博弈论答案第二章
博弈论教程答案
博弈论教程答案【篇一：《经济博弈论》课后答案、补充习题答案】 2345篇二：经济博弈论(谢织予)课后答案及补充习题答篇三：博弈论课后习题么是博弈？博弈论的主要研究内容是什么？2、设定一个博弈模型必须确定哪几个方面？3、举出烟草、餐饮、股市、房地产、广告、电视等行业的竞争中策略相互依存的例子。
4、“囚徒的困境”的内在根源是什么？举出现实中囚徒的困境的具体例子。
5、博弈有哪些分类方法，有哪些主要的类型？6、你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的：你决定开，则0.35的概率你讲收益300万元（包括投资），而0.65的概率你将全部亏损；如果你不开，则你能保住本钱但也不会有利润，请你（a）用得益矩阵和扩展形式表示该博弈；（b）如果你是风险中性的，你会怎样选择？（c）如果你是风险规避的，且期望得益的折扣系数为0.9，你的策略选择是什么？(d)如果你是风险偏好的，期望得益折算系数为1.2，你的选择又是什么？7、一逃犯从关押他的监狱中逃走，一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线，看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可以少坐10年牢，但一旦被抓住则要加刑10年；看守抓住逃犯能得到1000元奖金。
请分别用得益矩阵和扩展形式表示该博弈，并作简单分析。
第二章完全信息静态博弈1、上策均衡、严格下策反复消去法和纳什均衡相互之间的关系是什么？2、为什么说纳什均衡是博弈分析中最重要的概念？3、找出现实经济或生活中可以用帕累托上策均衡、风险上策均衡分析的例子。
4、多重纳什均衡是否会影响纳什均衡的一致预测性质，对博弈分析有什么不利影响？5、下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡？博弈的结果是什么？6、求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
7、博弈方1和2就如何分10 000元进行讨价还价。
假设确定了以下规则：双方同时提出自己要求的数额s1和s2，,如果s1+s2≤10 000，则两博弈方的要求都得到满足，即分别得到s1和s2，但如果是s1+s2＞10 000,则该笔钱就被没收。
博弈论(第二章)讲义
纳什均衡的练习（1）
例1：囚徒困境
囚徒B
坦白
不坦白
坦白 囚徒A
不坦白
-5， -5 -8， 0
0， -8 -1， -1
纳什均衡的练习（2）
例2：智猪博弈
大猪
踩
不踩
小猪
踩 不踩
1.5， 3.5 5， 0.5
- 0.5， 6 0， 0
纳什均衡的练习（3）
例2：猜硬币的博弈
猜硬币者
正
反
正 盖硬币者
反
-1， 1 1， -1
博弈方2
U
L
R
U 博弈方1
D
1， 0 0， 3
1， 2 0， 1
0， 1 2， 0
三、划线法
其中心思想是根据博弈方策略之间的相对优劣关系，导 出博弈分析的“划线法”。
例：下图中的得益矩阵表示两博弈方的一个静态博弈，
试使用划线法进行分析。 博弈方2
左
中
右
上 博弈方1
下
1， 0 0， 4
1， 3 0， 2
二、严格下策反复消去法
（1）如果在一个博弈中，不管其它博弈方的策略如何变 化，一个博弈方的某种策略给他带来的得益，总是 比另一种策略给他带来的得益要小，那么称前一种 策略为相对于后一种策略的一个“严格下策” 。
（2）经“反复消去”博弈方的严格下策以后，每个博弈 方
可选策略都缩小为一个策略。因此，每个博弈方都 选择各自剩下的一个策略所组成的策略组合，是这 个博弈的均衡解 。
0， 1 2， 0
划线法的练习（1） 例2：囚徒困境
坦白 囚徒A
不坦白
囚徒B
坦白
不坦白
-5， -5 -8， 0
第二章部分习题参考答案
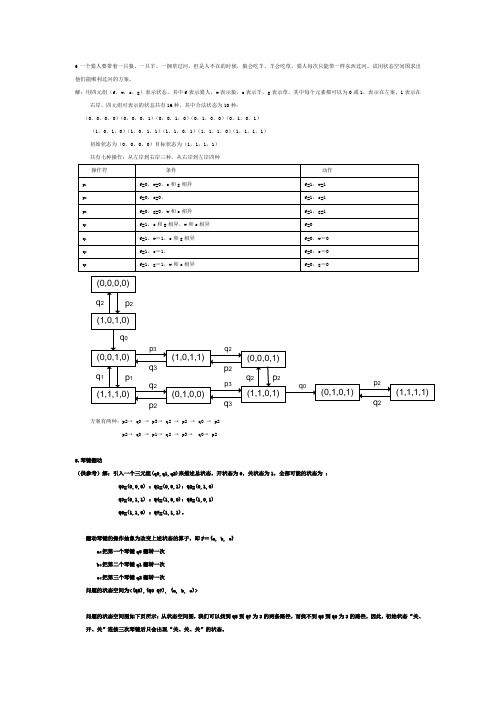
6一个猎人要带着一只狼、一只羊、一捆草过河，但是人不在的时候，狼会吃羊、羊会吃草，猎人每次只能带一样东西过河。
试用状态空间图求出他们能顺利过河的方案。
解：用四元组（f，w，s，g）表示状态，其中f表示猎人，w表示狼，s表示羊，g表示草，其中每个元素都可以为0或1，表示在左案，1表示在右岸。
四元组可表示的状态共有16种，其中合法状态为10种：（0，0，0，0）（0，0，0，1）（0，0，1，0）（0，1，0，0）（0，1，0，1）（1，0，1，0）（1，0，1，1）（1，1，0，1）（1，1，1，0）（1，1，1，1）初始状态为（0，0，0，0）目标状态为（1，1，1，1）共有七种操作：从左岸到右岸三种，从右岸到左岸四种方案有两种：p2→ q0 → p3→ q2 → p2 → q0 → p2p2→ q0 → p1→ q2 → p3→ q0→ p28.琴键翻动（供参考）解：引入一个三元组(q0,q1,q2)来描述总状态，开状态为0，关状态为1，全部可能的状态为：Q0=(0,0,0) ; Q1=(0,0,1); Q2=(0,1,0)Q3=(0,1,1) ; Q4=(1,0,0); Q5=(1,0,1)Q6=(1,1,0) ; Q7=(1,1,1)。
翻动琴键的操作抽象为改变上述状态的算子，即F＝{a, b, c}a:把第一个琴键q0翻转一次b:把第二个琴键q1翻转一次c:把第三个琴键q2翻转一次问题的状态空间为<{Q5},{Q0 Q7}, {a, b, c}>问题的状态空间图如下页所示：从状态空间图，我们可以找到Q5到Q7为3的两条路径，而找不到Q5到Q0为3的路径，因此，初始状态“关、开、关”连按三次琴键后只会出现“关、关、关”的状态。
11．代价树如图2-43所示。
其中，F 、I 、 J 、L 是目标结点。
（1）不考虑代价，给出广度和深度优先搜索过程和解。
（2）考虑代价，分别给出分支界限法和瞎子爬山法搜索策略下的搜索过程和解。
博弈论指定习题和参考答案
指定习题和参考答案Chapter 2: 1, 21. (a) D. There is so much amount and kinds of yogurt that each shopper need not consider whatothers do.(b) G. A prom is likely to be small enough that any participant can have some conceivable influence on others. For example, these two should prevent from dressing the same. However, in a BIG CITY, this may not be a case.(c) D. If he is not restricted to any specific university.(d) G. There are so few competitors for this specific product.(e) G. He must consider the interaction between him and his running mate. Even more, he must consider the response of the constituency when he chooses the mate.2. (a) Z; R/NR; I; F; NC.(b) NZ; NR; A; F; C.(c) NZ;NR; I; F; CChapter 3: 1, 2, 6, 71. (a) D=3, T=6(b) D=4, T=9(c) D=5, T=82. (a) #S(A)=2, S(A)={N,S}; #S(B)=2, S(B)={t, b}(b) #S(A)=2*2*2=8, S(A)={NNN, NNS, NSN, NSS, SNN, SNS, SSN, SSS}(left, right-up,right-down)#S(B)=2, S(B)={t, b}; #S(C)=2, S(C)={u,d}(c) #S(A)=2*2*2=8, S(A)= {NNN, NNS, NSN, NSS, SNN, SNS, SSN, SSS}(left, middle,right)#S(B)=8, S(B)={nnn, nns, nsn, nss, snn, sns, ssn, sss}6. (a) At the final run, B must take dimes. At the run next to final, if A choose to pass, given Btake dime at the final run, he can only get the reward accumulating at a speed of 5 cents per turn, initially 0 cents. If he takes dimes, he gets the dimes accumulating at a speed of 20 cents per turn, initially 10 cents. He surely takes dimes. Given this, B must take dimes at the run second next to final (B’s payoffs are the same as in our initial game) . Then A has the same reasoning as at the next to final run. And so on. So the rollback equilibrium strategy is always taking dime, for both players.(b) Using rollback method, let’s consider from the second round.No matter what payoffs both have got in the first round, they have sunk and cannot affect both players’ decisions in the second round. So two players play the second round as if it is a single-round centipede. So each plays is always choosing to take dimes, resulting payoffs of10 to A and 0 to B.Keeping this in both players’ mind, the first round is played almost as a single-roundcentipede, except that A always gets a reward of 10, whether she passes the dime or take it.But the fact that you always get something will neither affect your decision. So finally the first round game is exactly as a single-round centipede.Use rollback to this reduced single-round centipede. Notice the game is essential the same as before in the first 6 runs when the total amount is not accumulated to 50 when it’s player A’ s turn to play. If we can decide that the game after the 6th run will have an equilibrium of both players always taking dimes, we can be sure that B will get at most 20 when the 7th run comes and A (at most) takes 50.Now consider this ‘small’ equilibrium with only the last 4 runs. B will take dimes at in the final run (with a payoff of 90, otherwise 0). In any round before for A to play, taking dimes will leave her at least 50, but passing it will leave her at most 100-90=10 if B takes dimes then. In any round before for B, taking dime will leave him at least 60, but passing it will leave her at most 100-50=50 if A takes dimes then. Given the final run’s action of B (taking dimes), we can derive that both will always take dime in any round before, but after 6th run.Now let’s go back to our 6th run. B will take dimes at the 6th run (with a payoff of 60, otherwise 20). Given B’s choice, the game before the 6th run goes like the original one.The equilibrium is that both players always take dimes.(c) All the logic of (b) applies here until we begin to consider the last 5 runs (not 4 runs at thistime) of the first round game. Use rollback.B takes dimes in the final run, but get only 40 and leave 50 (as we restricts) to A. In the9th(second to the last) run, A can choose either to pass or take dimes(getting 50 both). The game essential the same when it ends in 9th run or 10th run.However, the 8th run is crucial. B can choose either to pass or to take dimes (getting 40 both). If B chooses to take dimes, A will definitely chooses to take dimes in the 7th run, and so on. The cooperation totally breaks and results in taking dimes always (our old equilibrium outcome).In any round before, but after 5th run, if both expect complete cooperation throughout the future, then they can either choose to pass or take. Any single deviation from cooperation (taking dimes) will result in total breakdown. So the 6-8th runs are all crucial points, given cooperation afterwards.Consider both pass dimes. Given this, at the 5th run, A chooses to pass is at least as good as to take. Taking them leads to breakdown as well. Suppose she passes it. B will also be indifferent with passing or taking dimes. So the 4-5th runs are also crucial points.However the 3rd run and the earlier are not crucial. If cooperation always happens afterward, passing dimes are always strictly better than taking dimes. If breakdown has already happen afterwards, taking dimes are definitely better choices.Summary: this game has multiple equilibria. Always passing dimes is one of them. Any deviations in one of 4-8th runs, given cooperation afterwards, will lead to breakdown from the very beginning. ( The number of equilbria is (1+5)*2=12, taking into account in the 9th run, both passing or taking dimes are indifferent for A.)7. (a) Amy; Beth.The player who reaches exactly 89 first will win; thus the player who reaches 78 first will win;thus 67,56, 45, 34, 23, 12, 1. Obviously Amy will reach 1 first.The player who reaches exactly 99 first will win. Then 88, 77, 66, 55, 44, 33, 22, 11.Obviously Beth will reach 11 first.(b) For Amy: 1 in the first run, then 11 no matter what Beth chooses, and 22, and so on. ForBeth, she can choose any amount between 1 and10.For Amy: any amount between 1 and 10. For Beth, 11 in his first run, 22 in his second run, and so on.Chapter 4: 2(d), 3(d), 5, 6, 9, 122. (d) Up is dominated by Straight (for Row). Then Left and Middle are both dominated by Right(for Column). Given Column plays Right, Row chooses Straight. The only NE is (Straight, Right).3. (d) (North, East) (unique NE). No dominant or dominated for both. Best-response analysis.5. Dominance solvable. (Up, Left). (Level, Center) has the same payoffs but not NE. There arealso other strategy configurations having strictly higher payoffs but not NEs.6. (1)JapaneseNorthern Southern AmericanNorthern 2 2Southern 1 3 (2) “Southern” is weakly dominated by “Northern” for Japanese. (North, North) is the only NE.(Check if “Southern” for Japanese can be part of any NE before you eliminate it.)9. (a) 3 NEs: (1, 1), (2, 2), (3, 3). The first is less likely to be focal point. But the other two areequally likely to be.(b) 12.5; Yes; Mixed strategy (just like flipping coins) can be used.12. (a) Two NEs: (Brunette, Blonde), and (Blonde, Brunette), yielding payoffs (5, 10) and (10, 5)respectively.Player 2Blonde BrunettePlayer 15Blonde 0,0 10,Brunette 5, 10 5, 5(b)Player 3Blonde BrunettePlayer 2 Player 2Blonde Brunette Blonde Brunette Player 1Blonde 0, 0, 0 0, 5, 0 0, 0, 5 10, 5, 5Brunette 5, 0, 0 5, 5, 10 5, 10, 5 5, 5, 53 NEs: (Blonde, Brunette, Brunette), (Brunette, Blonde, Brunette), and (Brunette, Brunette, Blonde), with payoffs 10 for who wins the Blonde, 5 for who wins Brunette.(c) The only possible NEs are those with only one pursues and wins the only Blonde and all others pursues and wins somehow excessive Brunettes.Or, follow the assumption given in text. Given k>=1, for any player, his payoffs of pursuing the Blonde is 0 and definitely worse than pursuing the Brunette with payoff 5. However, if k=0, you’d better pursue the Blonde.Consider this for a while, you will get the NE solutions.Thus All players choose Brunette cannot be a NE.。
博弈论及其应用-第二章4
3
3
∑ ∑ v1(σ1,σ
2
)
=
σ 11
σ 2 ju1(s11, s2 j ) + σ12
σ 2 ju1(s12 , s2 j )
j =1
j =1
2
3
23
∑ ∑ ∑ ∑ = σ1k σ 2 uj 1(s1k , s2 j ) =
σ σ 1k 2 ju1(s1k , s2 j )
k =1
j =1
k =1 j=1
张红霞 国民经济管理系
Homework
2. Find all mixed strategy NE to the football game shown below.
Defense
Run Pass
Run
Offense
张红霞 国民经济管理系
Pass
1, -1 15, -15
5, -5 0, 0
4
张红霞 国民经济管理系
案例分析
有人要打网球吗？？
张红霞 国民经济管理系
小结
混合策略的定义，含义 期望效用 混合策略纳什均衡：
– 定义 – 求解 – 含义
案例
张红霞 国民经济管理系
Homework
1. Find all “mixed” strategy NE to a Prisoners’ Dilemma. Comment on any connection with dominant strategies.
v2 (σ1,σ 2 ) = q(2 p + (1 − p) ⋅1) + (1 − q)(3p + (1 − p) ⋅ 0) = −q(2 p − 1) + 3p
张红霞 国民经济管理系
【博弈论基础】(吉本斯)课后习题答案
混 合 战 略 纳 什 均 衡 矛 盾 ， 假 设 不 成 立 ， 原 命 题 得 证 。
猪 头 非 整 理 ebwf@
3
Gibbons《博弈论基础》第二章习题解答（部分）
2.1 采用逆向归纳法，先最大化家长的收益：给定孩子的行动 A，来选择自己的行动 B,
MaxV ( I p − B) + k ( I c + B)
2 2 时 ， 生 产 qm / 2 的 一 方 的 利 润 为 π 2 = 5(a − c) / 48 ， 生 产 qc 的 一 方 的 利 润 为
π 3 = 5(a − c)2 / 36 ； 双 方 都 生 产 qc 时 ， 每 一 方 的 利 润 都 为 π 4 = (a − c) 2 / 9 。 以 标 准 式 表 示
2 1 2 2
{( (2w − w ) /(w + w ), (2w
1.14
− w1 ) /( w1 + w2 ) ) , ( (2 w1 − w2 ) /( w1 + w2 ), (2 w2 − w1 ) /( w1 + w2 ) )}
*
证 明 ： 在 混 合 战 略 纳 什 均 衡 中 ， 参 与 人 i 的 混 合 战 略 为 pi ， 其 中 选 择 第 j 个 纯 战 略 sij 的 概 率 为 pij 。 用 反 证 法 证 明 。 假 设 pij > 0 ， 且 sij 是 第 一 个 被 重 复 剔 除 劣 战 略 所 剔 除 的 战 略 。 那 么 参 与 人 i 必 定 存 在 另 一
针 对 上 面 的 博 弈 ， 设 参 与 人 1 的 战 略 为 （ p,1-p）， 参 与 人 2 的 战 略 为 （ q,1-q）。 则 对 于 1 来 说 ， 2q* + 4(1 − q* ) = 3q* + 2(1 − q* ) ， 得 ： q* = 2 / 3 ； 对 于 2 来 说 ， 4(1 − p ) = 2 p + 3(1 − p ) ， 得 p = 1/ 3 。
经济博弈论第二章a
以自身最大利益为目标：各生产 2单位产量，各自得益为4 以两厂商总体利益最大：各生产 1.5单位产量，各自得益为4.5
分析经营管理的实践案例
28
诚信之道
当一个社会缺乏信用、蔑视契约时，是难以建 立人与人之间的互信基础的。所以从建立对信 用和契约神圣的认知，并用强制措施加以保障。
29
诚信的选择
命题2.1 在n个博弈方的博弈 G S1,..., Sn ; u1,..., un 中，如果严格下
* * * * 以外的所有策略组合，则 策反复消去法排除了 (s1 (s1 ,..., sn ) ,..., sn ) 一定是G的唯一的纳什均衡。
命题2.2 在n个博弈方的博弈 G S1,..., Sn ; u1,..., un 中，如果
2 博弈方2利润： u2 q2 P(Q) C2q2 q2 8 (q1 q2 ) 2q2 6q2 q1q2 q2
* * * * 在本博弈中， 的最 (q1 , q2 ) 的纳什均衡的充分必要条件是 q1 和 q2 大值问题： * 2 max(6q1 q1q2 q1 ) q1 * 2 * * q2 q1 q2 q2 ) q q 2, u=8 max(6 1 2 q2
关键点：
寻找占优策略
检查一下你是否存在占优策略，如果有，就选择占优策略
站在对手的位置上思考问题
如果你没有占优策略，那么从你对手角度考虑博弈。如果对手 有占优策略，预期他将按占优策略行动
纳什均衡
我所做的是：给定你所做的，我所做的是最好的； 你所做的是：给定我所做的，你所做的是最好的
同步，一次博弈的应用
道德乎? 策略乎?
经济博弈论第二章a 博弈论课件
* 在本博弈中， ( q 1* , q 2 ) 的纳什均衡的充分必要条件是 q 大值问题： * 2
* 1
和q
q2 （0,6）
R1（q2）
（2，2） 6 R2（q1）
（0，3）
0
（3,0）
（6,0）q1
从左图可以看出，当一方的 选择为0时，另一方的最佳反应 为3，这正是我们前面所说过的 实现总体最大利益的产量，因为 一家产量为零，意味着另一家垄 断市场。当一方的产量达到6时， 另一方则被迫选择0，因为实际 上坚持生产已无利可图。
2.3.2 应用
混合策略的方法不仅可以解决不存在纯策略纳什均衡的博弈问题，同样 可应用于存在多个纯策略纳什均衡的博弈问题。 丈 夫 例 夫妻之争 时装 足球 该博弈与上一个博弈的不同之处在 0， 0 于每一方所希望对方知道自己的策略选 妻 时装 2，1 择以达到有利于自己的结果。现实中， 1， 3 子 足球 0，0 这类问题多通过协商解决以免两败俱伤。 在此我们假设夫妻双方不可协商，互不通消息。 令pw（时）， pw（足）分别表示妻子选择时装表演和足球的概率； ph（时）， ph（足）为丈夫选择时装表演和足球的概率。 同样的分析方法可得pw（时）=0.75, pw（足）=0.25; ph（时）=1/3, ph（足）=2/3.双方的期望得益分别为uwe＝0.67， uhe＝0.75。
d 2 b * 1 2 P ( a bc ) ( a b c ) 1 2 22 1 1 1 4 b b dd 4 b b dd 1 2 1 2 1 2 1 2 d 2 b * 2 1 P ( a b c ) ( a bc ) 2 1 11 2 22 4 b b dd 4 b b dd 12 1 2 12 1 2