与轴对称相关的最值问题
轴对称最值问题(线段和最小)(北师版)(含答案) (1)

学生做题前请先回答以下问题问题1:解决几何最值问题的理论依据有哪些?问题2:解决几何最值问题的主要方法是______,通过变化过程中_____________的分析,利用_______________________等手段把所求量进行转化,构造出符合几何最值问题理论依据的___________进而解决问题.轴对称最值问题(线段和最小)(北师版)一、单选题(共7道,每道14分)1.在平面直角坐标系中,点M的坐标是(4,3),点N的坐标是(1,-2),点P是y轴上一动点,若使PM+PN最小,则点P的坐标是( )A.(0,0)B.(0,1)C.(0,-1)D.(-1,0)答案:C解题思路:试题难度:三颗星知识点:轴对称最值问题2.如图,正方形ABCD的边长为8,点E,F分别在AB,BC上,AE=3,CF=1,P是对角线AC 上的动点,则PE+PF的最小值是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:轴对称最值问题3.如图,在Rt△AOB中,∠AOB=90°,OA=OB=8,C是OB的中点,D是AB边上一动点,则DC+OD的最小值是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:轴对称最值问题4.如图,等边三角形ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.且AE=2,则EM+CM的最小值为( )A. B.4 C. D.答案:A解题思路:试题难度:三颗星知识点:轴对称最值问题5.如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的负半轴上,顶点B的坐标为,点C的坐标为(-1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:轴对称最值问题6.如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上找一点Q,OB上找一点R,使得△PQR周长最小,则此时△PQR的周长为( )A.10B.C.20D.答案:A解题思路:试题难度:三颗星知识点:轴对称最值问题7.如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使得△AMN周长最小,则此时∠AMN+∠ANM=( )A.130°B.120°C.110°D.100°答案:B解题思路:试题难度:三颗星知识点:轴对称最值问题学生做题后建议通过以下问题总结反思问题1:解决几何最值问题的理论依据有哪些?问题2:解决几何最值问题的主要方法是______,通过变化过程中____________的分析,利用_______________________等手段把所求量进行转化,构造出符合几何最值问题理论依据的___________进而解决问题.问题3:在平面直角坐标系中,点M的坐标是(4,3),点N的坐标是(1,-2),点P是y 轴上一动点,若使PM+PN最小,则点P的坐标是( )A.(0,0)B.(0,1)C.(0,-1)D.(-1,0)本题的特征是什么?目标是什么?如何操作?。
轴对称相关最值问题

与轴对称有关的最值问题【典型题型一】:如图,直线 l 和 l 的异侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB最小。
APD BEC图(5)【典型题型二】如图,直线 l 和 l 的同侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB最小。
【练习】 1、( 温州中考题 ) 如图( 5),在菱形 ABCD中,AB=4a,E 在 BC上,EC=2a,∠ BAD=1200, 点 P 在 BD上,则 PE+PC 的最小值是()解:如图( 6),由于菱形是轴对称图形,因此 BC中点 E 对于对角线 BD的对称点 E 必定落在 AB的中点 E1,只需连结 CE1,CE1 即为 PC+PE的最小值。
这时三角形 CBE1 是含有 30 角的直角三角形, PC+PE=C1E=23 a 。
因此选( D)。
2、如图( 13),一个牧童在小河南 4 英里处牧马,河水向正东方流去,而他正位于他的小屋 B 西 8 英里北 7 英里处,他想把他的马牵到小河畔去饮水,而后回家,他可以达成这件事所走的最短距离是()(A) 4+ 185 英里(B) 16 英里(C) 17 英里(D) 18 英里3.如图, C为线段 BD上一动点,分别过点 B、D作 AB⊥BD,ED⊥BD,连结 AC、EC。
已知 AB=5,DE=1,BD=8,设 CD=x.请问点 C知足什么条件时, AC+CE的值最小 ?AC' 4.如图,在△ ABC中,AC=BC=2,∠ACB=90°, D是 BC边的中点, E是 AB边上一动点,则 EC+ED的最小值为 _______。
E即是在直线 AB上作一点 E,使 EC+ED最小作点 C对于直线 AB的对称点 C' ,连结 DC'交AB E DC' EC+ED DBC' DB=1 BC=2 于点,则线段的长就是的最小值。
在直角△中,,依据勾股定理可得, DC'= 55.如图,等腰 Rt△ABC的直角边长为 2,E是斜边 AB的中点, P 是 AC边CBD A上的一动点,则 PB+PE的最小值为E 即在 AC上作一点 P,使 PB+PE最小P作点 B对于 AC的对称点 B' ,连结 B'E,交 AC于点 P,则 B'E = PB'+PE = PB+PEB'E 的长就是 PB+PE的最小值B' CBF在直角△ B'EF 中,EF = 1 ,B'F = 3 依据勾股定理, B'E = 10A D6.如下图,正方形 ABCD的面积为 12,△ ABE是等边三角形,点 E 在正方形 ABCD内,E 在对角线 AC上有一点 P,使 PD+PE的和最小,则这个最小值为()P A.2 3 B.2 6 C.3 D. 6B C即在 AC上求一点 P,使 PE+PD的值最小点 D对于直线 AC的对称点是点 B,连结 BE交 AC于点 P,则 BE = PB+PE= PD+PE,BE的长就是 PD+PE的最小值 BE = AB = 2 37.如图,若四边形 ABCD是矩形, AB = 10cm ,BC = 20cm,E 为边 BC上的一个动点, P 为C'BD上的一个动点,求 PC+PD的最小值;A D作点 C对于 BD的对称点 C' ,过点 C',作 C'B⊥BC,交 BD于点 P,则 C'E 就是 PE+PC的最小20值直角△ BCD中,CH= 错误!不决义书签。
对称问题和最值问题

补充练习
1、如果AC 0, BC 0, 则直线Ax By C 0 不通过() ( A)第一象限( B)第二象限(C )第三象限( D)第四象限
2、已知 By C 0的图形如下,则() Ax
A、若C>0;0,B>0 C、若C<0,则A>0,B<0 D、若C<0,则A>0,B>0 y x
初中我们证明过这样一个问题:
等腰三角形底边上任一点到两腰的距离之和等于
一腰上的高。
你能用解析几何的方法证明此问题吗?
③点C(a,b)关于直线y=m的对称点为 C‘(a,2m-b)
④点D(a,b)关于直线x=n的对称点为 D‘(2n-a,b) ⑤点E(a,b)关于直线y=x的对称点为 E‘(b,a) ⑥点F(a,b)关于直线y=-x的对称点为 F‘(-b,-a) ⑦点P(a,b)关于直线y=x+m的对称点为 P‘(b-m,a+m) ⑧点Q(a,b)关于直线y=-x+n的对称点为 Q‘(-b+n,-a+n)
和l2:x+y+6=0截得的线段长为5,求直线l的方程。
例:一等腰三角形的底边所在直线l1的方程为x+y-1=0,
一腰所在直线l2方程为x-2y+1=0,又另一腰所在直 线l3过点(-2,0),求l3的直线方程。
补充练习
下列命题是真命题的是 A、 经 过 (x 0,y 0 的 直 线 都 可 以 写 成 P ) y - y 0 k ( x x0 ) B、 经 过 任 意 两 个 不 同 点P1 x1 , y1 ), P2 ( x 2 , y2 ) 的( 的 直 线 都 用 - y 1 )( x 2 x1 ) ( x x1 )( y2 y1 ) (y 表示 x y C、 不 经 过 原 点 的 直 线 可 以 用 1表 示 都 a b D、 经 过 定 点 (0, b )的 直 线 都 可 以 用 kx b表 示 A y
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
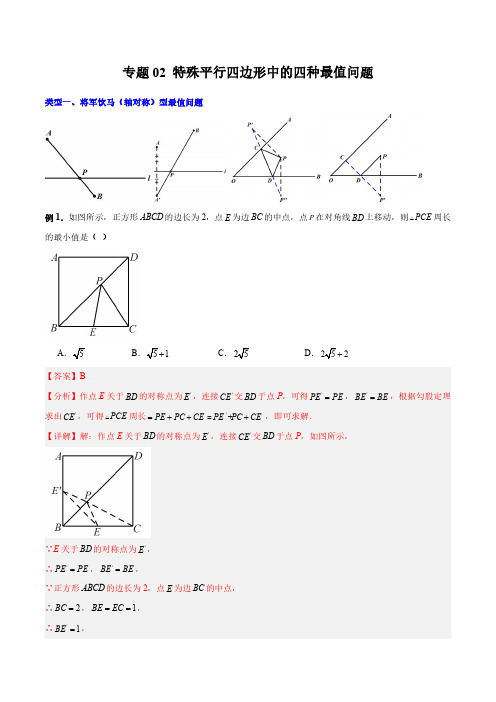
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
轴对称最值问题(讲义)(含答案)

轴对称最值问题(讲义)➢课前预习1.如图,要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站应建在什么地方,才能使A,B到奶站的距离之和最小?街道居民区B 居民区A➢知识点睛1.轴对称最值问题基本结构分析(1)求和最小:①特征:有定点,有动点,动点在____________上运动,求线段和(周长)最小.②解决方法:以动点所在的直线为对称轴,作定点的对称点,________________,利用两点之间线段最短进行处理.例题:在直线l上找一点P,使得在直线同侧的点A,B到点P的距离之和AP+BP 最小.BAl(2)求差最大:①特征:有定点,有动点,动点在____________上运动,求线段差最大.②解决方法:以动点所在的直线为对称轴,作定点的对称点,__________________,利用三角形两边之差小于第三边进行处理.例题:在直线l上找一点P,使得在直线两侧的点A,B到点P的距离之差AP BP最大.ABl2. 解决几何最值问题的理论依据:①___________________________________(已知两个定点)②___________________________________(已知一个定点、一条定直线) ③___________________________________(已知两边长固定或其和、差固定)➢ 精讲精练1. 某平原上有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水,某同学用直线l (虚线)表示小河,P ,Q 两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( )A .MlB .MQ PlC .lD.l2. 已知:如图,点P ,Q 分别是△ABC 的边AB ,AC 上的两个定点,在BC 上求作一点R ,使△PQR 的周长最小.PEDC B A第2题图 第3题图3. 如图所示,正方形ABCD 的边长是5,在正方形内作等边△ABE ,P 为对角线AC 上的一动点,则PD +PE 的最小值为__________. 4. 如图,等边三角形ABC 的边长为4,AD 是BC 边上的中线,F 是AD 边上的动点,E 是AC 边的中点.当EF +CF 取得最小值时,∠ECF 的度数为____________.FEDC B AM FED C B A第4题图 第5题图5. 如图,等腰三角形ABC 的底边BC 的长为4 cm ,面积是12 cm 2,腰AB 的垂直平分线EF 交AC 于点F ,若D 为BC 边的中点,M 为线段EF 上一动点,则△BDM 的最小周长为_________.6. 如图,在四边形ABCD 中,BC ∥AD ,CD ⊥AD ,P 是CD 边上的一动点,要使PA +PB 的值最小,则点P 应满足的条件是( ) A .PB =PA B .PC =PD C .∠APB =90°D .∠BPC =∠APD7. 如图,已知点P 为∠O 内一定点,分别在∠O 的两边上找点A ,B ,使△PAB 周长最小的是( )DC BAA.PO BAB.PO BAC.PO BAD.P2P1PO BA8.已知:如图,∠ABC=30°,P为∠ABC内部一点,BP=4,如果点M,N分别为边AB,BC上的两个动点,请画图说明当M,N在什么位置时使得△PMN的周长最小,并求出△PMN周长的最小值.9.如图,M为∠AOB内一定点,E,F分别是射线OA,OB上一点,当△MEF周长最小时,若∠OME=40°,则∠AOB的度数为__________.BO10.如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=110°,在BC,CD上分别找一点M,N.当△AMN周长最小时,∠MAN的度数为__________.A BCD MNDCBA11. 已知:如图,点P ,Q 为∠AOB 内部两点,点M ,N 分别为OA ,OB 上的两个动点,作四边形PMNQ ,请作图说明当点M ,N 在何处时,四边形PMNQ 的周长最小.12. 如图,在锐角三角形ABC 中,AB =4,△ABC 的面积为8,BD 平分∠ABC ,若M ,N 分别是BD ,BC 上的动点,则CM +MN 的最小值是( ) A .2B .4C .6D .8MNDCBABCD AMN第12题图 第13题图13. 如图,正方形ABCD 的边AB =8.在线段AC ,AB 上各有一动点M ,N ,则BM +MN 的最小值是__________.14. 如图,两点A ,B 在直线MN 的同侧,已知AB =5,点P 在直线MN 上运动,则|PA -PB |的最大值为_________.15.上的动点,则|PA -PB |的最大值为________.FE PCBA16. 如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有两个格点A ,B 和直线l .(1)求作点A 关于直线l 的对称点A 1;(2)P 为直线l 上一点,连接BP ,AP ,求△ABP 周长的最小值.【参考答案】➢课前预习1.图略➢知识点睛1.(1)①定直线;②折转直图略(2)①定直线;②折转直图略2.①两点之间,线段最短;②垂线段最短③三角形两边之差小于第三边➢精讲精练1. C2.图略3. 54.30°5.8 cm6. D7. D8.作图略,△PMN周长的最小值为4.9.50°10.40°11.如图所示:点M,N即为所求.12.B13.814.515.316.(1)图略;(2)△ABP周长最小为10。
轴对称最值
作法
图形
原理
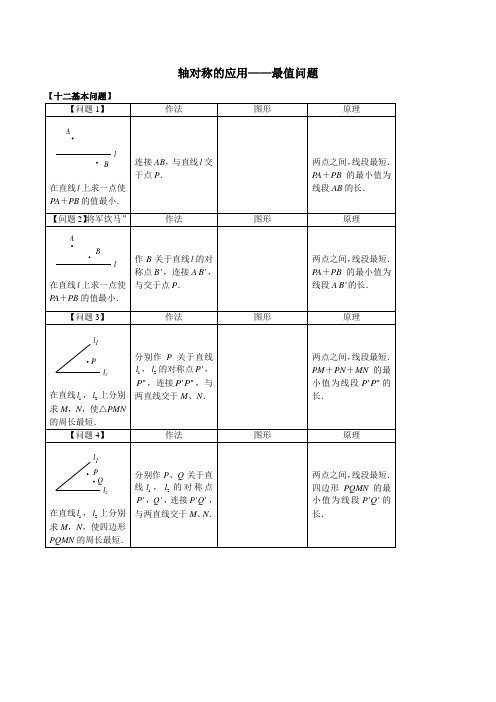
在直线 上求点A,在 上求B,使PA+AB的值最小.
作P点关于 的对称点 ,作 B⊥ 于B,交 于A.
点到直线的距离,垂线段最短.
【问题8】
作法
图形
原理
A为 上一定点,B为 上一定点,在 上求点M,在 上求点N,使AM+MN+NB的值最小.
作点A关于 的对称点 ,作点B关于 的对称点 ,连接 交 于M,交 于N.
轴对称的应用——最值问题
【十二基本问题】
【问题1】
作法
图形
原理
在直线 上求一点使PA+PB的值最小.
连接AB,与直线 交于点P.
两点之间,线段最短.
PA+PB的最小值为线段AB的长.
【问题2】将军饮马”
作法
图形
原理
在直线 上求一点使PA+PB的值最小.
作B关于直线 的对称点 ,连接A ,与交于点P.
17.(17-18-江汉-期中T24)如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,垂足为E,若M为BC边上一动点,D为EF上一动点,则BD+MD的最小值为cm.
18.(17-18-东西湖-期中T16)如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠OPM=α,∠PON=β,当MP+PQ+QN最小时,则α,β之间的相等数量关系是
9.(17-18-华一寄-12月T16)如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,2),D为OC的中点,P是线段BC上一动点,则当OP+PD值最小时点P的坐标为__________
10.(17-18-粮道街-12月T16)(2017-2018粮道街中学八上月考)如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值为___________
有关坐标对称及最值问题5种题型

坐标对称及最值问题是数学中的常见问题,常常出现在函数、几何、三角函数等领域。
这类问题需要运用对称思想,以及寻找最值的方法。
下面列举了5种常见的题型及相应的解法。
题型一:函数的最值对于函数f(x),其最值可能出现在最小值(f(x)min)和最大值(f(x)max)上。
对于这类问题,我们通常需要观察函数的对称性,例如,如果函数是关于原点对称的,那么最小值和最大值可能在左右两侧取得。
解法上,我们通常需要利用导数或其他方法来找到函数的极值点,从而确定最值。
题型二:两点之间的距离在两点之间的距离问题中,如果两个点关于某个轴对称,那么它们之间的距离可以通过简单的轴对称距离公式来计算。
解法上,我们通常需要利用轴对称距离公式,以及两点之间的距离公式来求解。
题型三:圆的半径的最值在圆的半径的最值问题中,如果圆关于某条直线对称,那么我们需要找到圆的半径与对称轴的位置关系,从而确定圆的半径的最值。
解法上,我们通常需要利用圆的半径公式,以及对称轴的位置关系来求解。
题型四:三角形的重心坐标在三角形的重心坐标问题中,如果三个顶点关于某条直线对称,那么我们需要找到重心坐标与对称轴的关系,从而确定重心的坐标。
解法上,我们通常需要利用重心的几何性质,以及对称轴的位置关系来求解。
题型五:椭圆的离心率在椭圆的离心率问题中,如果焦点关于某轴对称,那么我们需要找到椭圆的离心率与对称轴的关系,从而确定椭圆的离心率。
解法上,我们通常需要利用椭圆的离心率公式,以及对称轴的位置关系来求解。
总的来说,坐标对称及最值问题的解法主要依赖于对称性和位置关系。
对于不同类型的题目,我们需要灵活运用这些方法来解决问题。
同时,对于不同类型的题目,也需要进行相应的变化和拓展,以适应更复杂的情况。
希望以上信息对您有所帮助。
如果您有任何具体问题或需要进一步的解释,请随时告诉我。
中考数学《最值问题》及参考答案

中考数学《最值问题》及参考答案一、轴对称求最小值1.如图,四边形ABCD是边长为6的正方形,△ABC是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的值最小,求这个最小值.2.四边形ABCD中,∠BAD=122°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当△AMN周长最小时,求∠MAN的度数.3.如图,∠AOB =45°,OC为∠AOB内部一条射线,点D为射线OC上一点,OD=√2,点E、F分别为射线0A、OB上的动点,求△DEF周长的最小值.二、垂线段最短求最值4.如图,矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,求PQ 的最小值.5.如图,边长为6的等边三角形ABC中,E是对称轴AD上一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E运动的过程中,求DF的最小值.6.如图所示,在RtΔABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、 B重合),作PE ⊥AC于点E,PF⊥BC于点F,连接EF,求EF的最小值.7.如图,在ΔABC中,∠BAC=90,AB=6,BC=10,BD平分∠ABC,若P,Q分别是BD,AB上的动点,求PA+PQ的最小值.8.如图,Rt△ABC中,∠C=90°,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE,P,N分别为AC,BE上的动点,连接AN, PN,若DF=5,AC=9,求AN+PN的最小值.二、两点之间,线段最短求最值9.如图,等边△ABC的边长为4,过点B的直线l⊥AB,且△ABC与△A´B´C´公关于直线l对称,D为线段BC´上一动点,求AD+CD的最小值是( )10.如图,在长方形ABCD中,AB=3,AD=4,动点P满足S△PCD=14S长方形ABCD´,求点P到A,B两点的距离之和PA+PB的最小值.三、三角形三边的关系求最值问题11.如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(-1,0)、B(0,2)、 C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A´,求则A´C的最小值.参考答案1.析:连接BP.因为点B 与点D 关于直线AC 对称,所以PB=PD .所以PD+PE =PB+PE≥BE,所以PD+PE 的最小值即为BE 的长.BE =AB =6,则PD+PE 的值最小为6.2.析:如图,延长AB 到A ´使得BA ´=AB,延长AD 到A ´使得DA"=AD,连接A ´A"与BC 、CD 分别交于点M 、N.∵∠ABC=∠ADC=90° ∴ A 、A ´关于BC 对称,A 、A"关于CD 对称,此时ΔAMN 的周长最小∵BA=BA ´,MB ⊥ AB ∴MA =MA ´同理:NA=NA" ∴∠A ´=∠MAB,∠A"=∠NAD∵∠AMN =∠A ´+∠MAB =2∠A ´,∠ANM =∠A"+∠NAD =2∠A"∴∠AMN +∠ANM = 2(∠A ´+∠A")∵∠BAD=122° ∴ ∠A ´+LA"=180°-∠BAD=58° ∴∠AMN +∠ANM=2x58°=116∴∠MAN =180-116°=64°3.析:作点D 作关于OA 的对称点P,点D 关于OB 的对称点Q,连接PQ,与OA 的交点为点E,与OB 的交点为点F.△DEF 的最小周长为DE +EF +QF =PE+EF+QF =PQ连接OP 、OQ,则OP=0Q=√2 ∵∠POQ =2∠AOB=90°∴ΔOPQ 是等腰直角三角形∴PQ =√2OD=2∴ΔDEF 的周长的最小值是2.4.析:如图,连接CM∵MP ⊥CD 于点P,MQ ⊥BC 于点Q ∴∠CPM =∠CQM=90°∴四边形ABCD 是矩形∴BC=AD=3,CD=AB=4,∠BCD=90°∴四边形PCQM 是矩形,PQ =CM∴BD =√32+42=5当CM ⊥BD 时,CM 最小,则PQ 最小,此时,S △BCD =1 2BD ·CM=12BC ·CD ∴PQ 的最小值为125.5.析:取线段AC 的中点G,连接EG∵ΔABC 为等边三角形,AD 为△ABC 的对称轴∴CD=CG=1 2AB=3,∠ACD =60° ∵ ∠ECF =60°∴∠FCD =∠ECG在ΔFCD 和ΔECG 中,FC =EC,∠FCD=∠ECG,DC=GC∴ΔFCD ≌AECG ∴DF =GE当EG ⊥AD 时,EG 最短,即DF 最短∵点G 为AC 的中点,EG=DF=1 2CD=32 6.析: 连接CP.∵∠C=90,AC=3,BC =4 ∴AB =√32+42=5∵PE ⊥AC,PF ⊥BC,∠C=90°∴四边形CFPE 是矩形∴EF =CP由垂线段最短可得CP ⊥AB 时,线段EF 的值最小S △ABC=1 2BC ·AC=12AB ·CP ∴1 2×4×3=12×5·CP ∴CP =2.4 7.如图,作点Q 关于直线BD 的对称点Q ´∵BD 平分∠ABC ∴点Q 在BC 上连接PQ ´,则PA+PQ 的最小值即为PA+PQ ´的最小值∴当A 、P 、Q ´三点共线且AQ ´⊥BC 时,PA+PQ 的值最小过点A 作AM ⊥BC 于点M,则PA+PQ 的最小值即为AM 的长∵AB=6,BC=10 ∴AC ²=10²-6²=64 ∴AC=8∵ S △ABC =1 2AM ·BC=1 2AB ·AC ∴AM=AB·AC BC =48 10=4.88.析:连接AD ,与BE 交于点O∵四边形ABDE 是正方形 ∴BE ⊥AD,OD =OA ,点A 与点D 关于直线BE 对称 求PN + AN 的最小值,只需D ,N ,P 在同一条直线上,由于P ,N 分别是AC 和BE 上的动点,过点D 作DP ⊥AC 于P 交BE 于点 N ,此时PN + AN =PN+ND=PD ,由△ABC ≌ △BDF 可知,BF= AC = 9,BC=DF=5,易知四边形DFCP 是矩形,CF=PD=BF+BC=9+5=149.析:如图,连接AD∵△ABC 是边长为4的等边三角形 ∴AB =BC=4,∠ABC=60° ∵△ABC 与△ A ´B ´C ´关于直线l 对称∴A ´B=BC,∠AB ´C ´=60°∴∠CBC ´=60°=∠A ´BD∴△BCD ≌△BA ´D(SAS)∴A ´D=CD ∴CD +AD =AD +A ´D当A 、D 、A ´三点共线时,AD+A ´D 最小,此时CD+AD 最小,最小为4+4=8.10.析:如图,设APC 的CD 边上的高是h.∵S △PCD =1 2S 长形ABCD ,AD=4 ∴1 2·CD ·h =1 4CD ·AD ∴h=12AD=2 ∵动点P 在与CD 平行且与CD 的距离是2的直线l 上连接AC 交直线l 于点P ´∵l//CD,AD=4,四边形ABCD 是长方形 ∴l ⊥AD,l ⊥BC∴直线l 是BC 边的垂直平分线 ∴BP ´=CP ´∴AP ´+BP ´=AP ´+CP ´ ∴ AC 的长是最短距离∴AC=√32+4=5,PA +PB 的最小值为5.11.析:连接BA ´∵AB=√5,BC =4若点A 关于BP 的对称点为A ´ ∴BA ´=BA=√5在△BA ´C 中,A ´C ≥BC-BA ´,即AC ´≥4-√5∴AC ´的最小值为4-√5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图(5)CE D PBA 与轴对称相关的最值问题【典型题型一】:如图,直线l 和l 的异侧两点A 、B ,在直线l 上求作一点P ,使PA+PB 最小。
【典型题型二】如图,直线l 和l 的同侧两点A 、B ,在直线l 上求作一点P ,使PA+PB 最小。
【练习】1、(温州中考题)如图(5),在菱形ABCD 中,AB=4a,E 在BC 上,EC=2a ,∠BAD=1200,点P 在BD 上,则PE+PC 的最小值是( )解:如图(6),因为菱形是轴对称图形,所以BC 中点E 关于对角线BD 的对称点E 一定落在AB 的中点E 1,只要连结CE 1,CE 1即为PC+PE 的最小值。
这时三角形CBE 1是含有300角的直角三角形,PC+PE=CE 1=23a 。
所以选(D )。
2、如图(13),一个牧童在小河南4英里处牧马,河水向正东方流去,而他正位于他的小屋B 西8英里北7英里处,他想把他的马牵到小河边去饮水,然后回家,他能够完成这件事所走的最短距离是( )(A ) 4+185英里 (B ) 16英里 (C ) 17英里 (D ) 18英里3.如图,C 为线段BD 上一动点,分别过点B 、D 作AB ⊥BD ,ED ⊥BD ,连接AC 、EC 。
已知AB=5,DE=1,BD=8,设CD=x.请问点C 满足什么条件时,AC +CE 的值最小?4.如图,在△ABC 中,AC =BC =2,∠ACB =90°,D 是BC 边的中点,E 是AB 边上 一动点,则EC +ED 的最小值为_______。
即是在直线AB 上作一点E ,使EC+ED 最小作点C 关于直线AB 的对称点C',连接DC'交 AB 于点E ,则线段DC'的长就是EC+ED 的最小值。
在直角△DBC'中DB=1,BC=2, 根据勾股定理可得,DC'= 55.如图,等腰Rt △ABC 的直角边长为2,E 是斜边AB 的中点,P 是AC 边 上的一动点,则PB+PE 的最小值为 即在AC 上作一点P ,使PB+PE 最小作点B 关于AC 的对称点B',连接B'E ,交AC 于点P ,则B'E = PB'+PE = PB+PE B'E 的长就是PB+PE 的最小值在直角△B'EF 中,EF = 1,B'F = 3根据勾股定理,B'E = 106.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内, 在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( ) A .2 3 B .2 6 C .3 D . 6即在AC 上求一点P ,使PE+PD 的值最小点D 关于直线AC 的对称点是点B ,连接BE 交AC 于点P ,则BE = PB+PE = PD+PE ,BE 的长就是PD+PE 的最小值BE = AB = 2 3 7.如图,若四边形ABCD 是矩形, AB = 10cm ,BC = 20cm ,E 为边BC 上的一个动点,P 为BD 上的一个动点,求PC+PD 的最小值;作点C 关于BD 的对称点C',过点C',作C'B ⊥BC ,交BD 于点P ,则C'E 就是PE+PC 的最小值直角△BCD 中,CH = 205错误!未定义书签。
直角△BCH 中,BH = 8 5 △BCC'的面积为:BH ×CH = 160所以 C'E ×BC = 2×160 则CE' = 16FPB'EACBC'DACBEPE B CD AH PEC'DACB8.如图,若四边形ABCD 是菱形, AB=10cm ,∠ABC=45°,E 为边BC 上的一个动点,P 为BD 上的一个动点,求PC+PE 的最小值;点C 关于BD 的对称点是点A ,过点A 作AE ⊥BC ,交BD 于点P ,则AE 就是PE+PC 的最小值在等腰△EAB 中,求得AE 的长为5 29.如图,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN 弧的中点,P 是直径MN 上一动点,则PA +PB 的最小值为( )A 2 2B 2C 1D 2即在MN 上求一点P ,使PA+PB 的值最小作点A 关于MN 的对称点A',连接A'B ,交MN 于点P ,则点P 就是所要作的点A'B 的长就是PA+PB 的最小值连接OA'、OB ,则△OA'B 是等腰直角三角形所以 A'B = 210如图,一次函数 y = 12x 与反比例函数y = kx 交于点A ,AM ⊥x 轴于点M ,S △OAM = 1(1)求k 的值,(2)点B 为双曲线y=kx 上不与A 重合的一点,且B(1,n),在x 轴上求一点P ,使PA+PB 最小(1)由S △OAM = 1知,k = 2(2)作点A 关于x 轴的对称点A ’,连接A ’B ,交x 轴于点P ,连接PA ,则PA+PB 最小。
用待定系数法求直线A ’B 的解析式为y = - 3x + 5, 因为点P 在x 轴上,所以设 y = 0,即0 = - 3x + 5, 解得 x = 53 所以P( 53,0)11.如图,在平面直角坐标系中,直线l 是第一、三象限的角平分线.(1)由图观察易知A (0,2)关于直线l 的对称点A′的坐标为(2,0),请在图中分别标明B (5,3)、C (-2,5)关于直线l 的对称点B′、C′的位置,并写出他们的坐标:B′ 、C′ ;(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P (a ,b )关于第一、三象限的角平分线l 的对称点P′的坐标为 (不必证明); (3)已知两点D (1,-3)、E (-1,-4),试在直线l 上确定一点Q ,使点Q 到D 、E 两点的距离之和最小,并求出Q 点坐标. (1)点B(5,3)、C(-2,5)关于直线l 的对称点B'(3,5)、C'(5,-2) (2)坐标平面内任一点P(a ,b)关于直线l 的对称点P'的坐标为(b ,a)(3)作点E 关于直线l 的对称点E',连接DE',交直线l 于点Q 则QE+QD 的值最小设直线DE'的解析式为:y = kx+b ,因为D(1,-3)、E'(-4,-1),则-3 = k+b-1 = -4k+b解得:k = - 25 ,b = - 135 所以 y = - 25 x - 135当x = y 时,有x = y = - 137 则Q 点的坐标为(- 137 ,- 137)【典型题型三】:如图,点P 是∠MON 内的一点,分别在OM ,ON上作点A ,B 。
使△PAB 的周长最小12、如图(9),∠AOB=450,角内有一点P ,PO=10,在角两边上有两点Q 、R (均不同于点O ),则 ①△PQR 的周长最小值是____________。
②当ΔPQR 周长最小时,∠QPR 的度数=_________。
(答案:900)P ECA DB PA'BANOMx yl QE'C'B'ED CB A'A O BA 图(9)OP【典型题型四】求线段差的最大值:如图所示,已知直线MN 与MN 异侧两点A 、B ,在MN 上求作一点P ,使PA -PB 最大,并说明理由。
13.如图,两点A ,B 在直线MN 的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=6, CD=4,P 在直线MN 上运动,则 的最大值为( c ) A.B.C.D.14.如图,已知两点A ,B 在直线l 的异侧,A 到直线l 的距离AC=6,B 到直线l 的距离 BD=2,CD=3,点P 在直线l 上运动,则 的最大值为( d )A. B.3 C.1 D.515.如图,在平面直角坐标系中,已知A (0,1),B (3,-4),在x 轴上有一点P , 当 的值最大时,点P 的坐标是( b )A. B.(-1,0) C.(0,0) D.(3,0)16、在直角坐标系中,X 轴上的动点M (X ,0)到定点P (5,5)和到Q (2,1)的距离分别为MP 和MQ ,那么当MP+MQ 取最小值时,点M 的横坐标X=_ ___.(你能求出当MP-MQ 最大时点M 的横坐标X= ?)【典型题型四】17.如图,已知A (1,3),B (5,1),长度为2的线段PQ 在x 轴上平行移动,当 AP+PQ+QB 的值最小时,点P 的坐标为( b )A. B. C.(1,0) D.(5,0)18.在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A ,B 分别在 x 轴、y 轴的正半轴上,OA=3,OB=4,D 为边OB 的中点.若E ,F 为边OA 上的 两个动点,且EF=2,则当四边形CDEF 的周长最小时,点F 的坐标为( b )A. B. C.(2,0) D.(3,0)19.如图,当四边形PABN 的周长最小时,a 的值为( a )A. B.1 C.2 D.Q P A'B'P'AQ'20如图,矩形ABCD 中,AB=4,BC=8,E 为CD 边的中点,点P 、Q 为BC 边上 两个动点,且PQ=2,当BP=( )时,四边形APQE 的周长最小.21.已知A 和B 两地在一条河的两岸,现要在河上建造一座桥MN ,使从A 到B 的路径AM-MN-NB 最短,则应按照下列哪种方式来建造(假定河的两岸是平行直线,桥要与河岸垂直)( D )A. B. C. D.22.如图,村庄A 、B 位于一条小河的两侧,若河岸a 、b 彼此平行,现在要建设一座与河岸垂直的桥CD ,问桥址应如何选择,才能使A 村到B 村的路程最近?*逆向思维23.如图,已知点A (-4,8)和点B (2,n )在抛物线y = ax 2上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q 的坐标;(2) 平移抛物线y = ax 2,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式; ② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD 的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由. (1)直线AP 的解析式为:y = - 53 x + 43 则Q 的坐标为(45,0)(2)①解法一:CQ = |- 2 - 45 | = 145 则抛物线 y = 12 x 2向左移动145 个单位时,A ’C+B ’C 最短抛物线的解析式为:y = 12 (x+145)2(2) ②抛物线向左或向右平移时,使四边形A ′B ′CD 的周长最短,因为A ’B ’ + CD 是定值,只要使A ’D + B ’C 最短即可 当抛物线向右移动时,因为A ’D > AD ,B ’C > BC ,所以A ’D + B ’C > AD + BC ,则在不存在一个向右的位置,使四边形A ′B ′CD 的周长最短当抛物线向左移动时,设A ’(-4-a ,8),B ’(2-a ,2),因为CD = 2,则将点B ’向左平移2个单位得到点B ’’(-a ,2).点A ’关于x 轴的对称点是A ’’(-4-a ,-8),直线A ’’B ’’的解析式为:y = 52 x + 52m + 2要使A ’D + B ’’D 最短,点D 应在直线A ’’B ’’上将点D(-4,0)的坐标代入到直线A ’’B ’’的解析式,得m = 165 故将抛物线向左平移时,否存在一个位置,使四边形A ′B ′CD 的周长最短,抛物线函数解析式为y = 12 (x+165 )2【典型题型五】如图,直线1l 、2l 相交,两个固定点A 、B ,分别在1l 、2l 上确定两点M 、N ,使得AN MN BM ++之和最小。
