海浪谱公式总结
海洋要素计算与预报(海浪7)-文档资料
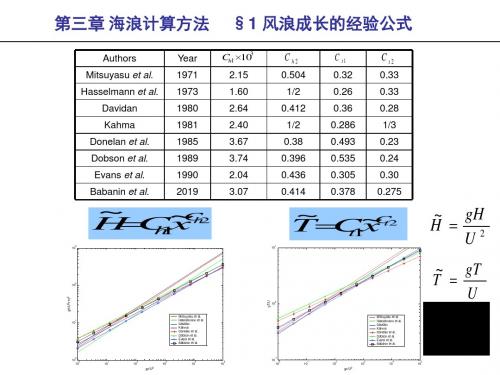
F F ( , ; x , y ; t )
cg k
--------------- 二维海浪谱 --------------- 群速度
d 1 d --------------- 波向空间的群速度 c dt k d m
有限深水的弥散关系为:
gk tanh( kd )
Mitsuyasu et al. Hasselmann et al. Davidan Kahma Donelan et al. Dobson et al. Evans et al. Babanin et al.
gx ~ x 2 U
10
5
10 0 10
0
10
1
10
2
10 gx/U
2
3
10
4
10
5
10
-1
10
0
10
1
10
2
10 gx/U2
3
10
4
§1 风浪成长的经验公式
10
2
10
2
10
1
10
gH/U2102
1
gH/U2102
10
0
10
0
10
-1
10 -1 10
-2
Mitsuyasu et al. Hasselmann et al. Davidan Kahma Donelan et al. Dobson et al. Evans et al. Babanin et al. 10 gT/U
§1 风浪成长的经验公式
Ch1 103
C h2
0.504 1/2 0.412 1/2 0.38 0.396 0.436 0.414
海浪谱公式总结

S f w H1 / 3 T
2
1m p
f
m
m 4 exp Tp f 4
10.Wallops谱
式中:
0.06238 mm1 / 4 m 21.057 w m 5 / 4 1 0.7458 4 m 1 TH 1 / 3 Tp 0.684 1 0.238m 1.5
0 0
A B exp d 4 5 4B A
因 W / 3 4m0 所以:B
1/ 2
m0
2
W /3
16
4A
2
W /3
由于P M谱中A 0.0081 g 2 0.78, B 代入后得ITTC谱:
4A
2
W /3
A
m1 0.30638A / B 3 / 4 T1 2m0 / m1 5.127/ B1 / 4或B 691/ T1 B W / 3 173 W /3 A 4 Bm 0 4 4 T1 代入后得到双参数海浪 谱:
2 2 4
691 173 W /3 S exp 4 4 4 5 T1 T 1
1.Neumann谱
由半经验的方法,假定海浪的某些外观特征反映其内部结构,由 观测到的波高和周期间的关系推导出来。于50年代首先提出。
2 1 2g S C exp 2 2 6 4 U
式中:U为海面上7.5米高处的风速;常数C=3.05m/s2
2.P-M谱
2
H1 / 3
4
4 1 1 5 exp1605 TH1 / 3 2
海浪谱公式总结

m,βw为两个参数,改变m即可改变谱的宽窄形状,βw用于调整
谱面积,使之等于波浪总能量。
形状参数m和JONSWAP谱中的γ一样,其选用依靠工程师的经验 和判断。一般小的无因次风距gX/U2和大的γ或m值相关,而大的无因
次风距值gX/U2导致γ=1或m=5。在浅水,上述谱中采用m=3或4是合
适的。
3.12
2
W /3
4
S
0.78
5
3.12 exp 2 4 W /3
式中:ζw/3为三一平均波高(不是波幅)。
4.双参数海浪谱
1978年第15届ITTC采用了双参数谱,双参数谱改进了ITTC谱,对成 长中的海浪也适用。
基于ITTC谱有: 1 A 3 B exp d 1 4 3/ 4 0 0 5 3B 4 3 式中:为函数, 1 0.91906 ,因此有: 4 m1 S d
11.方向谱
长峰不规则波是假定海浪沿单一方向传播的;实际海浪除了沿 主方向传播外,还向其他方向扩散,称为短峰不规则波;短峰不规则 波可以看成传播方向不同的长峰不规则波叠加而成。描述海浪沿不同 方向组成的波谱,称为方向谱。
S , S D,
式中:S(ω)为长峰不规则波的海浪谱;θ为组成波与主浪向的夹角。
9.六参数谱
奥启和汉伯尔(Ochi,Hubble, 1976)提出了一个六参数谱公式, 它把整个谱分成低频部分和高频部分两个组成部分,每一部分分别用 三个参数—有效波高Hs、谱峰频ωp和形状参数λ表示。
4 j 1 4 mj 4 2 H sj 4 j 1 mj 1 4 S exp 4 j 1 4 j j 4
第四章 海浪观测

H /m 0.6 1.4 1.6 1.1 1.6 2.1 1.1 3.0 2.6 1.7 1.5 3.9 3.0 2.4 3.3 2.0 1.1 2.5 2.1 3.5
T /s 11.4 6.6 6.5 5.3 8.3 6.0 23.0 6.9 6.9 8.8 4.5 7.1 8.1 16.1 6.2 6.4 6.2 5.8 5.3 7.1
波高模比系数
Ki
波高分组
Hi / m
出现次数
ni
区间频率
fi
平均频率
fi / ∆H H
累积次数
累积频率
F /%
∑n
6 2 3 6 11 20 30 39 57 80 94 98
i
1 2.4~2.2 2.2~2.0 2.0~1.8 1.8~1.6 1.6~1.4 1.4~1.2 1.2~1.0 1.0~0.8 0.8~0.6 0.6~0.4 0.4~0.2 0.2~0.0
2 .波高的经脸概率分布
为了探求波高的分布规律, 为了探求波高的分布规律,必须绘制频率直方图 ,以下 以下 所示的波浪观测序列为例简述其绘制方法。 表1所示的波浪观测序列为例简述其绘制方法。 所示的波浪观测序列为例简述其绘制方法
H /m 2.0 3.0 2.5 3.1
T /s 9.2 6.6 6.6 6.9 8.6 7.1 5.4 7.1 6.6 7.5 8.1 8.1 4.3 5.4 7.5 6.8 6.6 4.5 4.9 6.2
H /m 0.8 2.5 4.1 3.8 1.7 1.0 2.0 1.8 2.0 1.8 1.3 1.3 1.5 1.0 2.0 1.4 0.3 1.3 2.0 2.0
T /s 4.5 6.6 7.3 7.9 6.9 5.3 5.8 5.8 9.4 8.3 9.6 6.8 5.4 4.1 5.8 7.5 3.6 10.5 8.4 8.1
海浪谱公式总结.

年提出。适用于充分成长的海浪。
4 ag g S 5 exp U 式中:a=0.0081; β=0.74; 2
g为重力加速度; U为离海面19.5m处的风速。
8.斯科特谱
斯科特(Scott,1965)对于充分发展的海浪建议用下列谱公式:
1/ 2 2 2 p S 0.214H s exp 0 . 065 0 . 26 p
式中:-0.26<ω-ωp<1.65, Hs为有效波高;ωp为谱峰频率。 此谱和北大西洋以及印度西海岸实测谱符合得很好。
b.由波高和波浪周期表示的谱公式
0.159 Tp 1 2 exp 2 2
1948 S 319 .34 4 5 3.3 4 Tp Tp
2
W /3
式中:Tp为谱峰周期,波谱峰值对应的周期。
0 0
A B exp d 4 5 4B A
因 W / 3 4m0 所以:B
1/ 2
m0
2
W /3
16
4A
2
W /3
由于P M谱中A 0.0081 g 2 0.78, B 代入后得ITTC谱:
4A
2
W /3
P一M谱为经验谱,依据的资料比较充分,分析方法合理,使用也方便。
目前采用都的大多数标准波谱主要是基于P-M谱的形式建立的。但是它仅包 含一个参数U,不足以表征复杂的海浪情况。
3. ITTC谱
第七章海浪——精选推荐

第七章海浪第七章海浪第五节海浪的统计特性与海浪谱理论波动可以解释⾃然界中⽐较简单的理想规则波动,实际海洋中的海浪并不那样具有规律性,⽽是具有很⼤的随机性,海浪可视为⼀个随机过程。
海浪可视为⽆数随机正弦波动的叠加,且位相也是随机的。
各正弦波有各⾃的振幅和频率,其关系未被讨论。
实际观测表明,频率很⼩和很⼤的海浪波⾼都不⼤,波⾼显著部分的频率则介于某个范围内。
1、随机海浪过程的平稳性和各态历经性某随机过程的数学期望为常值,协⽅差只是与时间间隔有关,即:则该随机过程为平稳随机过程。
平稳随机过程的特点:过程的统计特征不随时间变化。
如果当时,该平稳过程具有各态历经性。
平稳随机过程各态历经性的特点:⼀个样本(⼀次现实)可代替总体。
实际海浪可视为⽆数正弦波动的叠加。
在较短的时间内,海浪过程为准平稳过程,同时具有各态历经性。
2、波剖⾯的分布对于随机变量X,最常见的⼀种概率分布为正态分布实际海浪可视为具有各态历经性的平稳随机过程;同时将海浪视为⽆数位相不同振幅不等的正弦波的叠加。
固定点处波⾯⾼度可写成:每个随机波⾯的期望值和⽅差为:合成波⾯的期望值和⽅差为:由于简单波动的振幅⽆限⼩,各组成正弦波动相互独⽴,且数⽬极⼤,则根据李亚普诺夫定理,波⾯的概率分布为正态分布。
经实测资料验证,波剖⾯服从正态分布,可近似认为实际海浪是由⽆数随机的正弦波动叠加⽽成。
海浪的内部结构海区测得的波⾯⾼度的概率分布(Kinsman ,1965)实验测得的波⾯⾼度的概率分布(Jacobson 和Colonell ,1972)3、波⾼的分布从外观上直接描述波⾯,固定点的波剖⾯可写成:和为实随机函数,分别代表波的包络线和位相函数。
振幅a 的概率分布为:波⾼H=2a ,平均波⾼,均⽅根波⾼波⾼的概率分布遵从瑞利分布。
4、各种波⾼之间的关系海浪波⾼是随机出现的,其统计性质可由概率分布描述。
实际应⽤中,常根据使⽤的⽬的,采⽤具有某种代表意义的特征波⾼(平均波⾼、均⽅根波⾼、最⼤波⾼等)。
海浪谱公式总结84313
exp
1.03
1 TH1/
3
4
S
400.5
Hs T2
H1/ 3
2
1
5
exp1605
1
T H1/ 3
4
式中:Hs为有效波高,表示波列中波高最大的1/3波浪的平均波高; TH1/3为有效波周期,表示波列中波高最大的1/3波浪周期的平均值。
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
◆语文•选修\中国小说欣赏•(配人教版)◆
1.Neumann谱
由半经验的方法,假定海浪的某些外观特征反映其内部结构,由 观测到的波高和周期间的关系推导出来。于50年代首先提出。
S
C
4
1
6
exp
2g2
U 22
式中:U为海面上7.5米高处的风速;常数C=3.05m/s2
金品质•高追求 我们让你更放心!
S f
H T2 1m w 1/3 p
f
m
exp
m 4
Tp f
4
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
10.Wallops谱
式中:
w
0.06238mm1/ 4 4m5/ 4 m 1
1 0.7458 m 2 1.057
Tp
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
2.P-M谱
皮尔逊和莫斯克维奇根据在北大西洋一定点上测得的大量数据,于1964
年提出。适用于充分成长的海浪。
S
式中:a=0.0081;
β=0.74;
ag2
5
exp
海浪谱
描述海浪内部能量相对于频率和方向的分布。
为研究海浪的重要概念。
通常假定海浪由许多随机的正弧波叠加而成。
不同频率的组成波具有不同的振幅,从而具有不同的能量。
设有圆频率ω的函数S(ω),在ω至(ω+ω)的间隔内,海浪各组成波的能量与S(ω)ω成比例,则S(ω)表示这些组成波的能量大小,它代表能量对频率的分布,故称为海浪的频谱或能谱。
同样,设有一个包含组成波的圆频率ω和波向θ的函数S(ω,θ),且在ω至(ω+ω)和θ至(θ+ω)的间隔内,各组成波的能量和S(ω,θ)ωθ成比例,则S(ω,θ)代表能量对ω和θ的分布,称为海浪的方向谱。
将组成波的圆频率换为波数,可得到波数谱;将ω换为2π(频率为周期的倒),得到以表示的频谱S()数。
以上各种谱统称为海浪谱。
海浪谱不仅表明海浪内部由哪些组成波构成,还能给出海浪的外部特征。
比如,理论上可由谱计算各种特征波高和平均周期,利用这些特征量连同波高与周期的概率密度分布,可推算海浪外观上由哪些高低长短不同的波所构成。
若已知海浪的谱,海浪的内外结构都可得到描述,因此谱是非常有用的概念。
事实上,海浪的研究(包括许多应用问题),大多和谱有关。
频谱在海浪谱中,风浪频谱得到最广泛的研究,因为它的应用最广,也最易于得到。
但尚无基于严格理论的风浪频谱。
已提出的经验的或半经验的频谱很多,大多数用[245-1]的乘积来表达。
通常p为5~7,q为2~4,在正量A和B之内。
除了数值常数外,还包含风要素(如风速、风时和风区)或浪要素(如特征波高和周期)作为参量,故谱的形状随风的状态或对应的浪的状态而变化。
上述两项的乘积代表的谱,在ω=0处为0,在0附近的值很小,ω增加时,它骤然增大至一个峰值,然后随频率的增大而迅速减小,在ω→∞ 时趋于0。
这表明谱的频率范围在理论上虽为0~∞,但其显著部分却集中在谱峰附近。
海面上存在的许多波,其显著部分的周期范围很小,恰和理论结果相对应。
随着风速的增大,谱曲线下面的面积(从而风浪的总能量或波高)增大,峰沿低频率方向推移,表明风浪显著部分的周期增大。
常见海浪波谱word版本
常见海浪波谱word版本1.Neumann谱由半经验的方法,假定海浪的某些外观特征反映其内部结构,由观测到的波高和周期间的关系推导出来。
于50年代首先提出。
式中:U为海面上7.5米高处的风速;常数C=3.05m/s2。
2.P-M谱皮尔逊和莫斯克维奇根据在北大西洋一定点上测得的大量数据,于1964年提出。
适用于充分成长的海浪。
式中:a=0.0081;β=0.74;g为重力加速度;U为离海面19.5m处的风速。
P-M谱为经验谱,依据的资料比较充分,分析方法合理,使用也方便。
目前采用的大多数标准波谱主要是基于P-M谱的形式建立的。
但是它仅包含一个参数U,不足以表征复杂的海浪情况。
3.ITTC谱国际拖曳水池会议(ITTC,1972)对P-M谱进行了修改,得到ITTC谱。
基于P-M谱有:由于P-M谱中:代入后得ITTC 谱:式中:ζw/3为三一平均波高,不是波幅。
4.双参数海浪谱1978年第15届ITTC 采用了双参数谱,双参数谱改进了ITTC 谱,对成长中的海浪也适用。
基于ITTC 谱有:3/410.30638m A /B =1/4410112 5.127691T m /m /B B /T π===或代入后得到双参数海浪谱:5.ISSC 谱国际船舶结构会议ISSC1964推荐下列谱公式,且常称之为ISSC 谱。
()24250.10.1110.110.44s H S f exp T f T f ⎡⎤⎛⎫⎛⎫⎢⎥=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦6.JONSWAP 谱该谱由“北海海浪联合计划”测量分析得到,在60年代末期提出,适合像北海那样风程被限定的海域,有两种表示形式。
a.由风速和风程表示的谱公式:()()()24225 1.25p p exp p g S exp ωωσωζωαωγωω⎡⎤-⎢⎥-⎢⎥⎢⎥⎣⎦⎧⎫⎛⎫⎪⎪=-⎨⎬ ⎪⎝⎭⎪⎪⎩⎭式中:α为无因次常数,可取α=0.0076(gx/U 2)-0.22;x 为风区长度(风程);U 为平均风速; ωp 为谱峰频率,可取ωp =22(g/U)(gx/U 2)-0.33 ; γ为谱峰提升因子,平均值为3.3;σ为峰形参数,当ω≤ωp 时,可取σ=0.07;当ω>ωp 时,取σ=0.09。
海洋工程环境 4-5波浪
0
m1 S d
m0为能量谱密度函数的0 谱矩(零阶矩)。
m1为能量谱密度函数一阶矩。
其他波高特征 H1/3 4.005 m0
相应的平均周期为:
平均频率为:
T 2 m0
m1
m1
m0
其中
mn nS d
0
为能量谱密度函数的n阶矩。顺便给出谱宽系数:
2 1 m22
m0m4
50
线性变换系统
• …….
方向能量谱密度函数 方向谱的一般形式:
S , S G
G 为方向函数,有
G d 1
G An cosn
ITTC : n=2, An=2/ ISSC : n=4, An=8/(3)
4.3.2 海浪要素特征
频谱与海浪特征值有密切关系
平均波高
H 2.507 m0
其中
m0 S d
浅水波:1/2>h/>1/25
C2
g 2
tanh
2 h
深水波(短波):h/≥1/2
C2 C02
0
tanh
2
h
C02
g0 2
C2 C02
0
tanh
2
h
假定周期T随水深不变。由C=λ/T,有
所以有
C C0 0
C2 C02
2 02
0
tanh
2 h
C C0
0
tanh
2 h
谱函数的特点:
• 谱函数在整个频率范围内,两端值极小,集中在较窄 频率带内。因此频率较小或较大的波提供的能量很小, 能量较大的波主要集中在某些频率范围内。
• 谱函数为非负函数,恒等于或大于零,于第一象限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
exp
1.03
1 TH1/
3
4
S
400.5
Hs T2
H1/ 3
2
1
5
exp1605
1
T H1/ 3
4
式中:Hs为有效波高,表示波列中波高最大的1/3波浪的平均波高; TH1/3为有效波周期,表示波列中波高最大的1/3波浪周期的平均值。
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
m0
S
d
0
0
A
5
exp
B
4
d
A 4B
因 W /3
4
m0
1/ 2
m0
2 W /3 16
所以:B
4A
2 W /3
由于P M谱中A 0.0081g 2
0.78,
B
4A
2 W /3
3.12
2
4
W /3
代入后得ITTC谱:
S
0.78
5
exp
3.12
2
4
W /3
式中:ζw/3为三一平均波高(不是波幅)。 金品质•高追求 我们让你更放心!
典型谱画图
%1.Neumann谱 C=3.05;U=11.5;g=9.8; w=0.3:0.01:4; S1neum=C*pi/4./w.^6.*exp(-2*g^2/U^2./w.^2); plot(w,S1neum,'b-'),hold on
%2.P-M谱 a=0.0081; b=0.74; g=9.8; U=11.5; w=0.3:0.01:4; S2pm=a*g^2./(w.^5).*exp(-b*(g/U./w).^4); plot(w,S2pm,'r-'),hold on
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
9.六参数谱
奥启和汉伯尔(Ochi,Hubble, 1976)提出了一个六参数谱公式, 它把整个谱分成低频部分和高频部分两个组成部分,每一部分分别用 三个参数—有效波高Hs、谱峰频ωp和形状参数λ表示。
S 1 4
j
4j
4
1
mj
4
j
j
H sj2
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
4
注:ITTC谱中的三一平均波幅是按照
风速U=11.5kn,U=6.85(ζw/3 )0.5 计 算得出h=2.8。
金品质•高追求 我们让你更放心!
返回
适的。
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
11.方向谱
长峰不规则波是假定海浪沿单一方向传播的;实际海浪除了沿 主方向传播外,还向其他方向扩散,称为短峰不规则波;短峰不规则 波可以看成传播方向不同的长峰不规则波叠加而成。描述海浪沿不同 方向组成的波谱,称为方向谱。
S, SD,
式中:S(ω)为长峰不规则波的海浪谱;θ为组成波与主浪向的夹角。
D(ω,θ)的一般形式为: D , kn cosn
(|θ|≤π)
国际船舶结构协会会议(ISSC)建议用一下两种n值
n=2, k2=2/π; n=4, k4=8/3π;
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
TH 1/ 3 1 0.238 m 1.5
0.684
m,βw为两个参数,改变m即可改变谱的宽窄形状,βw用于调整 谱面积,使之等于波浪总能量。
形状参数m和JONSWAP谱中的γ一样,其选用依靠工程师的经验
和判断。一般小的无因次风距gX/U2和大的γ或m值相关,而大的无因
次风距值gX/U2导致γ=1或m=5。在浅水,上述谱中采用m=3或4是合
%3.ITTC谱 h=2.8; w=0.3:0.01:4; S3ittc=0.78./(w.^5).*exp(-3.12/(h^2)./(w.^4)); plot(w,S3ittc,'g-'),hold on
%4.双参数海浪谱 h=2.8; w=0.3:0.01:4; B=3.12/(h^2)./(w.^4); T1=5.127./(B.^0.25); S4=173*h^2./(T1.^4)./(w.^5).*exp(-691./(T1.^4)./(w.^4)); plot(w,S4,'m-')
8.斯科特谱
斯科特(Scott,1965)对于充分发展的海浪建议用下列谱公式:
S
0.214H s 2
exp
0.065
p p
2
0.26
1/
2
式中:-0.26<ω-ωp<1.65, Hs为有效波高;ωp为谱峰频率。 此谱和北大西洋以及印度西海岸实测谱符合得很好。
金品质•高追求 我们让你更放心!
国际船舶结构会议ISSC1964推荐下列谱公式,且常 称之为ISSC谱。
2
S
f
0.11
Hs T2
0.1
1 f5
exp
0.44
1 T0.1
f
4
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
6.JONSWAP谱
该谱由“北海海浪联合计划”测量分析得到,在60年代末期提 出,适合像北海那样风程被限定是海域,有两种表示形式。
T1 2m0 / m1 5.127 / B1/ 4或B 691/ T14
A 4Bm0
B 2 W /3 4
173
2
W
T14
/3
代入后得到双参数海浪谱:
S
173
2
W
/3
T145
exp
691
T14 4
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
5.ISSC谱
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
7.Bretschneider谱
布氏于1959年由无因次波高和无因次波长的联合分布函数导出二参数 谱,适用于成长阶段或者充分成长的风浪。后经日本光易恒(Mitsuyasu)改进 如下:
S f
0.257
Hs T2
H1/ 3
2
1 f5
TH1/ 3
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
4.双参数海浪谱
1978年第15届ITTC采用了双参数谱,双参数谱改进了ITTC谱,对成 长中的海基浪于也IT适T用C谱。有:
m1
S
d
0
0
A
5
exp
B
4
d
1 3
A B3/4
1
3 4
式中:为函数,1
3 4
0.91906,因此有:
m1 0.30638A / B3/ 4
4 j1
exp
4j
4
1
mj
4
式中:j=1、2分别表示低频和高频部分。 六参数谱可表达任何发展阶段的风浪谱。
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
10.Wallops谱
1981年,美国Huang等基于理论研究和美国航空航天局wallops飞 行中心风浪流水槽实验资料,提出通用的二参数谱—wallops。他们认 为此谱适用于波浪发展、成熟和衰减各个阶段。合田把它改进成下列 形式,建议用于工程设计(Goda, 1999)
a.由风速和风程表示的谱公式
S
g 2 5
exp
1.25
p
4
e
xp
p 2 p 2
式中:α为无因次常数,可取α=0.0076(gx/U2)-0.22; x为风区长度(风程);U为平均风速; ωp为谱峰频率,可取 ωp=22(g/U)(gx/U2)-0.33 ; γ为谱峰提升因子,平均值为3.3; σ为峰形参数,当ω≤ωp时,可取 σ=0.07;当ω>ωp时,取σ=0.09.
。目前采用都的大多数标准波谱主要是基于P-M谱的形式建立的。但是它仅
包含一个参数U,不足以表征复杂的海浪情况。
金品质•高追求 我们让你更放心!
返回
3. ITTC谱 ◆语文•选修\中国小说欣赏•(配人教版)◆
国际拖曳水池会议(ITTC, 1972)对P-M谱进行了修改,得到ITTC谱 。
基于P M谱有:
S f
H T2 1m w 1/3 p
f
m
exp
m 4
Tp f
4
金品质•高追求 我们让你更放心!
返回
◆语文•选修\中国小说欣赏•(配人教版)◆
10.Wallops谱
式中:
w
0.06238mm1/ 4 4m5/ 4 m 1
1 0.7458 m 2 1.057
Tp
返回
◆语文•选修\中国小说欣赏•பைடு நூலகம்配人教版)◆
2.P-M谱
皮尔逊和莫斯克维奇根据在北大西洋一定点上测得的大量数据,于1964 年提出。适用于充分成长的海浪。
S
式中:a=0.0081;
β=0.74;
ag2
5
exp
g
U
4
g为重力加速度;
U为离海面19.5m处的风速。
P一M谱为经验谱,依据的资料比较充分,分析方法合理,使用也方便
◆语文•选修\中国小说欣赏•(配人教版)◆
1.Neumann谱
