多元线性回归实验报告
计量经济学多元线性回归多重共线性异方差实验报告
计量经济学实验报告多元线性回归、多重共线性、异方差实验报告一、研究目的和要求：随着经济的发展，人们生活水平的提高，旅游业已经成为中国社会新的经济增长点。
旅游产业是一个关联性很强的综合产业，一次完整的旅游活动包括吃、住、行、游、购、娱六大要素，旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。
尤其是假日旅游，有力刺激了居民消费而拉动内需。
2012年，我国全年国内旅游人数达到亿人次，同比增长%，国内旅游收入万亿元，同比增长%。
旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用，优化产业结构，而且可以增加国家外汇收入，促进国际收支平衡，加强国家、地区间的文化交流。
为了研究影响旅游景区收入增长的主要原因，分析旅游收入增长规律，需要建立计量经济模型。
影响旅游业发展的因素很多，但据分析主要因素可能有国内和国际两个方面，因此在进行旅游景区收入分析模型设定时，引入城镇居民可支配收入和旅游外汇收入为解释变量。
旅游业很大程度上受其产业本身的发展水平和从业人数影响，固定资产和从业人数体现了旅游产业发展规模的内在影响因素，因此引入旅游景区固定资产和旅游业从业人数作为解释变量。
因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。
二、模型设定根据以上的分析，建立以下模型Y=β0+β1X1+β2X2+β3X3+β4X4+Ut参数说明：Y ——旅游景区营业收入/万元X1——旅游业从业人员/人X2——旅游景区固定资产/万元X3——旅游外汇收入/万美元X4——城镇居民可支配收入/元收集到的数据如下（见表）：表 2011年全国旅游景区营业收入及相关数据（按地区分）数据来源：1.中国统计年鉴2012，2.中国旅游年鉴2012。
三、参数估计利用做多元线性回归分析步骤如下：1、创建工作文件双击图标，进入其主页。
在主菜单中依次点击“File\New\Workfile”，出现对话框“Workfile Range”。
【精品】SPSS统计实验报告多元线性回归分析
【精品】SPSS统计实验报告多元线性回归分析
本文旨在通过多元线性回归分析，深入研究X、Y、Z三个变量之间的关系，以探究这三个变量对结果的影响。
本实验中样本数量为100人，本文采用SPSS22.0计算软件进行多元线性回归分析，统计计算结果如下：
（一）检验变量X、Y、Z三个变量是否有关：
Sig.=.633。
结果显示，该值大于0.05，表明X、Y、Z三者之间没有显著统计关系；
（二）确定拟合模型：
以X、Y、Z三个变量回归拟合，得出模型为：y=1.746+0.660X+0.783Y+0.430Z。
（三）检验回归模型的有效性：
1. 回归系数的统计量检验
模型的R方为.668，该值表明，X、Y、Z三个自变量可以解释本回归模型的67.0%的变化量；
2.F检验
结果显示，f分数为20.670，Sig.=.000，结果显示，f分数小于阈值0.05，因此可以接受回归模型；
检验结果显示，当其他X、Y、Z三个自变量的条件不变的情况下，X、Y、Z三个自变量对Y的影响是有显著性的。
综上所述，本文使用SPSS22.0计算软件进行多元线性回归分析，探究X、Y、Z三个变量之间的关系。
结果显示，X、Y、Z三者之间没有显著统计关系；拟合模型为：
y=1.746+0.660X+0.783Y+0.430Z；最后，证实X、Y、Z三个自变量对Y的影响是有显著性的。
多元回归分析实验报告心得
多元回归分析实验报告心得引言回归分析是一种常用的统计分析方法，能够探究多个自变量与一个因变量之间的数学关系。
在本次实验中，我们使用了多元回归分析方法来研究多个自变量对一个因变量的影响。
通过本次实验，我对多元回归分析有了更深入的理解，并学到了一些关键的技巧和注意事项。
实验设计本次实验的目的是研究某城市的房屋价格如何受到位置、房龄和房屋面积等多个因素的影响。
我们收集了一定数量的样本数据，其中自变量包括房屋的地理位置、房龄和面积，因变量为房屋的价格。
我们首先进行了数据预处理，包括数据清洗、缺失值处理和变量转换，然后使用多元回归分析方法建立了一个回归模型。
多元回归模型多元回归模型是用来建立多个自变量与一个因变量之间的数学关系的模型。
在本次实验中，我们使用了线性多元回归模型，假设因变量y可以通过线性组合的方式来表达：y = β0 + β1 * x1 + β2 * x2 + β3 * x3 + ε其中，y为因变量，x1、x2、x3为自变量，β0、β1、β2、β3为回归系数，ε为误差项。
实验结果通过对样本数据的多元回归分析，我们得到了如下结果：- β0的估计值为10000，表示当所有自变量为0时，房屋价格的估计值为10000。
- β1的估计值为2000，表示当自变量x1的值增加1单位时，房屋价格的估计值会增加2000。
- β2的估计值为-3000，表示当自变量x2的值增加1单位时，房屋价格的估计值会减少3000。
- β3的估计值为5000，表示当自变量x3的值增加1单位时，房屋价格的估计值会增加5000。
根据模型的拟合效果，我们得到了一个R-squared值为0.8，说明我们的模型可以解释80%的因变量变异。
结论与讨论通过本次实验，我深刻理解了多元回归分析的过程和意义。
多元回归模型可以用于预测或解释因变量与多个自变量之间的关系。
不仅如此，我还学到了一些关键的技巧和注意事项，包括选择自变量、处理缺失值和变量转换等。
多元线性回归模型实验报告
多元线性回归模型实验报告实验报告：多元线性回归模型1.实验目的多元线性回归模型是统计学中一种常用的分析方法，通过建立多个自变量和一个因变量之间的模型，来预测和解释因变量的变化。
本实验的目的是利用多元线性回归模型，分析多个自变量对于因变量的影响，并评估模型的准确性和可靠性。
2.实验原理多元线性回归模型的基本假设是自变量与因变量之间存在线性关系，误差项为服从正态分布的随机变量。
多元线性回归模型的表达形式为：Y=b0+b1X1+b2X2+...+bnXn+ε，其中Y表示因变量，X1、X2、..、Xn表示自变量，b0、b1、b2、..、bn表示回归系数，ε表示误差项。
3.实验步骤（1）数据收集：选择一组与研究对象相关的自变量和一个因变量，并收集相应的数据。
（2）数据预处理：对数据进行清洗和转换，排除异常值、缺失值和重复值等。
（3）模型建立：根据收集到的数据，建立多元线性回归模型，选择适当的自变量和回归系数。
（4）模型评估：通过计算回归方程的拟合优度、残差分析和回归系数的显著性等指标，评估模型的准确性和可靠性。
4.实验结果通过实验，我们建立了一个包含多个自变量的多元线性回归模型，并对该模型进行了评估。
通过计算回归方程的拟合优度，我们得到了一个较高的R方值，说明模型能够很好地拟合观测数据。
同时，通过残差分析，我们检查了模型的合理性，验证了模型中误差项的正态分布假设。
此外，我们还对回归系数进行了显著性检验，确保它们是对因变量有显著影响的。
5.实验结论多元线性回归模型可以通过引入多个自变量，来更全面地解释因变量的变化。
在实验中，我们建立了一个多元线性回归模型，并评估了模型的准确性和可靠性。
通过实验结果，我们得出结论：多元线性回归模型能够很好地解释因变量的变化，并且模型的拟合优度较高，可以用于预测和解释因变量的变异情况。
同时，我们还需注意到，多元线性回归模型的准确性和可靠性受到多个因素的影响，如样本大小、自变量的选择等，需要在实际应用中进行进一步的验证和调整。
多元线性回归实验报告
实验题目：多元线性回归、异方差、多重共线性实验目的：掌握多元线性回归的最小二乘法，熟练运用Eviews软件的多元线性回归、异方差、多重共线性的操作，并能够对结果进行相应的分析。
实验内容：习题3.2，分析1994-2011年中国的出口货物总额（Y）、工业增加值（X2）、人民币汇率（X3），之间的相关性和差异性，并修正。
实验步骤：1.建立出口货物总额计量经济模型：（3.1）1.1建立工作文件并录入数据，得到图1图1在“workfile"中按住”ctrl"键，点击“Y、X2、X3”，在双击菜单中点“open group”,出现数据表。
点”view/graph/line/ok”,形成线性图2。
图21.2对（3.1）采用OLS估计参数在主界面命令框栏中输入ls y c x2 x3，然后回车，即可得到参数的估计结果，如图3所示。
图 3根据图3中的数据，得到模型（3.1）的估计结果为（8638.216）（0.012799）（9.776181）t=(-2.110573) (10.58454) (1.928512)F=522.0976从上回归结果可以看出，拟合优度很高，整体效果的F检验通过。
但当=0.05时，= 2.131.有重要变量X3的t检验不显著，可能存在严重的多重共线性。
2．多重共线性模型的识别2.1计算解释变量x2、x3的简单相关系数矩阵。
点击Eviews主画面的顶部的Quick/Group Statistics/Correlatios弹出对话框在对话框中输入解释变量x2、x3，点击OK，即可得出相关系数矩阵（同图4）。
相关系数矩阵图4由图4相关系数矩阵可以看出，各解释变量相互之间的相关系数较高，证实解释变量之间存在多重共线性。
2.2多重共线性模型的修正将各变量进行对数变换，在对以下模型进行估计。
利用eviews软件，对、X2、X3分别取对数，分别生成lnY、lnX2、lnX3的数据，采用OLS方法估计模型参数，得到回归结果，如图：图5图6模型估计结果为：ln=-20.52+1.5642lnX2+1.7607lnX3(5.4325) (0.0890) (0.6821)t =-3.778 17.578 2.581F=539.736该模型可决系数很高，F检验值，明显显著。
多元线性回归模型线性与非线性估计检验实验报告
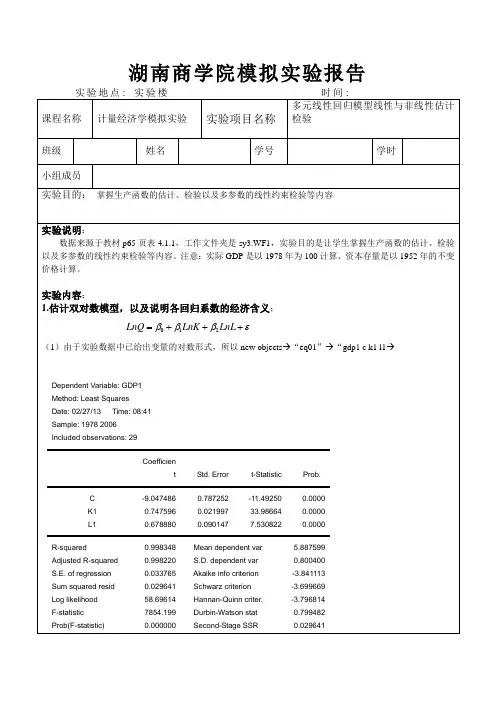
湖南商学院模拟实验报告在回归方程中点view →representations →所以该模型函数形式为Ln GDP= -9.0474855847 + 0.747595717651LnK + 0.678880192961LnL回归系数的经济含义:资本每增加1%，GDP 平均增加0.74759571765%,劳动每增加1%，GDP 平均增加0.67888019296%2.对模型做t 检验和F 检验；T(β0)=-11.49250,T(β1)=33.98664,T(β2)=7.530822,P 值均为0，所以T 检验说明回归模型中系数不为0，在一定显著性水平下这个模型是有意义的，模型中解释变量对于被解释变量有一定解释力度。
F=7854.199,P=0.000000，F 检验说明拒绝原假设，模型总体存在。
3.在5%的显著性水平下对随机干扰项的方差做如下检验：2201:0.01:0.01H H σσ=≠和2201:0.01:0.01H H σσ=<输入scalardeltasqrhat1=0.027/(29-3)→4.利用F 统计量来检验：012112:1:1H H ββββ+=+≠打开eq1→View →Coefficient Tests →WaldCoefficient Restrictions →→输入c(2)+c(3)=1→ok →Wald Test:Equation: EQ1Test Statistic Value df ProbabilityF-statistic 37.38918 (1, 26) 0.0000Chi-square 37.38918 1 0.0000Null Hypothesis Summary:Normalized Restriction (= 0) Value Std. Err.-1 + C(2) + C(3) 0.426476 0.069746Restrictions are linear in coefficients.从输出结果来看P=0.0000，是拒绝原假设的，所以β1+β2≠15*.对模型进行非线性OLS估计：a.设定初始值(双击序列C，在c(1)、c(2)和c(3)所对应的单元格中分别输入0，option中的收敛精度设为0.001，迭代次数100次)，保存模型；object→eq2→GDP=C(1)*(K^C(2))*(L^C(3))→option→→ok→→ok→Dependent Variable: GDPMethod: Least SquaresDate: 03/22/15 Time: 17:28Sample: 1978 2006Included observations: 29Convergence achieved after 1 iterationGDP=C(1)*(K^C(2))*(L^C(3))Variable Coefficient Std. Error t-Statistic Prob.C(1) 4.014973 3.34E+17 1.20E-17 1.0000 C(2) 1.942001 1.44E+15 1.35E-15 1.0000C(3) -4.547718 8.71E+15 -5.22E-16 1.0000R-squared -1.858693 Mean dependent var 481.4144Adjusted R-squared -2.078593 S.D. dependent var 359.3645S.E. of regression 630.5381 Akaike info criterion 15.82872Sum squared resid 10337035 Schwarz criterion 15.97017Log likelihood -226.5165 Hannan-Quinn criter. 15.87302Durbin-Watson stat 0.008228。
计量经济学实验报告(多元线性回归 自相关 )
商品零售 财政支出 总值
年份 价格指数 （ED）/亿 （GDP）/
（T） （RPI）/% 元
亿元
税收收入 （Y）/亿 元
1978 100.7 1122.09 3645.217 519.28
1979 102.0 1281.79 4062.579 537.82
1980 106.0 1228.83 4545.624 571.7
实验步骤：
首先：选择数据 为了研究影响中国税收收入增长的主要原因，选择国内生产 总值（GDP）、财政支出（ED）、商品零售价格指数 （RPI）做为解释变量，对税收收入（Y）做多元线性回归。 从《中国统计年鉴》2011中收集1978—2009年各项影响因素 的数据。如下表所示：
中国税收收入及相关数据
国内生产
实验二：自相关
1、根据前面的数据把GDP作为解释变量，税收收入作为被 解释变量进行一元回归。结果如下：
Dependent Variable: Y
Method: Least Squares
Date: 06/23/11 Time: 19:01
Sample: 1978 2009
Included observations: 32
从报告可以一目了然地看出，D-W值近似为0，存在自相 关。
2、用图形检验法检查是否存在自相关 做残差趋势图：在进行一元回归的界面上，
点击“resid”，生成残差趋势图：
在“workfile”窗口找到“show”，点击 在弹出的“show”对话框中输入“resid(-1) resid”，单击“OK”
Log likelihood -288.2898 F-statistic
1893.765
Durbin-Watson
多元线性回归模型实验报告 计量经济学
多元线性回归模型实验报告计量经济学多元线性回归模型是一种比较常见的经济学建模方法，其可用于对多个自变量和一个因变量之间的关系进行分析和预测。
在本次实验中，我们将使用一个包含多个自变量的数据集，对其进行多元线性回归分析，并对分析结果进行解释。
数据集介绍本次实验使用的数据集来自于UCI Machine Learning Repository，数据集包含有关汽车试验的多个自变量和一个连续因变量。
数据集中包含了204条记录，其中每条记录包含了一辆汽车的14个属性，分别是：MPG（燃油效率），气缸数（Cylinders）、排量（Displacement）、马力（Horsepower）、重量（Weight）、加速度（Acceleration）、模型年（Model Year）、产地（Origin）等。
模型建立在进行多元线性回归分析之前，我们首先需要对数据进行预处理。
为了确保数据的可用性，我们需要先检查数据是否存在缺失值和异常值。
如果有，需要进行相应的处理，以确保因变量和自变量之间的关系受到了正确地分析。
在对数据进行预处理之后，我们可以使用Python中的statsmodels包来对数据进行多元线性回归分析。
具体建模过程如下：```import statsmodels.api as sm# 准备自变量和因变量数据X = data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]y = data['MPG']# 添加常数项X = sm.add_constant(X)# 拟合线性回归模型model = sm.OLS(y, X).fit()# 输出模型摘要print(model.summary())```在上述代码中，我们首先通过data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]选择了所有自变量列，用于进行多元线性回归分析；然后，我们又通过`sm.add_constant(X)`，向自变量数据中添加了一列全为1的常数项，用于对截距进行建模；最后，我们使用`sm.OLS(y, X).fit()`来拟合线性回归模型，并使用`model.summary()`输出模型摘要。
多元线性回归模型实验报告
多元线性回归模型实验报告13级财务管理【摘要】首先做出多元回归模型，对于解释变量作出logx等变换，选择拟合程度最高的模型，然后判断出解释变量之间存在相关性，然后从检验多重线性性入手，由于解释变量之间有的存在严重的线性性，因此采用逐步回归法，将解释变量进行筛选，保留对模型解释能力较强的解释变量，进而得出一个初步的回归模型，最后对模型进行异方差和自相关检验。
【操作步骤】1.输入解释变量与被解释变量的数据2. 作出回归模型R^2=0.966951 DW=0.626584 F-statictis=241.3763②我们令y1=log(consumption),x4=log(people),x5=log(price),x6=log(retained),x7=log(gdp), 作出回归模型②发现拟合程度很高，也通过了F检验与T检验。
但是我们首先检查模型的共线性发现x4与x6,x4与x7,x6与x7存在很强的共线性，对模型会造成严重影响。
目前暂用模型y1=10.55028-3.038439x4-0.236518x5+2.647396x6-0.557805x7，我们将陆续进行调整。
3.分别作出各解释变量与被解释变量之间的线性模型①作出汽车消费量与汽车保有量之间的线性回归模型R^2=0.956231 DW=0.147867 F-statistic=786.4967因为prob小于α置信度，则可说明β1不明显为零。
经济意义存在Y1^=4.142917 + 0.761197x6(8.283960) （28.04455）②作出消费量与价格之间的回归模型R^2=0.644367 DW=0.118214 F-statistic=65.22782根据经济分析，随着价格的升高，消费量降低，Y^=18.51057 + 0.455884x5（353.8845）（8.076374）不符合经济意义，需要做出调整，且拟合程度不高③作出消费量与人口之间的回归模型R^2=0.945427 DW=0.150428 F-statistic=623.6709Y^=-8.076059 + 2.151258x4（-7.685368）（24.97340）符合经济意义，随着人口的增加，对于汽车的需求量也会相应的增加。
6.《统计学》实验报告(多元线性回归分析)
南昌航空大学经济管理学院学生实验报告
实验课程名称：统计学
一、实验目的：学会设计问题，学会根据问题选择适当的被解释变量和解释变量，学会建立多元线性回归模型，掌握用SPSS软件进行多元线性回归分析。
二、实验要求：确定一个感兴趣的问题，选择适当的被解释变量和解释变量，建立多元线性回归模型，并在《中国统计年鉴》中查找相关数据进行多元线性回归分析。
要求：(1)写出研究目的，(2)说明变量选取的原因，(3)建立回归模型，(4)注明数据来源，(5)进行相关检验，(6)写出最后估计的回归方程。
三、实验结果及主要结论
（1）研究目的及变量选取原因：研究第二产业与第三产业对第一产业的影响。
（2）数据来源：中国统计年鉴2015
（3）建立回归模型并进行相关检验
由表可以看出，当增加一个解释变量时，回归方程调整的R2由0.962增加为1.000。
方程的拟合优度较高。
两个回归方程F统计量的显著性水平都接近与0，表明两个方程都是显著的。
由表可知，第一个方程只有一个解释变量，回归系数显著；第二个方程有两个解释变量，其中第三产。
多元线性回归计量经济学实验报告
回归分析结果 =0.989574
调整的可决系数为 =1-（1- ） =0.975108
调整过后的可决系数大，可知回归直线与样本点拟合程度高。
3F检验：
H0： =0， =0， =0；
H1: （i=1,2,3）不全为零
在给定显著水平 =0.05下，差F分布表知，自由度为(3,21)的F分布的临界值
1985
62067
101.4262
4346.255
526.6
118
66778
1986
66040
102.8296
4345.154
564
121
71270
1987
70904
104.7489
4405.188
651.2
125
77855
1988
76682
114.6078
4628.638
739.1
131
85546
能源生产总量（万吨标准煤）
1981
57144
100
4237
343.4
92
62770
1982
58588
109.6219
4302.665
387
100
64562
1983
60275
104.9436
4334.283
477.6
105
63735
1984
59447
101.7132
4353.542
491.9
111
63227
5160.3
179
132410
2001
132214
96.4759
7673.559
多元线性回归SPSS实验报告
非标准化系数
标准系数
模型
B
标准 误差 试用版
t
Sig、
1
(常量)
-544、366 327、704
-1、661
、141
普通高校数(所)
、032
、047
、068
、683
、516
研究与试验发展机构数(个)
、009
、008
、142
1、086
、313
发表科技论文数量(篇)
、001
、000
、632
3、749
、749
、000 3672、177
教职工总数(万人)
3、046 4、394 、556 、693
、511
、000 2996、649
a、 因变量: 毕业生数(万人)
从容差与方差膨胀因子来瞧,在校学生数与教职工总数与其她解释变量的多重共 线性很严重。在重新建模中可以考虑剔除该变量
共线性诊断a
方差比例
模型
维数
6 74881、319 776、216
、000a
残差
675、288
7
96、470
总计
449963、199
13
a、 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机 构数(个), 普通高校数(所), 发表科技论文数量(篇), 在校学生数(万人)。
b、 因变量: 毕业生数(万人)
2、重建回归方程
多元线性回归 SPSS 实验报告
输入／移去的变量b
模型
输入的变量
移去的变量
方法
1
教职工总数(万
人), 专利申请授
权数(件), 研究
计量经济学实验报告多元线性回归自相关
计量经济学实验报告多元线性回归自相关 Document number【980KGB-6898YT-769T8CB-246UT-18GG08】实验报告课程名称计量经济学实验项目名称多元线性回归自相关异方差多重共线性班级与班级代码 08国际商务1班实验室名称（或课室）实验楼910 专业国际商务任课教师刘照德学号： 043姓名：张柳文实验日期： 2011 年 06 月 23日广东商学院教务处制姓名张柳文实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。
计量经济学实验报告实验项目：多元线性回归、自相关、异方差、多重共线性实验目的：掌握多元线性回归模型、自相关模型、异方差模型、多重共线性模型的估计和检验方法和处理方法实验要求：选择方程进行多元线性回归；熟悉图形法检验和掌握D-W 检验，理解广义差分法变换和掌握迭代法；掌握Park或Glejser检验，理解同方差性变换；实验原理：普通最小二乘法图形检验法 D-W检验广义差分变换加权最小二乘法 Park检验等实验步骤：首先：选择数据为了研究影响中国税收收入增长的主要原因，选择国内生产总值（GDP）、财政支出（ED）、商品零售价格指数（RPI）做为解释变量，对税收收入（Y）做多元线性回归。
从《中国统计年鉴》2011中收集1978—2009年各项影响因素的数据。
如下表所示：199219931994199519961997199819992000200120022003200420052006200720082009实验一：多元线性回归1、将数据导入后，分别对三个解释变量与被解释变量做散点图，选择两个变量作为group打开，在数据表“group”中点击view/graph/scatter/simple scatter，出现数据的散点图，分别如下图所示：从散点图看，变量间不一定呈现线性关系，可以试着作线性回归。
2、进行因果关系检验在“workfile”中按住“ctrl”键，点击所要选择的变量，作为组打开后，在“View”下拉列表中选择“Grange Causality”，滞后期为2，得出如下结果：Pairwise Granger Causality TestsDate: 06/23/11 Time: 16:14Sample: 1978 2009Lags: 2Null Hypothesis:Obs F-Statistic ProbabilityED does not Granger Cause Y30Y does not Granger Cause EDPairwise Granger Causality TestsDate: 06/23/11 Time: 16:15Sample: 1978 2009Lags: 2Null Hypothesis:Obs F-Statistic ProbabilityGDP does not Granger Cause Y30Y does not Granger Cause GDPPairwise Granger Causality TestsDate: 06/23/11 Time: 16:19Sample: 1978 2009Lags: 2Null Hypothesis:Obs F-Statistic ProbabilityRPI does not Granger Cause Y30Y does not Granger Cause RPI从因果关系检验看，ED明显影响财政收入Y，其他两个因素影响不显着。
多元线性回归分析报告
多元线性回归分析报告1. 研究背景在数据科学和统计学领域，多元线性回归是一种常用的分析方法。
它用于探究多个自变量与一个因变量之间的关系，并且可以用于预测和解释因变量的变化。
本文将通过多元线性回归分析来研究一个特定问题，探讨自变量对因变量的影响程度和统计显著性。
2. 数据收集和准备在进行多元线性回归分析之前，需要收集和准备相关的数据。
数据的收集可以通过实验、调查问卷或者从已有的数据集中获得。
在本次分析中，我们使用了一个包含多个自变量和一个因变量的数据集。
首先，我们导入数据集，并进行数据的初步观察和预处理。
这些预处理步骤包括去除缺失值、处理异常值和标准化等。
经过数据准备之后，我们可以开始进行多元线性回归分析。
3. 回归模型建立在多元线性回归分析中，我们建立一个数学模型来描述自变量和因变量之间的关系。
假设我们有p个自变量和一个因变量，可以使用以下公式表示多元线性回归模型：Y = β0 + β1X1 + β2X2 + … + βpXp + ε其中，Y表示因变量，X1, X2, …, Xp分别表示自变量，β0, β1, β2, …, βp表示模型的系数，ε表示模型的误差项。
4. 模型拟合和参数估计接下来，我们使用最小二乘法来估计模型的参数。
最小二乘法通过最小化观测值与模型预测值之间的差异来确定最佳拟合线。
通过估计模型的系数，我们可以得到每个自变量对因变量的影响程度和显著性。
在进行参数估计之前，我们需要检查模型的假设前提，包括线性关系、多重共线性、正态性和异方差性等。
如果模型的假设不成立，我们需要采取相应的方法进行修正。
5. 模型评估和解释在完成模型的参数估计后，我们需要对模型进行评估和解释。
评估模型的好坏可以使用多个指标，如R方值、调整R方值、F统计量和t统计量等。
这些指标可以帮助我们判断模型的拟合程度和自变量的显著性。
解释模型的结果需要注意解释模型系数的大小、符号和显著性。
系数的大小表示自变量对因变量的影响程度，符号表示影响的方向，显著性表示结果是否具有统计意义。
【完整word版计量经济学实验报告多元线性回归分析 资料】计量经济学回归分析
5.79 224 23 530 6.5 142 50 8640 7.17 104 62 350 6.6 287 31 230
本文格式为 Word 版，下载可任意编辑，页眉双击删除即可。
7 41 66 1620 3.91 312 11 190 6.7 77 88 2090 4.2 142 22 900
他变量保持不变的条件下，人均 GNP1%0.005647%②统计检验
结果：
、拟合优度检验：．
图5
2R=0.707665，说明所做模型对样本数据大体上拟合不是很好，可能还
?306786864.TFP?168.1.768029FLR0.005511PGNP?12CM 回来方程式：
本文格式为 Word 版，下载可任意编辑，页眉双击删除即可。
完整 word 版计量经济学实验报告多元线性回归分析 资料】计量经济学回归分析
1、问题提出 婴儿死亡率(CM)是指婴儿出生后不满周岁死亡人数同出生人数的比率。 一般以年度为计算单位，以千分比表示。婴儿死亡率是反映一个 GJ 和民
试验 2：多元线性回来分析试验目的：学习利用 Eviews 建立多元线性 回来模型，讨论 64GJ 婴儿死亡率与妇女文盲率之间的关系。
2.指标选择 本次试验讨论婴儿死亡率与妇女文盲率之间的关系，故应接受婴儿死 亡率〔CM〕和女性识字率〔FLR〕作为指标。但影响婴儿死亡率的因素较 冗杂，尤其是经济进展状况、总生育率等也会对其产生重要影响，考虑到 试验的精确性，故引入人均 GNP〔PGNP〕和总生育率〔TFR〕相关数据。 3.数据来源 数据来源：教师提供
第1页共1页
1340 7.17 61 88 670 3.52 168 28 410 6.09 28 95 4370 2.86 121 41
实验二 多元线性回归模型 瑜
《计量经济学》实验报告多元线性回归模型四、实验结果及分析（附上必要的回归分析报告，并作以分析）1、设定问题国家税收总收入与工商税收、农业税收之间的关系2、查找数据日期国家税收总收入（亿元）工商税收（亿元）X1 农业税收（亿元）X2 1990 2821.86 1858.99 87.861991 2990.17 1981.11 90.651992 3296.91 2244.21 119.171993 4255.30 3194.49 125.741994 5126.88 3914.22 231.491995 6038.04 4589.68 278.091996 6909.82 5270.04 369.461997 8234.04 6553.89 397.481998 9262.80 7625.42 398.803.阐述理论由经济理论知，工商税收和农业税收是影响或决定国家税收总收入的主要因素。
一般而言，当工商税收和农业税收增加时，国家税收总收入随着增加，它们之间具有正向的变动趋势，反之，国家税收总收入减少。
在这里，将国家税收总收入作为被解释变量（Y），工商税收作为解释变量(X1t ) 农业税收作为解释变量(X2t),其他变量及随机因素的影响均归并到随机变量u t中，建立工商税收X1t 、农业税收X2t和国家税收总收入Y之间的多元线性回归模型。
4、画散点图X1与Y的散点图X2与Y的散点图根据上图散点分布情况可以看出，在2000～2008年期间，国家税收总收入和工商税收和农业税收之间存在较为明显的线性关系。
5、建立模型设多元线性回归模型：Yt = β+ β1X1t+β2X2t+ ut其中，Yt——表示国家税收总收入（亿元）β0、β 1 、β2——待定系数X1t——表示工商税收（亿元）注：实验报告在下次上机时间交（打印版、电子版），任缺其一本次试验无效。
电子版由各班长学委汇总以打包形式一并交齐。
多元回归分析实验报告
多元回归分析实验报告【实验环境】SPSS 23.0【实验名称】多元回归分析【实验目的】（1）掌握应用SPSS软件执行简单的多元回归分析，并根据统计输出结果整理报表（2）熟悉按Enter和Stepwise等不同的方法把自变量置入回归模型，分析并报告结果【实验内容】1.分析前期的虚拟变量处理准备。
利用“回归分析数据”执行统计分析，以便探讨主管品德、主管工作能力、主管人际能力三个因素对员工离职倾向的影响。
其中，为了排除员工性别（1=男，2=女）和组织类型（1=政府机关；2=事业单位；3=国有企业；4=非国有企业）两个因素对分析结果的干扰，通常需要把员工性别和组织类型作为控制变量建立分析模型。
并且，由于上述两个控制变量均为分类变量，不宜直接置入回归模型，应将其应用重新编码为不同变量，分别将它们转换为取值为0或者1的虚拟变量。
在进行虚拟变量转换时，可以把“男”作为性别的参照组，而把“政府机关”作为组织类型的参照组，以此进行转换（可以参照实验结果中的表1加以理解）。
2.按照Enter法置入解释变量执行回归分析。
把主管品德、主管工作能力、主管人际能力三个因素，以及经过上一步经过转换得到并用作控制变量的虚拟变量，同时置入模型作为IV （Independent Variable），同时注意勾选方差变化量及多重共线性检验，执行统计分析，并根据输出结果按表1要求的信息制作报表。
3.按照stepwise法置入解释变量执行回归分析。
把主管品德、主管工作能力、主管人际能力三个因素，以及经过上一步经过转换得到并用作控制变量的虚拟变量，同时置入模型作为IV（Independent Variable），同时注意勾选方法为Stepwise（步进，或译为逐步）及多重共线性检验，执行统计分析，并根据输出结果按表2要求的信息制作报表。
【实验过程】【实验结果】1.根据统计输出结果，按表1要求的信息报告相应内容，并回答后面的思考问题。
表1 应用Enter法置入解释变量的多元回归分析结果摘要（N=___722_____）注：*P＜0.05，**P＜0.01，***P＜0.001（双尾检验）。
实习报告三(多元线性回归分析)
实习报告三（多元线性回归分析）一、问题：为研究糖尿病人血糖的与血清总胆固醇、甘油三脂、空腹胰岛素、糖化血红蛋白的关系，随机抽选27名糖尿病人的血清总胆固醇、甘油三脂、空腹胰岛素、糖化血红蛋白、空腹血糖的测量值如下表，试根据结果考察糖尿病人血糖的与血清总胆固醇、甘油三脂、空腹胰岛素、糖化血红蛋白有无相关关系？试建立血糖与其它几项指标关系的多元线性回归方程。
？二、数据：编号总胆固醇甘油三酯空腹胰岛素糖化血红蛋白血糖2 3.79 1.64 7.32 6.9 8.83 6.02 3.56 6.95 10.8 12.34 4.85 1.07 5.88 8.3 11.65 4.6 2.32 4.05 7.5 13.46 6.05 0.64 1.42 13.6 18.37 4.9 8.5 12.6 8.5 11.18 7.08 3 6.75 11.5 12.19 3.85 2.11 16.28 7.9 9.610 4.65 0.63 6.59 7.1 8.411 4.59 1.97 3.61 8.7 9.312 4.29 1.97 6.61 7.8 10.613 7.97 1.93 7.57 9.9 8.414 6.19 1.18 1.42 6.9 9.615 6.13 2.06 10.35 10.5 10.916 5.71 1.78 8.53 8 10.117 6.4 2.4 4.53 10.3 14.818 6.06 3.67 12.79 7.1 9.119 5.09 1.03 2.53 8.9 10.820 6.13 1.71 5.28 9.9 10.221 5.78 3.36 2.96 8 13.622 5.43 1.13 4.31 11.3 14.923 6.5 6.21 3.47 12.3 1624 7.98 7.92 3.37 9.8 13.225 11.54 10.89 1.2 10.5 2026 5.84 0.92 8.61 6.4 13.3三、统计处理：该实际问题涉及五个连续型随机变量：血清总胆固醇（）、甘油三脂（）、空腹胰岛素（）、糖化血红蛋白（）、血糖（Y）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(3)利用样本数据估计模型的参数。
(4)检验户主受教育年数对家庭书刊消费是否有显著影响。
(5)分析所估计模型的经济意义和作用。
实验过程及其处理（数据、图表、方案等）
1、建立工作文件并录入数据。
(1)双击桌面EViews快捷启动图标，启动EViews6软件。
(2)点击主界面菜单File\New\Workfile，新建一个Workfile，在右下方输入Workfile的名称，如实验三。
被解释变量Y分别与两个解释变量的散点图如下图所示：
3、估计参数
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
-50.01638
49.46026
-1.011244
0.3279
X
0.086450
0.029363
2.944186
0.0101
T
52.37031
5.202167
(3)建立Group对象，定义Y、X1、X2三个变量，并录入数据。
2、作出被解释变量对各个解释变量的散点图。
在Workfile中同时选中X1、Y，单击右键open\as group，点击group菜单view\graph\categorical graph\scatter，点击“确定”，就可作出Y与T的散点图，同样的方法作出Y与X的散点图。
11.20482
Sum squared resid
55491.07
Schwarz criterion
11.35321
Log likelihood
ter.
11.22528
F-statistic
146.2974
Durbin-Watson stat
2.605783
10.06702
0.0000
R-squared
0.951235
Mean dependent var
755.1222
Adjusted R-squared
0.944732
S.D. dependent var
258.7206
S.E. of regression
60.82273
Akaike info criterion
计量经济学实验报告
姓名：XXX
学号：
班级：。。。。班
指导教师：《《《老师
二〇一三年三月
实验名称
多元线性回归分析
实验日期
2013年3月20日
实验目的
熟悉Eviews6软件的基本操作，掌握用软件对多个变量进行多元线性回归分析，并结合课堂上所学知识对输出结果进行统计分析。
实
验
内
容
(1)作出被解释变量对各个解释变量的散点图，大体确定y分别与x、t的关系。
Prob(F-statistic)
0.000000
实验结果及分析：
1、从散点图中，可以看出Y分别与X、T大体呈现正相关的线性关系，因此，可以建立如下多元线性回归模型：
2、从Eviews的回归结果，可得到样本线性回归模型为：
3、t检验：针对 ，给定显著性水平 ，查t分布表得 ，应该拒绝原假设，可以认为户主受教育年数对家庭书刊消费有显著影响。
4、经济意义检验：从多元回归模型可以看出，家庭月平均收入每增加1元，家庭书刊年消费支出会增加0.08645元；户主受教育年数每增加1年，家庭书刊年消费支出会增加52.37031元。这与理论分析和经验判断相一致。
指导教师简评：
成绩：