人均国内生产总值和人均消费水平相关回归分析课堂练习题
《统计学》-第7章-习题答案

第七章思考与练习参考答案1.答:函数关系是两变量之间的确定性关系,即当一个变量取一定数值时,另一个变量有确定值与之相对应;而相关关系表示的是两变量之间的一种不确定性关系,具体表示为当一个变量取一定数值时,与之相对应的另一变量的数值虽然不确定,但它仍按某种规律在一定的范围内变化。
2.答:相关和回归都是研究现象及变量之间相互关系的方法。
相关分析研究变量之间相关的方向和相关的程度,但不能确定变量间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况;回归分析则可以找到研究变量之间相互关系的具体形式,并可变量之间的数量联系进行测定,确定一个回归方程,并根据这个回归方程从已知量推测未知量。
3.答:单相关系数是度量两个变量之间线性相关程度的指标,其计算公式为:总体相关系数,样本相关系数。
复相关系数是多元线性回归分析中度量因变量与其它多个自变量之间的线性相关程度的指标,它是方程的判定系数2R 的正的平方根。
偏相关系数是多元线性回归分析中度量在其它变量不变的情况下两个变量之间真实相关程度的指标,它反映了在消除其他变量影响的条件下两个变量之间的线性相关程度。
4.答:回归模型假定总体上因变量Y 与自变量X 之间存在着近似的线性函数关系,可表示为t t t u X Y ++=10ββ,这就是总体回归函数,其中u t 是随机误差项,可以反映未考虑的其他各种因素对Y 的影响。
根据样本数据拟合的方程,就是样本回归函数,以一元线性回归模型的样本回归函数为例可表示为:tt X Y 10ˆˆˆββ+=。
总体回归函数事实上是未知的,需要利用样本的信息对其进行估计,样本回归函数是对总体回归函数的近似反映。
两者的区别主要包括:第一,总体回归直线是未知的,它只有一条;而样本回归直线则是根据样本数据拟合的,每抽取一组样本,便可以拟合一条样本回归直线。
第二,总体回归函数中的0β和1β是未知的参数,表现为常数;而样本回归直线中的0ˆβ和1ˆβ是随机变量,其具体数值随所抽取的样本观测值不同而变动。
第七章 相关回归分析 思考题及练习题

实用价值越小。
13、在相关分析中,要求相关的两个变量( )
A、都是随机变量
B、都不是随机变量
C、其中因变量是随机变量 D、其中自变量是随机变量
14、在简单回归直线
中,
表示( ) A、当
增加一个单位时,
增加
的数量 B、当
增加一个单位时,
增加
的数量 C、当
增加一个单位时,
的平均增加值 D、当
增加一个单位时,
按一定数额变化时,变量
也随之近似地按固定的数额变化,那么,这时变量
和
之间存在着( )
A、正相关关系
B、负相关关系
C、直线相关关系 D、曲线相关关系
18、两个变量间的相关关系称为( )
A、单相关
B、无相关
C、复相关
D、多相关
19、如果两个变量之间的相关系数
,说明这两个变量之间存在( )。 A、低度相关关系 B、高度相关关系 C、完全相关关系 D、显著相关关系 20、已知
第七章 思考题及练习题
(一) 填空题
1、 1、 在相关关系中,把具有因果关系相互联系的两个变
量中起影响作用的变量称为_______,把另一个说明观察结果的
变量称为________。
2、 2、 现象之间的相关关系按相关的程度分有________相
关、________相关和_______相关;按相关的方向分有________
E、 E、回归方程实用价值大小的指标 10、现象之间相互联系的类型有( )
A、函数关系 B、回归关系 C、相关关系 D、随机关系 E、结构关系 11、相关关系种类( ) A、从相关方向分为正相关和负相关 B、从相关形态分为线性相关和非线性相关 C、从相关程度分为完全相关、不完全相关和零相关
回归分析练习试题和参考答案解析

1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
α=)。
(5)检验回归方程线性关系的显著性(0.05(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:系数a模型非标准化系数标准系数t Sig.相关性B标准误差试用版零阶偏部分1(常量).003人均GDP.309.008.998.000.998.998.998 a. 因变量: 人均消费水平有很强的线性关系。
(3)回归方程:734.6930.309y x=+系数a模型非标准化系数标准系数t Sig.相关性回归系数的含义:人均GDP没增加1元,人均消费增加元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1(常量)人均GDP(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1.998a.996.996a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的 R 方估计的标准差1.998(a)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F检验:Anova b模型平方和df均方F Sig.1回归.6801.680.000a 残差5总计.7146a. 预测变量: (常量), 人均GDP。
回归分析练习题及参考答案
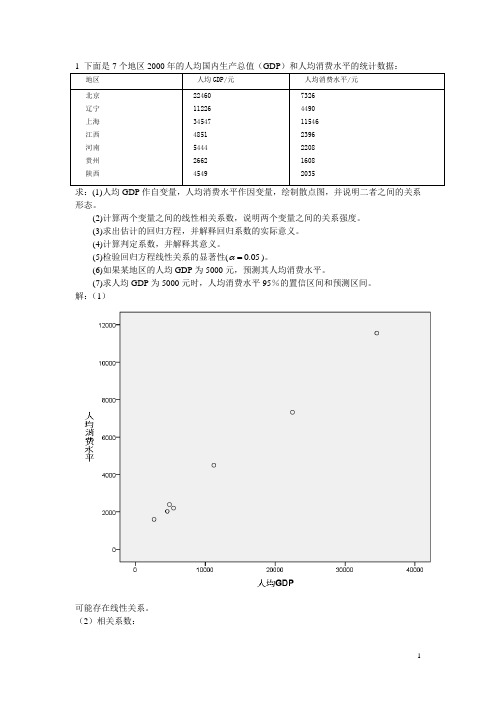
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
回归分析案例

年人均收入 (元)x2
1250 1650 1450 1310 1310 1580 1490 1520 1620 1570
回归方程 (模型) 的显著性谁对销售 额的影响 更显著一 点?
人均 消费金额
643 690 713 803 947 1148
解:根据样本相关系数的计算公式有
r n xy x y
2
n x 2 x n y 2 y
2
2
13 9156173.99 12827.5 7457 13 16073323.77 12827.5 13 5226399 7457
回归分析案例
Spss-回归分析
【例10.1】在研究我国人均消费水平的问题中,把全国人均消费额记 为y,把人均国民收入记为x。我们收集到1981~1993年的样本数据(xi , yi),i =1,2,…,13,数据见表10-1,计算相关系数。
表10-1 我国人均国民收入与人均消费金额数据
年份
1981 1982 1983 1984 1985 1986 1987
单位:元
人均 国民收入
393.8 419.14 460.86 544.11 668.29 737.73 859.97
人均 消费金额
249 267 289 329 406 451 513
年份
1988 1989 1990 1991 1992 1993
人均 国民收入
1068.8 1169.2 1250.7 1429.5 1725.9 2099.5
712.5734.469
人均消费金额95%的预测区间为678.101元~747.039元之间
到2010年若国民收入到10000元,消费金额会 是多少?置信区间?
应用回归分析课后习题

使用其中的一个。
2.12* 如果把自变量观测值都乘以 2,回归参数的最小二乘估计 ˆ0 和 ˆ1 会发生什么变化?
#;
.
如果把自变量观测值都加上 2,回归参数的最小二乘估计 ˆ0 和 ˆ1 会发生什么变化?
2.13 如果回归方程 yˆ ˆ0 ˆ1x 相应的相关系数 r 很大,则用它预测时,预测误差一定较小。
#;
.
第三章 习题
3.1 写出多元线性回归模型的矩阵表示形式,并给出多元线性回归模型的基本假设。 3.2 讨论样本量 n 与自变量个数 p 的关系,它们对模型的参数估计有何影响?
3.3 证明ˆ 2 1 SSE 是误差项方差 2 的无偏估计。 n p 1
3.4 一个回归方程的复相关系数 R=0.99,样本决定系数 R2 0.9801 ,我们能判断这个回归
2.15 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。经过 10
周时间,收集了每周加班工作时间的数据和签发的新保单数目,x 为每周签发的新保单数目,
y 为每周加班工作时间(小时)。见表
周序 1
2
3
4
5
6
7
8
9
10
号
X
825 215 1070 550 480 920 1350 325 670 1215
基于回归分析的居民人均消费水平与人均GDP的研究

基于回归分析的居民人均消费水平与人均GDP的研究居民消费在社会经济的持续发展中有着重要作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长。
本文是对1978年至2009年的居民消费水平数据进行分析并预测。
标签:回归分析检验居民消费水平一、简介改革开放以来,随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也在不断增长。
研究中国全体居民的消费水平与经济发展的数量关系,对于探寻居民消费增长的规律性,预测居民消费的发展趋势有重要意义。
在本研究中,通过在《国家统计数据库》选取了1978年~2009年的年度人均GDP和年度全国居民平均消费水平,并对人均GDP对居民消费水平的影响以及2010年居民消费水平进行预测。
二、一元线性回归分析可以看出.居民消费水平(Y)和人均GDP(X)大体呈现为线性关系,为分析中国居民消费水平随人均GDP变动的数量规律性,建立线性Y=a+bx。
回归模型。
参数估计及检验应用Eviews进行操作得下表:根据分析结果,可以得出回归方程为:y=a+bx=0.360x+327.3329,常数项和GDP系数的参数估计分别对应系数为327.3329和0.3598。
此外,残差平方和是2611591,对数似然值是-226.3618,分别是最小二乘估计和最大似然估计目标函数的值。
1978年到2009年这期间的居民人均消费和人均GDP之间的相关系数为0.987,说明我国人均GDP与居民人均消费之间存在着高度的相关关系,我国人均GDP每增长一元,我国居民的人均消费就增加0.36元。
这符合我国的国情,也符合宏观经济理论框架。
在结果中,参数估计量的标准差分别是70.49,0.00749。
对应常数项C和变量X系数两个参数估计的T的统计量分别是32.81,114.52,反映两个参数都是显著的。
2.检验T检验:是对回归系数的线性统计关系的检验,得出t值4.643139查表得tα/2 (30)=2.042。
计量经济学 课后练习题答案解析
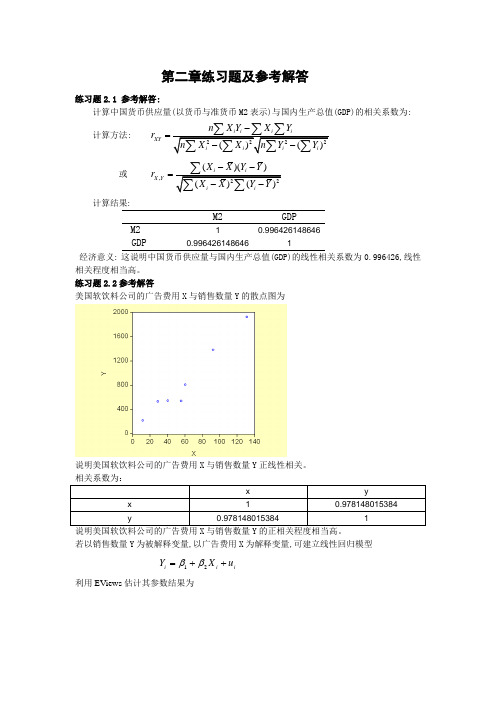
第二章练习题及参考解答练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或,()()X Y X X Y Y r --=计算结果:M2GDPM2 10.996426148646GDP0.9964261486461经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
练习题2.2参考解答美国软饮料公司的广告费用X 与销售数量Y 的散点图为说明美国软饮料公司的广告费用X 与销售数量Y 正线性相关。
相关系数为:说明美国软饮料公司的广告费用X 与销售数量Y 的正相关程度相当高。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
练习题2.3参考解答:1、 建立深圳地方预算内财政收入对GDP 的回归模型,建立EViews 文件,利用地方预算内财政收入(Y )和GDP 的数据表,作散点图可看出地方预算内财政收入(Y )和GDP 的关系近似直线关系,可建立线性回归模型: t t t u GDP Y ++=21ββ 利用EViews 估计其参数结果为即 ˆ20.46110.0850t tY GDP =+ (9.8674) (0.0033)t=(2.0736) (26.1038) R 2=0.9771 F=681.4064经检验说明,深圳市的GDP 对地方财政收入确有显著影响。
20.9771R =,说明GDP 解释了地方财政收入变动的近98%,模型拟合程度较好。
模型说明当GDP 每增长1亿元时,平均说来地方财政收入将增长0.0850亿元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章相关回归分析课堂练习题:
对15个地区2006年的人均国内生产总值(GDP)和人均消费水平的统计数据进行相关回归分析,以人均GDP作自变量,人均消费水平作因变量,利用EXCEL的具体计算结果如下:
方差分析
试根据以上数据处理结果,分析:
(1)根据散点图,说明两个变量之间存在什么相关关系,写出他们的相关系数。
(2)写出判定系数,并解释其意义。
(3)写出估计的回归方程,并解释回归系数的实际意义。
(4)在 =0.05显著性水平下,检验回归方程线性关系的显著性。
(5)写出标准误差S y,并解释其意义。
(6)如果人均GDP为5000元,预测其人均消费水平;如果给定95%的概率保证,估计人均消费水平的预测区间。
解:(1) 根据散点图,说明两个变量之间存在什么相关关系,写出他们的相关系数。
答:两个变量之间存在正线性相关关系。
相关系数r=0.9981,因为r ﹥0.8,根据经验可认
为两个变量之间存在高度线性相关。
(2) 写出判定系数,并解释其意义。
答:判定系数R 2=0.9963。
说明在人均消费水平的变动中,有99.63%可以由人均GDP 和人
均消费水平之间的线性关系来解释。
(或者答:在人均消费水平的变动中,有99.63%可以由人均GDP 来决定。
)
(3) 写出估计的回归方程,并解释回归系数的实际意义。
答:估计的回归方程是0.74x 457.28ˆ+==y。
回归系数2.457ˆ0=β是截距,没具体的经济意义。
回归系数74.ˆ
1o =β是斜率,表示人均GDP 每增加1单位,人均消费水平平均增加0.74单位。
(4) 在α=0.05显著性水平下,检验回归方程线性关系的显著性。
答:0:10=βH
因为Significance F=3.61282E-17﹤=0.05,所以拒绝H0,表明人年均消费水平和人
均GDP 之间的线性关系是显著的。
(5)标准误差S e =167.29元,说明根据人均GDP 来估计人均消费水平时,平均的估计误差为167.29元。
(6) 如果人均GDP 为5000元,预测其人均消费水平;如果给定95%的概率保证,估计人均消费水平的预测区间。
答:(元)28.4157500074.028.457ˆ=⨯+=y
)63.4518,93.3795(35.36128.415729.16716.228.4157ˆ)215(2/=±=⨯±=±-e S t y α。
