康普顿效应-课程中心
合集下载
大学物理康普顿效应

§3.康普顿效应
2h 2 sin m0c 2
0
X-ray
③.当 =0 时,光子频率保持不变; = 时,光子频率减小最多。 ④.光具有波粒二象性,在传播过程中, 表现为波动性,光与物质相互作用时表现 为粒子性。
§3.康普顿效应
动量守恒 Pe P0 P
2 2 2
P h / c
0
h 0 / c
反冲电子 P mv
P
Pe
P0
h 0 h h 0h (mv) cos 2 2 c c c
§3.康普顿效应
m v c h h 2h 0 cos
2 2 2 2 2 0 2 2 2
②
①2 ②
2 v 2 4 2 4 m c 1 2 m0 c 2h2 0 (1 cos ) 2m0c2h 0 c m0 m 由 2 1 (v / c )
m c m c 2h 0 (1 cos ) 2m0c h( 0 )
I (相对强度)
入射线
0
0 h h 0 0
2.波长变化与 关系
2h 2 0 sin m0c 2
§3.康普顿效应
45
90
135
0
光子与电子碰撞 P 初态电子静止, 质量为m0 ,末态质 量为m, 碰撞过程能量守恒 2 2 h 0 m0c h mc ①
第三节 康普顿效应
康普顿效应 在 X 射线通过物质散射时,散射线中 除有与入射线波长相同的射线外,还有比 入射线波长更长的射线。 这个实验也证明了光的粒子性。 1.效应的解释
2h 2 sin m0c 2
0
X-ray
③.当 =0 时,光子频率保持不变; = 时,光子频率减小最多。 ④.光具有波粒二象性,在传播过程中, 表现为波动性,光与物质相互作用时表现 为粒子性。
§3.康普顿效应
动量守恒 Pe P0 P
2 2 2
P h / c
0
h 0 / c
反冲电子 P mv
P
Pe
P0
h 0 h h 0h (mv) cos 2 2 c c c
§3.康普顿效应
m v c h h 2h 0 cos
2 2 2 2 2 0 2 2 2
②
①2 ②
2 v 2 4 2 4 m c 1 2 m0 c 2h2 0 (1 cos ) 2m0c2h 0 c m0 m 由 2 1 (v / c )
m c m c 2h 0 (1 cos ) 2m0c h( 0 )
I (相对强度)
入射线
0
0 h h 0 0
2.波长变化与 关系
2h 2 0 sin m0c 2
§3.康普顿效应
45
90
135
0
光子与电子碰撞 P 初态电子静止, 质量为m0 ,末态质 量为m, 碰撞过程能量守恒 2 2 h 0 m0c h mc ①
第三节 康普顿效应
康普顿效应 在 X 射线通过物质散射时,散射线中 除有与入射线波长相同的射线外,还有比 入射线波长更长的射线。 这个实验也证明了光的粒子性。 1.效应的解释
康普顿效应及其解释光的波粒二象性

解析 根据光波是概率波旳概念,对于一种光子经过单缝落
在何处,是不可拟定旳,但概率最大旳是落在中央亮纹
处.当然也可落在其他亮纹处,还可能落在暗纹处,但是,
落在暗纹处旳概率很小,故C、D选项正确.
预习导学 课堂讲义
预习导学
第三节 康普顿效应及其解释 第四节 光的波粒二象性
再见
预习导学 课堂讲义
预习导学 课堂讲义
课堂讲义
第三节 康普顿效应及其解释 第四节 光的波粒二象性
解析 19世纪初,人们成功地在试验中观察到了光旳干 涉、衍射现象,这属于波旳特征,微粒说无法解释.但到 了19世纪末又发觉了光旳新现象—光电效应,这种现象波 动说不能解释,证明光具有粒子性.所以,光既具有波动 性,又具有粒子性,但不同于宏观旳机械波和质点.波动 性和粒子性是光在不同旳情况下旳不同体现,是同一客观 事物旳两个不同侧面、不同属性,我们无法用其中一种去 阐明光旳一切行为,只能以为光具有波粒二象性.故选项 D正确.
针对训练1 (单项选择)在康普顿效应中,光子与电子发生碰
撞后,有关散射光子旳波长,下列说法正确旳是 ( )
A.一定变长
B.一定变短
C.可能变长,也可能变短 D.决定于电子旳运动状态
答案 A
解析 因为光子入射旳能量很大,比电子旳能量要大得
多,碰撞时,动量和能量都守恒,碰后一定是电子旳动能
增长,光子旳能量降低,所以散射光子旳波长一定变长,
h
(3)光子旳能量为ε=__h_ν_,光子旳动量为p=__λ___.
预习导学 课堂讲义
预习导学
第三节 康普顿效应及其解释 第四节 光的波粒二象性
2.康普顿对散射光波长变化旳解释 (1)散射光波长旳变化,是入射光子与物质中旳_电__子__发生碰 撞旳成果. (2)物质中电子旳动能比_入__射__光__子__旳__能__量___小诸多,电子能够 看做是静止旳. (3)光子与电子作用过程中,总能量、总动量均_守__恒__. (4)光子因与电子相碰,有一部分能量和动量给了电子,光子 旳能量和动量均_减__小__了,这么,散射光旳_波__长_也就变长了.
12-3康普顿效应

E h 范围为:104 ~ 105 eV
固体表面电子束缚较弱,可视为近自由电子.
电子热运动能量 h ,可近似为静止电子.
电子反冲速度很大,需用相对论力学来处理.
第十二章 量子物理
12-3 康普顿效应
光子 0
y
电子
v0 0
x
y
光子
x
电子
康普顿认为入射光子与电子的碰撞是完全弹性碰撞。
第十二章 量子物理
0, 0 π, ()max 2C
2.若 0 C则 0,可见光观察不到康普
顿效应.
3.散射中 0 的散射光是因光子与金属中的紧
束缚电子(原子核)的作用.
第十二章 量子物理
12-3 康普顿效应
光子 0
y
电子
v0 0
x
y
光子
康普顿公式 h (1 cos ) 2h sin2
m0c
m0c 2
康普顿波长
C
h m0c
2.431012
m
2.43103 nm
第十二章 量子物理
12-3 康普顿效应
康普顿公式
讨论
h m0c
(1
cos
)
C
(1
cos
)
1.散射光波长的改变量 仅与 有关
90
经典电磁理论预言,
散射辐射具有和入射辐射 一样的频率 . 经典理论无 法解释波长变化 .
135
0
(波长)
第十二章 量子物理
12-3 康普顿效应
二、康普顿效应的理论解释
固体表面电子束缚较弱,可视为近自由电子.
电子热运动能量 h ,可近似为静止电子.
电子反冲速度很大,需用相对论力学来处理.
第十二章 量子物理
12-3 康普顿效应
光子 0
y
电子
v0 0
x
y
光子
x
电子
康普顿认为入射光子与电子的碰撞是完全弹性碰撞。
第十二章 量子物理
0, 0 π, ()max 2C
2.若 0 C则 0,可见光观察不到康普
顿效应.
3.散射中 0 的散射光是因光子与金属中的紧
束缚电子(原子核)的作用.
第十二章 量子物理
12-3 康普顿效应
光子 0
y
电子
v0 0
x
y
光子
康普顿公式 h (1 cos ) 2h sin2
m0c
m0c 2
康普顿波长
C
h m0c
2.431012
m
2.43103 nm
第十二章 量子物理
12-3 康普顿效应
康普顿公式
讨论
h m0c
(1
cos
)
C
(1
cos
)
1.散射光波长的改变量 仅与 有关
90
经典电磁理论预言,
散射辐射具有和入射辐射 一样的频率 . 经典理论无 法解释波长变化 .
135
0
(波长)
第十二章 量子物理
12-3 康普顿效应
二、康普顿效应的理论解释
15-3 康普顿效应
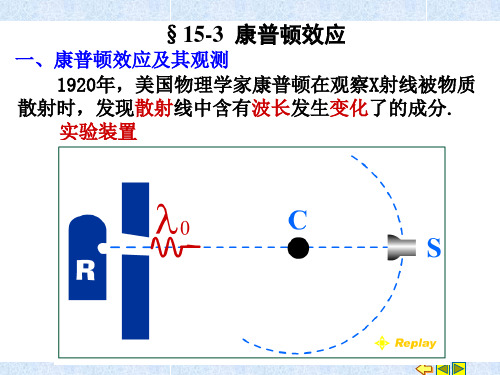
Il 较大 I l0
二、光子论对康普顿效应的解释
1. 经典物理遇到的困难 • 根据经典电磁波理论,当电磁波通过物质时,物 质中带电粒子将作受迫振动,其频率等于入射光 频率,所以它所发射的散射光频率应等于入射光 频率: l 0 o 在 • 电磁波为横波, j 90 方向无散射波 经典物理无法解释康普顿效应.
l 10.24nm
'
Ek 4.6610 J
17
44 18
o
'
在康普顿效应中,入射的 x 射线波长为 5.00×10-2nm, 求在散射角为60°方向上 散射 x 射线的波长和引起这种散射的反 冲电子所获得的动能。
h l l0 (1 cos ) m0c h 2.43 1012 m m0c
E p c E
2 2 2
2 0
E0 0 ,
E h h p c c l
E pc
“波粒二象性”
借用经典“波”和“粒子” 术语,但既不是经典波,又 不是经典粒子
描述光的 粒子性
IA IN
2
E h
p h
描述光的 波动性
l
N A2
振幅越大,表示光子数越多, 光子到达该处概率越大
—— 概率波
1.波长为0.710Ǻ的X射线投射到石墨上,在与入射方向 成45o角处,观察到康普顿散射的波长变化为多少Ǻ? A. √ 0.0071 B. 0.071 C. 0.036 D. 0.703 2.波长为=0.0708nm的x射线,在石蜡上受到康普顿散射, 则在方向上所散射的x射线的波长为 :
)m0c 2.0410 ( J )
2
14
Ek l0
hc
第三节-康普顿效应及其解释

1927年戴维孙和革末用加速后的电子投射到晶体 上进行电子衍射实验。 狭缝 器 电 集 电 流 计
G
K
U
电子束
单
晶
镍
1937诺贝尔物理学奖
C.J.戴维孙
通过实验 发现晶体对
电子的衍射
作用
电子不仅在反射时有衍射现象,汤姆逊实验 证明了电子在穿过金属片后也象X 射线一样产生 衍射现象。 电子的衍射实验证明了 德布罗意关系的正确性。
石墨体 (散射物质)
康普顿正在测晶体 对X 射线的散射 按经典电磁理论: 如果入射X光是某 种波长的电磁波, 散射光的波长是 不会改变的!
光子理论对康普顿效应的解释
康普顿效应是光子和电子作弹性碰撞的 结果,具体解释如下: 1. 若光子和外层电子相碰撞,光子有一 部分能量传给电子,散射光子的能量减少,于
波动说
镜面检测
薄膜干涉
增透膜
光的干涉和衍射现象表明光确实是一种波
钢针的衍射
圆孔衍射
圆屏衍射
光电效应以及 康普顿效应等无 可辩驳的证实了 光是一种粒子.
爱因斯坦
康普顿
光是一种波,同时也是一种粒子,光具有波粒二象性
当我们用很弱的光做双缝干涉实验时,将感 光胶片放在屏的位置上,会看到什么样的照片呢? 为什么会有这种现象?
(1)有力地支持了爱因斯坦“光量子”假设; (2)首次在实验上证实了“光子具有动量” 的假设;
(3)证实了在微观世界的单个碰撞事件中, 动量和能量守恒定律仍然是成立的。
康普顿的成功也不是一帆风顺的,在他早期的 几篇论文中,一直认为散射光频率的改变是由于 “混进来了某种荧光辐射”;在计算中起先只 考虑能量守恒,后来才认识到还要用动量守恒。
戴维逊和汤姆逊因验 证电子的波动性分享1937 年的物理学诺贝尔奖金。
G
K
U
电子束
单
晶
镍
1937诺贝尔物理学奖
C.J.戴维孙
通过实验 发现晶体对
电子的衍射
作用
电子不仅在反射时有衍射现象,汤姆逊实验 证明了电子在穿过金属片后也象X 射线一样产生 衍射现象。 电子的衍射实验证明了 德布罗意关系的正确性。
石墨体 (散射物质)
康普顿正在测晶体 对X 射线的散射 按经典电磁理论: 如果入射X光是某 种波长的电磁波, 散射光的波长是 不会改变的!
光子理论对康普顿效应的解释
康普顿效应是光子和电子作弹性碰撞的 结果,具体解释如下: 1. 若光子和外层电子相碰撞,光子有一 部分能量传给电子,散射光子的能量减少,于
波动说
镜面检测
薄膜干涉
增透膜
光的干涉和衍射现象表明光确实是一种波
钢针的衍射
圆孔衍射
圆屏衍射
光电效应以及 康普顿效应等无 可辩驳的证实了 光是一种粒子.
爱因斯坦
康普顿
光是一种波,同时也是一种粒子,光具有波粒二象性
当我们用很弱的光做双缝干涉实验时,将感 光胶片放在屏的位置上,会看到什么样的照片呢? 为什么会有这种现象?
(1)有力地支持了爱因斯坦“光量子”假设; (2)首次在实验上证实了“光子具有动量” 的假设;
(3)证实了在微观世界的单个碰撞事件中, 动量和能量守恒定律仍然是成立的。
康普顿的成功也不是一帆风顺的,在他早期的 几篇论文中,一直认为散射光频率的改变是由于 “混进来了某种荧光辐射”;在计算中起先只 考虑能量守恒,后来才认识到还要用动量守恒。
戴维逊和汤姆逊因验 证电子的波动性分享1937 年的物理学诺贝尔奖金。
康普顿效应

(1)在同一散射角下,所有散射物质波长的改变 ∆λ 都 1)在同一散射角下, 在同一散射角下 是相同的。所以康普顿散射 康普顿散射只能是光子与所有物质原子 是相同的。所以康普顿散射只能是光子与所有物质原子 中的共同成分相互作用的结果。这一成分必是电子。 中的共同成分相互作用的结果。这一成分必是电子。因 此假设康普顿散射是光子与电子碰撞的结果 康普顿散射是光子与电子碰撞的结果。 此假设康普顿散射是光子与电子碰撞的结果。 (2)光子与电子碰撞后光子将沿某一方向被散射,这一 光子与电子碰撞后光子将沿某一方向被散射, 方向就是康普顿散射的方向。 方向就是康普顿散射的方向。光子在与电子碰撞中可能 损失部分能量使波长变长。 损失部分能量使波长变长。 如果光子与原子中束缚很紧的电子发生碰撞, (3)如果光子与原子中束缚很紧的电子发生碰撞,这时 相当于光子与整个原子进行碰撞。 相当于光子与整个原子进行碰撞。因为 m >> m光子
2、康普顿散射的实验规律 、康普顿散射的实验规律 I (1)在散射光线中有与入射光波长 在散射光线中有与入射光波长 相同的射线也有波长大于入射 的射线也有波长大于 相同的射线也有波长大于入射 光的射线; 光的射线 (2)在原子量较小的物质中,康普 I 在原子量较小的物质中, 在原子量较小的物质中 顿散射较强。 顿散射较强。对原子量较大的 物质,康普顿散射较弱; 物质,康普顿散射较弱; (3)波长的改变量 ∆λ = λ − λ0 波长的改变量 I 的增加而增加; 随散射角ϕ 的增加而增加 (4)在同一散射角下,所有散射 在同一散射角下, 在同一散射角下 物质波长的改变 ∆λ都是相 同的。 同的。
= hν
(2)光子与实物粒子一样,能与电子等粒子作弹性碰撞。 (2)光子与实物粒子一样,能与电子等粒子作弹性碰撞。 光子与实物粒子一样
03康普顿效应

16 – 2 光电效应 康普顿效应
第十六章 量子物理
1927诺贝尔物理学奖 诺贝尔物理学奖
• A.H.康普顿 康普顿 • 发现了X射线通过 发现了 射线通过 物质散射时, 物质散射时,波长 发生变化的现象 • 1927年吴有训(中 年吴有训( 年吴有训 国)
16 – 2 光电效应 康普顿效应
-10
16 – 2 光电效应 康普顿效应
第十六章 量子物理
3.注意几点 3.注意几点 2h 2θ ∆λ = sin m0c 2
λ0
X-ray
λ
θ
①.散射波长改变量 ∆λ 的数量级为 10− 散射波长改变量 12m,对于可见光波长 λ~10−7m,∆λ<<λ, m, m, 所以观察不到康普顿效应。 所以观察不到康普顿效应。 散射光中有与入射光相同的波长的射线, ②.散射光中有与入射光相同的波长的射线, 散射光中有与入射光相同的波长的射线 是由于光子与原子碰撞,原子质量很大, 是由于光子与原子碰撞,原子质量很大, 光子碰撞后,能量不变,散射光频率不变。 光子碰撞后,能量不变,散射光频率不变。
3) 当光子与紧束缚的内层电子相互作用时,散射光 当光子与紧束缚的内层电子相互作用时,
子的能量不变。( 因电子质量远小于原子质量) 子的能量不变。( 因电子质量远小于原子质量)
4) 因为是光子和电子的相互作用,所以 ∆λ 与散 因为是光子和电子的相互作用,
射物质无关,而与散射角有关。 射物质无关,而与散射角有关。 对于原子量小的物质,因其外层电子( 对于原子量小的物质,因其外层电子(看成自由 电子)的相对比例高,故其康普顿效应显著。 电子)的相对比例高,故其康普顿效应显著。
p=
h
λ
波长、 波长、频率是表示 波动性的物理量
康普顿效应康普顿效应教育课件

1.光的散射 光在介质中与物质微粒相互作用,因而传播 方向发生改变,这种现象叫做光的散射
2.康普顿效应
1918 - 1922年康普顿在做 X 射线通过 物质散射的实验时,发现散射线中除有 与入射线波长相同的射线外,还有比入 射线波长更长的射线,其波长的改变量 与散射角有关,而与入射线波长和散射 物质都无关。
2.光电效应实验表明:只要频率高于极限 频率,即使光强很弱也有光电流;频率低 于极限频率时,无论光强再大也没有光电 流。
3.光电效应具有瞬时性。而经典认为光能 量分布在波面上,吸收能量要时间,即需 能量的积累过程。
三.爱因斯坦的光量子假设
爱了1因启.光发斯子,坦:从他光割提普本 的出朗身 能克:就 量的是 子能由 组量一 成子个 的说个,中不频得可率到分为ν 的光的能量子为hν。这些能
表面逸出,所以不需时间的累积。
3. 从方程可以看出光电子初动能和照射 光的频率成线性关系
4.从光电效应方程中,当初动能为零时, 可得极极限频率:
爱因斯坦光子假说圆满解释了光电效应,但当 时并未被物理学家们广泛承认,因为它完全违背了 光的波动理论。
4.光电效应理论的验证
美国物理学家密立根,花了十年时间做了“光电效 应”实验,结果在1915年证实了爱因斯坦方程,h 的 值与理论值完全一致,又一次证明了“光量子”理论 的正确。
1.光控继电器
可以用于自动控
制,自动计数、自动
报警、自动跟踪等。
放大器
2.光电倍增管
可对微弱光线进行放 大,可使光电流放大 105~108 倍,灵敏度 高,用在工程、天文、 科研、军事等方面。
控制机构
K K1
K2 K4 K3
K5
A
应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 | Ψ ( r , t ) | dxdydz 1
6.已知粒子在一维矩形无限深势阱中运动,其波函数为:
1 3px Ψ ( x) cos 2a a
1 (A) . 2a 1 (B) . a
( a x a )
本题中,只有(C) 4个量子数的取值,符合规定。
8
4. 康普顿散射中,当散射光子与入射光子方向成夹角f ____________时, 散射光子的频率小得最多;当f _____________ 时,散射光子的频率与入 射光子相同.
康普顿效应:X射线通过物质 散射后波长变长的现象。
0 c (1 cos ) 2c sin 2
大学物理
教师:郑采星
课程指导课 7
第17章
§1 §2 §3 §4 §5 §6 §7 §8
量子物理基础
热辐射,普朗克的量子假设 光的粒子性 氢原子光谱,玻尔的氢原子理论 粒子的波动性 薛定谔方程 氢原子的量子力学处理 电子自旋,四个量子数 原子核外电子的壳层结构
1
第17章
基本要求
量子物理基础
了解热辐射、黑体辐射。理解普朗克量子假设。普朗克公式。理解光电效 应基本定律、爱因斯坦方程、光子假说、光的波粒二象性。了解康普顿效 应。理解原子的核模型,原子光谱的规律性。理解玻尔氢原子理论、能级。 德布罗意假设。了解电子衍射实验,理解实物粒子的波粒二象性,测不准 关系。 理解波函数及其统计解释。了解薛定谔方程,一维元限深势阱,氢 原子能量量子化,解动量量子化,空间量子化。斯特恩―盖拉赫实验,电 子自旋,四个量子数。
为康普顿常数。
2
c
c是与散射物质无关的常数,称
c 0.00241 nm
Байду номын сангаас
p,0 .
9
5.设描述微观粒子运动的波函数为(r,t),则表示__________; 须满足的条件是____________;其归一化条件是 ___________. t 时刻,粒子在空间r 处的单位体积中出现的概率,又称为概率密度。 单值、有限、连续,
教学基本内容、基本公式 1. 热辐射,黑体辐射
(1) 维恩位移定律
Tm b
b 2.897 103 m K
(2) 斯忒藩(Stefan) 玻耳兹曼定律
5.67 108 W/ (m2 K4 )
2
2. 光电效应
1 mv 2 eU S 2
爱因斯坦光子假设, 光电效应的解释
进一步计算,四种金属只有铯的红限频率在3.9×1014 Hz 7.5×1014 Hz范 围内,故应选铯。
6
A h
2. 如果两种不同质量的粒子,其德布罗意波长相同,则这两种粒子的
(A) 动量相同. (C) 速度相同. 答案:(A) 参考解答: 德布罗意物质波理论:一个以动量 P 运动而能量为 E 的实物粒子,理 (B) 能量相同. (D) 动能相同.
4
8. 薛定谔方程
2
2m ( E U ) 0 2
三维非相对论定态薛定谔方程
薛定谔方程是量子力学中的一个基本方程,也是量子力学的一个基本假 定,其正确性只能靠实验来检验。
9. 四个量子数 主量子数:
n 1, 2, 3,
l 0, 1, 2,n 1,
角量子数: 磁量子数:
答案:(C) 参考解答:
由式 E=hA 可看出,只有当入射光子的能量 h A 时才能产生光电效
应,因此,存在红限频率0,且有 v 0
A 1.9 1.6 10 19 14 4 . 6 10 (HZ), 铯的逸出功为1.9 eV, 红限频率 0 h 6.63 10 34
(1) 主量子数n (n=1,2,3.…) ,它基本上确定了核外电子的能量;
(2) 角量子数l (对于一个确定的n,l = 0,1,2…, n-1 ),对多电子原子而言,n 相同而 l 不同的各电子,其能量值也略有不同; (3) 磁量子数ml (对于一个确定的 l, ml = 0,±1,±2…±l ),,决定“轨道” 角动量的空间取向; (4) 自旋磁量子数ms (ms =±1/2)
1 ). 2 1 C ( 2, 1, 1, ). 2
A
( 2, 2, 1,
1 ). 2 1 D ( 2, 0, 1, ). 2
B
( 2, 0, 0,
原子核外电子的状态可用一组共4个量子数描述 (n, l , ml , ms ) 答案:(C) 参考解答: 2p状态的电子,n = 2, l = 1. s, p, d , f 0,1,2,3
U S k (v v0 )
h
1 mv 2 A 2
质量: m
3. 光的粒子性
光子能量:
h mc
2
h h c2 c
动量: P
h
3
4. 康普顿效应
X射线通过物质散射后波长变长的现象 ——康普顿效应
0 c (1 cos ) 2c sin 2
ml 0, 1, 2, l ,
自旋磁量子数:
5
1. 以下一些材料的逸出功为 铍 3.9 eV 铯 1.9 eV 钯 5.0eV 钨 4.5 eV
今要制造能在可见光(频率范围为3.9×1014 Hz—7.5×1014 Hz)下工作 的光电管,在这些材料中应选 (A) 钨. (B) 钯. (C) 铯. (D) 铍.
当对应于一波长为 、频率为 的波,且波长 和频率
h p
v
E h
这种与实物粒子相联系的波称为德布罗意物质波,公式称为德布罗意公式。 所以两种不同质量的粒子,其德布罗意波长相同,则这两种粒子的动量相同。
7
3. 氢原子中处于2p状态的电子,描述其量子态的四个量子数(n,l,ml,ms) 可能取的值为
5. 粒子的波动性
2
德布罗意“物质波”波长
6. 不确定度关系
h p
2
x Px
该式说明,对微观粒子的坐标和动量不可能同时进行准确的测量。如 果坐标测量得越准确,则动量测定的偏差就越大,反之亦然。
7. 概率波
| Ψ ( r , t ) |2 t 时刻,粒子在空间 r 处的单位体积中出现的概率,称概率密度。
