光栅基本方程
光栅自由光谱范围

光栅自由光谱范围(Free Spectral Range,FSR)是光栅的一个重要参数,指的是在光栅衍射光谱中相邻两个衍射峰之间的波长范围。
FSR的计算公式为:
FSR = λ / N
其中,λ是光栅的工作波长(中心波长),N是光栅的阶数(衍射级数)。
光栅衍射原理中,当入射光被光栅衍射后,不同的衍射级数会产生具有不同波长的衍射光,这些衍射光会形成一系列的衍射峰。
FSR表示了相邻两个衍射峰之间的波长差值,反映了光栅衍射的分辨能力和波长范围。
以一个光栅的工作波长为500 nm、阶数为1的情况为例,假设该光栅是一个正常反射光栅,那么它的FSR为:
FSR = 500 nm / 1 = 500 nm
这意味着在该光栅的衍射光谱中,相邻两个衍射峰之间的波长范围为500 nm。
需要注意的是,光栅的设计和工作波长、阶数等参数都会影响FSR的大小,因此在实际应用中,需要根据具体光栅的特性进行计算和分析。
光栅衍射光栅方程

λ
d
P ·
sin α E E m α
sin α I I m α
2
f
π a sin φ α λ
单缝衍射振幅曲线
相邻两缝发出的光在 P 点引起的光振动相位差为
2π δ d sin φ λ δ π d sin φ 取 β 由几何关系可得: 2 λ E φ 2 R s in β E P 2 R s in N β
(2) 主极大光强是相应位置处单缝引起光强的 52 倍。
6
2. N 缝干涉 对N 缝干涉两主极大间 有N - 1个极小, N - 2 个次极大。 衍射屏上总能量
m 1
4I 强度分布
25 I 0
I
EN
m 1
主极大的强度 I N 2 由能量守恒,主极大的
π π ( ) 最多明条纹数 2 2
B
k max
d π (sin sin ) 2
k max
d π (sin - sin ) 2
18
N k m ax k m ax 1
d cos φ1,k Δφ1,2, k kΔλ
其中 Δφ1,2,k φ2, k
kΔλ φ1,k = d cos φ1,k
...(1)
λ 波长 1 第 k 级 Δφ1,k 主极大半角宽度 Nd cos φ1,k
根据瑞利判据: 当 1, 2 , k 1, k 时刚好能分辨 由(1) 、(2) 得 讨论
N δ 2m π
2π d sin 为相邻缝光振动矢量夹角 其中 δ
N d sin m
m 1, 2 , , N 2 , N 1, N 1, N 2
大学物理下册衍射光栅
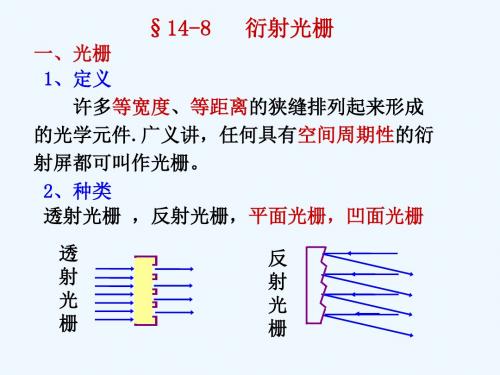
衍射角 L
P
Q
o
f
1、光栅方程
任意相邻两缝对应点在衍射角为 方向的两衍射光
到达P点的光程差为
dsin
衍射角
由双缝干涉可知,当满足
dsink
d
k 0 , 1 , 2 ,
干涉相长,在方向形成明条纹。
(1)主极大
光栅方程
dsin k (k0 ,1 ,2.....)
2
1
(2)由 sin1,可求得最高明纹级次为
2
ka b4 .8 1 6级 0 9 .6 级 9 级
m
5 1 70
例3 以氢放电管发出的光垂直照射在某光栅上,在
衍射角 410方向上看到165.62nm和241.10nm
的谱线重合,求光栅常数的最小值。
满足上面条件时出现明纹。
k=0称为中央明纹,k=1,2分别称为第一级,
第二级主极大。
(2)极小 可以证明:在两个相邻主极大之间有N-1个暗纹。
(3)次极大 相邻两极小之间有一个次极大,相邻两主极大间 有N - 2个次极大;次极大的亮度很小,实验中观 察不到。
五、衍射条纹在屏上的分布
1、主极大明纹在屏幕上的位置
§14-8 衍射光栅
一、光栅 1、定义 许多等宽度、等距离的狭缝排列起来形成
的光学元件.广义讲,任何具有空间周期性的衍 射屏都可叫作光栅。
2、种类 透射光栅 ,反射光栅,平面光栅,凹面光栅
透
反
射
射
光
光
栅
栅
3.光栅常量 a是透光部分的宽度,
b是不透光部分的宽度,
光栅常量d = a + b,是光
光栅常量和刻痕条数的关系

光栅常量和刻痕条数的关系
光栅常数d与刻痕条数N成倒数关系,即光栅常数d是指光栅上单位长度内的刻痕数,常用单位是每毫米或每厘米的刻痕数。
光栅常数与刻痕条数的关系可以用以下数学公式表示:
d = 1/N
其中,d表示光栅常数,单位为每毫米或每厘米的刻痕数,N表示刻痕条数。
这个公式说明,光栅常数越小,刻痕条数越多;反之,光栅常数越大,刻痕条数越少。
光栅常数是光栅的一个重要参数,它决定了光栅的分辨本领和测量精度。
在实际应用中,需要根据具体需求选择合适的光栅常数和刻痕条数。
光栅的原理及应用方法图解

光栅的原理及应用方法图解1. 光栅的原理光栅是一种具有周期性结构的光学元件,由一系列平行且等间距的透明槽或凹槽组成。
光栅的原理基于衍射现象,通过改变入射光的传播方向和干涉效应来实现光的分光和光谱分析。
1.1 衍射原理光栅的衍射原理是基于赖奥的法尔久衍射理论,即光在通过光栅时会发生衍射现象。
当光线通过光栅的时候,会出现多个次级波源,这些次级波源会发生干涉,使得光的传播方向发生改变。
由于光栅的周期性结构,干涉的结果会产生一系列有序的主峰和次级峰,形成衍射图样。
1.2 光栅的构造光栅通常由一系列平行的凹槽或透明槽组成,这些凹槽或透明槽之间具有固定的间距。
光栅的刻线密度决定了它的分光能力,刻线越密集,分光能力越强。
1.3 光栅方程光栅方程描述了光栅的衍射现象,它可以用来计算光通过光栅后的衍射角度和波长之间的关系。
光栅方程通常写作:nλ = d(sinθ + sinϕ)其中,n是衍射级次,λ是入射光的波长,d是光栅的间距,θ是入射角,ϕ是衍射角。
2. 光栅的应用方法光栅具有广泛的应用,特别是在光谱分析、波长选择和光学成像等领域。
以下列举了光栅的一些常见应用方法。
2.1 光谱分析光栅可以将入射光按照不同的波长进行分离,从而实现光谱的分析。
通过调节光栅的刻线密度,可以选择不同的波长范围进行分离,从而得到光的光谱信息。
光谱分析在物质分析、天文学研究等领域具有重要的应用价值。
2.2 光学成像光栅可以用于光学成像,在光学显微镜、光学望远镜等领域发挥重要作用。
通过调整光栅的参数,可以实现对特定波长的光进行成像,从而得到清晰的图像。
光栅在光学成像设备中的应用可以提高分辨率和减小像差。
2.3 波长选择光栅也可以用作波长选择器,通过选择特定的衍射级次,可以将特定波长的光分离出来。
这种波长选择器广泛应用于激光器、光通信等领域,可以实现光信号的调制和多路复用。
2.4 光栅衍射实验光栅也常用于光学教学实验中。
通过光栅的衍射现象,可以观察到明显的衍射图样,让学生直观地感受到光的波动性。
光栅
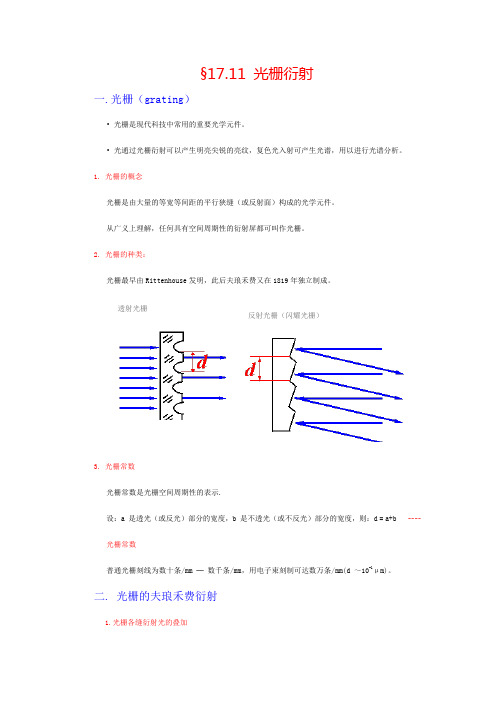
§17.11 光栅衍射一.光栅(grating)• 光栅是现代科技中常用的重要光学元件。
• 光通过光栅衍射可以产生明亮尖锐的亮纹,复色光入射可产生光谱,用以进行光谱分析。
1. 光栅的概念光栅是由大量的等宽等间距的平行狭缝(或反射面)构成的光学元件。
从广义上理解,任何具有空间周期性的衍射屏都可叫作光栅。
2. 光栅的种类:光栅最早由Rittenhouse发明,此后夫琅禾费又在1819年独立制成。
透射光栅反射光栅(闪耀光栅)3. 光栅常数光栅常数是光栅空间周期性的表示.设:a 是透光(或反光)部分的宽度,b 是不透光(或不反光)部分的宽度,则:d = a+b ----光栅常数普通光栅刻线为数十条/mm ─ 数千条/mm,用电子束刻制可达数万条/mm(d ~10-1μm)。
二. 光栅的夫琅禾费衍射1.光栅各缝衍射光的叠加衍射角相同的光线,会聚在接收屏的相同位置上。
衍射:每个缝衍射在衍射角相同的地方有相同的条纹干涉:缝与缝之间将产生干涉,这是一种多缝干涉•以双缝的夫琅和费衍射光的叠加为例来分析:干涉条纹各级主极大的强度将不再相等,而是受到了衍射的调制。
但是各个干涉主极大的位置仍由 d 决定,而没有变化。
2. 多光束干涉(multiple-beam interference)先不考虑衍射对光强的影响▲ 明纹(主极大)条件:——正入射光栅方程(k = 0,1,2,…)光栅方程是光栅的基本方程设有 N 个缝,每个缝发的光在对应衍射角θ方向的 p 点的光振动的振幅为 E p,相邻缝发的光在 p 点的相位差为△φp 点为干涉主极大时,▲ 暗纹条件:各振幅矢量构成闭合多边形,多边形外角和:由(1),(2)得:由(3)和相邻主极大间有 N-1个暗纹和 N-2个次极大。
例如: N = 4,在 0 级和 1 级亮纹之间 k' 可取1、2、3,即有三个极小:N 大时光强向主极大集中,使条纹亮而窄3. 光栅衍射(grating diffraction)(1)各干涉主极大受到单缝衍射的调制。
3.光谱仪器的色散系统—光栅

m 1
即光栅的自由光谱范围与光谱的衍射级次成反比。
例:对于500nm应用100级时,自由光谱范围仅为5nm
措施:滤光片,常用前置棱镜或光栅色散器,前置 色散器的色散方向和主仪器的色散方向互相垂直。
4、光栅的横向放大率
光栅在主截面内的横向放大率与棱镜一样,决定于 入射光束入射角余弦和衍射光束衍射角余弦之比。
3、光栅的叠级和自由光谱范围
由光栅方程,在给定光栅和入射角条件下,同一衍 射角方向可以有不同级次不同波长的光谱重叠。
d sin
1 1
2
1
2
3
1
3
级次m越大,光谱的 重叠现象越严重,没 有重叠的光谱波段范 围越小。
一个光谱级中不被其他级次光谱重叠的波段称为 自由光谱范围。
可由两个相邻的级次能够重叠的谱线波长差求出:
得到斜入射光线的光栅方程 即光栅方程的一般形式为:
d cos (sin i sin ) m
i , 分别为入射、衍射光束在主截面投影与光栅法线的夹角
为入射光束与光栅主截面夹角
Ao Bo (n n')z m
2、光栅谱线弯曲
对于狭缝中点的出射光束 0, i i0 , 0
根据光栅方程
c'常数, a刻槽宽度
u a sin
v d sin
正入射时相隔刻槽宽度的两衍射 光束相位差的一半
正入射时相隔光栅周期宽度的 两衍射光束相位差的一半
当u=v=0,即入射角与衍射角都为0时光强最大,零级主极大 的强度最大,集中了80%以上的光能量, 但零级光谱无色散, 对光谱分析无用,反而会增加杂散光,形成干扰。
sin i b , sin b' 或者 cos a , cos a'
光栅衍射光栅方程

1
sin( k
) sin k
d
sin d
k
cos k
/ Nd
Nd cos k
主极大的半角宽度与 N d 成反比,
N d 越大, k 越小,这意味着主
极大的锐度越大(条纹越细)
在给定光栅常数之后,主极大的位置就被确定 单缝衍射因子不改变主极大的位置和半角宽度
d (sin sin ) k
最多明条纹数
(π 2
π) 2
kmax
d
(sin
π 2
sin
)
k max
d
(sin
-
π 2
sin
)
N kmax kmax 1
18
例 一束波长为 480 nm 的单色平行光,照射在每毫米内有600 条刻痕的平面透射光栅上。
d sin 1,k k1 d sin 2,k k2
其中
d cos φ1,k Δφ1,2,k kΔλ
Δφ1,2,k
φ2,k
φ1,k
=
d
kΔλ cos φ1,k
...(1)
波长 1 第 k 级 主极大半角宽度
λ Δφ1,k Nd cos φ1,k
...(2)
根据瑞利判据:当 1,2,k 1,k 时刚好能分辨
暗纹公式
2π d sin 2kπ
d sin k
sin( β ) 0
I
I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光栅基本方程是什么
光栅方程是:
方程:d(sinα+sinβ)=ml(l是波长)。
如果光栅处于介质中:d*n(sinα+sinβ)=ml(n是折射率),一般情况下,光栅是在空气中的,故n=1;并且一般入射光会是正入射,则a=0,那么如果d<l,可以从光栅方程直接得到m只能是0,即不存在光栅衍射了。
含义
由大量等宽等间距的平行狭缝构成的光学器件称为光栅(grating)。
一般常用的光栅是在玻璃片上刻出大量平行刻痕制成,刻痕为不透光部分,两刻痕之间的光滑部分可以透光,相当于一狭缝。
精制的光栅,在1cm宽度内刻有几千条乃至上万条刻痕。
这种利用透射光衍射的光栅称为透射光栅,还有利用两刻痕间的反射光衍射的光栅,如在镀有金属层的表面上刻出许多平行刻痕,两刻痕间的光滑金属面可以反射光,这种光栅称为反射光栅。
