光的衍射 习题集
光的衍射习题(附答案)1

光的衍射(附答案)一.填空题1.波长λ=500nm(1nm=109m)的单色光垂直照射到宽度a=0.25mm的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹.今测得屏幕上中央明条纹之间的距离为d=12mm,则凸透镜的焦距f为3m.2.在单缝夫琅禾费衍射实验中,设第一级暗纹的衍射角很小,若钠黄光(λ1≈589nm)中央明纹宽度为4.0mm,则λ2≈442nm(1nm=109m)的蓝紫色光的中央明纹宽度为3.0mm.3.8mm,则4.时,衍射光谱中第±4,±8,…5.6.f7.8.9.λ210.X11.λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问:(1)这两种波长之间有何关系?(2)在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合?解:(1)由单缝衍射暗纹公式得a sinθ1=1λ1a sinθ2=2λ2=θ2,sinθ1=sinθ2由题意可知θ1代入上式可得λ1=2λ2(2)a sinθ1=k1λ1=2k1λ2(k1=1,2,…)sinθ1=2k1λ2/aa sinθ2=k2λ2(k2=1,2,…)sinθ2=2k2λ2/a=2k1,则θ1=θ2,即λ1的任一k1级极小都有λ2的2k1级极小与之重合.若k212.在单缝的夫琅禾费衍射中,缝宽a=0.100mm,平行光垂直如射在单缝上,波长λ=500nm,会聚透镜的焦距f=1.00m.求中央亮纹旁的第一个亮纹的宽度Δx.解:单缝衍射第1个暗纹条件和位置坐标x1为a sinθ1=λ13.9m).已(1)(2)所以x1=fλ1/ax2=fλ2/a则两个第一级明纹之间距为Δx=x2?x1=fΔλ/a=0.27cm1(2)由光栅衍射主极大的公式d sinφ1=kλ1=1λ1d sinφ2=kλ2=1λ2且有sinφ=tanφ=x/f=x2?x1=fΔλ/a=1.8cm所以Δx114.一双缝缝距d=0.40mm,两缝宽度都是a=0.080mm,用波长为λ=480nm(1nm=109m)的平行光垂直照射双缝,在双缝后放一焦距f=2.0m的透镜.求:(1)在透镜焦平面的屏上,双缝干涉条纹的间距l;(2)在单缝衍射中央亮纹范围内的双缝干涉数目N和相应的级数.解:双缝干涉条纹15.(1)(2)λ'=510.3nm(2)a+b=3λ/sinφ=2041.4nmφ'=arcsin(2×400/2041.4)nm(λ=400nm)2φ''=arcsin(2×760/2041.4)nm(λ=760nm)2''?φ2'=25°白光第二级光谱的张角Δφ=φ216.一束平行光垂直入射到某个光栅上,该光栅有两种波长的光,λ1=440nm,λ2=660nm.实验发现,两种波长的谱线(不计中央明纹)第二次重合于衍射角φ=60°的方向上,求此光栅的光栅常数d.解:由光栅衍射主极大公式得d sinφ=kλ11d sinφ2=kλ2===当两谱线重合时有φ1=φ2即====两谱线第二次重合即是=,k1=6,k2=4由光栅公式可知d sin60°=6λ1∴d==3.05×103mm17.将一束波长λ=589nm(1nm=109m)的平行钠光垂直入射在1厘米内有5000条刻痕的平面衍射(1)(2)18.30°,且第三级是缺级.(1)光栅常数(a+b)等于多少?(2)透光缝可能的最小宽度a等于多少?(3)在选定了上述(a+b)和a之后,求在衍射角–<φ<范围内可能观察到的全部主极大的级次.解:(1)由光栅衍射的主极大公式得a+b==2.4×104cm(2)若第三级不缺级,则由光栅公式得(a+b)sinφ'=3λ由于第三级缺级,则对应于最小可能的a,φ'方向应是单缝衍射第一级暗纹:两式比较,得a sinφ'=λa==8.0×103cm(3)(a+b)sinφ=kλ(主极大)a sinφ=k'λ(单缝衍射极小)(k'=1,2,3,…)因此k=3,6,9,…缺级;又∵k max==4,∴实际呈现出的是k=0,±1,±2级明纹(k=±4在π/2处不可见).19.在通常亮度下,人眼瞳孔直径约为,若视觉感受最灵敏的光波长为λ=480nm(1nm=109m),试问:(1)人眼最小分辨角是多大?(2)在教室的黑板上,画的等号两横线相距2mm,坐在距黑板10m处的同学能否看清?(要有计算过程)20.θ的两条谱λ2当k'=2时,a=d=×2.4μm=1.6μm21.某单色X射线以30°角掠射晶体表面时,在反射方向出现第一级极大;而另一单色X射线,波长为0.097nm,它在与晶体表面掠射角为60°时,出现第三级极大.试求第一束X射线的波长.解:设晶面间距为d,第一束X射线波长为λ1,掠射角θ1=30°,级次k1=1;另一束射线波长为λ2=0.097nm,掠射角θ2=60°,级次k2=3.根据布拉格公式:第一束2d sinθ1=k1λ1第二束2d sinθ2=k2λ2两式相除得λ==0.168nm.1。
5.3光的衍射基础训练(word版含答案)
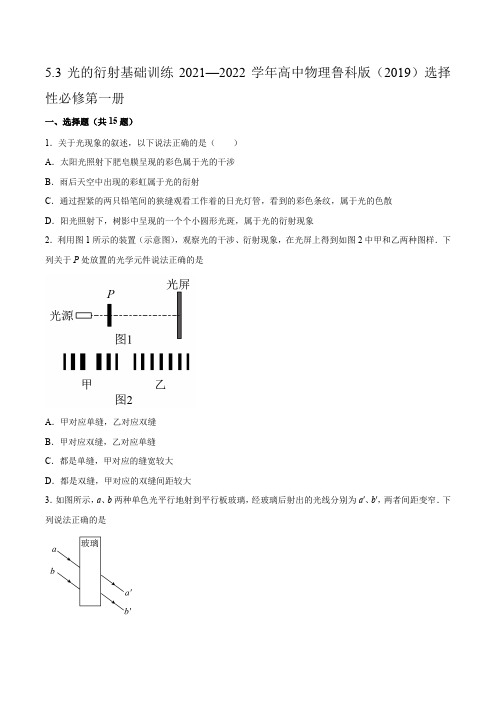
5.3光的衍射基础训练2021—2022学年高中物理鲁科版(2019)选择性必修第一册一、选择题(共15题)1.关于光现象的叙述,以下说法正确的是()A.太阳光照射下肥皂膜呈现的彩色属于光的干涉B.雨后天空中出现的彩虹属于光的衍射C.通过捏紧的两只铅笔间的狭缝观看工作着的日光灯管,看到的彩色条纹,属于光的色散D.阳光照射下,树影中呈现的一个个小圆形光斑,属于光的衍射现象2.利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样.下列关于P处放置的光学元件说法正确的是A.甲对应单缝,乙对应双缝B.甲对应双缝,乙对应单缝C.都是单缝,甲对应的缝宽较大D.都是双缝,甲对应的双缝间距较大3.如图所示,a、b两种单色光平行地射到平行板玻璃,经玻璃后射出的光线分别为a′、b′,两者间距变窄.下列说法正确的是A.光线a在玻璃中的折射率比光线b大B.光线a在玻璃中的传播速度比光线b小C.做双缝干涉实验时,用光线a产生的干涉条纹间距比b大D.光线b比a容易产生明显的衍射现象4.下列现象中属于光的衍射现象的是()A.太阳光通过透明的装满水的金鱼缸后在地面上形成彩色光带B.通过遮光板上的小孔观察远处明亮的电灯,看到电灯周围有一圈彩色光环C.油滴滴在潮湿水泥路面上形成油膜,在阳光照射下油膜上有一圈圈的彩色光环D.吹出的肥皂泡上出现彩色条纹5.关于光的现象,下列说法正确的是()A.某单色光从真空射入普通玻璃,光线传播速度将增大B.光导纤维传输信号,应用了全反射原理C.刮胡须的刀片的影子边缘模糊不清是光的干涉现象D.在镜头前加装一个偏振片可以增强入射光的强度。
6.如图所示的四种明暗相间的条纹,分别是红光、蓝光各自通过同一个双缝干涉仪器形成的干涉图样以及黄光、紫光各自通过同一个单缝形成的衍射图样(灰黑色部分表示亮纹).则在下面四个图中从左往右排列,亮条纹的颜色依次是()A.红蓝紫黄B.红紫蓝黄C.紫黄蓝红D.黄紫红蓝7.唐代储光羲的《钓鱼湾》诗句“潭清疑水浅,荷动知鱼散”中“疑水浅”是由于发生了()A.光的反射B.光的折射C.光的干涉D.光的衍射8.下列说法正确的是()A.汽车灯光夜间照着自行车“尾灯”,就变得十分明亮,是利用了光的折射B.当波源与观察者相互远离时,波源的频率会减小C.只有狭缝宽度与波长相差不多或比波长小的情况下,才发生衍射现象D.用透明的标准样板和单色光检查工件平面的平整度,利用了光的干涉9.如图,a、b两图是由单色光分别入射到a圆孔和b圆孔形成的图像,由两图可以得出()A.a图是衍射图像,a孔直径小于b孔直径B.a图是干涉图像,a孔直径大于b孔直径C.b图是衍射图像,a孔直径小于b孔直径D.b图是干涉图像,a孔直径大于b孔直径10.下列四种情形中,不属于干涉现象的是()A.图1中激光通过双缝形成等距条纹B.图2中肥皂膜的彩色条纹C.图3中圆盘后呈现泊松亮斑D.图4中检查平面的平整程度11.下列现象中,属于光的衍射现象的是()A.雨后天空出现彩虹B.通过一个狭缝观察日光灯可看到彩色条纹C.镀膜后,望远镜的镜头透入光的亮度增强D.海市蜃楼12.关于甲、乙、丙三个光学现象,下列说法正确的是()甲:激光束通过双缝产生明暗条纹乙:单色光通过劈尖空气薄膜产生明暗条纹丙:激光束通过细丝产生明暗条纹A.三个现象中产生的明暗条纹均为干涉条纹B.甲中,双缝的间距越大,条纹间距越大C.乙中,若被检查平面上有个凹陷,此处对应条纹会向右凸出D.丙中,如果屏上条纹变宽,表明抽制的丝变细了13.下列说法正确的是()A.物体做受迫振动时,驱动力频率越高,受迫振动的物体振幅越大B.医生利用超声波探测病人血管中血液的流速应用了多普勒效应C.两列波发生干涉,振动加强区质点的位移总比振动减弱区质点的位移大D.树荫下的太阳光斑大多成圆形是因为光的衍射14.下列所示的图片、示意图或实验装置图大都来源于课本,则下列判断错误是()A.甲图是薄膜干涉的图像,照相机、望远镜的镜头镀的一层膜是薄膜干涉的应用B.乙图是小孔衍射的图样,也被称为“泊松亮斑C.丙图是在平静无风的海面上出现的“蜃景”,上方是蜃景,下方是景物D.丁图是衍射图像,其最明显的特征是条纹间距不等15.在五彩缤纷的大自然中,我们常常会见到一些彩色光现象,下列现象中,属于光的衍射现象的是()A.雨后天空出现彩虹B.肥皂泡在阳光照射下呈现彩色C.雨后公路上的油膜在阳光照射下出现彩色条纹D.通过一狭缝观察日光灯看到彩色条纹二、填空题(共4题)16.光通过单缝发生衍射时,衍射条纹是一些________的条纹,中央条纹最________、最________,离中央条纹越远,亮条纹的宽度越_________,亮度越________.17.用单色平行光照射狭缝,当缝很窄时,光没有沿直线传播,它绕过了缝的边缘,传播到了_______的地方.这就是光的衍射现象。
光的衍射习题
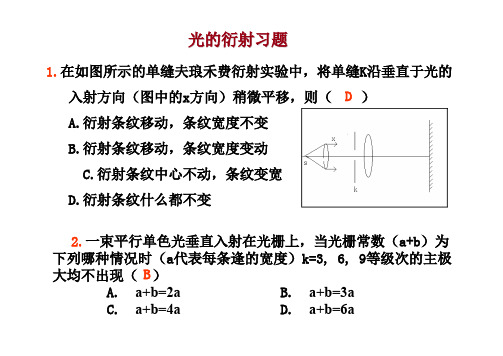
2.一束平行单色光垂直入射在光栅上,当光栅常数(a+b)为下列哪种情况时(a代表每条逢的宽度)k=3, 6, 9等级次的主极大均不出现( )A. a+b=2aB. a+b=3aC. a+b=4aD. a+b=6a1.在如图所示的单缝夫琅禾费衍射实验中,将单缝K沿垂直于光的入射方向(图中的x方向)稍微平移,则( )A.衍射条纹移动,条纹宽度不变B.衍射条纹移动,条纹宽度变动C.衍射条纹中心不动,条纹变宽D.衍射条纹什么都不变光的衍射习题B D4.如图所示,波长为λ=480nm 的平行光束垂直照射到宽度为a=0.40mm 的单缝上,单缝后透镜的焦距为 f =60cm,当单缝两边缘点A B射向P点的两条光线在P点的位相差为π 时,P点的明暗程度和离透镜焦点O的距离等于多少?A. 2, 3, 4, 5……B. 2, 5, 8, 11……C. 2, 4, 6, 8……D. 3, 6, 9, 12……3.某元素的特征光谱中含有波长分别为 和 的光谱线,在光栅光谱中,这两种波长的谱线有重叠现象,重叠处 的谱线的级次将是( )1λ=450nm 2λ=750nm 2λ D 解:由A. B 两边缘发出的光线到P 点的位相差为πδλπϕ==∆2可得其光程差为:2λδ=又因为两光线到P 点的光程差是: 是奇数个半波带所以P 点是明纹2λθδ==sin a mm.f sin f tan f OP 360=⋅=⋅≈⋅=2a λθθ5. 用可见光做单缝夫琅禾费衍射实验,已知狭缝宽度a=0.6mm ,透镜焦距f = 0.4m ,观察屏上离中心1.4 mm 出现亮条纹中心。
求:入射光的波长 ?k =3→λ=600nm; n =4→467nm由可见光波长范围,有解: 第k 级明条纹的位置θtan f x ⋅=∆第 k 级明条纹212λθ)k (sin a +=a )k (sin tan 212λθθ+=≈a)k (f tan f x 212λθ+⋅=⋅=∆()()nm .k .k ...k f a x 5021005040604150+=+⨯=+⋅∆=λ8.右下图为夫琅和费双缝衍射实验示意图, S 为缝光源, S 1、S 2为衍射缝, S 、S 1、S 2的缝长均垂直纸面。
第二章 光的衍射 习题

光的衍射一、填空题1. 衍射可分为 和 两大类。
2. 光的衍射条件是_障碍物的限度和波长可比拟____。
3. 光波的波长为λ的单色光,通过线度为L 的障碍物时,只有当___λ>>L_________才能观察到明显的衍射现象。
4. 单色平面波照射到一小圆孔上,将其波面分成半波带.若几点到观察点的距离为1m ,单色光的波长为4900Å,则此时第一半波带的半径为_________。
5. 惠更斯-菲涅尔原理是在惠更斯原理基础上,进一步考虑了__次波相干叠加______________,补充和发展了惠更斯原理而建立起来的。
6. 在菲涅尔圆孔衍射中,单色点光源距圆孔为R ,光波波长为λ,半径为ρ的圆孔露出的波面对在轴线上的距圆孔无限远处可作的半波带数为__λρR /2_______________。
7. 在菲涅尔圆孔衍射中,圆孔半径为 6 mm ,波长为6000οA 的平行单色光垂直通过圆孔,在圆孔的轴线上距圆孔6 m 处可作_____10___个半波带。
8. 在菲涅尔圆孔衍射中,入射光的强度为I 0,当轴线上P 点的光程差为2λ时,P 点的光强与入射光强的比为_____4__________。
9. 在菲涅尔圆孔衍射中,入射光的振幅为A 0,当轴线上P 点恰好作出一个半波带,该点的光强为__________20A ______。
10. 在夫琅禾费单缝衍射中,缝宽为b ,在衍射角为方向θ,狭缝边缘与中心光线的光程差为____________。
11. 在夫琅禾费单缝衍射中,缝宽为b ,波长为λ,在衍射角为方向θ,狭缝两边缘光波的位相差为____________。
12. 在夫琅禾费单缝衍射中,缝宽为b ,波长为λ,观察屏上出现暗纹的条件,衍射角θ可表示为_____________。
13. 夫琅禾费双缝衍射是___________与___________的总效果,其光强表达式中______________是单缝衍射因子,______________是双缝干涉因子。
光的衍射习题(附答案)

光的衍射(附答案)一.填空题1.波长λ = 500 nm(1 nm = 109 m)的单色光垂直照射到宽度a = mm的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹.今测得屏幕上中央明条纹之间的距离为d = 12 mm,则凸透镜的焦距f 为3 m.2.在单缝夫琅禾费衍射实验中,设第一级暗纹的衍射角很小,若钠黄光(λ1 ≈589 nm)中央明纹宽度为mm,则λ2 ≈ 442 nm(1 nm = 109 m)的蓝紫色光的中央明纹宽度为mm.3.平行单色光垂直入射在缝宽为a = mm的单缝上,缝后有焦距为f = 400 mm的凸透镜,在其焦平面上放置观察屏幕.现测得屏幕上中央明纹两侧的两个第三级暗纹之间的距离为8 mm,则入射光的波长为500 nm(或5×104mm).4.当一衍射光栅的不透光部分的宽度b与透光缝宽度a满足关系b = 3a 时,衍射光谱中第±4, ±8, …级谱线缺级.5.一毫米内有500条刻痕的平面透射光栅,用平行钠光束与光栅平面法线成30°角入射,在屏幕上最多能看到第5级光谱.6.用波长为λ的单色平行红光垂直照射在光栅常数d = 2 μm(1 μm = 106 m)的光栅上,用焦距f= m的透镜将光聚在屏上,测得第一级谱线与透镜主焦点的距离l = m,则可知该入射的红光波长λ=或633nm.7.一会聚透镜,直径为3 cm,焦距为20 cm.照射光波长550nm.为了可以分辨,两个远处的点状物体对透镜中心的张角必须不小于×105rad.这时在透镜焦平面上两个衍射图样中心间的距离不小于μm.8.钠黄光双线的两个波长分别是nm和nm(1 nm = 109 m),若平面衍射光栅能够在第二级光谱中分辨这两条谱线,光栅的缝数至少是500.9.用平行的白光垂直入射在平面透射光栅上,波长为λ1 = 440 nm的第3级光谱线将与波长为λ2 =660 nm的第2级光谱线重叠(1 nm = 109 m).10.X射线入射到晶格常数为d的晶体中,可能发生布拉格衍射的最大波长为2d.二.计算题11.在某个单缝衍射实验中,光源发出的光含有两种波长λ1和λ2,垂直入射于单缝上.假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问:(1) 这两种波长之间有何关系(2) 在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合解:(1) 由单缝衍射暗纹公式得a sinθ1= 1 λ1 a sinθ2= 2 λ2由题意可知θ1= θ2, sinθ1= sinθ2代入上式可得λ1 = 2 λ2(2) a sinθ1= k1λ1=2 k1λ2(k1=1, 2, …)sinθ1= 2 k1λ2/ aa sinθ2= k2λ2(k2=1, 2, …)sinθ2= 2 k2λ2/ a若k2= 2 k1,则θ1= θ2,即λ1的任一k1级极小都有λ2的2 k1级极小与之重合.12.在单缝的夫琅禾费衍射中,缝宽a = mm,平行光垂直如射在单缝上,波长λ= 500 nm,会聚透镜的焦距f= m.求中央亮纹旁的第一个亮纹的宽度Δx.解:单缝衍射第1个暗纹条件和位置坐标x1为a sinθ1= λx1 = f tanθ1≈ f sinθ1≈ f λ / a (∵θ1很小)单缝衍射第2个暗纹条件和位置坐标x2为a sinθ2 = 2 λx2 = f tanθ2≈ f sinθ2≈ 2 f λ / a (∵θ2很小)单缝衍射中央亮纹旁第一个亮纹的宽度Δx1 = x2x1≈ f (2 λ / a λ / a)= f λ / a=××107/×104) m=.13.在单缝夫琅禾费衍射中,垂直入射的光有两种波长,λ1 = 400 nm,λ2 = 760nm(1 nm = 109 m).已知单缝宽度a = ×102 cm,透镜焦距f = 50 cm.(1)求两种光第一级衍射明纹中心间的距离.(2)若用光栅常数a= ×10-3cm的光栅替换单缝,其它条件和上一问相同,求两种光第一级主极大之间的距离.解:(1) 由单缝衍射明纹公式可知a sinφ1= 12(2 k + 1)λ1 =12λ1(取k = 1)a sinφ2= 12(2 k + 1)λ2=32λ2tanφ1= x1/ f,tanφ2= x1/ f由于sinφ1≈ tanφ1,sinφ2≈ tanφ2所以x1= 32f λ1 /ax2= 32f λ2 /a则两个第一级明纹之间距为Δx1= x2x1= 32f Δλ/a = cm(2) 由光栅衍射主极大的公式d sinφ1= k λ1 = 1λ1d sinφ2= k λ2 = 1λ2且有sinφ = tanφ = x / f所以Δx1= x2x1 = fΔλ/a = cm14.一双缝缝距d = mm,两缝宽度都是a = mm,用波长为λ = 480 nm(1 nm =109 m)的平行光垂直照射双缝,在双缝后放一焦距f= m的透镜.求:(1) 在透镜焦平面的屏上,双缝干涉条纹的间距l;(2) 在单缝衍射中央亮纹范围内的双缝干涉数目N和相应的级数.解:双缝干涉条纹(1) 第k级亮纹条件:d sinθ = kλ第k级亮条纹位置:x1= f tanθ1≈ f sinθ1≈ k f λ / d相邻两亮纹的间距:Δx= x k +1x k = (k + 1) fλ / d k λ / d= f λ / d = ×103 m = mm(2) 单缝衍射第一暗纹:a sinθ1= λ单缝衍射中央亮纹半宽度:Δx= f tanθ1≈ f sinθ1≈ k f λ / d = 12 mm Δx0/ Δx = 5∴双缝干涉第±5级主极大缺级.∴在单缝衍射中央亮纹范围内,双缝干涉亮纹数目N = 9分别为k = 0, ±1, ±2, ±3, ±4级亮纹或根据d /a= 5指出双缝干涉缺第±5 级主极大,同样可得出结论。
人教版高中物理选修3-4同步练习:《光的衍射》(含答案)

人教版高中物理选修3-4同步练习:《光的衍射》(含答案)光的衍射同步练习一.选择题(每小题5分,共60分)1.对衍射现象的下述定性分析中,不正确的是()A.光的衍射是光在传播过程中绕过障碍物发生弯曲传播的现象B.衍射花纹图样是光波互相叠加的结果C.光的衍射现象为光的波动说提供了有力的证据D.光的衍射现象完全否定了光的直线传播结论2.下列现象哪些是光的衍射产生的()A,著名的泊松亮斑B.阳光下茂密树阴中地面上的圆形亮斑C.光照到细金属丝后在其后面屏上的阴影中间出现亮线D.阳光经凸透镜后形成的亮斑3.在一次观察光衍射的实验中,观察到如图所示的清晰的明暗相间的图样,那么障碍物应是(黑线为暗纹)()A.很小的不透明的圆板B.很大的中间有大圆孔的不透明的圆板C.很大的不透明的圆板D.很大的中间有小圆孔的不透明的圆板4.点光源照射到一个障碍物,在屏上所成的阴影的边缘部分模糊不清.产生的原因是()A.光的反射B.光的折射C.光的干涉D.光的衍射5.关于衍射的下列说法中正确的是()A.衍射现象中衍射花样的明暗条纹的出现是光干涉的结果B.双缝干涉中也存在着光的衍射现象C.影的存在是一个与衍射现象相矛盾的客观事实D.一切波都可以产生衍射6.下列现象中能产生明显衍射现象的是()A.光的波长比孔或障碍物的尺寸大B.光的波长与孔或障碍物的尺寸可相比C.光的波长等于孔或障碍物的尺寸D.光的波长比孔或障碍物的尺寸小得多7.一束平行单色光,通过双缝后,在屏上得到明暗相间的条纹,则()A.相邻的明条纹或暗条纹的间距不等B.将双缝中某一缝挡住,则屏上一切条纹将消失,而出现一亮点C.将双缝中某一缝挡住,屏上出现间距不等的明、暗条纹D.将双缝中某一缝挡住,则屏上条纹与原来一样,只是亮度减半8.用单色光做双缝干涉实验和单缝衍射实验,比较屏上的条纹,正确的是()A.双缝干涉条纹是等间距的明暗相间的条纹B.单缝衍射条纹是中央宽、两边窄的明暗相间的条纹C.双缝干涉条纹是中央宽、两边窄的明暗相间的条纹D.单缝衍射条纹是等间距的明暗相间的条纹9.关于光的干涉和衍射现象,下面各种说法中正确的是()A.光的干涉和衍射是相同的物理过程,只是干涉图样和衍射图样不同B.光的干涉只能用双缝,而光的衍射只能用单缝C.在双缝干涉过程中,也有衍射现象存在D.单缝衍射过程中也存在着干涉现象10.在用单色平行光照射单缝观察衍射现象的实验中,下列哪些说法是正确的()A.缝越窄,衍射现象越显著B.缝越宽,衍射现象越显著C.照射光的波长越长,衍射现象越显著D.照射光的频率越高,衍射现象越显著11.下列关于光的干涉和衍射的叙述中正确的是()A.光的干涉和衍射都遵循光波的叠加原理B.光的干涉说明光的波动性,光的衍射说明光不是沿直线传播C.光的干涉呈黑白间隔条纹,光的衍射呈彩色条纹D.光的干涉遵循光波叠加原理,光的衍射不遵循这一原理12.下列哪些现象是光的衍射产生的()A.阳光下茂密的树荫下地面上的圆形亮斑B.泊松亮斑C.点光源照到不透明物体上,在物体背后的光屏上形成的阴影的边缘部分模糊不清D.透过树叶的缝隙观看太阳呈现产生的光环。
光的衍射习题

四 几种衍射的情况表格(一)
光强分布 决定光强 分布因素 极值条件 极大条件 极小条件 花样特 征 特征量
菲 半波(奇 1 氏 A a a 或偶) k 1 k 圆 2 2 1 1 孔 圆孔中心轴上 k r R 衍 0 任一点的光强 射
ห้องสมุดไป่ตู้sin u
例3.波长为 的光经过常数为d 的光栅衍射时,能观察的最 高级次为什么?衍射光谱中能够得到的最大波长决定于什么? 求能使波长达 100 m 的红外线产生的衍射光谱的光栅所应 具有的光谱常数.
解: (1)由光栅方程知:
j
d sin j
d sin
与d一定时,j的最
2
3 6 10
5
2
7
可知
2
cm
2 3 1
2
七个半波带 九个半波带
4 4 . 7 10
5
cm
2 4 1
2
9
2
讨论:一般此时的半波带形形状为平行狭缝的带状,也满足 相邻两半波带上的对应点到P点的光程差为 2(即该两点 到P点的振幅 a k 相等)
1)单缝衍射中央明纹宽度 2)在该宽度内有几个光栅衍射主极大 3)总共可以看到多少条谱线 4)若将垂直入射改为入射角 i 30 的斜入射,衍射光谱的 最高级次和可看到的光谱线总数
0
解:1)由暗纹条件 对于单缝衍射第一级极小
sin 1
b sin k b sin
b
当 0 . 5 mm 时, k 1 当
1mm
时, k 4
(完整版)光的衍射习题(附答案)

光的衍射(附答案)一.填空题1.波长λ= 500 nm(1 nm = 10−9 m)的单色光垂直照射到宽度a = 0.25 mm的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹.今测得屏幕上中央明条纹之间的距离为d = 12 mm,则凸透镜的焦距f为3 m.2.在单缝夫琅禾费衍射实验中,设第一级暗纹的衍射角很小,若钠黄光(λ1 ≈589 nm)中央明纹宽度为4.0 mm,则λ2 ≈ 442 nm(1 nm = 10−9 m)的蓝紫色光的中央明纹宽度为3.0 mm.3.平行单色光垂直入射在缝宽为a = 0.15 mm的单缝上,缝后有焦距为f = 400mm的凸透镜,在其焦平面上放置观察屏幕.现测得屏幕上中央明纹两侧的两个第三级暗纹之间的距离为8 mm,则入射光的波长为500 nm(或5×10−4mm).4.当一衍射光栅的不透光部分的宽度b与透光缝宽度a满足关系b = 3a 时,衍射光谱中第±4, ±8, …级谱线缺级.5.一毫米内有500条刻痕的平面透射光栅,用平行钠光束与光栅平面法线成30°角入射,在屏幕上最多能看到第5级光谱.6.用波长为λ的单色平行红光垂直照射在光栅常数d = 2 μm(1 μm = 10−6 m)的光栅上,用焦距f= 0.500 m的透镜将光聚在屏上,测得第一级谱线与透镜主焦点的距离l= 0.1667 m,则可知该入射的红光波长λ=632.6或633nm.7.一会聚透镜,直径为3 cm,焦距为20 cm.照射光波长550nm.为了可以分辨,两个远处的点状物体对透镜中心的张角必须不小于2.24×10−5rad.这时在透镜焦平面上两个衍射图样中心间的距离不小于4.47μm.8.钠黄光双线的两个波长分别是589.00 nm和589.59 nm(1 nm = 10−9 m),若平面衍射光栅能够在第二级光谱中分辨这两条谱线,光栅的缝数至少是500.9.用平行的白光垂直入射在平面透射光栅上,波长为λ1 = 440 nm的第3级光谱线将与波长为λ2 =660 nm的第2级光谱线重叠(1 nm = 10−9 m).10.X射线入射到晶格常数为d的晶体中,可能发生布拉格衍射的最大波长为2d.二.计算题11.在某个单缝衍射实验中,光源发出的光含有两种波长λ1和λ2,垂直入射于单缝上.假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问:(1) 这两种波长之间有何关系?(2) 在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合?解:(1) 由单缝衍射暗纹公式得a sinθ1= 1 λ1a sinθ2= 2 λ2由题意可知θ1 = θ2, sinθ1= sinθ2代入上式可得λ1 = 2 λ2(2) a sinθ1= k1λ1=2 k1λ2(k1=1, 2, …)sinθ1= 2 k1λ2/ aa sinθ2= k2λ2(k2=1, 2, …)sinθ2= 2 k2λ2/ a若k2= 2 k1,则θ1= θ2,即λ1的任一k1级极小都有λ2的2 k1级极小与之重合.12.在单缝的夫琅禾费衍射中,缝宽a = 0.100 mm,平行光垂直如射在单缝上,波长λ= 500 nm,会聚透镜的焦距f = 1.00 m.求中央亮纹旁的第一个亮纹的宽度Δx.解:单缝衍射第1个暗纹条件和位置坐标x1为a sinθ1= λx 1 = f tanθ1≈f sinθ1≈f λ/ a (∵θ1很小)单缝衍射第2个暗纹条件和位置坐标x2为a sinθ2 = 2 λx 2 = f tanθ2≈f sinθ2≈ 2 f λ/ a (∵θ2很小)单缝衍射中央亮纹旁第一个亮纹的宽度Δx1= x2− x1≈f (2 λ/ a −λ/ a)= f λ/ a=1.00×5.00×10−7/(1.00×10−4) m=5.00mm.13.在单缝夫琅禾费衍射中,垂直入射的光有两种波长,λ1 = 400 nm,λ2 = 760nm(1 nm = 10−9 m).已知单缝宽度a = 1.0×10−2 cm,透镜焦距f = 50 cm.(1)求两种光第一级衍射明纹中心间的距离.(2)若用光栅常数a= 1.0×10-3cm的光栅替换单缝,其它条件和上一问相同,求两种光第一级主极大之间的距离.解:(1) 由单缝衍射明纹公式可知a sinφ1=12(2 k + 1)λ1=12λ1(取k = 1)a sinφ2=12(2 k + 1)λ2=32λ2tanφ1= x1/ f,tanφ2= x1/ f由于 sin φ1 ≈ tan φ1,sin φ2 ≈ tan φ2 所以 x 1 = 32 f λ1 / ax 2 = 32f λ2 / a则两个第一级明纹之间距为Δx 1 = x 2 − x 1 = 32f Δλ / a = 0.27 cm(2) 由光栅衍射主极大的公式d sin φ1 = k λ1 = 1 λ1 d sin φ2 = k λ2 = 1 λ2且有sin φ = tan φ = x / f所以Δx 1 = x 2 − x 1 = f Δλ / a = 1.8 cm14. 一双缝缝距d = 0.40 mm ,两缝宽度都是a = 0.080 mm ,用波长为λ = 480 nm (1 nm = 10−9 m )的平行光垂直照射双缝,在双缝后放一焦距f = 2.0 m 的透镜.求:(1) 在透镜焦平面的屏上,双缝干涉条纹的间距l ;(2) 在单缝衍射中央亮纹范围内的双缝干涉数目N 和相应的级数. 解:双缝干涉条纹(1) 第k 级亮纹条件:d sin θ = k λ第k 级亮条纹位置:x 1 = f tan θ1 ≈ f sin θ1 ≈ k f λ / d 相邻两亮纹的间距:Δx = x k +1 − x k = (k + 1) f λ / d − k λ / d = f λ / d = 2.4×10−3m = 2.4 mm(2) 单缝衍射第一暗纹:a sin θ1 = λ单缝衍射中央亮纹半宽度:Δx 0 = f tan θ1 ≈ f sin θ1 ≈ k f λ / d = 12 mm Δx 0 / Δx = 5∴ 双缝干涉第 ±5级主极大缺级.∴ 在单缝衍射中央亮纹范围内,双缝干涉亮纹数目N = 9 分别为k = 0, ±1, ±2, ±3, ±4级亮纹或根据d / a = 5指出双缝干涉缺第 ±5 级主极大,同样可得出结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 光的衍射5.1光源S 以速度V 沿一方向运动,它发出的光波在介质中的传播速度为v ,试用惠更斯原理证明:当V>v 时,光波具有圆锥形波前,其半圆锥角为1sin ()v V α-=5.2点光源向平面镜发出球面波,用惠更斯作图法求出反射波的波前。
2题图5.3试从场论中的散度公式*F d Fdv σ=∇⎰⎰⎰⎰⎰导出格林公式(5-6)。
[提示:令F= ~~G E ∇ 。
并利用恒等式~~~~~2()G E G E G E ∇∇=∇∇+∇±]5.4对题5.2图中所示的平面屏上孔径∑的衍射,证明:若选取格林函数 ~exp()exp(')'ikr ikr G r r =- (r=r ’,p 和p ’对衍射屏成镜像关系),则p 点的场值为~exp()exp()()cos(,)A ikl ikr E p n r d i l r σλ=∑⎰⎰5.5在图中,设 2∑ 上的场是由发散球面波产生的,证明它满足索末菲辐射条件。
5题图5.6波长λ=500nm 的单色光垂直入射到边长为3cm 的方孔,在光轴(它通过方孔中心并垂直方孔平面)附近离孔z 处观察衍射,试求出夫琅和费衍射区的大致范围。
5.7求矩孔夫琅和费衍射图样中,沿图样对角线方向第一个次极大和第二个次极大相对于图样中心的强度。
5.8将长为500nm 的平行光垂直照射在宽度为0.025mm 的单缝上,以焦距为50cm 的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;(3)第一亮纹和第二亮纹相对于中央亮纹的强度。
5.9.证明平行光斜入射到单缝上时,单缝夫琅和费衍射强度为0sin[(sin sin )]{}(sin sin )a i I I a i πθλπθλ-=- 式中,I 0央亮纹中心强度,a 是缝宽,θ 是衍射角,i 是入射角(见图)。
(2)中央亮纹的角半宽度为cos a i λθ∆=9题图5.10在不透明细丝的夫琅和费衍射图样中,测得暗条纹的间距为1.5mm ,所用透镜的焦距为300mm, 光波波长为632.8nm 。
问细丝直径是多少?5.11用物镜直径为4cm 的望远镜来观察10km 远的两个相距0.5m 的光源。
在望远镜前置一可变宽度的狭缝,缝宽方向与两光源连线平行。
让狭缝宽度逐渐减小,发现当狭缝宽度减小到某一宽度时,两光源产生的衍射像不能分辨,问这时狭缝宽度为?(设光波波长为550nm.)5.12试利用 第五章 5-5的结果,导出外径和内径分别为a 和b 的圆环的夫琅和费衍射强度公式。
并求出当b=a/2时。
(1)圆环衍射与半径为a 的圆孔衍射图样的中心强度之比;(2)圆环衍射图样第一个暗环的角半径。
12题图5.13用望远镜观察远处两个等强度的发光点S1和S2。
当S1的像(衍射图样)中央和S2的像的第一个强度零点相重合时,两像之间的强度极小值与两个像中央强度之比是?5.14(1)一束直径为2mm 的氦氖激光(λ=632.8nm )自地面射向月球,已知地面和月球相距3.76*103km ,问在月球上得到的光斑有多大?(2)如果用望远镜倒用作为扩束器将该光束扩展成直径为4m 的光束,该用多大倍数的望远镜?将扩束后的光束再射向月球,在月球上的光斑为多大?5.15人造卫星上的宇航员声称,他恰好能够分辨离他100km 地面上的两个点光源。
设光波的波长为550nm ,宇航员眼瞳直径为4mm ,这两个点光源的距离是?5.16若望远镜能分辨角距离为3*10 -7 rad 的两颗星,它的物镜的最小直径是?同时为了充分利用望远镜的分辨本领,望远镜应有多大的放大率?5.17若要使照相机感光胶片能分辨2μm 的线距,(1)感光胶片的分辨本领至少是每毫米多少线;(2)照相机镜头的相对孔径D/f 至少有多大?(设光波波长为550nm 。
)5.18一台显微镜的数值孔径为0.85,问(1)它用于波长λ= 400nm 时的最小分辨距离是多少?(2)若利用油浸物镜使数值孔径增大到1.45,分辨本领提高了多少倍?(3)显微镜的放大率应设计成多大?(设人眼的最小分辨角为1’.)5.19一块光学玻璃对谱线435.8nm 和546.1nm 的折射率分别为1.6525和1.6245。
试计算用这种玻璃制造的棱镜刚好能分辨钠D 双线时底边的长度。
钠D 双线的波长为589.0nm 和589.6nm 。
5.20在双缝夫琅和费衍射实验中,所用光波波长为λ=632.8nm ,透镜焦距为f=50cm ,观察到两相邻亮条纹之间的距离为e=1.5mm ,并且第4级亮纹缺级。
试求(1)双缝的缝距和缝宽;(2)第1,2,3级亮纹的相对强度。
5.21在双缝的一个缝前贴一块厚0.001mm ,折射率为1.5的玻璃片,设双缝间距为1.5m ,缝宽为0.5 m ,用波长为500nm 的平行光垂直入射,分析该双缝的夫琅和费衍射图样。
5.22一块光栅的宽度为10cm ,每毫米内有500条缝,光栅后面放置的透镜焦距为500mm 。
问(1)它产生的波长λ=632.8nm 的单色光的1级和2级谱线的半宽度为?(2)若入射光是波长为632.8nm 和波长与之相差0.5nm 的两种单色光,它们的1级和2级谱线之间的距离是多少?5.23计算光栅(光栅常数)是缝宽5倍的光栅的第0,1,2,3,4,5级亮纹的相对强度。
并对N=5的情形画出光栅衍射的强度分布曲线。
5.24设计一块光栅,要求(1)使波长λ=600nm 的第2级谱线的衍射角,(2)色散尽可能大,(3)第3级谱线缺级,(4)在波长λ=600nm 的第2级谱线处能分辨0。
02的波长差。
在选定光栅的参数后,问在透镜的焦面上只可能看到波长600nm 的几条谱线?5.25为在一块每毫米1200条刻线的光栅的1级光谱中分辨波长为632.8nm 的一束氦氖光的模结构(两个模之间的频率差为450MHz ),光栅需要有多宽?5.26证明光束斜入射时,(1)光栅衍射强度分布公式为220sin sin ()()a N I I a ββ= 式中,(sin sin ),(sin sin )a d i i ππαθβθλλ=-=- θ 为衍射角,i 为入射角(见图),N 为光栅常数。
(2)若光栅常数d>>λ ,光栅形成主极大的条件可以写为(cos )()d i i m θλ-= m=0,±1,±2……26题图5.27有一多缝衍射屏如图所示,缝数为2N,缝宽为a,缝间不透明部分的宽度依次为a和3a,试求正入射情况下,这一衍射屏的夫琅和费衍射强度分布公式。
27题图5.28一块每毫米1000个刻槽的闪耀光栅,以平行光垂直于槽面入射,一级闪耀波长为546nm。
问(1)光栅的闪耀角为?(2)若不考虑缺级,有可能看见546nm的几级谱线;(3)各级谱线的衍射角是多少?5.29一块闪耀光栅宽260mm,每毫米有300个刻槽,闪耀角77012’。
(1)求光束垂直于槽面入射时,对于波长500nm的光的分辨本领;(2)光栅的自由光谱范围有多大?(3)试问空间间隔为1cm,精细度为25的法布里-珀罗标准具的分辨本领和自由光谱范围作一比较。
5.30一透射式阶梯光栅由20块玻璃板叠成,板厚为1cm,玻璃折射率n=1.5,阶梯高度为0.1cm,以波长500nm的单色光垂直照射,试计算(1)入射光方向上干涉主极大的级数;(2)光栅的角色散和分辨本领(假定玻璃折射率不随波长变化)5.31 一块位相光栅如图所示,在透明介质薄板上做成栅距为d 的刻槽,刻槽的宽度与凸阶宽度相等,且都是透明的。
设刻槽深度为t,介质折射率为n,平行光正入射。
试导出这一光栅的夫琅和费强度分布公式,并讨论它的强度分布图样。
31题图5.32 如图所示, 是单色点光源S发出的光波波面。
试利用基尔霍夫衍射公式(5-19),计算相对于考察点P 划分的波面上第j 个波带在P 点产生的复振幅。
设波面的半径为 R ,S 到P 的距离为R+r 0.32题图5.33 如图所示,单色点光源(波长λ=500nm )安放在离光阑1m 远的地方,光阑上有一个内外半径分别为0.5mm 和1mm 的通光圆环。
考察点P 离光阑1m (SP 连线通过圆环中心,并垂直于圆环平面)。
问在P 点的光强度和没有光阑时的光强度之比是多少?33题图5.34 波长λ=563.3nm 的平行光正入射直径D=2.6mm 的圆孔,与孔相距r 0=1m 处放一屏幕。
问(1)屏幕上正对圆孔中心的P 点是亮点还是暗点?(2)要使P 点变成与(1)相反的情况,至少把屏幕向前(同时求出向后)移动多少距离?5.35 单位振幅的单色平面波垂直照明半径为1的圆孔,试利用式(5-24)证明,圆孔后通过圆孔中心的光轴上的点的光强分布为24sin 2I zπλ= 式中,z 为考察点到圆孔中心的距离。
5.36 一波带片离点光源2m ,点光源发光的波长λ=546nm ,波带片成点光源的像于2.5m 远的地方,问波带片第一个波带和第二个波带的半径是多少?5.37 一波带片主焦点的强度约为入射光强度的310倍,在400nm 的紫光照明下的主焦距为81cm 。
问(1)波带片应有几个开带;(2)波带片半径是多少?5.38 两个同频的平面波同时射向一张全息底板(设为xoy 平面),它们的方向余弦分别为(1cos α,1cos β,1cos γ)和(2cos α,2cos β,2cos γ),振幅分别为A1和A2。
(1)写出全息底板上干涉条纹强度分布的表达式;(2)说明干涉条纹的形状;(3)写出x 方向和y 方向上条纹间距的表达式。
5.39 在图所示的全息记录装置中,若060O= -θR ,是证明全息图上干涉条纹的间距为 2sin()2e λθ= 式中,θ是两平行光束的夹角。
当采用氦氖激光记录(λ=632.8nm )。
并且θ是010和060,条纹间距分别是多少?39题图5.40 试对于上题条件下所获得的全息图,讨论分别采用下面两种再现照明方法时衍射光波的变化:(1)再现光波的波长和方向与参考光波相同;(2)再现光波(波长仍与参考光波相同)正入射于全息图。
5.41 如图a 所示,全息底板H 上记录的是参考点源S R (坐标为x R , y R ,z R )和物电源S O (坐标为x O ,y O ,z O )发出的球面波(波长为λ1)的干涉图样。
(1)写出H 平面上干涉条纹强度分布的表达式;(2)记录下的全息图,若以位于点(x p ,y p ,z p )的点光源发出的球面波(波长为λ2)来再现(图b ),试决定像点的位置坐标。
41题图5.42波长为500nm 的平行光垂直照在宽度为0.025mm 的单缝上,以焦距为50cm 的会聚透镜将衍射光聚焦于焦平面上进项观察,求单缝衍射中央亮纹的半宽度。
