李萨如图形
李萨如图形PPT课件全

简谐运动。李萨如图形是物理学的重要内容之一,在工程技术领域也有很
重要的应用。利用李萨如图形可以测量未知振动的频率和初相位,掌握李
萨如图形的形成过程有很重要的意义。因而动态显示李萨如可以深入理解
其形成过程。
-
1
假定形成李萨如图形的两个简谐运动,一个在X轴上,一个在Y 轴上,它们的运动方程为(假设它们的振幅相等):它们的合运动 轨迹就是李萨如图形。为了能够形象地描述李萨如图形的形成过程, 一般是把X轴和Y轴上的简谐运动分别用旋转矢量图来描述,如图1 所示。由上式计算出不同时刻的质点的坐标(x,y),依次连接这 些点,得到的图形就是李萨如图形。
-
2
-
3
嫦娥二号在L2点沿李萨如轨道飞行
-
4
示波器
-
5
X Y的比例不一样会出现各种图形哦~
-
6
-
7
实验1用“李萨如图形法”测量简谐振动的频率

实验一 简谐振动幅值测量试验一 实验目的1、了解并掌握简谐振动信号位移、速度、加速度幅值之间的关系。
2、学会用速度传感器测量简谐振动位移、速度、加速度的幅值。
3、正确理解和分析各种计算值与测试值之间的误差及其产生的原因。
二 实验原理振动体的位移、速度、加速度是系统振动的重要参数,正确测试其值对探索振动参量之间关系、全面了解和掌握振动规律有着重要的作用。
它们的值可用位移传感器、速度传感器或加速度传感器来直接测取,也可根据位移、速度、加速度的关系,用一种传感器来进行测量,或者利用测振仪的微分、积分电路来测量。
对于位移、速度、加速度三个振动参量,只要知道其中一个,就可以通过微分和积分变换求出另外两个振动参量。
在工程实践中,对有的参量,由于受条件限制无法测得时,可以通过参量变换求得。
另外,当三个振动参量的时间过程都测得时,可以通过参数变换进行相互检验。
将实测波形与参数变换得到的波形比较,进一步分析测量精度和误差范围,为测试波形的基线修正和测试结果的修正提供条件。
设某一简谐振动其固有园频率为n ω,初相位为0ϕ,该振动的位移、速度、加速度分别计为x 、v 、a 。
若)sin(0ϕω+=n B x (1-1)则)2sin( )cos(00πϕωωϕωω++=+==n n n n B B xv (1-2))sin( )sin(0202πϕωωϕωω++=+-==n n n n B B x a (1-3)由(1-1)~(1-3)式可知,速度v 、加速度a 是与位移x 具有相同频率的简谐振动,但是其相位角分别超前2/π或π。
如果已知加速度a ,也可以通过积分求得速度v 及位移x变化规律。
位移x 、速度v 和加速度a 的相应的幅值分别记为B 、V 、A ,则其幅值关系为B f B V n 2πω== (1-4)B f B A n 2224πω== (1-5)上式中:f 为简谐振动的频率。
本实验主要由激振信号源通过电动式激振器对振动实验台上的简支梁施加谐激振,用速度传感器测量简支梁上某一位置在不同激振频率条件下的振动响应的位移、速度和加速度的幅值,这相当于测量简支梁在谐激振作用下该位置的稳态振动响应的位移、速度和加速度的幅值。
matlab研究李萨如图形

关于李萨如图形的探讨nx 指的是假想的水平线跟图形的交点数,ny 指的是假想的垂直线跟图形的交点数。
当fy/fx 8,即∞ 所以fy 如果越大的话,横向圆的数量就越多,反之,纵向的圆的数量就越多。
【借助matlab 编程】>> clear>>A1=10;A2=12; %设定两振幅>>delda=pi/2; %设定相位差>>phi1=0; phi2=phi1+delda; %设定两振动的相位>>k=10; %设定两频率的比例>>w1=1;w2=k*w1; %设定两振动的频率>>t=1:.01:50; %设定计算时间>>x=A1*cos(w1*t+phi1); %计算x 方向的位移>>y=A2*cos(w2*t+phi2); %计算y 方向的位移>>plot(x,y) %描绘李萨茹图形>> xlabel('x');>> ylabel('y');>> title('李萨如图形 fy:fx=10:1');fy=10,fx=1 △φ=0fy=10,fx=1 △φ=π/4fy=10,fx=1 △φ=π/2fy=100,fx=1 △φ=0fy=100,fx=1 △φ=π/4fy=100,fx=1 △φ=π/2fy=10000000,fx=1 △φ=0fy=10000000,fx=1 △φ=pi/4fy=10000000,fx=1 △φ=π/2fy=500,fx=50 △φ=0fy=500,fx=50 △φ=π/4fy=500,fx=50 △φ=π/2fx=10,fy=1 △φ=0fx=10,fy=1 △φ=π/4fx=10,fy=1 △φ=π/2fx=50,fy=1 △φ=0fx=50,fy=1 △φ=π/4fx=50,fy=1 △φ=π/2fx=500,fy=50 △φ=0fx=500,fy=50 △φ=π/4fx=500,fy=50 △φ=π/2。
李萨如图形的相关研究

李萨如图形的相关研究姓名:XXX班级:XXX学号:XXX指导教师:XXX班级序号:XXX摘要:探究李萨茹图形形成的原因以及影响其形状的因素,并通过matlab软件模拟出李萨茹图形,给出其原程序,及其相关图形;利用示波器和信号源,演示出一个李萨茹图形,探究李萨如图形的应用并设计出一个简易演示李萨茹图形的教具,并做简单说明。
关键词:李萨如图形;matlab;应用;设计教具1、李萨如图形简介(1)形成原因两个相互垂直的简谐振动,当他们的频率比是整数比时,合振动的轨迹是稳定的闭合曲线,此时就形成了李萨如图形。
(2)影响李萨如图形形状的因素:设两个互相垂直的简谐运动的方程为x=A1cos(2πn1t+Φ1)y=A2cos(2πn2t+Φ2)①设n1/n2=m1/m2(m1、m2是互质的整数),李萨如图形的形状由分振动振幅、频率比和cos(m1Φ1-m2Φ2)确定。
②萨如图形具有对称性。
设n1/n2=m1/m2(m1、m2是互质的整数)。
当m1为为偶数时,图形关于x轴对称;当m2为偶数时,图形关于y轴对称;当m1、m2均为奇数时,图形关于原点对称。
③李萨如图形具有周期性。
取a= =Φ2-Φ1当Φ1为定值时,图形随Φ2变化的周期是2π/m1;当Φ2取定值时,图形随Φ1变化的周期为2π/m2;a取定值,图形随Φ1或Φ2变化的周期为|2π/(m1-m2)|。
2、MATLAB制图①一个振动初相位为零时的振动合成设wx和wy,为x、y两个方向的振动频率.先讨论简单情况:不妨设y方向初相位Φy为零,则初相位差Φx-Φy=Φx程序设计:wx=input(‘wx=’);wy=input(‘wy=’);nx=input(‘nx=’);t=0:0.02:200;x=cos(wx*t+nx*3.1415926);y=cos(wy*t);plot(x,y)图像:②两个振动初相位均不为零时的振动合成程序设计:wx=input(‘wx=’);wy=input(‘wy=’);nx=input(‘nx=’);ny=input(‘ny=’);t=0:0.02:200;x=cos(wx*t+nx*3.1415926);y=cox(wy*t+ny*3.1415926);plot(x,y)图像:首先绘制几组不同y初相位条件下的图形,如图所示.为减少频率比的特殊性,选取频率比为3:2。
实验制作用激光显示李萨如图形
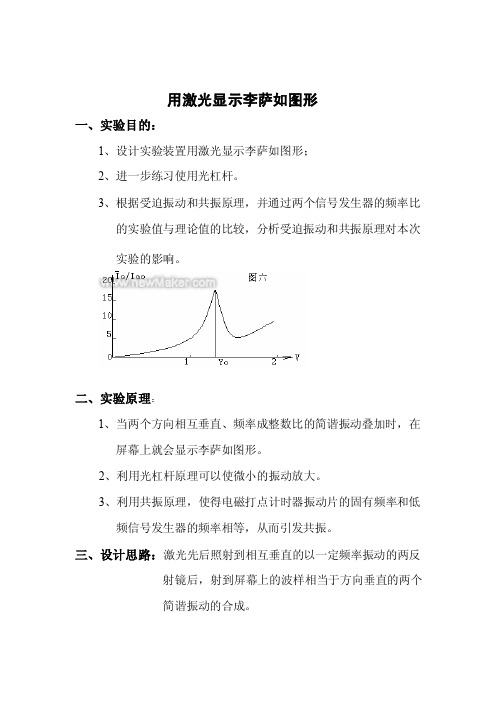
用激光显示李萨如图形一、实验目的:1、设计实验装置用激光显示李萨如图形;2、进一步练习使用光杠杆。
3、根据受迫振动和共振原理,并通过两个信号发生器的频率比的实验值与理论值的比较,分析受迫振动和共振原理对本次实验的影响。
二、实验原理:1、当两个方向相互垂直、频率成整数比的简谐振动叠加时,在屏幕上就会显示李萨如图形。
2、利用光杠杆原理可以使微小的振动放大。
3、利用共振原理,使得电磁打点计时器振动片的固有频率和低频信号发生器的频率相等,从而引发共振。
三、设计思路:激光先后照射到相互垂直的以一定频率振动的两反射镜后,射到屏幕上的波样相当于方向垂直的两个简谐振动的合成。
四、实验器材:电磁打点计时器两个、半导体激光器或氦氖激光器1台(半导体激光器效果更好,优先考虑;注意激光不要直射眼睛)、固2、激光照射到反光镜上的入射角的调整;3、整个实验装置的设计与调试。
4、如何使屏幕上的李萨如图形变得稳定。
六、实验内容:(1)取两个电磁打点计时器,去掉打点针与塑料罩,在振动片的振动端贴上反射镜。
(2)测定两个打点计时器振动片的固有频率(基频)。
将打点计时器与低频信号发生器相连接,逐渐改变信号发生器的频率,当振动片的振幅出现最大值时,此时信号发生器的频率就是振动片的固有频率。
如果两个打点计时器的固有振动频率不等,可改变振动片的长度或加上配重,使其振动频率相等。
(3)将两个打点计时器相互垂直放置,使激光照射在第一个打点计时器振动片的反射镜上后,经反射照射在第二个打点计时器振动片的反射镜上,反射后再投射在远处屏上。
(4)把两台低频信号发生器的输出端分别与两个打点计时器相连接。
开启发生器使振动条振动,发生器的输出频率分别与振动片的固有频率相同。
(5)演示二维同频(频率比为1:1)振动合成:李萨如图形激光演示装置调制好以后,平放在桌上,激光照射在远处屏上。
首先,打开X方向振动开关,演示X方向振动;然后,关闭X方向振动开关,打开Y方向振动开关,演示Y方向振动,最后打开X、Y方向振动开关,演示两个相互垂直方向的简谐振动合成。
对李萨如图形的探讨

卜’ ` ’ “
’
、
门
a
l
几
曰
”
`
『
`
`
’
F
谬
~
’
、
~ O
_
八
,
L
k
.z I _ 一。 k ~ 1
, ’ 一
n
_
__
m
,
则 ”
、J
口
_ _ 八 一心令 、
一 ’
_
a
,
且
_ 一
井
L ,
`
_ _
, ,
份 2
k一 1
k
`
~ O 则
,
“:
~
一
等等 要
乙
”
文
,
参
,
. .
考
献
1 98 2
.
漆 安 填 杜 掸 英 力 学 基 础 北 京 高 等教育 出版 社
A
一e
o s
Za t ,
A
Ze
o s
(。
t
一
汀
、
牙
少
一 八
25,
“
C l , L
其 速 度分 量 可 用 坐 标 对 时 间导 数表 示
、 V l X
. ` 、 ,
= 一 ~
A
Z
田 ZA 一
s
田 in Z
t
t
忱 2 /
`
0
5
田
,
当 2以 ~
k ;r
k 一 (
0
,
1
,
2
`
,
… ) 时 毖一
,
李萨如图

李萨如图形的应用摘要:李萨如图形是波与波叠加的结果,通过对波形的观察,可以比较出两组波的差异,在已知一组波的相关数据的情况下可以得出另一组波的相关数据,根据这些数据又可以得出与那一组波的相关的一些数据等,从而求出所需数据,如求频率,电阻,电阻的变化情况,容抗阻抗,电压大小……关键词:李萨如图形,对比,数据1.李萨如图的形成原理李萨如图形就是利用一个示波器,在X轴和Y轴上输入不同的正弦信号,把他们有机的叠加起来所形成的一种图形,如图所示,把X轴的信号换成正弦信号,就形成了李萨如图形。
由于输入信号是加在X方向偏转电压和Y方向的偏转电压上,从电子枪里头喷出的电子就会在这两个电压的影响下,向不同的方向偏转,然后打在屏上,显示出不同的波形。
所以,通过对波形的研究,我们就可以了解到两个方向所加的信号得特征,如果已经知道一个方向的型号特征,就可以通过对比,得出另一个信号的特征,再根据这些特征来求出一些需要的值。
2.影响李萨如图的因素要想通过一个信号的特征推出另一个信号特征,那么就必须了解影响李萨如图形的一些关键因素,通过比较这些因素,才能得出结果。
通常情况下能够影响图形形状的有输入信号的振幅大小,两个输入信号的初始相位的不同,两个信号的频率的不同等。
2.1频率对李萨如图的影响李萨如图形的周期与频率是分不开的,设一个方向上的频率为fx,另一个的为fy,那么李萨如图形的周期T即为1/fx和1/fy的最小公倍数,因为在T时间内,X方向和Y方向都经过了几个完整的周期,之后又重头开始,和刚开始时一样。
有时示波器调出的波形会移动,就是因为周期没有调好的缘故。
根据对李萨如图形一个周期的测量,在已知一个信号的频率的情况下,就可求出另一个信号的频率;李萨如图形本身还具有一个特点,图形边界与水平方向的交点和竖直方向的交点的比等于fy/fx,如图,因为图形的最低点即为Y方向信号的波谷,图形最左端与竖直的交点即为X方向信号的波谷,在一个李萨如图形周期T内,有几个交点,则对应X方向和Y方向信号就经历了多少个周期,正好与fy/fx相吻合。
对利萨如图形的探究

对利萨如图形的探究徐奕(04011512)(东南大学,南京 211189)摘要:示波器是一种用途广泛的电子测量仪器,它能对电压信号的波形进行直接的观察和定量分析,示波器分两种,其中模拟示波器长期以来被广泛应用来观察常规波形,对周期信号的观察与测量尤为适用,因此也用来观察利萨如图形。
关键词:利萨如图形频率比示波器The study of Lissajou figureXu Yi(Southeast University, Nanjing, 211189)Abstract: The oscilloscope is a widely used electronic measuring instrument.It can directly observe and quantitatively analyze the waveform of the voltage signal.Between the two kind of oscilloscopes,the analog oscilloscope has long been widely used to observe regular waveform,particularly applicable to the observation of the periodic signals.So it is often used to observe the Lissajou figure.Abstract: Lissajou figure ; the rate of frequency ; oscilloscope1利萨如图形概念1.1定义一个质点同时在X轴和Y轴上作简谐运动,形成的图形就是李萨如图形。
具体来说,相互垂直的两个简谐振动,如果振动频率相同,则可形成稳定的椭圆曲线,而对于振动频率不同的垂直振动叠加,一般合振动的轨迹不能形成稳定的图案,但如果两振动频率成整数比,则合振动的轨迹为封闭曲线,称为利萨如图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探
究
李
萨
如
图
形
环境科学10-2班
李洋旸2010012208
探究李萨如图形
环科10-2班李洋旸2010012208
李萨如(Jules Antoine Lissajous),法国数学家,生卒:1822年3月4日~1880年6月24日。
物理、工程中常用的李萨如图形便是以他的名字命名的。
在众多的创造中,李萨如发明了李萨如仪器,一种用来绘制李萨如图形的装置。
在这个装置中,一束光被一面固定在音叉上的镜子反射,然后再被第二面固定在音叉上的镜子反射,两个音叉震动方向互相垂直,两者音高也经常被设置为不同,以取得不同的谐振频率。
光束最后被打在墙上,得到了我们如今所称的李萨如图形。
这项发明是之后许多仪器的基础,如谐振仪(谐振记录仪)。
定义
一个质点同时在X轴和Y轴上作简谐运动,形成的图形就是李萨如图形。
形成李萨如图形的另一种方法:把两个圆斜着放,在两个圆上任取两点,将这两点向右上角做垂线,交于一点。
然后将这两个点在圆上运动,点也随之运动。
点运动的轨迹形成李萨如图形。
公式
李萨如图上的每一个点都可以用以下的公式进行表示:
X=A1sin(ω1t+ψ1)
Y=A2sin(ω2t+ψ2)
从这里可以看出,李萨如图实际上是一个质点同时在X轴和Y轴上作简谐运动形成的。
但是,如果这两个相互垂直的振动的频率为任意值,那么它们的合成运动就
会比较复杂,而且轨迹是不稳定的。
然而,如果两个振动的频率成简单的整数比,这样就能合成一个稳定、封闭的曲线图形,这就是李萨如图形。
性质
若以Nx和Ny分别表示李萨如图形与外切水平线与外切垂直线的切点数,则其切点数与正弦波频率之间有如下关系:
Fy/Fx=Nx/Ny
用途
设一信号为X=Asinωt,另一信号为Y=Bsin(ωt+ψ),分别输入示波器的x轴和y 轴输入端,可以通过在示波屏上显示的椭圆的性质确定其相位差。
ψ=arcsin(b/B),其中b是椭圆与X轴正半轴的交点值,B是椭圆上的点能取到的最大的X坐标的值。
深入研究。
