数学建模案例之多变量有约束最优化共22页文档
合集下载
数学建模～最优化模型(课件)
投资组合优化
在风险和收益之间寻求平衡，通 过优化投资组合实现最大收益。
03
非线性规划模型
非线性规划问题的定义
目标函数
一个或多个非线性函数，表示 要最小化或最大化的目标。
约束条件
决策变量的取值受到某些限制 ，通常以等式或不等式形式给 出。
决策变量
问题中需要求解的未知数，通 常表示为x1, x2, ..., xn。
这是一种常用的求解整数规划问题的算法，通过不断将问题分解为更 小的子问题，并确定问题的下界和上界，逐步逼近最优解。
割平面法
该方法通过添加割平面来限制搜索区域，从而逼近最优解。
迭代改进法
该方法通过不断迭代和改进当前解，逐步逼近最优解。
遗传算法
这是一种基于生物进化原理的优化算法，通过模拟自然选择和遗传机 制来寻找最优解。
定义域
决策变量的取值范围，通常是 一个闭区间或开区间。
非线性规划问题的求解方法
梯度法
利用目标函数的梯度信息，通过迭代方法寻 找最优解。
共轭梯度法
结合梯度法和牛顿法的思想，通过迭代方法 寻找最优解。
牛顿法
利用目标函数的二阶导数信息，通过迭代方 法寻找最优解。
信赖域方法
在每次迭代中，通过限制搜索步长来保证求 解的稳定性。
02
线性规划模型
线性规划问题的定义
01
02
03
线性规划问题
在给定一组线性约束条件 下，求一组线性函数的最 大值或最小值的问题。
约束条件
包括资源限制、物理条件 等，通常以等式或不等式 形式给出。
目标函数
需要最大化或最小化的线 性函数，通常表示为决策 变量的线性组合。
线性规划问题的求解方法
约束问题的最优化方法
(k ) (k ) m
1 u 1 g ( x ) u
m
其中：gu ( x) 0, u 1,2,...m
1 u 1 g ( x ) u m 1 (k ) (k ) ③ . ( x, r ) f ( x) ru u 1 g u ( x) m 1 (k ) (k ) ④ .( x, r ) f ( x) r 2 u 1 [ g ( x )] u
min . g k x s.t. x Rn gu x g k x gu x 0
0
0
u 1, 2,..., S 1 u S 1,..., m
以求得的设计点作为新初始点，继续其判断可行性，若仍有不
满足的约束，则重复上述过程，直至初始点可行。
的选择：
要求： ①
② 方法： ①
在可行域内；
不要离约束边界太近。 人工估算，需要校核可行性；
②
计算机随机产生，也需校核可行性。
§5.2 内点惩罚函数法
方法： ③ 搜索方法： 任意给出一个初始点； 判断其可行性，若违反了S个约束，求出不满足约束中的最大值： g k ( x 0 ) max{ gu x 0 } u 1,2,..., S； 应用优化方法减少违反约束：
uI
Z
I为违反约束的集合。
g u x ， 当 g u x 0时， maxg u x ,0 { 0 ，当g u x 0时， x, r
(k )
{
f x r k maxg u x ,0 f x
uI
Z
Z一般取2。
k
k
(k )
H [h ( x
1 u 1 g ( x ) u
m
其中：gu ( x) 0, u 1,2,...m
1 u 1 g ( x ) u m 1 (k ) (k ) ③ . ( x, r ) f ( x) ru u 1 g u ( x) m 1 (k ) (k ) ④ .( x, r ) f ( x) r 2 u 1 [ g ( x )] u
min . g k x s.t. x Rn gu x g k x gu x 0
0
0
u 1, 2,..., S 1 u S 1,..., m
以求得的设计点作为新初始点，继续其判断可行性，若仍有不
满足的约束，则重复上述过程，直至初始点可行。
的选择：
要求： ①
② 方法： ①
在可行域内；
不要离约束边界太近。 人工估算，需要校核可行性；
②
计算机随机产生，也需校核可行性。
§5.2 内点惩罚函数法
方法： ③ 搜索方法： 任意给出一个初始点； 判断其可行性，若违反了S个约束，求出不满足约束中的最大值： g k ( x 0 ) max{ gu x 0 } u 1,2,..., S； 应用优化方法减少违反约束：
uI
Z
I为违反约束的集合。
g u x ， 当 g u x 0时， maxg u x ,0 { 0 ，当g u x 0时， x, r
(k )
{
f x r k maxg u x ,0 f x
uI
Z
Z一般取2。
k
k
(k )
H [h ( x
约束条件下的最优化问题
在约束条件下的最优化问题是指在一定的限制条件下，寻找使目标函数达到最大或最小值的最优解。
这类问题可以通过数学建模和优化算法来解决。
常见的约束条件包括等式约束和不等式约束。
等式约束要求某些变量之间的关系满足特定的等式关系，而不等式约束则要求某些变量之间的关系满足特定的不等式关系。
数学上，约束条件可以表示为：
1. 等式约束：g(x) = 0，其中g(x)是一个关于变量x的函数。
2. 不等式约束：h(x) ≤0，其中h(x)是一个关于变量x的函数。
最优化问题的目标函数可以是线性的、非线性的，甚至是在某些特殊情况下可能是非凸的。
根据问题的具体形式，可以选择适合的优化算法进行求解，如线性规划、非线性规划、整数规划等。
常见的优化算法包括：
1. 梯度下降法：用于求解无约束或有约束的凸优化问题，在连续可导的情况下通过迭代调整参数来逐步接近最优解。
2. KKT条件法：用于求解有约束的凸优化问题，通过构建拉格朗日函数和KKT条件来确定最优解。
3. 内点法：用于求解线性规划和凸优化问题，通过在可行域内寻找目标函数的最优解。
4. 遗传算法：用于求解复杂的非线性优化问题，通过模拟自然进化过程中的选择、交叉和变异操作来搜索最优解。
5. 模拟退火算法：用于求解非线性优化问题，通过模拟固体退火的过程来逐步降低温度并接近最优解。
在实际应用中，约束条件下的最优化问题广泛应用于工程、经济、运筹学、物流等领域。
通过合理地建立数学模型，并选择合适的优化算法，可以有效地解决这类问题，并得到最优解或接近最优解的结果。
数学建模分配问题模型
数学建模分配问题模型数学建模是一种通过数学方法解决实际问题的方法。
在实际生活中，我们经常会遇到分配问题，即将一定数量的资源分配给不同的需求方。
这些资源可以是金钱、人力、材料等，需求方可以是个人、企业、机构等。
为了合理地分配资源，我们可以使用数学建模的方法进行分析和优化。
一般来说，分配问题可以分为两类：最优化问题和约束问题。
最优化问题的目标是使得某个指标达到最大或最小值，比如最大化利润、最小化成本等。
约束问题则是在一定的条件下寻找满足需求的最优解。
下面我们将分别介绍这两类问题的数学建模方法。
对于最优化问题，我们首先需要确定一个目标函数。
目标函数描述了我们希望优化的指标，可以是一个或多个变量之间的函数关系。
然后，我们需要确定一组约束条件。
约束条件反映了资源的限制以及需求方的限制，可以是等式或不等式。
最后，我们需要确定决策变量，即需要分配的资源量或决策方案。
通过求解目标函数在约束条件下的最优解，就可以得到最佳的分配方案。
以货物运输为例，假设有一批货物需要从仓库分配给不同的销售点，我们希望通过最优化分配来降低运输成本。
我们可以将每个销售点的需求量作为约束条件，将货物的运输成本作为目标函数。
然后，我们需要确定每个销售点的分配量作为决策变量，通过求解目标函数在约束条件下的最优解，就可以得到最佳的分配方案，从而降低运输成本。
对于约束问题，我们需要确定一组约束条件，这些条件可能是资源的限制、需求方的限制或其他限制。
然后，我们需要确定决策变量，即需要分配的资源量或决策方案。
通过在约束条件下寻找满足需求的最优解，就可以得到合理的分配方案。
以人力资源分配为例，假设有一定数量的员工需要分配到不同的项目中，每个项目对员工的技能要求不同。
我们希望通过合理的分配来最大化项目的效益。
我们可以将每个项目的效益作为约束条件，将员工的技能水平作为决策变量。
通过在约束条件下寻找满足需求的最优解，就可以得到最佳的分配方案，从而最大化项目的效益。
约束问题的最优化方法
m
⑤ .Φ ( x, r ) = f ( x) − r ∑ ln[− g u ( x)]
(k )
其中：惩罚（加权）因子 降低系数 c：
r ( 0 ) > r (1) > ....r ( k )
0< c <1
r ( k −1) ⋅ c = r ( k )
xk * → x *
当lim r ( k ) → 0
新目标函数： Φ ( x, r1 , r2 ) =
(k ) M
(k ) p
G[ g u ( x)] + r2 ∑ H [hv ( x)] f ( x) + r1 ∑ u =1 v =1
m
p
H [hv ( x)] 其中r ∑ G[g u ( x)] 和 r ∑ 称为加权转化项，并根据它们在惩 v =1 u =1 罚函数中的作用，分别称为障碍项和惩罚项。
2、等式约束优化问题（EP型）
x ∈ D ⊂ Rn s.t. hv ( x ) = 0, v = 1,2,..., q min F ( x )
3、一般约束优化问题（GP型）
x ∈ D ⊂ Rn s.t. g u ( x ) ≥ 0, u = 1,2,..., p hv ( x ) = 0, v = 1,2,..., q min F ( x )
(k ) u =1 m
lim r2 H [hv ( x ( k ) )] = 0
k →∞
lim[Φ ( x ( k ) , r1 , r2 ) − f ( x ( k ) )] = 0 k →∞
(k ) (k )
分类： 根据约束形式和定义的泛函及罚因子的递推方法等不同，罚函 数法可分为内点法、外点法和混合罚函数法三种。 这种方法是1968年由美国学者A．V．Fiacco和G．P．Mcormick 提出的，把不等式约束引入数学模型中，为求多维有约束非线性规 划问题开创了一个新局面。 适用范围：求解等式约束优化问题和一般约束优化问题。
数学建模最优化模型
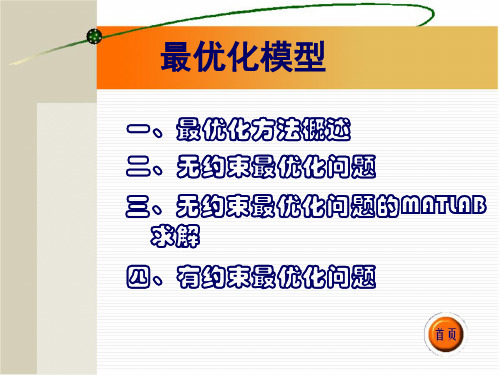
解 设剪去的正方形的边长为 x ，则水槽的容积为： (3 2x)2 x
建立无约束优化模型为：min y =- (3 2x)2 x ， 0< x <1.5
先编写M文件fun0.m如下:
function f=fun0(x)
f=-(3-2*x).^2*x; 主程序为wliti2.m:
[x,fval]=fminbnd('fun0',0,1.5);
计算机技术的出现，使得数学家研究出了许 多最优化方法和算法用以解决以前难以解决的问 题。
最优化：在一定的条件下，寻求 使得目标最大（最小）的策略
• 约一半以上的问题与最优化问题有关。如： 飞行管理问题（95A） 最优捕鱼策略（96A） 节水洗衣机（96B） 零件的参数设计(97A) 投资收益和风险(98A) 钢管订购和运输(2000B)
一般的模型简化工作包括以下几类： （1）将离散变量转化为连续变量。 （2）将非线性函数线性化。 （3）删除一些非主要约束条件。
建立最优化问题数学模型的三要素：
（1）决策变量和参数。
决策变量是由数学模型的解确定的未知数。参数表 示系统的控制变量，有确定性的也有随机性的。
（2）约束或限制条件。
由于现实系统的客观物质条件限制，模型必须包括 把决策变量限制在它们可行值之内的约束条件，而这 通常是用约束的数学函数形式来表示的。
min f (x) x
2、约束条件下极值问题的数学模型
min f (x) x
s.t. gi (x) 0, i 1, 2,..., m hi (x) 0, i 1, 2,..., n
其中，极大值问题可以转化为极小值问题来
进行求解。如求： max f (x) x 可以转化为：min f (x) x
第二章多变量最优化
问题1中的全部常量包括：
1.两种彩电的初始定价：339美元和399美元； 2.其对应的成本分别为：195美元和225美元； 3.每种彩电多销售一台，平均售价下降系数a=0.01 美元（称为价格弹性系数），两种彩电之间的销售 相互影响系数分别为0.004美元和0.003美元； 4.固定成本为400000美元。
–
– 因此，原问题转化为求s≥0和t≥0，使得y=P
取得最大值。
2.选择建模方法
概述选定的建模方法
– 这个问题我们视为无约束的多变量最优化问题。这类
问题通常在多元微积分得入门课程中都有介绍。我们 这里只给出模型的要点和一般的求解过程。
2.选择建模方法
的子集S上的函数 y f ( x1 , , xn ) 。我们要求 f 在集合S上的最大值或最小值。一个定 理给出：若 f 在S的某个点内 ( x1 , , xn ) 达到极大值或 极小值，设 f 在这点可微，则在这个点上 f 0 。也 就是说，在极值点有 f f ( x1 , , xn ) 0 ( x1 , , xn ) 0 （2-1） xn x1 据此我们可以在求极大或极小点时，不考虑那些在S内 部使 f 的某一个偏导数不为0的点。因此，要求极大或 极小点，我们就要求解方程组(2-1)给出的n个未知数、 n个方程的联立方程组。然后我们还要检查S的边界上的 点,以及那些一个或多个偏导数没有定义的点。
S x1 , x2 : x1 0, x2
y f x1 , x2 339 0.01x1 0.003 x2 x1 339 0.04 x1 0.01x2 x2 400 000 195 x1 225 x2
4.利用第二步确定的标准过程求解
数学建模最优化模型
曲线不一定通过那m个测量点,而要产生“偏差”.
将测量点沿垂线方向到曲线的距离的
y
平方和作为这种“偏差”的度量.即
2
x
S
m i 1
yi
a1
1 a3
a2 ln 1 exp
xi a4 a5
显然偏差S越小,曲线就拟合得越好,说明参数值就选择得越好，从而 我们的问题就转化为5维无约束最优化问题。即：
计算机技术的出现，使得数学家研究出了许 多最优化方法和算法用以解决以前难以解决的问 题。
最优化：在一定的条件下，寻求 使得目标最大（最小）的策略
• 约一半以上的问题与最优化问题有关。如： 飞行管理问题（95A） 最优捕鱼策略（96A） 节水洗衣机（96B） 零件的参数设计(97A) 投资收益和风险(98A) 钢管订购和运输(2000B)
2
min
m i 1
yi
a1
1
a3
a2 ln 1 exp
xi
x4 a5
有约束最优化
最优化方法分类
（一）线性最优化：目标函数和约束条件都是线 性的则称为线性最优化。
非线性最优化：目标函数和约束条件如果含 有非线性的，则称为非线性最优化。
（二）静态最优化：如果可能的方案与时间无关， 则是静态最优化问题。
或[x，fval，exitflag，output]= fminsearch（...）
例 用fminsearch函数求解 输入命令:
f='100*(x(2)-x(1)^2)^2+(1-x(1))^2'; [x,fval,exitflag,output]=fminsearch(f,[-1.2 2])
运行结果:
f x* f x 则称 x*是最优化问题的整体最优解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第 3 步：计算边界上的极大值
由于可行域由 5 条直线围成，因此需要分别计算 P(s,t)在每一条边界线段上的极大值，下面
分别计算，重点介绍如何计算 P(s,t)在直线 s t 10000 上的最大值。
（1）P(s,t)在约束直线 s t 10000 上的极大值
此时，需要求解问题
max P(s, t) s.t. g(s, t) s t 10000
2．建立数学模型
根据前面的分析，原问题的数学模型如下：
max P(s, t) (339 as 0.003t)s (399 0.004s 0.01t)t (400000 195s 225t),
s.t. s t 10000, s 5000 , t 8000 , s 0,t 0
其 Lagrange 乘子方程为 P g ，即
144 0.02s 0.007t 174 0.007s 0.02t
与约束方程
联立求解，得到
s t 10000
s0 3846
t0
6154
24
代入目标函数 P(s,t)可得极大值为 P(s0 , t0 ) 532308 。
（2.3） （2.4）
第 4 步：比较边界极大值，求出最大值点 比较函数 P(s,t)在区域 S 的五段边界直线上的最大值，可得到 P(s,t)在区域上的
最大值为 532308 美元，在点(3846,6154)处取得。
这里 a=0.01。
（2.1）
3．模型求解
3.1 求解方法----Lagrange 乘子法 这是一个带有多个约束条件的多变量最优化问题，可以使用 Lagrange 乘子法求解。 第 1 步：确定目标函数 P(s,t)的可行域 S 目标函数 P(s,t)的可行域 S（见图 1）为：
S {(s, t) : s t 10000,0 s 5000,0 t 8000}
清晰问题：问每种彩电应该各生产多少台，使得利润最大化？
1．问题分析、假设与符号说明
这里涉及的变量和问题１相同： s：19 英寸彩电的售出数量（台）； t：21 英寸彩电的售出数量（台）； p：19 英寸彩电的售出价格（美元/台）； q：21 英寸彩电的售出价格（美元/台）； C：生产彩电的成本（美元）； R：彩电销售的收入（美元）； P：彩电销售的利润（美元）
这里涉及的常量同问题１： 两种彩电的初始定价分别为：339 美元和 399 美元； 每种彩电的生产成本分别为：195 美元和 225 美元； 每种彩电每多销售一台，平均售价下降系数 a=0.01 美元（称为价格弹性系数）； 种彩电之间的销售相互影响系数分别为 0.04 美元和 0.03 美元； 固定成本 400000 美元。
10000 8000 6000 4000 2000
可行域
2000 4000 6000 8000 10000 图 1 目标函数的可行域图
第 2 步：计算 P
P
(
P s
,
P t
)
(144
0.02s
0.007t , 174Leabharlann 0.007s0.02t
)
（2.2）
在可行域 S 的内部， P 0 ，因此，最大值一定在边界上达到。
图 2 可行域及水平集图
上面的图 2 给出了可行域以及 P(s,t)的水平集图像。水平集 P(s,t)=C 为一 簇同心环，这些环与可行域相交，水平集 P(s,t)=532308 为最小的环。这个集
合刚刚接触到可行域 S，且与直线 s t 10000 在极值点相切。由图 2 还可以 看出，利用 Lagrange 乘子法在约束直线 s t 10000 上找到的临界点就是
问题 2[1]（续问题 1）：在问题 1 中，我们假设公司每年有能力生产任何数量的彩电。现
在我们根据允许的生产能力引入限制条件。公司考虑投产者两种新产品是由于计划停止黑白 电视机的生产。这样装配厂就有了额外的生产能力。这些额外的生产能力就可以用来提高那 些现有产品的产量，但公司认为新产品会带来更高的利润。据估计，现有的生产能力允许每 年可以生产 10000 台电视（约每周 200 台）。公司有充足的 19 英寸、21 英寸彩色显像管、 底盘及其他标准配件。但现在生产立体声电视所需要的电路板供给不足。此外，19 英寸彩 电所需要的电路板与 21 英寸彩电的不同，这是由于其内部的结构造成的。只有进行较大的 重新设计才能改变这一点，但公司现在不准备做这项工作。电路板的供应商每年可以提供 8000 块 21 英寸彩电的电路板和 5000 块 19 英寸彩电的电路板。考虑到所有这些情况， 彩电公司应该怎样确定其生产量？
变量之间的相互关系确定： 假设 1：对每种类型的彩电，每多售出一台，平均销售价格会下降 1 美分。 假设２：对于每种类型的彩电，受到生产所需要的电路板的限制，其售出数量有限制
s 5000, t 8000 ； 假设３：公司年内的生产能力有上限 c=10000 台，即 s t 10000 ；
假设４：据估计，每售出一台 21 英寸彩电，19 英寸的彩电平均售价会下降 0.3 美分， 而每售出一台 19 英寸的彩电，21 英寸彩电的平均售价会下降 0.4 美分。
P(s,t)在整个可行域上的最大值。
（2）P(s,t)在其它约束直线上的极大值 采用与（1）类似的方法可以求出在剩余的其它约束直线上对 P(s,t)的极大
值点，结果如下：
直线段 s 5000：极大值点（5000，5000），极值为 515000 美元； 直线段 t 8000：极大值点（2000，8000），极值为 488000 美元； 直线段 s 0 ：极大值点（0，8000），极值为 352000 美元； 直线段 t 0 ：极大值点（5000，0），极值为 70000 美元。
因此，19 英寸彩电的销售价格为： p=339 - a×s - 0.03×t，此处 a=0.01
21 英寸彩电的销售价格为： q=399 - 0.01×t - 0.04×s
因此，总的销售收入为： R=p×s + q×t
生产成本为： C=400000 + 195×s + 225×t
净利润为： P=R-C