第四章 静水压力计算习题及答案
《流体力学》所有做过的习题答案
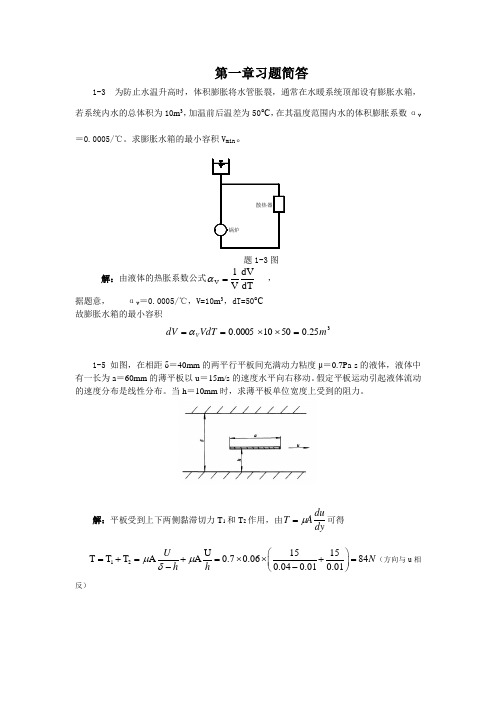
第一章习题简答1-3 为防止水温升高时，体积膨胀将水管胀裂，通常在水暖系统顶部设有膨胀水箱，若系统内水的总体积为10m 3，加温前后温差为50°С，在其温度范围内水的体积膨胀系数αv＝0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解：由液体的热胀系数公式dTdVV 1V =α ， 据题意， αv ＝0.0005/℃，V=10m 3，dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图，在相距δ＝40mm 的两平行平板间充满动力粘度μ＝0.7Pa·s 的液体，液体中有一长为a ＝60mm 的薄平板以u ＝15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h ＝10mm 时，求薄平板单位宽度上受到的阻力。
解：平板受到上下两侧黏滞切力T 1和T 2作用，由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭（方向与u 相反）1-7 温度为20°С的空气，在直径为2.5cm 的管中流动，距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少？解：温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系，且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250，c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ （与课本后的答案不一样。
工程流体水力学第四章习题答案
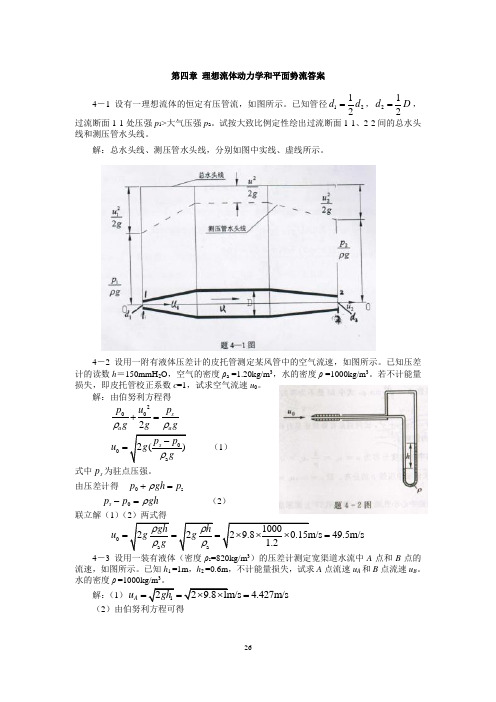
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。
已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解：总水头线、测压管水头线，分别如图中实线、虚线所示。
4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。
已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。
若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。
解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。
已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
《水力学》作业题参考答案
详细描述
流速是影响水头损失的重要因素，流速越大，水流阻力越 大，水头损失也越大。流体性质对水头损失也有影响，例 如水的黏滞性、密度和表面张力等都会影响水头损失。管 道材料和管道形状也是影响水头损失的因素，不同材料的 管道对水流的阻力不同，管道的弯曲、分叉等形状也会影 响水头损失。了解水头损失的影响因素有助于更好地控制 和减少水头损失，提高水流运动的效率。
液体流动的能量平衡特性
液体流动的能量平衡具有守恒性， 即流动过程中各种形式的能量总和 保持不变。 能量平衡与流体的状态变化密切相 关，例如流体从高压状态向低压状 态流动时，压力能会转化为动能。 液体流动的能量平衡特性决定了流 体的运动规律和特性，例如流速、 压强、水位等参数的变化。
液体流动的能量平衡计算
PA R T. 0 2
流体运动
单击此处添加文本具体内容
流体运动的分类
层流运动 湍流运动 过渡流 自由表面流 流体在流动过程中，流层之间互不掺混，呈层状流动。 流体在流动过程中，流层之间有强烈的动量交换，流动呈现紊 乱、无规则状态。 介于层流与湍流之间的流动状态，具有某些层流和湍流的特性。 流体在流动过程中，存在自由表面的流动，如河流、洪水等。
水头损失
单击此处添加文本具体内容
水头损失的概念
总结词
水头损失是指水流在运动过程中，由于克服水流阻力而消耗的能量。
详细描述
水头损失是水流在运动过程中由于克服水流阻力而消耗的能量。水 流在运动过程中会遇到各种阻力，如摩擦阻力、局部阻力等，这些 阻力会导致水流的能量损失，即水头损失。
水头损失的计算
总结词
离有关。
静水压强的特性
静水压强具有方向性，垂直指向作用面， 即垂直指向受压物体表面。
流体力学静水压强练习题
流体力学静水压强练习题一、基本概念题1. 列出静水压强的定义。
2. 静水压强与哪些因素有关？3. 什么是绝对压强和相对压强？4. 简述液体压强随深度的变化规律。
5. 如何计算液体在某一点的静水压强？二、公式应用题1. 已知水的密度为1000 kg/m³，求深度为10m处的静水压强。
2. 某容器内液体深度为5m，液体密度为800 kg/m³，求容器底部的静水压强。
3. 一根直径为0.1m的管道内，水流速度为2m/s，求管道中心处的静水压强。
4. 某封闭容器内气体压强为1.5×10^5 Pa，容器内液体深度为3m，液体密度为1200 kg/m³，求气体对容器底部的压强。
5. 在一水坝底部，水深为20m，求水坝底部的静水压强。
三、综合分析题1. 分析液体内部压强分布规律，并说明原因。
2. 举例说明静水压强在实际工程中的应用。
3. 讨论液体静压强与液体密度的关系。
4. 如何利用静水压强原理计算液体在容器内的压力？5. 分析在深海潜水过程中，潜水员所承受的静水压强变化。
四、计算题1. 已知一圆形水池直径为10m，水深为4m，求水池底部的静水压强。
2. 一矩形水槽长20m，宽5m，水深6m，求水槽底部的静水压强。
3. 某圆柱形容器高1m，直径0.5m，容器内液体密度为1500kg/m³，求容器底部的静水压强。
4. 一潜水员在海底作业，水深为50m，求潜水员所承受的静水压强。
5. 一艘船在海上航行，船底距海平面深度为15m，求船底的静水压强。
五、判断题1. 液体内部的压强处处相等。
（）2. 静水压强与液体深度成正比。
（）3. 液体压强与液体密度无关。
（）4. 绝对压强总是大于相对压强。
（）5. 液体静压强在水平方向上是不变的。
（）六、选择题A. 液体的密度B. 液体的温度C. 液体的深度D. 重力加速度2. 在同一液体中，下列哪个深度处的静水压强最大？A. 5m深处B. 10m深处C. 15m深处D. 20m深处A. 静水压强随深度增加而减小B. 静水压强在液体表面处最大C. 静水压强在液体内部处处相等D. 静水压强与液体密度成正比4. 在一个密闭容器内，液体上方气体的压强为50kPa，液体深度为2m，液体密度为1000 kg/m³，容器底部的总压强为多少？A. 100 kPaB. 150 kPaC. 200 kPaD. 250 kPaA. P = ρghB. P = ρgh^2C. P = ρg/hD. P = ρg^2h七、填空题1. 液体的静水压强是由__________、__________和__________共同作用产生的。
水力学答案完整版
第一章 绪论答案1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆ 1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%。
1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。
试求m h 5.0=时渠底（y =0）处的切应力。
[解] μρ/)(002.0y h g dy du -=)(002.0y h g dydu -==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑y u AT mg d d sin μθ== 001.0145.05.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg =s Pa 08376.0⋅ 1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律y ud d μτ=，定性绘出切应力沿y[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。
第四章静水压力计算习题及答案
第四章静水压力计算一、是非题1O重合。
2、静止液体中同一点各方向的静水压强数值相等。
3、直立平板静水总压力的作用点与平板的形心不重合。
4、静止水体中,某点的真空压强为50kPa，则该点相对压强为-50kPa。
5、水深相同的静止水面一定是等压面。
6、静水压强的大小与受压面的方位无关。
7、恒定总流能量方程只适用于整个水流都是渐变流的情况。
二、选择题1、根据静水压强的特性，静止液体中同一点各方向的压强（1）数值相等（2）数值不等（3）水平方向数值相等（4）铅直方向数值最大m，则该点的相对压强为2、液体中某点的绝对压强为100kN/2m（1）1kN/2m（2）2kN/2m（3）5kN/2m（4）10kN/2m，则该点的相对压强为3、液体中某点的绝对压强为108kN/2m（1）1kN/2m（2）2kN/2m（3）8kN/2m（4）10kN/24、静止液体中同一点沿各方向上的压强（1）数值相等（2）数值不等（3）仅水平方向数值相等5、在平衡液体中，质量力与等压面（1）重合（2）平行（3）正交6、图示容器中有两种液体，密度ρ2 > ρ1 ，则A、B 两测压管中的液面必为（1）B 管高于A管（2）A管高于 B 管（3）AB 两管同高。
7、盛水容器 a 和b 的测压管水面位置如图(a)、(b) 所示，其底部压强分别为pa和pb。
若两容器内水深相等，则pa和pb的关系为（1）pa>pb（2）pa< pb（3）pa=pb（4）无法确定8（1）牛顿（2）千帕（3）水柱高（4）工程大气压三、问答题1、什么是相对压强和绝对压强？2、在什么条件下“静止液体内任何一个水平面都是等压面”的说法是正确的？3、压力中心D和受压平面形心C的位置之间有什么关系？什么情况下D点与C点重合？4、图示为几个不同形状的盛水容器，它们的底面积AB、水深h均相等。
试说明：（1）各容器底面所受的静水总压力是否相等？（2）每个容器底面的静水总压力与地面对容器的反力是否相等？并说明理由（容器的重量不计）。
静水压力计算
第四章静水压力计算一、是非题1O重合。
2、静止液体中同一点各方向的静水压强数值相等。
3、直立平板静水总压力的作用点与平板的形心不重合。
4、静止水体中,某点的真空压强为50kPa，则该点相对压强为-50kPa。
5、水深相同的静止水面一定是等压面。
6、静水压强的大小与受压面的方位无关。
7、恒定总流能量方程只适用于整个水流都是渐变流的情况。
二、选择题1、根据静水压强的特性，静止液体中同一点各方向的压强（1）数值相等（2）数值不等（3）水平方向数值相等（4）铅直方向数值最大m，则该点的相对压强为2、液体中某点的绝对压强为100kN/2m（1）1kN/2m（2）2kN/2m（3）5kN/2m（4）10kN/2m，则该点的相对压强为3、液体中某点的绝对压强为108kN/2m（1）1kN/2m（2）2kN/2m（3）8kN/2m（4）10kN/24、静止液体中同一点沿各方向上的压强（1）数值相等（2）数值不等（3）仅水平方向数值相等5、在平衡液体中，质量力与等压面（1）重合（2）平行（3）正交6、图示容器中有两种液体，密度ρ2 > ρ1 ，则A、B 两测压管中的液面必为（1）B 管高于A 管（2）A 管高于B 管（3）AB 两管同高。
7、盛水容器a 和b 的测压管水面位置如图(a)、(b) 所示，其底部压强分别为pa和pb。
若两容器内水深相等，则pa和pb的关系为（1）pa>pb（2）pa< pb（3）pa=pb（4）无法确定8（1）牛顿（2）千帕（3）水柱高（4）工程大气压三、问答题1、什么是相对压强和绝对压强？2、在什么条件下“静止液体内任何一个水平面都是等压面”的说法是正确的？3、压力中心D和受压平面形心C的位置之间有什么关系？什么情况下D点与C点重合？4、图示为几个不同形状的盛水容器，它们的底面积AB、水深h均相等。
试说明：（1）各容器底面所受的静水总压力是否相等？（2）每个容器底面的静水总压力与地面对容器的反力是否相等？并说明理由（容器的重量不计）。
第四章静水压力计算习题及答案
第四章静水压力计算一、是非题1、图中矩形面板所受静水的形心点O重合。
2、静止液体中同一点各方向的静水压强数值相等。
3、直立平板静水总压力的作用点与平板的形心不重合。
4、静止水体中,某点的真空压强为50k Pa，则该点相对压强为-50kPa。
5、水深相同的静止水面一定是等压面。
6、静水压强的大小与受压面的方位无关。
7、恒定总流能量方程只适用于整个水流都是渐变流的情况。
二、选择题1、根据静水压强的特性，静止液体中同一点各方向的压强（1）数值相等（2）数值不等（3）水平方向数值相等（4）铅直方向数值最大m，则该点的相对压强为2、液体中某点的绝对压强为100kN/2m（1）1kN/2m（2）2kN/2m（3）5kN/2m（4）10kN/2m，则该点的相对压强为3、液体中某点的绝对压强为108kN/2m（1）1kN/2m（2）2kN/2m（3）8kN/2m（4）10kN/24、静止液体中同一点沿各方向上的压强（1）数值相等（2）数值不等（3）仅水平方向数值相等5、在平衡液体中，质量力与等压面（1）重合（2）平行（3）正交6、图示容器中有两种液体，密度ρ2 > ρ1 ，则A、B 两测压管中的液面必为（1）B 管高于A管（2）A管高于 B 管（3）AB 两管同高。
7、盛水容器 a 和b 的测压管水面位置如图 (a)、(b) 所示，其底部压强分别为pa和pb。
若两容器内水深相等，则pa和pb的关系为（1）pa>pb（2）pa< pb（3）pa=pb（4）无法确定8、下列单位中，（1）牛顿（2）千帕（3）水柱高（4）工程大气压三、问答题1、什么是相对压强和绝对压强？2、在什么条件下“静止液体内任何一个水平面都是等压面”的说法是正确的？3、压力中心D和受压平面形心C的位置之间有什么关系？什么情况下D点与C点重合？4、图示为几个不同形状的盛水容器，它们的底面积A B、水深h均相等。
水静力学全部习题---经典,好
解题步骤
解：
由图可知１－１、２－２ 为等压面，
A
1
hA 1
则在这两个等压面之间 两端的液柱产生的压力 之和相等，即
ρ
ρ
hB
2
2
B
A ghA B ghB ghA ghB
则容器内液体的密度为 AhA BhB
hA hB
静止液体作用在物面上的总压力
MF2TD0251006
(H 13.6 10 3 kg/m3 , 110 3 kg/m3 )
解题步骤
解：
已知断面1上作用着大气 压，因此可以从点1开始，通 ， 过等压面，并应用流体静力 学基本方程式，逐点推算， 最后便可求得A点压强。
， 因2-2、3-3、4-4为等压面，根据静压强公式可得
p2 H g(1 2 )
p3 p2 g(3 2 )
p4 p3 H g(3 4 ) p A p5 p4 g(5 4 )
解题步骤
联立求得
pA H g(1 2 ) g(3 2 ) H g(3 4 ) g(5 4 )
得C点绝对压强为
p p0 gh
85kN/m2 1000kg/m3 9.8m/s2 1m 94.8kN/m2
由公式 p p pa ，C点的相对压强为
p p pa 94.8kN/m 2 98kN/m 2 3.2kN/m 2
相对压强为负值，说明C点存在真空。
h1 h
h2 h3
P1 P2 P3
y 1 y2 y3
解题步骤
解：
首先画出平板闸门所受的
静水压强分布图。
单位宽闸门上所受的静水总 P 压力可以由图解法计算静水
流体力学习题集与答案解析
流体力学与叶栅理论课程考试试题一、选择题（每小题1分，共10分）1、在括号填上“表面力”或“质量力”：摩擦力（）；重力（）；离心力（）；浮力（）；压力（）。
2、判断下列叙述是否正确（对者画√，错者画╳）：(a) 基准面可以任意选取。
（）(b) 流体在水平圆管流动，如果流量增大一倍而其它条件不变的话，沿程阻力也将增大一倍。
（）(c) 因为并联管路中各并联支路的水力损失相等，所以其能量损失也一定相等。
（）(d) 定常流动时，流线与迹线重合。
（）(e) 沿程阻力系数λ的大小只取决于流体的流动状态。
（）二、回答下列各题（1—2题每题5分，3题10分，共20分）1、什么是流体的连续介质模型？它在流体力学中有何作用？2、用工程单位制表示流体的速度、管径、运动粘性系数时，管流的雷诺数4Re ，10问采用国际单位制时，该条件下的雷诺数是多少？为什么？3、常见的流量的测量方法有哪些？各有何特点？三、计算题（70分）1、如图所示，一油缸及其中滑动栓塞，尺寸D=120.2mm，d=119.8mm，L=160mm，间隙充满μ=0.065Pa·S的润滑油，若施加活塞以F=10N的拉力,试问活塞匀速运动时的速度是多少？（10分）题1图2、如图所示一盛水容器，已知平壁AB=CD=2.5m，BC及AD为半个圆柱体，半径R=1m，自由表面处压强为一个大气压，高度H=3m，试分别计算作用在单位长度上AB面、BC面和CD面所受到的静水总压力。
（10分）题2图3、原型流动中油的运动粘性系数υp=15×10-5m2/s，其几何尺度为模型的5倍，如确定佛汝德数和雷诺数作为决定性相似准数，试问模型中流体运动粘性系数υm=？（10分）4、如图所示，变直径圆管在水平面以α=30。
弯曲，直径分别为d1=0.2m，d2=0.15m，过水流量若为Q=0.1m3/s，P1=1000N/m2时，不计损失的情况下，求水流对圆管的作用力及作用力的位置。
土力学习题及答案--第四章
Q2第4章土中应力一简答题1．何谓土中应力？它有哪些分类和用途？2．怎样简化土中应力计算模型？在工程中应注意哪些问题？3．地下水位的升降对土中自重应力有何影响？在工程实践中，有哪些问题应充分考虑其影响？4．基底压力分布的影响因素有哪些？简化直线分布的假设条件是什么？5．如何计算基底压力和基底附加压力？两者概念有何不同？6．土中附加应力的产生原因有哪些？在工程实用中应如何考虑？7．在工程中，如何考虑土中应力分布规律？二填空题1.土中应力按成因可分为和。
2.土中应力按土骨架和土中孔隙的分担作用可分为和。
3.地下水位下降则原水位出处的有效自重应力。
4.计算土的自重应力应从算起。
5.计算土的自重应力时，地下水位以下的重度应取。
三选择题1．建筑物基础作用于地基表面的压力，称为（）。
(A)基底压力；(B)基底附加压力；(C)基底净反力；(D)附加应力2．在隔水层中计算土的自重应力c时，存在如下关系（）。
(A) =静水压力(B) =总应力，且静水压力为零(C) =总应力，但静水压力大于零(D)=总应力—静水压力，且静水压力大于零3．当各土层中仅存在潜水而不存在毛细水和承压水时，在潜水位以下的土中自重应力为（）。
(A)静水压力(B)总应力(C)有效应力，但不等于总应力(D)有效应力，但等于总应力4．地下水位长时间下降，会使（）。
(A)地基中原水位以下的自重应力增加(B)地基中原水位以上的自重应力增加(C)地基土的抗剪强度减小(D)土中孔隙水压力增大5．通过土粒承受和传递的应力称为（）。
(A)有效应力；(B)总应力；(C)附加应力；(D)孔隙水压力6．某场地表层为4m厚的粉质黏土，天然重度=18kN/m3，其下为饱和重度sat=19 kN/m3的很厚的黏土层，地下水位在地表下4m处，经计算地表以下2m处土的竖向自重应力为（）。
(A)72kPa ； (B)36kPa ；(C)16kPa ；(D)38kPa7．同上题，地表以下5m处土的竖向自重应力为（）。
《流体力学与流体机械》计算题及答案
1 2
总结词
掌握流体流动阻力和能量损失的计算方法，了解 流体流动过程中阻力和能量的变化规律。
流体流动阻力计算
根据流体流动的雷诺数和流体性质，计算流体在 管道中的流动阻力，包括直管阻力和局部阻力。
3
能量损失计算
根据伯努利方程和流体流动的能量守恒原理，计 算流体在管道中的能量损失，包括沿程损失和局 部损失。
分析流体在流动过程中 的温度变化，以及由此
产生的热能转换。
03
探讨流体流动与热能转 换之间的关系，以及其 对流体机械性能的影响。
05
详细描述
02
计算流体在流动过程中 由于热传导、对流和辐 射等热传递方式而产生
的热量交换。
04
流体流动与化学能转换计算
总结词：计算流体在流动 过程中由于化学反应而产 生的化学能转换。
详细描述
分析流体在流动过程中可 能发生的化学反应，以及 由此产生的化学能转换。
探讨流体流动与化学能转 换之间的关系，以及其在 化工、制药等领域中的应 用。
计算化学反应过程中流体 的能量变化，以及其对流 体机械性能的影响。
THANKS
感谢观看
计算流体在流动过程中由于机械能转换 而产生的能量损失或增益。
分析流体在流动过程中所受的阻力，如 摩擦力和局部阻力，对机械能转换的影 响。
详细描述
计算流体在管道中流动时的压力能变化 ，以及由此产生的速度和流量的变化。
流体流动与热能转换计算
总结词：计算流体在流 动过程中由于温度变化
而产生的热能转换。
01
必需汽蚀余量（NPSHr）
泵开始发生汽蚀时，所必须的最低有效汽蚀余量。
有效汽蚀余量（NPSHa）
泵在实际运行中，所实际具有的有效汽蚀余量。
水力学试题和答案
思考题1.1静水压强有哪些特性？静水压强的分布规律是什么？1.2试分析图中压强分布图错在哪里？1.3何谓绝对压强，相对压强和真空值？它们的表示方法有哪三种？它们之间有什么关系？1.4图示一密闭水箱，试分析水平面A—A，B—B，C—C是否皆为等压面？何谓等压面？等压面的条件有哪些？1.5一密闭水箱(如图)系用橡皮管从C点连通容器Ⅱ，并在A，B两点各接一测压管，问：思 1 . 4 思1 . 5（1）AB两测压管中水位是否相同？如相同时，问AB两点压强是否相等?（2）把容器Ⅱ提高一些后，p比原来值增大还是减小？两测压管中水位变化如何？1.6什么叫压力体？如何确定压力体的范围和方向？习 题1.1 图示为一密闭容器，两侧各装一测压管，右管上端封闭，其中水面高出容器水3 m ，管内液面0p 压强为78 kPa ；左管与大气相通。
求：（1）容器内液面压强c p ；（2）左侧管内水面距容器液面高度h 。
1.2 盛有同种介质(密度==B A ρρ 1 132.6 kg/m 3)的两容器，其中心点A 与B 位于同一高程，今用U 形差压计测定A 与B 点之压差(差压计内盛油，密度=0ρ867.3 kg/m 3 )， A 点还装有一水银测压计。
其他有关数据如图题1.2所示。
问：（1）A 与B 两点之压差为多少？（2）A 与B 两点中有无真空存在，其值为多少？1.3 图示一圆柱形油桶，内装轻油及重油。
轻油密度1ρ为6 632.6 kg / m 3，重油密度2ρ为887.75k g/m 3，当两种油重量相等时，求：（1）两种油的深度1h 及2h 为多少？（2）两测压管内油面将上升至什么高度？1.4 在盛满水的容器盖上， 加上6 154N 的荷载G （包括盖重），若盖与容器侧壁完密合，试求A ，B ，C ，D 各点的相对静水压强（尺寸见图）。
1.5 今采用三组串联的U 形水银测压计测量高压水管中压强，测压计顶端盛水。
当M 点压强等于大气压强时，各支水银面均位于0一0水平面上。
水力学课后习题详解
冲击损失
水流在高速流动中，由于 水流的剧烈波动、水流的 分离和再附着等过程所引 起的水头损失。
水头损失的计算方法
伯诺里方程法
利用伯诺里方程计算沿程水头损失，该方法适用于计算均 匀流动的水管中的水头损失。
尼古拉兹实验曲线法
根据尼古拉兹实验结果，绘制出的沿程阻力系数与雷诺数 的关系曲线，通过查表和曲线拟合计算沿程水头损失。
静水压强具有方向性，其方向垂直于 作用面，并指向作用面内。
静水压强的基本规律
静水压强分布规律
在同一深度处，各点所受的静水压强相等。
静水压强与深度关系
随着深度的增加，静水压强逐渐增大。
静水压强与液体密度关系
在相同深度和重力加速度条件下，液体密度越大，所受的静水压强 越大。
静水压强的计算公式
1 2 3
使用减小阻力的材料
选择具有较小阻力的材料可以 降低流体流动的阻力。
04
水头损失
水头损失的类型
01
02
03
沿程水头损失
水流在管道、渠道等直线 型流动中，由于水流与边 界壁面的摩擦和黏性阻力 所引起的水头损失。
局部水头损失
水流在流经管道的弯头、 阀门、扩散管等局部构件 时，由于流速分布的急剧 变化而引起的水头损失。
解答
首先，我们需要计算孔口的面积，使用公式$A = pi r^2$，其中$r$是孔的半径。然后，我们需要计算每秒流出 的水量，使用公式$Q = A times v$，其中$v$是水流速度。最后，我们用总水量除以每秒流出的水量，得到所 需时间。
习题二解答
问题
一个水坝的横截面是一个梯形，上底为6米，下底为12米，高为30米。当水坝内蓄满水时，水的深度 为20米。求水对坝底的压强和压力。
水力学课后计算题及答案解析
水力学课后计算题及答案第一章 绪论1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。
试求m h 5.0=时渠底（y =0）处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yuAT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律yud d μτ=，定性绘出切应力沿y 方向的分布图。
[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。
流体力学（刘鹤年）第4章答案
4.1一变直径管段AB ，直径d A =0.2m ，d B =0.4m ，高差△h=1.5m，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ．水在管中的流动方向。
解：s m d d v v ABB A 62.04.05.1442222=⨯=⋅=ππ以过A 点的水平面为等压面，则OmH g v g p h H OmH g v g p H B B B A A A 2222226964.58.925.18.9405.128980.48.9268.9302=⨯++=++==⨯+=+=ρρ可以看出：，水将从B 点流向A 点。
A B H H >或：wB B B A A A h gvg p z g v g p z +++=++2222ρρ解得水头损失为：，水将从B 点流向A 点。
O mH h w 27984.0-=4.2利用毕托管原理，测量水管中的流速u 。
水银差压计读书⊿h =60mm ，求该点流速。
解：m/s8530606128922....h g u =⋅⋅⋅=∆=汞ρ4.3水管直径50mm ，末端阀门关闭时，压力表读值为21kPa ，阀门打开后读值降为5.5kPa ，求不计水头损失时通过的流量Q.解：所以 m/s 57555212221.g .g g p p g V =-=⎪⎪⎭⎫ ⎝⎛-=ρρQ=VA=5.57×π(0.05)2/4=10.9 l/s4.4水在变直径竖管中流动，已知粗管直径d 1=300mm ，流速v 1=6m/s ，为使两断面的压力表读值相同，试求细管直径（水头损失不计）。
gV g p g p 20221++=ρρ解： gvg P g v g P 223222211+⋅=+⋅+ρρ21P P =流量相等222121v d v d =mmd 2352=4.5 为了测量石油管道的流量，安装文丘里流量计，管道直径d 1 =200mm ，流量计喉管直径d 2 =100mm ，石油密度ρ=850kg/m ，流量计流量系数μ=0.95。
静水总压力试题及答案
静水总压力试题及答案一、选择题1. 静水总压力是指（）。
A. 作用在物体表面上的流体压力B. 作用在物体表面上的气体压力C. 作用在物体表面上的固体压力D. 作用在物体表面上的静水压力答案：D2. 静水总压力的计算公式为（）。
A. F = ρghB. F = ρvC. F = pAD. F = ρghA答案：D3. 静水总压力的方向是（）。
A. 垂直向下B. 垂直向上C. 水平D. 与物体表面平行答案：A二、填空题4. 静水总压力是指作用在物体表面上的____压力。
答案：静水5. 静水总压力的计算公式为F = ____。
答案：ρghA6. 静水总压力的方向是____。
答案：垂直向下三、计算题7. 已知一物体浸没在水中，水的密度ρ为1000 kg/m³，重力加速度g为9.8 m/s²，物体的底面积A为0.5 m²，物体底部到水面的距离h为10 m，求物体底部所受的静水总压力。
答案：F = ρghA = 1000 kg/m³ × 9.8 m/s² × 10 m × 0.5 m² = 49000 N四、简答题8. 静水总压力与哪些因素有关？答案：静水总压力与水的密度、物体底部到水面的距离以及物体底面积有关。
9. 静水总压力的方向为什么总是垂直向下？答案：静水总压力的方向总是垂直向下，因为水是不可压缩的流体，其内部压力在各个方向上都是相等的，而物体底部所受的压力是水柱的重量，因此压力的方向与重力的方向一致，即垂直向下。
水力学大纲习题解答
qV
l
4 12104 V 2 0.239（m/s） 2 d 3.14 0.008 4qV
雷诺数
0.239 0.008 Re 127.5 2000 6 1510 Vd
为层流列截面1-1和2-2的伯努利方程
图示 润滑油管路
pa pa V12 V 22 h 1 0 2 hf g 2g g 2g
Re
vd
979 2000
为层流
每小时流量为：
若重油的流动为层流，则：
1 v umax 1.175 m / s 2
用v =1.175m/s计算Re
1 2 Q 1.175 d 3600 4 18.68m 3 / h
例题 : 如图所示水泵管路系统 , 已知：流量 Q=101m3/h,管径d=150mm，管路的总水头 损失 hw1-2=25.4m, 水泵效率 η=75.5% ，试求： （1）水泵的扬程Hp（2）水泵的功率Np
1
1 0
2 0
z
解：由连续性方程得
A2 0.42 v1 v2 1 4m / s 2 A1 0.2
v2 30.2 12 81 H 02 z 1 m 2g 9.8 2 9.8 19.6 P2
2
H 01 H 02
1 2
以0-0为基准面计算两断面的总能量
H0
2
1
解：水头损失
hw h f h j l v2 v2 ( 进 2 弯 出） d 2g 2g
写出1-1到2-2断面的伯努利方程
2
H 00 0 0 0 0 hw
9v 2 hw H0 4 2g
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章静水压力计算
一、是非题
1O重合。
2、静止液体中同一点各方向的静水压强数值相等。
3、直立平板静水总压力的作用点与平板的形心不重合。
4、静止水体中,某点的真空压强为50kPa，则该点相对压强为-50kPa。
5、水深相同的静止水面一定是等压面。
6、静水压强的大小与受压面的方位无关。
7、恒定总流能量方程只适用于整个水流都是渐变流的情况。
二、选择题
1、根据静水压强的特性，静止液体中同一点各方向的压强
（1）数值相等
（2）数值不等
（3）水平方向数值相等
（4）铅直方向数值最大
m，则该点的相对压强为
2、液体中某点的绝对压强为100kN/2
m
（1）1kN/2
m
（2）2kN/2
m
（3）5kN/2
m
（4）10kN/2
m，则该点的相对压强为
3、液体中某点的绝对压强为108kN/2
m
（1）1kN/2
m
（2）2kN/2
m
（3）8kN/2
m
（4）10kN/2
4、静止液体中同一点沿各方向上的压强
（1）数值相等
（2）数值不等
（3）仅水平方向数值相等
5、在平衡液体中，质量力与等压面
（1）重合
（2）平行
（3）正交
6、图示容器中有两种液体，密度ρ2 > ρ1 ，则A、B 两测压管中的液面必为
（1）B 管高于A 管
（2）A 管高于B 管
（3）AB 两管同高。
7、盛水容器a 和b 的测压管水面位置如图(a)、(b) 所示，其底部压强分别为pa和pb。
若两容器内水深相等，则pa和pb的关系为
（1）pa>pb
（2）pa< pb
（3）pa=pb
（4）无法确定
8、下列单位中，哪一个不是表示压强大小的单位
（1）牛顿
（2）千帕
（3）水柱高
（4）工程大气压
三、问答题
1、什么是相对压强和绝对压强？
2、在什么条件下“静止液体内任何一个水平面都是等压面”的说法是正确的？
3、压力中心D和受压平面形心C的位置之间有什么关系？什么情况下D点与C点重合？
4、图示为几个不同形状的盛水容器，它们的底面积AB、水深h均相等。
试说明：
（1）各容器底面所受的静水总压力是否相等？
（2）每个容器底面的静水总压力与地面对容器的反力是否相等？并说明理由（容器的重量不计）。
四、绘图题
1、绘出图中注有字母的各挡水面上的静水压强分布。
2、绘出图中二向曲面上的铅垂水压力的压力体及曲面在铅垂投影面积上的水平压强分布图。
五、计算题
1、如图所示为一溢流坝上的弧形门。
已知：R=10m,门宽b=8m,α=30ο,试求：作用在弧形闸门上的静水总压力；压力作用点位
置。
2、用一简单测压管测量容器中A 的的压强，如下图所示，计算A 点的静水压强及其测压管水头。
3、图示圆弧形闸门AB(1/4圆), A 点以上的水深H ＝1.2m ，闸门宽B=4m ，圆弧形闸门半径R=1m ，水面均为大气压强。
确定圆弧形闸门AB 上作用的静水总压力及作用方向。
4、求图中矩形面板所受静水总压力的大小及作用点位置，已知水深H=2 m ，板宽B ＝3m 。
5、一容器内有密度不同的三种液体,123ρρρ<<如图所示问：
（1）三根测压管中的液面是否与容器中的液面相齐平?如不齐平,试比较各测压管中液面的高度。
（2）图中1-1,2-2,3-3三个水平面是否是等压面?
6、有一水银测压计与盛水的封闭容器连通,如图所示.已知H=3.5m,1h =0.6m,2h =0.4m,求分别用绝对压强,相对压强及真空压强表示容器内的表面压强0p 的值。
7、有一盛水封闭容器,其两侧各接一根玻璃管,如图所示,一管顶端封闭,其水面压强
2
0/3.88m KN asb =ρ,水面与大气接触,已知
m
h 20=.
求：（1）容器内的水面压强c p
； （2）敞口管与容器内的水面高差χ; (3)以真空压强
v
p 表示
p 的大小。
8、有一引水涵洞如图所示，涵洞进口处装有圆形平面闸门，其直径D=0.5m ，闸门上
缘至水面的斜距l = 2 m ,闸门与水面的夹角0
60=α，求闸门上的静水总压力及其作用点的位置。
9、有一距形平面闸门，宽度b=2m,两边承受水压力，如图所示，已知水深
,8,421m h m h ==求闸门上的静水总压力P 及其作用点e 的位置。
10、有一自动开启的距形平面闸门，如图所示，门高h=2m,门宽h=1.5m,其轴O —O 在门的重心C 以下a=0.15m 处，问闸门顶上水深超过多少时，此门将自动开启？并问，作用于闸门上的静水总压力为多少？（不计磨擦和闸门自重）
11、某直径为d 的球形容器内充满水，作用水头为H ，容器上、下两个半球在径向断面AB 的同围用几个铆钉连接，如图所示，设该容器的上半球重量为G ，作用每个铆钉上的拉力。
12、如图所示为一船闸闸室的人字门，已知闸室的宽度B=30m ，闸门偏角0
20=α，
上游水深101=h m,闸室中水深62=h m,求每扇闸门上的静水总压力P 及其作用点e 的位置。
13、有一弧形闸门，闸门宽度b=4m, 闸门前水深H=3m ，对应的圆心角0
45=α，如图所示，求弧形闸门上的静水总压力P 及其作用线的方向。