信号与系统实验题目及答案
信号与系统实验答案1
实验一 离散时间信号的表示及可视化一、实验目的学会对离散时间信号进行标识和可视化处理。
二、实验源程序 (1)f(n)= )(n δn=-5:1:5; f=dirac(n); plot(n,f,'.'); xlabel('(n)'); ylabel('(f)'); axis([-5 5 -0.5 1.5])(2) f(n)=ε(n)f=Heaviside(n)n=-5:1:5; f=heaviside(n); plot(n,f,'.'); xlabel('(n)'); ylabel('(f)');axis([-5 5 -0.5 1.5]) (3) f(n)= ane (分别取a>0及a<0)a=1时 n=-5:1:5; f=exp(n); plot(n,f,'.');a=-1时 n=-5:1:5; f=exp(-n); plot(n,f,'.');(4) f(n)=R N (n) (分别取不同的N 值)N=10时 n=0:1:9; f=1;plot(n,f,'.');N=15时 n=0:1:14; f=1;plot(n,f,'.') (5) f(n)=Sa(nw)w=0.1时n=-45:1:45;f=sinc(0.1*n);plot(n,f,'.');xlabel('n');ylabel('f');axis([-50 50 -1 1])w=0.2时n=-45:1:45;f=sinc(0.2*n);plot(n,f,'.');xlabel('n');ylabel('f');axis([-50 50 -1 1])(6)f(n)=Sin(nw)(分别取不同的w值)w=100时n=-15:1:15;f=sin(100*n);plot(n,f,'.');xlabel('n');ylabel('f');w=200时n=-15:1:15;f=sin(200*n);plot(n,f,'.');xlabel('n');ylabel('f');三、程序运行结果及波形图（1）（2）（3）-5-4-3-2-1012345(n)(f)-5-4-3-2-1012345(n)(f)（4）0123456789024********（5）（6）-50-40-30-20-1001020304050-1-0.8-0.6-0.4-0.200.20.40.60.81nf-50-40-30-20-1001020304050-1-0.8-0.6-0.4-0.200.20.40.60.81nffnf-15-10-5051015n四、实验调试体会实验二 连续时间信号的表示及可视化一、实验目的熟练掌握连续时间信号的表示及可视化处理。
信号与系统练习题(带答案)
信号与系统练习题（带答案）1. 信号f(t)的波形如图所示。
分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形，并且写出其表达式。
答案：2. 信号f ( t )的图形如下所示，对(a)写出f ' ( t )的表达式，对(b)写出f " ( t )的表达式，并分别画出它们的波形。
解 (a)20,21≤≤tf ' (t)= δ(t -2)， t = 2-2δ(t -4)， t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示，试画出f(t)的波形。
52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析（）右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得－2t ，即f(5-2t)左移(52)(2)f t f t -−−−→-时移由（2）反转：f(-2t)中以-t 代替t ，可求得f(2t),表明f(-2t)的波形 以t ＝0的纵轴为中心线对褶，注意()t δ是偶数，故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由（3）尺度变换：以12t 代替f(2t)中的t ，所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。
4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。
解：{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。
(完整word版)信号与系统专题练习题及答案
信号与系统专题练习题一、选择题1．设当t 〈3时，x(t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。
A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-22．设当t 〈3时，x （t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。
A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—23．设当t<3时，x(t ）=0，则使x （t/3)=0的t 值为 C 。
A t>3 B t=0 C t<9 D t=34．信号)3/4cos(3)(π+=t t x 的周期是 C 。
A π2 B π C 2/π D π/2 5．下列各表达式中正确的是 BA. )()2(t t δδ= B 。
)(21)2(t t δδ= C. )(2)2(t t δδ= D 。
)2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。
已知 系统的激励e(t ）与响应r （t)的关系为:)()(2t e t r = 则该系统为 C .A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。
⎰∞-=t d ττττδ2sin )( A 。
A 2u （t ） B )(4t δ C 4 D 4u （t) 10. dt t t )2(2cos 33+⋅⎰-δπ等于 B 。
A 0 B —1 C 2 D —211．线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置；B 激励信号的形式;C 系统起始状态；D 以上均不对。
12．若系统的起始状态为0，在x （t)的激励下，所得的响应为 D . A 强迫响应;B 稳态响应；C 暂态响应;D 零状态响应。
(完整版)信号与系统练习及答案
信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（ ） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（ ） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（ ） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（ ） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。
2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。
3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。
信号与系统考题参考解答(完整版)
《信号与系统》作业参考解答第一章（P16-17）1-3 设)(1t f 和)(2t f 是基本周期分别为1T 和2T 的周期信号。
证明)()()(21t f t f t f +=是周期为T 的周期信号的条件为T nT mT ==21 （m ,n 为正整数） 解：由题知)()(111t f mT t f =+ )()(222t f mT t f =+要使)()()()()(2121t f t f T t f T t f T t f +=+++=+则必须有21nT mT T == （m ,n 为正整数） 1-5 试判断下列信号是否是周期信号。
若是，确定其周期。
（1）t t t f πsin 62sin 3)(+= （2）2)sin ()(t a t f =（8）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2cos 28sin 4cos )(k k k k f πππ解：（1）因为t 2sin 的周期为π，而t πsin 的周期为2。
显然，使方程n m 2=π （m ,n 为正整数）成立的正整数m ,n 是不存在的，所以信号t t t f πsin 62sin 3)(+=是非周期信号。
（2）因为)2cos 1()sin ()(22t a t a t f -==所以信号2)sin ()(t a t f =是周期π=T 的周期信号。
（8）由于)4/cos(k π的周期为8)4//(21==ππN ，)8/sin(k π的周期为16)8//(22==ππN ，)2/cos(k π的周期为4)2//(23==ππN ，且有16412321=⨯=⨯=⨯N N N所以，该信号是周期16=N 的周期信号。
1-10 判断下列系统是否为线性时不变系统，为什么？其中)(t f 、][k f 为输入信号，)(t y 、][k y 为零状态响应。
（1）)()()(t f t g t y = （2）)()()(2t f t Kf t y += 解：（1）显然，该系统为线性系统。
信号与系统实验答案
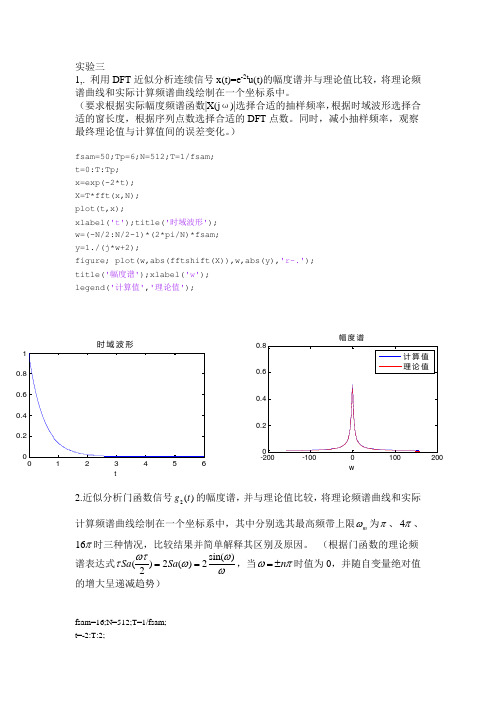
实验三1,. 利用DFT 近似分析连续信号x(t)=e -2t u(t)的幅度谱并与理论值比较，将理论频谱曲线和实际计算频谱曲线绘制在一个坐标系中。
（要求根据实际幅度频谱函数|X(j ω)|选择合适的抽样频率，根据时域波形选择合适的窗长度，根据序列点数选择合适的DFT 点数。
同时，减小抽样频率，观察最终理论值与计算值间的误差变化。
）fsam=50;Tp=6;N=512;T=1/fsam; t=0:T:Tp; x=exp(-2*t); X=T*fft(x,N); plot(t,x);xlabel('t');title('时域波形'); w=(-N/2:N/2-1)*(2*pi/N)*fsam; y=1./(j*w+2);figure; plot(w,abs(fftshift(X)),w,abs(y),'r-.'); title('幅度谱');xlabel('w'); legend('计算值','理论值');2.近似分析门函数信号2()g t 的幅度谱，并与理论值比较，将理论频谱曲线和实际计算频谱曲线绘制在一个坐标系中，其中分别选其最高频带上限m ω为π、4π、16π时三种情况，比较结果并简单解释其区别及原因。
（根据门函数的理论频谱表达式sin()()2()22Sa Sa ωτωτωω==，当n ωπ=±时值为0，并随自变量绝对值的增大呈递减趋势）fsam=16;N=512;T=1/fsam; t=-2:T:2;12345600.20.40.60.81t时域波形-200-100010020000.20.40.60.8幅度谱wx=[(t>=-1)&(t<=1)];X=T*fft(x,N);%消除1/T 因子的影响 plot(t,x);xlabel('t');title('时域波形'); w=(-N/2:N/2-1)*(2*pi/N)*fsam; y=2*sin(w)./w;%理论频谱值figure; plot(w,abs(fftshift(X)),w,abs(y),'r-.'); title('幅度谱');xlabel('w'); legend('计算值','理论值');-2-1.5-1-0.500.51 1.5200.20.40.60.81t时域波形-60-40-20020406000.511.522.5幅度谱w实验四。
信号与系统课后习题参考答案
1试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。
题图1-51-6试画出下列信号的波形图：⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。
信号与系统习题(陈后金版)
4-8 已知周期信号f(t)=2cos(2лt-3)+sin(6лt), 求傅立叶级数指数表示式，并画出其频谱．
0 2
f (t ) e
j ( 2t 3 )
e
j ( 2t 3 )
• 3-16
• 3-24
解：
•
3-26
3-39 计算序列卷积和。 （1）2ku[k]*u[k-4] （3）（1/2）k u[k]*u[k]
(1)
n
2 u[n] u[k n 4] 2 n u[k 4]
n n0
k 4
1 2 k 3 u[k 4] (2 k 3 1)u[k 4] 1 2
动态方程式的特征根s1，2 = -1,2, 且n>m, 故h(t)的形式为
3 8 为y(t ) (3te
2 t
e
2 t
e )u(t )
t
1 t 1 3 t 2 t 3 7 y f (t ) ( e e e )u (t ) 2 2
3-14
3-14
• （2） y"(t ) 4 y' (t ) 4 y(t ) 3 f＇) 2 f (t ),t 0; f (t ) et u(t )，y(0 ) 2, y' (0 ) 3 (t
动态方程式的特征根s1，2 =
2, 则零输入响应的形式为
2 t
y x (t ) K1e
动态方程式的特征根s1，2 = -1,2, 且n>m, 故h(t)的形式为
3 8 为y(t ) (3te
信号与系统试题及解答8
1. 试判断下图所示周期信号的傅氏级数展开式中，含有哪些分量。
【答】：观察此信号的波形可看出，)(t f 为奇函数且是奇谐函数（波形平移后，与原信号的波形以横轴成镜像对称），所以，)(t f 的傅氏级数展开式中只含有奇次谐波的正弦分量，而不会含有余弦分量和偶次谐波分量。
4.2 试判断下图所示周期信号)(t f 的傅氏级数展开式中，含有哪些分量。
【答】：观察)(t f 波形，可看出)(t f 是偶函数且是偶谐函数（波形平移后，与原信号的波形完全重合），所以，)(t f 的傅氏级数展开式中只含有直流分量和偶次谐波的余弦分量，而不会含有正弦分量和奇次谐波分量。
2. 试求下列信号)(t f 的傅氏变换)(ωj F 。
（1）)()(3t et f tε-=； （2）)1()(3-=-t e t f t ε； （3）)()()1(3t e t f t ε--=；（4）t t f 4cos )(=； （5）)4()(t Sa t f =； （6）t t g t f 0cos )()(ωτ=； 【解】：（1）因为 αωεα+−→←-j t et1)(，所以31)(+=ωωj j F（2）因为 )1()1()()1(333-⋅=-=----t ee t e tf t t εε， αωεωα+−→←----j e t ej t )1()1(， 所以 33)()3(3+=+=+---ωωωωωj e j e ej F j j（3）因为 )()()(33)1(3t e e t et f t t εε---==，而αωεα+−→←-j t e t 1)(所以 31)(3+⋅=-ωωj ej F（4）因为 [])()()(cos 000ωωδωωδπεω-++−→←t t所以 [])4()4()(4cos -++−→←ωδωδπεt t （5）因为 [])()()()(0002000ωωεωωεωπωωπωω--+=−→←g t Sa 所以 [])4()4(4)(4)4(8--+=−→←ωεωεπωπg t Sa（6） 因为 {})]([)]([21)(cos )(000ωωωωεω+++−→←⋅j F j F t t t f)2()(τωττSa t g −→←所以 ⎭⎬⎫⎩⎨⎧-++−→←⋅)](2[)](2[2)(cos )(000ωωτωωττεωτSa Sa t t t g3. 试求门函数)(4t g 的频谱密度函数，并指出此门函数的等效频带宽度是多少。
信号与系统实验网上答案
信号与系统实验网上答案第一篇：信号与系统实验网上答案目的：通过MATLAB编程实现对时域抽样定理的验证，加深抽样定理的理解。
同时训练应用计算机分析问题的能力。
任务：连续信号f(t)=cos(8*pi*t)+2*sin(40*pi*t)+cos(24*pi*t)，经过理想抽样后得到抽样信号fs(t)，通过理想低通滤波器后重构信号f(t)。
方法：1、确定f(t)的最高频率fm。
对于无限带宽信号，确定最高频率fm的方法：设其频谱的模降到10-5左右时的频率为fm。
2、确定Nyquist抽样间隔TN。
选定两个抽样时间：TSTN。
3、MATLAB的理想抽样为n=-200:200;nTs=n*Ts;或 nTs=-0.04:Ts:0.044、抽样信号通过理想低通滤波器的响应理想低通滤波器的冲激响应为系统响应为由于所以MATLAB计算为ft=fs*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));要求（画出6幅图）：当TS1、在一幅图中画原连续信号f(t)和抽样信号fS(t)。
f(t)是包络线，fS(t)是离散信号。
2、画出重构的信号y(t)。
3、画出误差图，即error=abs(f(t)-y(t))的波形。
当TS>TN时同样可画出3幅图。
%a wm=40*pi;wc=1.2*wm;%理想低通截止频率Ts=[0.02 0.03];N=length(Ts);for k=1:N;n=-100:100;nTs=n*Ts(k);fs=(cos(8*pi*nTs)+2*sin(40*pi*nTs)+cos(24*pi*nTs)).*(u(nTs+ pi)-u(nTs-pi));t=-0.25:0.001:0.25;ft=fs*Ts(k)*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));t1=-0.25:0.001:0.25;f1=(cos(8*pi*t1)+2*sin(40*pi*t1)+cos(24*pi*t1)).*(u(t1+0.25) -u(t1-0.25));%在一副图中画原连续信号f(t)和样信号f_s(t)。
信号与系统实验答案
实验十二：连续时间系统的频域分析例题：1、使用MATLAB 函数实现下列信号的傅里叶变换，并画出变换后的曲线 求出e -|2t|的傅里叶变换，并画出变换后的曲线clear all; syms t f;f=fourier(exp((-2)*abs(t))); ezplot(f);-6-4-224600.10.20.30.40.50.60.70.80.91w4/(4+w 2)1、 使用MATLAB 函数实现下列信号的傅里叶逆变换 已知F （jw ）=1/1+w 2,求信号的逆傅里叶变换syms t w;ifourier(1/(1+(w^2)),t);ans1/2*exp(-t)*heaviside(t)+1/2*exp(t)*heaviside(-t)3、使用MATLAB函数实现傅里叶的时移特性画出f（t）=1/2e-2t u(t)和f(t-1)的频谱图，观察信号时移对频谱的影响clear all;r=0.02;t=-5:r:5;N=200;w=2*pi;k=-N:N;w=k*w/N;f1=1/2*exp(-2*t).*stepfun(t,0);F=r*f1*exp(-j*t'*w);F1=abs(F);P1=angle(F);subplot(3,1,1);plot(t,f1);grid on;ylabel('f(t)');title('f(t)'); subplot(3,1,2); plot(w,F1); xlabel('w');grid on;ylabel('F(jw)'); subplot(3,1,3); plot(w,P1*180/pi); grid;xlabel('w'); ylabel('相位度');。
-5-4-3-2-10123450.5tf (t )f(t)-8-6-4-20246800.20.4wF (j w )-8-6-4-202468-100100w相位(度)4、 使用MATLAB 函数实现下列信号的频移变换已知f （t ）为门函数，求f 1（t ）= f （t ）e -j5t 以及f 2（t ）e j5t 的频谱图clear all; R=0.02; t=-2:R:2;f=stepfun(t,-1)-stepfun(t,1); f1=f.*exp(-j*5*t); f2=f.*exp(j*5*t); N=500; W1=5*pi; k=-N:N; W=k*W1/N;。
信号与系统试题及答案
信号与系统试题1第一部分 选择题（共32分）一、单项选择题(本大题共16小题，每小题2分，共32分。
在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内)1．积分e d t --∞⎰2τδττ()等于（ ）A ．δ()tB ．ε()tC ．2ε()tD ．δε()()t t +2．已知系统微分方程为dy t dt y t f t ()()()+=2，若y f t t t (),()sin ()012+==ε，解得全响应为y t e t t ()sin()=+-︒-54242452，t ≥0。
全响应中24245sin()t -︒为（ ） A ．零输入响应分量 B ．零状态响应分量C ．自由响应分量D ．稳态响应分量3．系统结构框图如图示，该系统的单位冲激响应h(t)满足的方程式为（ ）A ．dy t dt y t x t ()()()+= B ．h t x t y t ()()()=- C ．dh t dt h t t ()()()+=δ D ．h t t y t ()()()=-δ4．信号f t f t 12(),()波形如图所示，设f t f t f t ()()*()=12，则f()0为（ ）A ．1B ．2C ．3D ．45．已知信号f t ()的傅里叶变换F j ()()ωδωω=-0，则f t ()为（ ）A ．120πωe j t B ．120πωe j t - C ．120πεωe t j t () D ．120πεωe t j t -()6．已知信号f t ()如图所示，则其傅里叶变换为（ ）A ．τωττωτ2422Sa Sa ()()+B ．τωττωτSa Sa ()()422+ C ．τωττωτ242Sa Sa ()()+ D ．τωττωτSa Sa ()()42+7．信号f t 1()和f t 2()分别如图（a ）和图(b)所示，已知 [()]()f t F j 11=ω，则f t 2()的 傅里叶变换为（ ）A ．F j e j t 10()--ωωB ．F j e j t 10()ωω-C ．F j e j t 10()-ωωD ．F j e j t 10()ωω8．有一因果线性时不变系统，其频率响应H j j ()ωω=+12，对于某一输入x(t)所得输出信号的傅里叶变换为Y j j j ()()()ωωω=++123，则该输入x(t)为（ ） A ．--e t t 3ε()B ．e t t -3ε()C ．-e t t 3ε()D ．e t t 3ε()9．f t e t t ()()=2ε的拉氏变换及收敛域为（ ）A ．122s s +>-,Re{} B ．122s s +<-,Re{} C ．122s s ->,Re{} D ．122s s -<,Re{} 10．f t t t ()()()=--εε1的拉氏变换为（ ） A ．11s e s ()--B ．11s e s ()-C ．s e s ()1--D ．s e s ()1-11．F s s s s s ()Re{}=+++>-25622的拉氏反变换为（ ）A ．[]()e e t t t --+322εB ．[]()e e t t t ---322εC ．δε()()t e t t +-3D ．e t t -3ε()12．图（a ）中ab 段电路是某复杂电路的一部分，其中电感L 和电容C 都含有初始状态，请在图（b ）中选出该电路的复频域模型。
信号与系统试卷及参考答案
试卷及答案信号与系统试卷（1）（满分：100分，所有答案一律写在答题纸上）考试班级学号姓名成绩考试日期：年月日，阅卷教师：考试时间120分钟，试卷题共2页一一线性非时变离散系统，具有一初始状态x(0)，当激励为时f(k)，响应为y(k)=((1/2)k+1)u(k)；若初始状态不变，当激励为-f(k)时，响应y(k)=((-1/2)k-1)u(k)为；试求当初始状态2x(0)为，激励为4f(k)时，系统的响应？（10分）二绘出下列函数的图形（1）.已知一连续时间信号x(t)如图所示，试概略画出信号y(t)=x(2-t/3)的波形图。
（8分）t-1 0 1 2 3(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
（8分）三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt （4分） (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) （8分）(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) （8分） （4） 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 （8分） （5）y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? （8分） （6）. y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? （8分）四 一线性非时变因果系统，当激励为u(t)时，响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ，求当激励f(t)=δ(t)时的响应)(t h 。
（10分）五 某一子系统，当输入f(t)=e -t u(t)时，零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时，总系统的冲激响应。
信号与线性系统分析试题及答案(10套)
标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。
3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。
4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。
5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。
信号与系统习题及答案
10通信 信号与系统习题及答案1、无失真传输系统，其幅频特性为 ，相频特性为 。
2、某连续LTI 系统的单位冲激响应为h(t)，则该系统稳定的充要条件是 。
3、某连续LTI 系统的单位冲激响应为h(t)，则该系统因果的充要条件是 。
4、信号Sa(500t)的频谱密度函数为 ，频带宽度为 Hz(只计正频率)。
5、信号)(cos )(0t t w t f ε=的拉普拉斯变换表达式是 。
6、描述线性时不变连续系统的输入输出方程是 。
7、单边拉普拉斯变换F(s)=1+s 的原函数f(t)= 。
8、 描述线性时不变连续系统的输入输出方程是 。
已知离散信号 请问：该信号是否是周期信号 ，若是，则周期应为多少 。
9、已知,0)(≥t f )()1()(*)(t e t t f t f t ε--='，则)(jw F = ，)(t f = 。
1、下列各表达式中正确的是（ ）（A ）)()2(t t δδ= （B ）)(21)2(t t δδ=（C ）)(2)2(t t δδ= （D ）)2(21)(2t t δδ= 2、设：f(t)↔F(jω) 则f 1(t)=f(at+b)，a>0，的频谱F 1(jω)为( )(A) F 1(jω)=aF(j a ω)e -j bw (B) F 1(jω)=a 1F(j aω)e -j bw (C) F 1(jω)= a 1F(j a ω)ω-a b j e (D) F 1(jω)=aF(j aω)ω-a b j e 3、如图所示周期信号)(t f ，设其傅立叶系数为n C ，则0C = 。
A. 10B. 5C. 20D. 154、若矩形脉冲信号的脉宽加宽，则它的频带宽度（ ）(A) 不变 (B) 变窄 (C) 变宽 (D) 与脉冲宽度无关238cos()(πk k f =t f 1 (t)121-10tf 2 (t)121-10f(t)t0115、 无失真传输的条件是( )(A) 幅频特性等于常数 (B) 相位特性是通过原点的直线(C) 幅频特性等于常数，相位特性是通过原点的直线(D) 幅频特性是通过原点的直线，相位特性等于常数6、信号)()1()(2t u e t t f t --=的拉氏变换为（ ）(A) 2)2(1+s (B) 2)2(+s s (C) 22)2(+s s (D) 2)2(1++s s7、积分式⎰-+++4422)]dt -(t 2(t))[23(δδt t 的积分结果是（ ）（A) 14 （B) 24 （C ）26 （D ）288、若连续时间系统是因果稳定的，则其系统函数的极点 。
信号与系统 测试题(附答案)
《信号与系统》测试题2一、选择题（共10题，每题3分 ，共30分，每题给出四个答案，其中只有一个正确的）1、 卷积f 1(k+5)*f 2(k-3) 等于 。
（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
（A ）1.25（B ）2.5（C ）3（D ）5 3、 序列f(k)=-u(-k)的z 变换等于 。
（A ）1-z z （B ）-1-z z（C ）11-z （D ）11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
（A ）)2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —tu(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t)（C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性（C ）离散性、周期性 （D ）离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换()se ss s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D10、信号()()23-=-t u te t f t 的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s ()()()2323++-s se C s ()()332++-s s e D s二、填空题（共9小题，每空3分，共30分）1、 卷积和[（0.5）k+1u(k+1)]*)1(k -δ=________________________2、 单边z 变换F(z)=12-z z的原序列f(k)=______________________3、 已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________ 4、 频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、 单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、 已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、 已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=20)()(t dxx f t y 的单边拉氏变换Y(s)=______________________________ 8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=k t 22三、（8分）已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
信号与系统实验答案
信号与系统实验答案验教（实验报告）班级:姓名:程实目录实验一：连续时间信号与系统的时域分析-------------------------------------------------4一、实验目的及要求---------------------------------------------------------------------------4二、实验原理-----------------------------------------------------------------------------------41、信号的时域表示方法------------------------------------------------------------------52、用MATLAB仿真连续时间信号和离散时间信号----------------------------------53、LTI系统的时域描述-----------------------------------------------------------------10三、实验步骤及内容--------------------------------------------------------------------------14四、实验报告要求-----------------------------------------------------------------------------26实验二：连续时间信号的频域分析---------------------------------------------------------27一、实验目的及要求--------------------------------------------------------------------------27二、实验原理----------------------------------------------------------------------------------271、连续时间周期信号的傅里叶级数CTFS---------------------------------------------272、连续时间信号的傅里叶变换CTFT--------------------------------------------------283、离散时间信号的傅里叶变换DTFT-------------------------------------------------294、连续时间周期信号的傅里叶级数CTFS的MATLAB实现------------------------295、用MATLAB实现CTFT及其逆变换的计算---------------------------------------33三、实验步骤及内容----------------------------------------------------------------------35四、实验报告要求-------------------------------------------------------------------------49实验三：连续时间LTI系统的频域分析---------------------------------------------------50一、实验目的及要求--------------------------------------------------------------------------50二、实验原理----------------------------------------------------------------------------------501、连续时间LTI系统的频率响应-------------------------------------------------------502、LTI系统的群延时---------------------------------------------------------------------513、用MATLAB计算系统的频率响应--------------------------------------------------52三、实验步骤及内容----------------------------------------------------------------------53四、实验报告要求-------------------------------------------------------------------------59实验四：通信系统仿真------------------------------------------------------------------------60一、实验目的及要求--------------------------------------------------------------------------60二、实验原理----------------------------------------------------------------------------------601、信号的抽样及抽样定理---------------------------------------------------------------602、信号抽样过程中的频谱混叠----------------------------------------------------------6323、信号重建-------------------------------------------------------------------------------644、调制与解调----------------------------------------------------------------------------------665、通信系统中的调制与解调仿真---------------------------------------------------------68三、实验步骤及内容------------------------------------------------------------------------68四、实验报告要求---------------------------------------------------------------------------78实验五：连续时间LTI系统的复频域分析----------------------------------------------79一、实验目的及要求------------------------------------------------------------------------79二、实验原理--------------------------------------------------------------------------------791、连续时间LTI系统的复频域描述--------------------------------------------------792、系统函数的零极点分布图-----------------------------------------------------------------813、拉普拉斯变换与傅里叶变换之间的关系-----------------------------------------------814、系统函数的零极点分布与系统稳定性和因果性之间的关系------------------------825、系统函数的零极点分布与系统的滤波特性-------------------------------------------836、拉普拉斯逆变换的计算-------------------------------------------------------------84三、实验步骤及内容------------------------------------------------------------------------86四、实验报告要求---------------------------------------------------------------------------913实验一信号与系统的时域分析一、实验目的1、熟悉和掌握常用的用于信号与系统时域仿真分析的MATLAB函数；2、掌握连续时间和离散时间信号的MATLAB产生，掌握用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号的MATLAB编程；3、牢固掌握系统的单位冲激响应的概念，掌握LTI系统的卷积表达式及其物理意义，掌握卷积的计算方法、卷积的基本性质；4、掌握利用MATLAB计算卷积的编程方法，并利用所编写的MATLAB程序验证卷积的常用基本性质；掌握MATLAB描述LTI系统的常用方法及有关函数，并学会利用MATLAB求解LTI系统响应，绘制相应曲线。
信号与系统实验指导全部实验答案
信号与系统实验指导全部实验答案实验一连续时间信号的MATLAB 表示实验目的 1．掌握MATLAB 语言的基本操作，学习基本的编程功能； 2．掌握MATLAB 产生常用连续时间信号的编程方法；3．观察并熟悉常用连续时间信号的波形和特性。
实验原理：1. 连续信号MA TLAB 实现原理从严格意义上讲，MATLAB 数值计算的方法并不能处理连续时间信号。
然而，可用连续信号在等时间间隔点的取样值来近似表示连续信号，即当取样时间间隔足够小时，这些离散样值能够被MATLAB 处理，并且能较好地近似表示连续信号。
MATLAB 提供了大量生成基本信号的函数。
比如常用的指数信号、正余弦信号等都是MATLAB 的内部函数。
为了表示连续时间信号，需定义某一时间或自变量的范围和取样时间间隔，然后调用该函数计算这些点的函数值，最后画出其波形图。
实验内容：正弦信号抽样信号矩形脉冲信号单位跃阶信号实验编程：（1）t=0:0.01:3;K=2;a=-1.5;w=10; ft=K*exp((a+i*w)*t); A=real(ft); B=imag(ft); C=abs(ft);D=angle(ft);subplot(2,2,1),plot(t,A),grid on;title('实部');subplot(2,2,2),plot(t,B),grid on;title('虚部'); subplot(2,2,3),plot(t,C),grid on;title('取模'); subplot(2,2,4),plot(t,D),grid on;title('相角');实部2211-1-2-1取模相角25100-5（2）t=0:0.001:3;y=square(2*pi*10*t,30);方波信号plot(t,y);axis([0,1,-1,1]); title('方波信号');0.5-0.5-1 00.20.40.60.81（3）t=-2:0.01:2;y=uCT(t+0.5)-uCT(t-0.5); plot(t,y),grid on axis([-2,2,0,1.5]); xlabel('t(s)'),ylabel('y(s)') title('门函数')10.50 -2-1.5-1-0.5门函数y (s )0t(s)0.511.52实验二连续时间LTI 系统的时域分析实验目的1．运用MATLAB 符号求解连续系统的零输入响应和零状态响应； 2．运用MATLAB 数值求解连续系统的零状态响应； 3．运用MATLAB 求解连续系统的冲激响应和阶跃响应；4．运用MATLAB 卷积积分法求解系统的零状态响应。
(完整版)信号与系统练习及答案
信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（ ） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（ ） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（ ） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（ ） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。
2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。
3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一个信号实验的题目1实现下列常用信号 （1）(5)u t +；（2）(1)t δ-；（3）cos(3)sin(2)t t +；（4）()[(1)(2)]f t t u t t u t t =⨯---； （5）0.5()4cos(),010t f t e t t π-=⨯= 2连续信号的基本运算与波形变换已知信号22,21()33t t f t ⎧-+-≤≤⎪=⎨⎪⎩，试画出下列各函数对时间t 的波形： （1）()f t -（2）(2)f t -+（3）(2)f t （4）1(1)2d f t dt +（5）(2)t f d ττ-∞-⎰3连续信号的卷积运算实现12()()f t f t *，其中1()f t 、2()f t 从第2个题目中任选3对组合。
4连续系统的时域分析（1） 描述某连续系统的微分方程为()2()()()2()y t y t y t f t f t ''''++=+，求当输入信号为2()2()t f t e u t -=时，该系统的零状态响应()y t 。
（2） 已知描述某连续系统的微分方程为2()()3()()y t y t y t f t '''+-=，试用MATLAB 绘出该系统的冲激响应和阶跃响应的波形。
实验一答案：（1）(5)u t +在MATLAB 软件的输入程序及显示波形如下：（2）(1)t δ-在MATLAB 软件的输入程序及显示波形如下：（3）cos(3)sin(2)t t +在MATLAB 软件的输入程序及显示波形如下：（4）()[(1)(2)]f t t u t t u t t =⨯---在MATLAB 软件的输入程序及显示波形如下：（5）0.5()4cos(),010t f t e t t π-=⨯=在MATLAB 软件的输入程序及显示波形如下：（1）()f t-的输入程序及波形如下：（2）(2)f t-+的输入程序及波形如下：（3）(2)f t的输入程序及波形如下：（2）系统的冲激响应和阶跃响应如下：（4）1(1)2df tdt+的输入程序及波形如下：（5）(2)t f d ττ-∞-⎰的输入程序及波形如下：（1）()f t -和（2）(2)f t -+组合的卷积运算如下：（2）(2)f t -+和（3）(2)f t 组合的卷积运算如下：（1）()f t 和（3）(2)f t 组合的卷积运算如下：（1）系统的零状态响应()y t 如下：第二个信号实验题目1（1）用数值法求门函数4()G t 的傅里叶变换，并给出门函数的幅频特性曲线和相频特性曲线。
（2）用符号法给出函数5()2()()3t f t e u t -=的傅里叶变换。
（3）已知系统函数为3421()3s s H s s s ++=++，画出该系统的零极点图。
2（1）用数值法给出函数5(2)2()(2)3t f t e u t --=-幅频特性曲线和相频特性曲线。
（2）对函数5(2)2()(2)3t f t e u t --=-进行采样，采样间隔为0.01。
（3）已知输入信号为()sin(100)f t t =，载波频率为1000Hz ，采样频率为5000 Hz ，试产生输入信号的调幅信号。
3（1）用符号法实现函数4()G t 的傅里叶变换，并给出门函数的幅频特性曲线和相频特性曲线。
（2）已知系统函数为3421()3s s H s s s ++=++，输入信号为()sin(100)f t t =，求该系统的稳态响应。
（3）已知输入信号为()sin(100)f t t =，载波频率为100Hz ，采样频率为400 Hz ，试产生输入信号的调频信号。
4（1）已知系统函数为231()3s s H s s s ++=++，画出该系统的零极点图。
（2）已知函数5()2()()3t f t e u t -=用数值法给出函数(3)f t 的幅频特性曲线和相频特性曲线。
（3）实现系统函数3421()3s s H s s s ++=++的频率响应。
（4）已知输入信号为()cos(100)f t t =，载波频率为100Hz ，采样频率为400 Hz ，试产生输入信号的调相信号。
5（1）用数值法给出函数5(2)2()(2)3t f t e u t -+=+幅频特性曲线和相频特性曲线。
（2）用符号法实现函数22i ω+的傅里叶逆变换。
（3）已知输入信号为()5sin(200)f t t =，载波频率为1000Hz ，采样频率为5000 Hz ，试产生输入信号的调频信号。
实验二答案：（1） 用数值法求门函数4()G t 的傅里叶变换，并给出门函数的幅频特性曲线和相频特性曲线。
t=linspace(-4,4,200); f=0*t;f(t>=-2&t<=2)=1;W=linspace(-4*pi,4*pi,200); F=0*W; for N=1:200 for M=1:200F(N)=F(N)+8/200*f(M).*exp(-j*W(N)*t(M)); end endsubplot(4,4,1); plot(t,f); subplot(4,4,2); plot(W,F); subplot(4,4,3); plot(W,abs(F)); H=freqs(6,9,W); subplot(4,4,4); plot(W,angle(F))（2） 用符号法给出函数5()2()()3t f t e u t -=的傅里叶变换。
syms t f ;f=sym('(2/3)*exp(-5*t)*heaviside(t)'); F=fourier(f); pretty(F)（3） 已知系统函数为3421()3s s H s s s ++=++，画出该系统的零极点图。
num=[0 1 0 1 1]; den=[1 0 1 0 3]; G=tf(num,den); subplot(2,2,1); pzmap(G);0.51 1.52 2.53 3.54 4.550.511.5幅频曲线00.51 1.52 2.53 3.54 4.55-4-224相频曲线0123456789100.10.20.30.40.50.60.7-1-0.8-0.6-0.4-0.20.20.40.60.81时间(s)幅值1计算序列)(2)(1n u n f n =与序列)5()()(2--=n u n u n f 的卷积和；2已知离散系统的差分方程为()5(1)6(2)()y n y n y n f n --+-=，求系统的频率响应，若()2()n f n u n =，求系统的零状态响应。
3利用SIMULINK 画出（2）的系统框图。
实验三答案：1. 计算序列)(2)(1n u n f n=与序列)5()()(2--=n u n u n f 的卷积和；n=0:1:10;x=2.^nstem(n,x)n=0:1:4x1=ones(1,5)stem(n1,x1)y=conv(x,x1)n2=0:1:14stem(n2,y)2. 已知离散系统的差分方程为()5(1)6(2)()y n y n y n f n --+-=，求系统的频率响应，若()2()n f n u n =，求系统的零状态响应。
b=[1];a=[1,-5,6];w=linspace(0,50,200);freqs(b,a,w)n=[0:10];f=2.^n;a=[1,-5,6];b=[1];y=[0];xic=filtic(b,a,y);y1=filter(b,a,f,xic)1求()cos()()f n an u n =的Z 变换和2()()az F z z a =-的Z 反变换。
2已知某离散系统的系统函数为23221()0.50.0050.3z z H z z z z ++=--+，试用MATLAB 求出该系统的零极点，并画出零极点图，求系统的单位冲激响应和幅频响应，并判断系统是否稳定。
3 一系统的微分方程为()5()10()()y t y t y t f t '''++=，试利用MA TLAB 求其系统的状态方程。
4 已知某连续时间系统的状态方程和输出方程为.111.222()()()230101()10()()x t x t f t x t f t x t ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥=⋅+⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 111222()()()1110()01()10()y t x t f t y t x t f t ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=⋅+⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 试用M ATLAB 计算其系统函数矩阵()H s 。
实验四答案：求()cos()()f n an u n =的Z 变换和2()()az F z z a =-的Z 反变换。
1. syms a nf=cos(a*n);F=ztrans(f);pretty(F)syms k zFz=a*z/(z-a)^2;fk=iztrans(Fz,k);pretty(fk);2. 已知某离散系统的系统函数为23221()0.50.0050.3z z H z z z z ++=--+，试用MATLAB 求出该系统的零极点，并画出零极点图，求系统的单位冲激响应和幅频响应，并判断系统是否稳定。
b=[0,1,2,1]a=[1,-0.5,-0.005,0.3][R,P,K]=tf2zp(b,a)figure(1)zplane(b,a)legend('零点','极点');grid on ;num=[0 1 2 1]den=[1 -0.5 -0.005 0.3]h=impz(num,den)figure(2)stem(h)[H,w]=freqz(num,den)figure(3)plot(abs(H))3. 一系统的微分方程为()5()10()()y t y t y t f t '''++=，试利用MATLAB 求其系统的状态方程。
a=[1]; a = 1b=[1 5 10 ]; b = 1 5 10[A B C D]=tf2ss(a,b); A = -5 -10 B = 1 1 0 0C = 0 1D = 04. 已知某连续时间系统的状态方程和输出方程为.111.222()()()230101()10()()x t x t f t x t f t x t ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥=⋅+⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 111222()()()1110()01()10()y t x t f t y t x t f t ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=⋅+⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦试用MATLAB 计算其系统函数矩阵()H s 。