信号与系统实验指导全部实验答案
信号与系统matlab实验及答案
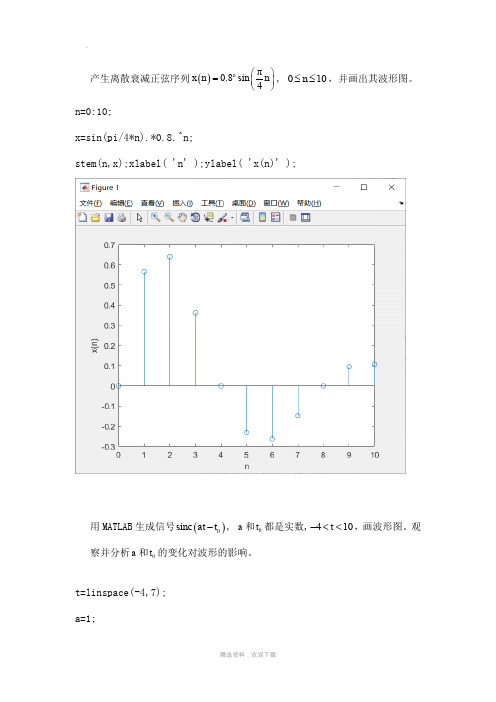
产生离散衰减正弦序列()π0.8sin 4n x n n ⎛⎫= ⎪⎝⎭, 010n ≤≤,并画出其波形图。
n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB 生成信号()0sinc at t -, a 和0t 都是实数,410t -<<,画波形图。
观察并分析a 和0t 的变化对波形的影响。
t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a 越大最大值越小,t0越大图像对称轴越往右移某频率为f 的正弦波可表示为()()cos 2πa x t ft =,对其进行等间隔抽样,得到的离散样值序列可表示为()()a t nT x n x t ==,其中T 称为抽样间隔,代表相邻样值间的时间间隔,1s f T=表示抽样频率,即单位时间内抽取样值的个数。
抽样频率取40 Hz s f =,信号频率f 分别取5Hz, 10Hz, 20Hz 和30Hz 。
请在同一张图中同时画出连续信号()a x t t 和序列()x n nT 的波形图,并观察和对比分析样值序列的变化。
可能用到的函数为plot, stem, hold on 。
fs = 40;t = 0 : 1/fs : 1 ;% ƵÂÊ·Ö±ðΪ5Hz,10Hz,20Hz,30Hz f1=5;xa = cos(2*pi*f1*t) ; subplot(1, 2, 1) ;plot(t, xa) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('t(s)') ;ylabel('Xa(t)') ;line([0, max(t)],[0,0]) ; subplot(1, 2, 2) ;stem(t, xa, '.') ;line([0, max(t)], [0, 0]) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('n') ;ylabel('X(n)') ;频率越高,图像更加密集。
信号与信号处理实验参考答案
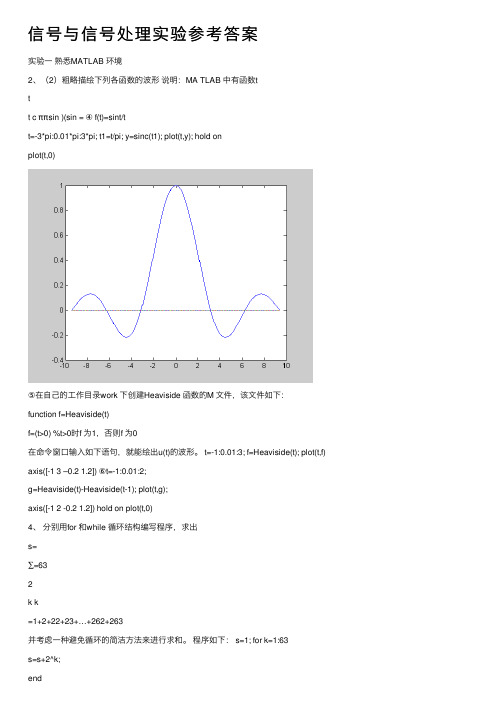
信号与信号处理实验参考答案实验⼀熟悉MATLAB 环境2、(2)粗略描绘下列各函数的波形说明:MA TLAB 中有函数ttt c ππsin )(sin = ④ f(t)=sint/tt=-3*pi:0.01*pi:3*pi; t1=t/pi; y=sinc(t1); plot(t,y); hold onplot(t,0)⑤在⾃⼰的⼯作⽬录work 下创建Heaviside 函数的M ⽂件,该⽂件如下:function f=Heaviside(t)f=(t>0) %t>0时f 为1,否则f 为0在命令窗⼝输⼊如下语句,就能绘出u(t)的波形。
t=-1:0.01:3; f=Heaviside(t); plot(t,f) axis([-1 3 –0.2 1.2]) ⑥t=-1:0.01:2;g=Heaviside(t)-Heaviside(t-1); plot(t,g);axis([-1 2 -0.2 1.2]) hold on plot(t,0)4、分别⽤for 和while 循环结构编写程序,求出s=∑=632k k=1+2+22+23+…+262+263并考虑⼀种避免循环的简洁⽅法来进⾏求和。
程序如下: s=1; for k=1:63s=s+2^k;s运⾏结果是:s =1.8447e+019(2)s=1;k=1;while k<=63s=s+2^k;k=k+1;ends运⾏结果:s =1.8447e+019(3)k=0:63;s=sum(2.^k)实验⼆信号的卷积与系统的响应和阶跃响应1.n=0:20;hn=0.9.^n;xn=[0,0 ones(1,8),0,0];yn=conv(hn,xn);stem(yn)3. 利⽤MA TLAB绘制下列信号的卷积积分f1(t)*f2(t)的时域波形。
(1)f1(t)=2[u(t+1)-u(t-1)], f2(t)=u(t+2)-u(t-2)(2)f1(t)=tu(t), f2(t)=u(t)(3)f1(t)=u(t)-u(t-4), f2(t)=sin(лt)u(t);(4)f1(t)=e-2t u(t), f2(t)=e-t u(t)(1) 先编写实现连续信号卷积的通⽤函数sconv(),程序如下:function[f,k]=sconv(f1,f2,k1,k2,p)%计算连续信号卷积积分f(t)=f1(t)*f2(t)%f:卷积积分f(t)对应的⾮零样值向量%k:f(t)的对应时间向量%f1:f1(t)⾮零样值向量%f2:f2(t)⾮零样值向量%k1:f1(t)的对应时间向量%k2:序列f2(t)的对应时间向量%p:取样时间间隔f=conv(f1,f2); %计算序列f1与f2的卷积ff=f*p;k0=k1(1)+k2(1); %计算序列f的⾮零样值的起点位置k3=length(f1)+length(f2)-2; %计算卷积和f的⾮零样值的宽度k=k0:p:((k3-(0-k0)/p)*p); %确定卷积和f⾮零样值的时间向量subplot(2,2,1)plot(k1,f1) %绘制f1(t)title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h) %将第三个⼦图的横坐标范围扩为原来的2.5倍title('f(t)=f1(t)*f2(t)') xlabel('t')ylabel('f(t)')p=0.01;k1=-1:p:1;f1=2*ones(1,length(k1));k2=-2:p:2;f2=ones(1,length(k2));[f,k]=sconv(f1,f2,k1,k2,p)(2)p=0.01;k1=0:p:10;k2=0:p:10;f2=ones(1,length(k2)); [f,k]=sconv(f1,f2,k1,k2,p)第(2)题图上实验⼆信号的卷积与系统的响应1.n=0:20;hn=0.9.^n;xn=stepseq(2,0,20)-stepseq(10,0,20);yn=conv(hn,xn);stem(yn)2.(1)p=0.01;k1=-2:p:2;f1=2*(u(k1+1)-u(k1-1));f2=u(k2+2)-u(k2-2);[f,k]=sconv(f1,f2,k1,k2,p)p=0.01;k1=-1:p:10;f1=k1.*u(k1);k2=k1;f2=u(k2);[f,k]=sconv(f1,f2,k1,k2,p)(3)p=0.01;k1=-4:p:10; f1=u(k1)-u(k1-4);k2=k1;f2=sin(pi*k2).*u(k2); [f,k]=sconv(f1,f2,k1,k2,p)5.已知描述某连续系统的微分⽅程为:y’’(t)+5y’(t)+8y(t)=3f’’(t)+2f(t)绘出系统的冲激响应波形,求出t=0.5s, 1s, 1.5s, 2s系统冲激响应的数值解。
信号与系统实验答案1

实验一 离散时间信号的表示及可视化一、实验目的学会对离散时间信号进行标识和可视化处理。
二、实验源程序 (1)f(n)= )(n δn=-5:1:5; f=dirac(n); plot(n,f,'.'); xlabel('(n)'); ylabel('(f)'); axis([-5 5 -0.5 1.5])(2) f(n)=ε(n)f=Heaviside(n)n=-5:1:5; f=heaviside(n); plot(n,f,'.'); xlabel('(n)'); ylabel('(f)');axis([-5 5 -0.5 1.5]) (3) f(n)= ane (分别取a>0及a<0)a=1时 n=-5:1:5; f=exp(n); plot(n,f,'.');a=-1时 n=-5:1:5; f=exp(-n); plot(n,f,'.');(4) f(n)=R N (n) (分别取不同的N 值)N=10时 n=0:1:9; f=1;plot(n,f,'.');N=15时 n=0:1:14; f=1;plot(n,f,'.') (5) f(n)=Sa(nw)w=0.1时n=-45:1:45;f=sinc(0.1*n);plot(n,f,'.');xlabel('n');ylabel('f');axis([-50 50 -1 1])w=0.2时n=-45:1:45;f=sinc(0.2*n);plot(n,f,'.');xlabel('n');ylabel('f');axis([-50 50 -1 1])(6)f(n)=Sin(nw)(分别取不同的w值)w=100时n=-15:1:15;f=sin(100*n);plot(n,f,'.');xlabel('n');ylabel('f');w=200时n=-15:1:15;f=sin(200*n);plot(n,f,'.');xlabel('n');ylabel('f');三、程序运行结果及波形图(1)(2)(3)-5-4-3-2-1012345(n)(f)-5-4-3-2-1012345(n)(f)(4)0123456789024********(5)(6)-50-40-30-20-1001020304050-1-0.8-0.6-0.4-0.200.20.40.60.81nf-50-40-30-20-1001020304050-1-0.8-0.6-0.4-0.200.20.40.60.81nffnf-15-10-5051015n四、实验调试体会实验二 连续时间信号的表示及可视化一、实验目的熟练掌握连续时间信号的表示及可视化处理。
信号与系统--完整版答案--纠错修改后版本
1)
3)
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)5)
3.9、求图所示各系统的单位序列响应。
(a)
(c)
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)
4.34 某LTI系统的频率响应,若系统输入,求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入,求该系统的输出。
4.39 如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?
(1)如,求的频谱函数(或画出频谱图)。
(2)如,求的频谱函数(或画出频谱图)。
(1) (2) (3) (4) (5)
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知,试求下列函数的频谱:
(1)(3) (5)
(8)(9)
4下列方式求图4-25示信号的频谱函数 (1)利用xx和线性性质(门函数的频谱可利用已知结果)。
(1)
5-18 已知系统函数和初始状态如下,求系统的零输入响应。
(1),
(3),
5-22 如图5-5所示的复合系统,由4个子系统连接组成,若各子系统的系统函数或冲激响应分别为,,,,求复合系统的冲激响应。
5-26 如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。
5-28 某LTI系统,在以下各种情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。
(7)(8)
1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
重庆大学信号与系统实验(附标准答案)

2.当2π/ω为有理数时,则有2π/ω=N/M,这里N和M均为正整数,令N=2πM/ω,则
sinω(n+N)= sinω(n+ M2π/ω)= sin(ωn+ 2πM)= sinωn。
即这时正弦序列也是周期序列,且序列的最小周期为N=2πM/ω。
平移:将函数 沿横坐标平移 就得到函数
相乘:将 与 相乘,得到 。两波形重叠部分相乘有值,不重叠部分乘积为零
积分: 曲线下的面积即为 时刻的卷积。
2.2离散信号卷积和
输入为 ,输出为 的离散时间线性时不变系统的作用是用卷积求和来描述的:
信号 是系统对于单位冲激输入的响应。其计算步骤为:
横坐标 换成
翻转:将函数 以纵坐标为轴翻转,得到其对称函数
问题1:详细说明正弦离散时间信号的周期性与信号频率的关系,为什么?
答:根据周期序列的定义来讨论正弦离散时间信号的周期性,根据其周期性来找出其与信号频率
的关系。即找到一个正整数N使得恒等式sin(ωn)=sinω(n+N)成立。
分为几种情况讨论:
1.当2π/ω为整数时,令N=2π/ω,则
sinω(n+N)= sinω(n+2π/ω)= sin(ωn+2π)= sinωn。
12电科02班
姓名
艾渝
成绩
课程
名称
信号与系统(双语)
实验项目
名称
信号的时域表示、变换、采样及系统的时域特性
指导教师
文静
教师评语
()深入理解了实验原理,完成了实验步骤,实验过程原始记录翔实、清晰、准确,实验结果正确,分析透彻,很好地达到了实验目的。
信号与系统实验答案
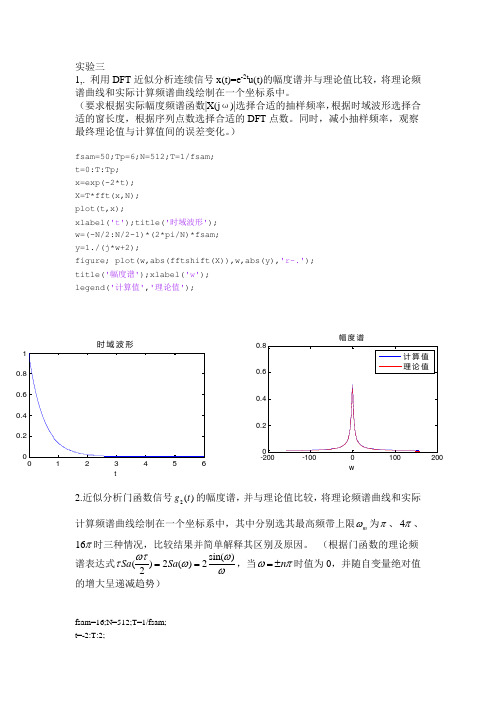
实验三1,. 利用DFT 近似分析连续信号x(t)=e -2t u(t)的幅度谱并与理论值比较,将理论频谱曲线和实际计算频谱曲线绘制在一个坐标系中。
(要求根据实际幅度频谱函数|X(j ω)|选择合适的抽样频率,根据时域波形选择合适的窗长度,根据序列点数选择合适的DFT 点数。
同时,减小抽样频率,观察最终理论值与计算值间的误差变化。
)fsam=50;Tp=6;N=512;T=1/fsam; t=0:T:Tp; x=exp(-2*t); X=T*fft(x,N); plot(t,x);xlabel('t');title('时域波形'); w=(-N/2:N/2-1)*(2*pi/N)*fsam; y=1./(j*w+2);figure; plot(w,abs(fftshift(X)),w,abs(y),'r-.'); title('幅度谱');xlabel('w'); legend('计算值','理论值');2.近似分析门函数信号2()g t 的幅度谱,并与理论值比较,将理论频谱曲线和实际计算频谱曲线绘制在一个坐标系中,其中分别选其最高频带上限m ω为π、4π、16π时三种情况,比较结果并简单解释其区别及原因。
(根据门函数的理论频谱表达式sin()()2()22Sa Sa ωτωτωω==,当n ωπ=±时值为0,并随自变量绝对值的增大呈递减趋势)fsam=16;N=512;T=1/fsam; t=-2:T:2;12345600.20.40.60.81t时域波形-200-100010020000.20.40.60.8幅度谱wx=[(t>=-1)&(t<=1)];X=T*fft(x,N);%消除1/T 因子的影响 plot(t,x);xlabel('t');title('时域波形'); w=(-N/2:N/2-1)*(2*pi/N)*fsam; y=2*sin(w)./w;%理论频谱值figure; plot(w,abs(fftshift(X)),w,abs(y),'r-.'); title('幅度谱');xlabel('w'); legend('计算值','理论值');-2-1.5-1-0.500.51 1.5200.20.40.60.81t时域波形-60-40-20020406000.511.522.5幅度谱w实验四。
信号与系统实验网上答案

信号与系统实验网上答案第一篇:信号与系统实验网上答案目的:通过MATLAB编程实现对时域抽样定理的验证,加深抽样定理的理解。
同时训练应用计算机分析问题的能力。
任务:连续信号f(t)=cos(8*pi*t)+2*sin(40*pi*t)+cos(24*pi*t),经过理想抽样后得到抽样信号fs(t),通过理想低通滤波器后重构信号f(t)。
方法:1、确定f(t)的最高频率fm。
对于无限带宽信号,确定最高频率fm的方法:设其频谱的模降到10-5左右时的频率为fm。
2、确定Nyquist抽样间隔TN。
选定两个抽样时间:TSTN。
3、MATLAB的理想抽样为n=-200:200;nTs=n*Ts;或 nTs=-0.04:Ts:0.044、抽样信号通过理想低通滤波器的响应理想低通滤波器的冲激响应为系统响应为由于所以MATLAB计算为ft=fs*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));要求(画出6幅图):当TS1、在一幅图中画原连续信号f(t)和抽样信号fS(t)。
f(t)是包络线,fS(t)是离散信号。
2、画出重构的信号y(t)。
3、画出误差图,即error=abs(f(t)-y(t))的波形。
当TS>TN时同样可画出3幅图。
%a wm=40*pi;wc=1.2*wm;%理想低通截止频率Ts=[0.02 0.03];N=length(Ts);for k=1:N;n=-100:100;nTs=n*Ts(k);fs=(cos(8*pi*nTs)+2*sin(40*pi*nTs)+cos(24*pi*nTs)).*(u(nTs+ pi)-u(nTs-pi));t=-0.25:0.001:0.25;ft=fs*Ts(k)*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));t1=-0.25:0.001:0.25;f1=(cos(8*pi*t1)+2*sin(40*pi*t1)+cos(24*pi*t1)).*(u(t1+0.25) -u(t1-0.25));%在一副图中画原连续信号f(t)和样信号f_s(t)。
信号与系统实验答案
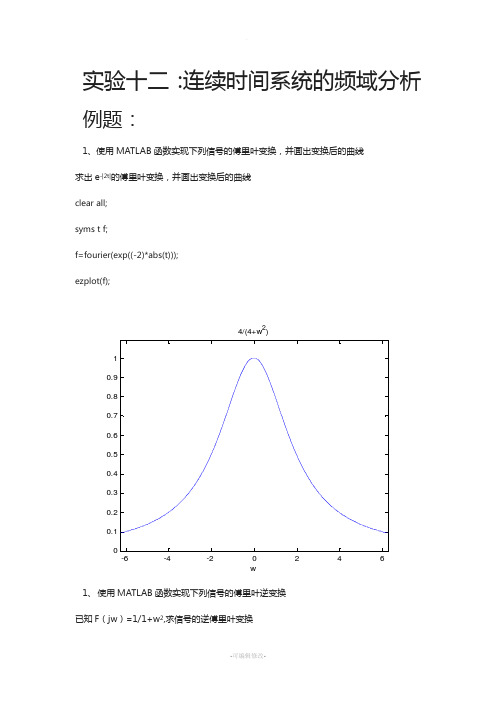
实验十二:连续时间系统的频域分析例题:1、使用MATLAB 函数实现下列信号的傅里叶变换,并画出变换后的曲线 求出e -|2t|的傅里叶变换,并画出变换后的曲线clear all; syms t f;f=fourier(exp((-2)*abs(t))); ezplot(f);-6-4-224600.10.20.30.40.50.60.70.80.91w4/(4+w 2)1、 使用MATLAB 函数实现下列信号的傅里叶逆变换 已知F (jw )=1/1+w 2,求信号的逆傅里叶变换syms t w;ifourier(1/(1+(w^2)),t);ans1/2*exp(-t)*heaviside(t)+1/2*exp(t)*heaviside(-t)3、使用MATLAB函数实现傅里叶的时移特性画出f(t)=1/2e-2t u(t)和f(t-1)的频谱图,观察信号时移对频谱的影响clear all;r=0.02;t=-5:r:5;N=200;w=2*pi;k=-N:N;w=k*w/N;f1=1/2*exp(-2*t).*stepfun(t,0);F=r*f1*exp(-j*t'*w);F1=abs(F);P1=angle(F);subplot(3,1,1);plot(t,f1);grid on;ylabel('f(t)');title('f(t)'); subplot(3,1,2); plot(w,F1); xlabel('w');grid on;ylabel('F(jw)'); subplot(3,1,3); plot(w,P1*180/pi); grid;xlabel('w'); ylabel('相位度');。
-5-4-3-2-10123450.5tf (t )f(t)-8-6-4-20246800.20.4wF (j w )-8-6-4-202468-100100w相位(度)4、 使用MATLAB 函数实现下列信号的频移变换已知f (t )为门函数,求f 1(t )= f (t )e -j5t 以及f 2(t )e j5t 的频谱图clear all; R=0.02; t=-2:R:2;f=stepfun(t,-1)-stepfun(t,1); f1=f.*exp(-j*5*t); f2=f.*exp(j*5*t); N=500; W1=5*pi; k=-N:N; W=k*W1/N;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦信号抽样信号矩形脉冲信号单位跃阶信号实验一 连续时间信号的MATLAB 表示实验目的 1.掌握MATLAB 语言的基本操作,学习基本的编程功能; 2.掌握MATLAB 产生常用连续时间信号的编程方法;3.观察并熟悉常用连续时间信号的波形和特性。
实验原理:1. 连续信号MA TLAB 实现原理从严格意义上讲,MATLAB 数值计算的方法并不能处理连续时间信号。
然而,可用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能够被MATLAB 处理,并且能较好地近似表示连续信号。
MATLAB 提供了大量生成基本信号的函数。
比如常用的指数信号、正余弦信号等都是MATLAB 的内部函数。
为了表示连续时间信号,需定义某一时间或自变量的范围和取样时间间隔,然后调用该函数计算这些点的函数值,最后画出其波形图。
实验内容:-2-112实部-112虚部012取模-505相角00.20.40.60.81-1-0.50.5方波信号实验编程:(1)t=0:0.01:3;K=2;a=-1.5;w=10; ft=K*exp((a+i*w)*t); A=real(ft); B=imag(ft); C=abs(ft); D=angle(ft);subplot(2,2,1),plot(t,A),grid on;title('实部'); subplot(2,2,2),plot(t,B),grid on;title('虚部'); subplot(2,2,3),plot(t,C),grid on;title('取模'); subplot(2,2,4),plot(t,D),grid on;title('相角');(2)t=0:0.001:3;y=square(2*pi*10*t,30);plot(t,y);axis([0,1,-1,1]); title('方波信号');-2-1.5-1-0.500.51 1.5200.511.5t(s)y (s )门函数(3)t=-2:0.01:2;y=uCT(t+0.5)-uCT(t-0.5); plot(t,y),grid on axis([-2,2,0,1.5]);xlabel('t(s)'),ylabel('y(s)')title('门函数')实验二 连续时间LTI 系统的时域分析实验目的1.运用MATLAB 符号求解连续系统的零输入响应和零状态响应; 2.运用MATLAB 数值求解连续系统的零状态响应; 3.运用MATLAB 求解连续系统的冲激响应和阶跃响应; 4.运用MATLAB 卷积积分法求解系统的零状态响应。
0.51t零输入响应123456780.10.2t零状态响应123456780.511.5t完全响应0123456780.050.10.150.20.25t(s)y (t )零状态响应实验内容:0.51 1.52 2.53 3.54-2024t(s)h (t )冲击响应0.51t(s)s (t )阶跃响应012340.20.40.60.811.2f1(t)t01234-1012f2(t)t0.20.40.6f(t)=f1(t)*f2(t)t实验编程: (1)ts=0;te=8;dt=0.01; sys=tf([1,16],[1,2,32]); t=ts:dt:te; f=exp(-2*t); y=lsim(sys,f,t); plot(t,y),grid on;xlabel('t(s)'),ylabel('y(t)') title('零状态响应')t(s)y (t )零状态响应0123456780.10.20.30.4t(s)h (t )冲激响应01234567800.20.40.60.8t(s)s (t )阶跃响应(2)t=0:0.01:8;sys=tf([1],[1,3,2]); h=impulse(sys,t); s=step(sys,t);subplot(2,1,1);plot(t,h),grid on xlabel('t(s)'),ylabel('h(t)') title('冲激响应')subplot(2,1,2);plot(t,s),grid on xlabel('t(s)'),ylabel('s(t)') title('阶跃响应')-10-8-6-4-202468100123ω(rad/s)|H (ω)|H(w)的频率特性-10-8-6-4-20246810-4-2024ω(rad/s)|p h i (ω)|H(w)的相频特性0.51 1.52Time(sec)矩形脉冲信号u 1t (t )-10010ω(rad/s)矩形脉冲频谱X (ω)Time(sec)响应的时域波形u 2(t)ω(rad/s)响应的频谱U 2(ω)实验三 连续时间LTI 系统的频率特性及频域分析实验目的1.运用MATLAB 分析连续系统的频率特性; 2.运用MATLAB 进行连续系统的频域分析。
实验内容:02468101214161820-10-50510Time(sec)f (t )输入信号的波形02468101214161820-2-1012Time(sec)y (t )稳态响应的波形实验编程: (1)w1=1;w2=10;A=5;B=2; t=0:0.01:20;H1=1/(-w1^2+3*j*w1+2); H2=1/(-w2^2+3*j*w2+2); f=5*cos(w1*t)+2*cos(w2*t);y=A*abs(H1)*cos(w1*t+angle(H1))+B*abs(H2)*cos(w2*t+angle(H2)); subplot(211),plot(t,f),grid on; xlabel('Time(sec)'),ylabel('f(t)'); title('输入信号的波形');subplot(212),plot(t,y),grid on; xlabel('Time(sec)'),ylabel('y(t)'); title('稳态响应的波形')-1.5-0.50.51.5实验四 连续时间LTI 系统的零极点分析实验目的1.运用MATLAB 求解系统函数的零极点;2.运用MATLAB 分析系统函数的零极点分布与其时域特性的关系; 3.运用MATLAB 分析系统函数的零极点分布与其系统稳定性的关系。
实验原理1. 系统函数及其零极点的求解系统零状态响应的拉普拉斯变换与激励的拉普拉斯变换之比称为系统函数H (s ),即m m-10m m-110n n-1n n-110()()()mjjj nii i b sb s b s b s b Y s H s F s a s a s a s a a s==++++===++++∑∑在连续时间LTI 系统的复频域分析中,系统函数起着十分重要的作用,它反映了系统的固有特性。
系统函数H (s )通常是一个有理分式,其分子和分母均为可分解因子形式的多项式,各项因子表明了H (s )零点和极点的位置,从零极点的分布情况可确定系统的性质。
H (s )零极点的计算可应用MA TLAB 中的roots 函数,分别求出分子和分母多项式的根即可。
实验内容:-2-1.5-1-0.500.511.52P ole-Zero M ap Real Axis I m a g i n a r y A x is00.51 1.52 2.52468101214I m pulse ResponseTim e (sec)A m p l i t u d e-8-6-4-202468P ole-Zero M ap Real Axis I m a g i n a r y A x is00.51 1.52 2.5-2-1.5-1-0.50.511.5I m pulse ResponseTim e (sec)A m p l i t u d ep =-2.0000 + 1.0000i -2.0000 - 1.0000i z =2-2-1.5-1-0.500.511.52P ole-Zero M apR eal AxisI m a g in a r y A x is-1-0.8-0.6-0.4-0.200.20.40.60.81I m pulse R esponseTim e (sec)A m p li t u d e实验编程: b1=[1]; a1=[1,-1];sys1=tf(b1,a1); subplot(121) pzmap(sys1) axis([-2,2,-2,2]) subplot(122) impulse(b1,a1) figure b2=[1];a2=[1,-2,50]; sys2=tf(b2,a2); subplot(121) pzmap(sys2) axis([-2,2,-8,8]) subplot(122) impulse(b2,a2) figure b3=[1]; a3=[1,0,1]; sys3=tf(b3,a3); subplot(121) pzmap(sys3)axis([-2,2,-2,2]) subplot(122) impulse(b3,a3)-202-8-6-4-202468P ole-Zero MapReal AxisI m a g i n a r y A x i s0246-0.08-0.06-0.04-0.0200.020.040.060.080.10.12Impulse ResponseTime (sec)A m p l i t u d e代码:b=[1]; a=[1,2,50]; sys2=tf(b,a); subplot(121) pzmap(sys2) axis([-2,2,-8,8]) subplot(122) impulse(b,a)-202-8-6-4-202468P ole-Zero MapReal AxisI m a g i n a r y A x i s051015-1-0.50.511.52Impulse ResponseTime (sec)A m p l i t u d e代码:b=[1,4,3]; a=[1,1,7,2]; sys2=tf(b,a); subplot(121) pzmap(sys2) axis([-2,2,-8,8]) subplot(122) impulse(b,a)实验五 典型离散信号及其MATLAB 实现实验目的1.掌握MATLAB 语言的基本操作,学习基本的编程功能; 2.掌握MATLAB 产生常用离散时间信号的编程方法; 3.掌握MATLAB 计算卷积的方法。
