大学物理 第七章 稳恒磁场
大学物理 稳恒磁场的基本性质
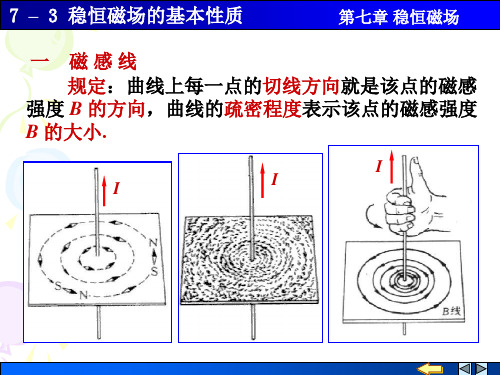
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
四 安培环路定理的应用举例
例1 求长直密绕螺线管内磁场
解 1 ) 对称性分析螺旋管内为均匀场 , 方向沿
轴向, 外部磁感强度趋于零 ,即 B 0 .
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
2 ) 选回路 L .
磁场 B 的方向与
电流 I 成右螺旋.
s
B dS B dS
S
S
-Br 2
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
例 如图载流长直导线的电流为 I ,
形面积的磁通量.
解 先求
试求通过矩 B ,对变磁场
B
给B出dΦ后0I 积分求BΦ// S
I
l
2π x dΦ BdS
0I
ldx
M
NB
++++++++++++
P
LO
B dl B dl B dl BPM
B MN 0nMNI B 0nI
无限长载流螺线管内部磁场处处相等 , 外部磁场 为零.
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
例3 无限长载流圆柱体的磁场
I
解 1)对称性分析 2)选取回路
RR
rR
Bdl l
0I
L
2π rB 0I
B 0I
2π r
r B
0 r R
l
B
d
l
0
π π
大学物理第七章 恒定磁场

dr
0dI 0 dB dr 2r 2 0 R 0R B dr 2 0 2
解法2:运动点电荷的磁场
R o r
dB
0 dqv
4π r
2
dq 2 π rdr
dr
B
dB
0
2
dr
vr
0
2
R
0
dr
0R
2
§7.5 磁通量 磁场的高斯定理
i j k, 记忆:i j k i, k i j j k i j
z 0 x y
方向:垂直于 A,B 平面,右手螺旋
A
叉积的基本性质: ① a a 0; a b b a 体积 ② 混合积:( a b ) c
I
I
环形螺线管 的磁感线
二. 磁通量
m B dS
单位:Wb = T· m2 闭合曲面的磁通量:
S
B
dS
dS
m
S
B dS (外法线)
例 如图载流长直导线的电流为 I,试求 通过矩形面积的磁通量.
d2
I
dS
d1
l
dΦ BdS
§7.3 §7.4 §7.5 §7.6
磁场 磁感强度 毕奥-萨伐尔定律 磁通量 磁场的高斯定理 安培环路定理
§7.7 带电粒子在电场和磁场中的运动 §7.8 载流导线在磁场中所受的力
本章基本要求
• 理解毕奥-萨伐尔定律,能利用它 计算一些简单问题中的磁感强度。 • 理解稳恒磁场的高斯定理和安培环路定理, 理解用安培环路定理计算磁感强度的条件 和方法。
7第七章稳恒磁场课件

稳恒磁场是涡旋场,静电场不是涡旋场。
例题: P237 7-19
电场与磁场比较
力线
电场 起于正电荷止于负电荷 不形成闭合曲线
高斯定理
S
E
dS
10(s内)qi
磁场
无头无尾闭合曲线
B dS 0
S
环路定理 E dl 0 L
B dl L
0 I
enB
B
s s
通过任意面元dS的磁通 量: d B dS
穿过整个曲面S的磁通量为:
d B dS
S
S
B cosdS
S
B
dS
B
规定:外法线方向为正
(1)当 < 90°时: 0
s
(2)当 > 90°时: 0
B Bx L dBx dBsin
0IR 4 r3
2 R dl 0
0
2
R2I r3
0
2
(R2
R2I x2)3/2
Idl
r
dB
o
P
R
x
*
x
I
方向:图示沿x轴正向,即沿圆电流的轴线,与电流的环绕 方向成右手螺旋关系。
如果令x=0,则圆电流圆心O处的磁感应强度的大小为
第七章 稳恒磁场
第七章 稳恒磁场
7-1 磁感应强度 磁场的高斯定理 7-2 安培定律 7-3 毕奥-萨伐尔定律 7-4 安培环路定律
7-1 磁感应强度 磁场的高斯定理
一.磁感应强度
1. 磁场
第7章稳恒磁场

电源电动势的大小等于把单位正电荷从负极经电源内
部移至正极时非静电力所做的功。
电源内部电势升高的方向,(即从负极经电源内部到正 极的方向)规定为电动势的方向
7.2 磁场 磁感应强度
实验指出,运动点电荷在磁场中任一指定点处所受的磁场力 具有如下性质:
(1)电荷速度 的方向与某一特定方向平
行(或反平行)时,磁场力 Fm 0
稳第 恒七 磁章 场
主要内容
7.1 恒定电流 7.2 磁场 磁感应强度 7.3 毕奥-萨伐尔定律 7.4 磁场基本定理 7.5 带电粒子在电场和磁场中的运动 7.6 磁场对电流的作用 7.7 磁场中的介质
7.1 恒定电流
7.1.1 电流 电流密度
电流是由大量电荷作有规则的定向运动形成的,电 荷的携带者叫载流子。
(2)定义载流线圈的磁矩 m ISen m 的大小等于IS
方向与线圈平面的法线方向相同
B
0m
3
2π(x2 R2 )2
B 0I
2π 2R
问题7-7 如图,一根无限长直导线,
通有电流 I ,中部一段弯成圆弧形,
求圆心点O 的磁感应强度 B。
解如图,将导线分成1、2、3三部分,设各部分在点P处产生
(2)当电荷q 以不同于上述特定方向的速度
通过 磁场中某点时,所受的磁场力 总是F垂m 直
于 与该特定方向组成的平面,大小与q 和 的
乘积成正比;改变q的符号,磁场力 的方向F反m向
(3)当速度 与该上述特定方向垂直时,
磁场力最大。力的大小正比于电荷的电量和速率的乘积 q
定义磁感应强度 B 的方向和大小如下
例7-2 圆形电流轴线上的磁场
解 取图示电流元 Idl
磁感应强度
第7章_稳恒磁场集美大学物理答案

班级____________ 姓名______________ 学号_________________ 第7-1 毕奥—萨伐尔定律 一.选择题:1.一根载有电流I 的无限长直导线,在A 处弯成半径为R 的圆形,由于导线外有绝缘层,在A 处两导线靠得很近但不短路,则在圆心处磁感应强度B 的大小为:( C ) (A) (μ0+1)I /(2πR ) (B) μ0I /(2πR ) (C) μ0I (-1+π)/(2πR )(D) μ0I (1+π)/(4πR )2.将半径为R 的无限长导体薄壁管(厚度忽略) 沿轴向割去一宽度为h (h <<R )无限长狭缝后,再沿轴向均匀地流有电流,其面电流密度为i (即沿圆周每单位长度的电流),则管轴线上磁感应强度的大小是:( A )(A) R h i πμ2/0 (B) 0(C) R h i πμ4/0(D) h i 0μ二、计算题:3.载有电流为I 的无限长导线,弯成如图形状,其中一段是半径为R 的半圆,则圆心处的磁感应强度B 的大小为多少? 解: 选为正方向123B B B B →→→→=++1(14IB Rομπ=--2,42I B R ομπ=⋅ 34I B R ομ=∴)12(4-+=ππμοRIB4.用相同的导线组成的一导电回路,由半径为R 的圆周及距圆心为R /2的一直导线组成(如图),若直导线上一电源ε,且通过电流为I ,求圆心O处的磁感应强度。
解 设大圆弧的电流为1I ,小圆弧的电流为2I ,则12I I I +=,选为正方向根据电阻定律有1122l I Sl I S ερερ⎧=⎪⎪⎨⎪=⎪⎩可得:1122I l I l =大圆弧电流在圆心处O 产生的磁感应强度:大小为01114I l B R μπ=,方向为 小圆弧电流在圆心处O 产生的磁感应强度:大小为02224I lB Rμπ=,方向为⊗直导线电流在圆心处O 产生的磁感应强度:大小为0035cos cos 66242I I B R R μππππ⎛⎫=-= ⎪⎝⎭,方向为所以,总电流在圆心处O 产生的磁感应强度:312B B B B =++,大小为:02IB Rπ=,方向为5.如图,两线圈共轴,半径分别为1R 和2R ,电流分别为I 1 和I 2 ,电流方向相同,两圆心相距2 b ,联线的中点为O 。
7 稳恒磁场

讨 1)若线圈有 N 匝
论
B
N (2 x2
0 IR2
R2)32
2)x 0 B 的方向不变( I 和 B成右螺旋关系)
3) x 0 4)x R
B 0I
2R
B
0IR 2
2x3
,
B
0 IS
2π x3
比一比
I
R
ox
B
*x
B
0 IR2
(2 x2 R2)32
B
如图所示,有一长为 l , 半径为R的载流密绕直螺线管,螺 线管的总匝数为N,通有电流 I. 设把螺线管放在真空中,求 管内轴线上一点处的磁感强度.
R
o
p*
dx x
x
+++++++++++++ +
解 由圆形电流磁场公式
B
0IR 2
(2 x2 R2)3/ 2
稳恒磁场
1
x1 o p 2
x
方向:磁场中的每一点都
有一个特征方向,当试探 电荷q0沿这个方向运动时 不受力。这一特征方向定
义为磁场的方向。
稳恒磁场
直带于电v粒 子与在磁B 场组中成沿的运平动面时.
F
垂
磁场中的带电粒子速度垂直于
受力最大.
B时
F Fmax F
Fmax qv
大小: 荷无关
,该比值只取决于该点磁场的性质,与试探电
磁偶极子的磁矩: m ISen
B
0 IS 2 x3
大学物理稳恒磁场理论及习题解读
250 0 方向垂直A面
B
BC
0 N C I C
2 RC
0 20 5
2 0.10
O BA
5000 方向垂直C面
B
2 BA
2 BC
7.02 10 T 方向 : tan
4
1
BC 63.4 BA
NIZQ
第14页
大学物理学
恒定磁场
NIZQ
问题: 磁现象产生的原因是什么?
第 2页
大学物理学
恒定磁场
• 电流的磁效应 1820年奥斯特实验表明: 电流对磁极有 力的作用. 1820年 9月 11日在法国科学院演示的奥 斯特的实验 ,引起了安培的兴趣 .一周之后 安培发现了电流间也存在着相互作用力.
此后安培又提出了著名的安 培定律 : 磁体附近的载流导线 会受到力的作用而发生运动.
NIZQ
第 3页
大学物理学
恒定磁场
结论: 磁现象与电荷的运动有着密切的关系 . 运动电荷既能产 生磁效应,也受到磁力的作用. 安培把磁性归结为电流之间的相互作用 . 1822年安培提 出了分子电流假说:
• 一切磁现象起源于电荷的运动.
• 磁性物质的分子中存在分子电流, 每个分子电流相当于一基元磁体。
写成矢量表示:
0 Idl sin
2 4π r 0 Idl r dB 4π r 3
真空中的磁导率: 0= 410-7亨利· 米-1 (H· m-1)
NIZQ
第 8页
大学物理学
恒定磁场
• 毕奥—萨伐尔定律的应用 恒定磁场的计算: 1.选取电流元或某些典型电流分布为积分元. 2.由毕-萨定律写出积分元的磁场dB .
第07章 稳恒磁场01电流与电动 比奥萨伐尔定律PPT课件
运动一周,非静电力所做的功。
Ek dl
L
7
第八章 稳恒磁场
7.1 电流与电动势 7.2 磁场 磁感应强度 7.3 毕奥-萨伐尔定律 7.4 安培环路定理 7.5 磁场载流导体的作用 7.6 磁介质对磁场的影响 7.7 铁磁质
8
§7.2 磁场 磁感应强度
一、 基本磁现象 磁场
1. 基本磁现象
1.磁体与磁体(磁极、磁力)
第七章 稳恒磁场
7.1 电流与电动势 7.2 磁场 磁感应强度 7.3 -萨伐尔定律 7.4 安培环路定理 7.5 磁场载流导体的作用 7.6 磁介质对磁场的影响 7.7 铁磁质
1
§7.1 电流与电动势 一、电流 电流密度
1. 电流强度
单位时间内通过截面S 的电量
I dq dt
电流单位: A(安培)
受力F m ax ,将Fmax v 方向定义为该点B 的方向。
磁感应强度大小B Fmax
F m ax
qv
单位:特斯拉(T) 1T1NA-1m -1
q&#
FqvB ——洛仑兹力
14
补充: 带电粒子在磁场中的运动
运动电荷在稳恒磁场中受力 FmqvB
匀强磁场中
1 . 若 v // B , 磁场对粒子的作用力为零,粒子仍将以 v 作匀速直线运动。
18
3. 一般情F况m下,qvv与BB有一R夹角mqBv ,
T 2 m qB
v// vcos
v
v
v vsin
螺距:
h
v//T
2 m
qB
v cos
v //
h
B
应用: 磁聚焦
非均匀磁场
19
由于地磁场俘获带电粒子而出现的现象
大学物理第七章稳恒磁场习题答案
第七章 稳恒磁场习题7-1 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量为多少?解:取平面S ’与半球面S 构成闭合曲面,根据高斯定理有 0m mS mS ΦΦΦ'=+=2cos mS mS r E ΦΦπα'=-=-球面外法线方向为其正方向7-2 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感应强度各为多少?08IR μ垂直画面向外0022II RR μμπ-垂直画面向里 00+42I IR Rμμπ垂直画面向外 7-3 如图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连。
已知圆环的粗细均匀,求环中心O 的磁感应强度。
解: 如图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
且θ-πθ==21221R R I I 电阻电阻 1I 产生1B 方向⊥纸面向外πθπμ2)2(2101-=R I B2I 产生2B 方向⊥纸面向里πθμ22202R I B =∴1)2(2121=-=θθπI I B B 有0210=+=B B B7-4 如图所示,已知地球北极地磁场磁感强度B 的大小为6.0×10-5T 。
如设想此地磁场是由地球赤道上一圆电流所激发的,此电流有多大?流向如何?(已知圆电流轴线上北极点的磁感强度()R IRR IR B 24202/32220μμ=+=)解:9042 1.7310A RBI μ==⨯方向如图所示7-5 有一同轴电缆,其尺寸如题图所示.两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
试计算以下各处的磁感应强度:(1)r<R 1;(2)R 1<r<R 2;(3)R 2<r<R 3;(4)r>R 3。
解:同轴电缆的电流分布具有轴对称性在电缆各区域中磁感应线是以电缆轴线为对称轴的同心圆。
大学物理A(一)课件第七章 稳恒磁场习题及答案
第七章 练习题1、在磁感强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n与B 的夹角为α ,则通过半球面S的磁通量(取弯面向外为正)为(A) πr 2B .. (B) 2 πr 2B . (C) -πr 2B sin α. (D) -πr 2B cos α.2、如图所示,电流I 由长直导线1经a 点流入由电阻均匀的导线构成的正方形线框,由b 点流出,经长直导线2返回电源(导线1、2的延长线均通过O 点).设载流导线1、2和正方形线框中的电流在框中心O 点产生的磁感强度分别用 1B 、2B、3B 表示,则O点的磁感强度大小 (A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0、B 3≠ 0,但0321=++B B B. (C) B ≠ 0,因为虽然021=+B B,但B 3≠ 0.(D) B ≠ 0,因为虽然B 3= 0,但021≠+B B.3、通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为: (A) B P > B Q > B O . (B) B Q > B P > B O . (C) B Q > B O > B P . (D) B O > B Q > B P .4、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)~(E)哪一条曲线表示B -x 的关系?[ ]5、如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll B d 等于(A) I 0μ. (B)I 031μ. (C) 4/0I μ. (D) 3/20I μ.IBxOR (D )Bx O R(C )BxO R (E )电流筒6、如图,在一固定的载流大平板附近有一载流小线框能自由转动或平动.线框平面与大平板垂直.大平板的电流与线框中电流方向如图所示,则通电线框的运动情况对着从大平板看是: (A) 靠近大平板. (B) 顺时针转动.(C) 逆时针转动.(D) 离开大平板向外运动.7、在一根通有电流I 的长直导线旁,与之共面地放着一个长、宽各为a 和b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为b ,如图所示.在此情形中,线框内的磁通量Φ =______________.8、如图所示,在真空中有一半圆形闭合线圈,半径为a ,流过稳恒电流I ,则圆心O 处的电流元l Id 所受的安培力F d 的大小为____,方向________.9、有一根质量为m ,长为l 的直导线,放在磁感强度为 B的均匀磁场中B的方向在水平面内,导线中电流方向如图所示,当导 线所受磁力与重力平衡时,导线中电流I =___________________.10、图示为三种不同的磁介质的B ~H 关系曲线,其中虚线表示的是B = μ0H 的关系.说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线:a 代表____________________的B ~H 关系曲线.b 代表____________________的B ~H 关系曲线.c 代表____________________的B ~H 关系曲线.11、AA '和CC '为两个正交地放置的圆形线圈,其圆心相重合.AA '线圈半径为20.0 cm ,共10匝,通有电流10.0 A ;而CC '线圈的半径为10.0 cm ,共20匝,通有电流 5.0 A .求两线圈公共中心O 点的磁感强度的大小和方向.(μ0 =4π×10-7 N ·A -2)12、如图所示,一无限长载流平板宽度为a ,线电流密度(即沿x 方向单位长度上的电流)为δ ,求与平板共面且距平板一边为b 的任意点P 的磁感强度.I 1I 2IlI dIB13、螺绕环中心周长l = 10 cm ,环上均匀密绕线圈N = 200匝,线圈中通有电流I = 0.1 A .管内充满相对磁导率μr = 4200的磁介质.求管内磁场强度和磁感强度的大小.14、一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成.中间充满磁导率为μ的各向同性均匀非铁磁绝缘材料,如图.传导电流I 沿导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的.求同轴线内外的磁感强度大小B 的分布.答案:一 选择题1、D2、A3、D4、B5、D6、B7、2ln 20πIaμ 8、a l I 4/d 20μ 垂直电流元背向半圆弧(即向左)9、)/(lB mg10、铁磁质、 顺磁质、 抗磁质 11、解:AA '线圈在O 点所产生的磁感强度002502μμ==AAA A r I NB (方向垂直AA '平面)CC '线圈在O 点所产生的磁感强度 005002μμ==CCC C r I N B (方向垂直CC '平面)O 点的合磁感强度 42/1221002.7)(-⨯=+=C AB B B T B 的方向在和AA '、CC '都垂直的平面内,和CC '平面的夹角︒==-4.63tg1AC B B θC A12、解:利用无限长载流直导线的公式求解.(1) 取离P 点为x 宽度为d x 的无限长载流细条,它的电流 x i d d δ=(2) 这载流长条在P 点产生的磁感应强度 xiB π=2d d 0μxxπ=2d 0δμ 方向垂直纸面向里.(3) 所有载流长条在P 点产生的磁感强度的方向都相同,所以载流平板在P点产生的磁感强度==⎰B B d ⎰+πba bxdx x20δμbb a x+π=ln20δμ 方向垂直纸面向里.13、解: ===l NI nI H /200 A/m===H H B r μμμ0 1.06 T14、解:由安培环路定理:∑⎰⋅=iI l Hd0< r <R 1区域: 212/2R Ir rH =π 212R Ir H π=, 2102R Ir B π=μR 1< r <R 2区域: I rH =π2rI H π=2, rIB π=2μR 2< r <R 3区域: )()(22223222R R R r I I rH ---=π )1(22223222R R R r rI H ---π=)1(2222322200RR R r rIH B ---π==μμr >R 3区域: H = 0,B = 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当 r > R3 时,
ww
7-9 一根很长的同轴电缆,由一导线圆柱(半径为 a)和一同轴的导线圆管(内、外半径分 别为 b、c)构成。使用时,电流 I 从一导体流出,从另一导体流回。设电流都是均匀分布在 导体的横截面上,求: (1)导体圆柱内( r<a );( 2)两导体之间( a<r<b);(3)导体圆管内 (b<r<c); (4)电缆外(r>c)各点处磁感应强度的大小。 解 如图 7.13 所示,由电流分布具有轴对称性可知,相应的磁场分布也具有轴对称性。根 据安培环路定理有
B=
圆弧段在 P 点所产生的磁感应强度为
µ0 I ⎛ 5π 3⎞ ⎞ µI⎛ − cos π ⎟ = 0 ⎜ 1 − ⎟ ⎜ cos 2π r ⎝ 6 2 ⎟ ⎠ 2π r ⎜ ⎝ ⎠
B=∫
2π 3 0
µ0 Idl µ0 I 2π µI = r= 0 2 2 4π r 4π r 3 6r
O 点总的磁感应强度为
I ′ = 0, B = 0
dF = Idl × B
把 dF 沿轴正交分解,有图 7.14 有
dFx = dF cos θ = BI cos θ dl
dFx = BI cos θ Rdθ dFy = BI sin θ Rdθ
因此
整个圆弧 ab 所受的安培力为
ww
7-12
7-11 用铅丝制作成半径为 R = 0.05m 的圆环,圆环中载有电流 I = 7 A ,把圆环放在磁场 中,磁场的方向与环面垂直,磁感应强度的大小为1.0T ,试问圆环静止时,铅丝内部张力 为多少? 解 如图 7.15 所示,整个圆环所受的合力为零,圆环静止不动。欲求圆环内部任意一点的 张力,可把圆环沿直径分为左右两部分,其中左半部分所受的安培力为,而左半部分又保持 静止不动,则必有
π , θ 2 = π , r0 = a 。所以 2 B= µ0 I π (cos − cos π ) = 4.0 × 105 (T ) 4π a0 2
方向垂直纸面向里。 7-3 如图 7.8 所示,用毕奥—萨伐尔定律计算图中 O 点的磁感应强度。 解 圆心 O 处的磁感应强度可看作由 3 段载流导线的磁场叠加而成, AB 段在 P 点所产生的磁感应强度为
的 a,b 两点的磁感应强度为 B。 解 截流长直导线在空间产生磁感应强度为
长直导线在 a,b 两点产生磁感应强度为
B1a =
方向垂直纸面向里
µ0 I1 µ 0 I1 , B1b = 2π × 0.05 2π × 0.15
长直导线 L2 在 a 点产生磁感应强度为
方向垂直纸面向里 在 b 点产生磁感应强度为
µ0 I 2dl µ0 I 2l2 = 4π R 2 4π R 2
答 案
µ0 I1dl µ0 I1l1 = 4π R 2 4π R 2
w.
B = B1 + B2 + B3 =
网
µ0 I ⎛ 3 ⎞ µ0 I ⎛ 3 ⎞ µ0 I 1 − + 1 − ⎜ ⎟ ⎜ ⎟+ ⎜ 2π r ⎜ 2 ⎟ 2 ⎟ ⎝ ⎠ 2π r ⎝ ⎠ 6r
方向垂直纸面向内。半圆弧在 O 点产生的磁感应强度为
B=∫
πR
0
µ0 Idl µ0 I µI = πR = 0 2 2 4π R 4π R 4R
方向垂直纸面向内,1/4 圆弧电流在 O 点产生的磁感应强度为
ww
式中 θ1 =
w.
B= B=
方向垂直纸面向里。 7.2 如图 7.7 所示,有一被折成直角的无限长直导线有 20A 电流,P 点在折线的延长线上, 设 a 为,试求 P 点磁感应强度。 解 P 点的磁感应强度可看作由两段载流直导线 AB 和 BC 所产生的磁场叠加而成。AB 段 在 P 点所产生的磁感应强度为零,BC 段在 P 点所产生的磁感应强度为
w.
铅丝内部张力 T 为
通以电流 I 的导线 abcd 形状如图 7.16 所 示 ,ab = cd = l ,bc 弧是半径为 R 的半圆周,
置于磁感应强度为 B 的均匀磁场中, B 的方向垂直纸面向里。 求此导线受到的安培力 的大小和方向。 解 建立如图 7.16 所示的坐标系。由安培定理得两线段和受力大小相等,方向相反,二力 合力为零,导线所受力即为半圆弧所受力。
I ′ = 0, B = 0 I′ = I = I ′, B = I (r 2 − a 2 ) µ0 I r 2 − a 2 , B = b2 − a 2 2π r b 2 − a 2
当 a < r < b 时, 当 r > b 时, 7-8
µ0 I 2π r
一根很长的电缆由半径为 R1 的导体圆柱,以及内外半径分别为 R2 和 R3 的同轴导体圆
网
co m
dB =
µ0 Idl 4π R 2
式中 θ1 = 0, θ 2 =
π , r0 = r 2 ,所以 6 B= µ0 I ⎛ π ⎞ µ0 I ⎛ 3⎞ 1− ⎜ ⎟ ⎜ cos 0 − cos ⎟ = ⎜ 2π r ⎝ 6 ⎠ 2π r ⎝ 2 ⎟ ⎠
方向垂直纸面向里。 同理,DE 段在 P 点所产生的磁感应强度为
ww
方向垂直纸面向里。 第一段圆弧在 O 点所产生的磁感应强度为
方向垂直纸面向里。 同理,第二段圆弧在 O 点所产生的磁感应强度为
方向垂直纸面向外。
kh da
后
I1R1 = I 2 R2 I1l1 = I 2l2 µ0 I1dl 4π R 2 dB1 = B1 = ∫
l1
0
方向垂直纸面向里。 7-4 如图 7.9 所示,两根长直导线沿半径方向接到粗细均匀的铁环上的 A、B 两点,并与很 远处的电源相接,试求环中心 O 点的磁感应强度。 解 因为 O 点在两根长直导线上的延长线上,所以两根长直导线在 O 点不产生磁场,设第
Bb = B1b + B2b =
ww
µ0 I µI dS = 0 ldx 2π x 2π x b µ I µ Il b 通过矩形面积的总磁通量为 φm = ∫ 0 ldx = 0 ln a 2π x 2π a 7-7 一载流无限长直圆筒,内半径为 a,外半径为 b,传到电流为 I ,电流沿轴线方向流动 ,
有 可得
� ∫ B • dl = b� ∫ dl = B2π r = µ I ′
0
L
L
B=
µ0 I ′ 2π r
当 r < R 时,
答 案
I′ =
µI r Ir 2 ,B = 0 2 R1 2π R12 µ0 I 2π r
2 2 I (r 2 − R22 ) I ( R3 − r ) µ0 I R32 − r 2 I′ = I − 2 = , B = 2 2 2 R3 − R2 R32 − R2 2π r R32 − R2
co m
7-10 一载有电流 I = 7.0 A 的硬导线,转折处为半径为 r = 0.10m 的四分之一圆周 ab。均 匀外磁场的大小为 B = 1T ,其方向垂直于导线所在的平面,如图 7.14 所示,求圆弧 ab 部分 所受的力。 解 在圆弧 ab 上取一电流元 Idl ,此电流元所受安培力为
kh da
后
Ba = B1a + B2 a =
答 案
B2 a =
µ0 I 2 µ0 I 2 , B2b = 2π × 0.05 2π × 0.05
课
µ0 I1 µ0 I 2 + = 1.2 × 10−4 (T ) 2π × 0.05 2π × 0.05
µ0 I1 µ0 I 2 + = −1.33 × 10 −5 (T ) 2π × 0.15 2π × 0.05
4
其中 I ′ 是通过圆周 L 内部的电流 (1)当 r < a 时,
I′ =
网
co m
柱构成。电流 I 从一导体流出,又从另一导体流回,电流都沿轴线方向流动,并均匀分布在 其横截面上,设 r 为到轴线的垂直距离,试求磁感应强度随 r 的变化。 解 由电流分布具有轴对称性,可知相应的磁场分布也具有轴对称性,根据安培环路定理,
kh da
课 后
Fx = ∫ dFx = BIR Fy = ∫ dFy = BIR F = Fx i + Fy j = BIRi + BIRj BI 2 R = 2T T = BIR = 0.35( N )
答 案
由于 dl = Rdθ ,所以
w.
5
网
dFy = dF sin θ = BI sin θ dl
为 R2 ,因为 1、2 两段圆弧两端电压相等,可得
课
一段圆弧的长为 l1 ,电流强度为 I1 ,电阻为 R1 ,第二段圆弧长为 l2 ,电流强度为 I 2 ,电阻
w.
B2 = ∫
l2
0
电阻 R = ρ
1 ,而同一铁环的截面积为 S 和电阻率是相同的,于是有 S
由于第一段圆弧上的任一线元在 O 点所产生的磁感应强度为
w.
课
当
kh da
后
R2 < r < R3 I ′ = 0, B = 0
当 R1 < r < R2 时,
I′ = I, B =
w.
时 ,
0
其中是通过圆周 L 内部的电流,
� ∫ Bdl = B � ∫ dl = B 2π r = µ I ′
L L
可得
B=
µ0 I ′ 2π r Ir 2 µI r ,B = 0 2 2 a 2π a
习题精解
7-1 一条无限长直导线在一处弯折成半径为 R 的圆弧,如图 7.6 所示,若已知导线中电流强 度为 I,试利用比奥—萨伐尔定律求: ( 1)当圆弧为半圆周时,圆心 O 处的磁感应强度; ( 2) 当圆弧为 1/4 圆周时,圆心 O 处的磁感应强度。 解(1)如图 7.6 所示,圆心 O 处的磁感应强度可看作由 3 段载流导线的磁场叠加而成。因 为圆心 O 位于直线电流 AB 和 DE 的延长线上,直线电流上的任一电流元在 O 点产生的磁 感应强度均为零,所以直线电流 AB 和 DE 段在 O 点不产生磁场。 根据比奥—萨伐尔定律,半圆弧上任一电流元在 O 点产生的磁感应强度为
