1自由度习题
自由度计算举例1
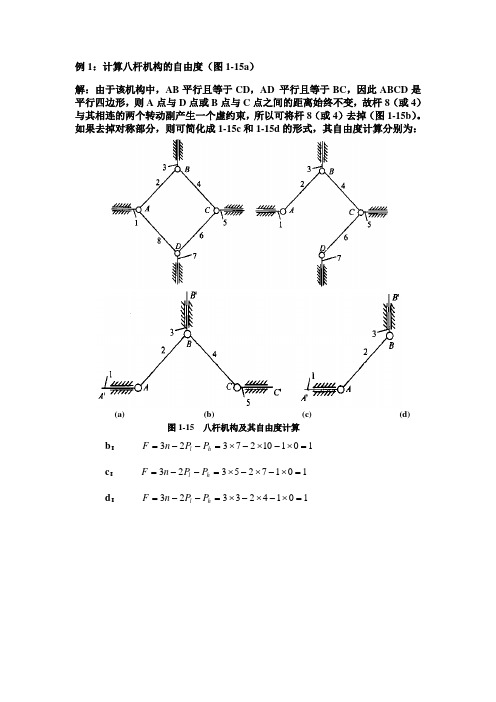
例1：计算八杆机构的自由度（图1-15a ）解：由于该机构中，AB 平行且等于CD ，AD 平行且等于BC ，因此ABCD 是平行四边形，则A 点与D 点或B 点与C 点之间的距离始终不变，故杆8（或4）与其相连的两个转动副产生一个虚约束，所以可将杆8（或4）去掉（图1-15b ）。
如果去掉对称部分，则可简化成1-15c 和1-15d 的形式，其自由度计算分别为：(a) (b) (c) (d) 图1-15 八杆机构及其自由度计算b ： 1011027323=⨯-⨯-⨯=--=h l P P n Fc ： 101725323=⨯-⨯-⨯=--=h l P P n Fd ： 101423323=⨯-⨯-⨯=--=h l P P n F例2、试计算图示机构的自由度。
（若有复合铰链、局部自由度或虚约束，必须明确指出。
）并指出杆组的数目与级别以及机构级别。
例3、试对图示机构：(本小题15分)（1）计算自由度；（3分）（2）分别取构件1和7 为原动件，拆出所有杆组，并确定机构的级别（必须画出各杆组）。
（8分）（3）求构件2、8和2、5之间的速度瞬心p和25p（4分）28例4、试对图示机构：(本小题11分)（1）计算自由度；（3分）（2）对图示机构进行高副低代和结构分析，并确定该机构的级别。
（8分）例5、计算图示机构的自由度，如有复合铰链、虚约束及局部自由度，直接在图中指出(本小题10 分)。
例6：计算如图所示机构的自由度并确定机构的级别解：例7、(本小题8分)计算图示机构的自由度，并在高副低代后判断机构的级别。
例8、已知图示机构的尺寸和位置(本小题10分)：1、画出高副低代机构的运动简图，直接在图上作图（4分）；2、拆分基本杆组，并判断机构的级别（6分）。
例9：计算如图所示的双缸曲柄滑块机构的自由度并确定机构的级别解：1011027323=⨯-⨯-⨯=--=h l P P n F 以4为原动件以2为原动件以8为原动件。
1 平面机构运动简图和自由度 习题答案
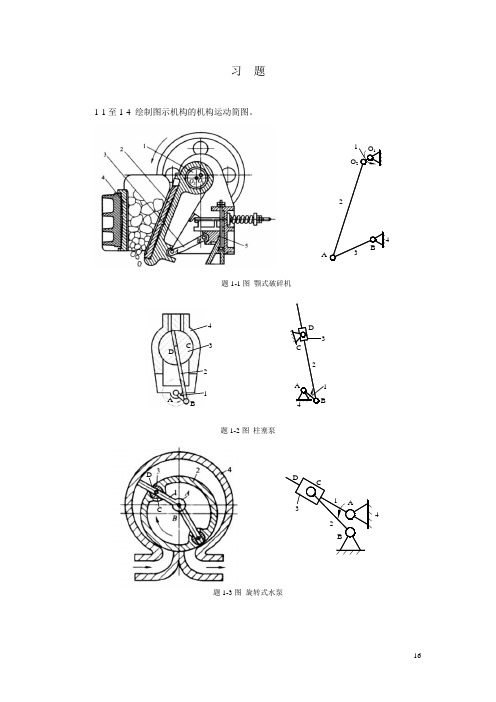
习 题1-1至1-4 绘制图示机构的机构运动简图。
题1-1图 颚式破碎机题1-2图 柱塞泵题1-3图 旋转式水泵O 1O 2AB1 234ABCD 1 2 3 4 A B CD1 234 AB CD1 2 34CD题1-4图 冲压机构1-5至1-10 指出机构运动简图中的复合铰链、局部自由度和虚约束，并计算各机构的自由度。
题1-6图解：构件3、4、5在D 处形成一个复合铰链，没有局部自由度和虚约束。
32352701L H F n P P =--=⨯-⨯-=解：没有复合铰链、局部自由度和虚约束。
323921301L H F n P P =--=⨯-⨯-= 题1-5图题1-5图56 ABCDEFO 1 O 2 D F1 2 345 6EGFEG题1-7图题1-8图题1-9图 题1-10图解：A 处为复合铰链，没有局部自由度和虚约束。
323721001L H F n P P =--=⨯-⨯-=解：A 处为复合铰链，没有局部自由度和虚约束。
323721001L H F n P P =--=⨯-⨯-=解：B 处为局部自由度，没有复合铰链和虚约束。
32352710L H F n P P =--=⨯-⨯-=解：C 处为复合铰链，E 处为局部自由度，没有虚约束。
32372912L H F n P P =--=⨯-⨯-=AB C DE IFG HADBECAEBCDGF1-11图示为一手动冲床机构，试绘制其机构运动简图，并计算自由度。
试分析该方案是否可行；如果不可行，给出修改方案。
题1-11图手动冲床答：此方案自由度为0，不可行。
改进方案如图所示：手动冲床运动简图手动冲床改进方案。
第1章--单自由度系统的自由振动题解
习 题1-1一单层房屋结构可简化为题1-1图所示的模型，房顶质量为m ，视为一刚性杆；柱子高h ，视为无质量的弹性杆，其抗弯刚度为EJ 。
求该房屋作水平方向振动时的固有频率。
解：由于两根杆都是弹性的，可以看作是两根相同的弹簧的并联。
等效弹簧系数为k 则 mg k δ=其中δ为两根杆的静形变量，由材料力学易知δ=324mgh EJ=则 k =324EJh设静平衡位置水平向右为正方向，则有 "m x kx =- 所以固有频率3n 24mhEJp =1-2 一均质等直杆，长为 l ，重量为W ，用两根长h 的相同的铅垂线悬挂成水平位置，如题1-2图所示。
试写出此杆绕通过重心的铅垂轴作微摆动的振动微分方程，并求出振动固有周期。
解：给杆一个微转角2a ＝h题1-1图题1-2图θF sin α2θαhmgθ2F cos ＝mg由动量矩定理：aha mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ&&其中12cossin ≈≈θααhl ga p ha mg ml n 22222304121==⋅+θθ&& g h a l gah l p T n 3π23π2π222===1-3求题1-3图中系统的固有频率，悬臂梁端点的刚度分别是k 1和k 3，悬臂梁的质量忽略不计。
解：悬臂梁可看成刚度分别为k 1和k 3的弹簧，因此，k 1与k 2串联，设总刚度为k 1ˊ。
k 1ˊ与k 3并联，设总刚度为k 2ˊ。
k 2ˊ与k 4串联，设总刚度为k 。
即为21211k k k k k +='，212132k k kk k k ++='，4241213231421432421k k k k k k k k k k k k k k k k k k k k ++++++=)(42412132314214324212k k k k k k k k k k m k k k k k k k k k p ++++++=1-4求题1-4图所示的阶梯轴一圆盘系统扭转振动的固有频率。
机械原理复习题2.
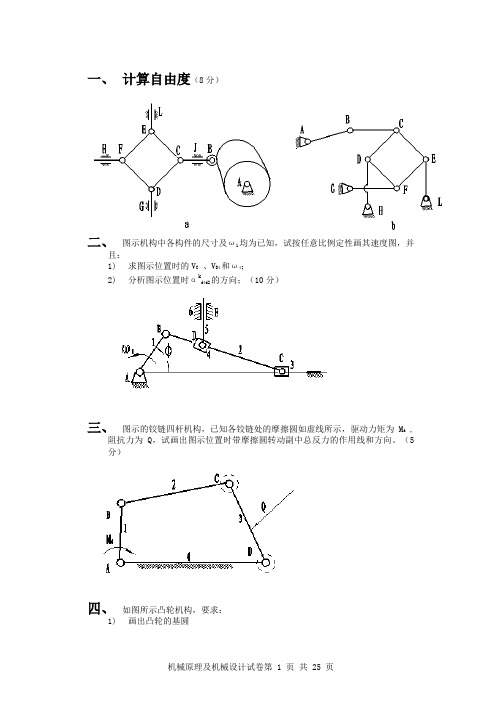
一、计算自由度（8分）二、图示机构中各构件的尺寸及ω1均为已知，试按任意比例定性画其速度图，并且：1)求图示位置时的V C、V D4和ω4；2)分析图示位置时αk d4d2的方向；（10分）三、图示的铰链四杆机构，已知各铰链处的摩擦圆如虚线所示，驱动力矩为M d ,阻抗力为Q，试画出图示位置时带摩擦圆转动副中总反力的作用线和方向。
（5分）四、如图所示凸轮机构，要求：1)画出凸轮的基圆2)画出从升程开始到图示位置时推杆的位移s，相对应的凸轮转角φ，B点的压力角α；（8分）五、计算题在图示机构中，已知各直齿圆柱齿轮模数均为m=2mm，z1 =15，z2=32，z2´=20，z3 =30，要求齿轮1、3同轴线。
试问：1)齿轮1、2和齿轮2´、3应选什麽传动类型最好？为什麽？2)齿轮1、2改变为斜齿轮传动来凑中心距，当齿数不变，模数不变时，斜齿轮的螺旋角为多少？3)若用范成法来加工齿数z1=15的斜齿轮1时，是否会产生根切？（14分）七、简答题：（20分）1.转动副的自锁条件是什麽？螺旋副的自锁条件是什麽？2.在曲柄摇杆机构中，当以曲柄为原动件时，机构是否一定存在急回运动，为什麽？3.若凸轮是以逆时针转动，采用偏置直动推杆时，推杆的导路应偏置于回转中心的哪一侧较合理？为什麽？4.外啮合斜齿圆柱齿轮的正确啮合条件是什麽？5.变位齿轮的分度圆、基圆、周节和基节大小都发生变化了吗？为什麽？6.压力角为15º的齿条（模数可为非标准值）能否与压力角为20º（标准模数）的齿轮正确啮合？为什麽？7.i H GK是不是周转轮系中G、K两轮的传动比？为什麽？8.槽轮机构运动特性系数k的取值范围是什麽？9. 双万向铰链机构传动比恒为1的条件是什麽？10. 什麽是机构稳定运转状态下的周期性速度波动，如何进行调节？一． 选择与填空（本题共12小题，选择题每小题2分，填空题每空1分，满分27分） （1）设图示回转体的材料均匀，制造精确，安装正确，当它绕AA 轴线回转时是处于 状态。
1单自由度系统振动总结与习题
n
U=
max A n
1 k ( a ) 2 2 A
T max U max ；
2 1 2 2 1 2 ml A Ka 2 . A 2 n 2 2
n
a l
k ； m
周期 T=
2l a
m k
利用等效能量法求图示系统的固有频率
解:真实系统:T=
l 1 1 2 ) 2 + m2. x m1( 2 x 2 2 l4 l 1 l 1 2 2 U= k1 ( 1 .x) k 2. ( 3 .x) 2 l4 2 l4 1 2 等效系统 T e = me. x 2 1 2 V e = ke x 2 l 2 T=T e m e =m 2 +m 1 ( 2 ) l4 l 2 l 2 V=V e k e ( 1 ) +k 2 ( 3 ) l4 l4
4 、细杆 OA 可绕水平轴 O 转动，如图，在静平衡位置时成水平，杆端 重锤的质量为m，杆与弹簧的质量均可忽略不计，求自由振动的固有周期。
解: 为小球偏角时,弹簧伸长以及锤的位移可表示成 a ,l ,
1 m (l) 2 ； 2 令 A sin( n t ) A sin( )
l
x sin( n t )
因此梁上各点的速度分布为
( x, t ) A sin v
l
x n cos( n t )
因而动能最大值为 1 1q l 2 Tmax M n A 2 ( A sin x n ) 2 dx 2 2g 0 l 1 A 2 2 ( M 1 Q ) n 2 2g 1 1 48 EI 2 A 在最大振幅位置 Vmax KA 2 2 2 l3 48EI 由 Vmax Tmax 求得： n = 1 Q 3 M 2 g l
1平面机构自由度
二、运动副的分类
低副（面接触） 转动副：引入两个约束，保留一个自由度（转动） 移动副：引入两个约束，保留一个自由度（移动） 高副（点或线接触）： 引入一个约束，保留两个自由度（切向移动＋转动） 如：滚动副、凸轮副、齿轮副 。
1 自由度 1
举例：内燃机
转动副: 活塞－连杆 连杆－曲轴
气缸体
活塞
顶杆
曲轴－气缸体
1 自由度 11
1.3 平面机构的自由度 ---机构所具有的独立运动
三、计算平面机构自由度应注意的事项
(2) 局部（多余）自由度 若某构件的运动与其它构件运动无关，则该构件所具有的自由度为局部自由度。 对于含有局部自由度的机构在计算自由度时，不考虑局部自由度。
如认为F = 3×3 - 2×3 - 1=2 (错误) n = 2、pL= 2、pH = 1 F = 3n -2pL - pH =3×2 -2×2 – 1 =1(正确)
大、小齿轮－气缸体 凸轮－气缸体 凸轮
连杆 曲轴
移动副：
活塞－气缸体 顶杆－气缸体 高副： 凸轮－顶杆 大齿轮－小齿轮 小齿轮 返回 1 自由度 2 大齿轮
1.2 平面机构运动简图
一、平面机构的组成
机架：固定构件。如机床床身、车辆底盘、气缸体； －1个
构件 原(主)动件(输入构件): 运动规律已知的活动构件； 从动件：随原动件运动而运动的其余活动构件。 输出构件: 输出预期运动的从动件。 运动副 －1个或几个 －若干个
返回
4
构件的表示方法
1. 将构件上所有运动副用线 条连接起来; 2.画构件时应撇开构件的实 际外形，而只考虑运动副的 性质。
返回
5
绘制步骤
1. 分析机构运动 先找原动件； 缓慢转动原动件，找出传动路线 及输出构件; 确定机架，沿传动路线“两两分 析相对运动”，确定各构件间运 动副性质。 2. 恰当选择投影面，确定合适瞬 时位置，按传动路线画草图。 3. 测量各运动副间尺寸，选择比 例尺，画正规运动简图。 原动件上标箭头；
机械原理试题库1
机械原理自测题库——分析计算题（共88题）1、试计算图示机构的自由度（若有复合铰链、局部自由度或虚约束，必须明确指出）。
并判断该机构的运动是否确定（标有箭头的机构为原动件）。
若其运动是确定的，要进行杆组分析，并显示出拆组过程，指出各级杆组的级别、数目以及机构图a 图b)题 1 图2、计算图示机构自由度，并判定该机构是否具有确定的运动（标有箭头的构件为原动件）。
图 a) 图 b)题 2 图3、计算图示机构自由度，并确定应给原动件的数目。
图a 图b题 3 图4、在图示机构中试分析计算该机构的自由度数，若有复合铰链、局部自由度或虚约束，则在图上明确指出。
图a 图b题 4 图5、计算图示机构的自由度，并作出它们仅含低副的替代机构。
第 1 页共24 页图 a) 图 b)题 5 图6、试计算图示机构的自由度。
(若有复合铰链、局部自由度或虚约束，必须明确指出。
)并指出杆组的数目与级别以及机构级别。
LG I题 6 图7、计算下列机构的自由度（有复合铰链、虚约束和局部自由度请指出）图 a) 图 b)题 7 图8、图示的铰链四杆机构中,已知mmlAB65=，mmlCD90=，mmlAD125=，sradmmlBC/10,1251==ω,顺时针转动,试用瞬心法求:1)当φ=15°时,点C的速度V C;2)当φ=15°时,构件BC上(即BC线上或其延长线上)速度最小的一点E的位置及其速度值。
题 8 图9、在图示的凸轮机构中，已知凸轮1以等角速度ω1=10rad/s转动。
凸轮为一偏心圆，其半径R1=25mm，L AB=15mm，L AD=50mm，φ1=90°，试用瞬心法求机构2的角速度ω2。
第 2 页共24 页题 9 图10、在图示机构中，已知长度L AB=L BC=20 mm ,L CD=40mm ,∠a=∠β=90°W1=100(1/S),请用速度瞬心法求C点的速度的大小和方向题 10 图11、如图所示偏置曲柄滑块机构。
1 平面机构及其自由度
常用运动副运动简图符号
常用构件运动简图符号
1.2 平面机构运动简图
1.2.1 机构运动简图及作用 1.2.2 构件的分类
1.2.2 构件的分类
机构中的构件可分为三类： 机构中的构件可分为三类： 三类 固定件 原动件 从动件
研究机构运动时作为参考坐标系的构件；又称为 研究机构运动时作为参考坐标系的构件； 机架。 机架。 是运动规律已知的活动构件。它的运动是由外界 是运动规律已知的活动构件。 输入的，所以又称为输入件 输入件。 输入的，所以又称为输入件。 机构中随着原动件运动而运动的其余活动构件。 机构中随着原动件运动而运动的其余活动构件。 其中输出机构预期运动的从动件称为输出件 输出件。 其中输出机构预期运动的从动件称为输出件。
小型压力机及其机构运动简图
颚式破碎机及其机构运动简图绘制
腭式破碎机
活塞泵及其机构运动简图绘制
1 平面机构及其自由度
1.1 运动副及其分类 1.2 平面机构运动简图 1.3 平面机构的自由度及其计算
1.3 平面机构的自由度及其计算
1.3.1 平面机构的自由度
1.3.1 平面机构的自由度
机构的自由度: 机构中各构件相对机架所有的独立运动的数目。 机构的自由度: 机构中各构件相对机架所有的独立运动的数目。 一个作平面运动的自由构件具有三个自由度。 一个作平面运动的自由构件具有三个自由度。 每个低副引入两个约束，使构件失去两个自由度； 每个低副引入两个约束，使构件失去两个自由度； 每个高副引入一个约束，使构件失去一个自由度。 每个高副引入一个约束，使构件失去一个自由度。 个构件。 设平面机构共有 K 个构件。 活动构件数为 活动构件数为 低副数： 低副数：PL 高副数： 高副数：PH
机构具有确定运动的条件是： 机构具有确定运动的条件是： F ＞ 0 并且给定机构的输入运动数（原动件数） 并且给定机构的输入运动数（原动件数） 等于机构的自由度数。 等于机构的自由度数。
1自由度分析
是
不是
3. 虚约束（难点）
不产生实际约束效果的重复约束。在特定的几何条 件下出现。（或称消极约束）
（1）暗含的几何条件： 两构件组成若干转动副，但转动副轴线互相重合 两构件组成若干移动副，但移动副导路互相平行 两构件组成若干高副，但各接触点公法线互相重合
（2）明确给定的几何条件： 平行、垂直、长度关系
通过严格的几何证明识别 熟悉教材例题
目的：为了改善构件的受力情况
虚约束常出现的场合—特定几何条件
场合一：用双转动副杆联接两构件上距离保持不变的两点
B 2E
C
1
3
A
D
F 33 24 1
去除构件4及其上运动副
B 2E
C
1
4
3
A
F
D
5
AB CD EF
? F 3 4 2 6 0
B
2 EC B
2EC
1
31
5
3
A
4F
A
4F
D
D
AB
EF CD
F=3n-2PL-Ph=33
-A2B4=E1F
CD
B
2
E
C
1
5
A
F
4
3
D
F=3n-2PL-Ph=33 -24=0 桁架-非虚约束
距离不变两点例2
例各构件的尺寸有如下的几何关系：
，
，
，
F = 3×4 - 2×6 = 0 ？
去除虚约束构件及其上运动副
F 33 24 1
• 机构要能运动，它的自由度必须大于零。
F≤0，构件间无相对运动，不成为机构。
原动件数W=F，运动确定
2
(完整版)机械设计基础1自由度
（约束了一个自由度）
此外，还有球面副和螺旋副，均属于空间相对运动。本课程不进行讨论。
§1-2.平面机构的运动简图
1．平面运动副的表示方法：
转动副表示方法
2．构件表示方法：
移动副表示方法
高副表示方法
两个转动副构件
一个转动副 一个移动副构件
5 F=3×5 - 2×7 = 1 ✓
(2) 局部自由度： 与整个机构运动无关的自由度。 计算机构自由度时应予排除。
F=3×3 - 2×3 -1 = 2 ×
F=3×2 - 2×2 -1 = 1 ✓
目的：变滑动磨擦为滚动磨擦，以减少磨损。计 算时应将该构件连同运动副一起除去。
(3) 虚约束： 对机构自由度是重复的约束。
第一章 平面机构的自由度 和速度分析
平面机构：所有的构件都在同一平面或在相互平行平 面内运动的机构。
§1-1.运动副及分类
自由构件：在平面内不受约束做自由运动的构件。
自由度：做平面运动的自由构件的独立的自由运动 数（三个自由度）X、Y、 。
Y
y
0
x
X
1．运动副（关节）：两构件间的可动联接
定义：使两构件直接接触并能产生一定相对运动的联接。
即该机构只有一个自由度，与原 动件数相同（齿轮3为原动件）。 所以,满足机构具有确定运动的条 件。
例题3. 已知一机构如图所示，求其自由度？
解：1. A、B、C、D处为复合铰 链
2. n=7 PL= 10 PH=0
F=3n-2PL-PH=37-2100=1
即该机构只有一个自由度，与原 动件数相同（杆8为原动件）。所 以,满足机构具有确定运动的条件
结构动力学【习题课】(单自由度体系1)
EI l
m
4.图 所示结构周期为T 则图b 4.图a所示结构周期为Ti,则图b所示体系的周期为
T =
T1 + T + T
2 2 2
2 3
ki m
k1 k2 k3 m
(a) 5.图示体系的自振频率为 5.图示体系的自振频率为 .
(b)
EI = ∞ k
l l
m
6.图示体系的动力自由度为5. 6.图示体系的动力自由度为5. 图示体系的动力自由度为 EI=常数
第1 、2 章
小结 动力特性计算 公式法 能量守恒 幅值方程 动力反应计算 简谐荷载 周期荷载 阶跃荷载 冲击荷载 一般荷载
动荷载及其分类 自由度及其确定 运动方程的建立 惯性力法 虚功法 运动方程的求解方法 经典解法 频域解法 时域解法 数值解法 确定动力特性的试验方法 阻尼力假定及阻尼的影响
1.若使单自由度体系的阻尼增大,其结果是周期变短. 1.若使单自由度体系的阻尼增大,其结果是周期变短. 若使单自由度体系的阻尼增大 错
EA = ∞
7.体系的振幅和自振频率与初始条件有关. 7.体系的振幅和自振频率与初始条件有关. 体系的振幅和自振频率与初始条件有关
8.在图示体系中,若要使其自振频率增大,可以 8.在图示体系中,若要使其自振频率增大, 在图示体系中 A.增大 ; A.增大P; 增大 C.增大 ; C.增大m; 增大 B.增大EI; B.增大EI; 增大 D.增大 l . D.增大
ωD = ω 1−ξ 2
&& + 2ξω y + ω 2 y = P ( t ) / m & y
)
2.单自度体系运动方程为 2.单自度体系运动方程为 其中未考虑质体重力,这是因为( 其中未考虑质体重力,这是因为(
1平面机构运动简图和自由度习题答案
1-1至1-4绘制图示机构的机构运动简图。
题1-1图顿式破碎机
题1-2图柱塞泵
题1-3图旋转式水泵
I
題1-4图冲压机构
1-5至1-10指岀机构运动简图中的复合铁链、局部自由度和虚约束，并计算各机构的
自由度。
解：构件3、4、5在D处形成一个复合钱
链，没有局部自由度和虚约朿。
F=3H —2P L—P H=3X5-2X7-0=1
题1-5图
解：没有复合铁链、局部自由度和虚约束。
F = 3n-2P L-P H=3X9-2X13-0=1
题1-6图
1
1
解：A处为复合绞链，没有局部自由度和虚约
朿。
F = 3n-2R —P H=3X7-2X10-0=1
解：C处为复合较链，E处为局部自由度, 没有
虚约束。
F=3H_2P I_P H=3X7-2X9-1=2
题1-10图
题1-8图
1-11图示为一手动冲床机构，试绘制其机构运动简图，并计算自由度。
试分析该方案 是否可行；如果不可行，给出修改方案。
答：此方案自由度为0,不可行。
改进方案如图所示:
于•动冲床改进方
案。
机械设计基础习题1
习 题2-1 试画出题2-1图中各平面机构的运动简图，并计算其自由度。
a)b)c)d)2-2 题2-2图所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。
2-3 试计算题2-3图所示凸轮—连杆组合机构的自由度。
并指出图中的复合铰、局部自由度和虚约束。
2431234153421BA432143512b)a)A EMDFELKJIFBCCDBA题2-2图题2-1图2-4 试计算题2-4图所示齿轮—连杆组合机构的自由度。
并指出图中的复合铰、局部自由度和虚约束。
2-5 计算题2-5图所示各机构的自由度。
并指出图中的复合铰、局部自由度和虚约束。
题2-5图（a ） 题2-5图（b ）CB D CDB A A(b) (a)题2-5图（c ） 题2-5图（d ）题2-5图（e ） 题2-5图（f ） 题2-4图2-6 计算题2-6图所示机构的自由度，其中图（a）为液压挖掘机构，图（b）为差动轮系。
（a) （b)2-7 题2-7图所示，箭头所示构件为原动件，试判断该机构是否有确定相对运动。
ACEDFACBEF（a) （b)题2-7图题2-6图习 题3-1 简答题1）平面四杆机构的基本型式是什么？它的演化方法有哪几种？ 2）机构运动分析包括哪些内容？ 3）什么叫三心定理？3-2 举出至少3个基本型式的平面四杆机构应用实例，并画出机构运动简图。
3-3题3-3图所示铰链四杆机构中，已知 BC=100mm ， CD=70mm ， AD=60mm ，AD 为机架。
试问：（1）若此机构为曲柄摇杆机构，且AB 为曲柄，求AB 的最大值； （2）若此机构为双曲柄机构，求AB 最小值； （3）若此机构为双摇杆机构，求AB 的取值范围。
3-4 题3-4图所示四杆机构简图中，各杆长度为a =30 mm ，b =60 mm ，c =75 mm ，d =80 mm ，试求机构的最大传动角和最小传动角、最大压力角和最小压力角、行程速比系数。
1自由度
?
B
2 4
F
E
C
B
2 5 4
F
E
C
1
A
3 AB EF CD
D
1
A
3
D
F=3n-2PL-Ph=33 -24=1
B
AB EF CD
E C
2 5 4
1
A F
3
D
F=3n-2PL-Ph=33 -24=0 桁架-非虚约束
距离不变两点例2 例各构件的尺寸有如下的几何关系： ， ， ，
F = 3× 4 - 2 × 6 = 0
1.3.3 计算机构自由度的注意事项
1. 复合铰链 由两个以上构件在同一转动轴线处构成的转动 副称为复合铰链。 由m个构件汇集而成的复合铰链应当包含(m-1) 个转动副。
◆计算中注意观察是否有复合铰链，以免漏算转动副数目，出现
计算错误。
需注意由齿轮、凸轮及机架等构件构成的复合铰链
判断是否为复合铰：
注：只有有小滚子处，且小滚子几何中心与转动中 心重合，才是局部自由度。
是
不是
3. 虚约束（难点）
不产生实际约束效果的重复约束。在特定的几何条 件下出现。（或称消极约束）
（1）暗含的几何条件： 两构件组成若干转动副，但转动副轴线互相重合 两构件组成若干移动副，但移动副导路互相平行 两构件组成若干高副，但各接触点公法线互相重合 （2）明确给定的几何条件： 平行、垂直、长度关系 通过严格的几何证明识别 熟悉教材例题
n=6, PL=8, PH=1 F=3n－2PL－PH =3×6-2×8-1 =1
自由度例题(6)
已知： DE=FG=HI，且相互平行；DF=EG，且相互平行；
DH=EI，且相互平行。
机械设计基础习题答案
平面机构及其自由度1、如图a 所示为一简易冲床的初拟设计方案，设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析其是否能实现设计意图？并提出修改方案。
解 1）取比例尺l μ绘制其机构运动简图（图b ）。
图 b ）2）分析其是否能实现设计意图。
由图b 可知，3=n ，4=l p ，1=h p ，0='p ，0='F故：00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此，此简单冲床根本不能运动（即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架），故需要增加机构的自由度。
3）提出修改方案（图c ）。
为了使此机构能运动，应增加机构的自由度（其方法是：可以在机构的适当位置增加一个活动构件和一个低副，或者用一个高副去代替一个低副，其修改方案很多，图c 给出了其中两种方案）。
图 c 1） 图 c 2） 2、试画出图示平面机构的运动简图，并计算其自由度。
解：3=n ，4=l p ，0=h p ，123=--=h l p p n F解：4=n ，5=l p ，1=h p ，123=--=h l p p n F3、计算图示平面机构的自由度。
解：7=n ，10=l p ，0=h p ，123=--=h l p p n F解：8=n ，11=l p ，1=h p ，123=--=h l p p n F ，局部自由度解：9=n ，12=l p ，2=h p ，123=--=h l p p n F解： D,E,FG 与D ，H ，J ，I 为对称结构，去除左边或者右边部分，可得，活动构件总数为7，其中转动副总数为8，移动副总数为2，高副数为0，机构自由度为1。
（其中E 、D 及H 均为复合铰链）4、试求图示各机构在图示位置时全部瞬心的位置（用符号ij P 直接标注在图上）。
工业机器人课后答案
工业机器人课后答案【篇一：工业机器人技术习题答案.pdf】>一、填空1、自由度2、操作机、控制器、示教器、末端执行器、操作机、控制器、示教器3、点位运动（ptp）、连续路径运动（cp）、cp4、正向二、选择1、d2、d 三、判断2、示教再现机器人、感知机器人、智能机器人3、日系、欧系二、选择1、d2、d3、c 三、判断第一章绪论第二章工业机器人的机械结构和运动控制第三章手动操纵工业机器人一、填空 1、机器人轴、基座轴、基座轴、外部轴 2、工具 3、点动二、选择1、d2、d 三、判断表手动移动机器3-6 人要领一、填空 1、示教、程序、再现 2、跟踪 3、离线编程二、选择1、b 2、d 3、d三、判断四、综合应用表4-6第四章初识工业机器人的作业编程直线轨迹作业示教第五章搬运机器人的作业编程一、填空 1、龙门式搬运机器人、悬臂式搬运机器人、侧壁式搬运机器人、摆臂式搬运机器人 2、吸附式、夹钳式、仿人式 3、机器人控制柜、示教器、气体发生装置、气吸附手爪二、选择1、d2、d三、判断1、√2、√3、√四、综合应用略取式、组合式 3、第六章码垛机器人的作业编程一、填空 1、龙门式码垛机器人、摆臂式码垛机器人 2、吸附式、夹板式、抓操作机、机器人控制柜、示教器、真空发生装置、气体发生装置4、一进一出、一进两出、两进两出二、选择1、a2、a三、判断一、填空 1、关节式 2、c型、伺服3、弧焊、示教器、焊枪、操作机、弧焊电源4、双、双、h 二、选择1、b2、d3、d 四、综合应用略第七章焊接机器人的作业编程三、判断（2）略2、1、√ √ 3、√ 四、综合应用（1）表 7-圆弧轨迹作业13 示教【篇二：工业机器人考点大全--习题答案】p class=txt>答：工业机器人是一种用于移动各种材料、零件、工具或专用装置，通过可编程动作来完成各种任务并具有编程能力的多功能机械手。
智能机器人是一种自动化的机器，所不同的是这种机器具备一些与人或生物相似的智能能力，如感知能力、规划能力、动作能力和协同能力，是一种具有高度灵活性的自动化机器。
机械原理习题及答案(1-1至4-3)
2-5
K 1 1.5 1 180 180 36 K 1 1.5 1
作以 C1C2 为弦其所 对圆角为 的圆，圆 与偏心距位置线的交 点即为所要求的铰链 中心A。
l AB 21.75m m lBC 46.75m m m l 0.001 mm
l AC1 lBC l AB 25 0.001 0.25m 25mm
3.15mm < 答：
l AB
< 45mm
解：1.当AD为机架，此机构为曲柄摆杆机构， 且AB为曲柄，即AB为最短杆，据曲柄存在条件：
l AB l BC lCD l AD
l AB 50 35 30 l AB 15
答：l AB
15 mm
2.当AD为机架，此机构为双曲柄机构， 则AD为最短杆，据曲柄存在条件，分两种情况； （1）若 l AB 为最长杆，则 l AD l AB l BC lCD
l AB 15mm 即此时 l AB 应大于15mm，但由上述（2）知 45 l AB 55 时， 此机构为双曲柄机构。如此机构为双摇杆机构，则必须15< l AB <45。 如 l AB 为最长杆
l AB 50 35 30
2-3 试分别标出下列机构图示位置时的压力角和传动角，箭头标 注的构件为主动件。
1 2 A 90，它说明没有
滑块4时，C点仍沿y轴运动，故 滑块4产生虚约束，应除去不计。
1-4 计算图示平面机构的自由度。将其中的高副用低副代替，确 定机构所含杆组的数目和级别，以及机构的级别。
2-3-4-5为III级组，故为III 级机构。
n 4, pL 5, pH 1
结构力学1
《结构力学》第一阶段作业一、判断题。
1、如果平面体系的约束数等于自由度数，那么体系一定是几何不变的。
（×）2、如果平面体系的计算自由度W=0，那么该体系一定为无多余约束的几何不变体系。
（×）3、如果平面体系的计算自由度W＜0，那么该体系是有多余约束的几何不变体系。
（×）二、请对图示各平面体系进行几何组成分析。
解：图2-1是无多余约束的几何不变体系。
解：图2-2是无多余约束的几何不变体系。
解：图2-3是具有一个多余约束的几何不变体系。
解：图2-4是具有一个多余约束的几何不变体系。
解：图2-5是无多余约束的几何不变体系。
解：图2-6是无多余约束的几何不变体系。
解：图2-7是无多余约束的几何不变体系。
解：图2-8是无多余约束的几何不变体系。
解：图2-9是无多余约束的几何不变体系。
解：图2-10是无多余约束的几何不变体系。
三、名词解释。
1、自由度答：一个体系的自由度，是指该体系在运动时，确定其位置所需的独立坐标的数目。
2、计算自由度答：计算一个体系在运动时，确定其位置所需的独立坐标的数目。
3、几何不变体系答：在任意荷载作用下，其原有的几何形状和位置保持不变的，称为几何不变体系。
4、几何可变体系答：在任意荷载作用下，其几何形状和位置发生变化的，称为几何可变体系。
5、刚片答：对体系进行几何组成分析时，由于不考虑材料的应变，故可将每一根杆件都视为刚体，在平面体系中又把刚体称为刚片。
6、二元体答：两根不共线的链杆连接一个结点的装置称为二元体。
7、二元体规则答：在一个体系上增加或减少二元体，不改变体系的几何可变或不可变性。
8、两刚片规则答：两刚片用不全交于一点也不全平行的三根链杆相互连接，或用一个铰及一根不通过铰心的链杆相连接，组成无多余约束的几何不变体系。
9、三刚片规则答：三刚片用不在同一直线上的三个铰两两连接，则组成无多余约束的几何不变体系。
机械运动自由度大于1的例子
机械运动自由度大于1的例子
1. 你看那台汽车在路上飞驰，它的轮子可以自由转动，这可不就是机械运动自由度大于 1 的典型例子嘛！四个轮子各自转动，多厉害呀！
2. 想想飞机在天空翱翔，它的机翼能摆动，机身能前进后退，这难道不是机械运动自由度大于 1 吗？这是多么神奇的存在呀！
3. 还记得公园里的摩天轮吗？它不仅能转圈，每个座舱还能小幅度晃动，这绝对是机械运动自由度大于 1 的有趣例子呀！哇哦！
4. 就说那台洗衣机吧，桶会转动清洗衣服，同时还会有一些震动，这不正说明了机械运动自由度大于 1 嘛，真了不起呢！
5. 大型起重机在工地工作时，起重臂可以上下左右移动，这不是机械运动自由度大于 1 是什么呢，太酷了吧！
6. 你注意过家里的风扇没有呀，扇叶能转动，风扇本身还能摇头呢，这可是机械运动自由度大于 1 的生动体现呀，神奇吧！
7. 观察一下船在水面行驶，它能前进后退，还能左右转向，这不就是机械运动自由度大于 1 的例子嘛，太有意思了！
8. 机器人的手臂呀，既能弯曲又能伸展，还能旋转，这就是机械运动自由度大于 1 呀，简直太帅了！
结论：生活中有这么多机械运动自由度大于 1 的例子，真是无处不在呀，让我们的世界变得丰富多彩！。
1计算图示机构的自由度
1计算图示机构的自由度，并指出其中的复合铰链、局部自由度和虚约束。
2试计算图示构件系统的自由度，并指出它是否为机构。
将高副低代后，分析杆组的级别和机构的级别。
204 图示为冲压机构，试：（1）计算自由度，标出原动件（用箭头表示）。
（2）画出全是低副的瞬时替代机构。
（3）进行机构结构分析，判别机构级别。
212 图示机构中，点划线所画之圆为两渐开线齿轮的节圆，凸轮与大齿轮为同一构件，O点为接触点K处凸轮轮廓线的曲率中心，如取小齿轮为原动件时，该机构是否具有确定的运动？高副低代后，进行结构分析，判明它是几级机构。
214 将图示机构高副低代，然后计算自由度，并且进行结构分析，确定机构的级别（画箭头的构件为原动件）。
215 已知机构的尺寸和位置如图所示，试：（1）计算机构的自由度F。
是否存在复合铰链，局部自由度和虚约束？若存在，指出其位置；（2）画出高副低代的机构运动简图；（3）对该机构进行结构分析，并确定该机构为几级。
193 标明图示机构的虚约束、复合铰链、 局部自由度 ， 判断该机构运动是否确定。
经高副低代和拆分杆组后，判明该机构的级别。
302 当两个构件组成移动副时，其瞬心位于 处。
当两构件组成纯滚动的高副时， 其瞬心就在 ； 当求机构的不互相直接联接各构件间的瞬心时， 可应用 来求。
311铰链四杆机构共有 个速度瞬心，其中 个是绝对瞬心， 个是相对瞬心。
329 给定图示六杆机构的加速度多边形，可得出(A) 矢量c d ''→ 代表 a CD ， α5是顺时针方向； (B) 矢量c d ''→ 代表a CD ， α5是逆时针方向； (C) 矢量 c d ''→代表a DC ， α5是顺时针方向； (D) 矢量c d ''→ 代 表a DC ， α5是逆时针方向。
330 利用相对运动图解法来求解图示机构中滑块2上D 2点的速 度rv D 2，解题过程的恰当步骤和利用的矢量方程可选择[ ]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.计算自由度（如有复合铰链、虚约束、局部自由度，请指出）1. D 处构成复合铰链，滚子有局部自由度，H （K ）构成虚约束F=3n －2P L －P H ＝3×7-2×9-1=22. 计算图示机构的自由度，并判定其是否具有确定运动，（绘有箭头的构件为原动件）。
1）F=3n-2Pl-Ph---------=3*6-2*8-1=1，----------自由度数等于原动件数， 具有确定运动-OA BCDEFGHK3、计算自由度（如有复合铰链、虚约束、局部自由度，请指出）解：滚子B 为局部自由度，E 处为复合铰链。
F=3n –2P L –P h =3×7–2×9–2=1。
4、计算图示机构的自由度，并判定其是否具有确定的运动。
标有箭头的构件为原动件；如有复合铰链、局部自由度或虚约束的地方请明确指出。
解：（1）机构的自由度F ＝3n －2P L -P H =3×7-2×9-2=1 （2）具有确定的运动 （2）复合铰链 （3）局部自由度：滚子6、计算图示机构的自由度，如有复合铰链、局部自由度和虚约束，请指出。
并判断该机构是否具有确定运动。
解，有复合铰链 有虚约束F n p p =--=⨯-⨯-=32L H 362811该机构具有确定运动7、计算图示机构的自由度，如有复合铰链、局部自由度和虚约束，请指出。
并判断该机构是否具有确定运动。
(1)有复合铰链，位置在F 处； (2)有局部自由度，位置在A 、G 处； (3)有虚约束，位置在B 或C 处。
F n p p =--=⨯-⨯-=32372921L H因为自由度数等于原动件数，所以该机构具有确定运动。
8、计算下列机构的自由度，已知//AB =//CD =EF 。
在图中指出其复合铰链，局部自由度和虚约束，并说明该机构是否具有确定运动？（图中画有箭头的构件为原动件）解： CD 是虚约束A 、B 点是复合铰链 G 处存在局部自由度F=3n-2P L -P H = 3×8-2×11-1=1因为自由度数等于主动件数，该机构具有确定运动。
9、试计算图示机构的自由度。
若有复合铰链、局部自由度、虚约束，须在图中标出。
解： 复合铰链；局部自由度。
虚约束 n=6、P L = 8 、P H =1118263=--=X X F齿轮计算题1、某设备上一对标准直齿圆柱齿轮传动，其传动比12i =3，使用日久后齿面已严重损坏，在拆卸修配过程中，不慎将小齿轮丢失，现测得大齿轮齿数z 2=57，其齿顶圆直径d a2=236mm ，试确定：z 1、m 、d 1、d a1、a 。
解：（1） 由122112z z n n i ==得193571221===i z z（2）依式 m h mz d a a *222+= 得 mm z h d m a a 457223622*2=+=+=（3） mm mz d 7619411=⨯==（4）mm m h mz d a a 844121942*11=⨯⨯+⨯=+= （4）mm z z m a 1522)5719(42)(21=+⨯=+=2、 某变速箱中，原设计一对直齿轮，其参数为m=2.5mm ，z 1=15，z 2=38；由于两轮轴孔中心距为70mm ，试改变设计采用斜齿轮传动，以适应轴孔中心距。
试确定一对斜齿轮的主要参数（模数、齿数、压力角、螺旋角） 解：依题意，可知：斜齿轮的法面模数m n =2.5mm为了保证转动比不变，则z 1=15 z 2=38 因为是标准齿轮，所以法面压力角αn =20°3、若已知一对正常齿制标准斜齿圆柱齿轮传动的中心距为160mm ，其中一个齿轮的齿数Z 1=30，模数m n = 4 mm ，螺旋角β=150。
试求另一个齿轮的齿数Z 2、分度圆直径d 2、齿顶圆直径d a2和齿根圆直径d f 2。
63.192425.1263.202)(222=⨯⨯-=+-=**n n an f m c h d d （196.77）4、有一标准斜齿圆柱齿轮机构，不慎丢失了小齿轮，已知两轮中心距 a =134.5mm ，大齿轮齿顶圆d a2=192.35mm ，齿数Z 2=60，螺旋角β=150，今欲配制小齿轮，试计算其模数、齿数、分度圆直径和齿顶圆直径。
解：依式 βcos 2)(21z z m a n +=得 z 2 = 47(48); ，63.19415cos 474cos 022=⨯==βz m d n （198.77）; 63.202222=+=*n an a m h d d （206.77）()βCos Z Z m a n 221+=()()12 2.515380.9462270n m Z Z Cos a β+⨯+===⨯︒=8.18βmm z m d n 51.8315cos 273cos 011=⨯==β mm m h d d n an a 51.89211=+=*5、一对渐开线标准圆柱直齿轮外啮合传动，已知齿轮的齿数Z 1=30，Z 2=40，分度圆压力角20=α°，齿顶高系数*ah =1，径向间隙系数C*=0.25，标准中心距a=140mm 。
试求出：齿轮的模数m ；两个齿轮的分度圆半径r 1、r 2；基圆半径r b1、r b2；齿顶圆半径r a1、r a2。
解：依式 2)(21z z m a +=得 mm z z am 4221=+=; ， mm mz r 602304211=⨯==; mm mz r 802404222=⨯==; mm r r b 38.5620cos 60cos 11=︒==α; mm r r b 175.7520cos 80cos 22=︒==α;mm m h r r a a 6446011=+=+=*mm m h r r a a 8448022=+=+=*6、已知一对标准安装的渐开线直齿圆柱标准齿轮传动，中心距12100OO=mm ，模数m =4mm ，分度圆上压力角α=200，小齿轮主动，传动比i ==ωω1215/.，试计算齿轮1和2的齿数、分度圆、基圆、齿顶圆和齿根圆半径。
解：i d d 122115==. d d a 122+=算出1280 120d d ==，解：依式*22(2)cos a n a z d m h β=+ 得 m n =3mm 依式βcos 2)(21z z m a n +=解得 z 1=27z d m 1120==， z d m 2230==d d b cos .11207518=︒=mm ， d m z h aa *()11288=+=mm d d b cos .222011276=︒=mm ， d m z h a a *()222128=+=mmd m z h c f a **()112270=--=mm d m z h c f a **()2222110=--=mm7、已知某对渐开线直齿圆柱齿轮传动，中心距mm a 350=，传动比5.2=i ,分度圆压力角020=α， h a *=1，25.0*=c ，根据强度等要求模数m 必须在5、6、7 mm 三者中选择，试设计此对齿轮的以下参数和尺寸。
(1)齿轮的齿数z 1、z 2，模数m ；(2)分度圆直径d 1、d 2，齿顶圆直径d a1、d a2，齿根圆直径d f1、d f 2； 解：a mz z mz i mz =+=+=⨯=2212353501211()(). mmz m 1350235=⨯⨯. m z m z m z ======5406333372857111 mm mm mm.. z z m 124040251005==⨯== mm .为标准安装的标准齿轮。
d mz d mz 11225402005100500==⨯===⨯= mm mm mm 5101025)2( mm 210425)2(a 22a a 11a =⨯=+==⨯=+=**h z m d h z m dd m z h c f a ()(.).1122540251875=--=⨯-=** mm d m z h c f a ()(.).22225100254875=--=⨯-=** mm8、在一对正常齿制的渐开线标准外啮合直齿圆柱齿轮机构中，已知轮1齿数Z 1=20，i 12=2.5， 模数m=10mm ，试求：（1）轮2的齿数Z 2、分度圆半径r 2、基圆半径r b2和齿根圆半径r f2； （2）分度圆齿厚S 、基圆上的齿距P b ； （3）该对齿轮标准安装时的中心距a 。
解：（1） 505.2201212=⨯=⋅=i Z Z)(2505010212122mm Z m r =⨯⨯=⋅⋅=)(9.23420cos 250cos 22mm r r b =⨯=⋅= α)(5.23710)25.01(250*)*(2222mm m h c r h r r a f f =⨯+-=⋅+-=-=（2） )(7.15102121mm m S =⨯⨯==ππ)(5.2920cos 10cos cos mm m p p b =⨯⨯=⋅=⋅= παπα(3) ())(350)5020(10212121mm Z Z m a =+⨯⨯=+=9、一对外啮合直齿轮传动中，已知两轮的齿数1z =20、2z =40，模数m =3mm ，压力角α=︒20，正常齿制，标准安装。
求： （1）分度圆半径1r 和2r ； （2）中心距a ； （3）基圆半径1b r 和2b r ； （4）齿顶圆半径1a r 和2a r ；（5）齿根圆半径1f r 和2f r ； （6）法向齿距nP 。
解：（1）111302r mz mm == 221602r mz mm ==； （2）90a mm =；（3）11cos 30cos 2028.191b r r mm α==⨯=22cos 60cos 2056.382b r r mm α==⨯=；（4）*1133a ar r h m mm =+= *2263a a r r h m mm =+=（5）**11()26.25f a r r h m c m mm =-+=**22()56.25f a r r h m c m mm =-+=；（6）cos cos 3cos 208.856n b p p p m mm απαπ==⋅=⋅=⨯⨯=。