(完整版)大学物理振动习题含答案
大学物理(第四版)课后习题及答案 机械振动
13 机械振动解答13-1 有一弹簧振子，振幅A=×10-2m ，周期T=，初相=3π/4。
试写出它的运动方程，并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外，ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
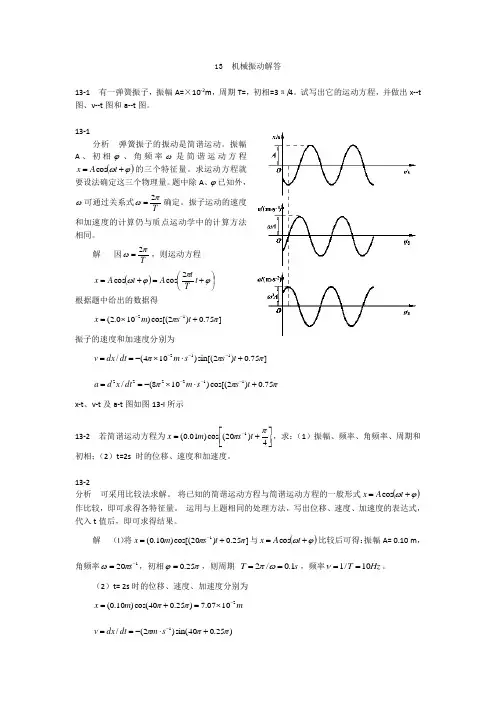
解 因Tπω2=，则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ，求：（1）振幅、频率、角频率、周期和初相；（2）t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量。
运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果。
解 （l ）将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得：振幅A= 0.10 m ，角频率120-=s πω，初相πϕ25.0=，则周期 s T 1.0/2==ωπ，频率Hz T 10/1==ν。
（2）t= 2s 时的位移、速度、加速度分别为m m x 21007.7)25.040cos()10.0(-⨯=+=ππ )25.040sin()2(/1πππ+⋅-==-s m dt dx v)25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体，密度ρ×103kgm -3。
江苏科技大学大学物理习题之-机械振动习题详解
一、选择题1．两个质点各自作简谐振动，它们的振幅相同、周期相同，第一个质点的振动方程为1cos()x A t ωα=+。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处，则第二个质点的振动方程为 [ ]（A ）)π21cos(2++=αωt A x ； （B ）)π21cos(2-+=αωt A x ；（C ）)π23cos(2-+=αωt A x ； （D ）)cos(2π++=αωt A x 。
答案：B解：由题意，第二个质点相位落后第一个质点相位π/2，因此，第二个质点的初相位为π21-α，所以答案应选取B 。
2．劲度系数分别为k 1和k 2的两个轻弹簧串联在一起，下面挂着质量为m 的物体，构成一个竖挂的弹簧振子，则该系统的振动周期为 ［ ］（A ）21212)(2k k k k m T +π=； （B ）)(221k k mT +π= ；（C ） 2121)(2k k k k m T +=π； （D ）2122k k mT +π=。
答案：C解：两根弹簧串联，其总劲度系数2121k k k k k +=，根椐弹簧振子周期公式，k mT π2=，代入2121k k k k k +=可得答案为C 。
3．一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，（如图所示），作成一复摆．已知细棒绕通过其一端的轴的转动惯量231ml J =，此摆作微小振动的周期为 ［ ］ （A ）g l π2； （B ）g l 22π； （C ）g l 322π； （D ）gl 3π。
答案：C解：由于是复摆，其振动的周期公式为glmgl J T 322222πππ===ω，所以答案为C 。
4．一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为［ ］ 答案：B解：根椐题意，此简谐振动的初相位为3π-，或35π，所以答案为B 。
大学物理(第四版)课后习题与答案_机械振动
13 机械振动解答13-1 有一弹簧振子，振幅A=2.0×10-2m ，周期T=1.0s ，初相ϕ=3π/4。
试写出它的运动方程，并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外，ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
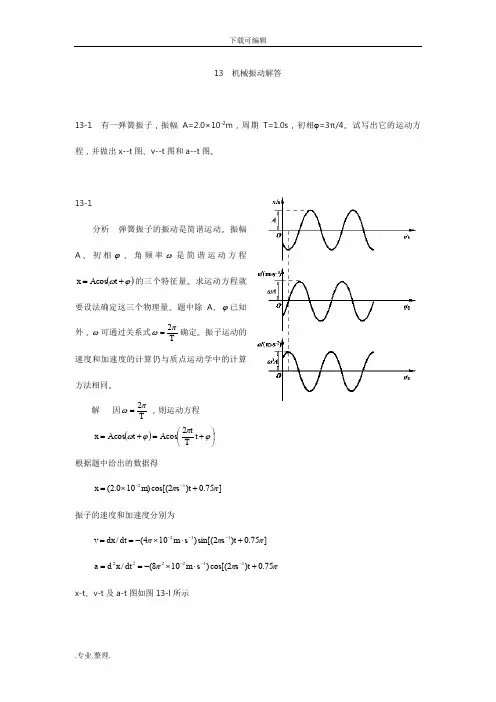
解 因Tπω2=，则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ，求：（1）振幅、频率、角频率、周期和初相；（2）t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量。
运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果。
解 （l ）将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得：振幅A= 0.10 m ，角频率120-=s πω，初相πϕ25.0=，则周期 s T 1.0/2==ωπ，频率Hz T 10/1==ν。
（2）t= 2s 时的位移、速度、加速度分别为m m x 21007.7)25.040cos()10.0(-⨯=+=ππ )25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体，密度ρ5.5×103kg •m -3。
大学物理试题精选(含答案)
单元一 简谐振动一、 选择、填空题1. 对一个作简谐振动的物体，下面哪种说法是正确的？ 【 C 】(A) 物体处在运动正方向的端点时，速度和加速度都达到最大值；(B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。
2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为π34，则t=0时，质点的位置在： 【 D 】(A) 过A 21x =处，向负方向运动； (B) 过A 21x =处，向正方向运动； (C) 过A 21x -=处，向负方向运动；(D) 过A 21x -=处，向正方向运动。
3. 将单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止释放任其振动，从放手开始计时，若用余弦函数表示运动方程，则该单摆的初相为： 【 B 】(A) θ； (B) 0； (C)π/2； (D) -θ4. 图(a)、(b)、(c)为三个不同的谐振动系统，组成各系统的各弹簧的倔强系数及重物质量如图所示，(a)、(b)、(c)三个振动系统的ω (ω为固有圆频率)值之比为：【 B 】(A) 2：1：1； (B) 1：2：4； (C) 4：2：1； (D) 1：1：25. 一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的： 【 C 】(A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动；(B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动； (C) 两种情况都可作简谐振动；)4(填空选择)5(填空选择(D) 两种情况都不能作简谐振动。
6. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： 【 C 】A2332,3)D (;A 22,43or ,4)C (;A 23,65,6)B (;A 21,32or ,3)A (±±±±±±±±±±±±，ππππππππ7. 如果外力按简谐振动的规律变化，但不等于振子的固有频率。
大学物理习题答案12简谐振动
大学物理练习题十二一、选择题1. 一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t=21T （T 为周期）时，质点的速度为 [ B ](A) φωsin A - (B) φωsin A(C) φωcos A - (D) φωcos A解: 当2/T t =,即π=π=ω=ω2/22/T t 时,()()=+-=+-==φπωφωωsin sin A t A dtdx v φωsin A2. 一物体作简谐振动，振动方程为)4/cos(πω+=t A x 。
在t=T/4(T 为周期)时刻，物体的加速度为 [ B ](A) 2212ωA - (B) 2212ωA(C) 2213ωA - (D) 2213ωA解: 当4/T t =,即2/4/24/T t π=π=ω=ω时, )4/cos(222πωω+-==t A dtxda=+-=)4/2/cos(2ππωA3. 劲度系数分别为k 1和k 2的两个轻弹簧串联在一起，下面挂着质量为m 的物体，构成一个竖挂的弹簧振子，则该系统的振动周期为 [ C ](A) 21212)(2k k k k m T +π= (B) )(221k k mT +π=(C) 2121)(2k k k k m T +π= (D) 2122k k mT +π=解: 由kx x k x k ==2211，21x x x +=可得21212111212111/1/1k k k k k k k x x k x x x k k +=+=+=+=，mk T /22ππ==ω4. 一质点沿x 轴作简谐振动，振动方程为()ππ3122cos 104+⨯=-t x (SI)。
从t=0时刻起，到质点位置在x= -2cm 处，且向X 轴正方向运动的最短时间间隔 (A) 1/8s (B) 1/4s (C) 1/2s (D) 1/3s (E) 1/6s [ C ]解: 由题意作知量图如右，πω=∆t，)(212s t ===∆ππωπ5．一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 [ B ]二、填空题1. 如图所示，一质量为m 的滑块，两边分别与倔强系数为k 1和k 2的轻弹簧连接，两弹簧的另外两端分别固定在墙上。
《大学物理学》(网工)简谐振动部分练习题(解答)
2
2
拓展题：一弹簧振子作简谐运动，当位移为振幅的一半时，其动能为总能量的
（D）
1
1
3
3
（A） ；（B） ；（C） ；（D） 。
2
2
2
4
【考虑到动能为 Ek
1 m 2 2
1 2
kA2
sin2 ( t
) ，位移为振幅的一半时，有 t
3
,
2 3
，那么，
Ek 1 kA2 ( 3 )2 】
2
3
4
A
3
5
（4）当 x
且正向时，由旋转矢量知4 2
4
（或4
4
）。
A
A
2
1
2
2
2
2
由周期 T 知 ，有： x1 A cos( t ) ；（ x1 A cos( t ) 也行）
T
T
T
2
2
2 3
x2 A cos( t ) ； x3 A cos( t ) ； x4 A cos( t ) 。
6
3
3
2
2 【可用旋转矢量考虑，两矢量的夹角应为 】
3
第九章机械振动-2
合肥学院《大学物理 B》自主学习材料
二、填空题 1．一质点在 X 轴上作简谐振动，振幅 A＝4cm，周期 T＝2s，其平衡位置取作坐标原点。若
t＝0 时质点第一次通过 x＝－2cm 处且向 X 轴负方向运动，则质点第二次通过 x＝－2cm 处
（A）落后 ； （B）超前 ；
2
2
o t
大学物理习题册答案
第15单元 机械振动[ B ]1. 已知一质点沿y 轴作简谐振动，其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是:[ B ] 2. 一质点在x 轴上作简谐振动，振幅A = 4cm ，周期T = 2s, 其平衡位置取作坐标原点。
若t = 0时刻质点第一次通过x = -2cm 处，且向x 轴负方向运动，则质点第二次通过x = -2cm 处的时刻为： (A) 1s (B)s 32 (C) s 34(D) 2s [ C ] 3. 如图所示，一质量为m 的滑块，两边分别与劲度系数为k1和k2的轻弹簧联接，两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动，O 点为系统平衡位置。
现将滑块m 向左移动x0，自静止释放，并从释放时开始计时。
取坐标如图所示，则其振动方程为：⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210 ⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D)⎥⎦⎤⎢⎣⎡+=t mk k x x 210cos (E)[ E ] 4. 一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的： (A)167 (B) 169 (C) 1611 (D) 1613(E) 1615 [ B ] 5. 图中所画的是两个简谐振动的振动曲线，若这两个简谐振动可叠加，则合成的余弦振动的初相为：(A) π21(B)π(C) π23(D) 0二 填空题1. 一水平弹簧简谐振子的振动曲线如图所示，振子处在位移零、速度为A ω-、加速度为零和弹性力为零的状态，对应于曲线上的 b,f 点。
振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力-kA 的状态，对应于曲线的 a,e点。
2两个同方向同频率的简谐振动，其合振动的振幅为20.cm,与第一个简谐振动的相位差为1ϕϕ-=π/6，若第一个简谐振动的振幅为103cm ，则第二个简谐振动的振幅为____10___cm ，第一、二个简谐振动的相位--(C)/A -A-差21ϕϕ-为2π-。
大学物理机械振动与机械波综合练习题(含答案)
20
T
11．一谐波沿直径为 0.14 m 的圆柱管行进，波的平均强度为 9 10−3 W/m 2 ，频率为 300 Hz ，
波 速 为 300 m/s ， 波 的 平 均 能 量 密 度 为 = 3 10 −5 J/m 3 ； 最 大 能 量 密 度 为
m = 6 10 −5 J/m 3 。
6-2
7．一平面谐波，频率为 100 Hz ，波速 360 m/s ，在波线上有 A 、 B 两点，相位差为
A − B = / 3 ，则两点的距离为 (A) 0.6 m ，且 A 点距波源较近；
(B) 1.2 m ，且 A 点距波源较近；
(C) 0.6 m ，且 B 点距波源较近； (D) 1.2 m ，且 B 点距波源较近。
A2 = A12 + A22 + 2 A1 A2 cos( 2 − 1 )
= ( 2 − 1 ) = 82
5．右图为沿 x 轴正向传播的平面谐波在 t = 0
y
时刻的 y − x 曲线。由图可知原点 O 和 1、2、
3、4 点的振动初位相分别为 、 0 、 −
2
2 o 12 3 4
T 2
T 2
(C)
y
=
Asin 2
t T
+ 2
−
2x
；
(D)
y
=
Asin 2
t T
−
2x
。
解：设波源振动方程为 y = Asin( t + 0 )
t
=
0，
y
=
A，0
=
2
y
=
Asin 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为：(A))21cos(2++=αωt A x (B) )21cos(2-+=αωt A x (C))23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B)ω2(C) 2/ω(D) ω /2［］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为(A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6(E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >'［］6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61 (C) s 41 (D) s 31 (E) s21［］7．5179：一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。
当重物通过平衡位置且向规定的正方向运动时，开始计时。
则其振动方程为：(A))21/(cos π+=t m k A x (B))21/cos(π-=t m k A x (C))π21/(cos +=t k m A x (D))21/cos(π-=t k m A x (E) t m /k A x cos =［］8．5312：一质点在x 轴上作简谐振动，振辐A = 4 cm ，周期T = 2 s ，其平衡位置取作坐标原点。
若t = 0时刻质点第一次通过x = -2 cm 处，且向x 轴负方向运动，则质点第二次通过x = -2 cm 处的时刻为21(A) 1 s (B) (2/3) s (C) (4/3) s (D) 2 s ［］9．5501：一物体作简谐振动，振动方程为)41cos(π+=t A x ω。
在 t = T /4（T 为周期）时刻，物体的加速度为(A) 2221ωA -(B) 2221ωA (C) 2321ωA - (D) 2321ωA ［］10．5502：一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A - (B) φωsin A(C) φωcos A -φωcos A ［ ］11．3030：两个同周期简谐振动曲线如图所示。
x 1的相位比x 2的相位(A) 落后π/2(B) 超前π/2 (C) 落后π(D) 超前π ［ ］12．3042：一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A21，且向x轴的正方向运动，代表此简谐振动的旋转矢量图为 ［ ］13．3254：一质点作简谐振动，周期为T 。
质点由平衡位置向x 轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为(A) T /4 (B) T /6 (C) T /8 (D) T ［ ］14．3270：一简谐振动曲线如图所示。
则振动周期是(A) 2.62 s (B) 2.40 s(C) 2.20 s (D) 2.00 s ［ ］15．5186：已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒。
则此简谐振动的振动方程为：(A))3232cos(2π+π=t x (B) )3232cos(2π-π=t x (C))3234cos(2π+π=t x (D) )3234cos(2π-π=t x (E))4134cos(2π-π=t x ［］16．3023：一弹簧振子，当把它水平放置时，它可以作简谐振动。
若把它竖直放置或放在固定的光滑斜面上，试判断下面哪种情况是正确的：3270图(B)(D)x (A)(C)A/(A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动(B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动(C) 两种情况都可作简谐振动(D) 两种情况都不能作简谐振动 ［ ］17．3028：一弹簧振子作简谐振动，总能量为E 1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E 2变为(A) E 1/4 (B) E 1/2 (C) 2E 1 (D) 4 E 1 ［ ］18．3393：当质点以频率ν 作简谐振动时，它的动能的变化频率为(A) 4 ν(B) 2 ν (C) ν (D) ν21［ ］19。
3560：弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(A) kA 2 (B) 221kA(C) (1/4)kA 2(D) 0［ ］20．5182：一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的(A) 1/4 (B) 1/2(C) 2/1(D) 3/4(E)2/3［ ］21．5504：一物体作简谐振动，振动方程为)21cos(π+=t A x ω。
则该物体在t = 0时刻的动能与t = T /8（T 为振动周期）时刻的动能之比为：(A) 1:4 (B) 1:2 (C) 1:1 (D) 2:1 (E) 4:1 ［］22．5505：一质点作简谐振动，其振动方程为)cos(φω+=t A x 。
在求质点的振动动能时，得出下面5个表达式： (1) )(sin 21222φωω+t A m (2) )(cos 21222φωω+t A m (3) )sin(212φω+t kA (4) )(cos 2122φω+t kA (5) )(sin 22222φω+πt mA T其中m 是质点的质量，k 是弹簧的劲度系数，T 是振动的周期。
这些表达式中(A) (1)，(4)是对的 (B) (2)，(4)是对的 (C) (1)，(5)是对的(D) (3)，(5)是对的 (E) (2)，(5)是对的 ［ ］23．3008：一长度为l 、劲度系数为k 的均匀轻弹簧分割成长度分别为l 1和l 2的两部分，且l 1 = n l 2，n 为整数. 则相应的劲度系数k 1和k 2为(A) 11+=n kn k ， )1(2+=n k k (B) n n k k )1(1+=， 12+=n kk (C) n n k k )1(1+=， )1(2+=n k k (D)11+=n kn k ， 12+=n k k ［］24．3562：图中所画的是两个简谐振动的振动曲线。
若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23(B) π(C) π21(D) 0［］二、填空题：1．3009：一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示。
若0=t 时，(1) 振子在负的最大位移处，则初相为______________；(2) 振子在平衡位置向正方向运动，则初相为__________；(3) 振子在位移为A /2处，且向负方向运动，则初相为______。
2．3390：一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm 。
若令速度具有正最大值的那一时刻为t = 0，则振动表达式为_________________________。
3．3557：一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点。
已知周期为T ，振幅为A 。
(1)若t = 0时质点过x = 0处且朝x 轴正方向运动，则振动方程为 x=____________。
（2）若t = 0时质点处于Ax 21=处且向x 轴负方向运动，则振动方程为 x=_______________。
4．3816：一质点沿x 轴以 x = 0为平衡位置作简谐振动，频率为 0.25 Hz 。
t = 0时，x = -0.37 cm 而速度等于零，则振幅是___________，振动的数值表达式为_____________________。
5．3817：一简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相φ =________________。
6．3818：两个弹簧振子的周期都是0.4 s ，设开始时第一个振子从平衡位置向负方向运动，经过0.5 s 后，第二个振子才从正方向的端点开始运动，则这两振动的相位差为____________。
7．3819：两质点沿水平x 轴线作相同频率和相同振幅的简谐振动，平衡位置都在坐标原点。
它们总是沿相反方向经过同一个点，其位移x 的绝对值为振幅的一半，则它们之间的相位差为___________。
8．3820：将质量为 0.2 kg 的物体，系于劲度系数k = 19 N/m 的竖直悬挂的弹簧的下端。
假定在弹簧不变形的位置将物体由静止释放，然后物体作简谐振动，则振动频率为__________，振幅为____________。
9．3033：一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为A =_____________；ω =________________；φ =_______________。
t = 2s 时刻质点的位移为____________，速度为__________________。
11．3046：一简谐振动的旋转矢量图如图所示，振幅矢量长2cm ，则该简谐振动的初相为__________。
振动方程为______________________________。
12．3398：一质点作简谐振动。
其振动曲线如图所示。