指数函数对数函数专练习题(含答案)
指数函数对数函数练习题(含答案)
B、
1 2 3
C、
1 2 2
)
D、
1 3 3
2 6、函数 y lg 1 的图像关于( 1 x
A、 x 轴对称
B、 y 轴对称
C、原点对称 )
D、直线 y x 对称
7、函数 y log(2 x1) 3x 2 的定义域是(
2 A、 ,1 3 2 C、 , 3
曲线|y|=2 +1 与直线 y=b 的图象如图所示,由图象可得:如果|y|=2 +1 与直线 y=b
x x
没有公共点,则 b 应满足的条件是 b∈[-1,1].
答案:[-1,1] 9. 解析:如图满足条件的区间[a,b],当 a=-1,b=0 或 a=0,b=1 时区间长度最 小,最小值为 1,当 a=-1,b=1 时区间长度最大,最大值为 2,故其差为 1. 答案:1 10. 解:要使函数有意义,则只需-x -3x+4≥0,即 x +3x-4≤0,解得-4≤x≤1.
2 2
∴函数的定义域为{x|-4≤x≤1}. 3 2 25 2 2 令 t=-x -3x+4,则 t=-x -3x+4=-(x+ ) + , 2 4 25 3 ∴当-4≤x≤1 时,tmax= ,此时 x=- ,tmin=0,此时 x=-4 或 x=1. 4 2 25 ∴0≤t≤ .∴0≤ 4 ∴函数 y= ( ) 5 2 -x -3x+4≤ . 2 的值域为[ 2 ,1]. 8
3 3 ∴函数的单调增区间是[- ,1],单调减区间是[-4,- ]. 2 2 11. 解:令 a =t,∴t>0,则 y=t +2t-1=(t+1) -2,其对称轴为 t=-1.该二次函数
x
2 2
在[-1,+∞)上是增函数. 1 x 2 ①若 a>1,∵x∈[-1,1],∴t=a ∈[ ,a],故当 t=a,即 x=1 时,ymax=a +2a-1=14,解得
(完整版)指数函数对数函数专练习题(含答案).docx
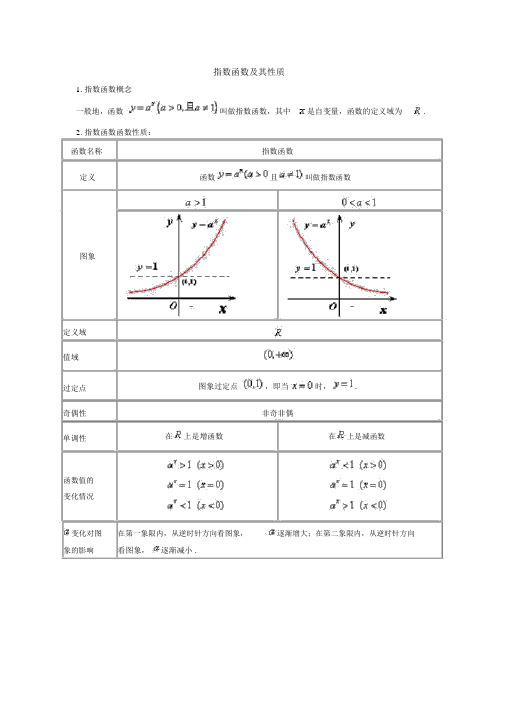
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称定义图象定义域值域过定点奇偶性单调性函数值的变化情况变化对图象的影响指数函数函数且叫做指数函数图象过定点,即当时,.非奇非偶在上是增函数在上是减函数在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小 .对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称定义函数对数函数且叫做对数函数图象定义域值域过定点奇偶性图象过定点,即当非奇非偶时,.单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,看图象,逐渐减小 .逐渐增大;在第四象限内,从顺时针方向指数函数习题一、选择题aa ≤ b,则函数 f ( x ) =1?2x 的图象大致为 ()1.定义运算 a ?b =>b a b2.函数 f ( x ) = x 2-bx + c 满足 f (1 + x ) =f (1 - x ) 且 f (0) =3,则 f ( b x ) 与 f ( c x ) 的大小关系是()xxA . f ( b ) ≤ f ( c ) x xB . f ( b ) ≥ f ( c )xxC . f ( b )> f ( c )D .大小关系随 x 的不同而不同3.函数 y = |2 x - 1| 在区间A . ( - 1,+∞ )C . ( - 1,1)( k - 1, k + 1) 内不单调,则 k 的取值范围是 ()B . ( -∞, 1)D . (0,2)4.设函数 f ( x ) =ln [( x -1)(2 -x)] 的定义域是 ,函数 ( ) = lg(x - 2x -1) 的定义域是 ,Ag xaB若 ?,则正数a 的取值范围 ()ABA . a >3B . a ≥ 3C . a > 5D . a ≥ 5.已知函数 f (x = 3- a x -3, x ≤ 7,若数列 { a n 满足 a n = f (n )(n ∈ * ,且 {a n }是递5 ) a x - 6, x >7. } N) 增数列,则实数a 的取值范围是 ()A . [ 9, 3)B . ( 9, 3) 44C . (2,3)D . (1,3)2x16.已知 a >0 且 a ≠ 1,f ( x ) = x - a ,当 x ∈ ( - 1,1) 时,均有 f ( x )< 2,则实数 a 的取值范围 是( )1 1 A . (0 , 2] ∪ [2 ,+∞ ) B . [ 4, 1) ∪ (1,4]11C . [ 2, 1) ∪ (1,2]D . (0 , 4) ∪ [4 ,+∞ )二、填空题xa7.函数 y = a ( a >0,且 a ≠ 1) 在 [1,2] 上的最大值比最小值大 2,则 a 的值是 ________.8.若曲线 | y | = 2 x + 1 与直线 y =b 没有公共点,则b 的取值范围是 ________.| x|的定义域为9. (2011 ·滨州模拟 ) 定义:区间 [x 1,x 2 ]( x 1<x 2) 的长度为 x 2- x 1. 已知函数 y = 2 [a , b] ,值域为 [1,2] ,则区间 [a , b] 的长度的最大值与最小值的差为 ________.三、解答题10.求函数y=2x2 3x 4 的定义域、值域和单调区间.11.(2011 ·银川模拟 ) 若函数y=a2x+ 2a x-1( a>0 且a≠ 1) 在x∈ [- 1,1]上的最大值为14,求a 的值.12.已知函数f (x) = 3x,(a+ 2) = 18, (x) =λ·3ax-4x的定义域为 [0,1] .f g(1)求 a 的值;(2) 若函数g( x) 在区间 [0,1] 上是单调递减函数,求实数λ的取值范围.1. 解析:由? = a a≤ b x2x x≤0,b a>b x>0 .1答案: A2. 解析:∵f (1 +x) =f (1 -x) ,∴f ( x) 的对称轴为直线x=1,由此得 b=2.又 f (0)=3,∴c=3.∴f ( x)在(-∞,1)上递减,在(1,+∞)上递增.x≥2x≥ 1,∴ (3 x) ≥(2 x) .若 x≥0,则3f f若 x<0,则3x<2x<1,∴f (3x)> f (2x).∴f (3x)≥ f (2x).答案: A3.解析:由于函数 y=|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间 ( k- 1,k+ 1) 内不单调,所以有答案: Ck-1<0<k+1,解得-1<k<1.4.解析:由题意得: A=(1,2)x x>1x x>1在(1,2)上恒成立,即,a- 2且 a>2,由 A? B知 a- 2x x上恒成立,令x x xln a-2xln2>0 ,所以函数a-2 - 1>0 在 (1,2)u( x)=a- 2- 1,则u′( x) =au ( x ) 在 (1,2) 上单调递增,则 u ( x )> u (1) = a - 3,即 a ≥ 3.答案: B*f ( n ) 为增函数,5. 解析: 数列 { a } 满足 a = f ( n )( n ∈ N ) ,则函数nna >18- 6- ) × 7- 3,所以 3- a >0注意 a>(3,解得 2<a <3.aa8-6> 3- a × 7-3答案: C1 2x1 21 x x21的图象,6. 解析: f ( x )<? x -a < ? x - <a ,考查函数 y = a与 y =x - 2222当 a >1 时,必有 a-1≥1,即 1<a ≤ 2,21 1当 0<a <1 时,必有 a ≥ ,即 ≤a <1,2 2 1 综上, 2≤ a <1 或 1<a ≤ 2. 答案: C7. 解析: 当 a >1 时, y x在 [1,2] 上单调递增,故 2a3x= a a - a = ,得 a = . 当 0<a <1 时, y = a2 22a在 [1,2] 上单调递减,故 a -a = 2,得 a = 2. 故 a =2或 2.1131 3答案: 2或28. 解析: 分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.x+1 与直线 y = b 的图象如图所示,由图象可得:如果x+ 1 与直线 y = b曲线 | y | = 2 | y | = 2没有公共点,则 b 应满足的条件是 b ∈ [- 1,1] .答案: [- 1,1]9. 解析: 如图满足条件的区间 [a , b] ,当 a =- 1, b = 0 或 a = 0, b = 1 时区间长度最小,最小值为 1,当 a =- 1,b = 1 时区间长度最大,最大值为2,故其差为 1.答案: 110. 解: 要使函数有意义,则只需- x 2-3x + 4≥ 0,即 x 2+ 3x -4≤ 0,解得- 4≤ x ≤ 1.∴函数的定义域为 { x | -4≤ x ≤ 1} .223225 令 t =- x - 3x + 4,则 t =- x - 3x + 4=- ( x + ) +4,2253∴当-4≤ x ≤ 1 时, t max = 4 ,此时 x =- 2, t min = 0,此时 x =- 4 或 x =1.∴0≤t ≤ 25 . ∴0≤ -x 2- 3x + 4≤ 5 .4 2∴函数 y = ( 1)x 23 x4的值域为 [ 2 , 1] .8223 225由 t =- x - 3x + 4=- ( x + )+4( - 4≤ x ≤ 1) 可知,23当- 4≤ x ≤- 2时, t 是增函数,3当- 2≤ x ≤1 时, t 是减函数.根据复合函数的单调性知:y = ( 1 )x 23 x 4在 [ - 4,- 3 3] 上是减函数,在 [ - ,1] 上是增函数.22 233∴函数的单调增区间是 [ - 2, 1] ,单调减区间是 [ - 4,- 2] . 11. 解: 令x22tt >0y= t+ 2t1= ( t+ 1)2,其对称轴为t =- 1.该二次函数a = ,∴ ,则--在[ - 1,+ ∞ ) 上是增函数.x12①若 a >1,∵x ∈ [ - 1,1] ,∴t = a ∈ [ a , a ] ,故当 t = a ,即 x =1 时, y max =a + 2a - 1=14,解得 a = 3( a =- 5 舍去 ) .②若 0<a <1,∵x ∈ [ - 1,1] ,∴ = x∈1 1=-时,a [ a , ] ,故当 t = ,即 1t a ax12y max = (a + 1) - 2= 14.11∴a =3或- 5( 舍去 ) .1综上可得 a = 3 或 3.12. 解: 法一: (1) 由已知得 a2 aa =log 32.3 += 18? 3 = 2?(2) 此时 g ( x ) = λ·2x - 4 x ,设 0≤ x 1<x 2≤ 1,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以 g ( x ) - g ( x ) = (2 x - 2x )( λ- 2x - 2x )>0 恒成立,即 λ<2x + 2x 恒成立.1 2 1 2 2 1 2 1由于 2x 2+ 2x 1>2 + 2 = 2,所以实数 λ的取值范围是λ≤ 2.法二: (1) 同法一.(2) 此时 g ( x ) = λ·2x - 4x ,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以有 g ′( x ) = λln2 ·2x - ln4 ·4x = ln2 [- 2 ·(2x )2+ λ·2x] ≤0 成立.x2 设 2 = u ∈ [1,2] ,上式成立等价于-2u+ λu ≤0 恒成立.因为 u ∈ [1,2] ,只需 λ≤2u 恒成立,所以实数 λ的取值范围是λ≤ 2.对数与对数函数同步练习一、选择题1、已知 3a2 ,那么 log3 8 2log 3 6 用 a 表示是()A 、 a 2B 、 5a2C 、 3a (1 a)2D 、 3a a 22、 2log a (M 2N ) log a Mlog a N ,则M的值为()A 、1NB 、4C 、1D 、 4 或 1413 、 已 知 x 2 y 2 1, x0, y 0 , 且 log a (1 x) m,log a n,则 log a y 等 于1 x()A 、 m nB 、 m nC 、 1m nD 、 1m n224、如果方程 lg 2 x (lg5lg 7)lgx lg5 glg 7 0 的两根是 ,,则 g的值是()A 、 lg5 glg 7B 、 lg35C 、 35D 、13515、已知 log 7[log 3 (log 2 x)] 0,那么 x2等于( )A 、1B 、13 C 、1D 、1322 2336、函数 ylg2 1 的图像关于()1 xA 、 x 轴对称B 、 y 轴对称C 、原点对称D 、直线 yx 对称7、函数 ylog (2 x 1) 3x2 的定义域是()A 、 2,1 U 1,B 、 1,1 U 1,32C 、 2,D 、 1,328、函数 ylog 1 (x 2 6x17) 的值域是()2A 、 RB 、 8,C 、, 3D 、 3,9、若 log m 9 log n 9 0 ,那么 m, n 满足的条件是( )A 、 m n 1B 、 n m 1C 、 0 n m 1D 、 0 m n 110、 log a 2 1,则 a 的取值范围是()3A 、 0, 2U 1,B 、 2,C 、 2,1D 、 0, 2U 2,3333 311、下列函数中,在 0,2 上为增函数的是()A 、 ylog 1 ( x1)B 、 y log 2 x 2 12C 、 ylog 2 1D 、 ylog 1 ( x 2 4x 5)x212、已知 g( x) log a x+1 ( a 0且a 1) 在 10, 上有 g( x)0 ,则 f ( x)a x 1 是( )A 、在 ,0上是增加的 B 、在 ,0 上是减少的C 、在, 1 上是增加的D 、在,0 上是减少的二、填空题13、若 log a 2 m,log a 3 n, a 2 m n 。
(完整版)指数函数对数函数专练习题含答案
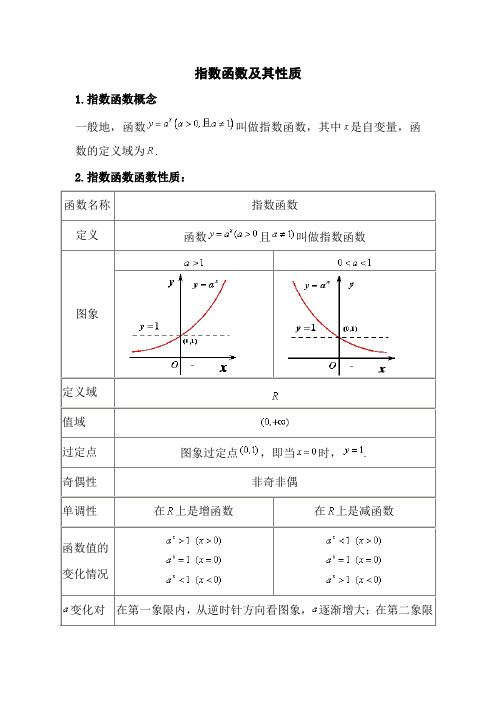
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称指数函数定义函数且叫做指数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限图象的影响内,从逆时针方向看图象,逐渐减小.对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.指数函数习题一、选择题1.定义运算a⊗b=⎩⎪⎨⎪⎧a(a≤b)b(a>b),则函数f(x)=1⊗2x的图象大致为( )2.函数f(x)=x2-bx+c满足f(1+x)=f(1-x)且f(0)=3,则f(b x)与f(c x)的大小关系是( )A .f (b x )≤f (c x )B .f (b x )≥f (c x )C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,则k 的取值范围是( )A .(-1,+∞)B .(-∞,1)C .(-1,1)D .(0,2)4.设函数f (x )=ln [(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x -2x -1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5 D .a ≥ 55.已知函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( )A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a的值是________.8.若曲线|y |=2x +1与直线y =b 没有公共点,则b 的取值范围是________.9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =211.(2011·银川模拟)若函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.1.解析:由a ⊗b =⎩⎪⎨⎪⎧a (a ≤b )b (a >b )得f (x )=1⊗2x=⎩⎪⎨⎪⎧2x(x ≤0),1 (x >0).答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2.又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x ). 若x <0,则3x <2x <1,∴f (3x )>f (2x ). ∴f (3x )≥f (2x ). 答案:A3.解析:由于函数y =|2x -1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x >1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎪⎨⎪⎧a >13-a >0a 8-6>(3-a )×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x在[1,2]上单调递增,故a 2-a =a2,得a =32.当0<a <1时,y =a x 在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32. 答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x +1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =1()2[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =1()2在[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x =t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去).②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a =2⇒a =log 32. (2)此时g (x )=λ·2x -4x , 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2, 所以实数λ的取值范围是λ≤2. 法二:(1)同法一. (2)此时g (x )=λ·2x -4x ,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x ]≤0成立. 设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.对数与对数函数同步练习一、选择题 1、已知32a=,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+D 、23a a -2、2log(2)log log a a a M N M N -=+,则NM 的值为( )A 、41 B 、4 C 、1 D 、4或1 3、已知221,0,0xy x y +=>>,且1log (1),log ,log 1y a aa x m n x+==-则等于( )A 、m n +B 、m n - C 、()12m n + D 、()12m n - 4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=g 的两根是,αβ,则αβg 的值是( )A 、lg5lg7gB 、lg35C 、35D 、3515、已知732log [log (log)]0x =,那么12x-等于( ) A 、13B 、C 、D6、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( )A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称 7、函数(21)logx y -= )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭U B 、()1,11,2⎛⎫+∞ ⎪⎝⎭U C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log9log 90mn <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a<,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭U B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭U 11、下列函数中,在()0,2上为增函数的是( ) A 、12log (1)y x =+ B 、2logy =C 、21logy x = D 、2log (45)y x x =-+ 12、已知()logx+1 (01)ag x a a =>≠且在()10-,上有()0g x >,则1()x f x a+=是( )A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题 13、若2log2,log 3,m n aa m n a +===。
指数函数与对数函数专项训练(解析版)

指数函数与对数函数专项训练一、单选题1.(23-24高一下·云南玉溪·期末)函数()()2lg 35f x x x =-的定义域为()A .()0,∞+B .50,3⎛⎫⎪C .()5,0,3∞∞⎛⎫-⋃+ ⎪D .5,3⎛⎫+∞ ⎪【答案】C【详解】由题意知,2350x x ->,即(35)0x x ->,所以0x <或53x >.故选:C.2.(23-24高一上·云南昭通·期末)函数()327x f x x =+-的零点所在的区间是()A .()0,1B .31,2⎛⎫ ⎪⎝⎭C .3,22⎛⎫⎪D .()2,3【答案】B【详解】∵3x y =和27y x =-均在R 上单调递增,∴()327x f x x =+-在R 上单调递增;又()12f =-,327402f ⎛⎫=-> ⎪⎝⎭,∴()f x 在31,2⎛⎫ ⎪⎝⎭上有唯一的零点,故选:B.3.(23-24高一上·云南昆明·期末)滇池是云南省面积最大的高原淡水湖,一段时间曾由于人类活动的加剧,滇池水质恶化,藻类水华事件频发.在适当的条件下,藻类的生长会进入指数增长阶段.滇池外海北部某年从1月到7月的水华面积占比符合指数增长,其模型为23 1.65x y -=⨯.经研究“以鱼控藻”模式能有效控制藻类水华.如果3月开始向滇池投放一定量的鱼群后,鱼群消耗水华面积占比呈现一次函数 5.213.5y x =-,将两函数模型放在同期进行比较,如图所示.下列说法正确的是(参考数据:671.6520.2,1.6533.3≈≈)()A .水华面积占比每月增长率为1.65B .如果不采取有效措施,到8月水华的面积占比就会达到60%左右C .“以鱼控藻”模式并没有对水华面积占比减少起到作用D .7月后滇池藻类水华会因“以鱼控藻”模式得到彻底治理【答案】B【详解】对于A ,由于模型23 1.65x y -=⨯呈指数增长,故A 错误;对于B ,当8x =时,8220.63 1.605326.y -⨯==⨯≈,故B 正确;对于C ,因为鱼群消耗水华面积占比呈现一次函数 5.213.5y x =-,所以“以鱼控藻”模式对水华面积占比减少起到作用,故C 错误;对于D ,由两函数模型放在同期进行比较的图象可知,7月后滇池藻类水华并不会因“以鱼控藻”模式得到彻底治理,故D 错误.故选:B.4.(23-24高一上·云南昭通·期末)()()1log 14a f x x =-+(0a >且1a ≠)的图象恒过定点M ,幂函数()g x 过点M ,则12g ⎛⎫⎪⎝⎭为()A .1B .2C .3D .4【答案】D【详解】()()1log 14a f x x =-+,令11x -=,得2x =,()124f =,则()()1log 14a f x x =-+(0a >且1a ≠)恒过定点12,4M ⎛⎫⎪⎝⎭,设()g x x α=,则124α=,即2α=-,即()2g x x -=,∴142g ⎛⎫= ⎪⎝⎭,故选:D.5.(23-24高一下·云南楚雄·期末)已知0.320.3lo g 3,2,lo g 2a b c -===,则()A .c b a <<B .<<b c aC .<<c a bD .a b c<<【答案】A【详解】因为2log y x =在(0,)+∞上单调递增,且234<<,所以222log 2log 3log 4<<,所以21log 32<<,即12a <<,因为2x y =在R 上递增,且0.30-<,所以0.300221-<<=,即01b <<,因为0.3log y x =在(0,)+∞上单调递减,且12<,所以0.30.3log 1log 2>,所以0.3log 20<,即0c <,所以c b a <<.故选:A6.(23-24高一上·云南·期末)若()21()ln 1||f x x x =+-,设()0.3(3),(ln2),2a f b f c f =-==,则a ,b ,c 的大小关系为()A .c a b >>B .b c a >>C .a b c >>D .a c b>>【答案】D【详解】由题意知()(),00,x ∈-∞⋃+∞,由()()()21ln 1f x x f x x⎡⎤-=-+-=⎣⎦-,所以()f x 为偶函数,图象关于y 轴对称,当0x >时,由复合函数的单调性法则知()f x 随x 的增大而增大,即()0,x ∈+∞,()21()ln 1||f x x x =+-单调递增,因为()()33a f f =-=,()0.3(ln2),2b f c f ==,且00.3112222=<<=,0ln2lne 1<<=,所以0.3ln 223<<,所以()()()0.3ln223f f f <<-,即b c a <<,也就是a c b >>.故选:D7.(23-24高一下·云南·期末)设222,0()log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若关于x 的方程2[()](2)()20f x a f x a -++=恰有5个不同实数解,则实数a 的取值范围是()A .[]1,2B .(2,3]C .()2,+∞D .()3,+∞【答案】B【详解】方程2[()](2)()20f x a f x a -++=化为[()2][()]0f x f x a --=,解得()2f x =或()f x a =,函数()f x 在(,0]-∞上单调递增,函数值的集合为(2,3],在(0,1]上单调递减,函数值的集合为[0,)+∞,在[1,)+∞上单调递增,函数值的集合为[0,)+∞,在同一坐标系内作出直线2,y y a ==与函数()y f x =的图象,显然直线2y =与函数()y f x =的图象有两个交点,由关于x 的方程2[()](2)()20f x a f x a -++=恰有5个不同实数解,则直线y a =与函数()y f x =的图象有3个交点,此时23a <≤,所以实数a 的取值范围是(2,3].故选:B8.(23-24高一下·云南昆明·期末)若()12:lo g 11,:39a p a q --<<,则p 是q 的()条件A .充分不必要B .必要不充分C .充要D .既不充分也不必要【答案】A【详解】对于()22:log 11log 2p a -<=,则012a <-<,解得13a <<;对于1:39a q -<,则12a -<,解得3a <;因为{}|13a a <<是{}|3a a <的真子集,所以p 是q 的充分不必要条件.故选:A.二、多选题9.(23-24高一上·云南迪庆·期末)已知函数()()2ln 2f x x x =-,则下列结论正确的是()A .函数()f x 的单调递增区间是[)1,+∞B .函数()f x 的值域是RC .函数()f x 的图象关于1x =对称D .不等式()ln 3f x <的解集是()1,3-【答案】BC【详解】对于A ,当1x =时,2210x x -=-<,此时()()2ln 2f x x x =-无意义,故A 错误;对于B ,由于()22y g x x x ==-的值域为[)1,-+∞,满足()[)0,1,+∞⊆-+∞,所以函数()f x 的值域是R ,故B 正确;对于C ,由题意()()()22ln 2ln 11f x x x x ⎡⎤=-=--⎣⎦,且定义域为()(),02,-∞+∞ ,它满足()()()21ln 11f x x f x+=-=-,即函数()f x 的图象关于1x =对称,故C 正确;对于D ,由于()f x 的定义域为()(),02,-∞+∞ ,故D 错误.故选:BC.10.(23-24高一上·云南昆明·期末)已知函数2212,0()2|log ,0x x x f x x x ⎧--≤⎪=⎨⎪⎩,若1234x x x x <<<,且()()()()1234fx fx fx fx ===,则下列结论中正确的是()A .122x x +=-B .1204x x <<C .()41,4x ∈D .342x x +的取值范围是332,4⎡⎫⎪⎢⎣⎭【答案】BC【详解】作出函数2212,0()2|log ,0x x x f x x x ⎧--≤⎪=⎨⎪⎩的图像如图.对于选项A,根据二次函数的对称性知,12()224x x +=⨯=--,故A 项错误;对于选项B ,因120x x <<,由上述分析知124x x +=-,则21212120()()()42x x x x x x --<=-⋅-≤=,因12x x ≠,故有1204x x <<,即B 项正确;对于选项C ,如图,因0x ≤时,2211()2(2)2222f x x x x =--=-++≤,0x >时,2()|log |f x x =,依题意须使20|log |2x <<,由2|log |0x >得1x ≠,由2|log |2x <解得:144x <<,故有3411,144x x <<<<,即C项正确;对于选项D ,由图知2324log log x x -=,可得341x x =,故431x x =,则343322x x x x ++=,3114x <<,不妨设21,(,1)4y x x x =+∈,显然函数2y x x =+在(1,14)上单调递减,故23334x x <+<,即342x x +的取值范围是(333,4),故D 项错误.故选:BC.11.(23-24高一上·云南昆明·期末)关于函数()ln f x x x =+,以下结论正确的是()A .方程()0f x =有唯一的实数解c ,且(0,1)c ∈B .对,0,()()()x y f xy f x f y ∀>=+恒成立C .对()1212,0x x x x ∀>≠,都有()()1212f x f x x x ->-D .对12,0x x ∀>,均有()()121222f x f x x x f ++⎛⎫≤⎪【答案】AC【详解】A 选项,由于1y x =在R 上单调递增,2ln y x =在()0,∞+上单调递增,故()ln f x x x =+在定义域()0,∞+上单调递增,又()11ln 30,11033f f ⎛⎫=-<=> ⎪⎝⎭,故由零点存在性定理可得,方程()0f x =有唯一的实数解c ,且(0,1)c ∈,A 正确;B 选项,()ln f xy xy xy =+,()()ln ln ln f x f y x x y y x y xy +=+++=++,显然,0x y ∀>,由于xy 与x y +不一定相等,故()()f x f y +与()f xy 不一定相等,B 错误;C 选项,由A 选项可知,()ln f x x x =+在定义域()0,∞+上单调递增,对()1212,0x x x x ∀>≠,都有()()12120f x f x x x ->-,C 正确;D 选项,12,0x x ∀>,均有121212ln 222x xx x x x f +++⎛⎫=+ ⎪⎝⎭,()()12112212121212ln ln ln ln 22222f x f x x x x x x x x x x x x x ++++++==+=+,由于12122x x x x +≥,当且仅当12x x =时,等号成立,故1212ln ln 2x x x x +≥,即()()121222f x f x x x f ++⎛⎫≥ ⎪⎝⎭,D 错误.故选:AC 三、填空题12.(23-24高一上·云南昆明·期末)()()2,(1)29,1x a x f x x ax a x ⎧>⎪=⎨-++-≤⎪⎩是R 上的单调递增函数,则实数a 的取值范围为.【答案】[]2,5【详解】因为在R 递增,则112129a a a a a⎧⎪⎪≥⎨⎪-++-≤⎪⎩>,解得:25a ≤≤,故答案为:[]2,513.(23-24高一下·云南昆明·期末)设函数()ln(1)f x x =+,2()g x x a =-+,若曲线()y f x =与曲线()y g x =有两个交点,则实数a 的取值范围是.【答案】(0,)+∞【详解】当0x ≥时,()ln(1),f x x =+当0x <时()ln(1),f x x =-+函数图象示意图为则2()g x x a =-+与()ln (1)f x x =+有两个零点知a 的取值范围是(0,)+∞.故答案为:(0,).+∞14.(23-24高一下·云南玉溪·期末)苏格兰数学家纳皮尔(J.Napier ,1550-1617)在研究天文学的过程中,经过对运算体系的多年研究后发明的对数,为当时的天文学家处理“大数”的计算大大缩短了时间.即就是任何一个正实数N 可以表示成10(110,)n N a a n =⨯≤<∈Z ,则lg lg (0lg 1)N n a a =+≤<,这样我们可以知道N 的位数为1n +.已知正整数M ,若10M 是10位数,则M 的值为.(参考数据:0.9 1.1107.94,1012.56≈≈)【答案】8或9【详解】依题意可得910101010M ≤<,两边取常用对数可得91010lg10lg lg10M ≤<,即910lg 10M ≤<,所以0.9lg 1M ≤<,即0.91010M ≤<,又M 为正整数,所以8M =或9M =.故答案为:8或9四、解答题15.(23-24高一上·云南昆明·期末)设函数()log (3)(,10a f x x a =-+>且1)a ≠.(1)若(12)3f =,解不等式()0f x >;(2)若()f x 在[4,5]上的最大值与最小值之差为1,求a 的值.【答案】(1)10(,)3+∞(2)2a =或12a =【详解】(1)由(12)3f =可得log (123)13a -+=,解得3a =,即3()log (3)1,(3)f x x x =-+>,则()0f x >,即3log (3)10x -+>,即310,1333x x x >⎧⎪∴>⎨->⎪⎩,故不等式()0f x >的解集为10(,)3+∞;(2)由于()f x 在[4,5]上的最大值与最小值之差为1,故log 11(log 21)1a a +-+=,即log 21,2a a =∴=或12a =,即a 的值为2a =或12a =.16.(23-24高一上·云南昭通·期末)化简求值:(1)()13103420.027π4160.49--++;(2)ln22311lg125lg40.1e log 9log 1632-+++⨯.【答案】(1)8(2)9【详解】(1)()13103420.027π4160.49--++()()()1313423420.3120.7⎡⎤⎡⎤⎡⎤=-++⎣⎦⎣⎦⎣⎦0.3180.78=-++=;(2)ln22311lg125lg4lg 0.1e log 9log 1632-++++⨯3211112lg34lg2lg5lg23222lg2lg3=+-++⨯lg 5lg28=++9=.17.(23-24高一上·云南·期末)已知定义域为R 的函数()11333xx m f x +-⋅=+是奇函数.(1)求m 的值并利用定义证明函数()f x 的单调性;(2)若对于任意t ∈R ,不等式()()22620f t t f t k -+-<恒成立,求实数k 的取值范围.【答案】(1)1m =,证明见解析(2)3k <-【详解】(1)因为()f x 是奇函数,函数的定义域为R ,所以(0)0f =,所以1033m-=+,所以1m =,经检验满足()()f x f x -=-易知()11312133331x x x f x +-⎛⎫==-+ ⎪++⎝⎭设12x x <,则2112122(33)()()3(31)(31)x x x x f x f x --=++因为3x y =在实数集上是增函数,故12()()0f x f x ->.所以()f x 在R 上是单调减函数(2)由(1)知()f x 在(,)-∞+∞上为减函数.又因为()f x 是奇函数,所以()()22620f t t f t k -+-<等价于()()2262f t t f k t-<-,因为()f x 为减函数,由上式可得:2262t t k t ->-.即对一切t R ∈有:2360t t k -->,从而判别式361203k k ∆=+<⇒<-.所以k 的取值范围是3k <-.18.(23-24高一下·云南昆明·期末)已知函数1()xx f x a a ⎛⎫=- ⎪⎝⎭ (0a >且1a ≠).(1)讨论()f x 的单调性(不需证明);(2)若2a =,(ⅰ)解不等式3()2≤f x x;(ⅱ)若21()(22))2(x g f x t x x f +=-+在区间[]1,1-上的最小值为74-,求t 的值.【答案】(1)答案见解析(2)(ⅰ)(](],10,1-∞-⋃;(ⅱ)2t =-或2t =【详解】(1)若1a >,则1()()x xf x a a=-在R 上单调递增;若01a <<,则1()()x xf x a a=-在R 上单调递减.(2)(ⅰ)3()2≤f x x ,即132()022xx x --≤,设13()2()22xx g x x=--,则(1)0g =,()()g x g x -=-,所以()g x 为奇函数,当0x >时,()g x 单调递增,由()(1)g x g ≤,解得01x <≤,根据奇函数的性质,当0x <时,()(1)g x g ≤的解为1x ≤-,综上所述,3()2≤f x x的解集为(](],10,1-∞-⋃.(ⅱ)2122()2(2)2()222(22)x x x x x g x f x tf x t +--=-+=++-,令22x x m --=,因为[]1,1x ∈-,则33,22m ⎡⎤∈-⎢⎥⎣⎦,所以2()()22g x h m m tm ==++,其图象为开口向上,对称轴为m t=-的抛物线,①当32t -≤-,即32t ≥时,min 39177()()3232444h m h t t =-=-+=-=-,解得2t =.②当3322t -<-<,即3322t -<<时,222min 7()()2224h m h t t t t =-=-+=-+=-,解得1152t =,2152t =-矛盾.③当32t -≥,即32t ≤-时,min 39177()()3232444h m h t t ==++=+=-,解得2t =-.综上所述,2t =-或2t =.19.(23-24高一上·云南昆明·期末)函数()e (0)x f x mx m =-<.(1)求(1)f -和(0)f 的值,判断()f x 的单调性并用定义加以证明;(2)设0x 是函数()f x 的一个零点,当1em <-时,()02f x k >,求整数k 的最大值.【答案】(1)1(1)e f m --=+,(0)1f =,()f x 在定义域R 上单调递增,证明见解析,(2)整数k 的最大值为1-【详解】(1)1(1)e f m --=+,(0)1f =,判断()f x 在定义域R 上单调递增,证明如下:在R 上任取1x ,2x ,且12x x <,则1212121212()()e (e )(e e )()x x x x f x f x mx mx m x x -=---=---,因为12x x <,0m <,所以12e e x x <,120x x -<,0m ->,所以12e e 0x x -<,12()0m x x --<,所以1212(e e )()0x x m x x ---<,即12())0(f x f x -<,所以12()()f x f x <,所以()f x 在定义域R 上单调递增.(2)由题意得0()0f x =,即00e 0x mx -=,1em <-,则10e m +<,即0(1)0()f f x -<=,由()f x 是R 上的增函数,所以01x -<,又0(0)10()f f x =>=,所以010x -<<,0200(2)e 2x f x mx =-002e 2e x x =-,令01e (ext =∈,1),则22()2(1)1g t t t t =-=--,所以()g t 在1(e ,1)上单调递减,所以()()11g t g >=-,即0(2)1f x >-,当1em <-时,0(2)f x k >,所以1k ≤-,所以整数k 的最大值为1-.。
指数函数与对数函数专项练习(含答案)

指数函数与对数函数专项练习1 设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是[ ] (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a2 函数y=ax2+ bx 与y= ||log b ax(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是[ ]3.设525bm ==,且112a b +=,则m =[ ](A (B )10 (C )20 (D )100 4.设a=3log 2,b=In2,c=125-,则[ ]A. a<b<cB. b<c<aC. c<a<b D . c<b<a 5 .已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是[ ] (A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞ 6.函数()()2log 31x f x =+的值域为[ ]A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣7.下列四类函数中,个有性质“对任意的x>0,y>0,函数f(x)满足f (x +y )=f (x )f (y )”的是 [ ](A )幂函数 (B )对数函数 (C )指数函数 (D )余弦函数 8. 函数y=log2x 的图象大致是[ ]PS(A) (B) (C) (D)8.设554a log 4b log c log ===25,(3),,则[ ] (A)a<c<b (B) b<c<a (C) a<b<c (D) b<a<c 9.已知函数 1()log (1),f x x =+若()1,f α= α=[ ](A)0(B)1(C)2(D)310.函数y =的值域是[ ](A )[0,+∞) (B) [0,4] (C) [0,4) (D) (0,4) 11.若372log πlog 6log 0.8a b c ===,,,则( )A .a b c >>B .b a c >>C .c a b >>D .b c a >>12.下面不等式成立的是( )A .322log 2log 3log 5<<B .3log 5log 2log 223<<C .5log 2log 3log 232<<D .2log 5log 3log 322<<13.若01x y <<<,则( )A .33y x <B .log 3log 3x y <C .44log log x y <D .11()()44x y<14.已知01a <<,log log a a x =,1log 52a y =,log log a a z =,则( )A .x y z >>B .z y x >>C .y x z >>D .z x y >>15.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <cB .c <a <bC . b <a <cD . b <c <a16.已知函数()log (21)(01)x a f x b a a =+->≠,的图象如图所示,则a b ,满足的关系是( ) A .101a b -<<< B .101b a-<<<C .101ba -<<<-D .1101ab --<<<18. 已知函数)1(122>-+=a a a y x x 在区间[-1,1]上的最大值是14,求a 的值.19.已知m x f x +-=132)(是奇函数,求常数m 的值;20.已知函数f(x)=11+-x x a a (a>0且a ≠1).(1)求f(x)的定义域;(2)讨论f(x)的奇偶性;(3)讨论f(x)的单调性.指数函数与对数函数专项练习参考答案1)A【解析】25y x =在0x >时是增函数,所以a c >,2()5xy =在0x >时是减函数,所以c b >。
指数函数对数函数专练习题含答案(1)

指数函数对数函数专练习题含答案(1)指数函数和对数函数是高中数学中的重要内容,在函数中成为了必学的一部分。
这两种函数在数学中应用非常广泛,除了在数学中,还常常运用于其他学科和实际生活中。
下面是介绍和练习这两种函数的一些题目及其答案。
一、指数函数:1. 求 f(x) = 2^(x+1) - 2^x 的零点。
答:f(x) = 2^(x+1) - 2^x = 2^(x+1) - 2^(x+1-1) = 2^(x+1) -2^x= 2^x * (2 - 1) = 2^x所以,f(x) = 0 时, x = 0。
2. 求解 3^x - 4^x + 3 = 0,其中 x 取值范围为 R。
答:将 4^x 用 2^x 表示,得到 3^x - (2^x)^2 + 3 = 0这是一个二次方程,需要使用求根公式解出 xD = b^2 - 4ac = 16 - 4*3*3 = 16 - 36 = -20由于 D < 0,因此无实数解。
3. 求解 2^(2x+1) - 2^(2x-2) = 12,其中 x 取值范围为 R。
答:将方程两边都取对数,得到(2x+1)log2 - (2x-2)log2 = log2(12)化简得到 2xlog2 + log2 - 4log2 + 3log2 = log2(12) 即 2xlog2 - log2 = log2(12) - 3log2即 2x = log2(4) + log2(3) - 3即 x = 1/2*log2(3) - 7/4二、对数函数:1. 解方程 log(a-1)x = logax + 1,其中 a>1。
答:由于 a>1,因此 a-1 > 0两边同时取指数,得到 x = a^2 / (a-1)2. 如果 a > 1,b > 1,且 a^logb = b,那么 loga b 是多少?答:将等式两边取对数,得到 loga (b^(logb a)) = loga a 即 (logb a) * loga b = 1即 loga b = 1 / logb a当 a^logb = b 时, loga b = 1 / logb a = 1 / (loga b / loga e)再次化简得到 loga b = logb a3. 求解方程 2log(x+1) + log(x-1) = log(x+2),其中 x > 1。
指数函数、对数函数、幂函数练习题大全(答案)

一.选择题(每小题4分,共计40分) 【1 】1.下列各式中成立的一项是( )A .7177)(m n mn =B .3339=C .43433)(y x y x +=+D .31243)3(-=-2.化简)31()3)((656131212132b a b a b a ÷-的成果( )A .a 9-B .a -C .a 6D .29a3.设指数函数)1,0()(≠>=a a a x f x,则下列等式中不准确...的是( )A .f (x +y )=f(x )·f (y )B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈=D .)()]([·)]([)]([+∈=N n y f x f xy f nnn4.函数210)2()5(--+-=x x y( )A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或 5.若指数函数xa y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于( )A .215+ B .215- C .215± D .251± 6.方程)10(2||<<=a x a x 的解的个数为( )A. 0个B. 1个C. 2个D. 0个或1个 7.函数||2)(x x f -=的值域是( )A .]1,0(B .)1,0(C .),0(+∞D .R8.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,知足1)(>x f 的x 的取值规模( )A .)1,1(-B . ),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或9.已知2)(xx e e x f --=,则下列准确的是 ( )A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数10.函数22)21(++-=x x y 得单调递增区间是( )A .]1,(--∞B .),2[+∞C .]2,21[D .]21,1[- 二.填空题(每小题4分,共计28分)11.已知0.622,0.6a b ==,则实数a b 、的大小关系为.12.不必盘算器盘算:48373271021.097203225.0+-⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛--π=__________________. 13.不等式x x 283312--<⎪⎭⎫ ⎝⎛的解集是__________________________.14.已知{}2,1,0,1,2,3n ∈--,若11()()25n n ->-,则=n ___________.15.不等式2221212-++⎪⎭⎫ ⎝⎛<⎪⎭⎫⎝⎛a x axx 恒成立,则a 的取值规模是.16.界说运算:⎩⎨⎧>≤=⊗)()(b a b b a a b a ,则函数()xx x f -⊗=22的值域为_________________(2m )与时光t (月)的关系:ty a =,有以下论述:② 第5个月时,浮萍的面积就会超出230m ; ③ 浮萍从24m 舒展到212m 须要经由1.5个月; ④ 浮萍每个月增长的面积都相等;⑤ 若浮萍舒展到22m .23m .26m 所经由的时光 分离为1t .2t .3t ,则123t t t +=. 个中准确的是.三.解答题:(10+10+12=32分) 18.已知17a a -+=,求下列各式的值: (1)33221122a a a a----; (2)1122a a-+; (3)22(1)a a a -->.)1(122>-+=a a a y x x 在区间[-1,1]上的最大值是14,求a 的值.20.(1)已知m x f x +-=132)(是奇函数,求常数m 的值; (2)画出函数|13|-=xy 的图象,并应用图象答复:k 为何值时,方程|31|x k -=无解?有一解?有两解?一.选择题:(本题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是相符标题请求的)1.已知32a=,那么33log 82log 6-用a 暗示是( )A.2a -B.52a -C.23(1)a a -+ D. 23a a - 2.2log (2)log log a a a M N M N -=+,则NM的值为( ) A.41B.4C.1D.4或1 3.已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a aa x m n x+==-则等于( ) A.m n + B.m n - C.()12m n + D.()12m n -4.假如方程2lg (lg5lg 7)lg lg5lg 70x x +++=的两根是,αβ,则αβ的值是A.lg5lg7B.lg35C.35D.351 5.已知732log [log (log )]0x =,那么12x -等于( )A.136.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A.x 轴对称 B.y 轴对称 C.原点对称 D.直线y x =对称7.函数(21)log x y -= )A.()2,11,3⎛⎫+∞⎪⎝⎭B.()1,11,2⎛⎫+∞⎪⎝⎭C.2,3⎛⎫+∞⎪⎝⎭ D.1,2⎛⎫+∞ ⎪⎝⎭8.函数212log (617)y x x =-+的值域是( )A.RB.[)8,+∞C.(),3-∞-D.[)3,+∞ 9.若log 9log 90m n <<,那么,m n 知足的前提是( ) A. 1 m n >> B.1n m >> C.01n m <<< D.01m n <<< 10.2log 13a <,则a 的取值规模是( ) A.()20,1,3⎛⎫+∞ ⎪⎝⎭B.2,3⎛⎫+∞⎪⎝⎭ C.2,13⎛⎫ ⎪⎝⎭ D.220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11.下列函数中,在()0,2上为增函数的是( )A.12log (1)y x =+ B.2log y =C.21log y x = D.2log (45)y x x =-+ 12.已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a+=是A.在(),0-∞上是增长的B.在(),0-∞上是削减的C.在(),1-∞-上是增长的D.在(),0-∞上是削减的二.填空题:(本题共4小题,每小题4分,共16分,请把答案填写在答题纸上) 13.若2log 2,log 3,m na a m n a+===.14.函数(-1)log (3-)x y x =的界说域是. 15.2lg 25lg 2lg 50(lg 2)++=. 16.函数()2()lg1f x x x =+是(奇.偶)函数.三.解答题:(本题共3小题,共36分,解答应写出文字解释,证实进程或演算步调.)17.已知函数1010()1010x xx x f x ---=+,断定()f x 的奇偶性和单调性.18.已知函数222(3)lg 6x f x x -=-,(1)求()f x 的界说域; (2)断定()f x 的奇偶性.19.已知函数2328()log 1mx x nf x x ++=+的界说域为R ,值域为[]0,2,求,m n 的值. 一.选择题1.下列所给出的函数中,是幂函数的是()A .3x y -=B .3-=x y C .32x y =D .13-=x y2.函数3yx =( )A .是奇函数,且在R 上是单调增函数B .是奇函数,且在R 上是单调减函数C .是偶函数,且在R 上是单调增函数D .是偶函数,且在R 上是单调减函数 3.函数43y x =的图象是()4.下列函数中既是偶函数又在(,0)-∞上是增函数的是()A .43y x = B .32y x = C .2y x -= D .14y x -=5.幂函数()3521----=m xm m y ,当x∈(0,+∞)时为减函数,则实数m 的值为()A.m =2B.m =-1C.m =-1或m =2D.251±≠m 6.当0<x <1时,f(x)=x 2,21)(x x g =,h(x)=x -2的大小关系是( )A.h(x)<g(x)<f(x)B.h(x)<f(x)<g(x)C.g(x)<h(x)<f(x)D.f(x)<g(x)<h(x) 7. 函数2-=xy 在区间]2,21[上的最大值是( )A .41B .1-C .4D .4- 8. 函数3x y =和31x y =图象满 ()A .关于原点对称B .关于x 轴对称C .关于y 轴对称D .关于直线x y =对称9. 函数R x x x y ∈=|,|,知足 ()A .是奇函数又是减函数B .是偶函数又是增函数C .是奇函数又是增函数D .是偶函数又是减函数10.鄙人列函数中界说域和值域不合的是( )A.31x y = B.21-=xy C.35x y = D.32x y =11.如图所示,是幂函数αx y =在第一象限的图象,比较1,,,,,04321αααα的大小为() A .102431<<<<<ααααB .104321<<<<<ααααC .134210αααα<<<<<D .142310αααα<<<<<12.设(),125212+⨯-=-x xx f 它的最小值是( )(A )21-(B )3- (C )169- (D )0二.填空题13.函数2223()(1)mm f x m m x --=--是幂函数,且在(0,)x ∈+∞上是减函数,则实数m =____14.函数y x=-32的界说域是15.下列命题中,准确命题的序号是 __________(写出你以为准确的所有序号)①当0=α时函数y x α=的图象是一条直线; ②幂函数的图象都经由(0,0)和(1,1)点;③若幂函数y x α=是奇函数,则y x α=是界说域上的增函数; ④幂函数的图象不成能出如今第四象限. 16.若22xx ≥,+∈R x ,则x 的取值规模是____________。
幂函数、指数函数、对数函数专练习题(含答案)

高中数学对数函数、指数函数、幂函数练习题1.函数f (x )=x21-的定义域是A.(-∞,0]B.[0,+∞)C.(-∞,0)D.(-∞,+∞) 2.函数x y 2log =的定义域是A.(0,1]B.(0,+∞)C.(1,+∞)D.[1,+∞)3.函数y =A.(3,+∞)B.[3,+∞)C.(4,+∞)D.[4,+∞)4.若集合{|2},{|xM y y N y y ====,则M N ⋂=A.}1|{≥y yB.}1|{>y yC.}0|{>y yD.}0|{≥y y5.函数y=-11-x 的图象是 6.函数y =1-11-x ,则下列说法正确的是A.y 在(-1,+∞)内单调递增B.y 在(-1,+∞)内单调递减C.y 在(1,+∞)内单调递增D.y 在(1,+∞)内单调递减7.函数y =的定义域是A.(2,3)B.[2,3)C.[2,)+∞D.(,3)-∞ 8.函数xx x f 1)(+=在]3,0(上是 A.增函数B.减函数C.在]10,(上是减函数,]31[,上是增函数D.在]10,(上是增函数,]31[,上是减函数 9.的定义域是函数 )2(x lg y -= A.(-∞,+∞)B.(-∞,2)C.(-∞,0]D(-∞,1]10.的取值范围是则若设函数o xx x x x f ,1)f(x 0)(x )0(,12)(o >⎪⎩⎪⎨⎧>≤-=-11.21||x y =函数A.是偶函数,在区间(﹣∞,0)上单调递增B.是偶函数,在区间(﹣∞,0)上单调递减C.是奇函数,在区间(0,+∞)上单调递增D.是奇函数,在区间(0,+∞)上单调递减 12.的定义域是函数xx x y -+=||)1(013.函数y =A.[1,)+∞B.23(,)+∞C.23[,1]D.23(,1]14.下列四个图象中,函数xx x f 1)(-=的图象是15.设A 、B 是非空集合,定义A ×B={x |x ∈A ∪B 且x ∉A ∩B}.已知A={x |y =22x x -},B={y |y =2x ,x >0},则A ×B 等于 A.[0,1)∪(2,+∞)B.[0,1]∪[2,+∞)C.[0,1]D.[0,2]16.设a =20.3,b =0.32,c =log3.02,则Aa >c >bB.a >b >cC.b >c >aD.c >b >a17.已知点(39在幂函数()y f x =的图象上,则()f x 的表达式是 A.()3f x x = B.3()f x x = C.2()f x x-=D.1()()2xf x =18.已知幂函数αx x f =)(的部分对应值如下表:则不等式1)(<x f 的解集是A.{}20≤<x x B.{}40≤≤x x C.{}22≤≤-x x D.{}44≤≤-x x19.已知函数的值为),则,的值域为)1(0[93)(2f a ax x f x∞+--+=A.3B.4C.5D.6指数函数习题一、选择题1.定义运算a ?b =?a ≤b ?,b ?a >b ?)),则函数f (x )=1?2x 的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x )的大小关系是( ) A .f (b x )≤f (c x ) B .f (b x )≥f (c x ) C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,则k 的取值范围是( )A.(-1,+∞)B.(-∞,1)C.(-1,1) D.(0,2)4.设函数f(x)=ln[(x-1)(2-x)]的定义域是A,函数g(x)=lg(-1)的定义域是B,若A?B,则正数a的取值范围( )A.a>3 B.a≥3C.a> D.a≥5.已知函数f(x)=若数列{a n}满足a n=f(n)(n∈N*),且{a n}是递增数列,则实数a的取值范围是( )A.[,3) B.(,3)C.(2,3) D.(1,3)6.已知a>0且a≠1,f(x)=x2-a x,当x∈(-1,1)时,均有f(x)<,则实数a的取值范围是( )A.(0,]∪[2,+∞)B.[,1)∪(1,4]C.[,1)∪(1,2] D.(0,)∪[4,+∞)二、填空题7.函数y=a x(a>0,且a≠1)在[1,2]上的最大值比最小值大,则a 的值是________.8.若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.9.(2011·滨州模拟)定义:区间[x1,x2](x1<x2)的长度为x2-x1.已知函数y=2|x|的定义域为[a,b],值域为[1,2],则区间[a,b]的长度的最大值与最小值的差为________. 三、解答题10.求函数y =211.(2011·银川模拟)若函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.对数与对数函数同步练习一、选择题 1、已知32a=,那么33log 82log 6-用a 表示是()A 、2a -B 、52a -C 、23(1)a a -+D 、23a a - 2、2log (2)log log a a a M N M N -=+,则NM的值为() A 、41B 、4C 、1D 、4或1 3、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a a a x m n x+==-则等于() A 、m n +B 、m n -C 、()12m n +D 、()12m n - 4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=的两根是,αβ,则αβ的值是()A 、lg5lg7B 、lg35C 、35D 、3515、已知732log [log (log )]0x =,那么12x -等于()A 、13B C D6、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于()A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称7、函数(21)log x y -=A 、()2,11,3⎛⎫+∞⎪⎝⎭B 、()1,11,2⎛⎫+∞⎪⎝⎭C 、2,3⎛⎫+∞⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是()A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞9、若log 9log 90m n <<,那么,m n 满足的条件是() A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<< 10、2log 13a <,则a 的取值范围是() A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中,在()0,2上为增函数的是()A 、12log (1)y x =+B 、2log y =C 、21log yx =D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是()A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的二、填空题13、若2log 2,log 3,m na a m n a+===。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为. 函数名称指数函数定义函数且叫做指数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限,从逆时针向看图象,逐渐增大;在第二象限,从逆时针向看图象,逐渐减小.对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限,从顺时针向看图象,逐渐增大;在第四象限,从顺时针向看图象,逐渐减小.指数函数习题一、选择题1.定义运算a ⊗b =⎩⎨⎧a (a ≤b )b (a >b ),则函数f (x )=1⊗2x的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x)的大小关系是( )A .f (b x )≤f (c x)B .f (b x )≥f (c x)C .f (b x )>f (c x)D .大小关系随x 的不同而不同3.函数y =|2x-1|在区间(k -1,k +1)不单调,则k 的取值围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1) D .(0,2) 4.设函数f (x )=ln[(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x-2x-1)的定义域是B ,若A ⊆B ,则正数a 的取值围( ) A .a >3 B .a ≥3C .a > 5D .a ≥ 55.已知函数f (x )=⎩⎨⎧(3-a )x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值围是( )A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x+1与直线y =b 没有公共点,则b 的取值围是________.9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =211.(2011·模拟)若函数y =a 2x +2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,数λ的取值围.1.解析:由a ⊗b =⎩⎨⎧ a (a ≤b )b (a >b )得f (x )=1⊗2x=⎩⎨⎧2x (x ≤0),1 (x >0).答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x).若x <0,则3x <2x <1,∴f (3x )>f (2x).∴f (3x )≥f (2x). 答案:A3.解析:由于函数y =|2x-1|在(-∞,0)单调递减,在(0,+∞)单调递增,而函数在区间(k -1,k +1)不单调,所以有k -1<0<k +1,解得-1<k <1.答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a8-6>(3-a )×7-3,所以⎩⎨⎧a >13-a >0a 8-6>(3-a )×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值围.曲线|y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1. ∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x --+的值域为[28,1]. 由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =2341()2x x --+在[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a=2⇒a =log 32.(2)此时g (x )=λ·2x -4x, 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2, 所以实数λ的取值围是λ≤2. 法二:(1)同法一.(2)此时g (x )=λ·2x -4x,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值围是λ≤2.对数与对数函数同步练习一、选择题1、已知32a =,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或13、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a a a x m n x+==-则等于( )A 、m n +B 、m n -C 、()12m n + D 、()12m n - 4、如果程2lg (lg5lg 7)lg lg5lg 70x x +++=g的两根是,αβ,则αβg 的值是( )A 、lg5lg 7gB 、lg35C 、35D 、3515、已知732log [log (log )]0x =,那么12x -等于( )A 、13 B C D 6、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称7、函数(21)log x y -= )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭UB 、()1,11,2⎛⎫+∞ ⎪⎝⎭UC 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<< 10、2log 13a<,则a 的取值围是( ) A 、()20,1,3⎛⎫+∞ ⎪⎝⎭U B 、2,3⎛⎫+∞ ⎪⎝⎭ C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭U11、下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是( )A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。
