计算复杂性-第一次作业
数据结构(C++)第一次作业参考答案

数据结构第一次作业数据结构第一次作业一.单项选择题(20分)( )1.已知一算术表达式的后缀形式为ABC *+DE-/,则其中缀形式为 _________。
a、(A+B *C)/(D-E)b、A+B*C /D-Ec、(A+B*C)/D-Ed、A+B*C/(D-E)( )2.若某链表中最常用的操作是在最后一个结点之后插入一个结点和删除第一个结点,则采用________存储方式最节省运算时间(假设链表仅设有一个first指针)。
a. 单链表b. 带头结点的双循环链表c. 单循环链表d. 双链表( )3.设一个栈的输入序列为A,B,C,D,则所得到的输出序列不可能是_______。
a. A,B,C,Db. D,C,B,Ac. A,C,D,Bd. D,A,B,C( )4.若线性表最常用的操作是存取第i个元素及其直接前驱的值,则采用_____存储方式节省时间。
a.顺序表 b.双链表 c.单循环链表 d.单链表( )5.若长度为n的线性表采用顺序存储结构,在其第i个位置插入一个新元素的算法的时间复杂度为_______。
(1≤i≤n+1)a、O(0)b、O(1)c、O(n)d、O(n2)( )6.若指针L指向一带头结点的循环单链表的头结点,该表为空表的条件是_______为真值;a. !( L -> link );b. L == (L -> link) -> link;c. L -> link;d. L == L -> link;( )7.用数组A[0..N-1]存放一个循环队列,一元素出队时,其队头指针front的修改方法是________:a. front = (front + 1) mod N;b. front = (front - 2)mod N;c. front = front + 1;d. front = front – 2;( )8.若用Head()和Tail()分别表示取广义表的表头和表尾,广义表A=(1,2,(3,4),(5,(6,7))),则Head(Tail(Head(Tail(Tail(A))))) 。
数字逻辑第一次大作业
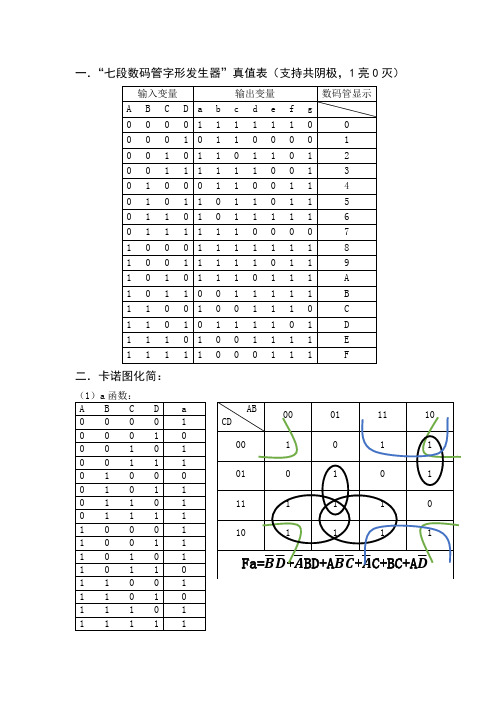
一.“七段数码管字形发生器”真值表(支持共阴极,1亮0灭)二.卡诺图化简:三.在Quartus 中,建工程,采用原理图设计方法,画整体电路图,设定I/O ,编译纠错第一次编译出错,Input与Output中部分名称重复,改Input中“A”为“In-A”,B、C、D同理。
第二次编译通过。
四.在Quartus中,对所设计的电路进行整体功能仿真:五.仅采用与非门实现的解决方案:根据摩根代换定律,将a~f的表达式改为与非式,在Quartus中重新用原理图的方法画出整体电路图,设定I/O,根据新表达式在电路中适当添加非门,编译纠错。
并对电路功能进行整体仿真。
六.支持共阳极数码管的解决方案:将a~f的输出信号按位取反。
即在各信号输出之前添加非门。
七.填写真值表:八.自定义三个4变量功能函数(不能重复前面的三变量函数功能),填写真值表:九.小结:首先明白了数码管工作原理后,通过写出a~f输出变量的表达式熟练了将真值表在卡诺图上表示的方法。
(由于BD字样不易显示,选用小写b和d)之后在摸索中掌握了Quartus中原理图的使用方法。
第一次编译得知在定义名称时字母不区分大写小写,A与a 将被视为重复命名。
第二次只是有几个warnings,给忽略了。
进行仿真时,由于和原理图设计是分两次进行的,在选择“Node Finder...”插入节点时系统没有自动选中我之前保存的bdf文件,显示“No node available”。
重新打开之前的工程文件重试后成功。
在仿真时不知道是否应该将ABCD连续设置16次分别观察是否显示0~F,还是将输入信号设为随即信号,整体观察。
后来一想没啥区别,后者逐个信号竖向观察就能知道显示的数字对不对,还更方便。
观察仿真波形发现,在固定输入信号时,确实输出的信号符合要求。
选做题没想出好方法,觉得只有同时连两条线路才可实现。
其实已开始对这个软件真是无从下手。
多亏几个朋友对我的帮助,我才掌握了基本使用方法。
对数学作业批语的思考

作, 也是学校工作 的重 中之重 。如今 , 学校 安 全 事 故 , 防 安 全 事 故 的发 生重 在 防 范 , 预
3建立健 全规章制度 , . 强化责任 。俗话
安 全事 故 频 发 , 人 防不 胜 防 。 埘学 生 安 似 严 防 , 不 可避 免 地 有 不 可 预 见 的 隐 患 说 “ 令 面 也 没有规矩 , 不成方圆” 有 了完善的规章 ,
…
系列教 育活动使师生的安 全意识得到加
要 安全 第一” 的思 事故 ; 1 校 组织 的大 型活 动 中 出现 的 强 。其 次, 1. 学 让学生掌握基本的安全知识 , 增 待安 全问题 , 牢固树立 “ 想, 时刻保持 清醒的头脑 , 要抓细 、 抓严 抓 事故。 强 预 防 、 理 意 外 事 故的 能 力 。 处 抓全, 使学校安全工作真正深人到每位 由此可见 , 校安全事故 的发生具有 学 2加 强师德 教育 , 强教师 工作 的责 实 、 . 增 教师 、 每位学生 、 每个家庭之 中。 复杂性 、 长期性及不可预见性 。 安全是一个 任心 。加强教师对《 教师法》 《 、未成年人保
事 故 ;. 体 育课 上 或 运 动 会 上 出 现 的 事 送到学校 , 4在 学校 和老师就有 责任和 义务做 严把安全关 ,杜绝 食物 中毒等安全事故 的 好 学生 安 全 的敦 育和 监 护 。 那 么 怎样 帮 助 发生 。 故 ;. 5上文 化课 和实 验课 时 出 现 的事 敞 ; 6劳 动 和卫 生 扫 除 时 出现 的 事故 ;. 生 之 学 生树 立 安 全 意 识 呢 ? 首 先 , 得 安 全 的 . 7学 懂
现代密码学总结

现代密码学总结现代密码学总结第⼀讲绪论1、密码学是保障信息安全的核⼼2、安全服务包括:机密性、完整性、认证性、不可否认性、可⽤性3、⼀个密码体制或密码系统是指由明⽂(m或p)、密⽂(c)、密钥(k)、加密算法(E)和解密算法(D)组成的五元组。
4、现代密码学分类:(1)对称密码体制:(⼜称为秘密密钥密码体制,单钥密码体制或传统密码体制)密钥完全保密;加解密密钥相同;典型算法:DES、3DES、AES、IDEA、RC4、A5 (2)⾮对称密码体制:(⼜称为双钥密码体制或公开密钥密码体制)典型算法:RSA、ECC第⼆讲古典密码学1、代换密码:古典密码中⽤到的最基本的处理技巧。
将明⽂中的⼀个字母由其它字母、数字或符号替代的⼀种⽅法。
(1)凯撒密码:c = E(p) = (p + k) mod (26)p = D(c) = (c –k) mod (26)(2)仿射密码:明⽂p ∈Z26,密⽂c ∈Z26 ,密钥k=(a,b)ap+b = c mod (26)(3)单表代换、多表代换Hill密码:(多表代换的⼀种)——明⽂p ∈(Z26)m,密⽂c ∈(Z26)m,密钥K ∈{定义在Z26上m*m的可逆矩阵}——加密 c = p * K mod 26解密p = c * K-1 mod 26Vigenere密码:查表解答(4)转轮密码机:2、置换密码:将明⽂字符按照某种规律重新排列⽽形成密⽂的过程列置换,周期置换3、密码分析:(1)统计分析法:移位密码、仿射密码和单表代换密码都没有破坏明⽂的频率统计规律,可以直接⽤统计分析法(2)重合指数法完全随机的⽂本CI=0.0385,⼀个有意义的英⽂⽂本CI=0.065实际使⽤CI 的估计值CI ’:L :密⽂长。
fi :密⽂符号i 发⽣的数⽬。
第三讲密码学基础第⼀部分密码学的信息论基础1、 Shannon 的保密通信系统模型(1)对称密码体制(2)(3)⼀个密码体制是⼀个六元组:(P , C, K 1, K 2, E, D )P--明⽂空间C--密⽂空间K 1 --加密密钥空间 K 2--解密密钥空间E --加密变换D --解密变换对任⼀k ∈K 1,都能找到k’∈K 2,使得D k’ (E k (m ))=m ,?m ∈M.2、熵和⽆条件保密(1)设随机变量X={xi | i=1,2,…,n}, xi 出现的概率为Pr(xi) ≧0, 且, 则X 的不确定性或熵定义为熵H(X)表⽰集X 中出现⼀个事件平均所需的信息量(观察前);或集X 中每出现⼀个事件平均所给出的信息量(观测后).(2)设X={x i |i=1,2,…,n}, x i 出现的概率为p (x i ) ≥0,且∑i=1,…,n p (x i )=1;0 )(1log )()(≥=∑ii ai x p x p X HY={y i |i=1,2,…,m}, y i 出现的概率为p (y i ) ≥0,且∑i=1,…,m p (y i )=1; 则集X 相对于集Y 的条件熵定义为(3) X 视为⼀个系统的输⼊空间,Y 视为系统的输出空间,通常将条件熵H (X|Y)称作含糊度,X 和Y 之间的平均互信息定义为:I (X,Y)=H (X)-H (X|Y) 表⽰X 熵减少量。
练习——简答题

练习——简答题1.什么是算法?算法有哪些特征?答:算法是求解问题的⼀系列计算步骤。
算法具有有限性、确定性、可⾏性、输⼊性和输出性5个重要特征。
2.算法设计应满⾜的⼏个⽬标答:算法设计应满⾜正确性、可使⽤性、可读性、健壮性和⾼效率与低存储量需求。
3.算法设计的基本步骤答:算法设计的基本步骤是:(1)分析求解问题(2)选择数据结构和算法设计策略(3)描述算法(4)证明算法正确性(5)算法分析各步骤之间存在循环和反复过程。
4.什么是算法复杂性?它主要有哪两个⽅⾯构成?答:算法复杂性是算法运⾏时所需要的计算机资源的量,它包括两个⽅⾯:时间复杂性(需要时间资源的量)和空间复杂性(需要空间资源的量)。
5.分析算法复杂性的意义是什么?算法的复杂性是算法效率的度量,是评价算法优劣的重要依据。
⼀个算法的复杂性的⾼低体现在运⾏该算法所需要的计算机资源的多少上⾯,所需的资源越多,我们就说该算法的复杂性越⾼;反之,所需的资源越低,则该算法的复杂性越低。
6.f(n)=O(g(n))答:f(n)=O(g(n))当且仅当存在正常量c和n0,使当n≥n0时,f(n)≤cg(n),即g(n)为f(n)的上界。
7.f(n)=W(g(n))答:f(n)=W(g(n))当且仅当存在正常量c和n0,使当n≥n0时,f(n)≥cg(n),即g(n)为f(n)的下界。
8.f(n)=Q(g(n))答:f(n)=Q(g(n))当且仅当存在正常量c1、c2和n0,使当n≥n0时,有c1g(n)≤f(n)≤c2g(n),即g(n)与f(n)的同阶。
9.算法的平均情况、最好情况、最坏情况,哪种情况的可操作性最好,最具有实际价值?答:设⼀个算法的输⼊规模为n,Dn是所有输⼊的集合,任⼀输⼊I∈Dn,P(I)是I出现的概率,有 =1,T(I)是算法在输⼊I下所执⾏的基本语句次数,则该算法的平均执⾏时间为:A(n)=算法的最好情况为:G(n)= ,是指算法在所有输⼊I下所执⾏基本语句的最少次数。
计算复杂性理论总结报告

人生有几件绝对不能失去的东西:自制的力量,冷静的头脑,希望和信心 1计算复杂性理论总结报告一、 图灵机(1) 图灵机基本模型图灵机是山图灵(Alan Mathisom Turing)在1936年提出的,它是一个通用的计算 模型。
通过图灵机,来研究递归可枚举集和部分递归函数,对算法和可计算性进行研究 提供了形式化描述工具。
图灵机的基本模型包括一个有穷控制器,一条含有无数个带方格的输入带和一个读 写头。
其直观物理模型如下图1所示。
基本图灵动作有以下三种:(1) 改写被扫描带方格内容,控制器转化为下一状态。
(2) 读写头向左移一个带方格,控制器转化为下一状态。
(3) 读写头向左移一个带方格,控制器转化为下一状态。
图1图灵机(2) 图灵机形式化定义,图灵机演算过程及语言描述定义:一个基本图灵机定义为一个七元组TM={Q,C,6,A.B,ql,F)o 其中Q 是状态集合,(图灵机所有的状态)非空有限集;C 是带符号表,(放在带方格中的符号集合)非空集;6是控制函数或过程转换函数(定义控制器)6: QxCTQxCU (R.L); A 是输入字母表,ACC ;B 是空白符,BGC :ql 是初始状态,qlSQ ;F 是终态集,F £ Q.TM 的扫描符号串主要山6来确定:(1)5 (q, s)二(q‘,s'); (2)8 (q, s) =(q* , R); (3)8 (q, s) =(q* , L); (4) 6 (q, s)无效,对应无定义时图灵机终止。
TM 的工作用“格局”的转换来描述。
格局:6 ala2a3...aj-lqajaj+l...其中 qWQ, aiGC ;帯(1)若8 (q, ai)无定义,称o为停机格局;(2)若qEF,称o为接受格局;人生有几件绝对不能失去的东西:自制的力量,冷静的头脑,希望和信心__(3) 若q为初始状态,称o为初始格局;格局O到格局T的转换a 卜mt 若成立go 1 |~mlo2 卜m2。
中科院计算机算法分析与设计_习题1-2_答案

2)证明:除结点v外,只有当结点w满足s[w]=0时才被压入栈中,因此每 个结点至多有一次被压入栈中,搜索不会出现重叠和死循环现象,对于每
template<class T> bool MinMax(T a[], int n, int& Min, int& Max) { if(n<1) return false; Min=Max=0; //初始化 for(int i=1; i<n; i++){ if(a[Min]>a[i]) Min=i; if(a[Max]<a[i]) Max=i; } return true; } 最好,最坏,平均比较次数都是 2*(n-1)
2-连通
割点
4 5
D E
4 5
(1,2,3,4,0,0,0) (1,1,1,4,1,0,0)
{(C,D)};
C
6
F
6
(1,1,1,4,1,6,0)
7
G
7
(1,1,1,4,1,5,5)
(E,A), {(G,E),(F,G), (E,F)} (B,C), (A,B) {(E,A),(B,C),(A,B)}
3.设G是具有n个顶点和m条边的无向图,如果G是连通的,而且满足m = n-1,
证明G是树。 4.假设用一个n×n的数组来描述一个有向图的n×n邻接矩阵,完成下面工作
:
1)编写一个函数以确定顶点的出度,函数的复杂性应为 2)编写一个函数以确定图中边的数目,函数的复杂性应为 3)编写一个函数删除边(i,j),并确定代码的复杂性。 5.实现图的D-搜索算法。要求用ALGEN语言写出算法的伪代码, 或者用一种计算机高级语言写出程序。 ; (n)
算法的计算复杂性概念

算法的计算复杂性概念
计算复杂性是一个相当普遍的概念,用来衡量算法的复杂程度及其所需要的计算和存储资源。
它指出了通过解决一个特定问题所需要的资源数量和时间,是计算机科学领域中应用非常广泛的计算时间和空间复杂度理论。
计算复杂性的基本思想是:给定的算法的运行时间,由其所执行的基本步骤的重复次数决定。
这些步骤机会包括读写输出、内存操作、比较和逻辑判断等。
每一次的重复,都会消耗算法所需的资源。
算法的运行时间,在某程度上可以用消耗的资源数量来衡量。
计算复杂性概念被用来衡量算法空间和时间复杂度,以及评价算法效率,它是一种定量量度。
运行时间和空间复杂度由大O表示法来表示,Big O表示法在数学里描述函数增加量的时候,使用主要步骤多少来表示算法的复杂程度。
算法中最耗时的基本步骤是核心步,而计算复杂性可以衡量算法的效率,并评估算法的运行性能。
计算复杂性的概念历经多年,今天已经成为计算机科学领域的核心技术,深受计算性能分析专家、软件开发者和算法设计者的重视。
它不仅能够帮助识别算法效率的关键瓶颈,而且能够用精准的度量标准来比较两个算法的性能,帮助推进算法的改进,提高计算性能。
因此计算复杂性是一个极为重要的计算机科学概念,它能够用精确的方式衡量算法的复杂程度,用于评估算法的性能,以及帮助算法设计者和开发者识别算法缺陷并进行改进。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算复杂性第一次作业
周雄(1152220101)
March21,2018
题目1:
①对于00010,我们有如下瞬间描述迁移序列:
q000010B⊢0q00010B⊢00q010B⊢000q010B⊢0000q10B⊢00000q1B⊢000000q2(接受)
②对于001000,我们有如下瞬间描述序列:
q0001000B⊢0q001000B⊢00q01000B⊢000q1000B⊢0000q100B⊢00000q10B⊢
000000q1B⊢0000000q2(接受)
③对于0010001,我们有如下瞬间描述序列:
q00010001B⊢0q0010001B⊢00q010001B⊢000q10001B⊢0000q1001B⊢00000q101B⊢
000000q11B(停机)
题目2:
start
题目3:
①对于0011,我们有如下瞬间描述迁移序列:
q00011B⊢Xq1011B⊢X0q111B⊢Xq20Y1B⊢q2X0Y1B⊢Xq00Y1B⊢XXq1Y1B⊢
XXY q11B⊢XXq2Y Y B⊢Xq2XY Y B⊢XXq0Y Y B⊢XXY q3Y B⊢XXY Y q3B⊢
XXY Y Bq4(接受)
②对于0101,我们有如下瞬间描述序列:
q00101B⊢Xq1101B⊢q2XY01B⊢Xq0Y01B⊢XY q301B(停机)
③对于00111,我们有如下瞬间描述序列:
q000111B⊢Xq10111B⊢X0q1111B⊢Xq20Y11B⊢q2X0Y11B⊢Xq00Y11B⊢XXq1Y11B⊢XXY q111B⊢XXq2Y Y1B⊢Xq2XY Y1B⊢XXq0Y Y1B⊢XXY q3Y1B⊢XXY Y q31B(停机)题目4:
(1)
start
(其中x表示任意字符)
(2)
start
(其中N表示空白符)
题目5:
start
←|1/1←下面我们用反证法来证明L ={0n 1n 2n |n ≥1}不是上下文无关语言.证:
假设L 是上下文无关语言,那么存在整数N 。
取z =0N 1N 2N 。
由泵引理,z =uvwxy ,其中|vwx |≤N,vx =ε。
其中vwx 显然不能同时包含0,1或2的,否则|vwx |>|1N |≥N 。
如果vwx 只包含0,1或2,那么uwy 不在L 中;vwx 若只包含0和1,或只包含1和2,uwy 也不在L 中.而由于泵引理uwy =uv 0wx 0,y ∈L ,因此假设不成立,L 不是上下文无关的.
题目6:
start
←
←
题目7:
start
←|1/1←。
