七年级动点问题专项练习
七年级数学专项练习全等中的动点问题(含答案解析)

1. 如图,在△ABC 中∠ACB =90°,BE 平分∠ABC ,DE ⊥AB 于D 七年级数学专项习题——全等中的动点问题(含答案解析),如果AC =3cm ,那么AE +DE 等于 .2. 如图,将一个长方形纸片ABCD 沿着BE 折叠,使C ,D 点分别落在点C 1,D 1处.若∠C 1BA =50°,则∠AB E 的度数为( )A .15°B .20°C .25°D .30°3. 如图a 是长方形纸带,∠BFE =15°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∠CFE 的度数是 .4. 如图,在3×3的网格中,以AB 为一边,点P 在格点处,则使△ABP 为等腰三角形的点P 有 个.5. 如图,矩形ABCD中,AB=2,AD=4,点E是边AD上的一个动点;把△BAE沿BE折叠,点A落在A'处,如果A'恰在矩形的对称轴上,则AE的长为.6. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在点E处,AE交DC于点O,若AO=5cm.⑴求证:△AOD≌△COE;⑵求AB的长.1. 解:∵∠ACB =90°,∴EC ⊥CB ,又BE 平分∠ABC ,DE ⊥AB ,∴CE =DE ,∴AE +DE =AE +CE =AC =3cm .2. 解:设∠ABE =x ,根据折叠前后角相等可知,∠C 1BE =∠CBE =50°+x , 所以50°+x +x =90°,解得x =20°.故选:B .3. 解:解:∵∠DEF =22°,长方形ABCD 的对边AD ∥BC , ∴∠EFB =∠DEF =22°,由折叠,∠EFB 处重叠了3层,∴∠CFE =180°-3∠EFB =180°-3×22°=114°.故选:B .4. 解:如图所示,以AB 为腰的等腰三角形的点P 有2个, 以AB 为底边的等腰三角形的点P 有3个,∴△ABP 为等腰三角形的点P 有5个.5. 解:分两种情况:①过点A ′作MN ∥CD 交AD 于点M ,交BC 于点N , 则直线MN 是矩形ABCD 的对称轴,∴AM =BN =21AD =2, ∵△ABC 沿直线BE 折叠得到△A ′BE ,∴AE =A ′E ,AB =A ′B =2,∴A ′N = =0,即A ′和N 重合, ∴A ′M =2=A ′E ,∴AE =2;②过点A ′作PQ ∥AD 交AB 于点P ,交CD 于点Q , 则直线PQ 是矩形ABCD 的对称轴,∴PQ ⊥AB ,AP =PB ,AD ∥PQ ∥BC ,∴A ′B =2PB ,∴∠P A ′B =30°,∴∠A ′BC =30°, ∴∠EBA ′=30°,设A ′E =x ,则BE =2x ,∴(2x )2=x 2+22,6.解:⑴全等易证.⑵根据折叠的性质可知∠BAC=∠EAC,∵四边形ABCD为矩形,∴AB∥CD,∴∠BAC=∠ACD,∴∠EAC=∠ACD,∴AO=CO=5cm,在直角三角形ADO中,AD=4cm,=3(cm),∴AB=CD=CO+OD=3+5=8(cm).。
初一数学动点问题例题集

初一数学动点问题集锦 【1 】1.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点. (1)假如点P 在线段BC 上以3厘米/秒的速度由B 点向C 点活动,同时,点Q 在线段CA 上由C 点向A 点活动.①若点Q 的活动速度与点P 的活动速度相等,经由1秒后,BPD △与CQP △是否全等,请解释来由;②若点Q 的活动速度与点P 的活动速度不相等,当点Q 的活动速度为若干时,可以或许使BPD △与CQP △全等?(2)若点Q 以②中的活动速度从点C 动身,点P 以本来的活动速度从点B 同时动身,都逆时针沿ABC △三边活动,求经由多长时光点P 与点Q 第一次在ABC △的哪条边上相遇?解:(1)①∵1t =秒, ∴313BP CQ ==⨯=厘米, ∵10AB =厘米,点D 为AB 的中点, ∴5BD =厘米. 又∵厘米,∴835PC =-=厘米8PC BC BP BC =-=,, ∴PC BD =. 又∵AB AC =, ∴B C ∠=∠,∴BPD CQP △≌△.(4分) ②∵P Qv v ≠,∴BP CQ ≠,又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,,∴点P,点Q活动的时光433BPt==秒,∴515443QCQvt===厘米/秒.(7分)(2)设经由x秒后点P与点Q第一次相遇,由题意,得153210 4x x=+⨯,解得803x=秒.∴点P共活动了803803⨯=厘米.∵8022824=⨯+,∴点P.点Q在AB边上相遇,∴经由803秒点P与点Q第一次在边AB上相遇.(12分)2.直线364y x=-+与坐标轴分离交于A B、两点,动点P Q、同时从O点动身,同时到达A点,活动停滞.点Q沿线段OA活动,速度为每秒1个单位长度,点P沿路线O→B→A活动.(1)直接写出A B、两点的坐标;(2)设点Q的活动时光为t秒,OPQ△的面积为S,求出S与t之间的函数关系式; 485S=(2)86OA OB ==,10AB ∴=点Q 由O 到A 的时光是881=(秒)∴点P 的速度是61028+=(单位/秒) 1分当P 在线段OB 上活动(或03t ≤≤)时,2OQ t OP t ==,2S t = 1分当P 在线段BA 上活动(或38t <≤)时,6102162OQ t AP t t ==+-=-,,如图,作PD OA ⊥于点D ,由PD AP BO AB =,得4865tPD -=, 1分21324255S OQ PD t t ∴=⨯=-+ 1分(自变量取值规模写对给1分,不然不给分.)(3)82455P ⎛⎫ ⎪⎝⎭, 1分12382412241224555555I M M 2⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,,, 3分 3如图,在平面直角坐标系中,直线l :y=-2x -8分离与x 轴,y 轴订交于A,B 两点,点P (0,k )是y 轴的负半轴上的一个动点,以P 为圆心,3为半径作⊙P.(1)贯穿连接PA,若PA=PB,试断定⊙P 与x 轴的地位关系,并解释来由;(2)当k 为何值时,以⊙P 与直线l 的两个交点和圆心P 为极点的三角形是正三角形?解:(1)⊙P 与x 轴相切.∵直线y=-2x -8与x 轴交于A (4,0), 与y 轴交于B (0,-8),∴OA=4,OB=8.由题意,OP=-k,∴PB=PA=8+k.在Rt△AOP中,k2+42=(8+k)2,∴k=-3,∴OP等于⊙P的半径,∴⊙P与x轴相切.(2)设⊙P与直线l交于C,D两点,贯穿连接PC,PD当圆心P在线段OB上时,作PE⊥CD于E.∵△PCD为正三角形,∴DE=12CD=32,PD=3,∴PE=33.∵∠AOB=∠PEB=90°,∠ABO=∠PBE,∴△AOB∽△PEB,∴332,45AO PEAB PB PB =即,∴315 PB=∴3158PO BO PB=-=,∴3158) P-,∴3158 k=.当圆心P在线段OB延伸线上时,同理可得P(0,-315-8),∴k=-315-8,∴当k=3152-8或k=-3152-8时,以⊙P与直线l的两个交点和圆心P为极点的三角形是正三角形.4(09哈尔滨)如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A 的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的解析式;(2)衔接BM,如图2,动点P从点A动身,沿折线ABC偏向以2个单位/秒的速度向终点C匀速活动,设△PMB的面积为S(S≠0),点P的活动时光为t秒,求S与t之间的函数关系式(请求写出自变量t的取值规模);(3)在(2)的前提下,当t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.解:B 5在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C动身沿CA以每秒1个单位长的速度向点A匀速活动,到达点AE后连忙以本来的速度沿AC 返回;点Q 从点A 动身沿AB 以每秒1个单位长的速度向点B 匀速活动.陪同着P.Q 的活动,DE 保持垂直等分PQ,且交PQ 于点D,交折线QB-BC-CP 于点E .点P.Q 同时动身,当点Q 到达点B 时停滞活动,点P 也随之停滞.设点P.Q 活动的时光是t 秒(t >0).(1)当t = 2时,AP = ,点Q 到AC 的距离是; (2)在点P 从C 向A 活动的进程中,求△APQ 的面积S 与 t 的函数关系式;(不必写出t 的取值规模)(3)在点E 从B 向C 活动的进程中,四边形QBED 可否成 为直角梯形?若能,求t 的值.若不克不及,请解释来由; (4)当DE 经由点C 时,请直接写出t 的值.解:(1)1,85;(2)作QF ⊥AC 于点F,如图3, AQ = CP= t,∴3AP t =-.由△AQF ∽△ABC,4BC ==,得45QF t =.∴45QF t=. ∴14(3)25S t t =-⋅,即22655S t t=-+. (3)能.①当DE ∥QB 时,如图4.∵DE ⊥PQ,∴PQ ⊥QB,四边形QBED 是直角梯形. 此时∠AQP=90°.由△APQ ∽△ABC,得AQ APAC AB =, 即335t t -=.解得98t =. ②如图5,当PQ ∥BC 时,DE ⊥BC,四边形QBED 是直角梯形. 此时∠APQ =90°.P图4P由△AQP ∽△ABC,得AQ APAB AC =, 即353t t -=.解得158t =. (4)52t =或4514t =.①点P 由C 向A 活动,DE 经由点C . 衔接QC,作QG ⊥BC 于点G,如图6.PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--.由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =. ②点P 由A 向C 活动,DE 经由点C,如图7.22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】6如图,在Rt ABC△中,9060ACB B ∠=∠=°,°,2BC =.点O 是AC 的中点,过点O 的直线l 从与AC 重合的地位开端,绕点O 作逆时针扭转,交AB边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的扭转角为α.(1)①当α=度时,四边形EDBC 是等腰梯形,此时AD 的长为;②当α=度时,四边形EDBC 是直角梯形,此时AD 的长为; (2)当90α=°时,断定四边形EDBC 是否为菱形,并解释来由. 解(1)①30,1;②60,1.5; ……………………4分 (2)当∠α=900时,四边形EDBC 是菱形. ∵∠α=∠ACB=900,∴BC//ED.∵CE//AB, ∴四边形EDBC 是平行四边形. ……………………6分 在Rt △ABC 中,∠ACB=900,∠B=600,BC=2,OE CDAα lOCA(备用图)∴∠A=300. ∴∴AO=12AC. ……………………8分在Rt △AOD 中,∠A=300,∴AD=2. ∴BD=2. ∴BD=BC.又∵四边形EDBC 是平行四边形,∴四边形EDBC 是菱形 ……………………10分 7如图,在梯形ABCD 中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点动身沿线段BC 以每秒2个单位长度的速度向终点C 活动;动点N 同时从C 点动身沿线段CD 以每秒1个单位长度的速度向终点D 活动.设活动的时光为t 秒. (1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探讨:t 为何值时,MNC △为等腰三角形.解:(1)如图①,过A .D 分离作AK BC ⊥于K ,DH BC ⊥于H ,则四边形ADHK 是矩形∴3KH AD ==. 1分在Rt ABK △中,sin 4542AK AB =︒==. 2cos 454242BK AB =︒==2分在Rt CDH △中,由勾股定理得,3HC == CM∴43310BC BK KH HC =++=++=3分(2)如图②,过D 作DG AB ∥交BC 于G 点,则四边形ADGB 是平行四边形 ∵MN AB ∥∴MN DG ∥ ∴3BG AD == ∴1037GC =-=4分由题意知,当M .N 活动到t 秒时,102CN t CM t ==-,. ∵DG MN ∥ ∴NMC DGC =∠∠ 又C C =∠∠ ∴MNC GDC △∽△∴CN CMCD CG =5分即10257t t -= 解得,5017t =6分(3)分三种情形评论辩论: ①当NC MC =时,如图③,即102t t =-∴103t =7分 (图①) ADCB KH(图②)ADCBG MN解法一:由等腰三角形三线合一性质得()11102522EC MC t t ==-=-在Rt CEN △中,5cos EC t c NC t -== 又在Rt DHC △中,3cos 5CH c CD ==∴535t t-= 解得258t =8分解法二:∵90C C DHC NEC =∠=∠=︒∠∠, ∴NEC DHC △∽△∴NC ECDC HC = 即553t t -=∴258t =8分③当MN MC =时,如图⑤,过M 作MF CN ⊥于F 点.1122FC NC t ==解法一:(办法同②中解法一)132cos 1025tFC C MC t ===-解得6017t = 解法二:(图⑤)ADCBH N MF∵90C C MFC DHC =∠=∠=︒∠∠, ∴MFC DHC △∽△∴FC MCHC DC = 即1102235tt-= ∴6017t =综上所述,当103t =.258t =或6017t =时,MNC △为等腰三角形 9分8如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =︒∠. (1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,贯穿连接PN ,设EP x =.①当点N 在线段AD 上时(如图2),PMN △的外形是否产生转变?若不变,求出PMN △的周长;若转变,请解释来由;②当点N 在线段DC 上时(如图3),是否消失点P ,使PMN △为等腰三角形?若消失,请求出所有知足请求的x 的值;若不消失,请解释来由. 解(1)如图1,过点E 作EG BC ⊥于点G . 1分 ∵E 为AB 的中点, ∴122BE AB ==.在Rt EBG △中,60B =︒∠,∴30BEG =︒∠. 2分A DE BF C图1图2A D EBF C PNM 图3 A D EBFC PNM 图1A D EB F CG∴112BG BE EG ====,即点E 到BC3分(2)①当点N 在线段AD 上活动时,PMN △的外形不产生转变. ∵PM EF EG EF ⊥⊥,,∴PM EG ∥. ∵EF BC ∥,∴EP GM =,PM EG == 同理4MN AB ==. 4分如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥, ∴6030NMC B PMH ==︒=︒∠∠,∠.∴12PH PM == ∴3cos302MH PM =︒=.则35422NH MN MH =-=-=.在Rt PNH △中,PN ===∴PMN △的周长=4PM PN MN ++=. 6分②当点N 在线段DC 上活动时,PMN △的外形产生转变,但MNC △恒为等边三角形. 当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.相似①,32MR =.∴23MN MR ==. 7分∵MNC △是等边三角形,∴3MC MN ==.图2A D E BFCPNMG H此时,6132x EP GM BC BG MC ===--=--=. 8分当MP MN =时,如图4,这时MC MN MP === 此时,615x EP GM ===-= 当NP NM =时,如图5,30NPM PMN ==︒∠∠. 则120PMN =︒∠,又60MNC =︒∠, ∴180PNM MNC +=︒∠∠.是以点P 与F 重合,PMC △为直角三角形.∴tan301MC PM =︒=.此时,6114x EP GM ===--=. 综上所述,当2x =或4或(5时,PMN △为等腰三角形. 10分9如图①,正方形 ABCD 中,点A.B 的坐标分离为(0,10),(8,4),点C 在第一象限.动点P 在正方形 ABCD 的边上,从点A 动身沿A→B→C→D 匀速活动,同时动点Q 以雷同速度在x 轴正半轴上活动,当P 点到达D 点时,两点同时停滞活动, 设活动的时光为t 秒.(1)当P 点在边AB 上活动时,点Q 的横坐标x (长度单位)关于活动时光t (秒)的函数图象如图②所示,请写出点Q 开端活动时的坐标及点P 活动速度; (2)求正方形边长及极点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标;图3A D E BFCPN M图4A D EBF CP MN 图5A D EBF (P ) CMN GGRG(4)假如点P.Q 保持原速度不变,当点P 沿A→B→C→D 匀速活动时,OP 与PQ 可否相等,若能,写出所有相符前提的t 的值;若不克不及,请解释来由.解:(1)Q (1,0)1分点P 活动速度每秒钟1个单位长度.2分(2)过点B 作BF ⊥y轴于点F ,BE ⊥x 轴于点E ,则BF =8,4OF BE ==.∴1046AF =-=.在Rt △AFB 中,228610AB =+= 3分 过点C 作CG ⊥x 轴于点G ,与FB 的延伸线交于点H . ∵90,ABC AB BC ∠=︒=∴△ABF ≌△BCH . ∴6,8BH AF CH BF ====. ∴8614,8412OG FH CG ==+==+=.∴所求C 点的坐标为(14,12). 4分 (3)过点P 作PM ⊥y 轴于点M,PN ⊥x 轴于点N, 则△APM ∽△ABF .∴AP AM MPAB AF BF ==.1068t AM MP ∴==. ∴3455AM t PM t ==,.∴3410,55PN OM t ON PM t==-==. 设△OPQ 的面积为S (平地契位)∴213473(10)(1)5251010S t t t t =⨯-+=+-(0≤t ≤10) 5分 解释:未注明自变量的取值规模不扣分.AB CDEF G H M NPQ Oxy∵310a =-<0 ∴当474710362()10t =-=⨯-时,△OPQ 的面积最大. 6分此时P 的坐标为(9415,5310).7分(4)当53t =或29513t =时, OP 与PQ 相等. 9分10数学课上,张先生出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F,求证:AE=EF . 经由思虑,小明展现了一种准确的解题思绪:取AB 的中点M,衔接ME,则AM=EC,易证AME ECF △≌△,所以AE EF =.在此基本上,同窗们作了进一步的研讨:(1)小颖提出:如图2,假如把“点E 是边BC 的中点”改为“点E 是边BC 上(除B,C 外)的随意率性一点”,其它前提不变,那么结论“AE=EF”仍然成立,你以为小颖的不雅点准确吗?假如准确,写出证实进程;假如不准确,请解释来由;(2)小华提出:如图3,点E 是BC 的延伸线上(除C 点外)的随意率性一点,其他前提不变,结论“AE=EF”仍然成立.你以为小华的不雅点准确吗?假如准确,写出证实进程;假如不准确,请解释来由.解:(1)准确.(1分)证实:在AB 上取一点M ,使AM EC =,衔接ME .(2分) BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°. CF 是外角等分线, 45DCF ∴∠=°, 135ECF ∴∠=°. AME ECF ∴∠=∠.ADF CG E B 图1 ADFC G E B 图2 ADFC G E B 图3 A DF CGEBM90AEB BAE ∠+∠=°,90AEB CEF ∠+∠=°,∴BAE CEF ∠=∠.AME BCF ∴△≌△(ASA ).(5分)AE EF ∴=.(6分)(2)准确.(7分)证实:在BA 的延伸线上取一点N . 使AN CE =,衔接NE .(8分)BN BE ∴=. 45N PCE ∴∠=∠=°.四边形ABCD 是正方形,AD BE ∴∥. DAE BEA ∴∠=∠.NAE CEF ∴∠=∠.ANE ECF ∴△≌△(ASA ).(10分)AE EF ∴=.(11分)11已知一个直角三角形纸片OAB ,个中9024AOB OA OB ∠===°,,.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D . ADFGE BN解(Ⅰ)如图①,折叠后点B 与点A 重合, 则ACD BCD △≌△. 设点C 的坐标为()()00m m >,.则4BC OB OC m =-=-. 于是4AC BC m ==-.在Rt AOC △中,由勾股定理,得222AC OC OA =+,即()22242m m -=+,解得32m =.∴点C 的坐标为302⎛⎫ ⎪⎝⎭,. 4分(Ⅱ)如图②,折叠后点B 落在OA 边上的点为B ', 则B CD BCD '△≌△.由题设OB x OC y '==,,则4B C BC OB OC y '==-=-,在Rt B OC '△中,由勾股定理,得222B C OC OB ''=+.()2224y y x ∴-=+,即2128y x =-+ 6分由点B '在边OA 上,有02x ≤≤,∴解析式2128y x =-+()02x ≤≤为所求. ∴当02x ≤≤时,y 随x 的增大而减小,y ∴的取值规模为322y ≤≤.7分(Ⅲ)如图③,折叠后点B 落在OA 边上的点为B '',且B D OB ''∥. 则OCB CB D ''''∠=∠. 又CBD CB D OCB CBD ''''∠=∠∴∠=∠,,有CB BA ''∥.Rt Rt COB BOA ''∴△∽△.有OB OC OA OB ''=,得2OC OB ''=. 9分 在Rt B OC ''△中, 设()00OB x x ''=>,则2OC x =.由(Ⅱ)的结论,得2001228x x =-+,解得000808x x x =-±>∴=-+,∴点C 的坐标为()016.10分12问题解决如图(1),将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E(不与点C ,D 重合),压平后得到折痕MN .当12CE CD =时,求AMBN 的值.类比归纳在图(1)中,若13CE CD =,则AM BN 的值等于;若14CE CD =,则AM BN 的值等于;若1CE CD n =(n为整数),则AMBN 的值等于.(用含n 的式子暗示)接洽拓广如图(2),将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C D ,重合),办法指点:为了求得AMBN的值,可先求BN .AM 的长,无妨设:AB =2 图(1)A BCDEFMN压平后得到折痕MN ,设()111AB CE m BC m CD n =>=,,则AMBN 的值等于.(用含m n ,的式子暗示)解:办法一:如图(1-1),衔接BM EM BE ,,.由题设,得四边形ABNM 和四边形FENM 关于直线MN 对称.∴MN 垂直等分BE .∴BM EM BN EN ==,. 1分∵四边形ABCD 是正方形,∴902A D C AB BC CD DA ∠=∠=∠=====°,.∵112CE CE DE CD =∴==,.设BN x =,则NE x =,2NC x =-.在Rt CNE △中,222NE CN CE =+.∴()22221x x =-+.解得54x =,即54BN =. 3分在Rt ABM △和在Rt DEM △中,222AM AB BM +=, 222DM DE EM +=,∴2222AM AB DM DE +=+. 5分设AM y =,则2DM y =-,∴()2222221y y +=-+. 解得14y =,即14AM =.6分 ∴15AM BN=. 7分 办法二:同办法一,54BN =.3分 如图(1-2),过点N 做NG CD ∥,交AD 于点G ,衔接BE .N图(1-1) A BCE FM第21页,共21页 ∵AD BC ∥,∴四边形GDCN 是平行四边形. ∴NG CD BC ==.同理,四边形ABNG 也是平行四边形.∴54AG BN ==. ∵90MN BE EBC BNM ⊥∴∠+∠=,°.90NG BC MNG BNM EBC MNG ⊥∴∠+∠=∴∠=∠,°,. 在BCE △与NGM △中90EBC MNG BC NG C NGM ∠=∠⎧⎪=⎨⎪∠=∠=⎩,,°.∴BCE NGM EC MG =△≌△,.5分∵114AM AG MG AM =--=5,=.4 6分 ∴15AM BN =. 7分 类比归纳25(或410);917;()2211n n -+10分接洽拓广 2222211n m n n m -++ 12分N 图(1-2) A B C D E F M G。
七年级平面直角坐标系动点问题专项练习
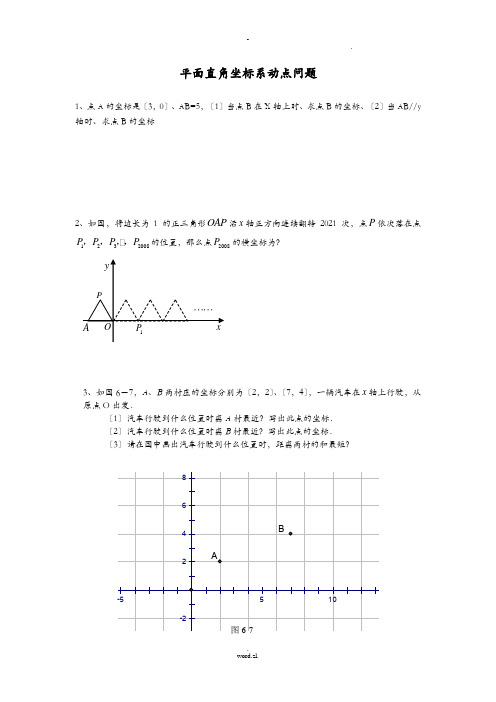
平面直角坐标系动点问题1、点A 的坐标是〔3,0〕、AB=5,〔1〕当点B 在X 轴上时、求点B 的坐标、〔2〕当AB//y 轴时、求点B 的坐标2、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2021次,点P 依次落在点1232008P P P P ,,,,的位置,那么点2008P 的横坐标为?3、如图6-7,A 、B 两村庄的坐标分别为〔2,2〕、〔7,4〕,一辆汽车在x 轴上行驶,从原点O 出发.〔1〕汽车行驶到什么位置时离A 村最近?写出此点的坐标. 〔2〕汽车行驶到什么位置时离B 村最近?写出此点的坐标. 〔3〕请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为〔-1,0〕,〔3,0〕,现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,假设存在这样一点,求出点P 的坐标,假设不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时〔不与B ,D 重合〕给出以下结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.(江岸)23.〔此题总分值12分〕如图,以直角三角形AOC 的直角顶点O 为原点,以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)20b -=.(1) 那么A 点的坐标为___________,C 点的坐标为__________;(2) 坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之完毕.AC 的中点D 的坐标是(1,2),设运动时间为t (t >0)秒.问:是否存在这样的t ,使S △ODP =S △ODQ ,假设存在,请求出t 的值;假设不存在,请说明理由;(3) 点F 是线段AC 上一点,满足∠FOC =∠FCO ,点G 是第二象限中一点,连OG ,使得∠AOG =∠AOF .点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACE OEC∠+∠∠的值是否会发生变化,假设不变,请求出它的值;假设变化,请说明理由.〔江汉〕28.〔此题总分值12分〕如图,长方形AOCB 的顶点A 〔m ,n 〕和C 〔p ,q 〕在坐标轴上,⎩⎪⎨⎪⎧x =m ,y =n 和⎩⎪⎨⎪⎧x =p ,y =q都是方程x +2y =4的解,点B 在第一象限.〔1〕求点B 的坐标;图1 图2〔2〕假设P 点从A 点出发沿y 轴负半轴以1个单位每秒的速度运动,同时Q 点从C 点出发沿x 轴负半轴方向以2个单位每秒的速度运动,问运动到多少秒时,四边形BPOQ 面积为长方形ABCO 面积的一半;〔3〕如图2,将线段AC 沿x 轴正方向平移,得到线段BD ,点E 〔a ,b 〕为线段BD 上任一点,试问式子a +2b 的值是否变化,假设变化,求其围;假设不变化,求其值.〔硚口〕24.〔12分〕如图1,在平面直角坐标系中,第一象限长方形ABCD , AB ∥y 轴,点A 〔1,1〕,点C 〔a , b 〕, 满足035=-+-b a .〔1〕求长方形ABCD 的面积.〔2〕如图2,长方形ABCD 以每秒1个单位长度的速度向右平移,同时点E 从原点O 出发沿x 轴以每秒2个单位长度的速度向右运动,设运动时间为t 秒. ①当t=4时,直接写出三角形OAC 的面积为 ; ② 假设AC ∥ED ,求t 的值;〔3〕在平面直角坐标系中,对于点()P x y ,,我们把点(11)P y x '-++,叫做点P 的伴随点,点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,…,这样依次得到点1A ,2A ,3A ,…,n A .①假设点1A 的坐标为〔3,1〕,那么点3A 的坐标为,点2014A 的坐标为;②假设点1A 的坐标为〔a ,b 〕,对于任意的正整数n ,点n A 均在x 轴上方,那么a ,b 应满足的条件为.探究案【例1】如图,在平面直角坐标中,A(0,1),B(2,0),C〔2,1.5〕.〔1〕求△ABC的面积;〔2〕如果在第二象限有一点P〔a,0.5〕,试用a的式子表示四边形ABOP的面积;〔3〕在〔2〕的条件下,是否存在这样的点P,使四边形ABOP的面积与△ABC的面积相等?假设存在,求出点P的坐标,假设不存在,请说明理由.【例2】在平面直角坐标系中,A〔-3,0〕,B〔-2,-2〕,将线段AB平移至线段CD,连AC、BD.图2〔1〕如图1,直接写出图中相等的线段,平行的线段;〔2〕如图2,假设线段AB移动到CD,C、D两点恰好都在坐标轴上,求C、D的坐标;〔3〕假设点C在y轴的正半轴上,点D在第一象限,且S△ACD=5,求C、D的坐标;〔4〕在y轴上是否存在一点P,使线段AB平移至线段PQ时,由A、B、P、Q构成的四边形是平行四边形面积为10,假设存在,求出P 、Q 的坐标,假设不存在,说明理由;【例3】如图,△ABC 的三个顶点位置分别是A 〔1,0〕,B 〔-2,3〕,C 〔-3,0〕. 〔1〕求△ABC 的面积;〔2〕假设把△ABC 向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C ''';〔3〕假设点A 、C 的位置不变,当点P 在y 轴上什么位置时,使2ACPABCS S=;〔4〕假设点B 、C 的位置不变,当点Q 在x 轴上什么位置时,使2BCQABCSS=.【例4】如图1,在平面直角坐标系中,A 〔a ,0〕,C 〔b ,2〕,且满足2(2)20a b ++-=,过C 作CB ⊥x 轴于B .〔1〕求三角形ABC 的面积;〔2〕假设过B 作BD ∥AC 交y 轴于D ,且AE ,DE 分别平分∠CAB ,∠ODB ,如图2,求∠AED 的度数;〔3〕在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等,假设存在,求出P点坐标;假设不存在,请说明理由.训练案1、如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A〔0,0〕,B〔7,0〕,C〔9,5〕,D〔2,7〕〔1〕在坐标系中,画出此四边形;〔2〕求此四边形的面积;(3)在坐标轴上,你能否找一个点P,使S△PBC=50,假设能,求出P点坐标,假设不能,说明理由.2、如图,A点坐标为〔-2,0〕,B点坐标为〔0,-3〕.(1)作图,将△ABO沿x轴正方向平移4个单位,得到△DEF,延长ED交y轴于C点,过O点作OG⊥CE,垂足为G;(2) 在(1)的条件下,求证: ∠COG=∠EDF;〔3〕求运动过程中线段AB扫过的图形的面积.A(-2,0)B(0,-3)yx3、在平面直角坐标系中,点B 〔0,4〕,C 〔-5,4〕,点A 是x 轴负半轴上一点,S 四边形AOBC =24.图1yxHOFEDAC B〔1〕线段BC 的长为,点A 的坐标为;〔2〕如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF⊥AE 点F ,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)假设点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON平分AOP ∠,BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.4、在平面直角坐标系中,OA =4,OC =8,四边形ABCO 是平行四边形.〔1〕求点B 的坐标及的面积ABCO S 四边形;〔2〕假设点P 从点C 以2单位长度/秒的速度沿CO 方向移动,同时点Q 从点O 以1单位长度/秒的速度沿OA 方向移动,设移动的时间为t 秒,△AQB 与△BPC 的面积分别记为AQB S ∆,BPC S ∆,是否存在某个时间,使AQB S ∆=3OQBPS 四边形,假设存在,求出t的值,假设不存在,试说明理由;〔3〕在〔2〕的条件下,四边形QBPO 的面积是否发生变化,假设不变,求出并证明你的结论,假设变化,求出变化的围.5、如图,在平面直角坐标系中,点A ,B 的坐标分别为〔-1,0〕,〔3,0〕,现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D 连结AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积S 四边形ABDC ;〔2〕在y 轴上是否存在一点P ,连结PA ,PB ,使S △PAB =S △PDB ,假设存在这样一点,求出点P 点坐标,假设不存在,试说明理由;〔3〕假设点Q 自O 点以0.5个单位/s 的速度在线段点就停顿,设移动的时间为t 秒,〔1〕是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?〔4〕是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?6、在直角坐标系中,△ABC 的顶点A 〔—2,0〕,B 〔2,4〕,C 〔5,0〕.〔1〕求△ABC 的面积〔2〕点D 为y 负半轴上一动点,连BD 交x 轴于E ,是否存在点D 使得ADE BCE S S ∆∆=?假设存在,请求出点D 的坐标;假设不存在,请说明理由.〔3〕点F 〔5,n 〕是第一象限一点,,连BF ,CF ,G 是x 轴上一点,假设△ABG 的面积等于四边形ABDC 的面积,那么点G 的坐标为〔用含n 的式子表示〕2021年初中数学组卷一.选择题〔共8小题〕1.〔2021春•北流市校级期中〕点P〔0,a〕在y轴的负半轴上,那么点Q〔﹣a2﹣1,﹣a+1〕在〔〕A.第一象限 B.第二象限C.第三象限 D.第四象限2.〔2021春•县校级月考〕点P〔x,y〕的坐标满足|x|=3,=2,且xy<0,那么点P的坐标是〔〕A.〔3,﹣2〕B.〔﹣3,2〕C.〔3,﹣4〕D.〔﹣3,4〕3.〔2021 •〕在平面直角坐标系中,假设点P的坐标为〔﹣3,2〕,那么点P所在的象限是〔〕A.第一象限 B.第二象限C.第三象限 D.第四象限4.〔2021 •〕直线L的方程式为x=3,直线M的方程式为y=﹣2,判断以下何者为直线L、直线M画在坐标平面上的图形?〔〕A.B.C.D.5.〔2021 •〕点P〔﹣2,﹣3〕向左平移1个单位,再向上平移3个单位,那么所得到的点的坐标为〔〕A.〔﹣3,0〕B.〔﹣1,6〕C.〔﹣3,﹣6〕D.〔﹣1,0〕6.〔2021 •〕在平面直角坐标系中,将点A〔x,y〕向左平移5个单位长度,再向上平移3个单位长度后与点B〔﹣3,2〕重合,那么点A的坐标是〔〕A.〔2,5〕B.〔﹣8,5〕C.〔﹣8,﹣1〕D.〔2,﹣1〕7.〔2021 春•校级期中〕如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒,它从原点运动到〔0,1〕,接着它按图所示在x轴、y轴的平行方向来回运动,〔即〔0,0〕→〔0,1〕→〔1,1〕→〔1,0〕→〔2,0〕→…〕且每秒运动一个单位长度,那么2021秒时,这个粒子所处位置为〔〕A.〔14,44〕B.〔15,44〕C.〔44,14〕D.〔44,15〕8.〔2021 •宝应县校级模拟〕点P〔m+3,m﹣1〕在x轴上,那么点P的坐标为〔〕A.〔0,﹣2〕B.〔2,0〕C.〔4,0〕D.〔0,﹣4〕二.填空题〔共8小题〕9.〔2021 •〕如图,将平面直角坐标系中“鱼〞的每个“顶点〞的纵坐标保持不变,横坐标分别变为原来的,那么点A的对应点A′的坐标是.10.〔2021 •二模〕如下图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断移动,每移动一个单位,得到点A1〔0,1〕、A2〔1,1〕、A3〔1,0〕、A4〔2,0〕,…,那么点A2021 的坐标为.11.〔2021春•洛龙区校级期中〕点O〔0,0〕,B〔1,2〕,点A在坐标轴上,且S△OAB=2,那么满足条件的点A的坐标为.12.〔2021春•信州区校级期中〕AB∥x轴,且AB=3,假设点A的坐标是〔﹣1,2〕,那么B 点的坐标是.13.〔2021春•区校级期中〕:点A〔0,5〕,B〔0,2〕,在坐标轴上找点C,使△ABC的面积为5,那么点C的坐标是.14.〔2021秋•靖江市校级期中〕在平面直角坐标系中,假设点M〔﹣2,6〕与点N〔x,6〕之间的距离是3,那么x的值是.15.〔2021春•江岸区期中〕在平面直角坐标系中,一个长方形的三个顶点坐标分别为〔﹣1,﹣1〕,〔﹣1,1〕,〔5,﹣1〕,那么第四个顶点的坐标是.16.〔2021春•鼓楼区校级期中〕A〔2,﹣6〕,B〔2,﹣4〕,那么线段AB=.三.解答题〔共14小题〕17.〔2021 •校级模拟〕在如下图的平面直角坐标系中描出下面各点:A〔0,3〕;B〔1,﹣3〕;C〔3,﹣5〕;D〔﹣3,﹣5〕;E〔3,5〕;F〔5,7〕;G〔5,0〕.〔1〕将点C向x轴的负方向平移6个单位,它与点重合.〔2〕连接CE,那么直线CE与y轴是什么关系?〔3〕顺次连接D、E、G、C、D得到四边形DEGC,求四边形DEGC的面积.18.〔2021 春•校级期末〕〔1〕在坐标平面画出点P〔2,3〕.〔2〕分别作出点P关于x轴、y轴的对称点P1,P2,并写出P1,P2的坐标.19.〔2021 秋•兴平市期末〕假设x,y为实数,且满足|x﹣3|+=0.〔1〕如果实数x,y对应为平面直角坐标系上的点A〔x,y〕,那么点A在第几象限?〔2〕求〔〕2021 的值?20.〔2021 春•平南县期末〕在平面直角坐标系中,点A〔a,3﹣2a〕在第一象限.〔1〕假设点A到x轴的距离与到y轴的距离相等,求a的值;〔2〕假设点A到x轴的距离小于到y轴的距离,求a的取值围.21.〔2021 秋•双柏县期末〕如图,A、B两点的坐标分别是〔2,﹣3〕、〔﹣4,﹣3〕.〔1〕请你确定P〔4,3〕的位置;〔2〕请你写出点Q的坐标.22.〔2021 秋•沭阳县校级期末〕如图,A〔﹣2,3〕、B〔4,3〕、C〔﹣1,﹣3〕〔1〕求点C到x轴的距离;〔2〕求△ABC的面积;〔3〕点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.23.〔2021 春•博兴县期末〕在平面直角坐标系中,四边形ABCD的顶点坐标分别为A〔1,0〕,B〔5,0〕,C〔3,3〕,D〔2,4〕.〔1〕求线段AB的长;〔2〕求四边形ABCD的面积.24.〔2021 春•丹江口市期末〕〔1〕两点A〔﹣3,m〕,B〔n,4〕,假设AB∥x轴,求m的值,并确定n的围;〔2〕假设点〔5﹣a,a﹣3〕在第一、三象限的角平分线上,求a的值.25.〔2021 秋•埇桥区期末〕点A〔m+2,3〕和点B〔m﹣1,2m﹣4〕,且AB∥x轴.〔1〕求m的值;〔2〕求AB的长.26.〔2021 春•建昌县期末〕:如图,在平面直角坐标系xOy中,A〔4,0〕,C〔0,6〕,点B 在第一象限,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周〔即:沿着O→A→B→C→O的路线移动〕.〔1〕写出B点的坐标〔〕;〔2〕当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;〔3〕在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.27.〔2021 春•文安县期末〕如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C 点坐标为〔1,2〕.〔1〕写出点A、B的坐标:A〔,〕、B〔,〕〔2〕将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,那么A′B′C′的三个顶点坐标分别是A′〔,〕、B′〔,〕、C′〔,〕.〔3〕△ABC的面积为.28.〔2021 春•校级期中〕我们规定以下三种变换:〔1〕f〔a,b〕=〔﹣a,b〕.如:f〔1,3〕=〔﹣1,3〕;〔2〕g〔a,b〕=〔b,a〕.如:g〔1,3〕=〔3,1〕;〔3〕h〔a,b〕=〔﹣a,﹣b〕.如:h〔1,3〕=〔﹣1,﹣3〕.按照以上变换有:f〔g〔2,﹣3〕〕=f〔﹣3,2〕=〔3,2〕,求f〔h〔5,﹣3〕〕的值.29.〔2021 春•繁昌县期中〕点A〔1+2a,4a﹣5〕,且点A到两坐标轴的距离相等,求点A 的坐标.30.〔2021 秋•务川县校级期中〕平面直角坐标系中,△ABC的三个顶点坐标分别为A〔0,4〕B〔2,4〕C〔3,﹣1〕.〔1〕试在平面直角坐标系中,标出A、B、C三点;〔2〕求△ABC的面积.〔3〕假设△DEF与△ABC关于x轴对称,写出D、E、F的坐标.2021年04月05日1148955744的初中数学组卷参考答案一.选择题〔共8小题〕1.B;2.D;3.B;4.B;5.A;6.D;7.A;8.C;二.填空题〔共8小题〕9.〔2,3〕;10.〔1007,0〕;11.〔2,0〕或〔-2,0〕或〔0,4〕或〔0,-4〕;12.〔-4,2〕或〔2,2〕;13.〔,0〕或〔-,0〕;14.1或-5;15.〔5,1〕;16.2;三.解答题〔共14小题〕17.D;〔-3,-5〕;18.;19.;20.;21.;22.;23.;24.;25.;26.〔4,6〕;27.2;-1; 4;3;0;0;2;4;-1; 3;5;28.;29.;30.;。
初中数学七年级上动点问题期末复习训练题(23道题,含答案)

七年级上期末复习动点问题专题训练1.如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是_________.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?2.已知数轴上两个点A、B所对应的数为a、b,且a、b满足|a+3|+(b﹣4)2=0.(1)求AB的长;(2)若甲、乙分别从A、B两点同时在数轴上运动,甲的速度是2个单位/秒,乙的速度比甲的速度快3个单位/秒,求甲乙相遇点所表示的数;(3)若点C对应的数为﹣1,在数轴上A点的左侧是否存在一点P,使P A+PB=3PC?若存在,求出点P所对应的数;若不存在,请说明理由.3.已知数轴上点A,B,C所表示的数分别是x,﹣6,4.(1)线段BC的长为_________,线段BC的中点D所表示的数是_________.(2)若AC=8,求x的值(3)在数轴上有两个动点P,Q,P的速度为1个单位长度/秒,Q的速度为2个单位/秒,点P,Q分别从点B,C 同时出发,在数轴上运动,则经过多少时间后P,Q两点相距4个单位?4.如图1,已知数轴上有三点A、B、C,AC=2AB,点A对应的数是400.(1)若AB=600,求点C到原点的距离;(2)在(1)的条件下,动点P、Q分别从C、A同时出发,其中P、Q向右运动,R向左运动如图2,已知点Q的速度是点R速度2倍少5个单位长度/秒,点P的速度是点R的速度的3倍,经过20秒,点P、Q之间的距离与点Q、R的距离相等,求动点Q的速度.5.已知:数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x(1)若点P到点A、点B的距离相等,则点P对应的数为_________.(2)若点P在A、B之间,请化简:|x+1|﹣|x﹣3|.(3)数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,请求出x的值;若不存在,请说明由.(4)当点P以每分钟1个单位长度的速度从O(原点)向左运动,同时,点A以每分钟5个单位长度的速度向左运动,点B以每分钟20个单位长度的速度向左运动.问它们同时出发,几分钟后点P到点A、点B的距离相等?6.如图,数轴上有A、B、C、D四个点,分别对应的数是a、b、c、d,且满足|a+9|=1,b=a+2,(c﹣16)2与|d﹣20|互为相反数.(1)求a、b、c、d的值.(2)如果点M为A、B两点的中点,点N到点C有5个单位长,求M、N两点之间的距离.(3)若A、B两点以6个单位长度/秒的速度向右匀速运动,同时C、D两点以2个单位长度/秒向左匀速运动,并设运动时间为t秒,当点B运动到点D的右侧时,问是否存在时间t,使B与C的距离是A与D的距离的4倍?若存在,求时间t;若不存在,请说明理由.7.如图1,数轴上E点表示的数是﹣10,Q点表示的数是20,P、F分别从Q、E点出发,沿箭头所示的方向运动,它们的速度都是5个单位长度/秒;它们的运动时间为t秒;(1)C为PF的中点,求C点表示的数,并用含t的式子表示F、P表示的数.(2)如图2,M是数轴上任意一点,线段PQ以P点的速度向左运动,点M以3个单位长度/秒的速度向右运动,点M在线段PQ上的时间为4秒,求线段PQ的长;(3)如图3,N是数轴上任意一点,线段EF、PQ在数轴上沿箭头所示的方向运动,它们的运动速度都是5个单位长度/秒,且EF=PQ,N向数轴正方向运动,已知N在线段PQ上的时间为6秒,N在线段EF上的时间为10秒,求PQ的长.8.已知数轴上顺次有A、B、C三点,分别表示数a、b、c,并且满足(a+12)2+|b+5|=0,b与c互为相反数.两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为3个单位/秒.(1)求A、B、C三点分别表示的数,并在数轴上表示A、B、C三点(2)运动多少秒时,甲、乙到点B的距离相等?(3)设点P在数轴上表示的数为x,且点P满足|x+12|+|x+5|+|x﹣5|=20,若甲运动到点P时立即调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.9.如图,数轴上点A、C对应的数分别为a,c,且a,c满足|a+4|+(c﹣1)2014=0,点B对应的数为﹣3,(1)求数a,c;(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值;(3)在(2)的条件下,若点B运动到点C处后立即以原速返回,到达自己的出发点后停止运动,点A运动至点C 处后又以原速返回,到达自己的出发点后又折返向点C运动,当点B停止运动时,点A随之停止运动,求在此运动过程中,A,B两点同时到达的点在数轴上表示的数.10.已知:数轴上A.B两点表示的有理数为a、b,且(a﹣1)2+|b+2|=0.(1)A、B各表示哪一个有理数?(2)点C在数轴上表示的数是c,且与A、B两点的距离和为11,求多项式a(bc+3)﹣|c2﹣3(a﹣c2)|的值;(3)小蚂蚁甲以1个单位长度/秒的速度从点B出发向其左边6个单位长度处的一颗饭粒爬去,3秒后位于点A的小蚂蚁乙收到它的信号,以2个单位长度/秒的速度也迅速爬向饭粒,小蚂蚁甲到达后背着饭粒立即返回,与小蚂蚁乙在数轴上D点相遇,则点D表示的有理数是什么?从出发到此时,小蚂蚁甲共用去多少时间?11.如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=BC.(1)求点C表示的数;(2)若数轴上有一点P,且PC+P A=19,求点P表示的数;(3)有一条2个单位长度的青色毛毛虫从点C出发,以每秒0.5个单位长度的速度沿数轴正方向匀速运动到点A 时,绕点A处的木杆(不考虑绕木杆所用的时间)改变方向后始终沿数轴负方向匀速运动,速度保持不变.青色毛毛虫从点C出发的同时,一条3个单位长度的白色毛毛虫从点B出发,始终沿数轴正方向以每秒0.2个单位长度的速度匀速运动.求两条毛毛虫在第几秒时头头相遇?在第几秒时尾尾相遇?每次从相遇到相离经过了多长时间?12.已知A、B在数轴上对应的数分别用a、b表示,且(ab+100)2+|a﹣20|=0.P是数轴上的一个动点(1)在数轴上标出A、B的位置,并求出A、B之间的距离;(2)数轴上一点C距A点24个单位长度,其对应的数c满足|ac|=﹣ac.当P点满足PB=2PC时,求P点对应的数;(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P移动到与A或B重合的位置吗?若能,请探究第几次移动是重合;若不能,请说明理由.13.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数_________,点P表示的数_________(用含t的代数式表示);(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.14.如图,已知数轴上A、B两点所表示的数分别为﹣2和8.(1)求线段AB的长;(2)若P为射线BA上的一点(点P不与A、B两点重合),M为P A的中点,N为PB的中点,当点P在射线BA 上运动时,线段MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.(3)若有理数a、b、c在数轴上的位置如图所示,且d=|a+b|﹣|﹣2﹣b|﹣|a﹣2c|﹣5,试求7(d+2c)2+2(d+2c)﹣5(d+2c)2﹣3(d+2c)的值.15.已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b﹣1)2=0,A、B之间距离记作|AB|,定义:|AB|=|a﹣b|.(Ⅰ)求线段AB的长|AB|;(Ⅱ)设点P在数轴上对应的数为x,当|P A|﹣|PB|=3时,求x的值;(Ⅲ)若点P在A的左侧,M、N分别是P A、PB的中点,当P在A的左侧移动时,下列两个结论:①|PM|+|PN|的值不变;②|PN|﹣|PM|的值不变,其中只有一个结论正确,请判断出正确结论,并求其值.16.如图1,点A、B分别在数轴原点O的左右两侧,且OA+50=OB,点B对应数是90.(1)求A点对应的数;(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离;(3)如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN 的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值.17.点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0(1)求线段AB的长;(2)如图1 点C在数轴上对应的数为x,且x是方程2x+1=x﹣5的根,在数轴上是否存在点P使P A+PB=BC+AB?若存在,求出点P对应的数;若不存在,说明理由;(3)如图2,若P点是B点右侧一点,P A的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,有两个结论:①PM﹣BN的值不变;②PM+BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值18.如图1,已知数轴上两点A、B对应的数分别﹣1、3,点P为数轴上一动点,其对应的数为x.(1)数轴上是否存在点P,使P到点A、点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;(2)当点P以每分钟1个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度的速度向左运动,点B 以每分钟20个单位长度的速度向左运动,问它们同时出发,几分钟时间P点到点A、点B的距离相等?(3)若P从B点出发向左运动(只在线段AB上运动),M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你在图2中画出图形,并求出线段MN的长.19.如图1,已知数轴上有三点A、B、C,AB=AC,点C对应的数是200.(1)若BC=300,求点A对应的数;(2)如图2,在(1)的条件下,动点P、Q分别从A、C两点同时出发向左运动,同时动点R从A点出发向右运动,点P、Q、R的速度分别为10单位长度每秒、5单位长度每秒、2单位长度每秒,点M为线段PR的中点,点N 为线段RQ的中点,多少秒时恰好满足MR=4RN(不考虑点R与点Q相遇之后的情形);(3)如图3,在(1)的条件下,若点E、D对应的数分别为﹣800、0,动点P、Q分别从E、D两点同时出发向左运动,点P、Q的速度分别为10单位长度每秒、5单位长度每秒,点M为线段PQ的中点,点Q在从是点D运动到点A的过程中,QC﹣AM的值是否发生变化?若不变,求其值;若不变,请说明理由.20.已知:A、B、C为数轴上三个运动的点,速度分别为a个单位/秒、b个单位/秒和c个单位/秒(a、b、c为正整数),且满足|5﹣a|+(b﹣3)2=1﹣c.(1)求A、B、C三点运动的速度;(2)若A、B两点分别从原点出发,向数轴正方向运动,C从表示+20的点出发同时向数轴的负方向运动,几秒后,C点恰好为AB的中点?(3)如图,若一把长16cm的直尺一端始终与C重合(另一端D在C的右边),且M、N分别为OD、OC的中点,在C点运动过程中,试问:MN的值是否变化?若变化,求出其取值范围;若不变,请求出其值.21.已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m﹣2n|=﹣(6﹣n)2.(1)求线段AB、CD的长;(2)M、N分别为线段AC、BD的中点,若BC=4,求MN;(3)当CD运动到某一时刻时,D点与B点重合,P是线段AB延长线上任意一点,下列两个结论:①是定值;②是定值,请选择正确的一个并加以证明.22.数轴上两个质点A、B所对应的数为﹣8、4,A、B两点各自以一定的速度在上运动,且A点的运动速度为2个单位/秒.(1)点A、B两点同时出发相向而行,在原点处相遇,求B点的运动速度;(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CB:CA=1:2,若干秒钟后,C停留在﹣10处,求此时B点的位置?23.如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.(1)问运动多少时BC=8(单位长度)?(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是_________;(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式=3,若存在,求线段PD的长;若不存在,请说明理由.参考答案1.如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是30.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?,×﹣;运动到或2.已知数轴上两个点A、B所对应的数为a、b,且a、b满足|a+3|+(b﹣4)2=0.(1)求AB的长;(2)若甲、乙分别从A、B两点同时在数轴上运动,甲的速度是2个单位/秒,乙的速度比甲的速度快3个单位/秒,(3)若点C对应的数为﹣1,在数轴上A点的左侧是否存在一点P,使PA+PB=3PC?若存在,求出点P所对应的数;若不存在,请说明理由.x=此时对应点为;﹣,故甲乙相遇点所表示的数为:3.已知数轴上点A,B,C所表示的数分别是x,﹣6,4.(1)线段BC的长为10,线段BC的中点D所表示的数是﹣1.(2)若AC=8,求x的值(3)在数轴上有两个动点P,Q,P的速度为1个单位长度/秒,Q的速度为2个单位/秒,点P,Q分别从点B,C 同时出发,在数轴上运动,则经过多少时间后P,Q两点相距4个单位?所表示的数是t=;、4.如图1,已知数轴上有三点A、B、C,AC=2AB,点A对应的数是400.(1)若AB=600,求点C到原点的距离;(2)在(1)的条件下,动点P、Q分别从C、A同时出发,其中P、Q向右运动,R向左运动如图2,已知点Q 的速度是点R速度2倍少5个单位长度/秒,点P的速度是点R的速度的3倍,经过20秒,点P、Q之间的距离与点Q、R的距离相等,求动点Q的速度.5.已知:数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x(1)若点P到点A、点B的距离相等,则点P对应的数为1.(2)若点P在A、B之间,请化简:|x+1|﹣|x﹣3|.(3)数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,请求出x的值;若不存在,请说明由.(4)当点P以每分钟1个单位长度的速度从O(原点)向左运动,同时,点A以每分钟5个单位长度的速度向左运动,点B以每分钟20个单位长度的速度向左运动.问它们同时出发,几分钟后点P到点A、点B的距离相等?;6.如图,数轴上有A、B、C、D四个点,分别对应的数是a、b、c、d,且满足|a+9|=1,b=a+2,(c﹣16)2与|d﹣20|互为相反数.(1)求a、b、c、d的值.(2)如果点M为A、B两点的中点,点N到点C有5个单位长,求M、N两点之间的距离.(3)若A、B两点以6个单位长度/秒的速度向右匀速运动,同时C、D两点以2个单位长度/秒向左匀速运动,并设运动时间为t秒,当点B运动到点D的右侧时,问是否存在时间t,使B与C的距离是A与D的距离的4倍?若存在,求时间t;若不存在,请说明理由.)或,<,t=,≤>;<,t=,满足<,t=>t=,满足>t=4t=,使7.如图1,数轴上E点表示的数是﹣10,Q点表示的数是20,P、F分别从Q、E点出发,沿箭头所示的方向运动,它们的速度都是5个单位长度/秒;它们的运动时间为t秒;(1)C为PF的中点,求C点表示的数,并用含t的式子表示F、P表示的数.(2)如图2,M是数轴上任意一点,线段PQ以P点的速度向左运动,点M以3个单位长度/秒的速度向右运动,点M在线段PQ上的时间为4秒,求线段PQ的长;(3)如图3,N是数轴上任意一点,线段EF、PQ在数轴上沿箭头所示的方向运动,它们的运动速度都是5个单位长度/秒,且EF=PQ,N向数轴正方向运动,已知N在线段PQ上的时间为6秒,N在线段EF上的时间为10秒,求PQ的长.8.已知数轴上顺次有A、B、C三点,分别表示数a、b、c,并且满足(a+12)2+|b+5|=0,b与c互为相反数.两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为3个单位/秒.(1)求A、B、C三点分别表示的数,并在数轴上表示A、B、C三点(2)运动多少秒时,甲、乙到点B的距离相等?(3)设点P在数轴上表示的数为x,且点P满足|x+12|+|x+5|+|x﹣5|=20,若甲运动到点P时立即调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.(不合题意舍去)+t.;(不合题意舍去)或﹣9.如图,数轴上点A、C对应的数分别为a,c,且a,c 满足|a+4|+(c﹣1)2014=0,点B对应的数为﹣3,(1)求数a,c;(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值;(3)在(2)的条件下,若点B运动到点C处后立即以原速返回,到达自己的出发点后停止运动,点A运动至点C处后又以原速返回,到达自己的出发点后又折返向点C运动,当点B停止运动时,点A随之停止运动,求在此运动过程中,A,B两点同时到达的点在数轴上表示的数.t=..,.在此,﹣10.已知:数轴上A.B两点表示的有理数为a、b,且(a﹣1)2+|b+2|=0.(1)A、B各表示哪一个有理数?(2)点C在数轴上表示的数是c,且与A、B两点的距离和为11,求多项式a(bc+3)﹣|c2﹣3(a﹣c2)|的值;(3)小蚂蚁甲以1个单位长度/秒的速度从点B出发向其左边6个单位长度处的一颗饭粒爬去,3秒后位于点A的小蚂蚁乙收到它的信号,以2个单位长度/秒的速度也迅速爬向饭粒,小蚂蚁甲到达后背着饭粒立即返回,与小蚂蚁乙在数轴上D点相遇,则点D表示的有理数是什么?从出发到此时,小蚂蚁甲共用去多少时间?c|c||×;11.如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=BC.(1)求点C表示的数;(2)若数轴上有一点P,且PC+PA=19,求点P表示的数;(3)有一条2个单位长度的青色毛毛虫从点C出发,以每秒0.5个单位长度的速度沿数轴正方向匀速运动到点A 时,绕点A处的木杆(不考虑绕木杆所用的时间)改变方向后始终沿数轴负方向匀速运动,速度保持不变.青色毛毛虫从点C出发的同时,一条3个单位长度的白色毛毛虫从点B出发,始终沿数轴正方向以每秒0.2个单位长度的速度匀速运动.求两条毛毛虫在第几秒时头头相遇?在第几秒时尾尾相遇?每次从相遇到相离经过了多长时间?AB=x=9(秒)=(秒)=,34+(秒)=12.已知A、B在数轴上对应的数分别用a、b 表示,且(ab+100)2+|a﹣20|=0.P是数轴上的一个动点(1)在数轴上标出A、B的位置,并求出A、B之间的距离;(2)数轴上一点C距A点24个单位长度,其对应的数c满足|ac|=﹣ac.当P点满足PB=2PC时,求P点对应的数;(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P移动到与A或B重合的位置吗?若能,请探究第几次移动是重合;若不能,请说明理由.13.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数﹣6,点P表示的数8﹣5t(用含t的代数式表示);(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.AP+BP==AB=14.如图,已知数轴上A、B两点所表示的数分别为﹣2和8.(1)求线段AB的长;(2)若P为射线BA上的一点(点P不与A、B两点重合),M为PA的中点,N为PB的中点,当点P在射线BA 上运动时,线段MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.(3)若有理数a、b、c在数轴上的位置如图所示:且d=|a+b|﹣|﹣2﹣b|﹣|a﹣2c|﹣5,试求7(d+2c)2+2(d+2c)﹣5(d+2c)2﹣3(d+2c)的值.AP+BPAP15.已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b﹣1)2=0,A、B之间距离记作|AB|,定义:|AB|=|a﹣b|.(Ⅰ)求线段AB的长|AB|;(Ⅱ)设点P在数轴上对应的数为x,当|PA|﹣|PB|=3时,求x的值;(Ⅲ)若点P在A的左侧,M、N分别是PA、PB的中点,当P在A的左侧移动时,下列两个结论:①|PM|+|PN|的值不变;②|PN|﹣|PM|的值不变,其中只有一个结论正确,请判断出正确结论,并求其值.(=|PM|=×16.如图1,点A、B分别在数轴原点O的左右两侧,且OA+50=OB,点B对应数是90.(1)求A点对应的数;(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离;(3)如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN 的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值.OA+50=OB,即OA+50=9017.点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0(1)求线段AB的长;(2)如图1 点C在数轴上对应的数为x,且x是方程2x+1=x﹣5的根,在数轴上是否存在点P使PA+PB=BC+AB?若存在,求出点P对应的数;若不存在,说明理由;(3)如图2,若P点是B点右侧一点,PA的中点为M,N为PB的三等分点且靠近于P点,当P在B的右侧运动时,有两个结论:①PM﹣BN的值不变;②PM+BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值PA+PB=PM=BN= BN②PM+2x+1=xBC+AB2|=PN=PB=BN=﹣××②PM+BN=××n(随BN18.如图1,已知数轴上两点A、B对应的数分别﹣1、3,点P为数轴上一动点,其对应的数为x.(1)数轴上是否存在点P,使P到点A、点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;(2)当点P以每分钟1个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度的速度向左运动,点B 以每分钟20个单位长度的速度向左运动,问它们同时出发,几分钟时间P点到点A、点B的距离相等?(3)若P从B点出发向左运动(只在线段AB上运动),M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你在图2中画出图形,并求出线段MN的长.;=,19.如图1,已知数轴上有三点A、B、C,AB=AC,点C对应的数是200.(1)若BC=300,求点A对应的数;(2)如图2,在(1)的条件下,动点P、Q分别从A、C两点同时出发向左运动,同时动点R从A点出发向右运动,点P、Q、R的速度分别为10单位长度每秒、5单位长度每秒、2单位长度每秒,点M为线段PR的中点,点N为线段RQ的中点,多少秒时恰好满足MR=4RN(不考虑点R与点Q相遇之后的情形);(3)如图3,在(1)的条件下,若点E、D对应的数分别为﹣800、0,动点P、Q分别从E、D两点同时出发向左运动,点P、Q的速度分别为10单位长度每秒、5单位长度每秒,点M为线段PQ的中点,点Q在从是点D运动到点A的过程中,QC﹣AM的值是否发生变化?若不变,求其值;若不变,请说明理由.AB=,进而得出y,得出﹣yAB=××=4×[600一半则是点为:y﹣AM=﹣20.已知:A、B、C为数轴上三个运动的点,速度分别为a个单位/秒、b个单位/秒和c个单位/秒(a、b、c为正整数),且满足|5﹣a|+(b﹣3)2=1﹣c.(1)求A、B、C三点运动的速度;(2)若A、B两点分别从原点出发,向数轴正方向运动,C从表示+20的点出发同时向数轴的负方向运动,几秒后,C点恰好为AB的中点?(3)如图,若一把长16cm的直尺一端始终与C重合(另一端D在C的右边),且M、N分别为OD、OC的中点,在C点运动过程中,试问:MN的值是否变化?若变化,求出其取值范围;若不变,请求出其值.3x+(OC=a OM=OD==8+MN=8+﹣21.附加题:已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m﹣2n|=﹣(6﹣n)2.(1)求线段AB、CD的长;(2)M、N分别为线段AC、BD的中点,若BC=4,求MN;(3)当CD运动到某一时刻时,D点与B点重合,P是线段AB延长线上任意一点,下列两个结论:①是定值;②是定值,请选择正确的一个并加以证明.AM=(BD=AM=(BD==2==2②是定值22.数轴上两个质点A、B所对应的数为﹣8、4,A、B两点各自以一定的速度在上运动,且A点的运动速度为2个单位/秒.(1)点A、B两点同时出发相向而行,在原点处相遇,求B点的运动速度;(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CB:CA=1:2,若干秒钟后,C停留在﹣10处,求此时B点的位置?=,,即:=,得,当=秒,的位置为.=,=,,处,所用时间为:=的位置为=.23.如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.(1)问运动多少时BC=8(单位长度)?(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是4或16;(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式=3,若存在,求线段PD的长;若不存在,请说明理由.)存在关系式=3时,点=3PC=,即t=PC=,即当t时,。
完整word版,七年级动点问题大全(给力)

七年级动点问题大全例 1 如图,在数轴上 A 点表示数 a,B 点表示数 b ,AB 表示 A 点和 B 点之间的距离,且a 、b 知足 |a+2|+ ( b+3a )2 =0(1)求 A 、B 两点之间的距离;(2)若在数轴上存在一点 C,且 AC=2BC ,求 C 点表示的数;( 3)若在原点O 处放一挡板,一小球甲从点 A 处以 1 个单位 /秒的速度向左运动;同时另一小球乙从点 B 处以 2 个单位 /秒的速度也向左运动,在碰到挡板后(忽视球的大小,可看作一点)以本来的速度向相反的方向运动,设运动的时间为t(秒),①分别表示甲、乙两小球到原点的距离(用t 表示);②求甲、乙两小球到原点的距离相等时经历的时间.例 3 动点 A 从原点出发向数轴负方向运动,同时,动点 B 也从原点出发向数轴正方向运动, 3 秒后,两点相距 15 个单位长度.已知动点 A 、B 的速度比是 1:4.(速度单位:单位长度 /秒)( 1)求出两个动点运动的速度,并在数轴上标出 A 、 B 两点从原点出发运动 3 秒时的地点;(2)若 A、 B 两点从( 1)中的地点同时向数轴负方向运动,几秒后原点恰巧处在两个动点正中间;( 3)在( 2)中 A 、 B 两点持续同时向数轴负方向运动时,另一动点 C 同时从B 点地点出发向 A 运动,当碰到 A 后,立刻返回向 B 点运动,碰到 B 点后立刻返回向 A 点运动,这样来回,直到 B 追上 A 时, C 立刻停止运动.若点 C 向来以 20 单位长度 /秒的速度匀速运动,那么点 C 从开始到停止运动,运动的行程是多少单位长度.例 2 如图,有一数轴原点为 O,点 A 所对应的数是 -1 2,点 A 沿数轴匀速平移经过例 4 已知数轴上两点 A 、 B 对应的数分别为 -1、 3,点 P 为数轴上一动点,其对应原点抵达点 B.的数为 x.(1)若点 P 到点 A,点 B 的距离相等,求点 P 对应的数;( 1)假如 OA=OB ,那么点 B 所对应的数是什么?( 2)从点 A 抵达点 B 所用时间是 3 秒,求该点的运动速度.( 2)数轴上能否存在点 P,使点 P 到点 A 、点 B 的距离之和为 6?若存在,恳求( 3)从点 A 沿数轴匀速平移经过点K 抵达点 C,所用时间是9 秒,且 KC=KA ,出 x 的值;若不存在,说明原因;分别求点 K 和点 C 所对应的数。
人教版七年级上册数学期末动点问题专题训练(含答案)

一、单选题
1.如图,数轴上一动点A向左移动4个单位长度到达点B,再向右移动1个单位长度到达点C,点C表示的数为-1,若将A,B,C三点表示的数进行混合运算(每个数只能用一次),则可得到最大数为()
A.9B.8C.6D.5
2.如图,数轴上的点O和点A分别表示0和10,点P是线段 上一动点.点P从点O出发沿 的方向以每秒2个单位的速度向A运动,B是线段 的中点,设点P运动时间为t秒(t不超过5秒).若点P在运动过程中,当 时,则运动时间t的值为______.
10.在数轴上点A所表示的数是-3,点B所表示的数为0,一个动点P从点B出发沿着数轴以每秒2个单位长度的速度运动,则3秒后点P到点A的距离为______个单位长度.
11.如图,在数轴上有A、B两个动点,O为坐标原点.点A、B从图中所示位置同时向数轴的负方向运动,A点运动速度为每秒2个单位长度,B点运动速度为每秒3个单位长度,当运动___________秒时,点O恰好为线段AB中点.
(2)点 为 的中点时, ______;
(3)当 时,求 的值.
参考答案:
1.A
2.D
3.C
4.B
5.D
6.D
7.B
8.D
9.3或13或1或
10.3或9
11.
12.2
13.
14. 秒或 秒或 秒或 秒
15.-328;
(2)M,N都向左运动,经过7秒或17秒时,点M、N两点间的距离为5个单位,M向左运动,N向右运动,经过1秒或 秒时,点M、N两点间的距离为5个单位.
(2)若点M以每秒4个单位的速度从A点出发,点N以每秒3个单位的速度运动从B点出发,设点M、N同时出发,运动时间为t秒,试探究:经过多少秒时,点M、N两点间的距离为5个单位?
完整版)七年级上期末动点问题专题(附答案)

完整版)七年级上期末动点问题专题(附答案)1.已知数轴上点A对应的数为a,点B对应的数为b,且满足|2b-6|+(a+1)^2=0,定义AB的长度为|a-b|。
1) 求线段AB的长度。
解:由定义可得,AB的长度为|a-b|。
2) 设点P在数轴上的坐标为x,且满足PA-PB=2,求x的值。
解:由题意得,PA-PB=|a-x|-|b-x|=2,分成两种情况讨论:当a>b时,有a-x-b+x=2,即a-b=2,解得x=a-1.当a<b时,有b-x-a+x=2,即b-a=2,解得x=b-1.综上所述,x的取值为a-1或b-1.3) 设M、N分别为PA、PB的中点,当P移动时,指出当下列结论分别成立时,x的取值范围,并说明理由:①PM÷PN的值不变,②|PM-PN|的值不变。
解:由题意得,M、N的坐标分别为[(a+x)/2,0]和[(b+x)/2,0],则① PM÷PN的值不变时,有|a-x|/|b-x|=|a-x0|/|b-x0|,其中x0是PM÷PN的值不变时的一个定值,化简得(a-x0)(b-x)=(b-x0)(a-x),即ax0-bx0=ax-bx0,解得x=(ax0-bx0+bx0)/2=a/2+b/2-x0/2.② |PM-PN|的值不变时,有[(a-x)/2-(b-x)/2]^2=K,其中K 是|PM-PN|的值不变时的一个定值,化简得(x-a+b)^2=4K,解得x=(a+b±2√K)/2.综上所述,当①成立时,x的取值为a/2+b/2-x0/2;当②成立时,x的取值为(a+b±2√K)/2.2.如图1,已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上的动点,其对应的数为x。
1) PA=|x-(-1)|=|x+1|,PB=|x-3|。
2) 若PA+PB=5,则有|x+1|+|x-3|=5,分成四种情况讨论:当x≤-1时,有-(x+1)-(x-3)=5,解得x=-2.当-1<x<3时,有-(x+1)+(x-3)=5,无解。
初一数学动点问题20题及答案

初一数学动点问题20题及答案数轴上动点问题1.已知:如图,数轴上点A表示的数为6,点B表示的数为2,点C表示的数为﹣8,动点P从点A出发,沿数轴向左运动,速度为每秒1个单位长度.点M为线段BC中点,点N为线段BP中点.设运动时间为t秒.(1)线段AC的长为__________个单位长度;点M表示的数为;(2)当t=5时,求线段MN的长度;(3)在整个运动过程中,求线段MN的长度.(用含t的式子表示).2.已知数轴上点A,B,C所表示的数分别是x,﹣6,4.(1)线段BC的长为_________,线段BC的中点D所表示的数是;(2)若AC=8,求x的值;(3)在数轴上有两个动点P,Q,P的速度为1个单位长度/秒,Q的速度为2个单位/秒,点P,Q分别从点B,C同时出发,在数轴上运动,则经过多少时间后P,Q两点相距4个单位?3.动点A、B同时从数轴上的原点出发向相反的方向运动,且A、B的速度之比是1:4(速度单位:长度单位/秒),3秒后,A、B两点相距15个单位长度.(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置.(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间?4.如图A、B两点在数轴上分别表示﹣10和20,动点P从点A出发以10个单位每秒的速度向右运动,动点Q从点B出发以每秒5个单位的速度出向右运动.设运动时间为t.(1)当点P运动到B点时,求出t的值;(2)当t为何值时,P、Q两点相遇,并求出此时P点对应的数?(3)在此运动过程中,若P、Q相距10个单位,直接写出运动时间t?5.已知a,b满足(a+2)2+|b﹣1|=0,请回答下列问题:(1)a=_______,b=_______;(2)a,b在数轴上对应的点分别为A,B,在所给的数轴上标出点A,点B;(3)若甲、乙两个动点分别从A,B两点同时出发沿x轴正方向运动,已知甲的速度为每秒2个单位长度,乙的速度为每秒1个单位长度,更多好题请进入:437600809,请问经过多少秒甲追上乙?6.在数轴上有A、B两动点,点A起始位置表示数为﹣3,点B起始位置表示数为12,点A的速度为1单位长度/秒,点B的运动速度是点A速度的二倍.(1)若点A、B同时沿数轴向左运动,多少秒后,点B与点A相距6单位长度?(2)若点A、点B同时沿数轴向左运动,是否有一个时刻,表示数﹣3的点是线段AB 的中点?如果有,求出运动时间;如果没有,说明理由.7.如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H 同时出发,问点P运动多少秒时追上点H?8.如图,数轴上的点A,B对应的数分别为﹣10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.(1)求线段AB的长;(2)直接用含t的式子分别表示数轴上的点P,Q对应的数;(3)当PQ=AB时,求t的值.9.如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O 出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B所表示的数______;当t=3时,OP=_______.(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R 同时出发,问点R运动多少秒时追上点P?10.如图.点A、点C是数轴上的两点,0是原点,0A=6,5AO=3CO.(1)写出数轴上点A、点C表示的数;(2)点P、Q分别从A、C同时出发,点P以每秒1个单位长度的速度沿数轴向右匀速运动,点Q以每4个单位长度的速度沿数轴向左匀速运动,问运动多少秒后,这两个动点到原点O的距离存在2倍关系?11.已知数轴上两点A,B对应的数分别为﹣1,3,P为数轴上的动点,其对应的数为x.(1)数轴上是否存在点P,使P到点A、点B的之和为5?若存在,请求出x的值;若不存在,说明理由;(2)当点P以每分钟1个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度的速度向左运动,点B以每分钟20个单位长度的速度向左运动.问,它们同时出发几分钟时点P到点A、点B的距离相等?12.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如下.(1)根据题意,填写下列表格;(2)A、B两点能否相遇?如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.13.如图1,点A,B是在数轴上对应的数字分别为﹣12和4,动点P和Q分别从A,B 两点同时出发向右运动,点P的速度是5个单位/秒,点Q的速度是2个单位/秒,设运动时间为t秒.(1)AB=.(2)当点P在线段BQ上时(如图2):①BP=______________(用含t的代数式表示);②当P点为BQ中点时,求t的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级“动点问题”专项练习
1、已知点 A 在数轴上对应的数为 a,点 B 对应的数为 b,且
|2b﹣6|+(a+1)2=0,A、B 之间的距离记作 AB,定义:AB=|a﹣b|.
(1)求线段 AB 的长.
(2)设点 P 在数轴上对应的数 x,当 PA﹣PB=2 时,求 x 的值.
(3)M、N 分别是 PA、PB 的中点,当 P 移动时,指出当下列结论分别成立时,x
的取值范围,并说明理由:①PM
PN
的值不变,②|PM﹣PN|的值不变.
2、如图 1,已知数轴上两点 A、B 对应的数分别为-1、3,点 P 为数轴上的
一动点,其对应的数为 x.
(1)PA=______________;PB=_____________(用含 x 的式子表示).
(2)在数轴上是否存在点 P,使 PA+PB=5?若存在,请求出 x 的值;若不存在,请说明理由.
(3)如图 2,点 P 以每秒 1 个单位的速度从点 D 向右运动,同时点 A 以每秒 5 个单位的速度向左运动,点 B 以每秒 20 个单位的速度向右运动,在运动过程中,M、N 分别是 AP、OB 的中点,问:的值是否发生变化?请说明理由.
3、如图,已知 A(﹣4,3)、B(﹣1,3)、C(﹣2,1),△ABC 中任意一 P(x0,y0)点平移后对应的点为 P1(x0+2,y0﹣1),将△ABC 作同样的平移得到△A1B1C1.
(1)画出△A
1B
1
C
1
.
(2)直接写出 A
1、B
1
、C
1
的坐标.
(3)在坐标轴上是否存在点 P,使△PB1C1的面积等于△ABC 的面积?若存在,求出点的坐标;若不存在,说明理由.
4、如图,在平面直角坐标系中,长方形 ABCD 的边BC∥x 轴.如果 A 点坐标是(),C 点坐标是(3,﹣).
(1)求 B 点和 D 点的坐标;
(2)将这个长方形向下平移个单位长度,四个顶点的坐标变为多少?请你写出平移后四个顶点的坐标;(3)如果 Q 点以每秒米的速度在长方形ABCD 的边上从 A 出发到 C 点停止,
沿着A→D→C 的路径运动,那么当 Q 点的运动时间分别是 1 秒、4 秒和 6 秒时,△BCQ 的面积各是多少?请你分别求出来.
5、长方形 ABCD 在平面直角坐标系中,点 A(1,8),B(1,6),C(7,6).(1)请直接写出 D 点的坐标______.
(2)连接线段 OB、OD、BD,请直接求出△OBD 的面积______.
(3)若长方形 ABCD 以每秒 1 个单位的速度向下运动,设运动的时间为 t 秒,问是否存在某一时刻,△OBD 的面积与长方形 ABCD 的面积相等?若存在,请求出 t
的值;若不存在,请说明理由.
6、如图,在平面直角坐标系中,A (a,0),B(0,b),且a、b满足
,点C、B关于x轴对称.
(1)求A、B、C两点坐标;
(2)点M为射线OA上A点右侧一动点,过点M作MN⊥CM交直线AB于N,连
BM,是否存在点M,使?若存在,求M点坐标;若不存在,说明理由.
(3)点P为第二象限角平分线上一动点,将射线BP绕B点逆时针旋转30°交x轴于点Q,连PQ,在点P运动过程中,当∠BPQ =45°时,求BQ的长.
7.在平面直角坐标系中,四边形ABCD是长方形, AB∥CD,AB=CD=8cm,
AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标.
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q 从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P、Q两点同时出发,当P到达点B时,P、Q同时停止,在此运动过程中,线段AQ,PC会将四边形ABCD分割成三部分,设运动时间为t秒,当t为何值时,其中有两部分面积相等?
(3)试问四边形AQCP面积能否达到57,若能,求出此时Q点坐标;若不能,请说明理由。
8.已知:在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°AB ∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标.
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q 从点C出发以每秒4个单位长度的速度I沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥BC?
(3)在Q的运动过程中,当Q运动到什么位置时,使△ADQ的面积为9? 求出此时Q点的坐标.
9.如图A(-4,0),B(6,0),C(2,4),D(-3,2).
10.(1)求四边形ABCD的面积;
11.(2)在y轴上找一点P,使△APB的面积等于四边形的一半.求P点坐标.。
