六年级数学阴影部分面积
小学六年级数学求阴影面积与周长
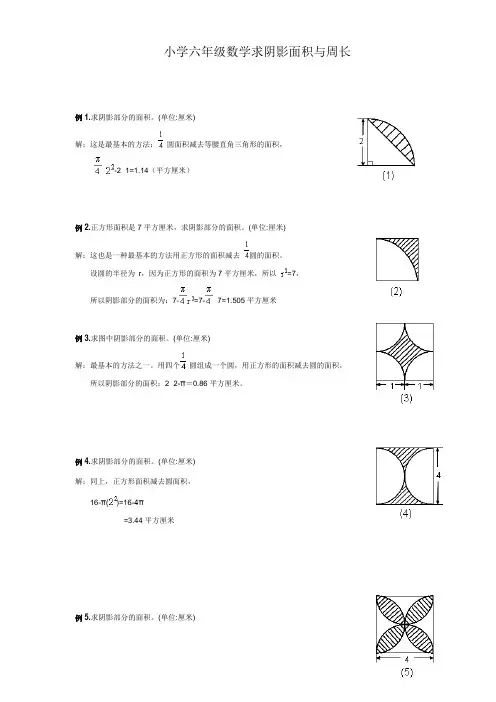
小学六年级数学求阴影面积与周长例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
阴影面积公式六年级知识点
阴影面积公式六年级知识点阴影面积公式是六年级数学中的一个重要知识点。
在学习这个知识点之前，我们首先需要了解什么是阴影面积以及如何计算阴影面积。
阴影面积是指光线照射在物体上产生的阴影部分所覆盖的面积。
它在日常生活中的应用非常广泛，比如我们可以利用阴影面积来计算建筑物在不同时间段内的阳光照射程度，或者推算出日晷和太阳光的夹角等。
在计算阴影面积时，我们可以使用不同的公式来适应不同的几何形状。
下面，我将为大家介绍几种常见的阴影面积公式。
一、矩形形状的阴影面积公式对于一个矩形的阴影面积，我们可以使用以下公式进行计算：阴影面积 = 阴影的长度 ×矩形的宽度其中，阴影的长度是指光线在物体上形成的影子部分的长度，矩形的宽度是阴影部分所投射物体的宽度。
二、三角形形状的阴影面积公式对于一个三角形的阴影面积，我们可以使用以下公式进行计算：阴影面积 = 阴影的长度 ×三角形的底边长度 ÷ 2与矩形不同的是，三角形的阴影面积需要先计算出底边的长度，然后乘以阴影的长度，最后再除以2。
三、圆形形状的阴影面积公式对于一个圆形的阴影面积，我们可以使用以下公式进行计算：阴影面积 = 阴影的长度 ×圆的周长 ÷ 2同样地，圆形的阴影面积需要结合阴影的长度和圆的周长进行计算。
需要注意的是，圆的周长可以通过直径乘以π来计算。
除了上述几种常见的几何形状，阴影面积的计算方法还可以应用于更多的形状，比如梯形、多边形等。
对于不同形状的阴影面积计算，我们需要根据实际情况来选择合适的公式进行计算。
阴影面积的计算涉及到对几何形状的理解和运用，对于六年级的学生来说，需要通过多次的练习和实际问题的应用来巩固和加深对阴影面积公式的理解。
总结一下，阴影面积公式是六年级数学中的一个重要知识点。
通过学习和掌握不同几何形状的阴影面积公式，我们可以更好地理解和应用阴影面积的概念，解决实际问题。
希望同学们在学习过程中能够认真思考和练习，掌握好这一知识点。
人教版六年级上册数学 求阴影部分的面积
判断对错：
（2）两个圆的周长相等，面
积也一定相等。
（√ ）
判断对错：
（3）圆的半径越大，圆所占
的面积也越大。
（√ ）
判断对错： （4）圆的半径扩大3倍，它
× 的面积扩大6倍。 （ ）
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
判断：
（1）下图哪个是圆环？
·
·
·
图1
图2
图3
×
√
×
9cm 3cm
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
思考： 计算圆环的面积需要知道哪些 条件呢？
外圆和内圆的半径
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
光盘的银色部分是一个圆环，内圆 半径是3cm，外圆半径是9cm。它 的面积是多少？
3.14×（92 －32） =3.14 ×72 =226.08（cm2）
答：它的面积是226.08 cm2。
一个圆形金鱼池的半径是8米，周 围有一条2米宽的小路（如图）。 这条小路的占地面积是多少平方米？
8+2＝10(m)
3.14×（102 －82）
=3.14 ×36
=113.04（m2）
2m
8m
答：它的面积是113.04 m2。
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
人 教 版 六 年 级上册 数学 求 阴 影部 分的面 积
小学六年级数学求阴影部份面积
小学六年级（求阴影部份面积练习题）1.求阴影部份面积(单位：cm)。
解：阴影部份的面积=正方形的面积-两个空白的面积；一个空白的面积=正方形的面积-半径为2的14圆面积；S阴=S正-2×S空×3.14×22）=2×2−2×（2×2−14=4−2×（4−3.14）=4−1.72=2.28cm22.求阴影部份面积(单位：cm)。
解：作辅助线如下图所示，空白①与阴影②的面积相等，所以：阴影部份的面积=边长为10的正方形面积。
S阴=S正=10×10=100cm23.求阴影部份面积(单位：cm)。
解：阴影部份的面积=两个阴影三角形的面积之和。
S阴=S左阴影三角形+ S右阴影三角形=1 2×10×6+12×6×6=30+18=48cm24.求阴影部份面积(单位：cm)。
解：阴影部份的面积=边长为10的正方形面积-空白部份的面积，经观察发现：空白部份可组合成一个直径为10的圆。
空白部份的面积=直径为10的圆面积。
S阴=S正方形- S直径为10的圆=10×10−12×3.14×52=100−39.25=60.75cm25. 求阴影部份面积(单位：cm)。
解：作辅助线如下图所示，阴影部份的面积=S甲+S乙+S丙+S丁。
观察发现，S 甲+S丁=直径为6的半圆的面积，恰好与空白半圆的面积一样。
所以阴影部分的面积=长为6、宽为3的长方形的面积。
S阴= 6×3=18cm26. 求阴影部份面积(单位：cm)。
解：作辅助线如下图所示，将阴影部份分成相等的四部分，阴影部份的面积=4×S②。
S②=半径为2的1圆面积-边长为2的直角等腰三4角形的面积S阴=4×S②=4×（14×3.14×22−12×2×2）=4×（3.14−2）=2.28cm27. 求阴影部份面积(单位：cm)。
六年级数学计算阴影部分的面积
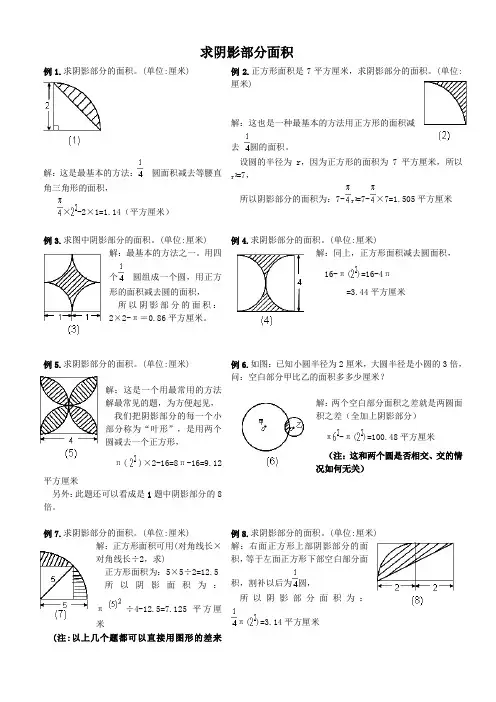
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来例8.求阴影部分的面积。
(单位:厘米) 解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米求,无需割、补、增、减变形)例9.求阴影部分的面积。
小学六年级数学之圆-阴影部分面积(含答案)
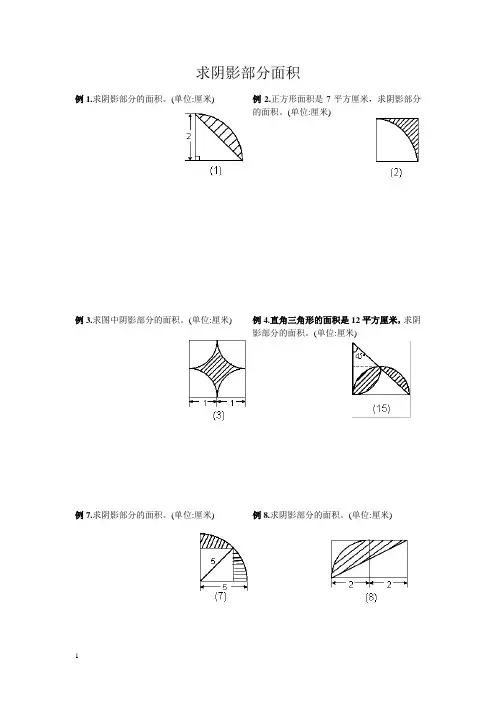
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.直角三角形的面积是12平方厘米，求阴影部分的面积。
(单位:厘米)例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解：同上，平移左右两部分至中间部分，则合成一个长方形，所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
(单位:厘米)解：这种图形称为环形，可以用两个同心圆的面积差或差的一部分来求。
（π-π）×=×3.14=3.66平方厘米例12.求阴影部分的面积。
(单位:厘米)解：三个部分拼成一个半圆面积．π()÷２＝14.13平方厘米例13.求阴影部分的面积。
(单位:厘米)解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为：8×8÷2=32平方厘米例14.求阴影部分的面积。
(单位:厘米)解：梯形面积减去圆面积，(4+10)×4-π=28-4π=15.44平方厘米.例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)解：［π＋π－π］=π(116-36)=40π=125.6平方厘米例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)解：上面的阴影部分以AB为轴翻转后，整个阴影部分成为梯形减去直角三角形，或两个小直角三角形AED、BCD面积和。
所以阴影部分面积为：5×5÷2+5×10÷2=37.5平方厘米例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
六年级数学计算阴影部分的面积
计算阴影部分的面积需要了解阴影是如何形成的以及数学中用到的相关知识。
在计算阴影面积时可以采用以下步骤：1.确定阴影的形状：阴影可以有多种形状，例如矩形、三角形、圆形等。
在计算阴影面积之前，首先要确定阴影的形状，以便选择合适的计算公式。
2.确定阴影的尺寸：测量阴影的尺寸是计算阴影面积的前提。
尺寸可以通过用尺子或者其他测量工具进行测量得到。
确保测量的准确性对于计算阴影面积非常重要。
3.选择合适的计算公式：根据阴影的形状选择合适的计算公式。
以下是常见的几种阴影形状及其对应的计算公式：a.矩形阴影的面积计算：阴影的面积等于其长度乘以宽度，即A=l*w。
b.三角形阴影的面积计算：阴影的面积等于底边乘以高度再除以2，即A=(b*h)/2c.圆形阴影的面积计算：阴影的面积等于圆的面积减去半圆的面积，即A=π*r^2-π*r^2/2=π*r^2/24.进行计算：根据选择的计算公式，将测量得到的尺寸代入计算公式中进行计算。
确保计算的准确性，并注意单位的一致性。
下面通过几个例子具体说明如何计算阴影部分的面积：例一：计算矩形阴影的面积假设一个矩形的长度为10cm，宽度为5cm，我们要计算其阴影的面积。
解：根据矩形阴影的面积计算公式A = l * w，代入已知的尺寸，得到A= 10cm * 5cm = 50cm²。
所以矩形阴影的面积为50cm²。
例二：计算三角形阴影的面积假设一个三角形的底边长度为6cm，高度为8cm，我们要计算其阴影的面积。
解：根据三角形阴影的面积计算公式 A = (b * h) / 2，代入已知的尺寸，得到A = (6cm * 8cm) / 2 = 24cm²。
所以三角形阴影的面积为24cm²。
例三：计算圆形阴影的面积假设一个圆的半径为5cm，我们要计算其阴影的面积。
解：根据圆形阴影的面积计算公式 A = π * r^2 / 2，代入已知的尺寸，得到A = π * 5cm^2 / 2 ≈ 7.85cm²。
六年级上第6讲阴影部分面积
六年级上第6讲阴影部分面积在六年级的数学学习中，计算阴影部分的面积是一个常见且重要的知识点。
这不仅考验着我们对基本图形面积公式的掌握，还锻炼着我们的空间想象力和逻辑思维能力。
让我们先来回顾一下常见的基本图形面积公式。
对于长方形，面积等于长乘以宽；正方形的面积则是边长的平方；三角形的面积是底乘以高再除以 2；平行四边形的面积是底乘以高；梯形的面积是（上底＋下底）乘以高除以 2。
当我们面对复杂的图形，其中包含阴影部分时，往往需要运用这些基本公式，通过巧妙的方法来求解。
比如说，有一种常见的题型是两个或多个基本图形重叠，形成阴影部分。
我们可以先分别算出各个基本图形的面积，然后通过加减运算得出阴影部分的面积。
举个例子，有一个长方形，长为 8 厘米，宽为 6 厘米。
在这个长方形内部，有一个直径为 6 厘米的半圆。
求半圆与长方形重叠部分之外的阴影面积。
首先，长方形的面积为 8×6 ＝ 48 平方厘米。
半圆的半径为 3 厘米，其面积为1/2×π×3² ≈ 1413 平方厘米。
然后，用长方形的面积减去半圆的面积，就能得到阴影部分的面积：48 1413 ＝ 3387 平方厘米。
还有一种情况，是一个图形中包含另一个图形，通过整体减去部分的方法来求阴影面积。
比如，有一个边长为 10 厘米的正方形，在其内部有一个半径为 5厘米的圆。
求正方形中圆之外的阴影部分面积。
正方形的面积为 10×10 ＝ 100 平方厘米。
圆的面积为π×5² ≈ 785 平方厘米。
那么阴影部分的面积就是 100 785 ＝ 215 平方厘米。
有时候，图形会更加复杂，需要我们进行一些转换和变形。
例如，有一个直角三角形，两条直角边分别为 6 厘米和 8 厘米。
以斜边为直径作一个半圆，求半圆内三角形之外的阴影部分面积。
首先，根据勾股定理算出斜边的长度为 10 厘米，所以半圆的半径为 5 厘米。
六年级上册数学阴影部分的题型
六年级上册数学阴影部分的题型一、求阴影部分面积（规则图形组合）1. 题目：在一个长方形中，长为8厘米，宽为6厘米，在长方形内部有一个最大的半圆，求除半圆外阴影部分的面积。
解析：长方形的面积 = 长×宽，即公式平方厘米。
因为长方形内最大的半圆，这个半圆的直径应该等于长方形的长公式厘米，所以半径公式厘米。
半圆的面积=公式平方厘米。
那么阴影部分面积 = 长方形面积半圆面积，即公式平方厘米。
2. 题目：正方形的边长为10厘米，以正方形的边长为直径在正方形内部画四个半圆，求阴影部分面积。
解析：把阴影部分进行拼接，可以发现阴影部分的面积等于正方形的面积减去中间空白部分（正方形减去四个半圆的重叠部分）。
正方形面积 = 边长×边长=公式平方厘米。
一个半圆的半径公式厘米，一个半圆的面积=公式平方厘米。
四个半圆的面积之和为公式平方厘米。
四个半圆重叠部分（中间空白部分）的面积计算：四个半圆的面积之和比正方形面积多了中间重叠部分的面积。
所以中间重叠部分（空白部分）面积 = 公式平方厘米。
阴影部分面积 = 正方形面积空白部分面积=公式平方厘米。
二、求阴影部分面积（利用割补法）1. 题目：有一个等腰直角三角形，直角边为8厘米，在这个三角形内有一个扇形（圆心角为公式），求阴影部分面积。
解析：等腰直角三角形的面积=公式平方厘米。
因为扇形的圆心角为公式，整个圆是公式，所以这个扇形的面积占所在圆面积的公式。
以等腰直角三角形的直角边为半径的圆的面积=公式平方厘米。
扇形面积=公式平方厘米。
阴影部分面积 = 等腰直角三角形面积扇形面积，即公式平方厘米。
2. 题目：在一个半径为6厘米的圆中，有一个圆心角为公式的扇形，将扇形的两条半径和弧所围成的部分剪去，剩余部分为阴影部分，求阴影部分面积。
解析：圆的面积=公式平方厘米。
扇形面积占圆面积的比例为公式。
扇形面积=公式平方厘米。
阴影部分面积 = 圆的面积扇形面积，即公式平方厘米。
六年级上册数学课件-《阴影部分面积》课件 (共15张PPT)人教版
3、求阴影部分面积。 10cm
5cm
4、求阴影部分面积。 8cm
4பைடு நூலகம்求阴影部分面积。
（1）
（2）
（3（）4）
（（4）3）
（2）
8cm
（1）
6. 生气，就是拿别人的过错来惩罚自己。原谅别人，就是善待自己。 8. 好习惯成就一生，坏习惯毁人前程。 18. 有事者，事竟成;破釜沉舟，百二秦关终归楚;苦心人，天不负;卧薪尝胆，三千越甲可吞吴。 17. 成功是什么?就是走过了所有通向失败的路，只剩下一条路，那就是成功的路。 17. 只要相信，就有可能 5. 有勇气并不表示恐惧不存在，而是敢面对恐惧克服恐惧。 12. 成功的法则极为简单，但简单并不代表容易。 9. 叹气是最浪费时间的事情，哭泣是最浪费力气的行径。 7. 一个人几乎可以在任何他怀有无限热忱的事情上成功。 11. 把自己当傻瓜，不懂就问，你会学的更多。 3. 崇高的理想就像生长在高山上的鲜花。如果要搞下它，勤奋才能是攀登的绳索。 12. 自己打败自己是最可悲的失败，自己战胜自己是最可贵的胜利。 19. 宁可辛苦一阵子，不要苦一辈子。 15. 体验自然是财富。风是一副透明的锦缎，雨是无数晶莹的珍珠，森林宛如翠绿的刺绣，而海湾湖泊则是湛蓝的宝石。 13. 失去金钱的人损失甚少，失去健康的人损失极多，失去勇气的人损失一切。 19. 凡事不要说“我不会”或“不可能”，因为你根本还没有去做! 15. 心灵激情不在，就可能被打败。 15. 一个人除非自己有信心，否则带给别人信心。1. 人要在挫折中成长，就在一次次失败中也逐渐明白，前面的路途将会更加的坚难，等着自 己的将会是各种的困难与挫折，要想不被它们打倒，那只有打倒它们。
请用一句话说一说下图中阴影部分面积 怎么求
8m
六年级上册数学期末必考《求阴影部分面积》
六年级上册数学期末必考：求阴影部分面积1、求阴影部分面积（单位：厘米）解：用割补法如图梯形上底DE=7-4=3（厘米）S阴影部分=S梯形=1/2（3+7）×4=20（平方厘米）2、求阴影部分面积（单位：厘米）解：S阴影部分=S梯形1/2×（2+4）×2=6（平方厘米）3、求阴影部分面积（单位：厘米）解：半圆的半径= 梯形的高=4÷2=2 厘米，S阴=S梯形-S半圆=(4+6) ×2 ÷2-3.14 ×2²÷2=10-6.28=3.72（cm²）4、下图是一个半圆形，已知AB=10厘米，阴影部分的面积为24.25平方厘米，求图形中三角形的高。
解：S三角形=S半圆-S阴影=1/2×π×（AB÷2）²-24.25=1/2×3.14×（10÷2）²-24.25=15（平方厘米）三角形的高：2S÷AB=2×15÷10=3（厘米）5、如图，已知半圆的面积是31.4 平方厘米，求长方形的面积。
解：S 半圆=31.4平方厘米圆的半径²=2×S半圆÷π=2×31.4÷3.14=20长方形的宽为r，长为2r，所以长方形的面积=r ×2r=2r²=2×20=40（cm²）。
6、求下图中阴影部分的面积和周长。
（单位：厘米）S阴=S正-S半圆=2²-1/2×π×（2÷2）²=2.43（dm²）C阴=3/4C正+C半圆=3×2+1/2×π×2=9.14（dm²）7、求阴影部分面积（单位：厘米）解：空白三角形是一个等腰直角三角形，且腰等于圆的半径，为3 cm 。
六年级上册数学 求阴影部分的面积简单技巧
六年级上册数学求阴影部分的面积简单技巧
求阴影部分的面积是一个常见的数学问题，对于六年级的学生来说，掌握一些简单的技巧是非常有帮助的。
1. 观察图形：首先，你需要仔细观察阴影部分的形状。
这可以帮助你确定使用哪种数学公式来求解。
2. 选择合适的公式：根据阴影部分的形状，选择合适的面积公式。
例如，如果阴影是一个矩形，你可以使用长×宽来计算面积；如果阴影是一个圆，你可以使用π×r^2来计算面积。
3. 减去其他部分的面积：如果阴影部分是由几个图形组成的，你可能需要先计算所有图形的面积，然后从总面积中减去其他部分的面积。
4. 利用对称性：如果图形是对称的，你可以只计算一半的面积，然后再乘以2。
5. 注意单位：确保所有的测量值都有相同的单位，这样你就可以正确地计算面积。
6. 检查答案：最后，检查你的答案是否合理。
你可以通过将答案代回原问题来验证答案是否正确。
下面是一个具体的例子：
假设你有一个长方形，长为8cm，宽为4cm，并且你知道其中有一个阴影部分。
这个阴影部分是一个正方形，边长为3cm。
首先，你可以计算长方形的总面积：8cm × 4cm = 32cm^2。
然后，你可以计算阴影部分的面积：3cm × 3cm = 9cm^2。
最后，你可以从长方形的总面积中减去阴影部分的面积：32cm^2 - 9cm^2 = 23cm^2。
所以，阴影部分的面积是23cm^2。
小学六年级数学求阴影部分面积(圆)-阴影部分面积(六年级)
计算图19-1中阴影部分面积是多少平方厘米？（圆的半径r=10厘米，∏取3.14）分析：要计算图19-1中阴影部分的面积，关键在于处理图中空白部分的面积。
利用割补进行转化，把空白部分转移到圆的边缘。
如图19-2所示，这样阴影部分面积就可以转化为41圆面积加上两个正方形的面积来计算。
解 ∏×102×41+102×2=25∏+200=78.5+200=278.5图19-3大小两圆相交部分面积是大圆面积的154，是小圆面积的53，量得小圆的半径是5厘米，问大圆的半径是多少厘米？分析：因为已知阴影部分与大圆，小圆的面积比，所以可以先求出两圆面积的比，继而求出它们的半径比。
，解 设阴影部分的面积为1.则小圆面积是415，小圆面积是35。
于是： 大圆面积：小圆面积=415：35=49=（23）2 5×23=7.5厘米如图19-4，正方形面积是8平方厘米。
求阴影部分的面积是多少平方厘米？分析：这道题按常规思路是：要求阴影部分的面积，用正方形的面积减去一个四分之一圆的面积。
因此，只要知道圆的半径，问题就得到解决了。
但是，从题中的已知条件知道，圆的半径是不可能求出的，问题难以得解。
这时，就必须改变解题思路，重新审题和分析图形，从图中不难看到，正方形的边长等于圆的半径，进而可以推出a ×a=r ×r=8平方厘米。
所以，在求四分之一圆的面积时，就不必按常规的方法，去求解圆的半径，而直接用8平方厘米代替r ×r 的面积，四分之一圆的面积是3.14×8×41=6.28平方厘米，则阴影部分的面积就是8-3.14×8×41=1.72平方厘米。
如图19-7，求空白部分的面积是正方形面积的几分之几？分析：因为圆和正方形它们的对称性，可以先画出两条辅助线帮助分析，即将正方形分成4个全等的小正方形。
先看上面的两个小正方形，从圆中可知，A=B ，C=D 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
六年级数学阴影部分面积1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。
③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。
的半径是3cm，求阴影部分的周长和面积。
（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积
小48平方厘米，
①比阴影②面积少3cm2，求EC的长。
AB=40cm，求BC的长。
⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD
的1/3，求三角形AEF的面积。