九年级上册数学第3章图形的相似单元测试题(湘教版含答案)
第一学期湘教版九年级上册数学第3章《图形的相似》单元测试卷(有答案)

第一学期湘教版九年级上册数学第3章《图形的相似》单元测试卷(有答案)一、填空题〔共10 小题,每题 3 分,共30 分〕1.如图,在Rt△ABC中,∠C=90∘,CD⊥AB于D.假定AD=2cm,DB=6cm,那么CD=________.2.如图,在△ABC中,D是AB边上一点,衔接CD,要使△ADC与△ABC相似,应添加的条件是________.3.两个位似图形的位似比为2:1,那么这两个位似图形的面积比为________.4.如图,在△ABC中,DE // BC,假定AD=1,DE=2,BD=3,那么BC=________.5.P是线段AB上一点,且APPB =25,那么APAB=________.6.如图,在△ABC中,D、E两点区分在边BC、AC上,AE:EC=CD:BD=1:2,AD与BE相交于点F,假定△ABC的面积为21,那么△ABF的面积为________.7.如图,在梯形ABCD中,AD // BC,AC平分∠BCD,∠BAC=∠D,假定AD=4,BC=10,那么AC=________.8.在同一时辰物高与影长成比例,小莉量得综合楼的影长为6米,同一时辰他量得身高1.6米的同窗的影长为0.6米,那么综合楼高为________米.9.如图是圆桌正上方的灯泡O收回的光线照射桌面后,在空中上构成阴影〔圆形〕的表示图.桌面的直径为1.2m,桌面距离空中1m,假定灯泡O距离空中3m,那么空中上阴影局部的面积为________m2.10.假定两个相似三角形的面积之比为1:16,那么它们的周长之比为________.二、选择题〔共10 小题,每题 3 分,共30 分〕11.ab+c =bc+a=cb+a=k,那么k的取值为〔〕A.1 2B.−1C.12或−1 D.−12或−112.下面四组线段中不能成比例线段的是〔〕A.3、6、2、4B.4、6、5、10C.1、√2、√3、√6D.2√5、√15、4、2√313.△ABC∽△DEF,假定对应边AB:DE=1:2,那么它们的周长比等于〔〕A.1:2B.1:4C.2:1D.4:114.如图,在三角形ABC中,E,F区分是AB,AC边上的点,且有EF // BC,假设EBAB =45,那么ACFC=()A.9 4B.59C.54D.9515.如下图,顶角为36∘的等腰三角形,其底边与腰之比等于k,这样的三角形叫做黄金三角形.AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为〔〕A.k2012B.k2013C.k2013(2+k)D.k20132+k16.如图,在△ABC中,点D在AB上,在以下四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD⋅AB;④AB⋅CD=AD⋅CB,能满足△ADC与△ACB相似的条件是〔〕A.①、②、③B.①、③、④C.②、③、④D.①、②、④17.如图,直线a // b // c,直线m、n与a、b、c区分交于点A、C、E和B、D、F,假定AC=4,AE=10,BF=152,那么DF的长为〔〕A.9 2B.10C.3D.7218.如图,直角梯形ABCD中,AB // CD,∠C=90∘,∠BDA=90∘,AB=a,BD=b,CD=c,BC=d,AD=e,那么以上等式成立的是〔〕A.b2=acB.b2=ceC.be=acD.bd=ae19.假定两个相似三角形的面积之比为a:b,那么它们的周长之比为〔〕A.a2:b2B.a:bC.√a:√bD.无法确定20.△ABC与△DEF的相似比为1:4,那么△DEF与△ABC的相似比为〔〕A.1:2B.1:3C.4:1D.1:16三、解答题〔共6 小题,每题10 分,共60 分〕21.如图,在△ABC中,∠ACB=90∘,CD⊥AB于点D,AC=6√3,BD=3.(1)求∠A的度数;(2)求BC的长及△ABC的面积.22.如图,在△ABC中,D为AC边上一点,∠DBC=∠A.(1)求证:△ACD∽△ABC;(2)假设BC=√6,AC=3,求CD的长.23.路边有两根相距4m的电线杆AB,CD,区分在高为3m的A处和高为6m的C处用铁丝将两电线杆固定(1)求铁丝AD与铁丝BC的交点M离空中的高度MH;(2)假定电线杆AB与CD的长区分为a,b,请猜想高度MH与a,b间的关系.24.小明想测量在太阳光下一栋楼高,他设计了一种测量方案如下:如图,小明站到点E处时,刚好使自己落在墙上的影子与这栋楼落在墙上的影子堆叠,且高度恰恰相反.此时,小明测得落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m〔点A、E、C在同不时线上〕,小明的身高EF是1.7m,请你帮小明求出楼高AB〔结果准确到0.1m〕.25.如图,小明站在竖立的电线杆AB前D处时的影子长为3m,他向电线杆走了4m抵达E处时的影子长为1m.假定小明的身高为1.8m.(1)求电线杆的长;(2)找出△ABF的位似图形,并指出位似中心.26.如图,:△ABC中,M为BC边的中点,O为AM上一点,BO的延伸线交AC于点D,CO延伸线交AB于点E,PQ // BC,且PQ过点O与AB、AC区分交于P和点Q,求证:(1)PO=OQ;(2)DE // BC.答案1.2√3cm2.∠ACD=∠B,∠ADC=∠ACB,ADAC =ACAB3.4:14.85.276.67.2√108.169.0.81π10.1:411-20:CBACC AAACC21.解:(1)∵∠ACB=90∘,CD⊥AB于点D,∴AC2=AD⋅AB,即(6√3)2=AD⋅(AD+3),整理得AD2+3AD−108=0,解得AD=9或AD=−12〔舍去〕,在Rt△ACD中,∵cosA=ADAC =6√3=√32,∴∠A=30∘;(2)∵AB=AD+BD=9+3=12,而∠A=30∘,∴BC=12AB=6,∴S△ABC=12⋅AC⋅BC=12⋅6√3⋅6=18√3.22.(1)证明:∵∠DBC=∠A,∠C=∠C,∴△ACD∽△ABC;(2)解:∵△ACD∽△ABC,∴BCAC =CDBC,∴√63=6,∴CD=2.23.铁丝AD与铁丝BC的交点M离空中的高度MH为2m;(2)猜想:MH=a2b.∵AB // CD,∴△ABM∽△DCM,∴ABCD =ab,∵MH // AB,∴△MDH∽△ADB,∴MHAB =DHBD=ab,即MHa=ab,∴MH=a2b.24.楼高AB约为20.0米.25.解:(1)在△ABF和△HEF中.∠B=∠HEF=90∘,∠BFA=∠EFH,那么△ABF∽△HEF,∴ABHE =BFEF,即ABHE =BE+11①,在△ABC和△GDC中,∠B=∠GDC=90∘,∠C=∠C,那么△ABC∽△GDC,∴ABGD =BCDC,即ABGD =BE+4+33②,而HE=GD③,由①、②、③可得BE+1=BE+73,解得BE=2.把BE=2代入①中,得AB=(2+1)HE=1.8×3=5.4(m);(2)△ABF的位似图形是△HEF.位似中心是点F.说明:以上各题假定用其它做法可参照此规范评分.26.证明:(1)∵PQ // BC,PO // BM,OQ // MC,∴PO:MB=AO:AM,OQ:MC=AO:AM,∴OP:BM=OQ:CM,∵MB=MC,∴PO=OQ.(2)∵PO // BC,OQ // BC,∴PO:BC=EO:EC,OQ:BC=DO:BD,∴EO:EC=DO:BD,∴DE // BC.。
第3章 图形的相似数学九年级上册-单元测试卷-湘教版(含答案)

第3章图形的相似数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是()A. B. C. D.2、已知=,则()A. B. C. D.3、下列命题正确的个数有()①若 x2+kx+25 是一个完全平方式,则 k 的值等于 10;②一组对边平行,一组对角相等的四边形是平行四边形;③顺次连接平行四边形的各边中点,构成的四边形是菱形;④黄金分割比的值为≈0.618.A.0 个B.1 个C.2 个D.3 个4、如图,CD为Rt△ABC斜边上的高,如果AD=6,BD=2,那么CD等于()A.2B.4C.D.5、如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是()A.图中有三个直角三角形B.∠1=∠2C.∠1和∠B都是∠A的余角 D.∠2=∠A6、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有()A.1个B.2个C.3个D.4个7、如图,在平面直角坐标系中,以原点为位似中心,在第一象限内,按照位似比将放大得到,且点坐标为,点坐标为,则线段长为()A. B.2 C. D.8、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积为()A.0.36 π米2B.0.81 π米2C.2 π米2D.3.24 π米29、已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是()A.2 -2B.2-C.2 -1D. -210、如图,在矩形中,E为中点,以为边作正方形,边交于点H,在边上取点M使,作交于点L,交于点N,欧几里得在《几何原本》中利用该图解释了,现以点为圆心,为半径作圆弧交线段于点P,连结,记的面积为,图中阴影部分的面积为.若点A,L,G在同一直线上,则的值为( )A. B. C. D.11、下面给出了一些关于相似的命题,其中真命题有()①菱形都相似;②等腰直角三角形都相似;③正方形都相似;④矩形都相似;⑤正六边形都相似.A.1个B.2个C.3个D.4个12、如图,在正方形中,以为边作等边,延长分别交于点,连接与相交于点,给出下列结论:①;②;③;④;其中正确的是()A.①②③④B.②③C.①②④D.①③④13、如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为()A.(8,﹣12)B.(﹣8,12)C.(8,﹣12)或(﹣8,12)D.(5,﹣12)14、如图,AB∥CD,AD与BC相交于点P,AB=3,CD=6,AP=4,则DP的长为()A.3B.4C.6D.815、如图,点A(6,3)、B(6,0)在直角坐标系内.以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,那么点C的坐标为()A.(3,1)B.(2,0)C.(3,3)D.(2,1)二、填空题(共10题,共计30分)16、如图,∠DAB=∠CAE,要使△ABC∽△ADE,则补充的一个条件可以是________(注:只需写出一个正确答案即可).17、已知△ABC~△DEF,AB:DE=3:5,△ABC的面积为9,则△DEF的面积为________.18、某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为________米.19、如图,平行四边形分别切于点,连接并延长交AD 于点H,连接与刚好平行,若,则的直径为________.20、如图, A、B是双曲线上的点, A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC= .则k的值是________.21、如图是小明在建筑物AB上用激光仪测量另一建筑物CD高度的示意图,在地面点P处水平放置一平面镜,一束激光从点A射出经平面镜上的点P反射后刚好射到建筑物CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=15米,BP=20米,PD=32米,B、P、D在一条直线上,那么建筑物CD的高度是________ 米.22、如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是________m.23、如图,AG:GD=4∶1, BD :DC=2∶3,则 AE∶EC的值为________.24、如图,在Rt△ABC中,AC=6,∠C=90°,∠B=30°,AD平分∠BAC交BC于点D,点E为AB上一点,作∠DEF=60°交AC于点F,若AE=,则AF的长是________.25、如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于________.三、解答题(共5题,共计25分)26、已知=,求的值.27、如图,为了测量一栋楼的高度,小明同学先在操场上处放一面镜子,向后退到处,恰好在镜子中看到楼的顶部;再将镜子放到处,然后后退到处,恰好再次在镜子中看到楼的顶部,,,,在同一条直线上),测得,,如果小明眼睛距地面髙度,为,试确定楼的高度.28、如图,Rt△ABC中,∠ACB=90°,cosA= ,D为AB上一点,且AD:BD=1:2,若BC=3 ,求CD的长.29、已知,求:的值.30、亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部,颖颖的头顶及亮亮的眼睛恰在一条直线上时,两人分别标定自己的位置,.然后测出两人之间的距离,颖颖与楼之间的距离(,,在一条直线上),颖颖的身高,亮亮蹲地观测时眼睛到地面的距离.你能根据以上测量数据帮助他们求出住宅楼的高度吗?参考答案一、单选题(共15题,共计45分)1、A2、C3、C4、C5、B6、B7、D8、B9、A10、C11、C13、D14、D15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
第3章 图形的相似数学九年级上册-单元测试卷-湘教版(含答案)

第3章图形的相似数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD,且AE、BD交于点F,则S△DEF:S△ADF:S△BAF等于()A.4:10:25B.4:9:25C.2:3:5D.2:5:252、下列各组中的四条线段成比例的是()A.1cm、2cm、20cm、30cmB.1cm、2cm、3cm、4cmC.5cm、10cm、10cm、20cmD.4cm、2cm、1cm、3cm3、正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M,N,则MN的长为( )A. B. ﹣1 C. D.4、已知,如图,E(﹣4,2),F(﹣1,﹣1).以O为位似中心,按比例尺1:2把△EFO 缩小,点E的对应点的坐标()A.(﹣2,1)B.(2,﹣1)C.(2,﹣1)或(﹣2,﹣1)D.(﹣2,1)或(2,﹣1)5、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足= ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ;④S△DEF=4 ,其中正确的是()A.①②③B.②③④C.①②④D.①③④6、如图,在△ABC中,DE∥BC,,DE=4cm,则BC的长为()A.8 cmB.12 cmC.11 cmD.10 cm7、按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1 个B.2 个C.3 个D.4 个8、如图,l1∥l2∥l3, BC=1,= ,则AB长为()A.4B.2C.D.9、若=,则的值为()A. B. C. D.10、如图,在矩形ABCD中,E,F分别是AD,AB边上的点,连接CE,DF,他们相交于点G,延长CE交BA的延长线于点H,则图中的相似三角形共有( )A.5对B.4对C.3对D.2对11、如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为()A.1:2B.1:4C.2:1D.4:112、如图,已知∠1=∠2,则添加下列一个条件后,仍无法判定△ABC∽△ADE的是()A.∠C=∠EB.∠B=∠ADEC.D.13、如图是著名画家达芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2a,则BE长为()A.(+1)aB.(﹣1)aC.(3﹣)aD.(﹣2)a14、如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE= AF;⑤=FG•DG,其中正确结论的个数为()A.2B.3C.4D.515、如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为()A.1B.C.2D.不确定二、填空题(共10题,共计30分)16、在中,AD是BC边上的高,,正方形EFGH的顶点E、F 分别在AB、AC上,H、G在BC上.那么正方形EFGH的边长是________.17、与相似且对应中线的比为3:5,则与面积的比为________.18、若,则=________.19、如图,已知矩形中,,,点M,分别在边,上,沿着折叠矩形,使点A,B分别落在E,F处,且点F在线段上(不与两端点重合),过点M作于点H,连接,给出下列判断:①;②折痕的长度的取值范围为;③当四边形为正方形时,N为的中点;④若,则折叠后重叠部分的面积为.其中正确的是________.(写出所有正确判断的序号).20、已知a、b、c、d是成比例线段,即=,其中a=3cm,b=2cm,c=6cm,则线段d=________ cm .21、如图,原点O是△ABC和△A’B’C’的位似中心,点A(1,0)与点A’(-2,0)是对应点,△ABC的面积是,则△A’B’C’的面积是________22、若x:y=1:2,则=________.23、如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1, P2, P3,…,P n,使OP1=1,P1P2=3,P2P3=5,…,P n﹣1P n=2n﹣1(n为正整数),分别过点P1, P2, P3,…,P n向射线OA作垂线段,垂足分别为点Q1, Q2, Q3,…,Q n,则点Q n的坐标为________ .24、如图,已知等边△ABC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D1;过D1作D1E1∥AB于E1,连接BE1交AD于D2;过D2作D2E2∥AB于E2,…,如此继续,若记S△BDE为S1,记为S2,记为S3…,若S△ABC面积为Scm²,则Sn=________cm²(用含n与S的代数式表示)25、 3月20日起,我国陆续公布了三星堆遗址考古最新发掘成果.地球表面纬度范围是0~90°,对其进行黄金分割,黄金分割点间地区特别适合人类生活,产生了包括三星堆在内的世界古文明,也囊括了大多发达国家.那么黄金地带纬度的范围是________.(黄金比为0.618)三、解答题(共5题,共计25分)26、,求的值.27、如图是一个铁夹子的侧面示意图,点是连接夹面的轴上一点,于点.这个侧面图是轴对称图形,直线是它的对称轴.已知,,.求点与点之间的距离.28、已知反比例函数y=(m为常数)的图象经过点A(-1,6).(1)求m的值;(2)如图,过点A作直线AC与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.29、如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.30、某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示,),村委会想在地带与地带种植单价为10元的太阳花,当地带种满花后,已经花了500元,请你计算一下,若继续在地带种植同样的太阳花,资金是否够用?并说明理由.参考答案一、单选题(共15题,共计45分)1、B2、C3、C4、D5、C6、B8、C9、C10、B11、B12、D13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、29、。
湘教版九年级数学上册第3章 图形的相似 单元测试题(含答案)

第3章 图形的相似一、选择题(本大题共7小题,每小题4分,共28分) 1.以下列数据为长度的线段中,能成比例的是( ) A .3 cm ,6 cm ,8 cm ,9 cm B .3 cm ,5 cm ,6 cm ,9 cm C .3 cm ,6 cm ,7 cm ,9 cm D .3 cm ,6 cm ,9 cm ,18 cm2.已知△ABC ∽△A ′B ′C ′,AD ,A ′D ′分别是对应边BC ,B ′C ′上的高,且BC =10 cm ,B ′C ′=6 cm ,AD =7 cm ,则A ′D ′为( )A.163 cm B .12 cm C.215cm D .以上都不正确 3.在△ABC 中,D ,E 分别为边AB ,AC 的中点,则△ADE 与△ABC 的面积之比为( ) A.12 B.13 C.14 D.164.在△ABC 和△DEF 中,AB =AC ,DE =DF ,根据下列条件,能判定△ABC 和△DEF 相似的是( )A.AB DE =AC DFB.AB DE =BC EF C .∠A =∠E D .∠B =∠D 5.宽与长的比是5-12(约0.618)的矩形叫作黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图1,作正方形ABCD ,分别取AD ,BC 的中点E ,F ,连接EF .以点F 为圆心,以FD 的长为半径画弧,交BC 的延长线于点G .作GH ⊥AD ,交AD 的延长线于点H ,则图中下列矩形是黄金矩形的是( )图1A .矩形ABFEB .矩形EFCDC .矩形EFGHD .矩形DCGH6.如图2,已知△ABC ,任取一点O ,连接AO ,BO ,CO ,并取它们的中点D ,E ,F ,得△DEF ,则下列说法正确的个数是( )①△ABC 与△DEF 是位似图形;②△ABC 与△DEF 是相似图形;③△ABC 与△DEF 的周长比为1∶2;④△ABC 与△DEF 的面积比为4∶1.A .1B .2C .3D .4图2 图37.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E ,标记好脚掌中心位置为B ,测得脚掌中心位置B 到镜面中心C 的距离是50 cm ,镜面中心C 距离旗杆底部D 的距离为4 m ,如图3所示.已知小丽同学的身高是1.54 m ,眼睛位置A 距离小丽头顶的距离是4 cm ,则旗杆DE 的高度为( )A .10 mB .12 mC .12.4 mD .12.32 m二、填空题(本大题共7小题,每小题5分,共35分) 8.已知ab =3,则a -b b=________.9.在△ABC 中,AB =6,AC =8,在△DEF 中,DE =4,DF =3,要使△ABC 与△DEF 相似,需添加一个条件是________.(写出一种情况即可)10.如图4,以点O 为位似中心,将△ABC 缩小得到△A ′B ′C ′,若AA ′=2OA ′,则△ABC 与△A ′B ′C ′的周长比为________.11.如果两个相似三角形的面积比是16∶9,那么它们对应的角平分线的比是________.图4 图512.如图5,在平面直角坐标系中,每个小方格的边长均为1,△AOB 与△A ′OB ′是以原点O 为位似中心的位似图形,且OA OA ′=32,点A ,B 都在格点上,则点B ′的坐标是________.13.如图6,为了测量一水塔的高度,小强用2 m 长的竹竿做测量工具,移动竹竿,使竹竿、水塔顶端的影子恰好落在地面上的同一点.此时,竹竿与这一点相距8 m ,与水塔相距32 m ,则水塔的高度为________m.图614.如图7,在Rt △ABC 中,∠C =90°,AC =6,BC =8,P ,Q 分别为边BC ,AB 上的两个动点,若要使△APQ 是等腰三角形且△BPQ 是直角三角形,则AQ =________.图7三、解答题(本大题共3小题,共37分)15.(10分)已知:如图8,△ABC 三个顶点的坐标分别为A (-2,-2),B (-5,-4),C (-1,-5).(1)在网格中画出△ABC 关于x 轴对称的△A 1B 1C 1;(2)以点O 为位似中心,将△ABC 放大为原来的2倍,得到△A 2B 2C 2,请在网格中画出△A 2B 2C 2,并写出点B 2的坐标.图816.(13分)如图9(示意图),小明把手臂水平向前伸直,手持长为a的小尺竖直,瞄准小尺的两端E,F,不断调整站立的位置,使站在点D处正好看到旗杆的底部和顶部.如果小明的手臂长l=40 cm,小尺的长a=20 cm,点D到旗杆底部的距离AD=25 m,求旗杆BA 的高度.图917.(14分)如图10,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,EF交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EF A;(2)若AB=12,BM=5,求DE的长.图101.[答案] D 2.[答案] C 3.[答案] C 4.[答案] B5.[解析] D 设正方形ABCD 的边长为2,则CD =2,CF =1.在直角三角形DCF 中,DF =CF 2+CD 2=12+22=5,∴FG =5,∴CG =5-1,∴CGCD =5-12,∴矩形DCGH为黄金矩形.故选D.6.[解析] C 根据位似的性质得出①△ABC 与△DEF 是位似图形,②△ABC 与△DEF 是相似图形.∵△DEF 是将△ABC 的三边缩小为原来的12得到的,∴△ABC 与△DEF 的周长比为2∶1,故③错误.根据面积比等于相似比的平方,可知④△ABC 与△DEF 的面积比为4∶1.故选C.7.[解析] B 由题意可得AB =1.5 m ,BC =0.5 m ,DC =4 m ,△ABC ∽△EDC ,则ABDE =BC DC ,即1.5DE =0.54,解得DE =12(m).故选B. 8.[答案] 29.[答案] ∠A =∠D (答案不唯一) 10.[答案] 3∶1[解析] 由题意可知△ABC ∽△A ′B ′C ′, ∵AA ′=2OA ′,∴OA =3OA ′, ∴AC A ′C ′=OA O ′A ′=31,∴C △ABC C △A ′B ′C ′=AC A ′C ′=31. 故答案为3∶1. 11.[答案] 4∶3 12.[答案] (-2,43)[解析] 由题意得OA OA ′=32.又∵B (3,-2),∴点B ′的横坐标是3×(-23)=-2,点B ′的纵坐标是-2×(-23)=43,即点B ′的坐标是(-2,43).故答案为(-2,43).13.[答案] 1014.154或307 [解析] 在Rt △ABC 中,由勾股定理,得AB =10.应分情况讨论:①当AQ =PQ ,∠QPB =90°时.设AQ =PQ =x .由题意,得PQ ∥AC ,∴△BPQ ∽△BCA , ∴BQ BA =PQ CA ,∴10-x 10=x 6, ∴x =154,∴AQ =154.②当AQ =PQ ,∠PQB =90°时.设AQ =PQ =y . 由题意,得△BQP ∽△BCA ,∴PQ AC =BQ BC ,∴y 6=10-y 8,∴y =307. ③当AQ =AP ,∠PQB =90°时.设AQ =z . 由题意,得△BQP ∽△BCA ,BQ =10-z . BQ BC =BP BA ,10-z 8=BP 10,BP =12.5-1.25z . 在Rt △ACP 中,AC =6,AP =z ,BP =12.5-1.25z ,∴CP =8-(12.5-1.25z )=1.25z -4.5.由勾股定理,得(12.5-4.5z )2+62=z 2,解得z =10,∴此情况不存在.综上所述,满足条件的AQ 的值为154或307.15.解:(1)(2)画图如下图所示,B 2(10,8).16.解:过点C 作CH ⊥AB 于点H ,交EF 于点P ,则CH =AD =25 m ,CP =40 cm =0.4 m ,EF =20 cm =0.2 m.由题意,得EF ∥AB , ∴△CEF ∽△CBA ,∴EFBA=CPCH,即0.2BA=0.425,解得BA=12.5(m).答:旗杆BA的高度为12.5 m.17.解:(1)证明:∵四边形ABCD是正方形,∴AD∥BC,∴∠AMB=∠EAF.又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EF A.(2)∵∠B=90°,AB=12,BM=5,∴AM=122+52=13.∵四边形ABCD为正方形,∴AD=AB=12.∵F是AM的中点,∴AF=FM=6.5.∵△ABM∽△EF A,∴BMF A=AMEA,即56.5=13EA,∴EA=16.9,∴DE=EA-AD=4.9.。
第3章 图形的相似数学九年级上册-单元测试卷-湘教版(含答案)

第3章图形的相似数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是()A.2:3B. :C.4:9D.8:272、如图,已知△ABC,P是边AB上的一点,连结CP,以下条件中不能确定△ACP与△ABC 相似的是()A.∠ACP=∠BB.∠APC=∠ACBC.AC 2=AP·ABD.3、若,则的值为()A.0.5B.1C.1.5D.24、如图,D、E分别是△ABC边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则的值为()A. B. C. D.5、如图,点 A1、A2、A3、A4 在射线上,点 B1、B2、B3在射线上,且,.若△A2B1B2、△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为()A.8B.9C.10D.10.56、如图,和是以点为位似中心的位似三角形,若为的中点,,则的面积为()A.15B.12C.9D.67、在下列四组线段中,成比例线段的是()A.3、4、5、6B.5、15、2、6C.4、8、3、5D.8、4、1、38、如图,在平行四边形ABCD中,E是BC延长线上一点,AE交CD于点F,且CE=BC,则=()A. B. C. D.9、如图,在中,,是角平分线,若,,则点到的距离是()A. B. C. D.10、下列各组中的四条线段是成比例线段的是( )A.4cm,4cm,5cm,6cmB.1cm,2cm,3cm,5cmC.3cm,4cm,5cm,6cmD.1cm,2cm,2cm,4cm11、如图,,,,则的长()A. B. C. D.12、如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB 的中点,EF交AC于点H,则的值为A.1B.C.D.13、在△ABC中,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB,若BD=2AD,则的值为()A. B. C. D.14、如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1∶,点A的坐标为(1,0),则E点的坐标为().A.( ,0)B.( ,)C.( ,)D. (2,2)15、如图,,则下列比例式错误的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为________.17、已知△ABC与△DEF的相似比为5∶1,则△ABC与△DEF的周长比为________ .18、如图,已知直线y=-2x+4与x轴交于点A,与y轴交于点B,与双曲线y=(x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为________。
九年级上册数学单元测试卷-第3章 图形的相似-湘教版(含答案)
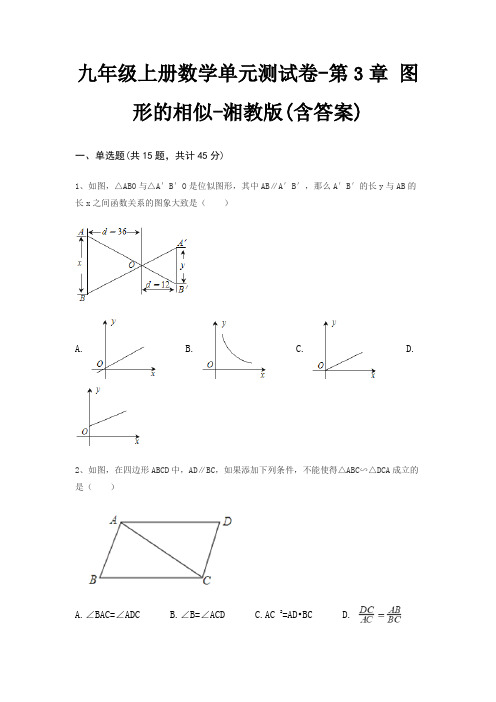
九年级上册数学单元测试卷-第3章图形的相似-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,那么A′B′的长y与AB的长x之间函数关系的图象大致是()A. B. C. D.2、如图,在四边形ABCD中,AD∥BC,如果添加下列条件,不能使得△ABC∽△DCA成立的是()A.∠BAC=∠ADCB.∠B=∠ACDC.AC 2=AD•BCD.3、若△ABC∽△A′B′C′,相似比为2:3,则△ABC与△A′B′C′的周长的比为()A.2:3B.4:9C.3:2D. :4、如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了()A.0.5米B.0.6米C.0.3米D.0.9米5、如图,在矩形ABCD中,DE⊥AC于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE的长度是()A.3B.5C.D.6、下面四个图案:不等边三角形、等边三角形、正方形和矩形,其中每个图案花边的宽度都相同,那么每个图形中花边的内外边缘所围成的几何图形不相似的个数有()A.4个B.3个C.2个D.1个7、如图,A,B两点分别在反比例函数和的图像上,连接OA,OB,若OA ⊥OB,OB=2OA,则k的值为()A.-2B.2C.-4D.48、如图,在△中,D,E两点分别在边, 上,∥.若,则为()A. B. C. D.9、如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;步骤2:作直线MN,分别交AC,BC于点E,F;步骤3:连接DE,DF。
若AC=4,BC=2,则线段DE的长为()A. B. C. D.10、如图,直线与双曲线(k>0,x>0)交于点A,将直线向上平移4个单位长度后,与y轴交于点C,与双曲线(k>0,x>0)交于点B,若OA=3BC,则k的值为( )A.3B.6C.D.11、如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是()A. 或B.C.D. 或12、如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3,则的值为( )A. B. C. D.13、如图,Rt△BOA与Rt△COA的斜边在x轴上,BA=6,A(10,0),AC与OB相交于点E,且CA=CO,连接BC,下列判断一定正确的是()①△ABE∽△OCE;②C(5,5);③BC=;④S△ABC=3.A.①③B.②④C.①②③D.①②③④14、如图,下列条件中不能判定△ACD∽△ABC的是()A.∠ADC=∠ACBB.C.∠ACD=∠BD.AC 2=AD•AB15、如图,在△ABC中,D、E、F分别是边AB、AC、BC上的点,连接EF,CD相交于点G,若四边形BDEF是平行四边形,则下列说法不正确的是()A. B. C. D.二、填空题(共10题,共计30分)16、在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是________.17、两个相似三角形的相似比为1:3,则它们周长的比为________.18、如图,铁道路口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高为________.(杆的宽度忽略不计)19、如果= ,那么的值等于________.20、有一块三角形的草地,它的一条边长为25m.在图纸上,这条边的长为5cm,其他两条边的长都为4cm,则其他两边的实际长度都是________m.21、正方形DEFG是的内接正方形,AM⊥BC于M,交DG于H,若AM=4cmcm,BC 长6cm, 则正方形DEFG的边长是________cm。
第3章 图形的相似数学九年级上册-单元测试卷-湘教版(含答案)

第3章图形的相似数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,已知AB∥CD∥EF,那么下列结论正确的是()A. B. C. D.2、如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④.其中单独能够判定△ABC △ACD的有()A.①②③④B.①②③C.①②④D.①②.3、如图,在3×3正方形网格中,顶点是网格线的交点的三角形叫做格点三角形,给出下列命题:①一定存在全等的两个格点三角形②一定存在相似且不全等的两个格点三角形③一定存在两个格点三角形是位似图形④一定存在周长和面积均为无理数的格点三角形其中真命题的个数是()A.4个B.3个C.2个D.1个4、如图1,在矩形中,动点从点出发,沿的路线运动,当点到达点时停止运动.若,交于点设点运动的路程为,,已知关于的图象如图2所示,则的值为()A. B.2 C.1 D.5、已知△ABC∽△DEF,S△ABC:S△DEF=1:9,若BC=1,则EF的长为()A.1B.2C.3D.96、如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF 交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=.在以上4个结论中,正确的有()A.1B.2C.3D.47、如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有A.1条B.2条C.3条D.4条8、如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为.其中,正确的结论是()A.①②④B.①③⑤C.②③④D.①④⑤9、如图,直线a∥b∥c,直线m交直线a、b、c于点A,B,C,直线n交直线a、b、c于点D,E,F,若= ,=().A. B.1 C. D.10、已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是()A. B. C. D.11、下列各组线段(单位:cm)中,成比例线段的是()A.1.2.3.4B.1 .2. 2. 4C.3. 5. 9. 13D.1. 2. 2. 312、如图,在等边中,,,分别是,,上的点,,,,则的面积与的面积之比等于()A.1∶3B.2∶3C. ∶2D. ∶313、如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是()A.- aB.- (a+1)C.- (a-1)D.- (a+3)14、如图,在△ABC中,,,,点F为边BC上一点,则下列条件不能保证△FDB与△ADE相似的是()A.∠A=∠BFDB.DF//ACC.D.15、如图,在Rt△ABC中,∠C=90°,点E在AC边上.将∠A沿直线BE翻折,点A落在点A'处,连接A'B,交AC于点F.若A'E⊥AE,cosA=,则()A. B. C. D.二、填空题(共10题,共计30分)16、如图,铁道口栏杆的短臂长(OA)为1.25m,长臂长(OB)为16.5m,当短臂端点下降0.85m时,长臂端点升高了________ m.(不计杆的宽度)17、已知:如图,△ABC的面积为16,点D、E分别是边AB、AC的中点,则△ADE的面积为________.18、在矩形ABCD中,AB=4,BC=3,取CD中点E,连接BD、BE,将沿BE翻折成为,过点C作CM⊥BF于M,则CM+FC=________.19、如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.已知点B′的坐标是(3,﹣1),则点B的坐标是________.20、如图,已知和均是等边三角形,点在同一条直线上,与交于点O,与交于点G,与交于点F,连接,则下列结论:①;②;③﹔④,其中正确结论有________个.21、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=________ .22、若△ABC∽△A′B′C′,AB=4,BC=5,AC=6,△A′B′C′的最大边长为15,那么它们的相似比是________,△A′B′C′的周长是________.23、若x:y=5:2,则(x+y):y的值是________24、如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=6,AD=2,若△ABC与△ACD 相似,AB=________.25、如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为________.三、解答题(共5题,共计25分)26、已知a、b、c满足,且,分别求出a、b、c的值.27、如图,将△ABC沿BC方向平移到△DEF,DE交AC于点G.若BC=2,△GEC的面积是△ABC的面积的一半,求△ABC平移的距离.28、如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求的值.29、如图,△ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少mm.30、如图,放映幻灯时,通过光源A,把幻灯片上的图形DE放大到屏幕BC上,若光源A 到幻灯片DE的距离AE长为20cm,幻灯片DE到屏幕BC的距离EC长为40cm,且幻灯片中的图形ED的高度为6cm,求屏幕上图形BC的高度.参考答案一、单选题(共15题,共计45分)1、A2、C3、B4、D5、C6、C7、C8、D9、C10、A11、B12、A13、D14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、30、。
第3章 图形的相似数学九年级上册-单元测试卷-湘教版(含答案)

第3章图形的相似数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,路灯距地面8米,身高1.6米的小李从点A处沿AO所在的直线行走14米到点B 时,人影长度()A.变长3.5米B.变长2.5米C.变短3.5米D.变短2.5米2、如图,Rt△ABC中,斜边为AB,且CD⊥AB于D,若,则△ADC的面积与△CDB的面积的比为()A. B. C. D.3、如图,在平面直角坐标系中,点A、B、C、D的坐标分别为、、、,若线段和是位似图形,位似中心在y轴上,则位似中心的坐标为()A. B. C. D.4、如图,直线a∥b∥c,直线m交直线a、b、c于点A,B,C,直线n交直线a、b、c于点D,E,F,若= ,=().A. B.1 C. D.5、下列各组中的四条线段成比例的是().A.1cm,2cm,20cm,40cmB.1cm,2cm,3cm,4cmC.4cm,2cm,1cm,3cm D.5cm,10cm,15cm,20cm6、下列各组数中,能成比例的是()A.3,4,5,6B.-1,-2, 2,4C.-3,1,3,0D.-1,2,-3,47、如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为()A. B. C. D.8、已知△ABC和△DEF相似,且△ABC的三边长为3、4、5,如果△DEF的周长为6,那么下列不可能是△DEF一边长的是()A.1.5B.2C.2.5D.39、若2a=3b,则=()A. B. C. D.10、如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:( 1 )图形中全等的三角形只有两对;(2)△ABC的面积等于四边形CDOE的面积的2倍;( 3 )CD+CE= OA;(4)AD2+BE2=2OP•OC.其中正确的结论有()A.1个B.2个C.3个D.4个11、如图,点G、F分别是△ACD的边AC、CD上的点,AD的延长线与GF的延长线相交于点B,DE∥AC交GB于点E,则下列结论错误的是()A. B. C. D.12、下面两个图形一定相似的是()A.两个矩形B.两个等腰三角形C.两个等腰梯形D.有一个角是35°的两直角三角形13、如图,已知在△ABC纸板中,AC=4,BC=8,AB=11,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是()A.0<CP≤1B.0<CP≤2C.1≤CP<8D.2≤CP<814、如图,矩形ABCD中,E为DC的中点,AD:AB=:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②=PB•EF;③PF•EF=2 ;④EF•EP=4AO•PO.其中正确的是()A.①②③B.①②④C.①③④D.③④15、如图,把绕点旋转到,当点D刚好落在上时,连结,设,相交于点,则图中相似三角形(不含全等)的对数有()A.1B.2C.3D.4二、填空题(共10题,共计30分)16、点D、E分别在等边△ABC的边AB、BC上,将△BDE沿直线DE翻折,使点B落在B1处,DB1、EB1分别交边AC于点F、G.若∠ADF=80°,则∠CGE=________.17、如下图,反比例函数(>0)图象上一点A,连结OA,作AB丄轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为________.18、如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是________.(只需写一个条件,不添加辅助线和字母)19、在平面直角坐标系中,O为原点,点,点B在y轴的正半轴上,.矩形的顶点D,E,C分别在上,.将矩形沿x轴向右平移,当矩形与重叠部分的面积为时,则矩形向右平移的距离为________.20、如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽________,△BAD∽△ACD(写出一个三角形即可).21、如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是________ cm.22、如图,与位似,点O为位似中心.已知,则与的面积比为________.23、如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD 于点E,则AE的长为________.24、已知两个相似三角形的面积之比是1:4,那么这两个三角形的周长之比是________.25、如图,菱形OABC的顶点A的坐标是(-5,0),点B,C在x轴上方,反比例函数y=(k>0,x>0)的图象分别与边OC、BC交于点D、点E,射线BD交y轴子点H,交反比例函数图象于点F,交x轴于点G,BD:DF:FG=2:3:1,若记△ODH的面积为S1,△CDE 的面积为S2,则的值是________三、解答题(共5题,共计25分)26、已知,且x+y-z=2,求x、y、z的值.27、如图,在锐角中,,,将绕点B按逆时针方向旋转,得到连接,若的面积为4,求的面积.28、如图,△ABC与△A′B′C′是位似图形,且位似比是1∶2,若AB=2 cm,则A′B′=▲ cm,并在图中画出位似中心O.29、已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3 .30、我们已经知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长,对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形.请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.参考答案一、单选题(共15题,共计45分)1、C2、A3、D4、C5、A6、B7、B8、D9、B10、C11、C12、D13、B14、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级上册数学第3章图形的相似单元测试题(湘教版含答案)
第3章图形的相似一、选择题 1.在1:1000000的地图上,A,B
两点之间的距离是5cm,则A,B两地的实际距离是() A. 5km B. 50km C. 500km D. 5000km 2.下列说法错误的是() A. 两个等边三角形一定相似 B. 两个等腰三角形一定相似 C. 两个等腰
直角三角形一定相似 D. 两个全等三角形一定相似 3.若
△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为() A. 1:2 B. 1:4 C. 2:1 D. 4:1 4.已知△ABC∽△DEF,如果∠A=55º,∠B=100º,则∠F=()A. 55º B. 100º C. 25º D. 30º 5.如图,若DC∥FE∥AB,则有() A. B. C. D. 6.如图,已知l1∥l2∥l3 , DE=4,DF=6,那么下列结论正确的是() A. BC:EF=1:1 B. BC:AB=1:2 C. AD:CF=2:3 D. BE:CF=2:3 7.某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是() A. 1.25m B. 10m C. 20m D. 8m 8.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S四边形DBCE=8S△ADE .那么AE:AC的值为() A. 1:8 B. 1:4 C. 1:3 D. 1:9 9.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A , BC=3,AC=6,则CD的长为() A. 1 B. 2 C. D. 10.如图,在▱ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于() A. 1:2 B. 1:3 C. 2:3 D. 以上都不正确二、填空题 11.若线段a,b,c,d成比例,其中a=3cm,b=6cm,c=2cm,则d=________ . 12.如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是________. 13.已知实数a,b,c 满足a+b+c=10,且 ,则的值是________ 14.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则 =________ . 15.如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 =________ .
16.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).①画出△ABC向下平移4个单位长度得到的△A1B1C1 ,点C1的坐标是________ ;②以点B为位似中心,在网格内画出
△A2B2C2 ,使△A2B2C2与△ABC位似,且位似比为2:1________ ,
点C2的坐标是________ ;③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________ . 17.如图,已知D , E分别
是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB ,那么BC:CD应等于________. 18.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =________ . 19.如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底
边离地面的高BC=________米. 20.一个等腰直角三角形和一个正方形如图摆放,被分割成了5个部分.①,②,③这三块的面积比依
次为1:4:41,那么④,⑤这两块的面积比是________ 三、解答题21.如图,在△ABC中,点D在边AB上,满足且∠ACD=∠ABC,若AC=2,AD=1,求DB的长.
22.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么? 23.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
24.已知:如图,.(1)求证:;(2)当时,求证:EC BC.
25.在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);(2)探究:如图②,点P在
矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
参考答案一、选择题 B B B C D B C C C C 二、填空题 11. 4cm 12. 1:9 13. 14. 15. . 16.(2,�2);;(1,0);(2a�3,2b�4)17. 18. 19. 2.5 20. 9:14 三、解答题 21.解∵∠ACD=∠ABC,
∠BAC=∠CAD,∴△ADC∽△ACB.∴ . ∵AC=2,AD=1,∴ . ∴DB=AB-AD=3.
22. 解:△ABE与△DEF相似.理由如下:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,设AB=AD=CD=4a,∵E为边AD的中点,CF=3FD,∴AE=DE=2a,DF=a,∴ =2, =2,∴ 而∠A=∠D,
∴△ABE∽△DEF. 23. 解:∵△PCD是等边三角形,∴∠PCD=60°,∴∠ACP=120°,∵△ACP∽△PDB,∴∠APC=∠B,又∠A=∠A,
∴△ACP∽△ABP,∴∠APB=∠ACP=120° 24. 证明:(1)∵
∴△ABC∽△DEF ∴ ,(2)∵ BAC= DAE ∴ BAD= CAE 又∵ ∴
∴△ABD∽△ACE ∴ ABD= ACE ∵ BAC=90° ∴ ABD+ ACD=90° ∴ ACE+ ACD=90° 即EC BC. 25. (1)证明:感知:如图①,∵四边形ABCD 为矩形,∴∠D=∠C=90°,∴∠DAE+∠DEA=90°,∵EF⊥AE,
∴∠AEF=90°,∴∠DEA+∠FEC=90°,∴∠DAE=∠FEC,∵DE=1,CD=4,∴CE=3,∵AD=3,∴AD=CE,∴△ADE≌△ECF(ASA)(2)探究:如图②,∵四边形ABCD为矩形,∴∠D=∠C=90°,
∴∠DPE+∠DEP=90°,∵EF⊥PE,∴∠PEF=90°,
∴∠DEP+∠FEC=90°,∴∠DPE=∠FEC,∴△PDE∽△ECF (3)2。
