5.3 方法专题 平行线的判定与性质的综合应用
平行线的判定与性质的综合应用 专题练习

平行线的判定与性质的综合应用专题练习平行线的判定与性质的综合运用专题一、推理填空题1.已知:如图,DE∥BC,∠ADE=∠XXX,将说明∠1=∠2成立的理由填写完整。
解:因为DE∥BC,所以∠ADE=∠XXX。
又因为DE∥BC,所以DB∥EF。
由平行线性质可知,∠1=∠ADE=∠XXX∠2.2.已知:如图所示,∠1=∠2,∠A=∠3.求证:XXX。
证明:因为∠1=∠2,所以XXX。
又因为∠A=∠3,所以AC∥BD。
由平行线性质可知,AC∥DE。
3.已知:如图,∠XXX∠ADC,BF、DE分别平分∠ABC 与∠ADC,且∠1=∠3.求证:AB∥DC。
证明:因为∠XXX∠ADC,所以∠XXX∠ADC。
又因为BF、DE分别平分∠ABC与∠ADC,所以∠1=∠ABC,∠3=∠ADC。
由∠1=∠3可得,∠2=∠ADC。
由平行线性质可知,AB∥DC。
二、证明题4.如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数。
证明:因为AB∥CD,所以∠A+∠D=180º。
又因为DE⊥AE,所以∠ADE=90º。
由∠A=37º可得,∠ADE=53º。
由三角形内角和定理可得,∠D=80º。
5.如图,已知AB∥CD,∠1=100°,∠2=120°,求∠α的度数。
证明:因为AB∥CD,所以∠1+∠α+∠2=180º。
由∠1=100º,∠2=120º可得,∠α= -40º。
由于∠α是角度,所以∠α=320º。
6.如图,XXX,AE平分∠BAD,求证:XXX与AE相交于F,∠XXX∠EAF。
证明:因为XXX,所以∠BAD=∠ACD。
又因为AE平分∠BAD,所以∠XXX∠DAF。
由相邻角的性质可得,∠EAF+∠DAF=∠BAD=∠ACD。
又因为CD与AE相交于F,所以∠CFE+∠EAF+∠ACD=180º。
平行线与平行线的性质及判定方法

平行线与平行线的性质及判定方法平行线是指在同一平面内永远不会相交的两条直线。
在数学中,平行线有着许多独特的性质和判定方法,对于几何学的研究和实际应用都具有重要意义。
一、平行线的性质1. 平行线上的两个点到另一直线的距离相等:如果两条直线L₁和L₂平行,那么这两条线上的任意两个点A和B到第三条直线L的距离都是相等的。
2. 平行线的内角和为180度:当一条直线与两条平行线相交时,两对内角之和是180度。
这可以通过数学证明得出。
3. 平行线的外角相等:当两条平行线被一条横截线相交时,这两条平行线的对应外角是相等的。
4. 平行线的平行线仍然平行:如果两条直线L₁和L₂平行,而L₃与L₁平行,那么L₃也与L₂平行。
二、平行线的判定方法1. 直角判定法:如果两条直线上的任意一对相邻内角之一是直角,那么这两条直线是平行线。
这种判定方法是由两条直线的垂直性质推导出来的。
2. 三角形内角和判定法:如果一条直线与一条平行线相交,那么直线上的一对内角与平行线上的一对内角之和为180度时,这两条直线是平行线。
3. 平行线定理:如果两条直线分别与第三条直线相交,并且两对同位角分别相等,那么这两条直线是平行线。
这个定理也被称为同位角定理。
4. 夹角判定法:如果两条直线分别与第三条直线相交,而且同位角相等或互补,则这两条直线是平行线。
5. 平行线公理(欧几里德公理):如果直线上的一点和直线外一点,有且只有一条通过这两个点的平行线。
这个公理是建立在欧几里德几何的基础上的。
以上是常见的一些关于平行线性质的说明和判定方法,通过这些性质和方法,我们可以在几何学中更好地理解和应用平行线。
在实际生活中,平行线也有着广泛的应用,例如建筑设计、道路规划、制图等领域都需要运用到平行线的概念和性质。
总结:在数学中,平行线是指在同一平面内永远不会相交的两条直线。
平行线有许多独特的性质,如平行线上的两个点到另一直线的距离相等、平行线的内角和为180度等等。
平行线的性质和判定及其综合运用

. 22
A
F1 F2 Fn
B E1
E2
Em
几何画板:探究平行线中动点问题.gsp
C
D
当左边有n个角,右边有m个角时: ∠A+∠F1 + ∠ F2 +…+ ∠Fn= ∠E1 +∠E2 +…+ ∠Em+ ∠D
. 16
当堂练习
1.填空:如图,
(1)∠1=∠2 时,AB∥CD. (2)∠3= ∠5或∠4时,AD∥BC.
2 F
(平行于同一条直线的两条直线平行).
∴ ∠3= ∠E(两直线平行,同位角相等).
. 20
5.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD
的度数.
C
解:∵EF∥AD, (已知)
∴∠2=∠3.(两直线平行,同位角相等) D 1 G
F
又∵∠1=∠2, (已知) ∴∠1=∠3.(等量代换)
解:作∠PCE =∠APC,交AB于E.
∴ AP∥CE ∴ ∠AEC=∠A,∠P=∠PCE.
∴ ∠A+∠P=∠PCE+∠AEC,
A
∵AB∥CD ∴ ∠ECD=∠AEC,
∴∠A+∠P =∠PCE+∠ECD=∠PCD. C
P EB
D
. 9
还可以怎样作辅助线?
例2:如图,AB∥CD,猜想∠BAP、∠APC 、∠PCD 的数量关系,并说明理由.
例1:如图,三角形ABC中,D是AB上一点,E是AC上
一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
D
A E
人教版七年级下册数学学案:5.3.1平行线的判定与性质的综合运用
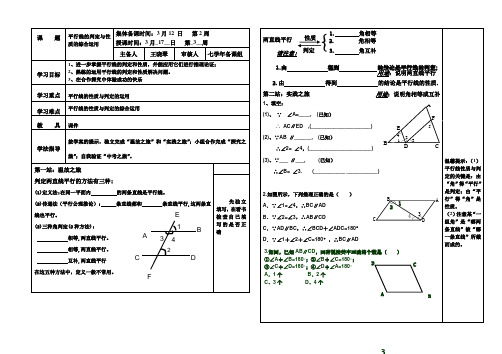
A.∠1=∠3
B.∠2+∠3=180º C.∠2+∠4<180º D.∠3+∠5=180º
第五站:反思之旅
本节课你有哪些收获? 布置作业:
C
O
A ╰1 ╯╮23
╰4 ╭5
B
D
A
B
教 学
反
思
课题 学习目标
平行线的判定与性 集体备课时间:3 月 12 日 第 2 周
质的综合运用
授课时间:3 月_17__日 第_3__周
主备人 王晓翠 审核人 七学年备课组
1、进一步掌握平行线的判定和性质,并能应用它们进行推理论证; 2、熟练的运用平行线的判定和性质解决问题。 3、在合作探究中体验成功的快乐
E
B
╰4
1╭
╮2 ╮3
D
F
╰5
C
(3)、∵___ ∥___, (已知) ∴∠B= ∠3. (___________ ___________)
2.如图所示,下列推理正确的是( ) A.∵∠1=∠4,∴BC∥AD
╰B2╮1
B.∵∠2=∠3,∴AB∥CD
C
4╭ ⌒3 D
C.∵AD∥BC,∴∠BCD+∠ADC=180°
学习重点 平行线的性质与判定的运用 学习难点 平行线的性质与温故之旅”和“实践之旅”;小组合作完成“探究之 旅”;自我验证“中考之旅”。
第一站:温故之旅
判定两直线平行的方法有三种:
(1)定义法;在同一平面内
的两条直线是平行线。
(2)传递法(平行公理推论);
D.∵∠1+∠2+∠C=180°,∴BC∥AD
3.如图,已知 AB∥CD,四种说法其中正确的个数是( )
①∠A+∠B=180°;②∠B+∠C=180°;
平行线的判定和性质的综合运用 (2)

第五章平行线的判定和性质的综合运用1、知识与技能:理解并掌握平行线的判定与性质,并能灵活运用。
(学习重点)2、过程与方法:领悟类比、转化等数学思想方法,能够综合运用平行线性质和判定解决问题.(学习难点)3、情感与态度:在学习过程中,通过师生的互动交流,培养良好的学习习惯,主动参与的意识,在独立思考的同时能够认同他人。
一、自学展示:1、①平行线的判定方法,其用途:②平行线的性质:其用途。
2、以下这6个小题,我们能否将它们放入各自该进的房间呢?并在括号内填上相应的理由。
请同学们不要放错了哦!二、合作学习例1:如图,AB∥CD,AD∥BC,试说明∠B与∠D的关系?变式训练:AB∥CD,且∠B=∠D,你能推理得出AD∥BC吗?三、质疑导学:例2:如图所示:点D为AE上的点,点B为FC上的点,AD∥BC,∠A=∠C,求证:AB∥DC.证明:变式1:如图所示:点D为AE上的点,点B为FC上的点,∠1=∠2,∠A=∠C,试说明 AE∥FC .如图所示,已知AB ∥CD,分别探索下列四个图形中∠P 与∠A,∠C 的关系, 请你从所得的四个关系中任选一个加以说明.(提示:过点P 做平行线)PD CBA P DBAP DCB A PDCB A(1) (2) (3) (4) 变式1:如图5所示,AB ∥CD,则∠A+∠E+∠F+∠C 等于( )A.180°B.360°C.540°D.720°变式2:如图6所示,A 1B ∥A n D ,则∠A 1+∠A 2+…+∠A n 等于(5) (6) (7) (8) 四、学习检测1)如图7所示,下列推理正确的是( ) A .∵∠1=∠4,∴BC ∥AD B .∵∠2=∠3,∴AB ∥CD C .∵AD ∥BC ,∴∠BCD +∠ADC=180° D .∵∠1+∠2+∠C=180°,∴BC ∥AD 2)如图8,已知∠3=∠2若要使∠1=∠4则还需( )A 、∠1=∠3B 、∠2=∠3C 、∠1=∠4D 、AB ∥CD3)如图,易拉罐的上下底面互相平等,用吸管吸饮料时,若∠1=1100,则∠2= , 理由可叙述如下: ∵AB//CD ( ) ∵∠1=110( )∴∠1=∠3=1100( )∵∠2+∠3=( ) ∴∠2=4).已知:如图,已知AB 、CD 被EF 所截,EG 平分∠BEF ,FG 平分∠EFD ,且∠1+∠2=900,求证:AB//CD证明: ∵EG 平分∠BEF ,FG 平分∠EFD ( ) ∴ ∠BEF=2∠1∠DFE=2∠2( )∵∠1+∠2=900( ) ∴∠BEF+∠DFE=1800( ) ∴AB//CD( )A 1A 3A 2A nBDFE D C BA教学反思:。
小学数学中的平行线和垂直线

小学数学中的平行线和垂直线在小学数学课程中,平行线和垂直线是非常基础的概念。
理解并能够准确识别平行线和垂直线,对于学生建立起几何形状的准确概念和进行几何运算都非常重要。
本文将详细介绍小学数学中的平行线和垂直线的概念、性质以及相关应用。
一、平行线的概念与性质1.1 平行线的定义在平面上,如果两条直线不相交,并且在同一个平面上不存在其他直线与这两条直线相交,那么这两条直线就是平行线。
1.2 平行线的判定在小学数学中,我们通常使用以下三种方法来判定两条直线是否平行:(1)同位角相等法:如果两条直线被一条横截线所截,那么同位角相等的话,这两条直线就是平行线;(2)转角法:如果两条直线被一条截线所截,而转角相等的话,则这两条直线是平行线;(3)平行线的性质:如果两条直线分别与第三条直线平行,那么这两条直线也是平行线。
二、垂直线的概念与性质2.1 垂直线的定义在平面上,如果两条直线相交,并且相交的角度为90度,那么这两条直线就是垂直线。
2.2 垂直线的判定在小学数学中,我们通常使用以下两种方法来判定两条直线是否垂直:(1)两条互相垂直的直线上的线段互成直角;(2)如果两条直线的斜率乘积等于-1,那么这两条直线是垂直的。
三、平行线与垂直线的应用平行线和垂直线在几何学中有广泛的应用,下面我们介绍几个常见的应用例子。
3.1 矩形的性质矩形是一种特殊的四边形,其中每条边都是两两平行且相等的。
所以在矩形中,每条边上的线段都互相平行,并且对角线互相垂直。
3.2 平行线分割线段如果一条直线与两条平行线相交,那么它将会把这两条平行线分割成多段线段,这些线段的长度比例是相等的。
这个性质在我们进行几何运算和问题求解时非常有用。
3.3 垂直平分线在数学中,如果一条直线与另一条直线相交,并且把另一条直线的中点划分成两个相等的部分,那么这条直线就是垂直平分线。
垂直平分线与被分割的线段互相垂直。
结语平行线和垂直线是小学数学中的基础概念,对于建立几何概念和进行几何运算非常重要。
平行线的判定、性质的综合运用-北京版七年级数学下册教案

平行线的判定、性质的综合运用-北京版七年级数学下册教案一、教学目标1.知道平行线的概念与判定方法;2.掌握平行线的性质,如平行线的交角补角相等等;3.能够灵活应用平行线的性质,解决一些实际问题。
二、教学重难点1.平行线的判定;2.平行线的性质综合运用。
三、教学过程1. 导入(5分钟)从品质行业的角度,通过老师讲述沿不同路线行走的两个工人,到达事先设定的目的地的时间不同的情况。
2. 平行线的判定(15分钟)1.讲述平行线的定义:在同一平面内,没有交点的两条直线。
2.讲述平行线的判定方法:–通过角度判定:如果两条直线所成的角度相等,则这两条线是平行线。
–通过距离判定:在比较短线段上,找点作垂线,并且两个垂线分别与另一条直线相交,如果这两个垂线的长度相等,那么这两条线就是平行的。
3.让学生通过习题进行巩固练习。
3. 平行线的性质(20分钟)1.讲述平行线的性质:–两条平行线的交角是补角;–同侧内角是180度;–同侧外角是补角;–对顶角相等。
2.让学生通过图判定来巩固这些性质。
4. 平行线性质的运用(35分钟)1.让学生通过图例来解题。
2.教案设计下列习题:–解决矩形的问题:两条对边互相平行,相对边相等。
–两条平行线各有一个点与另一直线相交,证明交点构成的两直线平行。
3.针对学生的问题进行讨论,解答。
5. 思考题(10分钟)向学生提出几个实际问题:•如何通过学习平行线性质,解决出现在日常生活中令人困扰的问题?老师可以引导学生分别给出实际例子,由学生进行分析和解答。
四、诊断评价根据学生们在课堂上的表现,老师可以对学生的学习情况进行评估。
并针对学生在学习过程中出现的问题进行诊断,帮助学生进行及时补救。
人教版七年级数学下册专题(教案):平行线的判定和性质的综合运用

此外,在小组讨论环节,学生们表现出了很高的积极性,能够主动提出自己的观点,并与其他同学进行交流。但我也发现,部分学生在讨论过程中过于依赖同伴,缺乏独立思考。为了解决这个问题,我计划在今后的教学中,多设置一些开放性问题,引导学生独立思考,培养他们的自主学习能力。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与平行线相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。这个操作将演示平行线的基本原理。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“平行线在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
举例:在复杂图形中,学生需要运用多种判定方法综合判断两条直线是否平行。
(2)性质的综合运用:学生需要将平行线的性质运用到解决实际问题中,特别是涉及多个平行线交叉的问题。
Байду номын сангаас举例:在给定图形中,已知一条直线平行于另一条直线,求证图形中其他直线之间的关系。
(3)逆向思维的培养:在解决平行线相关问题时,学生需要具备逆向思维能力,从已知条件推导出结论。
人教版七年级数学下册专题(教案):平行线的判定和性质的综合运用
一、教学内容
本节课选自人教版七年级数学下册第十一章“图形的性质”中的“平行线的判定和性质”一节。教学内容主要包括以下两部分:
