MATLABLE五跨连续梁
MATLAB实验(新)-梁

MATLAB实验讲义主编:梁迎春光电信息技术教学重点实验室2006年9月目录实验大纲 (2)实验一 MATLAB的基础操作 (3)实验二 MATLAB运算基础 (3)实验三循环结构程序设计 (4)实验四 MATLAB的绘图操作 (5)实验五函数和文件 (6)实验六线性代数中的数值计算问题 (6)实验七 MATLAB函数库的运用 (7)实验八 MATLAB在电路中的应用 (7)实验九 MATLAB在信号与系统中的应用 (8)《MATLAB》课程实验教学大纲课程名称:MATLAB(MATLAB)课程编号:16072327课程性质:选修实验总学时:18实验室名称:电子设计自动化一、课程简介:本课程是电气工程及其自动化、自动化、电力工程与管理专业本科生的学科基础选修课,它在线性代数、信号分析和处理、控制系统设计和仿真等方面有着广泛的应用。
主要是学习MATLAB的语法规则、基本命令和使用环境,使学生掌握MATLAB的基本命令和基本程序设计方法,提高使用该语言的应用能力,具有使用MATLAB语言编程和调试的能力,以便为后续多门课程使用该语言奠定必要的基础。
二、课程实验目的与要求:1.基本掌握MATLAB在线帮助功能的使用、熟悉MATLAB运行环境和MATLAB语言的主要特点,掌握MATLAB语言的基本语法规则及基本操作命令的使用,学会M文件的建立和使用方法以及应用MATLAB实现二维和三维图形的绘制方法,具有使用MATLAB语言编程和调试的能力。
2.初步掌握MATLAB在电路和信号与系统中的应用。
3.能根据需要选学参考书,查阅手册,通过独立思考,深入钻研有关问题,学会自己独立分析问题、解决问题,具有一定的创新能力。
三、主要仪器设备及台(套)数:计算机50台、MATLAB软件五、主要参考书目:1.《MATLAB及在电子信息课程中的应用》陈怀琛、杨吉斌编著,电子工业出版社,2002年1版2.《MATLAB7.0编程基础》王家文、王皓、刘海等;机械工业出版社,2005年7月3.《MATLAB教程——基于6.x版本》张志涌、徐彦琴等;北京航空航天大学出版,2001年4月出版实验一 MATLAB 的基础操作一、实验目的1、 掌握MATLAB 的启动和退出。
迈达斯软件实例教程之连续梁分析

1. 连续梁分析概述比较连续梁和多跨静定梁受均布荷载和温度荷载(上下面的温差)时的反力、位移、内力。
3跨连续两次超静定3跨静定3跨连续1次超静定图 1.1 分析模型2Ø材料钢材: Grade3Ø截面数值 : 箱形截面 400×200×12 mmØ荷载1. 均布荷载 : 1.0 tonf/m2. 温度荷载 : ΔT = 5 ℃ (上下面的温度差)设定基本环境打开新文件,以‘连续梁分析.mgb’为名存档。
单位体系设定为‘m’和‘tonf’。
文件/存档(连续梁分析 )工具 / 单位体系长度> m ; 力 > tonf¿图 1.2 设定单位体系3设定结构类型为 X-Z 平面。
模型 / 结构类型结构类型> X-Z 平面¿设定材料以及截面材料选择钢材GB(S)(中国标准规格),定义截面。
模型 / 材料和截面特性 /45建立节点和单元为了生成连续梁单元,首先输入节点。
捕捉轴线 (关)捕捉单元 (开), 建立节点坐标 ( x, y, z ) ( 0, 0, 0 ) ¿图 1.5 建立节点²参照用户手册的“输入单元时主要考虑事项”用扩展单元功能来建立连续梁。
模型 / 单元/全选扩展类型 > 节点à线单元单元属性> 单元类型 > 梁单元²材料 > 1:Grade3 ; 截面> 1: 400*200*12 ; Beta 角( 0 )生成形式> 复制和移动 ; 复制和移动 > 任意间距方向> x ; 间距( 3@5/3, 8@10/8, 3@5/3 )¿图 1.6 建立单元X Z²输入梁单元. 关于梁单元的详细事项参照在线帮助的“单元类型”的“梁单元”部分6输入边界条件3维空间的节点有6个自由度 (Dx, Dy, Dz, Rx, Ry, Rz)。
利用mathcad及力法原理计算多跨连续梁的内力

分析 连续梁在均布荷载作 用下的 内力分布规律 ,与计算 不等跨连 续梁 内力的传 统方法进 行 比较 ,比较 两种方 法计算不等 跨连 续梁的 内力可 以看 出f t . 1 用m a t h c a d计算显著提 高计算精度 ,给其 它结 构3 - . 程 中的连 续梁 内力计 算提 供参 考,证明 了
在水 工 钢结 构 或混 凝 土 结 构 中 ,涉 及 很 多 连续 梁
个未 知 力 X ( i ∈[ 1 ,n一1 ] ) 代替 ,这样 得 到 力法 的基
的设计 ,如 钢 闸 门 中 的水 平 次 梁 ,厂 房 楼 面 的 次 梁 , 闸坝 上 的工 作 桥和 交通 桥 中 的部 分 梁 系 等 。进 行 连续
A =6 l Xl+6 2 2+ … +6 , + … +6 m , 】+ A =0
一
梁 的设 计首 先需 计 算其 内力 ,按 弹性 理 论 计 算 连续 梁
的 内力 可采 用 弯矩 分 配 法或 力 法 ,以往 的计 算 多 通过 查 询现 成 的系数 表得 到各 控制 截 面的弯 矩值 和剪 力值 。 在 相关 书籍 中给 出了 2~5跨等 跨连 续梁 在常 用荷 载作
用 下 的 内力系 数 J ,2~7跨 等 跨 连续 梁 在 均 布荷
载 作用 下 的弯矩 和剪 力 系数 。例如水 工 钢 闸门结 构 中 ,
( 1 )
据 闸 门梁 系布 置特 点 ,水 平 次 梁一 般 连 续 地 支 承 在 隔
板 或竖 直次 梁 上 ,此 时 水 平 次梁 可 按 承 受 均 布 荷 载 的
= 一
多 跨连 续梁 计算 ,传 统 的钢 闸 门次 梁计 算 是 将 其 近 似 为 等跨 连续 梁 ,查 表求 得 其 跨 中 、支 座 处 的最 大 弯矩
基于MATLAB的平面五连杆机构的运动学分析_王锡霖

l1 + l2 = l 5 + l3 + l4 l1 = l 5 + l 4 即
l2 - l3 - l4 = - l1 + l5
( 1)
- l4 + l 1 = l5
( 2)
0
l4 sin 4
0
- l4cos 4
0 0 co s 1 sin 1
2
3
=
4
l1
l 1 sin( 1 + 180 ) - l 1 co s( 1 + 180 )
l1 sin 1 - l1cos 1
1. 3 加速度分析 用 1. 2 中得到的角速度方程式再求一次导数, 得:
- l2 sin 2 l2 cos 2 0 0
写成两个坐标方向上的投影式, 得到该机构 的位置方程:
l 2 cos 2 - l3 cos 3 - l 4 cos( 4 + 180 ) = - l 1 cos( 1 + 180 ) + l5 l 2 sin 2 - l3 sin 3 - l4 sin( 4 + 180 ) = - l 1 sin( 1 + 180 )
第3期
王锡霖, 等: 基于 M A T L A B 的平面五连杆机构的运动学分析
275
到非线性方程的雅克比矩阵 J[ 3-4] 。 在 MAT L AB 函数编写中用到了 w hile 条件
循环语句, 编写了名为 rrr posi 的 M 函数, 可以求 解 1. 1 中的位置函数, 再利用 fo r 循环语句得到 随原动件 BF 运动其它构件的位置图像[ 5-8] 。
matlab连续梁程序的编制与使用Word文档
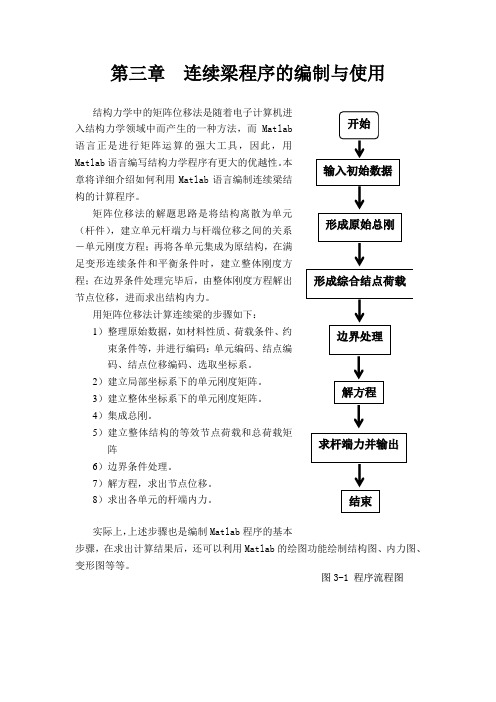
第三章连续梁程序的编制与使用入结构力学领域中而产生的一种方法,而Matlab语言正是进行矩阵运算的强大工具,因此,用Matlab语言编写结构力学程序有更大的优越性。
本章将详细介绍如何利用Matlab语言编制连续梁结构的计算程序。
矩阵位移法的解题思路是将结构离散为单元(杆件),建立单元杆端力与杆端位移之间的关系-单元刚度方程;再将各单元集成为原结构,在满足变形连续条件和平衡条件时,建立整体刚度方程;在边界条件处理完毕后,由整体刚度方程解出节点位移,进而求出结构内力。
用矩阵位移法计算连续梁的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,并进行编码:单元编码、结点编码、结点位移编码、选取坐标系。
2)建立局部坐标系下的单元刚度矩阵。
3)建立整体坐标系下的单元刚度矩阵。
4)集成总刚。
5)建立整体结构的等效节点荷载和总荷载矩阵6)边界条件处理。
7)解方程,求出节点位移。
8)求出各单元的杆端内力。
实际上,上述步骤也是编制Matlab程序的基本步骤,在求出计算结果后,还可以利用Matlab的绘图功能绘制结构图、内力图、变形图等等。
图3-1程序流程图3.1 程序说明%******************************************************************* % 矩阵位移法解连续梁主程序%******************************************************************* ●功能:运用矩阵位移法解连续梁的基本原理编制的计算主程序。
●基本思想:结点(结点位移)编码默认为从左至右,从1开始顺序进行;杆端弯矩的方向默认为逆时针。
●荷载类型:可计算结点荷载,每单元作用的跨中集中力和均布荷载。
●说明:主程序的作用是通过赋值语句、读取和写入文件、函数调用等完成算法的全过程,即实现程序流程图的程序表达。
%-----------------------------------------------------------------------------------------------------1 程序准备format short e %设定输出类型clear all %清除所有已定义变量clc %清屏●说明:format short e -设定计算过程中显示在屏幕上的数字类型为短格式、科学计数法;clear all -清除所有已定义变量,目的是在本程序的运行过程中,不会发生变量名相同等可能使计算出错的情况;clc -清屏,使屏幕在本程序运行开始时%-----------------------------------------------------------------------------------------------------2 打开文件FP1=fopen('input.txt','rt'); %打开输入数据文件存放初始数据FP2=fopen('output.txt','wt'); %打开输出数据文件存放计算结果●说明:FP1=fopen('input.txt','rt'); -打开已存在的输入数据文件input.txt,且设置其为只读格式,使程序在执行过程中不能改变输入文件中的数值,并用文件句柄FP1来FP2=fopen('output.txt','wt'); -打开输出数据文件,该文件不存在时,通过此命令创建新文件,该文件存在时则将原有内容全部删除。
连续梁按弹性理论五跨梁内力系数及弯矩分配法

附表25:等截面等跨连续梁在经常使用荷载作用下按弹性分析的内力系数(五跨梁)。
之宇文皓月创作弯矩分配法(弯矩分配法计算连续梁和刚架及举例)一、名词解释弯矩分配法在数学上属于逐次迫近法,但在力学上属于精确法的范畴,主要适用于连续梁和刚架的计算。
在弯矩分配法中不需要解联立方程,而且是直接得出杆端弯矩。
由于计算简便,弯矩分配法在建筑结构设计计算中应用很广。
(一)线刚度i杆件横截面的抗弯刚度EI被杆件的长度去除就是杆件的线刚度i:(a)当远端B为固定支座时,对于A点处,AB(b)当远端B为铰支座时,对于A点处,AB(c)当远端B为滑动支座时,对于A点处,AB(d)当远端B为自由端时,对于A点处,AB(二)转动刚度S转动刚度暗示靠近节点的杆件端部对该节点转动的反抗能力。
杆端的转动刚度以SA是暗示A端,第二个角标B是暗示杆的远端是B各杆A端的转动刚度成正比。
AB在A端的分配系数。
它暗示AB杆的A端AB的转动刚度与交于A点各杆的转动刚度之和的比值。
总之,加于节点A的外力矩,按各杆的分配系数分配于各杆的A端。
CC得出远端弯矩。
当远端为滑动边支座当远端为铰支边支座节点A作用的外力矩M,按各杆的分配系数μ分配给各杆的近端;远端弯矩等于近端弯矩乘以传递系数。
(五)杆端弯矩弯矩分配法解题过程中所指的杆端弯矩是所有作用于杆端的中间计算过程的最后总的效果。
计算杆端弯矩的目的,是因为杆端弯矩一旦求出,则每相邻节点之间的“单跨梁”将可以作为一根静定的脱离体取出来进行该杆的内力分析。
其上作用的荷载有外荷载,每一杆端截面上一般有一个剪力和一个弯矩,两端共有二个剪力和二个弯矩。
这两个弯矩就是两端的杆端弯矩,既然它们已经求出,那么余下的两个剪力可由两个静力平衡方程解出。
(六)近端弯矩和远端弯矩二、弯矩分配法的思路在求杆端弯矩时,其主要的目标是:(1)由于节点上有两根或多根杆件汇集,因此需确定每一根杆在维持节点不转动平衡过程中所作出的贡献。
基于Matlab的连续梁桥动力响应分析

基于M a tl ab的连续梁桥动力响应分析( 1. 中铁五局机械化工程有限责任公司, 湖南衡阳421002;2. 中南大学土木建筑学院, 湖南长沙410075 )摘要:利用插值振型函数法来获得多跨连续梁的振型函数。
建立连续梁桥振动方程,利用有限元分析软件A n sys对连续梁进行模态分析并将连续梁成千上万个自由度的有限元模型重构成数个自由度的动力学模型,且保持二者前几阶振型一致。
基于M a t lab数学分析软件模拟连续梁振型函数,利用OD E系列函数的二次开发函数来求解连续梁桥振动方程。
计算表明本文方法可行、有效,具有较高的精度。
关键词: M a t lab;连续梁;插值振型函数;模态分析中图分类号: U448. 21 + 5 文章编号: 1672 - 7029 ( 2010 )01 - 0016 - 05文献标志码: AD yn a m i c re s p o n s e a n a ly s i s o f c o n t i n u o u s b e am b rid g e b a s e d o n M A TLABL I Chang2song1 , HUAN G Fang2li n2( 1. M echan iza t ion Enginee ring L i m ited Comp any of Ch ina R a il way 5 th B u r eau Gr oup , H engyang 421002 , Ch ina;2. Schoo l of C i vil and A r ch itec tu r a l Enginee ring, Cen tr a l Sou th U n ive rsity, Changsha 410075 , Ch ina)A b s tra c t: Fo r a m u l ti - sp a n beam , the m e t hod t o ob t a i n the vi b ra t i o n mode func t i o n s by i n t e r po l a t i o n func2 ti o n wa s p r opo s ed. The vi b r a t i o n equa t i o n s of the con t i nuou s beam syste m we r e e s tab l ished.B y u s i ng fi n ite e l e2 m e n t soft w a r e A n s ys, the moda l ana l ysis of the con t i nuou s bea m wa s e s tab l ished. A l a r ge num b e r of freedom s of the fi n ite e l em e n t mode l of the con t i nuou s bea m we re grea t l y reduced and recon s truc t ed w ith seve r a l freedom s, and the first few mode s a r e i nva ri an t.The vi b ra t i o n mode func t i o n s of the con t i nuou s beam we re si m u l a t ed by u2 si ng M a t l ab p l a t f o r m. The vi b r a t i o n equa t i o n s of the con t i nuou s beam syste m we r e so l ved by the second - deve l2 op e d OD E func t i o n s. The ana l ysis re s u l ts show tha t the m e t hod p r opo s ed i n th i s p a p e r is fea s i b l e and effec t i ve, and ha s h i ghe r p rec i si o n.Key word s:M a t l ab; con t i nuou s bea m; i n t e r po l a t i ng vi b ra t i o n mode func t i o n; mode ana l ysis桥梁在移动荷载作用下的动力响应及机理研究一直是结构动力学的前沿课题。
):连续系统 梁的基础理论及 MATLAB 编程 Matlab (

(3)
将(3)式代入(2)式,可得应变能为:
U=
1 2 ∫0
L
⎛ ∂ 2u ⎞ EI ⎜ 2 ⎟ dx ⎜ ∂x ⎟ ⎝ ⎠
2
(4)
3.1.3 外力所做的功
外力所做的功可表示为: L
0
W = ∫ P( x) u dx
(5)
3.1.4 总势能
梁的总势能为应变能减去外力所做的功,可表示为:
V =U −W
ui、θ i、u j、θ j
将(8)式代入(7)式,有:
V =∫
L 0
T ⎤ ⎡1 ⎛ ∂2N ⎞ ⎛ ∂2 N ⎞ T ⎢ EI {φ} ⎜ 2 ⎟ ⎜ 2 ⎟{φ} − P[ N ]{φ}⎥ dx ⎜ ∂x ⎟ ⎜ ∂x ⎟ ⎥ ⎢2 ⎝ ⎠ ⎝ ⎠ ⎦ ⎣
(9)
(9)式的推导中,用到如下公式:
6EI ⎤ L2 ⎥ 2EI ⎥ ⎥ L ⎥ 6EI ⎥ − 2 L ⎥ 4EI ⎥ ⎥ L ⎦
⎡ Fiy ⎤ ⎢M ⎥ ⎢ i⎥ ⎢ Fjy ⎥ ⎢ ⎥ ⎢M j ⎥ ⎣ ⎦
(16)
3.2 Matlab 程序说明
clear x=sym( ‘x’ ); L=sym( ‘L’ ); N=[ 1 – 3 * (x^2) / (L^2) + 2 * (x^3) / (L^3), x – 2 * (x^2) / L + (x^3) / (L^2),…. 3 * (x^2) / (L^2) – 2 * (x^3) / (L^3), -(x^2) / L + (x^3) / (L^2) ]; Ni=diff ( N, 2 ); Nt=transpose ( Ni); kk=Nt * Ni; K=E * I * int (kk, 0, ‘L’);
