状态空间模型操作步骤
matlab tf、ss、和zpk的控制系统建模实验心得
matlab tf、ss、和zpk的控制系统建模实验心得1. 引言1.1 概述控制系统建模是设计和分析工程系统的重要步骤之一。
在这个过程中，我们需要选择适当的数学模型来描述系统的行为，并使其与实际物理现象相匹配。
MATLAB作为一个功能强大的工具，提供了多种方法来进行控制系统建模，其中包括传递函数模型(TF)、状态空间模型(SS)和零极点增益模型(ZPK)。
本文旨在总结和分享我在使用MATLAB中的TF、SS和ZPK进行控制系统建模实验中的经验和心得。
1.2 文章结构本文将按照以下结构展开讨论：- 第二部分将介绍在MATLAB中使用TF进行控制系统建模时的一些重要事项，包括理解传递函数模型以及如何建立该模型。
- 第三部分将介绍使用SS进行控制系统建模时所需注意的事项，包括理解状态空间模型和建立该模型的步骤。
- 第四部分将介绍使用ZPK进行控制系统建模时需要注意的事项，包括理解零极点增益模型和如何建立该模型。
最后，在第五部分中，将对TF、SS和ZPK三种建模方法进行比较，并总结心得体会，并对未来的研究方向进行展望。
1.3 目的本文的目的是帮助读者更好地理解和掌握MATLAB中TF、SS和ZPK建模方法，以便能够准确描述和分析控制系统的行为。
通过分享我的实验心得，我希望能够给读者提供一些在实际应用中使用这些模型时的指导和启示。
让我们开始吧！2. MATLAB中的TF模型建模实验心得2.1 理解传递函数模型在MATLAB中，传递函数（Transfer Function）是一种常用的控制系统建模方法。
它用于描述输入和输出之间的关系，并包含了系统的动态特性。
在进行TF 模型建模时，我们首先需要理解传递函数的含义和作用。
传递函数是指将系统的频率响应与拉普拉斯变换联系起来的函数表达式。
通过分子多项式和分母多项式的比值来表示系统，并使用频率域表达，可以方便地分析系统性能、稳定性以及设计控制器等。
2.2 建立传递函数模型的步骤在MATLAB中，建立传递函数模型可以遵循以下步骤：步骤1：确定系统的数学模型。
由传递函数转换成状态空间模型(1)
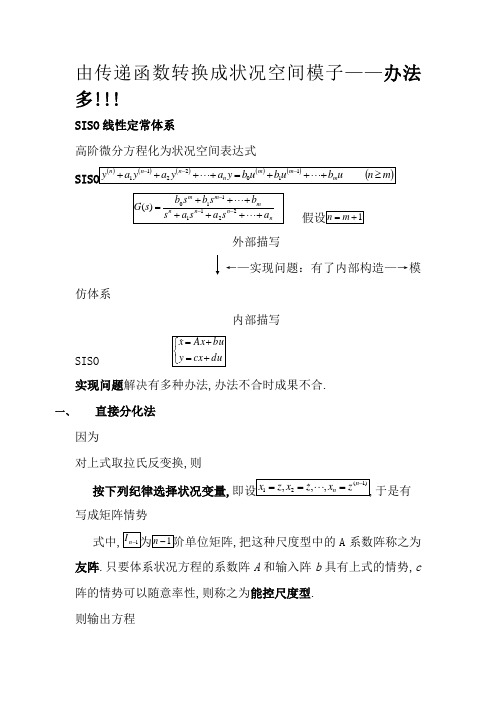
由传递函数转换成状况空间模子——办法多!!!SISO线性定常体系高阶微分方程化为状况空间表达式外部描写←—实现问题：有了内部构造—→模仿体系内部描写实现问题解决有多种办法,办法不合时成果不合.一、直接分化法因为对上式取拉氏反变换,则按下列纪律选择状况变量,于是有写成矩阵情势式中,把这种尺度型中的A系数阵称之为友阵.只要体系状况方程的系数阵A和输入阵b具有上式的情势,c 阵的情势可以随意率性,则称之为能控尺度型.则输出方程写成矩阵情势.在须要对现实体系进行数学模子转换时,不必进行盘算就可以便利地写出状况空间模子的A.b.c矩阵的所有元素.例：已知SISO体系的传递函数如下,试求体系的能控尺度型状况空间模子.解：直接得到体系进行能控尺度型的转换,即若选（若何斟酌？）斟酌式依次对第一式求导,并带入第二式;对第二式求导,并带入第三式;依次类推,便得到写成矩阵情势式中.只要体系状况空间表达式的A阵和c 阵具有上式的情势,b阵的情势可以随意率性,则称之为能不雅尺度型从情势上看,能控尺度型和能不雅尺度型的系数阵A是互为转置,能控尺度型输入阵b和能不雅尺度型输出阵c互为转置,这种互为转置的关系被称为对偶关系.将在第六章进一步评论辩论.经由过程以上对传递函数阵的能控尺度型或能不雅尺度型转换的评论辩论,对单输入体系而言,应留意如下问题：（1）传递函数转化成能控尺度型的状况空间表达式,状况方程的构造只由传递函数阵的顶点（特点）多项式肯定,而与其零点多项式无关,零点多项式只影响输出方程的构造.（2）从能不雅尺度型的转换可以看出,系数阵A的元素仅决议于传递函数顶点多项式系数,而其零点多项式则肯定输入阵B的元素.（3）只有当传递函数零点和顶点多项式同阶时,状况,.例：求前例的能不雅尺度型的状况空间模子解：直接得到能不雅尺度型的状况空间模子,即二、串联分化法若SISO体系的传递函数顶点互异,体系传递函数分子分母写成因式相乘情势图示！！三、并联分化法（对角尺度型/约旦尺度型——特点值尺度型）（一）若SISO体系的传递函数顶点互异,则可求得对角尺度型的模子.当体系的顶点互异时,体系传递函数分子分母写成因式相乘情势写成部分分式个中,其值为选择状况变量为（绘图示意状况变量的取法）即对上式拉氏反变换,得即写成矩阵情势式中,系数矩阵A为对角阵.对角线上的元素是传递函数G（s）的顶点,即体系的特点值.b阵是元素全为1的n×1矩阵.求对角尺度型模子的输出方程中c的构造对上式拉氏反变换,得假如体系的状况方程的A阵是对角阵,暗示体系的各个变量之间是解耦的.多变量的体系解耦是庞杂体系实现准确掌握的症结问题,关于若何实现解耦掌握将在第五章评论辩论.体系的状况构造图如图所示.例：设体系的闭环传递函数如下,试求体系对角尺度型的转换,得对角尺度型的转换为（二）对SISO体系式,当其有重特点值时,可以得到约当尺度型的状况空间模子.此时模子的系数矩阵A中与重特点值对应的那些子块都是与这些特点值相对应的约当块,即其重数为j,而其余为互异的特点值,则传递函数可以用部分分式睁开成式中,,其值为.绘图示意状况变量的取法：例：设体系的闭环传递函数如下,试求体系对约当准型的状况空间模子,该体系为四阶,有一个重顶点,重数为j=2,有两个互异的顶点,按部分分式睁开可得约当尺度型的模子为。
Eviews13章状态空间模型
本章小结：
• 了解状态空间模型的基本理论 • 掌握状态空间模型的建立方法 • 了解卡尔滤波方法
• 掌握状态空间模型的估计方法
EViews统计分析基础教程
四、状态空间模型的估计
当状态空间模型被定义好后，就可以对其进行模型的估计。 在 EViews 软 件 操 作 中 ， 选 择 状 态 空 间 对 象 工 具 栏 中 的 “Proc”|“Estimate…”选项，得到对话框。 在“Sample”中输入要估计的样本区间，系统默认下为整个 样本区间；在“Optimization algorithm”（最优化算法）中选 择 估 计 算 法 ， 包 括 “ Marquardt” （ 马 夸 特 测 定 法 ） 和 “BHHH”估计方法；在“Iteration Control”（循环控制）中 可以设定最大循环次数和收敛值；在“Derivatives”（导数方 法）中，有两种计算导数的方法，分别是“Accuracy”和 “Speed”。如果选择“Accuracy”计算的精度会更高，如果 选择“Speed”计算的速度会更快。
EViews统计分析基础教程
三、状态空间模型的建立
（2）在下图所示的状态空间对象的文本编辑栏中也可以对 状态空间模型进行定义。在该编辑栏中通过关键词和文本可 以描述量测方程、状态方程、初始条件、误差结构和待估参 数的初始值。
EViews统计分析基础教程
三、状态空间模型的建立
量测方程： 量测方程的关键词是“@signal”，如果该关键词缺失，系统 默认下会将该方程设定为量测方程。量测方程的因变量可以 包含表达式，例如 log(kg)=ss1 + c(1) + c(3)×x + ss2×y 其中，ss1和ss2是状态变量。 量测方程的右侧不能包含量测变量的当期值和未来值，即不 能包含因变量表达式中的变量。
matlab定义状态空间模型的初始状态
Matlab定义状态空间模型的初始状态1. 引言状态空间模型是一种描述动态系统的数学模型，它可以用于分析和控制各种复杂的系统，如机械系统、电气系统、控制系统等。
在Matlab中，我们可以使用一些函数和工具箱来定义和分析状态空间模型的初始状态。
本文将详细介绍如何使用Matlab来定义状态空间模型的初始状态，并且给出一些示例以帮助读者更好地理解。
2. Matlab中的状态空间模型在Matlab中，可以使用ss函数来定义状态空间模型。
ss函数的基本语法如下：sys = ss(A, B, C, D)其中，A是系统的状态转移矩阵，B是系统的输入矩阵，C是系统的输出矩阵，D是系统的直接传递矩阵。
3. 定义状态空间模型的初始状态在Matlab中，我们可以使用initial函数来定义状态空间模型的初始状态。
initial函数的基本语法如下：[y, t, x] = initial(sys, x0)其中，sys是状态空间模型，x0是系统的初始状态。
initial函数将返回系统的响应值y和时间向量t，以及系统的状态向量x。
4. 示例为了更好地理解如何使用Matlab定义状态空间模型的初始状态，我们将通过一个示例来进行说明。
假设我们有一个简单的电路系统，其状态空间模型如下：A = [-1, 0; 1, -2]B = [1; 0]C = [1, 0]D = 0我们希望定义该系统的初始状态为x0=[0.5; 0.5]，并观察系统的响应。
首先，我们需要使用ss函数定义状态空间模型：A = [-1, 0; 1, -2];B = [1; 0];C = [1, 0];D = 0;sys = ss(A, B, C, D);接下来，我们可以使用initial函数来定义系统的初始状态并观察系统的响应：x0 = [0.5; 0.5];[y, t, x] = initial(sys, x0);plot(t, y);xlabel('Time');ylabel('Output');title('System Response');运行以上代码，我们将得到系统的响应图像，该图像显示了系统的输出随时间的变化情况。
状态空间模型的建立过程
状态空间模型的建立过程嘿，咱今儿就来聊聊状态空间模型的建立过程哈！这可不是个简单的事儿呢，就好像盖房子，得一步步来，精心打造。
首先呢，你得明确自己要研究啥，就像你得知道要盖个啥样的房子，是小别墅还是大高楼。
这就是确定模型的状态变量，这可太关键啦，它们就像是房子的根基一样。
然后呢，根据这些状态变量，去找到它们之间的关系，这就好比是搭建房子的框架，得结实稳固才行。
这一步可不能马虎，得仔细琢磨，反复推敲。
接下来呀，还得考虑外界的影响因素呢，就跟房子会受到风雨雷电的影响一样。
这些外界因素会让模型变得更加复杂，但也更加真实。
你说，这状态空间模型建立起来，不就跟建了个小世界似的嘛！这里面的门道可多了去了。
咱得一点一点地去抠细节，去完善。
比如说，在确定状态变量的时候，要是没选好，那后面的一切不都白费功夫啦？这就好像盖房子一开始就把根基打歪了，那房子还能盖得稳吗？肯定不行呀！再比如，在构建关系的时候，要是弄错了，那模型不就乱套啦？就好比房子的框架歪七扭八的，能住人吗？建立状态空间模型可不只是个技术活，还得有耐心，有细心，更要有那份钻研的劲儿。
这就跟雕刻一件艺术品似的，得精心雕琢。
你想想，当你终于成功建立起一个完美的状态空间模型时，那得多有成就感呀！就好像看着自己亲手盖起来的漂亮房子，心里那个美呀！咱可不能小瞧了这状态空间模型的建立过程，这里面蕴含着无数的智慧和努力呢。
每一个步骤都得认真对待，不能有丝毫的马虎。
这就跟人生一样，每一步都得走得踏实，走得稳当。
只有这样，才能建成属于自己的那个精彩世界，不是吗？反正我是这么觉得的，你们呢？。
matlab离散化状态空间模型 -回复
matlab离散化状态空间模型-回复如何使用MATLAB 进行离散化状态空间模型的建模和分析离散化状态空间模型是一类广泛应用于系统建模和分析的数学工具。
它在控制论和动态系统理论中有着重要的作用。
MATLAB 是一个功能强大的数学软件，可以方便地进行离散化状态空间模型的建模和分析。
本文将介绍如何使用MATLAB 进行离散化状态空间模型的建模和分析。
一、离散化状态空间模型的概念和原理离散化状态空间模型是描述离散时间系统动态特性的一种数学模型。
它由状态方程和输出方程组成。
状态方程描述了系统状态的演化规律，输出方程描述了系统输出与状态的关系。
离散时间系统的状态方程和输出方程可以用矩阵形式表示如下：x(k+1) = Ax(k) + Bu(k)y(k) = Cx(k) + Du(k)其中，x(k) 表示系统在时刻k 的状态向量，u(k) 表示系统在时刻k 的输入向量，y(k) 表示系统在时刻k 的输出向量，A、B、C、D 分别为系统的状态矩阵、输入矩阵、输出矩阵和直接传递矩阵。
离散化状态空间模型的建模需要将连续时间系统的状态空间模型进行离散化处理。
离散化的基本原理是将连续时间系统的状态方程和输出方程在一段时间内进行离散化处理，使得系统的状态和输出在该离散时间内近似地描述系统的动态特性。
二、使用MATLAB 进行离散化状态空间模型的建模和分析的步骤1. 定义系统的连续时间状态空间模型首先，需要定义连续时间状态空间模型的状态矩阵A、输入矩阵B、输出矩阵C 和直接传递矩阵D。
这些矩阵的维度和元素值反映了系统的动态特性。
例如，假设我们有一个连续时间状态空间模型：dx(t)/dt = Ax(t) + Bu(t)y(t) = Cx(t) + Du(t)其中，状态向量x(t) 的维度为n，输入向量u(t) 的维度为m，输出向量y(t) 的维度为p。
那么，我们可以用MATLAB 编写如下代码定义连续时间状态空间模型：A = [a11, a12, ..., a1n; a21, a22, ..., a2n; ..., an1, an2, ..., ann];B = [b11, b12, ..., b1m; b21, b22, ..., b2m; ..., bn1, bn2, ..., bnm];C = [c11, c12, ..., c1n; c21, c22, ..., c2n; ..., cp1, cp2, ..., cpn];D = [d11, d12, ..., d1m; d21, d22, ..., d2m; ..., dp1, dp2, ..., dpm];2. 将连续时间状态空间模型离散化在MATLAB 中，可以使用c2d 函数将连续时间状态空间模型离散化为离散时间状态空间模型。
状态空间模型操作步骤
补充说明
需要强调指出的是，状态空间模型可以不必被对话框提 供的选择限制。如果发现自动指定对话框的限制了模型
指定，可以简单地使用它建立一个基本的指定，然后利
用更一般的文本工具描述模型。8 Nhomakorabea填写实例
生成下列状态空间模型
量测方程为
y t Zt α t z t γ u t ,
状态方程为 αt Tt αt 1 ct Rt εt ,
1
一
起动窗口
操作说明 Objects/New Object/Sspace
2
二 定义一个状态空间模型
◎自动指定法步骤
第一步 打开对话窗口
第二步 填写基本回部分 第三步 填写随机回归部分 第四步 选择状态空间模型的基本方差结构 备注：定义状态空间模型有两种方法：自动指定法 文本描 述法，本例以自动指定法为例，文本法略
1状态空间模型操作步骤一起动窗口二定义一个状态空间模型三估计状态空间模型四视图2操作说明objectsnewobjectsspace一起动窗口3自动指定法步骤第一步打开对话窗口第二步填写基本回部分第三步填写随机回归部分第四步选择状态空间模型的基本方差结构备注
状态空间模型操作步骤
一
二 三 四
起动窗口
定义一个状态空间模型 估计状态空间模型 视图
6
第四步 选择状态空间模型的基本方差结构
◎点击第三个标签对话框 Variance Specification， ◎为量测方程或状态方程选择 方差矩阵类型： 单位矩阵（Identity）、共同对 角矩阵（Common Diagonal， 对角元素是共同的方差）、一 般对角矩阵（Diagonal）、无 限制矩阵（Unrestricted）。 ◎对话框还允许为量测方程和 状态方程选择非零的误差协方 差阵。
4-3状态空间模型
则给出当年的各城镇人口，既可得出第二年的人口数量
M [q1q2q3q4q5 ] P q x
生于模式：胎数固定时，平均生育年龄早 人口更新快，状 态变化快，能较快达到人口目标 生育年龄区间：生育年龄区间越宽，则人口状态平缓 生育年龄区间越窄，则人口状态波动明显
三、状态空间模型(SSM)
人口迁移政策
迁移对人口总量及其结构会产生较大影响。 人口迁移常伴随一些重大事件的发生，比如大型 工程建设、战争冲突等。 政府可采取措施来控制迁移带来的人口状态 的突变。
交换设备:0.75u(t) -20%
y (t ) x1 (t ) x2 (t ) x2 (t )
u(t) 传输电缆:0.25u(t) +15%
0.25u (t ) x2 (t 1)
x1 (t ) 0.8 x1 (t 1) 0.75u (t ) 0.15x2 (t 1) x1 (t ) 0.8 0.15 0.75 状态空间向量： 0 x1 (t 1) 1 x2 (t 1) 0.25u (t ) x2 (t )
t0 t0
t
三、状态空间模型(SSM)
2.状态空间： 状态向量：将描述系统的一组状态写成列向量的 T 形式：x(t ) [ x1 (t ), x2 (t ),, xn (t )] x(t ) 称为系统的状态向量。
状态空间：所有n维状态向量的全体便构成了实数域 上的n维空间。
其中t是一个参变量，某一时刻t下的状态是空间中的一个点，而 一段时间下状态的集合称为系统在这一时间段的状态轨迹，也称作相 轨迹。
用系统的状态来描述系统的行为，称为状态 空间描述。对应地，系统的模型称为状态空间模 型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3
第一步 打开对话窗口
操 作 ◎Procs ◎Define State Space。
4
第二步 填写基本回部分
说 明 ◎Basic Regression 被用来描述
模型的基本回归部分。
◎键入因变量和带有固定或递
归系数的回归变量。在建立指
定时EViews使用系数对象代表 未知参数。 ◎在底部，可以指定误差项一 个ARMA结构。
估计状态空间模型，需要指定初值。 13
在选择各选项并点击OK以后，EViews在状态空间窗口显 示协方差 g = 0 时的估计结果(方程记为ss_ g):
14
协方差 g 0 时的估计结果(方程记为ss_c):
15
11
填写总规则
一 量测方程中所有外生变量填写进基础回归部分（量测方
程中常数项填写C） 二 量测方程中所有与状态方程相联系有变量全部在随机
系数部分，一般填入AR（1）中即可，因为状态方程可表示
成马可夫过程
12
三、估计状态空间模型
◎Procs/Estimate…。 ◎ EViews 允许选择估计样本区间，循环的
6
第四步 选择状态空间模型的基本方差结构
◎点击第三个标签对话框 Variance Specification， ◎为量测方程或状态方程选择 方差矩阵类型： 单位矩阵（Identity）、共同对 角矩阵（Common Diagonal， 对角元素是共同的方差）、一 般对角矩阵（Diagonal）、无 限制矩阵（Unrestricted）。 ◎对话框还允许为量测方程和 状态方程选择非零的误差协方 差阵。
7
补充说明
需要强调指出的是，状态空间模型可以不必被对话框提 供的选择限制。如果发现自动指定对话框的限制了模型
指定，可以简单地使用它建立一个基本的指定，然后利
用更一般的文本工具描述模型。
8
填写实例
生成下列状态空间模型
量测方程为
y t Zt α t z t γ u t ,
状态方程为 αt Tt αt 1 ct Rt εt ,
最大次数，收敛值，估计算法，导数计算设 置和是否显示初始值。对大部分问题，缺省 设置提供一个好的初始设置。
在进行模型估计时要注意下面两点：
(1) 尽管 EViews 中卡尔曼滤波程序可以自动处理
样本中的缺省值，但 EViews要求估计样本必须是连续 的，连续的观测值之间不能有缺口。
(2) 如果模型定义中有未知系数，为用卡尔曼滤波
状态空间模型操作步骤
一
二 三 四
起动窗口
定义一个状态空间模型 估计状态空间模型 视图
1
一
起动窗口
操作说明 Objects/New Object/Sspace
2
二 定义一个状态空间模型
◎自动指定法步骤
第一步 打开对话窗口
第二步 填写基本回部分 第三步 填写随机回归部分 第四步 选择状态空间模型的基本方差结构 备注：定义状态空间模型有两种方法：自动指定法 文本描 述法，本例以自动指定法为例，文本法略
5
第三步 填写随机回归部分
◎Stochastic Regressors被用来 加带有随机系数的回归变量。 在四个编辑区域中键入合适的 回归变量。 ◎EViews定义具有如下五项组 合的回归变量：无系数、固定 均值系数、AR(1)系数、随机 游动系数、带有漂移的随机游 动系数。例11.3是AR(1)系数的 形式。
9
填写Bic Regression 被用来描述模型的基
本回归部分（对照量测方程）。
◎因变量：y 固定系数的回归变量：c z 递归系数的回归变量：无
◎在底部，可以指定误差项一
个ARMA结构。 ◎注：Z有随机系数，不可观 察，将在下一步填写
10
填写随机系数
◎Stochastic Regressors 随机系数的回归变量：Z ◎EViews定义具有如下五项组 合的回归变量：无系数、固定 均值系数、AR(1)系数、随机 游动系数、带有漂移的随机游 动系数。例11.3是AR(1)系数的 形式。 ◎从状态方程可见是AR(1)系 数的形式。所以在AR(1)系数 项下填写 ：Z