后方交会法计算原理
后方交会
5.方茴说:"那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢,就算喜欢也是偷偷摸摸的。
"6.方茴说:"我觉得之所以说相见不如怀念,是因为相见只能让人在现实面前无奈地哀悼伤痛,而怀念却可以把已经注定的谎言变成童话。
"7.在村头有一截巨大的雷击木,直径十几米,此时主干上唯一的柳条已经在朝霞中掩去了莹光,变得普普通通了。
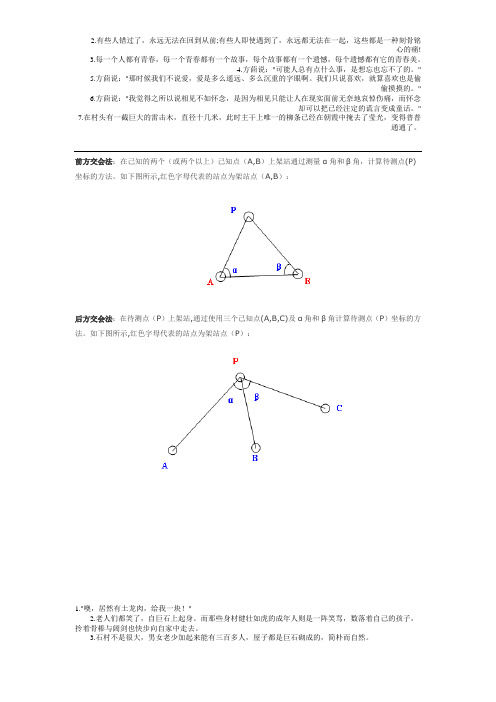
前方交会法:在己知的两个(或两个以上)己知点(A,B)上架站通过测量α角和β角,计算待测点(P)坐标的方法。
如下图所示,红色字母代表的站点为架站点(A,B):后方交会法:在待测点(P)上架站,通过使用三个己知点(A,B,C)及α角和β角计算待测点(P)坐标的方法。
如下图所示,红色字母代表的站点为架站点(P):1."噢,居然有土龙肉,给我一块!"2.老人们都笑了,自巨石上起身。
而那些身材健壮如虎的成年人则是一阵笑骂,数落着自己的孩子,拎着骨棒与阔剑也快步向自家中走去。
5.方茴说:"那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢,就算喜欢也是偷偷摸摸的。
"6.方茴说:"我觉得之所以说相见不如怀念,是因为相见只能让人在现实面前无奈地哀悼伤痛,而怀念却可以把已经注定的谎言变成童话。
"7.在村头有一截巨大的雷击木,直径十几米,此时主干上唯一的柳条已经在朝霞中掩去了莹光,变得普普通通了。
一、引言在工程测量中,内业资料计算占有很重要的比重,内业资料计算的准确无误与速度直接决定了测量工作是否能够快速、顺利地完成。
而内业资料的计算方法及其所需达到的精度,则又直接取决于外业所用仪器及具体的放样目标和内业计算所用到的办公软件和计算方法。
计算机辅助设计(Computer Aid Design 简写CAD,常称AutoCAD)是20世纪80年代初发展起来的一门新兴技术型应用软件。
如今在各个领域均得到了普遍的应用。
空间后方交会的解算

空间后方交会的解算一. 空间后方交会的目的摄影测量主要利用摄影的方法获取地面的信息,主要是是点位信息,属性信息,因此要对此进行空间定位和建模,并首先确定模型的参数,这就是空间后方交会的目的,用以求出模型外方位元素。
二. 空间后方交会的原理空间后方交会的原理是共线方程。
共线方程是依据相似三角形原理给出的,其形式如下111333222333()()()()()()()()()()()()A S A S A S A S A S A S AS A S A S A S A S A S a X X b Y Y c Z Z x f a X X a Y Y a Z Z a X X b Y Y c Z Z y f a X X a Y Y a Z Z -+-+-=--+-+--+-+-=--+-+-上式成为中心投影的构线方程,我们可以根据几个已知点,来计算方程的参数,一般需要六个方程,或者要三个点,为提高精度,可存在多余观测,然后利用最小二乘求其最小二乘解。
将公式利用泰勒公式线性化,取至一次项,得到其系数矩阵A ;引入改正数(残差)V ,则可将其写成矩阵形式:V AX L =-其中111333222333[,]()()()()()()()()()()()()()()Tx y A S A S A S x A S A S A S A S A S A S y A S A S A S L l l a X X b Y Y c Z Z l x x x fa X X a Y Y a Z Z a X Xb Y Yc Z Z l y y y fa X X a Y Y a Z Z =-+-+-=-=+-+-+--+-+-=-=+-+-+- 则1()T T X A A A L -=X 为外方位元素的近似改正数,由于采用泰勒展开取至一次项,为减少误差,要将的出的值作为近似值进行迭代,知道小于规定的误差三. 空间后方交会解算过程1. 已知条件近似垂直摄影00253.24mmx y 0f ===2. 解算程序流程图MATLAB 程序format long;s1=xlsread('data.xls');%读取数据a1=s1(1:4,1:2);%影像坐标b1=s1(1:4,3:5);%地面摄影测量坐标a2=s1.*10^-3;%影像坐标单位转化j1=a2(1,:)-a2(2,:);j2=j1(1,1)^2+j1(1,2)^2;lengh_a1=sqrt(j2); %相片某一长度j1=b1(1,:)-b1(1,:);j2=j1(1,1)^2+j1(1,2)^2;lengh_b1=sqrt(j2); %地面对应的长度m=lengh_b1/lengh_a1;%求出比例尺n0=0;p0=0;q0=0;x0=mean(b1(:,1));y0=mean(b1(:,2));f=153.24*10^-3;z0=m*f;x001={x0,x0,x0,x0};X0=cell2mat(x001)';y001={y0,y0,y0,y0};Y0=cell2mat(y001)';z001={z0,z0,z0,z0};Z0=cell2mat(z001)';%初始化外方位元素的值aa1=cos(n0)*cos(q0)-sin(n0)*sin(p0)*sin(q0);aa2=-sin(q0)*cos(n0)-sin(n0)*sin(p0)*cos(q0);aa3=-sin(n0)*cos(p0);bb1=sin(q0)*cos(p0);bb2=cos(q0)*cos(p0);bb3=-sin(p0);cc1=sin(n0)*cos(q0)+sin(p0)*cos(n0)*sin(q0);cc2=-sin(n0)*sin(q0)+sin(p0)*cos(q0)*cos(n0);cc3=cos(n0)*cos(p0);%计算改正数XX1=aa1.*(b1(:,1)-X0)+bb1.*(b1(:,2)-Y0)+cc1.*(b1(:,3)-Z0); XX2=aa2.*(b1(:,1)-X0)+bb2.*(b1(:,2)-Y0)+cc2.*(b1(:,3)-Z0); XX3=aa3.*(b1(:,1)-X0)+bb3.*(b1(:,2)-Y0)+cc3.*(b1(:,3)-Z0); lx=a1(:,1)+f.*(XX1./XX3);ly=a1(:,2)+f.*(XX2./XX3);l={lx',ly'};L=cell2mat(l)';%方程系数A=[-3.969*10^-5 0 2.231*10^-5 -0.2 -0.04 -0.06899;0 -3.969*10^-5 1.787*10^-5 -0.04 -0.18 0.08615;-2.88*10^-5 0 1*10^-5 -0.17 0.03 0.08211;0 -2.88*10^-5 -1.54*10^-5 0.03 -0.2 0.0534;-4.14*10^-5 0 4*10^-6 -0.15 -7.4*10^-3 -0.07663;0 -4.14*10^-5 2.07*10^-5 -7.4*10^-3 -0.19 0.01478;-2.89*10^-5 0 -1.98*10^-6 -0.15 -4.4*10^-3 0.06443;0 -2.89*10^-5 -1.22*10^-5 -4.4*10^-3 -0.18 0.01046];%L=[-1.28 3.78 -3.02 -1.45 -4.25 4.98 -4.72 -0.385]'.*10^-2; %第一次迭代X=inv(A'*A)*A'*L;3.结果X=1492.41127406195-554.4015671761941425.68660973544-0.0383847815608609 0.00911624039769785 -0.105416434087641S=1492.41127406195-554.401567176194 1425.68660973544 38436.9616152184 27963.1641162404-0.105416434087641。
后方交会法计算推导公式

后方交会法计算推导公式后方交会法是一种用于计算物体在空间中的坐标和距离的方法。
它基于两个观测者在不同位置观测同一个物体的现象。
假设有两个观测者A和B,在空间中观测同一个物体P。
观测者A 和B的位置分别为A(xA, yA, zA)和B(xB, yB, zB)。
物体P在观测者A和B的朝向上的投影分别为a和b,它们的长度分别为dA和dB。
根据几何关系,可以推导出以下公式:dA = sqrt((xA - xP)^2 + (yA - yP)^2 + (zA - zP)^2)dB = sqrt((xB - xP)^2 + (yB - yP)^2 + (zB - zP)^2)其中,(xP, yP, zP)是物体P的坐标。
如果已知dA、dB和相关观测者位置的坐标,可以使用这些公式来计算物体P的坐标(xP, yP, zP)。
同时,如果已知物体P在两个观测者朝向上的投影长度a和b,也可以利用这些公式计算物体P到观测者A和B的距离。
需要注意的是,后方交会法在实际应用中可能会受到观测误差的影响,因此在计算时需要考虑这些误差,并采取合适的数据处理和精度控制方法。
拓展:后方交会法是测量和定位的重要方法之一,广泛应用于地理测量、摄影测量、建筑工程等领域。
它可以通过精确的测量和计算,确定物体在三维空间中的准确位置和形状,对于工程设计、地理信息系统等具有重要的实际应用价值。
除了后方交会法,还有其他一些方法可以用于测量和定位物体的坐标和距离,比如三角测量法、三角高程测量法、全站仪测量法等。
每种方法都有其适用的场景和局限性,根据具体的测量需求和条件选择合适的方法是非常重要的。
此外,随着科技的进步和发展,新的测量和定位技术不断涌现,为实现更精确和高效的测量和定位提供了更多的选择。
后方交会残差值误差范围

后方交会残差值误差范围后方交会是摄影测量中常用的一种方法,用于确定地面上各个点的空间坐标。
在实际应用中,由于各种误差的存在,后方交会的结果会产生一定的残差值误差。
误差范围的确定对于保证测量结果的准确性和可靠性非常重要。
本文将从后方交会的基本原理、误差来源、误差计算方法以及误差范围的确定等方面进行详细的分析和论述。
一、后方交会的基本原理后方交会是一种基于像对几何关系的摄影测量方法,通过对各个像点的位置测量和相对方位角的观测,计算出地面控制点的空间坐标。
其基本原理可以简述如下:1. 反投影原理:根据像点在像空间上的位置,利用摄影测量的几何关系反推出这些像点所对应的地面点在物空间上的位置。
反投影原理是后方交会的理论基础,也是误差产生的根源。
2. 控制点观测:确定一定数量的控制点,并测量其像点位置及相对方位角。
控制点的选择应满足精度要求和实际情况,通常采用地面测量或其他摄影测量方法进行。
3. 几何模型:根据反投影原理和控制点观测,建立几何模型,描述像空间与物空间之间的几何关系。
模型包括相机的内外参数、像点的位置和相对方位角等。
4. 误差方程:利用几何模型,建立误差方程,将测量值与真实值之间的误差表示出来。
误差方程是分析误差来源、计算误差范围的基础。
二、后方交会误差的来源后方交会的误差主要来自于以下几个方面:1. 相机内外参数的误差:相机的内外参数是后方交会的重要参数,包括焦距、主点位置、旋转矩阵、平移向量等。
由于摄影测量设备和仪器的制造和使用限制,这些参数会存在误差,从而影响后方交会的结果。
2. 观测误差:观测误差包括控制点的像点测量误差和方位角观测误差。
像点测量误差可以由像点测量精度来描述,方位角观测误差可以由方位角观测精度来描述。
观测误差是由测量设备、操作人员和环境等因素共同引起的。
3. 地面控制点的精度:后方交会的精度还受到地面控制点的精度限制。
如果地面控制点的精度较差,那么后方交会的精度也会受到影响。
后方交会

后方交会-解释是工程测量中一种比较常用的一种测量方法.主要是通过两个或多已知点测量一个未知点.测角定位-正文利用测角仪器观测角度,以确定被测点位置的一种方法。
一般观测两个角,则有两条位置线,两线交点即为被测点位置。
在海洋测量中,测角定位通常使用的方法有:后方交会法,一般使用三标两角法,有时使用四标三角法,即在被测点上使用测角仪器观测3个或4个已知目标之间的夹角来确定点位;前方交会法,在两个或两个以上已知点上用测角仪器同时观测各已知点到某一被测点的夹角来确定点位;侧方交会法,综合使用后方交会法和前方交会法来实现定位的方法。
另外,还有一距离一方位法,也是通过测角测定方位和距离实现定位的。
因为测角仪器大部分是目视光学仪器,所以作用距离近,只适于近岸测量使用。
控制测量-正文在一定的区域内为地形测图或工程测量建立控制网(区域控制网)所进行的测量工作。
分为平面控制测量和高程控制测量。
平面控制网与高程控制网一般分别单独布设,也可以布设成三维控制网。
控制网具有控制全局,限制测量误差累积的作用,是各项测量工作的依据。
对于地形测图,等级控制是扩展图根控制的基础,以保证所测地形图能互相拼接成为一个整体。
对于工程测量,常需布设专用控制网,作为施工放样和变形观测的依据。
平面控制网常用三角测量、导线测量、三边测量和边角测量等方法建立。
三角测量是建立平面控制网的基本方法之一。
但三角网(锁)要求每点与较多的邻点相互通视,在隐蔽地区常需建造较高的觇标。
导线测量布设简单,每点仅需与前后两点通视,选点方便,特别是在隐蔽地区和建筑物多而通视困难的城市,应用起来方便灵活。
随着电磁波测距仪的发展,导线测量的应用日益广泛。
三边测量要求丈量网中所有的边长。
应用电磁波测距仪测定边长后即可进行解算。
此法检核条件少,推算方位角的精度较低。
边角测量法既观测控制网的角度,又测量边长。
测角有利于控制方向误差,测边有利于控制长度误差。
边角共测可充分发挥两者的优点,提高点位精度。
第2章后方交会

则
f sin H f a22 cos H y y0 a23 H ( x x0 )( y y0 ) ( y y0 ) 2 a24 cos ( f )sin f f a21 ( y y0 ) 2 ( x x0 )( y y0 ) a25 ( f ) cos sin f f
sin sin 0 0 cos cos
cos 0 sin
X Y 1 X X s 0 0 1 X X s Z R R 1 R 1 Y Y R 0 0 0 Y Y s s Z Z s 1 0 0 Z Z s
《摄影测量学》
第2 章
单片空间后方交会
主要内容
一、定义
二、误差方程和法方程 三、计算过程
一、定义 z
y s(Xs, Ys, Zs) Z
b a
x
c
根据影像覆盖范 围内一定数量的 分布合理的地面 控制点(已知其 像点和地面点的 坐标),利用共 线条件方程求解 像片外方位元素 C X
Y
B
A
注:如果我们有每张像片的六个外方位元素,就能恢复航摄像片 与被摄地面之间的几何关 R 1 Y Y s Z Z Z s
0 a 2 c1 a1c2 a c a c 3 1 1 3 0 b3 b 2 b3 0 b1
a1c2 a 2 c1 0 a 3 c 2 a 2 c3 b2 X b1 Y 0 Z
x f X X Z ( ) Z Z f b2 Z b3Y Z Y b2 f b3 f f Z X (b1Y b2 X ) Z X Y X (b1 b2 ) Z Z Z
测绘技术中的三角测量原理与方法解析

测绘技术中的三角测量原理与方法解析测绘技术是一门重要的工程学科,广泛应用于工程建设、地理空间信息等领域。
在测绘技术中,三角测量是一种基本的测量方法,其原理和方法对于准确测量地理空间位置、验证地理信息数据具有重要意义。
本文将详细解析三角测量的原理与方法,以帮助读者更好地理解这一测绘技术。
首先,三角测量基于三角形的几何性质进行测量,利用三角形的边长、角度和旁边之间的关系来计算未知距离或角度。
三角测量是建立在三角形的相似性原理上的,即在两个相似的三角形中,对应的角度是相等的,对应的边长之比是恒定的。
在实际测量中,三角测量的原理使用三角板、测距仪、全站仪等测量设备进行测量。
其中,最常见的是使用全站仪进行测量。
全站仪是一种先进的测量仪器,能够同时测量地形、测量地面点、测量建筑物等。
通过在目标物上设置测量点,测量仪器可以测量目标物与测量点之间的距离和角度,并根据三角测量原理推算出目标物之间的距离和角度。
除了全站仪,三角板也是一种常用的测量设备。
三角板是一个金属制成的三角形,用于测量目标物与测量点之间的角度。
通过目测三角板上对应角的刻度,可以推算出目标物之间的角度。
然后,结合已知边长,根据三角形的几何性质,可以计算出未知边长的长度。
三角测量的方法包括前方交会法、后方交会法和三边测量法。
前方交会法是利用已知点与未知点之间的角度和边长关系来计算未知点的坐标。
后方交会法是通过测量多个已知点与未知点之间的角度和边长,并结合已知点的坐标,推算出未知点的坐标。
三边测量法是通过测量三个已知点与未知点之间的角度和边长,计算出未知点的坐标。
三角测量在测绘技术中的应用广泛。
例如,在地理空间信息系统中,三角测量用于测量地形、道路、建筑物等。
在工程建设中,三角测量用于确定建筑物位置和高程。
三角测量还用于制图、制定土地规划等方面。
然而,三角测量也存在一些误差和限制。
由于测量仪器的精度和测量环境的影响,测量结果可能存在一定的误差。
此外,在测量过程中,如果参照点不准确或测量点位置选择不当,也可能导致测量结果的不准确性。
空间后方交会的直接解

空间后方交会的直接解空间后方交会,即由物方已知若干个控制点以及相应的像点坐标,解求摄站的坐标与影像的方位,这是一个摄影测量的基本问题。
通常采用最小二乘解算,由于原始的观测值方程是非线性的,因此,一般空间后方交会必须已知方位元素的初值,且解算过程是个迭代解算过程。
但是,在实时摄影测量的某些情况下,影像相对于物方坐标系的方位是任意的,且没有任何初值可供参考。
这时常规的空间后方交会最小二乘算法就无法处理,而必须建立新的空间后方交会的直接解法。
直接解法的基本思想是将它分成两步:先求出三个已知点i P 到摄站S 的距离i S ;然后求出摄站S 的坐标和影像方位。
物方一已知点()iiii,Z ,Y X P 在影像上的成像()iii,y x p ,根据影像已知的内方位元素()0,y f,x 可求得从摄站()SS S S ,Z ,Y X 到已知点i P 的观测方向i,βαi 。
()⎪⎪⎭⎪⎪⎬⎫-+-=-=2020tan tan x x f y y βf x x αi i i i i (1)距离方程组可以写成如下形式:⎪⎭⎪⎬⎫=+++=+++=+++020202312113312323233223221222211221b x x x a x b x x x a x b x x x a x (2)其中()j ;i ,,i,j S ,b a ijijijij≠===321cos ϕ。
因此,解算摄站S 到三个控制点的距离问题,被归结为解算一个三元二次联立方程组的问题。
这个方程组的解算方法选用迭代法。
迭代计算公式可写成:()()() ,,,K Ab Aa x K K 2101=+=+(3)其中,[]TS F S F S F a 231312232321212=()()()()()()()()()()[]T2K 1K 3312K 3K 2232K 2K 112K S S G S S G S S G b------=()()()()[]TK K K K S S S x 232221=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111111111---A⎪⎪⎭⎫ ⎝⎛=2sin 2122ij ij F ϕij ij ij F G ϕcos 22=因此,距离的初值,即当0=K 时,Aa x =0()()20i0iS S =()()()()()()()()()()[]T2010331203022320201120S S G S S G S S G b------=代入(2-24)式进行迭代。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
后方交会计算原理
一、已知参数:
A点(20515.6960,12164.6580)、B点(20546.1240,12497.4690)
A-架仪点平距:La、B-架仪点平距:Lb
二、求解方位角:
1、Aab=tan-1((Yb-Ya)/ (Xb-Xa))= tan-1((12164.658-12497.469)/
(20546.124-20515.696))= 84°46'34”
2、Lab=√((Xa-Xb)2+(Ya-Yb)2)=334.199=c
三、求解夹角:
1、C点处夹角c、A点处夹角a、B点处夹角b
2、C=cos-1√((C2- a2-b2)/2ab):由余弦定理公式得
3、A=sin-1 (La×sinC)/Lab):由正弦定理公式得
4、B=sin-1 (Lb×sinC)/Lab):由正弦定理公式得
四、求解方位角:
1、La边方位角a、Lb边方位角b
2、a=Aab+A
3、b=Aab-B
五、求解坐标:
1、C点处坐标:(由点A处推算)
Cx=Xa+La×cosa、Cy=Ya+La×sina
2、C点处坐标:(由点B处推算)
Cx=Xb+Lb×cosb、Cy=Yb+Lb×sinb
计算简图如下:
斜交放样方法:
一、已知参数
1、A点桩号:A
2、斜距离:S
3、斜交角:a
二、求解路线右幅:
Δx=S×sina、Δy=S×cosa 右幅桩号=A+Δy、边距=Δx 三、求解路线左幅:
Δx=S×sina、Δy=S×cosa
右幅桩号=A-Δy、边距=Δx 计算简图:。
