将军饮马问题的拓展与应用
“将军饮马”问题在空间几何中的应用与拓展

“将军饮马”问题在空间几何中的应用与拓展-中学数学论文“将军饮马”问题在空间几何中的应用与拓展湖北麻城第二中学袁少军一、什么是将军饮马问题将军饮马问题是这样的,传说古希腊的亚历山大城有一位精通数学和物理的学者,名叫海伦。
一天,一位将军专程去拜访他,向他请教一个百思不得其解的问题。
就是,将军每天要从山峰下的军营A出发,先到河边饮马,然后再到河岸同侧的军营B地开会,应该怎样走才能使路程最短?(如图1)据说这个问题,海伦略加思索就给出了解答(如图2)。
从此,这个被称为”将军饮马”的问题就广为流传。
这个问题可归纳为如下模型:在平面内给定一条直线L,以及在直线同侧的任意两点A,B,求在L上的点C,使CA+CB取得最小值。
这个问题中运用了对称性思想,并化折线段为直线段,依据三角形中两边之和大于第三边,可知点在C处时,CA+CB取最小值。
二、将军饮马问题在高中空间几何中的应用这个问题根据正方体的对称性,可以抽象为如下的数学问题:在如图3的正方体中,在棱BB1找一点P,求AP+C1P的最小值。
常见的解法有如下两种:评析:解法二中,选择边长为变量,建立相应函数,构造平面内三点,转化为“将军饮马”问题,使用了“以形助数,以数解形”的数形结合思想,使复杂问题简单化。
上述问题可归纳为如下模型:在空间中给定一条直线L,以及不在直线上的任意两点P,Q,求在L上的点R,使PR+QR取得最小值。
三、将军饮马问题在高中空间几何中的拓展如图7,在棱长为2的正方体ABCD-A1B1C1D1中,M是棱A1B1的中点,动点P在平面BB1D1D内运动,求PA+PM的最小值。
解:∵AC⊥面BB1D1D,且垂足为线段AC的中点。
故点A关于平面BB1D1D 的对称点为点C,根据对称性,∴PA=PC。
即PA+PM=PC+PM≥CM。
(如图8)评析:本题中求最小值是借助于对称思想来实现的,运用了类比思维,将二维空间中的“将军饮马”问题在三维空间做了相应的拓展。
将军饮马的原理和应用

将军饮马的原理和应用将军饮马,是一种古代的战术运用,指的是将军在战争中以一种饮马的姿势示弱,从而引诱敌方进攻,利用敌方的进攻来达到制胜的目的。
这一战术源自于古代马背上下文的文化背景,虽然随着战争形式的变化,将军饮马战术已不再实用,但其仍有一定的历史意义和传承。
将军饮马战术的原理是通过将军的饮马姿势来迷惑敌方,使敌方认为将军疲惫和无力,从而低估将军的实力和斗志。
将军饮马的姿势经常是将军坐在马背上,俯身倾斜,时而左右环顾,时而低头喝水。
这种姿势给人以疲惫和脆弱的印象,使敌方将领们心生轻敌之念,进而麻痹大意。
将军饮马战术的应用是多种多样的。
首先,将军饮马可以用来吸引敌方的注意力,从而分散敌军的注意力。
在战争中,战场上往往是混乱而紧张的,通过展示将军饮马的姿势,可以在一定程度上改变敌军的战略和战术布局,从而为己方的进攻创造有利的机会。
其次,将军饮马可以用来进一步破坏敌军士气。
在战争中,士气是极其重要的因素之一,高昂的士气可以激励士兵们奋勇作战,而低迷的士气则容易导致士兵心生退缩之念。
当敌方将领们看到将军饮马的样子,他们可能会认为将军已经疲惫不堪,士兵们的战斗力也会大大减弱,从而产生懈怠和退缩的情绪。
这为己方打击敌军士气提供了有利的条件。
此外,将军饮马还可以用来降低己方伤亡。
战争是血腥而残酷的,战场上的伤亡是家常便饭。
通过将军饮马战术,可以引诱敌方主动进攻,将己方兵力保持在更有利的防守地势。
同时,己方将军以示弱姿态出现,可以减少敌军对将军的攻击,为保护己方将军提供一定的安全保障。
当然,将军饮马战术也伴随着一定的风险和限制。
首先,敌方将领们是否会被将军饮马所迷惑,很大程度上取决于双方将领的军事素质和智慧。
如果敌方将领足够聪明,可以看穿将军饮马的伪装,那么将军饮马战术就会失败。
其次,将军饮马只是战争中的一种战术手段,无法单独决定战局的胜负,还需要与其他战术和策略相结合,以支撑整个作战计划的实施。
综上所述,将军饮马作为一种古代的战术运用,通过将军的饮马姿势来示弱,以达到引诱敌方和制胜的效果。
将军饮马问题的技巧

将军饮马问题的技巧1. 嘿,要记住找对称点啊!就像你要找另一个自己一样,比如在河的这岸找到与河对岸那个点相对称的点,这可是关键哟!就像你找好朋友,得找那个最懂你的呀!比如求 PA+PB 最小值时,找到 B 关于河的对称点B’,问题不就简单多了嘛!2. 哇塞,连接对称点和另一点呀!这就像搭起一座桥,把两个重要的地方连接起来。
比如找到了对称点后,把它和另外一个点连接起来,这不就是那条关键的路嘛!像要求 AC+CD+BD 最小值,先连接 A 和D’,多明显呀!3. 注意哦,这条线与河边的交点就是关键点呀!这就好比在茫茫人海中一下子找到那个对的人。
比如当那条连线与河边相交时,那个点就是将军饮马的最佳位置咯!就像你找宝藏,一下子就找到那个最特别的地方啦!比如在一个特定图形中,马上就能确定那个点。
4. 哎呀呀,可别小瞧了这简单的步骤哟!每一步都很重要呢,就像盖大楼,少了一块砖都不行。
比如明明知道要这样做,却粗心弄错,那不就可惜啦!像计算最小值,要是中间错了,结果不就不对啦!5. 还有还有,要多思考多尝试呀!别死脑筋只知道一种方法。
这就好像玩游戏,得各种攻略都试试。
比如有时候换个角度思考,或者尝试不同的对称点,说不定会有意外惊喜呢!比如一道复杂题,换个思路可能一下子就通了。
6. 真的呀,要把这些技巧深深印在脑子里哦!这样遇到问题就能马上想起来。
就像你记住最爱的美食做法一样。
比如考试的时候,这些技巧一用,难题瞬间变简单啦!就像武侠高手,轻松应对各种挑战。
7. 总之,熟练掌握将军饮马问题的技巧,你就无敌啦!相信自己一定可以的!这就像是拥有了一把神奇的钥匙,能打开各种难题的大门。
比如以后再碰到这类问题,你都能轻松搞定!。
将军饮马问题例题及应用
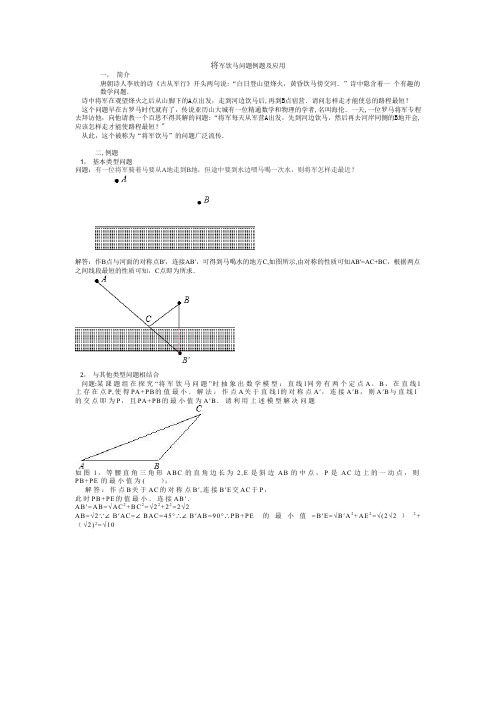
将军饮马问题例题及应用一,简介唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后,再到B点宿营.请问怎样走才能使总的路程最短?这个问题早在古罗马时代就有了,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:“将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?"从此,这个被称为“将军饮马”的问题广泛流传.二,例题1,基本类型问题问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?解答:作B点与河面的对称点B′,连接AB′,可得到马喝水的地方C,如图所示,由对称的性质可知AB′=AC+BC,根据两点之间线段最短的性质可知,C点即为所求.2,与其他类型问题相结合问题:某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l 上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l 的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决问题如图1,等腰直角三角形A B C的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为( );解答:作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小.连接AB′.AB′=AB=√AC2+B C2=√22+22=2√2AB=√2∵∠B′AC=∠B AC=45°∴∠B′AB=90°∴PB+PE的最小值=B′E=√B′A2+AE2=√(2√2)2+(√2)2=√10。
“将军饮马”模型详解与拓展

“将军饮马”模型详解与拓展平面几何中涉及最值问题的相关定理或公理有:① 线段公理:两点之间,线段最短. 并由此得到三角形三边关系;② 垂线段的性质:从直线外一点到这条直线上各点所连的线段中,垂线段最短. 在一些“线段和最值”的问题中,通过翻折运动,把一些线段进行转化即可应用①、② 的基本图形,并求得最值,这类问题一般被称之为“将军饮马”问题。
问题提出:唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.如图所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后再到B点宿营.请问怎样走才能使总的路程最短?模型提炼:模型【1】一定直线、异侧两定点直线l和l的异侧两点A、B,在直线l上求作一点P,使PA+PB最小解答:根据“两点之间,线段距离最短”,所以联结AB交直线l于点P,点P即为所求点模型【2】一定直线、同侧两定点直线l和l的同侧两点A、B,在直线l上求作一点P,使PA+PB最小解答:第一步:画点A关于直线l的对称点A'(根据“翻折运动”的相关性质,点A、A'到对称轴上任意点距离相等,如图所示,AP=A'P,即把一定直线同侧两定点问题转化为一定直线异侧两定点问题)第二步:联结A'B交直线l于点Q,根据“两点之间,线段距离最短”,此时“A'Q+QB”最短即“AQ+QB”最短模型【3】一定直线、一定点一动点已知直线l和定点A,在直线k上找一点B(点A、B在直线l同侧),在直线l上找点P,使得AP+PB最小解答:第一步:画点A关于直线l的对称点A'第二步:过点A'做A'B⊥k于点B且交直线l于点P,根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”,可知A'P+PB最小即AP+PB最小模型【4】一定点、两定直线点P是∠MON内的一点,分别在OM,ON上作点A,B,使△PAB的周长最小解答:策略:两次翻折第一步:分别画点P关于直线OM、ON的对称点P1、P2第二步:联结P1P2,交OM、ON于点A、点B(根据“翻折运动”的相关性质,AP=AP1,BP=BP2;根据“两点之间,线段距离最短”可知此时AP1+BP2+AB最短即△ABP周长最短)拓展如果两定点、两定直线呢?“如图,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。
数学将军饮马知识点总结

数学将军饮马知识点总结一、问题描述数学将军饮马问题的描述如下:一个将军率领一支骑兵队,要经过一片沙漠。
沙漠上有一口水井,水井的深度可以满足整支骑兵队的饮水需求。
将军骑着一匹马,可以携带一定数量的水。
现在问题来了,将军每小时可以骑马走一定的距离,而每匹马每小时可以喝一定的水。
现在需要确定将军携带多少水,才能保证整支骑兵队能够成功地跨越沙漠,而又不至于浪费水资源。
二、问题分析1. 数学模型建立数学将军饮马问题首先需要进行问题分析和建模,以确定针对这一问题的数学模型。
通过观察和分析可以得出,这是一个关于时间、距离和水量的问题,需要建立数学关系,建模求解。
2. 走距离与喝水在沙漠中骑马跋涉,对于骑马走的距离和喝水之间的关系需要进行合理的分析和计算。
根据数学将军饮马问题的描述,我们可以得知:将军每小时可以骑马走一定的距离,每匹马每小时可以喝一定的水。
3. 求解根据将军队伍的规模、马的喝水速度和水源的容量,我们需要求解将军携带多少水能够足够整支骑兵队顺利跨越沙漠的问题。
三、相关知识点总结1. 时间、距离与速度的关系在数学将军饮马问题中,时间、距离和速度是密不可分的。
根据题目描述,我们需要确定将军每小时可以骑马走的距离。
这就涉及到了时间、距离和速度的关系。
在实际生活和工作中,我们也经常会遇到时间、距离和速度的计算和关系问题,而这一问题正是数学知识在实际应用中的体现。
2. 水量的计算在数学将军饮马问题中,将军骑马携带的水量是一个重要的问题。
将军需要在保证整支骑兵队能够成功跨越沙漠的前提下,尽量减少携带的水量,避免浪费水资源。
因此,对于将军饮马问题,我们需要进行水量的计算和分析,以确定最合适的携带水量。
3. 最优化问题数学将军饮马问题可以理解为一个最优化问题,在保证整支骑兵队能够成功地跨越沙漠的前提下,需要尽量减少携带的水量,以达到最优化的效果。
这就涉及到了数学中的最优化问题的求解方法,需要通过建立数学模型、分析求解,找到最优的携带水量。
将军饮马的实际应用

将军饮马的实际应用将军饮马,是一个古老的典故,也有着实际的应用价值。
它源自于中国古代的一位著名将军,通过一杯美酒来判断马匹的状况。
这个典故在现代也有着一些实际应用,尤其在一些与决策相关的领域中。
本文将通过具体的案例来探讨将军饮马的实际应用。
在现代的商业领域中,将军饮马的思想可以被运用于市场调研。
市场调研是一个非常重要的环节,通过调查和分析市场的需求和竞争情况,可以为企业制定正确的市场策略提供依据。
而将军饮马的方法则可以帮助企业更好地理解市场的需求。
举个例子,假设一家公司计划推出一款新产品,并且已经完成了初步的市场调研,但仍然对市场潜在消费者的需求了解不够深入。
此时,将军饮马的方法可以派上用场。
公司可以选择一部分潜在消费者作为代表,并邀请他们参加一个市场调研会议。
在会议上,公司可以为参与者提供一些关于新产品的信息,并询问他们对于这个产品的看法和需求。
在参与者听取完产品的介绍之后,公司可以提供一款类似产品(可以是同种类别的其他产品,或者是一个样机),并邀请参与者使用以后分享他们的感受和意见。
通过参与者的反馈,公司可以更好地了解潜在消费者对于自家产品的看法和需求,通过这种方式可以更好地掌握市场的脉搏,从而制定出更合适的市场策略。
将军饮马的方法也可以应用于项目管理中的风险评估。
在项目管理中,风险评估是一个重要的环节,通过充分评估项目的风险,可以在项目执行阶段提前准备应对策略,从而最大限度地避免项目出现问题。
假设一个公司正在开发一个新的软件产品,并决定使用敏捷开发的方式进行项目管理。
在项目推进的过程中,开发团队发现有一个新的技术需要引入到项目中,这个技术尚未经过团队的认证和测试,存在一定的风险。
此时,将军饮马的方法可以派上用场。
团队可以选择一个技术熟悉的成员,并且让他负责这个新技术的验证和测试工作。
这个成员需要详细了解这个技术的原理和应用场景,并在项目中应用这个技术。
之后,团队可以通过这个成员的经验和反馈来评估这个新技术的可行性和稳定性。
初中数学将军饮马教案

初中数学将军饮马教案教学目标:1. 理解并掌握“将军饮马”问题的解题方法及其应用;2. 能够运用轴对称的性质解决实际问题;3. 提高学生的逻辑思维能力和解决问题的能力。
教学内容:1. 将军饮马问题的背景及解题思路;2. 轴对称的性质及其在解决问题中的应用;3. 将军饮马问题的拓展与应用。
教学过程:一、导入(5分钟)1. 引入问题:讲解唐朝诗人李颀的《古从军行》中的一句诗“白日登山望烽火,黄昏饮马傍交河”,提问学生是否知道这句诗中隐含着一个有趣的数学问题。
2. 学生思考并回答,教师总结:这个问题就是将军饮马问题。
二、新课讲解(20分钟)1. 讲解将军饮马问题的背景和解题思路,引导学生理解并掌握问题的解决方法。
2. 讲解轴对称的性质,引导学生了解轴对称在解决问题中的应用。
3. 通过例题讲解,让学生动手实践,巩固所学知识。
三、课堂练习(15分钟)1. 布置练习题,让学生独立完成,检验学生对知识的掌握程度。
2. 选取部分学生的作业进行讲解和评价,指出其中的错误和不足。
四、拓展与应用(10分钟)1. 讲解将军饮马问题的拓展,引导学生学会将问题进行拓展和应用。
2. 让学生举例说明轴对称在实际问题中的应用,分享自己的心得体会。
五、课堂小结(5分钟)1. 教师总结本节课的主要内容和知识点。
2. 学生分享自己在课堂上的收获和感悟。
教学评价:1. 课后作业的完成情况,检验学生对知识的掌握程度;2. 学生在课堂上的参与度和表现,评价学生的学习效果;3. 学生对拓展与应用部分的内容的理解和应用能力,评价学生的思维拓展能力。
教学反思:本节课通过讲解将军饮马问题,让学生了解了轴对称的性质及其在解决问题中的应用。
在教学过程中,要注意引导学生主动思考,培养学生的逻辑思维能力。
同时,要关注学生的学习反馈,及时调整教学方法和策略,提高教学效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B’
B
EF=a
A C
CD=a
A’
D
E
饮马人走的路径是A---C—D--B
F
应用1:
如图,已知点A(3,4),点B的坐标(-1,1),在X轴上另取 两点E,F(F在E的右侧),且EF=1.线段EF在X轴上平移, 线段EF平移至何处时,四边形ABEF的周长最小?求出此时点 E的坐标。
y
A
B E F
x
拓展2:
A’
M C
草地
河岸
N
A B D
B’
饮马人走的路程是A---C---D---B
应用:
A0 B 45 ,角内有一点P,PO=10,在角两边上有两 如图, 点Q,R(均不同于点0), 1)求 VPQR 的周长最小值是? 2)当 VPQR 周长最小时, QPR 的度数=( )
A
Q
P o
R
B
总结归纳升华
通过一系列的探索可知,将军饮马问题的本质:
1),求最短线路问题,通过几何变换找到对称图形。 2)把A,B两点在直线同侧的问题转化为在直线的两侧,化折线 为直线 3)利用“两点间线段最短”求解
结束语
今天我们共同经历了“饮马问题”拓展的探旅程, 相信你会有所感触,请你延续这种学习方法和探索方式, 你会发现数学其实挺好玩,你更会发现数学很有趣,数学也挺美。
.
二:探索数学本真
如图所示,诗中将军在观望烽火之后从山脚 下A点出发,走到河边饮马后再到B点宿营, 请问怎样走才能使总路程最短?
费马最短时间原理 :光是沿着光程为极值的路径传播的 B
A
河 流
c A’
两点之间,线段最短
将军饮马问题:
两线段之和最短这个问题早在古罗马时代就有 了,传说亚历山大城有一位精通数学和物理的学者, 名叫海伦.一天,一位罗马将军专程去拜访他,向 他请教一个百思不得其解的问题:
如图,A,B两点位于一条河的两岸,假定河的 两岸笔直且要在河上建一座桥,问把桥建在 何处,才能使点A经过这座桥到B点最短?
A
河 流 宽 度 为 X
C
河流
B’ B
B B’=X
拓展3:
如图,如果饮马人从点A出发,先到笔直的草地边 的某一处 饮马,再到笔直的河岸去饮马,然后回到B处,走什么样 的路程最短。
将军饮马问题的拓展与应用
苍南县青华学校 范叔阁 2015/6/16
看图思考: 为什么有的人会经常践踏草地呢?
禁止践踏 爱护草坪 绿地里本没有路,走的人多了… …
两点之间,线段最短
一:走进数学故事
唐 李 欣 《 古 从 军 行 》
年闻胡野行白 年道雁云人日 战玉哀万刁登 骨门鸣里斗山 埋犹夜无风望 荒被夜城沙烽 外遮飞郭暗火 ,,,,,, 空应胡雨公黄 见将儿雪主昏 蒲性眼纷琵饮 桃命泪纷琶马 入逐双连幽傍 汉轻双大怨交 家车落漠多河 。 。。。。。
变式一:
在直角坐标系中,有四个点A(-8,1), B(-4,5),C(0,n),D(m,0),当四边形ABCD的周长最 短时,求m/n
1,如何求AD的长度?
B
C
A
2,如何求AB的长度?
E
D
3,已知点A( X1,Y1),B(X2,Y2)如何求AB的长度?
( x 2) 1
2
表示哪两点的距离?
应用二:
求代数式
( x 2) 2 1 ( x 5) 2 25
的最小值
变式一:求函数 y x2 6 x 10 x 2 10 x 50 的最小值
三,探索拓展应用 拓展1:
如果饮马人从图中的A点出发到笔直的河岸L去饮马, 且沿河走一段路程a,然后再去B地,走什么样的路程最短呢?
将军每天骑马从城堡A出发,到城堡B,途中 马要到小溪边饮水一次。将军问怎样走路程最短? 这就是被称为"将军饮马"而广为流传的问题。
饮马问题的本质
B A B P A’ 图 2
异 侧
A
图1
P
变式一:思考,点p在直线L哪个位置的时候,有AP-BP最大?
A P P
图1
B A
图2
B’
同 侧
B
应用1, 如图,若A到直线L的距离AC是3KM,B到直 线L的距离BD是1KM,并且C,D的距离为4KM, 在直线L上找一点P,使PA+PB的值最小,并 求这个最小值。 A B P L C D H
A’
法二:
Y
A E P
(0,3)
B D
(4,1)
L
C
XA’Biblioteka (0,-3)变式一:
在直角坐标系中,有四个点A(-8,1), B(-4,5),C(0,n),D(m,0),当四边形ABCD的周长最 短时,求m/n
B
C A D
A’
B’
变式二:
如图,已知A(4,0),B(0,4),从点p(2,0)射出的光线经直线AB反 射后再射直线OB上,最后经直线OB反射又回到P点,则光线所经过的路程 是( A )(2013年湖南高考题) B:6 C: 3 3 A: 2 10 D: 2 5
