将军饮马问题27404PPT课件
2020中考数学复习 最值问题-将军饮马问题 (51张PPT)
02、将军饮马模型系列 ————“一定两动”之点到点
当P'、N、M、P''共线时，得△PMN周长的最小值，即线段P'P''长，连接OP'、 OP''，可得△OP'P''为等边三角形，所以P'P''=OP'=OP=8．
02、将军饮马模型系列 ————“两定两动”之点到点
在OA、OB上分别取点M、N使得四边 形PMNQ的周长最小。
05、将军过桥
【分析】 考虑MN长度恒定，只要求AM+NB最小值即可。问题 在于AM、NB彼此分离，所以首先通过平移，使AM与 NB连在一起，将AM向下平移使得M、N重合，此时A 点落在A'位置。
问题化为求A'N+NB最小值，显 然，当共线时，值最小，并得出 桥应建的位置．
05、将军过桥
通过几何变换将若干段原本彼此分离线段组合到一起，是解决问题的关键~
此处M点为折点，作点P关于OA对称 的点P'，将折线段PM+MN转化为 P'M+MN，即过点P'作OB垂线分别 交OA、OB于点M、N，得PM+MN 最小值（点到直线的连线中，垂线段 最短）
03、几何图形中的将军饮马
寻找几何图形中 端点关于折点所在直线的对称点位置
03、几何图形中的将军饮马 ----正方形中的“将军饮马”
则PC+PD的最小值为（ ）
A．4
B．5 C．6
D．7
03、几何图形中的将军饮马 ----正方形中的“将军饮马”
【分析】作点C关于P点所在直线AB的对称点C'，当C'、P、D共线时， PC+PD最小，最小值为5，故选B．
《最短路径-将军饮马问题》教学课件ppt
• A2
AB+BC+CA的和
为什么是最小呢？
·
M
A
两点之间
N
线段最短
反思验证
将军饮马问题
为什么AB+BC+CA的和最小？Fra bibliotek情节1：
O
B
C
• A2
A1 •
C′
B′ ·
M
A
N
两点之间 线段最短
反思验证
将军饮马问题
为什么AB+BC+CA的和最小？
情节2： A1 •
O
C
B
·
M
A
• A2
两点之间 线段最短
N
y
4
A′• 3 2 1•P
-4 -3 -2 -1 0 1 -1 -2 -3 -4
•A
2 3•P 4 x
•B
若换成y 轴呢？
一题多变
将军饮马问题
探究3 若将军要先让马到草地OM吃草，再到河边ON喝水 ，最后回到出发点A，你能画出最短路径吗？
O
A
M
N
探究新知
将军饮马问题
分析：1、建模：点在两直线的内部 2、在OM上找点B，在ON上找点C， 使AB+BC+CA的和最小。
O
B
·
M
A
考虑对称点的作用
C
1.将直线同侧两点问题转 化为直线异侧两点问题；
2.利用轴对称的性质可以 将相等线段转化。
N
方法揭晓
将军饮马问题
作法：
1、作点A关于直线OM的对称点A1，点A关于直线ON的对称点A2 ， 2、连接A1，A2，交OM于B，交ON于C,
则路径A-B-C-A是最短路径。
将军饮马(最完整讲义)
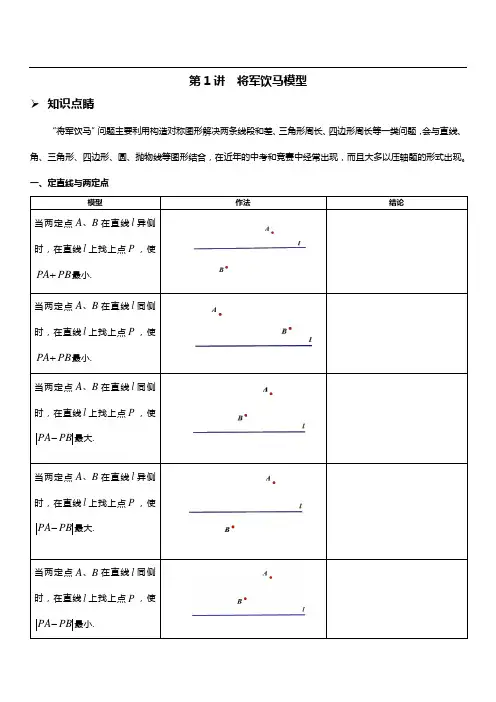
第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。
一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA+最小.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l异侧当两定点B时，在直线l上找上点P，使PA-最大.PBA、在直线l同侧当两定点B时，在直线l上找上点P，使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部，在OA 上找一点M ，在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部，在射线OA 上找一点P ，使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是，在OA 上找一点M ，在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、（M 在左），使NB MN AM ++最小,且d MN =.如图，21//l l ，21l l 、之间的距离为d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，且NB MN AM ++最小.如图，21//l l ，43//l l ,21l l 、之间的距离为1d ，43//l l 之间的距离为2d ，在21l l 、上分别找N M 、两点，使1l MN ⊥，在43l l 、上分别找Q P 、两点，使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图，在⊙O 上找一点N ，在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1：如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值．P OBAMN例2：如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值．例3：如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( )A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)第3题图 第4题图 第5题图例4：如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( ) A ．4B ．5C ．6D ．7例5：如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________． PDCBAA BCDMNNMDCBA例6：如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值．例7：如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3 B ．4 C ． D ．第7题图 第8题图 第9题图例8：如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( ) A B ．2 C ．D ．4例9：如图，在菱形ABCD 中，AC =BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，连接PE 、PM ，则PE +PM 的最小值是( ) A ．6B ．C ．D ．4.5NMDBA E AFCDBNM DCBAEPDCBAM例10：如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)3第10题图 第11题图 第12题图例11：如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A ．B ．C ．D 例12：如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( )A ．B ．C ．D ．例13：如图，∠AOB =60°，点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是( )A B C ．6D ．3第13题图 第14题图 CBH FGEDCB AA BMOPN例14：如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为 ．例15：如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为___________．第15题图例16：如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．例17：如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．AB CD EFMx例18：如图，正方形ABCD 的面积是12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，求PD+PE 的最小值。
将军饮马(最完整讲义)
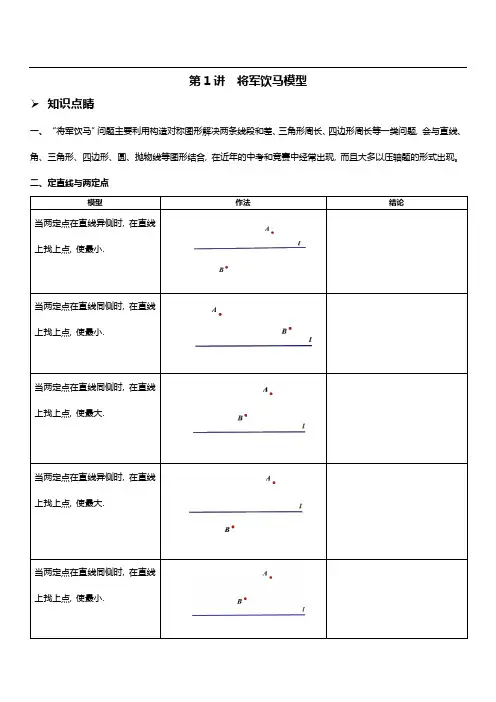
第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。
二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点（在左）, 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A ．例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A （4,4）, 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C ．,D ．第3题图 第4题图 第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5：如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________．A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图 第8题图 第9题图A ．例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA ．例10: 如图, 矩形ABOC 的顶点A 的坐标为（-4,5）, D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图 第11题图 第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图 第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N （3,0）是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15：如图, 已知正比例函数y=kx （k>0）的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为（0, 4）, P 为y 轴上的一个动点, M 、N 为函数y=kx （k>0）的图像上的两个动点, 则AM+MP+PN 的最小值为___________．第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为（6, 4）, E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17：如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值．x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。
将军饮马问题课件
将军饮马问题类型一、基本模式类型二、轴对称变换得应用(将军饮马问题)２、如图所示,如果将军从马棚M出发,先赶到河ＯＡ上得某一位置Ｐ,再马上赶到河OB上得某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P与Q),使得总路程MP+PQ+QN最短.【变式】如图所示,将军希望从马棚M出发,先赶到河ＯA上得某一位置P,再马上赶到河OB 上得某一位置Q。
请为将军设计一条路线(即选择点Ｐ与Q),使得总路程MＰ＋PＱ最短.３、将军要检阅一队士兵,要求(如图所示):队伍长为a,沿河ＯB排开(从点Ｐ到点Ｑ);将军从马棚M出发到达队头P,从P至Ｑ检阅队伍后再赶到校场N、请问:在什么位置列队(即选择点P与Q),可以使得将军走得总路程MP+PQ+ＱN最短？4。
如图,点Ｍ在锐角∠AOB内部,在OB边上求作一点P,使点P到点M得距离与点P到OA 边得距离之与最小5已知∠MON内有一点P,P关于OM,ON得对称点分别就是与,分别交OＭ, ＯＮ于点Ａ、B,已知=１5,则△ＰAB 得周长为( )ﻫＡ。
15 B 7、5 C。
10 D. ２4ﻫ6、已知∠AOB,试在∠AOB内确定一点P,如图,使P到OA、OB得距离相等,并且到M、N两点得距离也相等、7、已知∠MON=４０°,P为∠ＭON内一定点,OＭ上有一点A,OＮ上有一点B,当△ＰＡB得周长取最小值时,求∠ＡPB得度数、8、如图,在四边形ＡBCＤ中,∠A=９０°,ＡD＝4,连接ＢＤ,BD⊥ＣD,∠AＤＢ=∠C、若Ｐ就是BＣ边上一动点,则DP长得最小值为_＿__＿_.ﻫ练习1、已知点在直线外,点为直线上得一个动点,探究就是否存在一个定点,当点在直线上运动时,点与、两点得距离总相等,如果存在,请作出定点;若不存在,请说明理由、2、如图,在公路得同旁有两个仓库、,现需要建一货物中转站,要求到、两仓库得距离与最短,这个中转站应建在公路旁得哪个位置比较合理？３、已知:、两点在直线得同侧, 在上求作一点,使得最小。
将军饮马课件ppt
05
将军饮马问题的扩展和挑 战
变种问题
01
02
03
04
障碍物问题
在路径上设置障碍物，求最短 路径时需要避开障碍物。
多点折返问题
在路径上设置多个折返点，求 最短路径时需要多次折返。
限制条件问题
在求最短路径时加入限制条件 ，如步数限制、时间限制等。
动态变化问题
路径长度会随时间或其他因素 变化，需要求最短路径时考虑
这些变化。
计算复杂度
最坏情况下的时间复杂度
在最坏情况下，算法的时间复杂度可 能较高，需要优化算法以降低时间复 杂度。
空间复杂度
并行计算
为了提高算法的效率，可以考虑使用 并行计算来加速计算过程。
算法的空间复杂度也需要考虑，以评 估算法的内存消耗。
实际应用中的限制和优化
数据精度
在实际应用中，需要考虑 数据精度对算法的影响， 以避免误差累积导致结果 不准确。
在车辆调度方面，将军饮马问题同样 适用。通过优化车辆的出发时间和行 驶路线，物流公司可以最大化利用车 辆资源，提高运输效率。
计算机算法
图论算法
将军饮马问题作为图论中的经典问题，可以应用于计算机算法领域。通过解决将军饮马问题，可以开 发出更高效的图论算法，用于解决其他相关问题。
最短路径算法
最短路径算法是计算机算法中的重要组成部分。将军饮马问题可以作为最短路径算法的参考模型，帮 助开发人员找到图中两点之间的最短路径。
03
04
几何法是利用几何知识解决将 军饮马问题的方法。
它通过将问题转化为几何图形 ，利用几何定理和性质来找到
最短路径。
几何法适பைடு நூலகம்于具有明显几何特 征的问题，如两点之间的最短 距离、三角形中的最短路径等
将军饮马问题
A
B
编辑课件
河
7
(二)一次轴对称：两点在一条直线同侧
例2作法：
（1）作点B关于直线 MN 的对称点 B’ （2）连结B’A，交MN于点 C；
∴ 点C就是所求的点．
B
A
M
N
C
B’
编辑课件
8
(二)一次轴对称： 两点在一条直线同侧
例2证明：在MN 上任取另一点C’， B
A
连结BC、BC’、 AC’ 、 B’C’ ．
(2)连结A'和A''，交OM 于B，交ON于C。
则点B, C为所求。
编辑课件
12
(三)二次轴对称：一点在两相交直线内部
例3变式1：已知P是△ABC的边BC上的点， 你能在AB、AC上分别确定一点Q和R， 使△PQR的周长最短吗？
编辑课件
13
（四）二次轴对称：两点在两相交直线内部
例4：如图，A为马厩，B为帐篷，将军某一天要 从马厩牵出马，先到草地边某一处牧马， 再到河边饮马，然后回到帐篷， 请你帮助确定这一天的最短路线。
（3）可利用“两点之间线段最短” 加以解决。
编辑课件
19
反 思 阶是 梯进 步 的
我的收获；
我的疑惑；
面对一个新的求线段最短问题时， 我们可以通过怎样的途径去研究它？
编辑课件
20
编辑课件
9
(二)一次轴对称： 两点在一条直线同侧
例2变式1：已知：P、Q是△ABC的边AB、 AC上的点，你能在BC上确定一点R， 使△PQR的周长最短吗？
编辑课件
10
(三)二次轴对称：一点在两相交直线内部
例3.如图：一位将军骑马从驻地A出发，先牵马去草地 OM吃草，再牵马去河边ON喝水， 最后回到驻地A，
2.将军饮马模型-课件PPT
3
给妹妹讲初中数学
5 真题训练
2023·黑龙江省齐齐哈尔市
4
给妹妹讲初中数学
5 真题训练
2023·黑龙江省绥化市
5
给妹妹讲初中数学
5 真题训练
2023·广西
给妹妹讲初中数学 6
5 真题训练
2023·四川宜宾
给妹妹讲初中数学 7
5 真题训练
2023·湖南省邵阳市
8
给妹妹讲初中数学
5 真题训练
（2个动点不关联，转化为图形到图形的最值问题）
1个图形做对称图形，与另1个图形的最值。
点到点
图形到图形 直线到直线，垂直 直线到圆，过圆心 圆到圆，过两圆圆心
给妹妹讲初中数学 示例图
4 解题技巧
第五步：求最值。
解题技巧
找到图形中的最短值后，根据题意求解值即可。
给妹妹讲初中数学
4 解题技巧
解题技巧
2 模型探究
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
（2019，陕西）
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
（2020，云南）
给妹妹讲初中数学
4 解题技巧
（2019，沈阳）
给妹妹讲初中数学
4 解题技巧
1. 找出最值经过的所有点，标记定点和动点。
2. 画出所有动点的运动轨迹。
3. 判断最值的两个端点是动点还是定点。
4. 根据端点情况，做对称点/对称图形。
5. 求最值。
找动点 画轨迹 判两端 做对称 求最值
给妹妹讲初中数学
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则PB+PC的最小值是多少？
M
（2）若Q为x轴上一动点，则三角 形QCD的周长的最小值是多少？
（3）若M是x轴上一动点，N是y轴 一动点，则四边形MNCD的周长的 最小值是多少？
A
B
-1 0N 1Q 2 3
x
C′（2，-3）
.
6
学以致用：2017年莱芜市数学中考第9题
如图，菱形ABCD的边长为6，∠ABC=120°
yD 4
C（2,3）
上一动点，则PB+PC的最 小值=
A -1 O 1
B
3
x
（2）Q为x轴上一动点，则
三角形QCD周长的最小值=
（3）M是x轴上一动点，N
是y轴一动点，则四边形
.
12
，点M是BC边的一个三等分点，点P是AC上的动点， 当PB+PM的值最小时，PM的长是（ ）
D A
P
P
B
C E M .
7
堂堂清练习 1、在半径为1的⊙O 中，MN是直径，A为半圆的三等分点，
B为弧AN的中点，P为直径MN上的一动点，则PA+PB的最小值是 （ ）。
2、如图，边长为6的等边△ABC，AD ⊥ BC于D ，E为AC边
内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，
离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离
为(
)cm.
A
A
C蜂蜜
C蜂蜜
.
10
谢谢指导
.
11
探究二：已知二次函数交x
轴于A(-1,0)、B（3,0）两
点且过点C（2，3），写出 解析式并求出顶点D的坐标 。 （1）P为抛物线的对称轴
A.
B.
.l
. P P′
A′
.
2
“将军饮马”问题
------利用轴对称求最小值的问题
.
3
注意：
1、直线l是定直线,A、B两点是直线同侧的定点。 2、定点的对称点还是定点。 3、连接定点与对称点确定动点。 4、求出最小值即最短距离。
.
4
探究一：如图，正方形ABCD的边长是4，E
为BC边上一点，BE=1，P为对角线AC上一动点，
则 PE+PB的最小值=（
）
AP BE
D 解题要点：
1、 确定定直线和定点。
P
2、作对称，连接定点与对称点确 定动点.
3、求出最小值即最短距离
C
.
5
探究二： 已知二次函数交x轴于A(-1,0)、B
y
D′
D
（3,0）两点且过点C（2，3），写出解
析式并求出顶点D的坐标。
C(2,3)
（1）若P为抛物线的对称轴上一动点，
直击中考：
（2017年莱芜市数学中考题第9题）如图，
菱形ABCD的边长为6，∠ABC=120℃，点M是BC边
的一个三等分点，点P是对角线AC上的动点，当
PB+PM的值最小时，PM的长是（
）。
A
D
P
B
. MC
1
温情回顾： 如图，直线l是草原上的一条小河。将军
从草原的A地出发到河边饮马，然后再到B地军 营视察。那么走什么样的路线行程最短呢？
上一点，且AE:CE=1:2,点M为直线AD上一动点，则ME+MC的最
小值为( ) 。
A
.B
M
. O
N
…
..Βιβλιοθήκη .C8.
3、如图、在周长为12的菱形中AE=1，AF=2,若P为对角
线BD上一动点，则ＥＰ＋ＦＰ的最小值是（
）。
A E
F
B
P
D
C
.
9
附加题：
如图，圆柱形的玻璃杯的高为12cm,底面周长为18cm,在杯