9章-复功率
合集下载
复功率
有功功率是同相的UI乘积,无功功率是相位差为 的乘积. 有功功率是同相的 乘积,无功功率是相位差为90oUI的乘积. 乘积 的乘积 UR为U的有功分量 U X U UX为U的无功分量
UR
I
URI = P UX I = Q
P = UI cos
Q = UI sin
3. 无功功率 (reactive power) Q i + u i + u C L
功率因数提高 为什么要提高功率因数? 为什么要提高功率因数? (1) 充分利用设备容量 P=Scos S 负载 75kVA cos =1, P=S=75kW cos =0.7, P=0.7S=52.5kW cos = 0 则P = 0 (2)减少线路损耗. 减少线路损耗. 减少线路损耗 当P,U一定时 一定时
6. 有功功率的测量 单相功率表原理
电压线圈 * i1
*
i2
+
设电流i 从电流线圈" " 设电流 1从电流线圈"*"端流入 电压u正端接电压线圈" " 电压 正端接电压线圈"*"端 正端接电压线圈
u R
电流线圈 u U i2 ≈ = 2 sin(ωt φ) 设 i1 = i = 2 I sin ωt , R R U M = K I cos = K ' UI cos = K ' P 则力矩
已 知 f=50Hz , 且 测 得 U=50V , I=1A , P=3W .
V
P 30 解 P = I R ∴ R = 2 = 2 = 30 I 1 U 50 | Z |= = = 50 I 1 | Z |= R 2 + (ωL) 2
2
复功率及功率守恒.
串联
1 1 UC j I j U jQ U 0C R 0 C 0L U L jL I j U jQ U
UR RI U U I max R
并联
IG G U I
I max G 1 1 I L j U j I jQ I 0L G 0 L U
Y( j ) G j(C
1 ) L
I m [Y( j )] 0
Z ( j ) R
1 0 LC
1 Q R R 0 C R
Y( j ) G
0
L C
1 LC
1 G 0 L 1 C G L
0L
1
Q
0C
G
串、并联比较-----对偶原理
1 o L oC
1 0 LC
1)
I
即谐振时电流与电压同相 , I达到最大值
I( )
U R 2 (L 1 2 ) C
2) 各元件的电压相量为：
UR R I U
U L jL I j
I
+
R
1/jC - + U - + jL C U L _
1 1 Q ( ) 2 1
选择性
2) 通频带
网络函数的模不低于谐振时网络函数的模的
1 （0.707倍）的频率范围叫做 2
通频带。其宽度决定了幅频特性曲线的尖锐程度——通频带越窄， Q值越高，幅频
特性曲线越尖，选择性越好。
1 1 1 1 Q 2 ( ) 2 0.707 2
U R U 0.707
1 1 UC j I j U jQ U 0C R 0 C 0L U L jL I j U jQ U
UR RI U U I max R
并联
IG G U I
I max G 1 1 I L j U j I jQ I 0L G 0 L U
Y( j ) G j(C
1 ) L
I m [Y( j )] 0
Z ( j ) R
1 0 LC
1 Q R R 0 C R
Y( j ) G
0
L C
1 LC
1 G 0 L 1 C G L
0L
1
Q
0C
G
串、并联比较-----对偶原理
1 o L oC
1 0 LC
1)
I
即谐振时电流与电压同相 , I达到最大值
I( )
U R 2 (L 1 2 ) C
2) 各元件的电压相量为：
UR R I U
U L jL I j
I
+
R
1/jC - + U - + jL C U L _
1 1 Q ( ) 2 1
选择性
2) 通频带
网络函数的模不低于谐振时网络函数的模的
1 （0.707倍）的频率范围叫做 2
通频带。其宽度决定了幅频特性曲线的尖锐程度——通频带越窄， Q值越高，幅频
特性曲线越尖，选择性越好。
1 1 1 1 Q 2 ( ) 2 0.707 2
U R U 0.707
电路分析基础(第二版) 曾令琴 人民邮电出版社 课后答案 指导与解答4 课后答案【khdaw_lxywyl】
1、学习指导 （1）复功率
上等于电路中的有功功率 P，复功率的虚部在数值等于电路的无功功率 Q，复功率的模值等于 正弦交流电路中的视在功率 S。要注意的是，电路中各个元件上的有功功率可以相加，无功功 率可以相加减，但电路各部分的视在功率一般不能直接相加减，其中原因由读者自己考虑。 （2）功率因数的提高 由对功率的讨论我们引入了提高功率因数的问题。提高功率因数是指提高线路总电压与
初相， 任何一个正弦量都可以对应这样的一个复数， 而我们就把这个与正弦量相对应的复数称 为正弦量的相量，简称相量。换句话说，正弦量的相量就是特指用复数来表示的、与正弦量具 有一一对应关系的复数。 为区别与一般复数的不同， 相量头顶要带上标记 “· ” 。 值得注意的是， 一个相量可以充分表达正弦量的三要素， 只是由于电路中各量频率相同而省掉了频率而已 （如 上面 1.所述） 。相量仅为正弦量的一种表示方法，相量并不等于正弦量。 （3）复阻抗 复数形式的电阻和电抗称为复阻抗。相量分析法中的复阻抗的模对应正弦交流电路中的 电阻和电抗，例如单一电阻元件电路的复阻抗为R，是一个只有实部没有虚部的复数；单一电 感元件电路的复阻抗是jX L ，是没有实部，只有正值虚部的复数；单一电容元件电路的复阻抗
51
aw
案
（2）式中解析式不等于相量式，应改为
网
u 220 2 sin(t
)
U m 220 2e j 45 V
.c o
m
作好相量图是分析解决问题的关键环节， 也是一种基本的技能训练。 在正弦稳态电路的分析中， 利用相量图的帮助来分析和解决实际问题的例子很多， 相量图不仅能形象地表征出电路中各量 间的数量和相位关系， 有时通过对相量图能把隐含的问题浅显化， 藉助相量图往往可以方便地 定性分析电路中的某些特性， 使复杂问题从相量图的分析中显示的一目了然， 甚至能够起着四 两拨千斤的效果。 （2）RLC 串联电路的相量模型分析 相量分析法中，借助相量图分析电路很关键。相量图的画法，可根据具体问题的不同， 选择合适的一个电路变量作为参考相量， 串联电路的参考相量一般选用电流相量， 再根据各元 元件电压之间的相位关系和数量关系、 各电压与电流之间的相位关系一目了然。 注意相量图分 析中只有电压三角形是相量图，阻抗三角形不是相量图，它只反映了各元件参数的数量关系。 正弦并联电路采用相量分析法解题时，一般选取电压为电路的参考相量。然后根据 R、L、 后运用矢量图遵循的平行四边形法则或多角形法则， 定性地画出电路的相量图， 根据相量图分 2、学习检验结果解析 （1）一个 110V、60W 的白炽灯接到 50Hz、220V 正弦电源上，可以用一个电阻、或一个 电感、或一个电容和它串联。试分别求所需的 R、L、C 的值。如果换接到 220V 直流电源上， 这三种情况的后果分别如何？ （3）RLC 并联电路的相量模型分析 件上电压与电流的相位关系定性地画出各电压， 各电压比例尺应相同， 由这样的相量图可把各
最全第九章(正弦稳态电路分析)习题解答打印版.doc
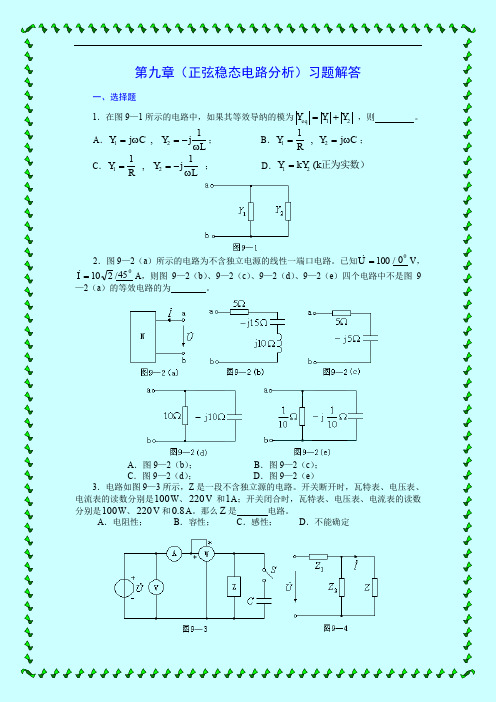
第九章（正弦稳态电路分析）习题解答一、选择题1．在图9—1所示的电路中，如果其等效导纳的模为21Y Y Y eq += ，则 。
A ．L Y C Y ω-=ω=1j, j 21； B ．C Y RY ω==j , 121；C ．L Y R Y ω-==1j , 121 ；D ．正为实数）k kY Y ( 21=2．图9—2（a ）所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ，045 /210=I A ，则图9—2（b ）、9—2（c ）、9—2（d ）、9—2（e ）四个电路中不是图9—2（a ）的等效电路的为 。
A ．图9—2（b ）；B ．图9—2（c ）；C ．图9—2（d ）；D ．图9—2（e ）3．电路如图9—3所示，Z 是一段不含独立源的电路。
开关断开时，瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ；开关闭合时，瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A ．电阻性；B ．容性；C ．感性；D ．不能确定4．电路如图9—4所示，U固定不变。
如果 ，则改变Z （Z 不等于无限大）时，I不变。
A ．21Z Z =； B ．21Z Z -=； C ．21Z Z =； D ．)Arg()Arg(21Z Z =5．Ω=10R 的电阻，F 1μ=C 的电容与电感L 串联，接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高，电感应取 。
A ．1H ；B ．π21Ｈ； C ．21H ； D ．241πＨ二、填空题1．若Ω=3R ，Ω=ω6L ，Ω=ω2011C ，Ω=ω2012C ，则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2．线性一端口电路如图9—6所示，A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率，有功功率、无功功率分别为V A 30/1000、W 350、50Var 。
复功率的物理意义
复功率的物理意义1. 复功率啊，那可太重要啦！就好比你要去完成一个大任务，有功功率就是你实际完成的部分，而无功功率就像是为了完成任务而做的那些辅助工作，复功率就是把这一切都综合起来啦！比如说在一个电路里，电流和电压相互作用，这就是复功率在起作用呀！2. 你想想看呀，复功率不就是把有功和无功功率都包含在内嘛！就像一场比赛，有功功率是直接得分，无功功率是那些精彩的配合和策略，而复功率就是这场比赛的整体表现呀！比如电动机运行的时候，不就是复功率在掌控全局嘛！3. 复功率的物理意义可别小瞧呀！它就如同一个团队的核心，有功功率和无功功率都是它的成员呀！像家里的电器工作时，复功率就在背后默默指挥着呢！4. 哎呀呀，复功率不就是有功和无功功率的完美结合嘛！好比一部电影，有功功率是精彩的剧情，无功功率是酷炫的特效，而复功率就是整部电影的魅力所在呀！就像变压器工作时体现的那样！5. 复功率真的很神奇的呀！它简直就像一个魔法盒子，把有功功率和无功功率都装进去啦！比如在电力系统中，复功率就是保证一切正常运转的关键呀！6. 你说复功率的物理意义是啥？那就是把各种力量汇聚在一起呀！就好像一场音乐会，有功功率是主旋律，无功功率是和声，而复功率就是那动人的乐章呀！像日光灯发光，就是复功率在起作用呢！7. 复功率啊，不就是对能量的一种全面描述嘛！就像一个人的综合素质，有功功率是能力，无功功率是魅力，而复功率就是这个人的整体呀！比如在电子电路中，复功率就是那个掌控者哟！8. 复功率的意义可大着呢！这不就是把有功和无功功率都整合起来的厉害角色嘛！像一个大工程，有功功率是主体建设，无功功率是配套设施，而复功率就是整个工程呀！例如在无功补偿装置中就体现明显呀！9. 复功率真的很关键呀！它就像是一个拼图的全貌，有功功率和无功功率是其中的小块呀！像在电力传输过程中，复功率的作用可不容忽视呀！10. 复功率的物理意义，那就是把有功功率和无功功率完美融合呀！就像一个完美的团队合作，有功功率是冲锋陷阵的战士，无功功率是提供支持的后勤，而复功率就是整个团队的战斗力呀！比如在大型工厂的用电中，复功率就是主宰呀！我的观点结论：复功率在电路和电力领域中有着极其重要的地位和意义，它全面地反映了能量的流动和利用情况，是我们理解和研究相关现象和系统的关键。
第九章 正弦稳态电路的分析
1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗（导纳） 分析阻抗（导纳）串、并联电路时，可以利用相关的 并联电路时， 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程，用相量平移求和法则，画出结点 方程， ③ 根据结点上的 方程 用相量平移求和法则， 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知：R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, （瞬时表达式）和各元件的 电路中的电流 瞬时表达式） 试求 电压相量； 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量；(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法： p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法： p UIcosϕ 恒定分量 恒定分量 u i
O
第9章 正弦稳态电路的分析(2010-2011第一学期 邱关源)
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
无源单口网络N0任一时刻输入的瞬时功率为该时刻 电压和电流的乘积，即
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
3. 视在功率 由于变压器等电力设备的容量是由它们的额定电压 和额定电流（均指有效值）的乘积决定的，为此引入视 在功率的概念，用大写字母S来表示
S UI
显然有
S 2 P 2 Q 2 S P2 Q 2
P S cos
Q S sin
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
瞬时功率还可以表示为
p UI cos UI cos 2t UI cos UI cos cos 2t UI sin sin 2t UI cos 1 cos 2t UI sin sin 2t
式中Y的实部就是电路中的电阻G，虚部即电抗B为
B BC BL C
1 BC C 为电容的电纳，简称容纳；BL 为电感的电 L
1 L
纳，简称感纳。
第九章 正弦稳态电路的分析
§9-1 阻抗和导纳
当 时，容纳的作用大于感纳的作用， 电路呈容性，这时， Y ,电流的相位超前于电压的 0 相位。 当 时，感纳的作用大于容纳的作 用，电路呈感性，这时，Y 0 ,电压的相位超前于电 流的相位。 B<0，即 C
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-3 正弦稳态电路的分析
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
无源单口网络N0任一时刻输入的瞬时功率为该时刻 电压和电流的乘积，即
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
3. 视在功率 由于变压器等电力设备的容量是由它们的额定电压 和额定电流（均指有效值）的乘积决定的，为此引入视 在功率的概念，用大写字母S来表示
S UI
显然有
S 2 P 2 Q 2 S P2 Q 2
P S cos
Q S sin
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
第九章 正弦稳态电路的分析
§9-4 正弦稳态电路的功率
瞬时功率还可以表示为
p UI cos UI cos 2t UI cos UI cos cos 2t UI sin sin 2t UI cos 1 cos 2t UI sin sin 2t
式中Y的实部就是电路中的电阻G，虚部即电抗B为
B BC BL C
1 BC C 为电容的电纳，简称容纳；BL 为电感的电 L
1 L
纳，简称感纳。
第九章 正弦稳态电路的分析
§9-1 阻抗和导纳
当 时，容纳的作用大于感纳的作用， 电路呈容性，这时， Y ,电流的相位超前于电压的 0 相位。 当 时，感纳的作用大于容纳的作 用，电路呈感性，这时，Y 0 ,电压的相位超前于电 流的相位。 B<0，即 C
9章_正弦稳态电路的分析n
9 正弦稳态电路的分析
9-1 阻抗和导纳 9-2 电路的相量图 9-3 正弦稳态电路的分析 9-4 正弦稳态电路的功率 9-5 复功率 9-6 最大功率传输
一、复阻抗Z
9-1 阻抗和导纳
I
+
U
无源 线性
-
I
+
U
Z
-
正弦激励下的无独立源线性网络，定义其入端等效复阻抗Z:
Z
UI
U I
(u
Z 2Ω I=8A ?
两个阻抗并联时,在什么情况下:
1 1 1 成立。
Z Z1 Z2
1. 图示电路中,已知 X L XC R 2Ω 电流表A1的读数为3A,
试问(1)A2和A3的读数为多少? + A1 A2 A3 (2)并联等效阻抗Z为多少? U L R C -
2. 如果某支路的阻抗 Z (8 j6)Ω, 则其导纳
阻抗三角形(impedance triangle)
|Z|
z
R
z > 0
X或
R
z
X |Z|
z < 0
| Z |
R2 X 2
φ arctan X R
R = |Z|cos z X = |Z|sin z
阻抗Z可以用加压求流法计算（含受控源），也可以用复阻 抗的串并联等效计算。
UL超 前I90°
由相量图可求得：
V 读数为141V
UL
100I1 10
U
45°I 45°
100UAB
10 2 I2
练习题
一、 如图电路中，已知：
i
u(t) 10cos(400π t 60o) V
9-1 阻抗和导纳 9-2 电路的相量图 9-3 正弦稳态电路的分析 9-4 正弦稳态电路的功率 9-5 复功率 9-6 最大功率传输
一、复阻抗Z
9-1 阻抗和导纳
I
+
U
无源 线性
-
I
+
U
Z
-
正弦激励下的无独立源线性网络，定义其入端等效复阻抗Z:
Z
UI
U I
(u
Z 2Ω I=8A ?
两个阻抗并联时,在什么情况下:
1 1 1 成立。
Z Z1 Z2
1. 图示电路中,已知 X L XC R 2Ω 电流表A1的读数为3A,
试问(1)A2和A3的读数为多少? + A1 A2 A3 (2)并联等效阻抗Z为多少? U L R C -
2. 如果某支路的阻抗 Z (8 j6)Ω, 则其导纳
阻抗三角形(impedance triangle)
|Z|
z
R
z > 0
X或
R
z
X |Z|
z < 0
| Z |
R2 X 2
φ arctan X R
R = |Z|cos z X = |Z|sin z
阻抗Z可以用加压求流法计算（含受控源），也可以用复阻 抗的串并联等效计算。
UL超 前I90°
由相量图可求得：
V 读数为141V
UL
100I1 10
U
45°I 45°
100UAB
10 2 I2
练习题
一、 如图电路中，已知：
i
u(t) 10cos(400π t 60o) V
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
o o
S1吸 U Y1 236 2 ( 1 )* 768 j1920 VA 10 j25
2 *
S2 吸 U Y2 1113 j3345 VA
2 *
S1吸 S2吸 S发
解2
o I1 100
5 j15 o 8.77(105.3 ) A 10 j25 5 j15
解法 2
PI R
2
P 30 R 2 2 30Ω I 1
又
2
U 50 Z 50Ω I 1
Z R 2 (L) 2
L
解法 3
1
1 Z R 50 2 30 2 0.127H 314
2
P UI cos
U 50 Z 50 Ω I 1
P 30 cos 0.6 UI 50 1
也可表示为：
I * ZI I * ZI 2 (R jX)I 2 RI 2 jXI 2 S U
* * 2 * S UI U (UY ) U (U Y ) U Y
结论
① ②
S是复数，而不是相量，它不对应任意正弦量； S 把 P、Q、S 联系在一起，它的实部是平均功率，虚
S P Q2Leabharlann 2SQ
P
功率三角形
5. R、L、C元件的有功功率和无功功率
i
u
+ i
R
PR =UIcos =UIcos0 =UI=I2R=U2/R QR =UIsin =UIsin0 =0
+ u i + u -
L
PL=UIcos =UIcos90 =0
QL =UIsin =UIsin90 =UI=I2XL
9.4 正弦稳态电路的功率
1. 瞬时功率
+ i
u _
无源 网络
u (t ) 2U cos(t u ) i (t ) 2 I cos(t i )
p(t ) ui 2U cos(t u ) 2I cos(t i ) UI [cos( u i ) cos(2t u i )] UI [cos φ cos(2t 2 u φ)]
第一种分解方法
第二种分解方法
UI cos φ[1 cos(2t 2 u )] UI sin sin(2t 2 u )
φ为u和i的相位差 φ u i
2 cos x cos y cos(x y ) cos(x y )
第一种分解方法：
p(t ) UI[cos φ cos(2t 2 u φ)]
可以用以下几种方法计算电压源发出的平均功率:
1. P发 出 U S I1 cos 2 2 cos45 2W ~ * 2. S U S I 1
~ 2 245 (2 j2) P Re(S ) 2W
2 3. P发 出 I12 R1 I 2 R2 (2 0.5 11) 2W
p u UIcos 恒定分量 i
o
t
UIcos (2t+2ψu－)为正弦分量 p 有时为正, 有时为负； p>0, 电路吸收功率； p<0，电路发出功率；
第二种分解方法：
p(t ) UI cosφ[1 cos(2t 2 u )] UI sin sin(2t 2 u )
不可逆分量
o
t
可逆分量
部分能量在电源和一端口之间来回交换。
2.平均功率 P
1 P T
1 T
T
0
T
pdt UI cosφ
[UI cos UI cos( 2t 2 u )]dt
0
P UI cos φ
cos ：功率因数。
单位： W(瓦)
=u-i：功率因数角。对无源网络，为其等效阻抗的
PC=UIcos =UIcos(-90)=0 QC =UIsin =UIsin (-90)= -UI= I2XC
C
6. 任意阻抗的功率计算
i + u Z PZ =UIcos =I2|Z|cos =I2R QZ =UIsin =I2|Z|sin =I2X
=I2(XL－XC)=QL－QC
分析 +
部是无功功率，模是视在功率；
③复功率满足守恒定理：在正弦稳态下，任一电路的所有 支路吸收的复功率之和为零。即
b b b P 0 k ( Pk jQk ) Sk k 1 b k 1 k 1 Qk 0 k 1 U U1 U 2 S S1 S2
2 I S I 1 14.9434.5o A I
S1吸 I1 Z1 8.77 (10 j25) 769 j1923 VA
2 2
S2 吸 I 2 Z 2 14.94 (5 j15) 1116 j3348 VA
2 2
* o S发 I1Z1 I S 10 8.77(105 .3 )(10 j25)
U _
B I
B
G I
B I
I
P UI cosφ UIG
U
Q UI sin φ UIB
称IG 为I的有功分量 称IB 为I的无功分量
P UI cos U R I
Q UI sin U X I
2 2 S P2 Q2 I U R UX IU
4. P发 出 I12 ReZ I12 Re1 j1 2 1 2W
9.* 正弦交流电路的两个功率问题
1. 功率因数的提高
功率因数低带来的问题： ① 设备不能充分利用 P=UIcos=Scos cos =1, P=S=75kW
S 75kVA
负载
cos =0.7, P=0.7S=52.5kW
当单口网络呈现纯电阻时，功率因数cos=1，功率利用 程度最高。当单口网络等效为一个电阻与电感或电容连接时， 即单口呈现电感性或电容性时，功率因数cos<1，以致于 P<UI。为了提高电能的利用效率，电力部门采用各种措施 力求提高功率因数。
例1
三表法测线圈参数。已知：f=50Hz，且测得U=50V，
用欧姆定律求出电流
U 2 0 S I 2 45 A 1 Z 1 j1
用分流公式求出电流
I 2
j1 j1 I2 I1 2 45 1 j1 2 45 j1 1 90 A
20 V I 2 45 A I 1 90 A U S 1 2
def
单位： VA (伏安)
它表示一个电气设备的容量，是单口网络所吸收平均功率
的最大值，为与其它功率相区别，用伏安(VA)为单位。例如我
们说某个发电机的容量为100kVA，而不说其容量为100kW。
有功，无功，视在功率的关系： 有功功率: 无功功率: 视在功率: P=UIcos Q=UIsin S=UI 单位：W 单位：var 单位：VA
某个家用电器消耗多少瓦的功率，就是指它的平均功率，
简称为功率。
3. 无功功率 Q
Q UI sin φ
def
单位： var(乏)
Q>0，表示网络吸收无功功率； Q<0，表示网络发出无功功率。 Q 的大小反映网络与外电路交换功率的规模，由储能元
件L、C的性质决定。
4. 视在功率S
S UI
1885 j1423 VA
例2 图(a)电路工作于正弦稳态，已知电压源电压为
uS (t ) 2 2 cos t V ，求电压源发出的平均功率。
解：图a)电路的相量模型，如图(b)所示。先求出连接电压 源单口网络的等效阻抗
( j1)(j1 1 j1) Z 0.5 j1.5 1 j1 0.5 j1.5 0.5 j0.5 (1 j1)
cosφD 0.8(感性） φD 36.8o
2200o 设U
5.68 36.8o I D
2200o jC j2.08 I C
I I 4.54 j1.33 4.73 16.3o I D C
cosφ cos[0o (16.3o )] 0.96
pC
i
uC
t
电压、电流的有功分量和无功分量： 以感性负载为例
P UI cos U R I
R _ +U I
+
U _
I
+
R
X U
+ X
U
Q UI sin U X I
X 称U R 为U 的 有 功 分 量 U
_
U R I
G I
G
称U X 为U 的 无 功 分 量
0
注意
复功率守恒，视在功率不守恒。
例1 解1
求电路各支路的复功率
+
1 I
2 I 10
j25
5 -j15
10∠0o A
Z (10 j25) //(5 j15)
U
_
100o Z 236(37.1o )V U
S发 236(37.1 ) 100 1882 j1424 VA
I=1A，P=30W。
I
+ A *
* W Z R
解法 1
S UI 50 1 50VA
V U
_
2 2 2 2 Q S P 50 30 L 40 var
P 30 R 2 30 I 1 XL
S1吸 U Y1 236 2 ( 1 )* 768 j1920 VA 10 j25
2 *
S2 吸 U Y2 1113 j3345 VA
2 *
S1吸 S2吸 S发
解2
o I1 100
5 j15 o 8.77(105.3 ) A 10 j25 5 j15
解法 2
PI R
2
P 30 R 2 2 30Ω I 1
又
2
U 50 Z 50Ω I 1
Z R 2 (L) 2
L
解法 3
1
1 Z R 50 2 30 2 0.127H 314
2
P UI cos
U 50 Z 50 Ω I 1
P 30 cos 0.6 UI 50 1
也可表示为：
I * ZI I * ZI 2 (R jX)I 2 RI 2 jXI 2 S U
* * 2 * S UI U (UY ) U (U Y ) U Y
结论
① ②
S是复数，而不是相量，它不对应任意正弦量； S 把 P、Q、S 联系在一起，它的实部是平均功率，虚
S P Q2Leabharlann 2SQ
P
功率三角形
5. R、L、C元件的有功功率和无功功率
i
u
+ i
R
PR =UIcos =UIcos0 =UI=I2R=U2/R QR =UIsin =UIsin0 =0
+ u i + u -
L
PL=UIcos =UIcos90 =0
QL =UIsin =UIsin90 =UI=I2XL
9.4 正弦稳态电路的功率
1. 瞬时功率
+ i
u _
无源 网络
u (t ) 2U cos(t u ) i (t ) 2 I cos(t i )
p(t ) ui 2U cos(t u ) 2I cos(t i ) UI [cos( u i ) cos(2t u i )] UI [cos φ cos(2t 2 u φ)]
第一种分解方法
第二种分解方法
UI cos φ[1 cos(2t 2 u )] UI sin sin(2t 2 u )
φ为u和i的相位差 φ u i
2 cos x cos y cos(x y ) cos(x y )
第一种分解方法：
p(t ) UI[cos φ cos(2t 2 u φ)]
可以用以下几种方法计算电压源发出的平均功率:
1. P发 出 U S I1 cos 2 2 cos45 2W ~ * 2. S U S I 1
~ 2 245 (2 j2) P Re(S ) 2W
2 3. P发 出 I12 R1 I 2 R2 (2 0.5 11) 2W
p u UIcos 恒定分量 i
o
t
UIcos (2t+2ψu－)为正弦分量 p 有时为正, 有时为负； p>0, 电路吸收功率； p<0，电路发出功率；
第二种分解方法：
p(t ) UI cosφ[1 cos(2t 2 u )] UI sin sin(2t 2 u )
不可逆分量
o
t
可逆分量
部分能量在电源和一端口之间来回交换。
2.平均功率 P
1 P T
1 T
T
0
T
pdt UI cosφ
[UI cos UI cos( 2t 2 u )]dt
0
P UI cos φ
cos ：功率因数。
单位： W(瓦)
=u-i：功率因数角。对无源网络，为其等效阻抗的
PC=UIcos =UIcos(-90)=0 QC =UIsin =UIsin (-90)= -UI= I2XC
C
6. 任意阻抗的功率计算
i + u Z PZ =UIcos =I2|Z|cos =I2R QZ =UIsin =I2|Z|sin =I2X
=I2(XL－XC)=QL－QC
分析 +
部是无功功率，模是视在功率；
③复功率满足守恒定理：在正弦稳态下，任一电路的所有 支路吸收的复功率之和为零。即
b b b P 0 k ( Pk jQk ) Sk k 1 b k 1 k 1 Qk 0 k 1 U U1 U 2 S S1 S2
2 I S I 1 14.9434.5o A I
S1吸 I1 Z1 8.77 (10 j25) 769 j1923 VA
2 2
S2 吸 I 2 Z 2 14.94 (5 j15) 1116 j3348 VA
2 2
* o S发 I1Z1 I S 10 8.77(105 .3 )(10 j25)
U _
B I
B
G I
B I
I
P UI cosφ UIG
U
Q UI sin φ UIB
称IG 为I的有功分量 称IB 为I的无功分量
P UI cos U R I
Q UI sin U X I
2 2 S P2 Q2 I U R UX IU
4. P发 出 I12 ReZ I12 Re1 j1 2 1 2W
9.* 正弦交流电路的两个功率问题
1. 功率因数的提高
功率因数低带来的问题： ① 设备不能充分利用 P=UIcos=Scos cos =1, P=S=75kW
S 75kVA
负载
cos =0.7, P=0.7S=52.5kW
当单口网络呈现纯电阻时，功率因数cos=1，功率利用 程度最高。当单口网络等效为一个电阻与电感或电容连接时， 即单口呈现电感性或电容性时，功率因数cos<1，以致于 P<UI。为了提高电能的利用效率，电力部门采用各种措施 力求提高功率因数。
例1
三表法测线圈参数。已知：f=50Hz，且测得U=50V，
用欧姆定律求出电流
U 2 0 S I 2 45 A 1 Z 1 j1
用分流公式求出电流
I 2
j1 j1 I2 I1 2 45 1 j1 2 45 j1 1 90 A
20 V I 2 45 A I 1 90 A U S 1 2
def
单位： VA (伏安)
它表示一个电气设备的容量，是单口网络所吸收平均功率
的最大值，为与其它功率相区别，用伏安(VA)为单位。例如我
们说某个发电机的容量为100kVA，而不说其容量为100kW。
有功，无功，视在功率的关系： 有功功率: 无功功率: 视在功率: P=UIcos Q=UIsin S=UI 单位：W 单位：var 单位：VA
某个家用电器消耗多少瓦的功率，就是指它的平均功率，
简称为功率。
3. 无功功率 Q
Q UI sin φ
def
单位： var(乏)
Q>0，表示网络吸收无功功率； Q<0，表示网络发出无功功率。 Q 的大小反映网络与外电路交换功率的规模，由储能元
件L、C的性质决定。
4. 视在功率S
S UI
1885 j1423 VA
例2 图(a)电路工作于正弦稳态，已知电压源电压为
uS (t ) 2 2 cos t V ，求电压源发出的平均功率。
解：图a)电路的相量模型，如图(b)所示。先求出连接电压 源单口网络的等效阻抗
( j1)(j1 1 j1) Z 0.5 j1.5 1 j1 0.5 j1.5 0.5 j0.5 (1 j1)
cosφD 0.8(感性） φD 36.8o
2200o 设U
5.68 36.8o I D
2200o jC j2.08 I C
I I 4.54 j1.33 4.73 16.3o I D C
cosφ cos[0o (16.3o )] 0.96
pC
i
uC
t
电压、电流的有功分量和无功分量： 以感性负载为例
P UI cos U R I
R _ +U I
+
U _
I
+
R
X U
+ X
U
Q UI sin U X I
X 称U R 为U 的 有 功 分 量 U
_
U R I
G I
G
称U X 为U 的 无 功 分 量
0
注意
复功率守恒，视在功率不守恒。
例1 解1
求电路各支路的复功率
+
1 I
2 I 10
j25
5 -j15
10∠0o A
Z (10 j25) //(5 j15)
U
_
100o Z 236(37.1o )V U
S发 236(37.1 ) 100 1882 j1424 VA
I=1A，P=30W。
I
+ A *
* W Z R
解法 1
S UI 50 1 50VA
V U
_
2 2 2 2 Q S P 50 30 L 40 var
P 30 R 2 30 I 1 XL