我国高校资金运营多目标非线性规划模型设计
合集下载
第5讲 整数规划、非线性规划、多目标规划1
第5讲整数规划、非线性规划、多目标规划一、整数规划1、概念数学规划中的变量（部分或全部）限制为整数时，称为整数规划。
若在线性规划模型中，变量限制为整数，则称为整数线性规划。
整数规划的分类:如不加特殊说明，一般指整数线性规划。
对于整数线性规划模型大致可分为两类：1）变量全限制为整数时，称纯（完全）整数规划。
2）变量部分限制为整数的，称混合整数规划。
2、整数规划特点(i)原线性规划有最优解，当自变量限制为整数后，其整数规划解出现下述情况：①原线性规划最优解全是整数，则整数规划最优解与线性规划最优解一致。
②整数规划无可行解。
例1原线性规划为21min x x z +=s.t.⎩⎨⎧≥≥=+0,05422121x x x x 其最优实数解为：01=x ，452=x ，45min =z ③有可行解（当然就存在最优解），但最优值变差。
例2原线性规划为21min x x Z +=s.t.⎩⎨⎧≥≥=+0,06422121x x x x 其最优实数解为：01=x ，232=x ，23min =z 若限制整数得：11=x ，12=x ，2min =z 。
（ii ）整数规划最优解不能按照实数最优解简单取整而获得。
3、0-1整数规划0−1型整数规划是整数规划中的特殊情形，它的变量j x 仅取值0或1。
这时j x 称为0−1变量，或称二进制变量。
j x 仅取值0或1这个条件可由下述约束条件：10≤≤j x ，且为整数所代替，是和一般整数规划的约束条件形式一致的。
在实际问题中，如果引入0−1变量，就可以把有各种情况需要分别讨论的线性规划问题统一在一个问题中讨论了。
引入10-变量的实际问题：（1）投资场所的选定——相互排斥的计划例3某公司拟在市东、西、南三区建立门市部。
拟议中有7个位置（点）)7,,2,1( =i A i 可供选择。
规定在东区：由321,,A A A 三个点中至多选两个；在西区：由54,A A 两个点中至少选一个；在南区：由76,A A 两个点中至少选一个。
非线性规划和多目标规划模型数学建模
i'j(ij2 )(m o d2 )
进一步考虑到角度的周期性，不碰撞的约束条件可写成：
ij i'jij 2ij
第5讲 非线性规划和多目标模型
最终，原非线性规划问题转化为
6
min i
iji'j 1 2 ( i ij) i2 6 1 , i ij,1i, 2,j,i,j , 61 ,2 , ,6
,
vsinyi0i'
,if
i'
3
2
,tani'
yi0 xi0
or 3
2
i'
2, tani'
yi0 Dxi0
（2）计算任意飞机在t时刻两者的距离：
d ij(i i,j j,t)2 (x i0 v tc o s (i i) x 0 j v tc o s (j j))2 (y i0 v ts in (i i) y 0 j v ts in (j j))2
s . t .
6
m in i i 1
d i j(i i,j j,t ) 8i j
i
6
目标函数也可以定义为
minmax 1i6
i
第5讲 非线性规划和多目标模型
我们来简单看一下其复杂程度
（1）区域内飞行时间：假设飞行角度为θi ’= θi + Δ θi
vDcosxi0i'
,if
0 i'
2
,
最优解 迭代法是主要求解方法: 通常从一个初始解出发，在可
行域中沿着使得目标函数降低的方向前进到下一个解。 一般求解方法：罚函数法，拉格朗日乘子法，近似规划
法等,或者采用智能算法，如：遗传算法，模拟退火算 法，蚁群算法等。
进一步考虑到角度的周期性，不碰撞的约束条件可写成：
ij i'jij 2ij
第5讲 非线性规划和多目标模型
最终，原非线性规划问题转化为
6
min i
iji'j 1 2 ( i ij) i2 6 1 , i ij,1i, 2,j,i,j , 61 ,2 , ,6
,
vsinyi0i'
,if
i'
3
2
,tani'
yi0 xi0
or 3
2
i'
2, tani'
yi0 Dxi0
（2）计算任意飞机在t时刻两者的距离：
d ij(i i,j j,t)2 (x i0 v tc o s (i i) x 0 j v tc o s (j j))2 (y i0 v ts in (i i) y 0 j v ts in (j j))2
s . t .
6
m in i i 1
d i j(i i,j j,t ) 8i j
i
6
目标函数也可以定义为
minmax 1i6
i
第5讲 非线性规划和多目标模型
我们来简单看一下其复杂程度
（1）区域内飞行时间：假设飞行角度为θi ’= θi + Δ θi
vDcosxi0i'
,if
0 i'
2
,
最优解 迭代法是主要求解方法: 通常从一个初始解出发，在可
行域中沿着使得目标函数降低的方向前进到下一个解。 一般求解方法：罚函数法，拉格朗日乘子法，近似规划
法等,或者采用智能算法，如：遗传算法，模拟退火算 法，蚁群算法等。
运用多元线性回归模型分析我国教育经费投入现状
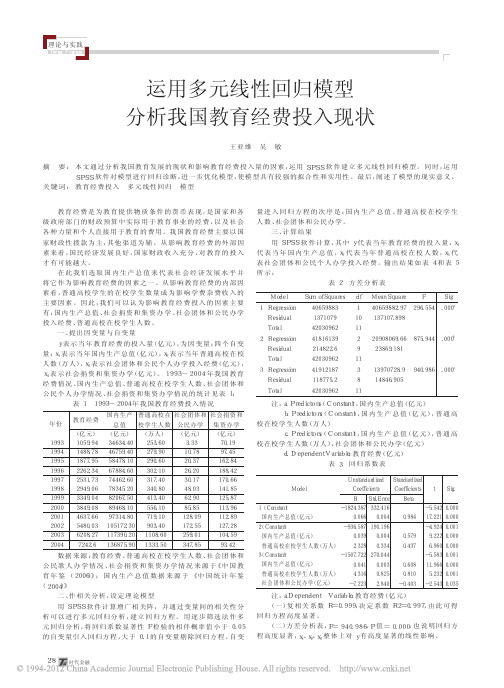
２ ２０９０８０６９．６６ ８７５．９４４ ．０００ｂ
Ｒｅｓｉｄｕａｌ
２１４８２２．６
９ ２３８６９．１８１
Ｔｏｔａｌ
４２０３０９６２ １１
３ Ｒｅｇｒｅｓｓｉｏｎ ４１９１２１８７
３ １３９７０７２８．９ ９４０．９８６ ．０００ｃ
Ｒｅｓｉｄｕａｌ
１１８７７５．２
８ １４８４６．９０５
Ｔｏｔａｌ
４２０３０９６２ １１
社会团体和公民办学（ 亿元）
－ ７．２２３ ２．８４０ － ０．４０３ － ２．５４３ ０．０３５
注： ａ．Ｄｅｐｅｎｄｅｎｔ Ｖａｒｉａｂｌｅ： 教育经费（ 亿元） （ 一） 复 相 关 系 数 Ｒ＝０．９９９， 决 定 系 数 Ｒ２＝０．９９７， 由 此 可 得 回归方程高度显著。 （ 二） 方差 分 析表 ， Ｆ＝ ９４０．９８６， Ｐ 值＝ ０．０００， 也 说 明 回归 方 程 高度 显 著 ， ｘ１、ｘ２、ｘ３ 整体 上 对 ｙ 有高 度 显 著的 线 性 影响 。
国内生产总值是教育经费投入的一个 决定和限制量， 教育经费的投入围绕着国内 生产总值的变化而上下波动， 这是教育受经
教育经费投入多元线性回归模型年份教育经费国内生产总值亿元346344046759405847810678846074462607834520820675089468109731480105172301173902013687590普通高校在校学生人数万人25360279902906030210317403408041340556107191090340110860133350社会团体和公民办学亿元333107820372620301748036290858512809172552590134785社会捐资和集资办学亿元701997451628418842170661418512587113961128912728104599342亿元10599414887818779522623425317329490633490438490846376654800362082772426199319941995199619971998199920002001200220032004modelsumofsquaresdfmeansquarefsig000a1regression4065988314065988297296554residual137107910137107898total42030962112regression4181613922090806966875944000bresidual2148226923869181total42030962113regression419121873139707289940986000cresidual1187752814846905total4203096211modelunstandardizedcoefficientsbstandardizedcoefficientsbetatsigstderror1constant182438733241655420000国内生产总值亿元0066000409841722100002constant93658719019649240001国内生产总值亿元00390004057992220000普通高校在校学生人数万人232803340437696000003constant150772227004455830001国内生产总值亿元004100030608119660000普通高校在校学生人数万人43160825081052320001社会
基于非线性优化算法的多目标决策研究
基于非线性优化算法的多目标决策研究在现代社会中，决策是普遍存在的。
而在实际的决策中，往往存在着多个目标，如何在这些目标之间做出权衡，使得决策达到最优，成为了一个相当重要的问题。
而传统的决策方法，往往会产生问题，比如不够灵活、难以处理多个目标等等。
因此，基于非线性优化算法的多目标决策研究日益被人们关注。
一、多目标决策的背景和重要性在实际的决策中，往往存在着多个目标，这些目标之间又往往存在着矛盾和制约。
因此，在做出决策时，需要考虑多个目标之间的权衡和协调，以达到最优决策的目的。
同时，由于决策的影响范围和目标的多样性，多目标决策在实际应用中十分普遍，如投资决策、环境保护、资源配置等等。
然而，传统的决策方法往往过于简单单一，无法处理多目标情况下的权衡和协调，造成了很多问题和损失。
因此，基于非线性优化算法的多目标决策研究显得尤为重要。
通过将优化和多目标分析技术结合起来，可以更好地处理复杂的多目标决策问题，为实际决策提供更好的支持和辅助。
二、非线性优化算法在多目标决策中的应用1. 多目标优化模型在多目标决策的研究中，多目标优化模型是一种基本的工具。
该模型可以将多个目标同时考虑进入，以求得满足多个目标的最优解。
其中，确定目标的权重和目标函数的线性/非线性特性是模型的主要难点。
在非线性优化算法中，基于多种方法的多目标优化模型已经得到了广泛的应用。
其中，常用的算法包括遗传算法、粒子群算法、人工免疫算法等等。
这些算法在多目标决策中具有较好的适用性，可以处理非线性目标函数，同时还可以给出较为全面的解集，方便决策者做出权衡决策。
2. 模糊优化模型在实际决策中，常常会涉及到模糊的目标和约束条件。
针对这种情况，非线性优化算法中的模糊优化模型应运而生。
模糊优化模型通过引入模糊度概念，将真实世界中存在的模糊目标和约束进行合理地处理，以便更好地完成多目标决策。
在模糊多目标优化模型中，常用的算法包括模糊遗传算法、模糊粒子群算法、模糊聚类和模糊神经网络等等。
非线性最优化模型
案例二：生产调度优化的应用
总结词
生产调度优化是利用非线性最优化模型来安排生产计划 ，以提高生产效率和降低生产成本。
详细描述
生产调度问题需要考虑生产线的配置、工人的排班、原 材料的采购等多个因素。非线性最优化模型能够综合考 虑这些因素，并找到最优的生产调度方案，提高生产效 率，降低生产成本，并确保生产计划的可行性。
04
非线性最优化模型的实例分析
投资组合优化模型
投资组合优化模型
通过非线性最优化方法，确定最佳投资组合配置，以实现预期收 益和风险之间的平衡。
目标函数
最大化预期收益或最小化风险，通常采用夏普比率、詹森指数等 作为评价指标。
约束条件
包括投资比例限制、流动性约束、风险控制等。
生产调度优化模型
01
生产调度优化模型
非线性最优化模型
• 非线性最优化模型概述 • 非线性最优化模型的分类 • 非线性最优化模型的求解方法 • 非线性最优化模型的实例分析 • 非线性最优化模型的挑战与展望 • 非线性最优化模型的应用案例
01
非线性最优化模型概述
定义与特点
定义
非线性最优化模型是指用来描述具有 非线性特性的系统或问题的数学模型 。
多目标非线性优化模型
多目标
多目标非线性优化模型中存在多个目标函数，这些目标函 数之间可能存在冲突。
01
求解方法
常用的求解方法包括权重法、帕累托最 优解法、多目标遗传算法等，这些方法 通过迭代过程逐步逼近最优解。
02
03
应用领域
多目标非线性优化模型广泛应用于各 种领域，如系统设计、城市规划、经 济分析等。
通过非线性最优化方法，合理安 排生产计划和调度，以提高生产 效率和降低成本。
数学实验报告-非线性规划与多目标规划实验
编写函数文件：
1）建立函数M文件：
functionf=fun(x)
f=-20*exp(-0.2*(0.5*(x(1)^2+x(2)^2)^0.5))-exp(0.5*(cos(2*pi*x(1))+cos(2*pi*x(2))))+22.713;
2）
x0=[0,0];
options=optimset('display', 'iter', 'tolfun',1e-10);
1982
0.117
0.465
0.215
0.187
0.213
0.311
-0.019
0.084
1983
0.092
-0.015
0.224
0.235
0.217
0.08
0.237
-0.128
1984
0.103
0.159
0.061
0.03
-0.097
0.15
0.074
-0.175
1985
0.08
0.366
0.316
[3]熟悉MATLAB软件求解非线性规划模型的基本命令；
[4]通过范例学习，了解建立非线性规划模型的全过程，与线性规划比较其难点何在。
本实验包括基础实验、应用实验和创新实验，基础实验和应用实验要求独立完成，创新实验要求合作完成。通过该实验的学习，使学生掌握最优化技术，认识面对什么样的实际问题，提出假设和建立优化模型，并且使学生学会使用MATLAB软件和Lingo软件求解非线性规划模型，注意初始解的选择不同会导致软件求出的解的变化（是局部最优解还是整体最优解）。解决现实生活中的最优化问题是本科生学习阶段中一门重要的课程，因此，本实验对学生的学习尤为重要。
1）建立函数M文件：
functionf=fun(x)
f=-20*exp(-0.2*(0.5*(x(1)^2+x(2)^2)^0.5))-exp(0.5*(cos(2*pi*x(1))+cos(2*pi*x(2))))+22.713;
2）
x0=[0,0];
options=optimset('display', 'iter', 'tolfun',1e-10);
1982
0.117
0.465
0.215
0.187
0.213
0.311
-0.019
0.084
1983
0.092
-0.015
0.224
0.235
0.217
0.08
0.237
-0.128
1984
0.103
0.159
0.061
0.03
-0.097
0.15
0.074
-0.175
1985
0.08
0.366
0.316
[3]熟悉MATLAB软件求解非线性规划模型的基本命令；
[4]通过范例学习，了解建立非线性规划模型的全过程，与线性规划比较其难点何在。
本实验包括基础实验、应用实验和创新实验，基础实验和应用实验要求独立完成，创新实验要求合作完成。通过该实验的学习，使学生掌握最优化技术，认识面对什么样的实际问题，提出假设和建立优化模型，并且使学生学会使用MATLAB软件和Lingo软件求解非线性规划模型，注意初始解的选择不同会导致软件求出的解的变化（是局部最优解还是整体最优解）。解决现实生活中的最优化问题是本科生学习阶段中一门重要的课程，因此，本实验对学生的学习尤为重要。
基于多目标多元非线性规划模型及“以大代小”方法的电力负荷预测方案设计
ｏ ｎ Ｍｕ ｌ ｔ ｉ ． ｏ ｂ ｊ ｅ ｃ ｔ ｉ ｖ ｅ Ｍｕ ｌ ｔ ｉ ｖ ａ ｒ ｉ ａ ｔ ｅ Ｎ ｏ ｎ — ｌ ｉ ｎ ｅ ａ ｒ Ｐ ｌ ａ ｎ ｎ ｉ ｎ ｇ Ｍｏ ｄ ｅ ｌ
ａ ｎ ｄ Ｒｅ ｐ ｌ ａ ｃ ｅ ｍｅ ｎ ｔ ｏ ｆ Ｓｍａ ｌ ｌ ｌ ｔ ｅ ｎｓ ｒ ｂ ｙ Ｌ ａ ｒ ｇ ｅ ０ｎ ｅ ｓ
ｉ ｎ ｔ ｈ ｅ ｓ ａ ｍ ｅ ｗ ａ ｙ ａ ｓ ｔ ｈ ａ ｔ ｏ ｆ ｒ ｓ ｉ ｎ ｇ ｌ ｅ — ｏ ｂ ｊ ｅ ｃ ｔ ｉ ｖ ｅ ｏ ｐ ｔ ｉ ｍ ｉ ｚ ａ ｔ ｉ ｏ ｎ ．
Ｋｅ ｙ ｗ ｏ ｒ ｄ ｓ ： ｒ ｅ ｐ ｌ ａ ｃ ｅ ｍ ｅ ｎ ｔ ｏ ｆ ｓ ｍ ａ ｌ ｌ ｉ ｔ ｅ ｍ ｓ ｂ ｙ ｌ ａ ｒ ｇ ｅ ｏ ｎ ｅ ｓ ； ｌ ｏ ａ ｄ ｄ ｉ ｓ ｔ ｉ ｒ ｂ ｕ ｔ ｉ ｏ ｎ ； ｍ ｕ ｌ ｔ ｉ — ｏ ｂ ｊ ｅ ｃ ｔ ｉ ｖ ｅ ｐ ｌ ａ ｎ ｎ ｉ ｎ ｇ ９ ‘ Ａ ｎ ｇ ｌ ｙ ｔ ｉ ｃ ｈ ｉ ｅ ｒ ａ ｒ ｃ ｈ ｙ ｐ ｒ ｏ ｃ ｅ ｓ ｓ ； Ｌ Ｉ Ｎ Ｇ Ｏ
［ 中图分类号 ］Ｔ Ｍ ６ ０ ［ 文献标志码 ］Ａ ［ 文章编号 ］１ ０ ０ ０—３ ８ ８ ６ （ ２ ０ １ ４ ） ０ １— ０ ０ ８ ２— ０ ３
Ｄｅ ｓ ｉ ｇ ｎ ｏ ｆ ａ Ｓｃ ｈ ｅ ｍｅ ｆ ｏ ｒ Ｅｓ ｔ ｉ ｍａ ｔ ｉ ｏ ｎ ｏ ｆ Ｐｏ ｗｅ ｒ Ｌ ｏ ａ ｄ Ｂａ ｓ ｅ ｄ
ｕ ｓ ｅ ｄ ｔ ｏ ｒ ｅ ｌｉ ａ ｚ ｅ ｓ ｉ ｎ ｇ ｌ ｅ — ｏ ｂ ｊ ｅ ｃ ｔ ｉ ｖ ｅ ｏ ｐ ｔ ｉ ｍ ｉ ｚ ａ ｔ ｉ ｏ ｎ ｏ ｎ ｔ ｈ ｅ ｍ ｏ ｄ ｅ １ ．Ｆ ｉ ｎ ａ ｌ ｌ ｙ ， ｔ ｈ ｅ ｏ ｐ ｔ ｉ ｍ ｌ ａ ｓ ｃ ｈ ｅ ｍ ｅ ｆ ｏ ｒ ｌ ｏ ａ ｄ ｄ ｉ ｓ ｔ ｒ ｉ ｂ ｕ ｔ ｉ ｏ ｎ ｉ ｓ ｓ ｏ ｌ ｖ ｅ ｄ ｔ ｈ ｒ ｏ ｕ ｇ ｈ Ｌ Ｉ Ｎ Ｇ Ｏ
《多目标规划模型》课件
02
权重法的主要步骤包括确定权重、构造加权目标函数、求解加权目标函数，最 后得到最优解。
03
权重法的优点是简单易行，适用于目标数量较少的情况。但缺点是主观性强， 依赖于决策者的经验和判断。
约束法
1
约束法是通过引入约束条件，将多目标问题转化 为单目标问题，然后求解单目标问题得到最优解 。
2
约束法的主要步骤包括确定约束条件、构造约束 下的目标函数、求解约束下的目标函数，最后得 到最优解。
多目标规划模型
目录
• 多目标规划模型概述 • 多目标规划模型的建立 • 多目标规划模型的求解方法 • 多目标规划模型的应用案例 • 多目标规划模型的未来发展与挑战
01 多目标规划模型概述
定义与特点
定义
多目标规划模型是一种数学优化方法 ，用于解决具有多个相互冲突的目标 的问题。
特点
多目标规划模型能够权衡和折衷多个 目标之间的矛盾，寻求满足所有目标 的最佳解决方案。
02 多目标规划模型的建立
确定目标函数
01
目标函数是描述系统或决策问题的期望结果的数学表达 式。
02
在多目标规划中，目标函数通常包含多个目标，每个目 标对应一个数学表达式。
03
目标函数的确定需要考虑问题的实际背景和决策者的偏 好。
确定约束条件
01 约束条件是限制决策变量取值范围的限制条件。 02 在多目标规划中，约束条件可以分为等式约束和
谢谢聆听
模型在大数据和人工智能时代的应用前景
要点一
总结词
要点二
详细描述
随着大数据和人工智能技术的快速发展，多目标规划模型 在许多领域的应用前景广阔。
大数据时代带来了海量的数据和复杂的问题，这为多目标 规划模型提供了广阔的应用场景。例如，在金融领域，多 目标规划可以用于资产配置和风险管理；在能源领域，多 目标规划可以用于能源系统优化和碳排放管理。同时，随 着人工智能技术的不断发展，多目标规划模型有望与机器 学习、深度学习等算法相结合，共同推动相关领域的发展 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
） ； ≥ ＼ ） ＼ 二 ） ； ） ） ；
本文采用面板数据 ， 通 过 构 建 动 态 模 型 对 我 国上 市银 行
部环境改善方 面 ， 减轻 国家控制约束 ， 健全相关法律制度 ， 实 现市场化 的 自由调整 。
资本结构 的影 响因素及动态调整作 了实证 分析 ， 得 出了如 下 研究结论 ： （ １ ） 我国上 市银行 资本结构是一个动态调整过程 ， 构建 动态模型才能更加 反映现实。（ ２ ） 银行规模 、 盈利能力 、
＝ ｐ ， 日 ， ） 。在贷款违约率确定 的情况下 ， 银行发放贷款 ｗ 的期望收益为 ：
＝ ， Ｗ ｐ （ ｒ ， ， ） ＋ （ 七 ） （ １ 一 ｐ （ ｒ ， 目 ， ｅ Ｏ ） 一 （ ｃ ｌ ， Ｃ ２ ） ＋ Ｑ １ （ １ ）
基于以上分析 ， 本文建立 了高校 资金运营多 目标非线性规划 模型 ， 在及时反 映高 校资金真 实状况 的前提下 ， 建立起 实用
［ ２ ］ 周文定我 国商 业银行 资本结构 与经 营绩效分析［ Ｊ 】 ． 吉林财 税高等专科学校 学报， ２ ０ ０ ３ （ ０ ４ ） ［ ３ ］ 钱健， 王瑛瑛． 商业银行 资本 结构 与经营绩效关系的统计分
析［ Ｊ ］ ． 金 融 经 济， ２ ０ 校 资金 运营 多目标非线
性 规 划模 型 ， 同 时把 这 个体 系放 到 整 个社 会 经 济 的 大 系统 中
进 行研 究， 从 而找 出 高 校 、 银 行 和 政 府 利 益 最 优 化 的 解 决 方
案， 最后 提 出我 国 高校 资金 运 营 的 对 策 建议 关键 字 ： 高校 ： 资金 运 营 ： 非 线性 模 型
ｉ ｃ Ｒｅ ｖ ｉ ｅ ｗ，１ ９ ５ ８ ， Ｖｏ １ ． ４ ８ ： ２ ６ １ — ２ ９ ７ ．
国有法人持 股 比例 与银行 负债 比率显著正相关 ，所得税率 、 管理层持股 比例 、 资 本充足性 、 经 济增长率 与银行负债 比率
显著负相关 ， 成长性 、 流 动性与银行 负债 比率 相关关 系不显
校、 政府 和银行 。 要 以最 大的经济效益支撑高校 的发展 ， 并实
现高校发 展最优化 与经济运行 最优化 的统一 ，就必须在 高 校、 政府 和银行 间做好协调和统一 。 因此 ， 可以构建多 目标非
引 言
近年来 ， 随着社 会主义市 场经济体 制的逐 步完善 ， 我 国 高校 自 １ ９ ９ ９年高 校扩大招生 以来取得 了前所未 有 的发展 ， 在经费投入 、 入学人数 、 学校规模 、 科研水平等各个方面体现 出突飞猛进的发展态势 。但是 ， 由于高校资金管理手段 和管 理水平的发展 尚未跟上高等教育快速发展 的需 求 ， 使高 校在
参考文献 ：
［ １ ］ Ｍｏ ｄ ｉ ｇ ｌ ｉ ａ ｎ ｉ ， Ｆ ． ａ ｎ ｄ Ｍ ｉ ｌ ｌ ｅ ｒ ， Ｍ． Ｈ ． Ｔ ｈ ｅ ｃ ｏ ｓ ｔ ｏ ｆ ｃ ａ ｐ ｉ ｔ ａ ｌ ， ｃ ｏ ｒ ｐ ｏ —
ｒ ａ ｔ ｅ ｆ ｉ ｎ ａ ｎ ｃ ｅ ， ａ ｎ ｄ ｔ ｈ ｅ ｔ ｈ ｅ ｏ ｒ ｙ ｏ ｆ ｉ ｎ ｖ ｅ ｓ ｔ ｍｅ ｎ ｔ ． Ａｍｅ ｒ ｉ ｃ ａ ｎ Ｅｃ ｏ ｎ ｏ ｍ－
迅速扩张 的趋势下 ， 财务管理方面 出现 了很多 弊端 。例如资 金使用机制 由按指令性计划 变为按经济规律办事 ， 而带 来的 投资效益 问题 ； 高校资 金由 国家无偿投人 变为多方投资 带来 的利益确认与利益分配 问题等。 这些 新情况 、 新 问题 ， 促使高校 亟需建立 起一整套 与社 会政 治 、经济 和文化 发展相协调的资金使用效果评价体 系。
线性规划模型 ， 即高校发展所需的资金在政府和银行 间进行
平衡 。
二、 高校、 政府和银行多 目标 非线性规划模型
假定高校从银行 的贷款额为 ｗ， 贷款利率为 ｒ ， 贷款不发
生违 约的概率为 Ｐ ， 贷 款违 约概 率为 １ － ｐ ， 当高校 资金运营不
善而 发生违约时 ， 银行在这笔 贷款的资本 回收 比率为 ｋ 。其 中 ｋ取决 于高校的资信和资产情况 、 经济发 展情 况以及政策 支持等因素； Ｐ取决 于贷款 的利 率 ｒ 、 高校面临 的政策 环境和 经济 因素 等外 部条件 （ ） 以及 高校 自身的资金 状况 （ ） ， 即
Ｆ Ｉ Ｎ ＡＮ ＣＥ Ｅ Ｃ ＯＮ ＯＭＹ 金 融经济
我国高校资金运营多 目标非线性规划模型设计
陈 启荣 徐爱 兰 （ 中南大 学资金 结 算 中心 ， 湖南 长沙 ４ １ ０ ０ ８ ４ ）
摘要： 本 文采 用系统研 究 方法 ， 把 高校 资金 运 营的 所有
问题 作 为一 个整 体 ， 将 高校 、 银 行 和 政 府 纳 入 研 究体 系． 充 分
性高 、 针对性强 的财务评价新 体系 ， 为推 动高校资 金运营顺 利发展的提供前提和制度保 障。
） ｐ ≯ ｐ
（ １ ） 式 中第一项表示贷款在不发生违约 的情 况下 ， 银行可 获得 的预期 收益 ； 第 二项表示贷款在 发生违约 的情 况下 ， 银 行可获得 的预期 收益 ； 第三项 ｃ ＝ ｃ （ ｃ ， Ｃ ） Ｗ表示银行发放数
一
、
我国高校资金运营的思路
我 国高校 资金运 营的思路应该 是按 照社 会主义市 场经 济的价值导 向 ， 把高 校的一切 资源都 当作资本 ， 借鉴 企业运 营模 式 ， 以求在办学 中获取最 大的经济 效益 ， 同时 以最 大 的 经济效益来获得最佳 的教育产 出。
从这层意 义上说 ， 高 校资金运 营涉及到三个 主体 ， 即高
本文采用面板数据 ， 通 过 构 建 动 态 模 型 对 我 国上 市银 行
部环境改善方 面 ， 减轻 国家控制约束 ， 健全相关法律制度 ， 实 现市场化 的 自由调整 。
资本结构 的影 响因素及动态调整作 了实证 分析 ， 得 出了如 下 研究结论 ： （ １ ） 我国上 市银行 资本结构是一个动态调整过程 ， 构建 动态模型才能更加 反映现实。（ ２ ） 银行规模 、 盈利能力 、
＝ ｐ ， 日 ， ） 。在贷款违约率确定 的情况下 ， 银行发放贷款 ｗ 的期望收益为 ：
＝ ， Ｗ ｐ （ ｒ ， ， ） ＋ （ 七 ） （ １ 一 ｐ （ ｒ ， 目 ， ｅ Ｏ ） 一 （ ｃ ｌ ， Ｃ ２ ） ＋ Ｑ １ （ １ ）
基于以上分析 ， 本文建立 了高校 资金运营多 目标非线性规划 模型 ， 在及时反 映高 校资金真 实状况 的前提下 ， 建立起 实用
［ ２ ］ 周文定我 国商 业银行 资本结构 与经 营绩效分析［ Ｊ 】 ． 吉林财 税高等专科学校 学报， ２ ０ ０ ３ （ ０ ４ ） ［ ３ ］ 钱健， 王瑛瑛． 商业银行 资本 结构 与经营绩效关系的统计分
析［ Ｊ ］ ． 金 融 经 济， ２ ０ 校 资金 运营 多目标非线
性 规 划模 型 ， 同 时把 这 个体 系放 到 整 个社 会 经 济 的 大 系统 中
进 行研 究， 从 而找 出 高 校 、 银 行 和 政 府 利 益 最 优 化 的 解 决 方
案， 最后 提 出我 国 高校 资金 运 营 的 对 策 建议 关键 字 ： 高校 ： 资金 运 营 ： 非 线性 模 型
ｉ ｃ Ｒｅ ｖ ｉ ｅ ｗ，１ ９ ５ ８ ， Ｖｏ １ ． ４ ８ ： ２ ６ １ — ２ ９ ７ ．
国有法人持 股 比例 与银行 负债 比率显著正相关 ，所得税率 、 管理层持股 比例 、 资 本充足性 、 经 济增长率 与银行负债 比率
显著负相关 ， 成长性 、 流 动性与银行 负债 比率 相关关 系不显
校、 政府 和银行 。 要 以最 大的经济效益支撑高校 的发展 ， 并实
现高校发 展最优化 与经济运行 最优化 的统一 ，就必须在 高 校、 政府 和银行 间做好协调和统一 。 因此 ， 可以构建多 目标非
引 言
近年来 ， 随着社 会主义市 场经济体 制的逐 步完善 ， 我 国 高校 自 １ ９ ９ ９年高 校扩大招生 以来取得 了前所未 有 的发展 ， 在经费投入 、 入学人数 、 学校规模 、 科研水平等各个方面体现 出突飞猛进的发展态势 。但是 ， 由于高校资金管理手段 和管 理水平的发展 尚未跟上高等教育快速发展 的需 求 ， 使高 校在
参考文献 ：
［ １ ］ Ｍｏ ｄ ｉ ｇ ｌ ｉ ａ ｎ ｉ ， Ｆ ． ａ ｎ ｄ Ｍ ｉ ｌ ｌ ｅ ｒ ， Ｍ． Ｈ ． Ｔ ｈ ｅ ｃ ｏ ｓ ｔ ｏ ｆ ｃ ａ ｐ ｉ ｔ ａ ｌ ， ｃ ｏ ｒ ｐ ｏ —
ｒ ａ ｔ ｅ ｆ ｉ ｎ ａ ｎ ｃ ｅ ， ａ ｎ ｄ ｔ ｈ ｅ ｔ ｈ ｅ ｏ ｒ ｙ ｏ ｆ ｉ ｎ ｖ ｅ ｓ ｔ ｍｅ ｎ ｔ ． Ａｍｅ ｒ ｉ ｃ ａ ｎ Ｅｃ ｏ ｎ ｏ ｍ－
迅速扩张 的趋势下 ， 财务管理方面 出现 了很多 弊端 。例如资 金使用机制 由按指令性计划 变为按经济规律办事 ， 而带 来的 投资效益 问题 ； 高校资 金由 国家无偿投人 变为多方投资 带来 的利益确认与利益分配 问题等。 这些 新情况 、 新 问题 ， 促使高校 亟需建立 起一整套 与社 会政 治 、经济 和文化 发展相协调的资金使用效果评价体 系。
线性规划模型 ， 即高校发展所需的资金在政府和银行 间进行
平衡 。
二、 高校、 政府和银行多 目标 非线性规划模型
假定高校从银行 的贷款额为 ｗ， 贷款利率为 ｒ ， 贷款不发
生违 约的概率为 Ｐ ， 贷 款违 约概 率为 １ － ｐ ， 当高校 资金运营不
善而 发生违约时 ， 银行在这笔 贷款的资本 回收 比率为 ｋ 。其 中 ｋ取决 于高校的资信和资产情况 、 经济发 展情 况以及政策 支持等因素； Ｐ取决 于贷款 的利 率 ｒ 、 高校面临 的政策 环境和 经济 因素 等外 部条件 （ ） 以及 高校 自身的资金 状况 （ ） ， 即
Ｆ Ｉ Ｎ ＡＮ ＣＥ Ｅ Ｃ ＯＮ ＯＭＹ 金 融经济
我国高校资金运营多 目标非线性规划模型设计
陈 启荣 徐爱 兰 （ 中南大 学资金 结 算 中心 ， 湖南 长沙 ４ １ ０ ０ ８ ４ ）
摘要： 本 文采 用系统研 究 方法 ， 把 高校 资金 运 营的 所有
问题 作 为一 个整 体 ， 将 高校 、 银 行 和 政 府 纳 入 研 究体 系． 充 分
性高 、 针对性强 的财务评价新 体系 ， 为推 动高校资 金运营顺 利发展的提供前提和制度保 障。
） ｐ ≯ ｐ
（ １ ） 式 中第一项表示贷款在不发生违约 的情 况下 ， 银行可 获得 的预期 收益 ； 第 二项表示贷款在 发生违约 的情 况下 ， 银 行可获得 的预期 收益 ； 第三项 ｃ ＝ ｃ （ ｃ ， Ｃ ） Ｗ表示银行发放数
一
、
我国高校资金运营的思路
我 国高校 资金运 营的思路应该 是按 照社 会主义市 场经 济的价值导 向 ， 把高 校的一切 资源都 当作资本 ， 借鉴 企业运 营模 式 ， 以求在办学 中获取最 大的经济 效益 ， 同时 以最 大 的 经济效益来获得最佳 的教育产 出。
从这层意 义上说 ， 高 校资金运 营涉及到三个 主体 ， 即高