鲁棒多目标线性规划模型及混合遗传算法

合集下载

【计算机应用研究】_混合遗传算法_期刊发文热词逐年推荐_20140722

2011年科研热词推荐指数遗传算法 4 粒子群优化 3 多目标优化 2 非支配遗传算法 1 遗传算子 1 车辆调度问题 1 装卸频率 1 约束性目标 1 粒子群优化算法 1 知识进化算法 1 混合算法 1 混合流水线车间调度 1 测试路径 1 测试数据 ' 1 模糊环境 1 模糊时间窗 1 模拟退火算法 1 智能交通系统 1 差异作业单机批调度 1 大规模车辆路径问题 1 多态 1 协同进化非支配遗传算法 1 协同进化 1 准最短路径 1 作业车间调度 1 优化性目标 1 soc软硬件划分 1 floyd算法 1 c-w节约算法 1 a*算法 1
科研热词遗传算法模糊环境集成优化量子pso 量化正交遗传算法遗传操作遗传pso 运输路径运输方式软件测试车间作业计划调度触发自由搜索聚类分析网格资源聚类结构化神经网络组合优化粒子群算法粒子群优化算法粒子群优化(pso) 混沌混合调度混合编码测试数据自动生成模拟退火pso 模拟退火柔性车间作业计划问题杂交最大完工时间最大互信息时间序列预测指数预测批处理机差异演化算法差异工件小生境多式联运图像配准参数初始化作业计划二阶振荡pso 丢弃算子 t混合模型 pso k-均值算法 ga-pso算法 fcm dna进化算法 dna计算 0-1背包问题
推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
4年序号 1 2 3 4
2014年科研热词遗传算法柔性工艺变邻域搜索作业车间调度推荐指数 1 1 1 1
推荐指数 8 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

分布鲁棒优化求解算法

分布鲁棒优化是指在考虑不确定性的条件下，寻找一个能够在各种情况下都表现良好的解的优化问题。

以下是一些常见的分布鲁棒优化求解算法：
1.随机优化：随机优化方法使用随机采样的方式来搜索解空间，在优化过程中可以通过多
次采样来减少不确定性的影响。

2.遗传算法：遗传算法基于生物进化理论，通过模拟基因遗传、交叉和变异等操作来搜索
解空间，并通过选择优秀个体进行繁殖，以逐步改进解的质量。

3.模拟退火算法：模拟退火算法模拟固体退火的过程，通过接受劣质解的概率逐渐降低，
以增加全局搜索的能力，并最终达到近似最优解。

4.置换算法：置换算法主要用于处理离散优化问题，通过生成候选解并逐步替换当前解来
进行搜索。

常用的置换算法包括领域搜索、模拟退火和遗传算法。

5.非线性规划：非线性规划方法可以应用于分布鲁棒优化问题，通过建立数学模型和约束
条件，利用优化算法求解最优解。

常见的非线性规划算法包括牛顿法、拟牛顿法和序列二次规划等。

6.鲁棒优化：鲁棒优化方法通过生成针对不确定性情况下的最坏情况的模型，以最小化规
划目标函数在这些情况下的损失。

鲁棒优化方法可以应用于各种优化问题，并提供了对不确定性的鲁棒性能保证。

需要根据具体的问题和要求选择合适的分布鲁棒优化求解算法。

同时，结合实际情况和经验，可能需要对算法进行调整和改进以获得更好的解决方案。

【国家自然科学基金】_pareto遗传算法_基金支持热词逐年推荐_【万方软件创新助手】_20140803

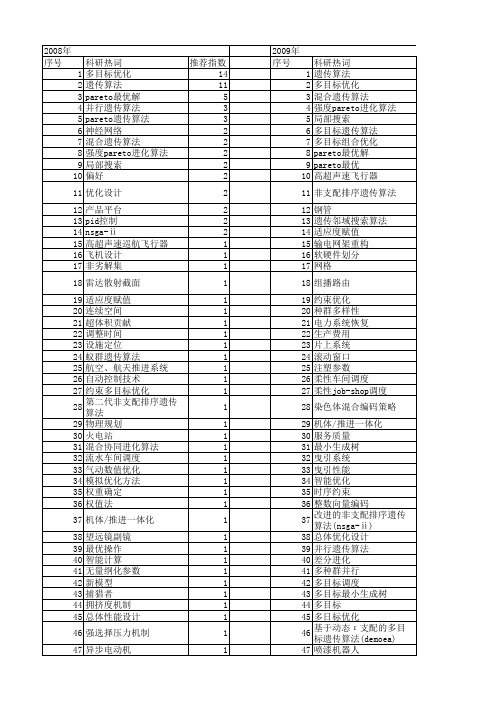
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
动态调度动态ε 支配划分进化方向公平全局优化作业车间调度优化调度仿真乘波布局主动控制一体化设计 β 分布 web服务组合 pareto适应度遗传算法 pareto最优集 nsga-ii算法 lyapunov方程 bp神经网络
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
射流元件天线分集大型注射成型机多载波码分多址多目标问题多目标负荷调度多目标蚁群遗传算法(moaga) 多目标组合优化多目标混合遗传算法多目标多用户检测多工况优化均匀设计地下水系统管理叶轮机械可调节变量产品族参数辨识压气机造型位姿精调机构产品族产品开发 stewart 平台 pareto集 pareto解集 pareto最优决策 pareto最优 pareto支配 pareto前沿 nsga-ⅱi算法 nsga-ii npga nash的系统分解法 nash-pareto策略 memetic算法 hysys gough-stewart平台机构 cad模型 ais

多目标优化算法综述

多目标优化算法综述随着科技的发展和社会进步，人们不断地提出更高的科学技术要求，其中许多问题都可以用多目标优化算法得到解决。

多目标优化算法的发展非常迅速，当前已经有各种综合性比较全面的算法，如：遗传算法、粒子群算法、蚁群算法、模拟退火算法等。

本文将进一步介绍这些算法及其应用情况。

一、遗传算法遗传算法（Genetic Algorithm，简称GA）是一种源于生物学进化思想的优化算法，它通过自然选择、交叉和变异等方法来产生新的解，并逐步优化最终的解。

过程中，解又称为个体，个体又组成种群，种群中的个体通过遗传操作产生新的个体。

遗传算法的主要应用领域为工程优化问题，如：智能控制、机器学习、数据分类等。

在实际应用上，遗传算法具有较好的鲁棒性和可靠性，能够为人们解决实际问题提供很好的帮助。

二、粒子群算法粒子群算法（Particle Swarm Optimization，简称PSO）是一种基于群体智能的优化算法，其核心思想是通过群体中的个体相互协作，不断搜索目标函数的最优解。

粒子群算法适用于连续和离散函数优化问题。

和遗传算法不同，粒子群算法在每次迭代中对整个种群进行更新，通过粒子间的信息交流，误差及速度的修改，产生更好的解。

因此粒子群算法收敛速度快，对于动态环境的优化问题有着比较突出的优势。

三、蚁群算法蚁群算法（Ant Colony Optimization，简称ACO）是一种仿生学启发式算法，采用“蚂蚁寻路”策略，模仿蚂蚁寻找食物的行为，通过“信息素”的引导和更新，粗略地搜索解空间。

在实际问题中，这些target可以是要寻找的最优解（minimum或maximum）。

蚁群算法通常用于组合优化问题，如：旅行商问题、资源分配问题、调度问题等。

和其他优化算法相比，蚁群算法在处理组合优化问题时得到的结果更为准确，已经被广泛应用于各个领域。

四、模拟退火算法模拟退火算法（Simulated Annealing，简称SA）是一种启发式优化算法，通过随机搜索来寻找最优解。

用混合遗传算法求解武器目标分配问题

ｍ
器，可以得到所有的武器个数ｍ１＝∑Ｒｉ．对第二个约束条件：对目标Ｔｊ（ｊ＝１，２，…，ｎ）最多可使用Ｓｊ个武ｉ＝１
器，假设实际待分配的武器总数ｍ１不会小于总目标数ｎ，则当Ｓｊ＝１时，染色体的长度取武器总个数ｍ１；当Ｓｊ≥ ２时，为了在每个目标都获得被Ｓｊ个武器迎击机会的基础上寻找最低失败概率，将每一个目标扩展为Ｓｊ个目标，则共有Ｔｊ×Ｓｊ个目标，故染色体的长度取Ｔｊ×Ｓｊ．其中，染色体的基因位表示武器的编号，每一个染色体表示一种可能的分配方案，分别代表Ｓｊ个编号为从１到Ｔｊ的目标武器编号．编号大于ｍ１的武器代表虚设的武器，该武器对应的目标分配无效．例如，ｍ＝３时，武器数分别为２，２，１，即武器总个数ｍ１＝５，若ｎ＝３，Ｓｊ＝２，则染色体长度取Ｔｊ×Ｓｊ＝６，一个染色体为
摘要：为了提高武器目标分配问题的求解效率，提出了一种求解武器目标分配问题的混合遗传算法．针对遗传算法局部搜索能力的不足，引入局部搜索能力很强的爬山算法与之结合，构造了武器目标分配问题的混合遗传算法．计算结果表明，混合遗传算法与传统优化算法相比，收敛速度更快，分配结果更优，具有很好的应用价值．关键词：武器目标分配问题；混合遗传算法；爬山算法；优化中图分类号：ＴＰ３０１；Ｅ９１７文献标志码：Ａ文章编号：１６７４－３３０Ｘ（２０１８）０１－００５３－０４
ＰｏｌｉｔｉｃａｌＦｏｕｎｄａｔｉｏｎ，ＡｒｔｉｌｌｅｒｙａｎｄＡｉｒＤｅｆｅｎｓｅＦｏｒｃｅｓＡｃａｄｅｍｙｏｆＡｒｍｙ，Ｈｅｆｅｉ２３００３１，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：Ｉｎｏｒｄｅｒｔｏｉｍｐｒｏｖｅｔｈｅｅｆｆｉｃｉｅｎｃｙｏｆｗｅａｐｏｎｔａｒｇｅｔａｓｓｉｇｎｍｅｎｔｐｒｏｂｌｅｍ，ａｈｙｂｒｉｄｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｉｓｐｒｏｐｏｓｅｄｔｏｓｏｌｖｅｔｈｅｗｅａｐｏｎｔａｒｇｅｔａｓｓｉｇｎｍｅｎｔｐｒｏｂｌｅｍ．Ｉｎｖｉｅｗｏｆｔｈｅｄｅｆｉｃｉｅｎｃｙｏｆｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｉｎｌｏｃａｌｓｅａｒｃｈａｂｉｌｉｔｙ，ａｈｙｂｒｉｄｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｆｏｒｗｅａｐｏｎｔａｒｇｅｔａｓｓｉｇｎｍｅｎｔｐｒｏｂｌｅｍｉｓｃｏｎｓｔｒｕｃｔｅｄｂｙｃｏｍｂｉｎｉｎｇｔｈｅｈｉｌｌｃｌｉｍｂｉｎｇａｌｇｏｒｉｔｈｍｗｉｔｈｓｔｒｏｎｇｌｏｃａｌｓｅａｒｃｈａｂｉｌｉｔｙ．Ｔｈｅｒｅｓｕｌｔｓｓｈｏｗｔｈａｔｔｈｅｈｙｂｒｉｄｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｈａｓｆａｓｔｅｒｃｏｎｖｅｒｇｅｎｃｅｓｐｅｅｄ，ｂｅｔｔｅｒｄｉｓｔｒｉｂｕｔｉｏｎｒｅｓｕｌｔａｎｄｂｅｔｔｅｒａｐｐｌｉｃａｔｉｏｎｖａｌｕｅｃｏｍｐａｒｅｄｗｉｔｈｔｈｅｔｒａｄｉｔｉｏｎａｌｏｐｔｉｍｉｚａｔｉｏｎａｌｇｏｒｉｔｈｍ．

基于NSGA-II_算法解决多目标优化实际应用的研究

Advances in Applied Mathematics 应用数学进展, 2023, 12(10), 4195-4207Published Online October 2023 in Hans. https:///journal/aamhttps:///10.12677/aam.2023.1210413基于NSGA-II算法解决多目标优化实际应用的研究向芷恒，王秉哲，雪景州，山晟北方工业大学理学院，北京收稿日期：2023年9月11日；录用日期：2023年10月5日；发布日期：2023年10月13日摘要优化问题是工业生产中十分常见的一类问题，但在具体的实际应用中，单目标优化往往无法满足实际的需求。

工厂需要在保证利润的前提下降低自己的成本，如能耗、人工、生产时间等。

此时单目标优化无法较好地给出需要的可行解，采用多目标优化能较为简单地解决此类问题。

NSGA-II算法在解决此类问题时具有较好的可行性，本文主要介绍NSGA-II算法的发展与原理，并以模拟工业生产的实际情况给出了简单的应用案例。

关键词多目标优化，NSGA-II算法，Pareto占优Research on the Practical Application ofNSGA-II Algorithm for Multi-ObjectiveOptimizationZhiheng Xiang, Bingzhe Wang, Jinzhou Xue, Shen ShanCollege of Science, North China University of Technology, BeijingReceived: Sep. 11th, 2023; accepted: Oct. 5th, 2023; published: Oct. 13th, 2023AbstractOptimization problems are common in industrial production, but in specific practical applications, single-objective optimization often fails to meet the actual requirements. Factories need to reduce their costs, such as energy consumption, labor, and production time, while ensuring profitabili-向芷恒等ty. In such cases, single-objective optimization cannot provide satisfactory feasible solutions, and multi-objective optimization can effectively address these problems. The NSGA-II algorithm demon-strates good feasibility in solving such problems. This paper primarily introduces the development and principles of the NSGA-II algorithm and provides a simple application case based on simulated industrial production scenarios.KeywordsMulti-Objective Optimization, NSGA-II Algorithm, Pareto Dominance Array Copyright © 2023 by author(s) and Hans Publishers Inc.This work is licensed under the Creative Commons Attribution International License (CC BY 4.0)./licenses/by/4.0/1. 绪论1.1. 引言多目标优化是现实生活中许多实际问题的重要组成部分，如工程设计、资源分配、机器学习等。

鲁棒优化模型和最优解解法毕业论文

鲁棒优化模型和最优解解法毕业论文1.简介装配线就是包括一系列在车间中进行连续操作的生产系统。

零部件依次向下移动直到完工。

它们通常被使用在高效地生产大量地标准件的工业行业之中。

在这方面，建模和解决生产线平衡问题也鉴于工业对于效率的追求变得日益重要。

生产线平衡处理的是分配作业到工作站来优化一些预定义的目标函数。

那些定义操作顺序的优先关系都是要被考虑的，同时也要对能力或基于成本的目标函数进行优化。

就生产（绍尔4999）产品型号的数量来说，装配线可分为三类：单一模型（SALBP），混合模型（MALBP）和多模式（MMALBP）。

在混合模型线和类似的生产流程中的同一产品的几个版本都需要他们。

凡生产流程有明显不同的生产线都需要计划并被称为多模型生产线。

从整体上对单一模型的装配线来说，对于一种均匀的产品的制造，就会有两个基本能力取向的问题：在给定一个所需的周期时间最小化工作站的数量，所有这是由工作站时间的最大值（SALBP1）中所定义；或在给定的工作站数目下最小化周期时间（SALBP2）。

AVORD版木.结合两种构想和优化工作站的数量和周期时间的效率问题(SALBP 2)，也经常被研究。

在现实生活中，装配过程中受到各种不确定性来源的影响，如操作时间的可变性、资源使用或可用性。

这些变化威胁到装配目标和避免它们造成的损失是至关重要的。

在这些资源中，操作时间的变化是重要的，特别是对于包含手动操作的生产线。

在大量变化的情况下，生产管理是昂贵的(生产线停工，工人的再分配，加班、短缺，等等)。

在这方面，本研究着重于预防这些成本的产生。

为此，我们制定了鲁棒SALBP-2。

在这个问题中，工作站被认为是预先确定的数量，因此变化影响生产周期和生产率。

开发一个算法来分配操作工作站，使其有可能在定义的最小周期完成。

因此，即使面对突发事件也能表现良好的更可靠的装配系统将会被设计出来。

我们强调，这项研究既有助于装配线设计的理论也有助于其实践。

控制系统鲁棒性优化的遗传算法策略

控制系统鲁棒性优化的遗传算法策略控制系统的鲁棒性是指系统对于外部扰动和变化的适应能力，是其保持稳定性和性能的关键要素。

然而，在现实工程中，控制系统往往面临各种不确定性因素，如模型参数的变化、传感器测量误差和外部环境变化等，这些因素都会对系统的性能造成不利影响。

因此，如何提高控制系统的鲁棒性成为了一个重要的研究领域。

遗传算法作为一种优化搜索方法，能够在解空间中寻找最优解。

其基本思想是通过模拟自然界中的生物进化过程，通过选择、交叉和变异等操作来搜索全局最优解。

在控制系统鲁棒性优化中，遗传算法可以被应用于设计控制器参数，以提高系统的抗扰性和稳定性。

首先，遗传算法通过对控制器参数进行编码，将参数空间映射到染色体空间中。

常见的编码方式有二进制编码和浮点数编码，根据问题的具体情况选择合适的编码方式。

然后，通过随机生成初始种群，每个个体代表一个可能的解。

根据目标函数对个体进行评估，评估函数可以是系统的性能指标，如时域响应曲线的峰值误差和稳定时间等。

评估之后，根据适应度函数对个体进行选择，优秀的个体将有更高的生存概率。

接着，选择的个体进行交叉操作，通过互换染色体中的基因片段来生成新的个体。

交叉操作可以增加种群的多样性，从而增加搜索空间的覆盖率。

同时，为了防止早熟收敛，需要引入变异操作，通过随机改变个体中的某些基因，引入新的解以避免陷入局部最优解。

在每一代的进化过程中，根据预先设定的终止准则，如达到最大迭代次数或收敛到一定误差范围内，选择适应度最高的个体作为最终的解。

最后，将找到的最优解解码回参数空间，并应用于控制系统中。

遗传算法策略在控制系统鲁棒性优化中具有以下优势：1. 全局优化能力：遗传算法通过随机生成初始种群，并且通过选择、交叉和变异等操作来搜索解空间，具有较强的全局搜索能力。

可以在复杂的参数空间中找到全局最优解。

2. 简单而有效：遗传算法的基本操作简单直观，易于实现。

不需要对控制系统的具体模型和行为进行复杂的数学建模，适用于各种类型的控制系统。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ｔｈｅｏｒｅｍａｎｄｐｒｏｏｆ．Ｔｈｅｒｅｆｏｒｅ。ｃｏｎｖｅｎｅｄｔｈｅｏｒｉｇｉｎｌａｕｎｃｅｒｔａｉｎＭＯＬＰｔｏｔｈｅｄｅｔｅｒｍｉｎｉｓｔｉｃＭ０ＬＰｃｏｎｓｔｒａｉｎｅｄｗｉｔｈｓｅｃｏｎｄ．ｏｒｄｅｒ
王君
（天津财经大学商学院，天津３００２２２）
摘要：针对目标函数系数和约束条件系数均在椭球扰动集下的不确定多目标线性规划，提出了椭球扰动集下
的鲁棒多目标线性规划问题。基于每个目标均需获得鲁棒解的假设下给出了定理及证明，以此把原问题转换为具有二阶锥约束的确定性多目标优化问题。设计了一种混合策略求解算法，整体流程采用多目标遗传算法，局部采用ＳＯＣＰ优化软件Ｓｅｄｕｍｉ进行计算，从而获得不确定多目标线性规划的鲁棒解集，并通过数值算例验证了
该算法的有效性。
关键词：多目标线性规划；鲁棒优化；二阶锥规划；椭球扰动；混合策略算法
中图分类号：ＴＰ３０１文献标志码：Ａ文章编号：１００１ — ３６９５（２０１３）０９ — ２６３３－０４
ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．１００１．３６９５．２０１３．０９．０１９
ｔｈｅｅｆｆｅｃｔｉｖｅｎｅｓｓｏｆｔｈｅａｌｇｏｒｉｔｈｍ．
ｃｏｎｅ．Ｔｈｅｎ，ｉｔｄｅｓｉｇｎｅｄｔｈｅｍｉｘｅｄｓｔｒａｔｅｇｙａｌｇｏｉｒｔｈｍ，ｉｎｗｈｉｃｈｔｈｅｏｖｅｒａｌｌｐｒｏｃｅｓｓｗａｓｍｕｌｔｉ — ｏｂｊｅｃｔｉｖｅｇｅｎｅｔｉｃａｌｇｏｉｒｔｈｍａｎｄ
ｃａｌｃｕｌａｔｅｄｔｈｅｌｏｃａｌｏｐｔｉｍｉｚａｔｉｏｎｂｙＳＯＣＰｓｏｆｔｗａｒｅＳｅｄｕｍｉ，ｔｏｏｂｔａｉｎｔｈｅｒｏｂｕｓｔｓｏｌｕｔｉｏｎｓｅｔ．Ａｎｕｍｅｒｉｃａｌｅｘａｍｐｌｅｄｅｍｏｎｓｔｒａｔｅｓ
ＷＡＮＧＪｕｎ
（Ｓｃｈｏｏｌ曰
ｓ，ＴｉａｎＵｎｉｖｅｒｓｉｔｙｏｆＦｉｎａｎｃｅ＆Ｅｃｏｎｏｍｉｃｓ，Ｔｉａｎｊｉｎ３００２２２，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：Ａｉｍｉｎｇａｔｓｏｌｖｉｎｇｔｈｅｕｎｃｅｎｍｎｍｕｌｉｔ－ｏｂｊｅｃｔｉｖｅｌｉｎｅａｒｐｒｏｇｒａｍｍｉｎｇ（ＭＯＬＰ）ｗｉｔｈｔｈｅｃｏｅｆｆｉｃｉｅｎｔｓｕｎｄｅｒｈｅｔｅｌｌｉｐ－ｓｏｉｄａｌｄｉｓｔｕｒｂａｎｃｅｉｎｏｂｊｅｃｔｉｖｅｆｕｎｃｔｉｏｎｓａｎｄｃｏｎｓｔｒａｉｎｃｏｎｄｉｔｉｏｎｓ，ｔｈｉｓｐａｐｅｒｐｒｏｐｏｓｅｄａｒｏｂｕｓｔＭＯＬＰｐｒｏｂｌｅｍｕｎｄｅｒｔｈｅｅｌｌｉｐ —
ｓｏｉｄａｌｄｉｓｔｕｒｂａｎｃｅ．Ｂａｓｅｄｏｎｔｈｅａｓｓｕｍｐｔｉｏｎｔｈａｔａｌｌｏｂｉｅｃｔｉｖｅｆｕｎｃｔｉｏｎｓｎｅｅｄｅｄｔｏａｃｑｕｉｒｅｔｈｅｒｏｂｕｓｔｓｏｌｕｔｉｏｎｓ．ｉｔｐｒｏｐｏｓｅｄｔｈｅ
Ｍｏｄｅｌａｎｄｈｙｂｒｉｄｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｆｏｒｒｏｂｕｓｔｍｕｌｔｉ — ｏｂｊｅｃｔｉｖｅ
ｌｉｎｅａｒｐｒｏｇｒａｍｍｉｎｇ
第３Ｏ卷第９期
２０１３年９月
计算机应用研究
ＡｐｐｌｉｃａｔｉｏｎＲｅｓｅａｒｃｈｏｆＣｏｍｐｕｔｅｒｓ
Ｖｏ１．３０Ｎｏ．９Ｓｅｐ．２０１３
鲁棒多目标线性规划模型及混合遗传算法