图论
图论及其应用

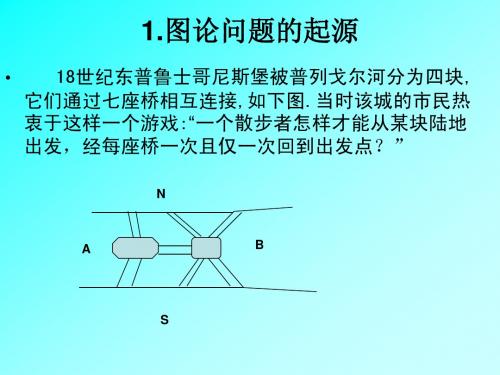
图论及其应用简介图论是计算机科学中的一个重要分支,研究的对象是由边与顶点组成的图形结构以及与其相关的问题和算法。
图论的应用广泛,涵盖了计算机科学、网络科学、物理学、社会学、生物学等多个领域。
本文将介绍图论的基本概念、常用算法以及一些实际的应用案例。
图的基本概念图由顶点(Vertex)和边(Edge)组成,记作G=(V, E),其中V为顶点的集合,E为边的集合。
图可以分为有向图和无向图两种类型。
有向图有向图中的边具有方向性,即从一个顶点到另一个顶点的边有明确的起点和终点。
有向图可以表示一种有序的关系,比如A到B有一条边,但B到A可能没有边。
有向图的表示可以用邻接矩阵或邻接表来表示。
无向图无向图中的边没有方向性,任意两个顶点之间都有相互连接的边。
无向图可以表示一种无序的关系,比如A与B有一条边,那么B与A之间也有一条边。
无向图的表示通常使用邻接矩阵或邻接表。
常用图论算法图论中有许多经典的算法,其中一些常用的算法包括:深度优先搜索(DFS)深度优先搜索是一种用于遍历或搜索图的算法。
通过从起始顶点开始,沿着一条路径尽可能深入图中的顶点,直到无法再继续前进时,返回上一个顶点并尝试下一条路径的方式。
DFS可以用于判断图是否连通,寻找路径以及检测环等。
广度优先搜索(BFS)广度优先搜索也是一种用于遍历或搜索图的算法。
不同于深度优先搜索,广度优先搜索逐层遍历顶点,先访问离起始顶点最近的顶点,然后依次访问与起始顶点距离为2的顶点,以此类推。
BFS可以用于寻找最短路径、搜索最近的节点等。
最短路径算法最短路径算法用于计算图中两个顶点之间的最短路径。
其中最著名的算法是迪杰斯特拉算法(Dijkstra’s A lgorithm)和弗洛伊德算法(Floyd’s Algorithm)。
迪杰斯特拉算法适用于没有负权边的图,而弗洛伊德算法可以处理带有负权边的图。
最小生成树算法最小生成树算法用于找到一个连通图的最小的生成树。
其中最常用的算法是普里姆算法(Prim’s Algorithm)和克鲁斯卡尔算法(Kruskal’s Algorithm)。
第一章(图论的基本概念)
第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理,图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
图论知识点

图论知识点摘要:图论是数学的一个分支,它研究图的性质和应用。
图由节点(或顶点)和连接这些节点的边组成。
本文将概述图论的基本概念、类型、算法以及在各种领域的应用。
1. 基本概念1.1 节点和边图由一组节点(V)和一组边(E)组成,每条边连接两个节点。
边可以是有向的(指向一个方向)或无向的(双向连接)。
1.2 路径和环路径是节点的序列,其中每对连续节点由边连接。
环是一条起点和终点相同的路径。
1.3 度数节点的度数是与该节点相连的边的数量。
对于有向图,分为入度和出度。
1.4 子图子图是原图的一部分,包含原图的一些节点和连接这些节点的边。
2. 图的类型2.1 无向图和有向图无向图的边没有方向,有向图的每条边都有一个方向。
2.2 简单图和多重图简单图是没有多重边或自环的图。
多重图中,可以有多条边连接同一对节点。
2.3 连通图和非连通图在无向图中,如果从任意节点都可以到达其他所有节点,则称该图为连通的。
有向图的连通性称为强连通性。
2.4 树树是一种特殊的连通图,其中任意两个节点之间有且仅有一条路径。
3. 图的算法3.1 最短路径算法如Dijkstra算法和Bellman-Ford算法,用于在加权图中找到从单个源点到所有其他节点的最短路径。
3.2 最大流最小割定理Ford-Fulkerson算法用于解决网络流中的最大流问题。
3.3 匹配问题如匈牙利算法,用于解决二分图中的匹配问题。
4. 应用4.1 网络科学图论在网络科学中有广泛应用,如社交网络分析、互联网结构研究等。
4.2 运筹学在运筹学中,图论用于解决物流、交通网络优化等问题。
4.3 生物信息学在生物信息学中,图论用于分析蛋白质相互作用网络、基因调控网络等。
5. 结论图论是数学中一个非常重要和广泛应用的领域。
它不仅在理论上有着深刻的内涵,而且在实际应用中也发挥着关键作用。
随着科技的发展,图论在新的领域中的应用将会不断涌现。
本文提供了图论的基础知识点,包括概念、图的类型、算法和应用。
图论的基本概念和应用

图论的基本概念和应用图论,顾名思义,是研究图的一门数学分支。
在计算机科学、网络科学、物理学等领域都有广泛的应用。
本文将从图的基本概念入手,介绍图论的基础知识和常见应用。
一、图的基本概念1.1 图的定义图是由若干点和若干边构成的。
点也被称为顶点,边也被称为弧或者线。
一个点可以与任意个点相连,而边则是连接两个点的线性对象。
一些有向边可以构成一棵树,而一些无向边则形成了一个回路。
1.2 图的表示图可以用一张二维平面图像表示。
这张图像由若干个点和连接这些点的线组成。
这种表示方式被称为图的平面表示。
图还可以用邻接矩阵、邻接表、关联矩阵等数据结构进行表示。
1.3 图的类型根据图的性质,可以将图分为有向图、无向图、完全图、连通图、欧拉图、哈密顿图等。
有向图:边有方向,表示从一个点到另一个点的某种关系。
无向图:边没有方向,表示两个点之间的某种关系。
完全图:任意两个点之间都有一条边,不存在自环。
\连通图:任意两个点之间都有至少一条通路,没有孤立的点。
欧拉图:一条欧拉通路是一条从一点开始经过所有边恰好一次后回到该点的通路。
哈密顿图:经过所有点恰好一次的通路被称为哈密顿通路。
二、图的应用2.1 最短路径问题图论在计算机算法中最常见的应用之一就是最短路径问题。
在一个有向图中,从一个点到另一个点可能有多条不同的路径,每条路径的长度也可能不同。
最短路径问题就是找到两个点之间长度最短的路径。
最短路径问题可以通过深度优先搜索、广度优先搜索等方法来解决,但是时间复杂度通常较高。
另外,使用Dijkstra算法、Floyd算法等优化算法可以大大缩短计算时间。
2.2 社交网络社交网络是图论应用的一个重要领域。
在社交网络中,人们之间的关系可以用图的形式表示。
例如,在微博网络中,每个用户和他/她所关注的人就可以形成一个有向图。
在这种图中,点表示用户,边表示一个人关注另一个人的关系。
通过对社交网络进行图论分析,可以研究用户之间的互动模式,了解到哪些用户之间联系较为紧密,哪些用户是网络中的“大咖”等。
图论期末总结

图论期末总结一、引言图论是一门研究图和网络结构的数学学科。
图论不仅在数学领域中有着广泛的应用,而且在计算机科学、物理学、化学、生物学等交叉学科中也扮演着重要的角色。
在本学期的图论课程中,我系统地学习了图论的基本概念、算法和应用,对图论的知识有了更深入的理解和认识。
在本文中,我将对本学期学习的图论知识进行总结和归纳。
二、基本概念1. 图的定义与表示:图是由一组顶点和一组边组成的数学模型。
在图中,顶点表示图中的实体,边表示顶点之间的关系。
图可以用邻接矩阵或邻接表来表示。
2. 图的类型:图可以分为有向图和无向图、加权图和非加权图、简单图和多重图等。
有向图的边具有方向性,无向图的边没有方向性。
加权图的边带有权重,非加权图的边没有权重。
简单图没有自环和平行边,多重图可以有自环和平行边。
3. 图的基本术语:顶点的度数是指与该顶点相关联的边的数量。
入度是有向图中指向该顶点的边的数量,出度是有向图中从该顶点发出的边的数量。
路径是由边连接的一系列顶点,路径的长度是指路径上边的数量。
连通图是指从一个顶点到任意其他顶点都存在路径。
三、图的算法1. 图的遍历算法:深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的图遍历算法。
DFS从一个顶点出发,探索所有可能的路径,直到无法继续深入为止。
BFS从一个顶点开始,逐层探索图中的其他顶点,直到所有顶点都被访问过为止。
2. 最短路径算法:最短路径算法用来计算图中两个顶点之间的最短路径。
迪杰斯特拉算法和弗洛伊德算法是两种常用的最短路径算法。
迪杰斯特拉算法适用于没有负权边的图,通过每次选择到某个顶点的最短路径来逐步扩展最短路径树。
弗洛伊德算法适用于有负权边的图,通过每次更新两个顶点之间的最短路径来逐步求解最短路径。
3. 最小生成树算法:最小生成树算法用于找到连接图中所有顶点的最小代价树。
克鲁斯卡尔算法和普林姆算法是两种常用的最小生成树算法。
克鲁斯卡尔算法通过每次选择代价最小的边来逐步扩展最小生成树。
图论课后习题答案

图论课后习题答案图论是数学中的一个分支,主要研究图的结构和性质。
图论的课后习题通常包括证明题、计算题和应用题。
下面给出一些典型的图论课后习题答案:1. 证明题:证明一个图是连通的当且仅当它的任意两个顶点都存在一条路径相连。
答案:首先定义连通图的概念:一个图是连通的,如果对于任意两个顶点,都存在一条路径将它们连接起来。
接下来,我们证明两个方向:- 如果一个图是连通的,那么对于任意两个顶点\( u \)和\( v \),根据定义,必然存在一条路径\( P \)将它们连接起来。
- 反之,如果对于任意两个顶点\( u \)和\( v \),都存在一条路径将它们连接起来,那么我们可以构造一个从任意顶点\( u \)出发,访问图中所有顶点的路径,这表明图是连通的。
2. 计算题:给定一个有\( n \)个顶点的完全图,计算它的边数。
答案:在完全图中,每个顶点都与其他所有顶点相连。
因此,对于一个顶点,它将与\( n-1 \)个其他顶点相连。
但是,每条边被计算了两次(因为它连接了两个顶点),所以边数应该是\( \frac{n(n-1)}{2} \)。
3. 应用题:在一个社交网络中,每个用户可以与其他人建立联系。
如果一个用户与至少一半的用户建立了联系,那么这个社交网络是连通的吗?答案:是的,这个社交网络是连通的。
假设社交网络中有\( n \)个用户,如果一个用户与至少\( \lceil \frac{n}{2} \rceil \)个用户建立了联系,那么我们可以构造一条从任意用户\( u \)到这个中心用户的路径。
由于中心用户与至少一半的用户建立了联系,我们可以继续通过这些联系到达其他用户,从而证明社交网络是连通的。
4. 证明题:证明在任何图中,边数至少是顶点数减一。
答案:考虑一个图的生成树,它是一个最小的连通子图,包含图中的所有顶点,并且没有环。
在生成树中,边数等于顶点数减一。
由于任何图都至少包含一个生成树,因此原图的边数至少与生成树的边数相同,即至少是顶点数减一。
第五章 图论

图论可应用于多个领域,如信息论,控制论, 运筹学,运输网络,集合论等(如用关系图来 描述一个关系)。
计算机领域,其可应用于人工智能,操作系统, 计算机制图,数据结构)
§1
图论基本概念
1-1 图的实例 问题1、哥尼斯堡桥问题
A C B D C B A D
问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点?
同理,结点间按别的对应方式,便都不存在一一对应
关系。
所以G1,G2不同构。
两图同构有必要条件:
(1)结点数相同; (2)边数同; (3)次数相同的结点数目相等。
1-5 多重图与带权图
1.5.1 多重图 定义11、一个结点对对应多条边,称为多重边。
包含多重边的图称为多重图,否则,成为简单图。
如:
如:基本通路:p1,p2,p3.
简单通路:p1,p2,p3,p5,p6. p4,p7既不是基本通路,也不是简单通路。
定义3、起始结点和终止结点相同的通路称为回路。 各边全不同的回路称为简单回路,各点全不同 的回路称为基本回路。
例2、上例中,1到1的回路有: c1: (1,1,),c2: (1,2,1),c3: (1,2,3,1), 1 2
例2、设有四个城市c1,c2,c3,c4;其中c1与c2间, c1与c4间,c2与c3间有高速公路直接相连,用图表 示该事实。 解:G=<V,E>,其中:V={c1,c2,c3,c4}, E={l1,l2,l3}={(c1,c2),(c1,c4),(c2,c3)} 例3、有四个程序p1,p2,p3,p4,其间调用关系为p1 p2, p1 p4,p2 p3,用图表示该事实。 解:G=<V,E>,V={p1,p2,p3,p4}, E={l1,l2,l3}={(p1,p2),(p1,p4),(p2,p3)}
图论教学大纲

图论教学大纲图论教学大纲引言:图论是离散数学的一个重要分支,它研究的是由节点和边组成的图结构。
图论在计算机科学、电信网络、社交网络等领域都有广泛的应用。
为了提高学生的图论理解和应用能力,制定一份完善的图论教学大纲是必要的。
一、基础概念与术语1. 图的定义与基本术语:节点、边、度、路径等。
2. 有向图与无向图的区别与应用场景。
3. 连通性与连通图的性质。
4. 子图与超图的概念及应用。
二、图的表示与存储1. 邻接矩阵与邻接表的比较与选择。
2. 图的存储结构的选择与实现。
3. 图的遍历算法:深度优先搜索与广度优先搜索。
三、图的性质与算法1. 图的同构与同构判定算法。
2. 图的连通性与连通分量的计算。
3. 图的割点与割边的定义与算法。
4. 最短路径算法:Dijkstra算法与Floyd-Warshall算法。
5. 最小生成树算法:Prim算法与Kruskal算法。
四、应用案例分析1. 电信网络规划与优化中的图论应用。
2. 社交网络中的图论算法与分析。
3. 交通网络与路径规划中的图论应用。
4. 电力系统与供应链管理中的图论应用。
五、拓展与深入研究1. 图的扩展应用领域与前沿研究方向。
2. 图论在人工智能与机器学习中的应用。
3. 图论与其他学科的交叉研究与合作。
结语:通过本教学大纲的学习,学生将能够掌握图论的基本概念与术语,理解图的表示与存储方法,掌握图的性质与算法,以及应用图论解决实际问题的能力。
同时,拓展与深入研究的内容将为学生提供更广阔的学术发展空间。
图论作为一门重要的学科,将为学生的学习和未来的职业发展带来巨大的价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 7.6 树与生成树(Trees and Spanning Trees)
• 7.7 根树及其应用(Rooted Trees and Its Applications)
7.1 图的基本概念
• 7.1.1 图的基本概念 • 7.1.2 图的结点的度数及其计算 • 7.1.3 子图和图的同构
7.1 图的基本概念
vV vV
7.1 图的基本概念
图7.1.4
7.1.3 子图和图的同构 • 1.子图 • 在研究和描述图的性质时,子 图的概念占有重要地位。 • 定义7.1.5 设有图G=〈V , E〉和图 • G′=〈 V′, E′ 〉 。 1) 若V′ V, E′ E, 则称G′是G的子 图。 • 2) 若G′是G的子图,且E′≠E,则称G′ 是G 的真子图。
7.1 图的基本概念
• 定理 7.1.1 图G=〈V ,E〉中结点度 数的总和等于边数的两倍, 即
V
deg( ) 2 E
• 证明: 因为每条边都与两个结点关联, 所以加上一条边就使得各结点度数的和 增加 2, 由此结论成立。 • 推论: 图G中度数为奇数的结点必为偶 数个。
7.1 图的基本概念
•
7.1 图的基本概念
我们将结点a、b的无序结点对记为(a,b), 有 序结点对记为〈a,b〉。 一个图G可用一个图形来表示且表示是不唯 一的。
• 【例7.1.2】 设G=〈V(G),E(G)〉,其中 • V(G)={a,b,c,d},E(G)={e1,e2,e3,e4,e5,e6 ,e7},e1=(a,b), • e2=(a,c),e3=(b,d),e4=(b,c),e5=(d,c),e6= (a,d),e7=(b,b) 。 则图G可用图7.1.2(a)或(b)表示。
定义7.1.4 在有向图中,射入结点v的 边数称为结点v 的入度, 记 为 deg(v) ;由结点v射出的边数称为 结点v 的出度, 记为 deg(v) 。结点v的 入度与出度之和就是结点v的度数。 deg(v)=2。 • 如图7.1.4中 deg(a) =1, • 定理 7.1.2 在任何有向图G=〈V ,E〉 中, 有 deg(v) deg(v) E
•
• 3) 若V′=V, E′ E,则称G′是G的生 成子图。 • 图7.1.7给出了图G以及它的真子图G1和 生成子图G2。
7.1 图的基本概念
图7.1.7 图G以及其真子图G 1和生成子图G2
7.1 图的基本概念
2. 图的同构 • 从图的定义可以看出,图的 最本质的内容是结点与结点的邻接 关系。例如例 7.1.1 也可以用图 7.1.8 中几种不同形状的图形表示。它们 与图 7.1.1 一样,都同样表示例 7.1.1 中4个队之间的比赛情况。从这个 意义上讲,我们说它们是同一个图, 并称图 7.1.1 与图 7.1.8 的 (a) 和 (b) 是 同构的。
第七章 图论(Graph Theory)
• 7.1 图的基本概念(Graph)
• 7.2 路与图的连通性(Walks & Connectivity of Graphs) • 7.3 图的矩阵表示(Matrix Notation of Graph) • 7.4 欧拉图与哈密尔顿图(Eulerian Graph & Hamilton-ian Graph ) • 7.5 平面图(Planar Graph)
7.1 图的基本概念
•
【例7.1.4】(拉姆齐问题)试证在任
何一个有6个人的组里, 存在3个人互 相认识, 或者存在3个人互相不认识。 • 我们用6个结点来代表人, 并用邻接性 来代表认识关系。 这样一来, 该例就是 要证明: 任意一个有6个结点的图 G中, 或者有3个互相邻接的点, 或者有3个 互相不邻接的点。 即, 对任何一个有6 G 个结点的图G, G或 中含有一个三角 形(即K3)。
•
定义 7.2.1 给定图G=〈V ,E〉, 设v0, v1, … , vk∈V,e1,e2,…,ek∈E, 其中ei是关联于结 点vi-1和vi的边, 称交替序列v0e1v1e2…ekvk为连 接 v0到vk的路, v0和 vk 分别称为路的起点与终 点。路中边的数目k称作路的长度。 当v0=vk时, 这条路称为回路。在简单图中一条路 v0e1v1e2…ekvk 由它的结点序列 v0v1…vk 确定 , 所 以简单图的路 ,可表示为 v0v1…vk 。如图7.1.1表 示的简单图中, 路ae1be4ce5d可写成abcd。
•
7.1 图的基本概念
图 7 .1. 3
7.1 图的基本概念
3. 图G的分类 (1)按 G 的结点个数和边数分为 (n,m) 图 , 即n个结点, m条边的图; (2)特别地, (n,0)称为零图, (1,0) 图称为 平凡图 。 (3) 按 G 中关联于同一对结点的边数分为 多重图和简单图; 多重图:含有平行边的图(如图7.1. 3) 。 简单图:不含平行边和自环的图。
7.1 图的基本概念
如例 7.1.1 中的图,结点集 V ={ a , b,c,d}, 边集 E={e1, e2, e3, e4, e5}, 其中 • e1=(a,b),e2=(a, c),e3 =(a,d), e4=(b, c), e5= (c, d)。 d与a、 d与c是邻接的, 但 d 与 b 不邻接, 边 e3 与 e5 是邻接的。
•
7.1 图的基本概念
图 7.1.8 同构的图
图 7.1.9
7.1 图的基本概念
• 定义7.1.6 设有图 G=〈V , E〉和图 G′=〈 V′, E′〉。 如果存在双射g: V→V′,使得e=(u, v) ∈E iff e′=(g (u),g(v))∈E′, 且(u, v)与(g(u),g (v))有相同的重数,则称G与G′同构。 记作G≌G′。 • 【例 7.1.5】考察图 7.1.9 中的两个图 G =〈V , E〉和G′=〈 V′, E′〉 。
•
7.2 路与图的连通性(
Walks & TheConnectivityof Graphs)
7.2.1通性( • The Connectivityof Graphs)
• •
7.2.1 路与回路(Wlaks and Circuits)
7.1 图的基本概念
• 7.1.2 图的结点的度数及其计算 • 我们常常需要关心图中有多少条边 与某一结点关联,这就引出了图的一个 重要概念——结点的度数。
• 定义7.1.3 图中结点v所关联的边数(有自 回路时计算两次)称为结点v 的度数,记 为deg(v)。 • 如图7.1.3中的deg(v1)=2,deg(v2) = 3, deg(v3)=5。
•
7.1 图的基本概念
【例7.1.3】设图G=〈V ,E〉 如图 7.1. 3所示。 • 这里V={v1,v2,v3}, • E={e1,e2,e3,e4,e5}, • 其中e1 =(v1, v2) ,e2=(v1,v3) , e3 =(v3, v3), e4 =(v2, v3), e5=(v2,v3)。 • 在这个图中,e3是关联同一个结点 的一条边,即自回路; 边e4和e5都与 结点v2、 v3关联, 即它们是多重边。
(3)按G的边有序、无序分为有向图、无向 图和混合图; 有向图:每条边都是有向边的图称为有向 图(图 7 .1.4 (b)); 无向图:每条边都是无向边的图称为无向图; 混合图:既有无向边 , 又有有向边的图称 为混合图。 本书主要研究无向图和有向图。 (4)按G的边旁有无数量特征分为边权图(如 图 7.1.4 (a)) 、无权图;
• 证明: 设V1和V2分别是G中奇数度数 和偶数度数的结点集。 • 由定理7.1.1知
vV1
deg(v) deg(v) 2 E
deg(v) 是偶数之和,
2
vV2
•
由于 vV 必为偶数, 而2|E|也为偶数, 故 V 由此|V1|必为偶数。
1
deg( )
• •
7.1 图的基本概念
7.1 图的基本概念
图 7.1.2
7.1 图的基本概念
图 7.1.2
7.1 图的基本概念
• • • • • • 2. 图G的结点与边之间的关系 邻接点: 同一条边的两个端点。 孤立点: 没有边与之关联的结点。 邻接边: 关联同一个结点的两条边。 孤立边: 不与任何边相邻接的边。 自回路(环):关联同一个结点的 一条边((v,v)或〈v,v〉)。 • 平行边 ( 多重边 ): 关联同一对结点的 多条边。
7.1 图的基本概念
显然,定义g:V→V′, g(vi)=v i ′, 可以验证g是满足定义7.1.6的双射, 所以G≌G′。 • 对于同构,形象地说,若图 的结点可以任意挪动位置,而边是完 全弹性的,只要在不拉断的条件下, 这个图可以变形为另一个图,那么这 两个图是同构的。故同构的两个图从 外形上看可能不一样,但它们的拓扑 结构是一样的。
图 7.1.1哥尼斯堡七桥问题
1.图的定义
7.1 图的基本概念
现实世界中许多现象能用某种图形 表示 ,这种图形是由一些点和一些连接 两点间的连线所组成。 • 【例7.1.1】a, b, c, d 4个篮球队进
• 行友谊比赛。 为了表示4个队之间比赛的 情况, 我们作出图 7.1.1的图形。 在图中 4个小圆圈分别表示这4个篮球队, 称之 为结点。 如果两队进行过比赛, 则在表示 该队的两个结点之间用一条线连接起来, 称之为边。 这样利用一个图形使各队之间 的比赛情况一目了然。
7.1 图的基本概念
• 证明: 设G=〈V ,E〉, |V|=6, v是G中一结点。 因为v 与G的其余5个 结点或者在 中邻接, 或者在G中邻接。 G 故不失一般性可假定,有3个结点 v1 , v2, v3在G中与v邻接。 • 如果这3个结点中有两个结点(如 v1, v2)邻接,则它们与v 就是G中一个三角 形的3个顶点。 如果这 3 个结点中任意 两个在G中均不邻接, 则v1, v2, v3就 是 G 中一个三角形的3个顶点。
