离散数学(图论部分)1-4章习题课
第1章 习题讲解 离散数学(共22张PPT)

设 P :今天是星期二 Q :我有一次计算方法测验 R :我有物理(wùlǐ)测验 S :物理(wùlǐ)
老前师提生(病qiántí): P ∧P → Q ∨ R, S → R
S,
步骤
断 言(真)
结论:Q
根据
1
2
3
4 5
6
7 8
2012-2013-2
P∧S
P P→Q∨R Q∨R
S
S→ R
R
Q
鲁东大学 第十四页,共22页。
鲁东大学 第十六页,共22页。 数学与统计科学学院 鲍永平
第一章 数理逻辑
习题(xítí)1.6
11.设 P(x, y, z) 表示 x * y =z,E( x, y )表示 x=y,G(x , y)表示 x > y,
论述域是整数(zhěngshù),将以下断言译成逻辑符。
2)如果(rúguǒ) xy 0,那么 x 0并且 y 0
〔i〕 Q (R ∧ P)
我去镇上当且仅当我有时间且天不下雪。
〔i v〕
(R ∨ Q )
说我有时间或我去镇上是不对的
2012-2013-2
鲁东大学 第四页,共22页。 数学与统计科学学院 鲍永平
第一章 数理逻辑
2. 否认以下(yǐxià)命题 〔1〕上海处处(chùchù)清洁
上海并非处处清洁 4. 给 P 和 Q 指派(zhǐpài)真值 T,给 R 和 S 指派(zhǐpài)
第一章 数理逻辑 14.试译出“ a 是 b 的外祖父〞,只允许用以下(yǐxià)谓词: P(x) 表示 “x是人〞,F(x , y)表示 “x 是 y 的父亲〞, M(x,y)表示 “ x 是 y 的母亲〞
x ( P(x) ∧ P(a) ∧ P(b) ∧ F( a , x) ∧ M(x, b) )
离散数学习题课图论

2021/6/28
6 of 220
练习2(续)
D的邻接矩阵的前4次幂.
1 2 0 0
A 0
0
1
0
1 0 0 1
0
0
1
0
1 2 2 0
A 2 1
0
0
1
1 2 1 0
1
0
0
1
3 2 2 2
A3
1
2
1
0
2 2 2 1
1
2
1
0
Hale Waihona Puke 5 6 4 2A4
2
2
2
1
4 4 3 2
2
2
2
1
2021/6/28
8 of 220
练习2(续)
(5) v1到v1长度为1,2,3,4的回路数分别为 1,1,3,5. 其中长度为1的是初级的(环);长度 为2的是复杂的;长度为3的中有1条是复杂 的,2条是初级的;长度为4的有1条是复杂 的,有4条是非初级的简单回路. (6) 长度为4的通路(不含回路)为33条. (7) 长度为4的回路为11条. (8) 长度4的通路88条,其中22条为回路. (9) 44的全1矩阵.
9阶无向图G中,每个顶点的度数不是5就 是6. 证明G中至少有5个6度顶点或至少有 6个5度顶点.
方法一:穷举法
设G中有x个5度顶点,则必有(9x)个6度顶点, 由握手定理推论可知,(x,9x)只有5种可能: (0,9), (2,7), (4,5), (6,3), (8,1)它们都满足要求.
方法二:反证法
〔1 n 6〕 熟练掌握求最优树的方法
2021/6/28
12 of 220
习题1
离散数学自考第一章(课后习题和答案)

每当P和Q的真值相同时,则(P↔Q)的真值 为“T”,否则(P↔Q)的真值为“F”。
(3)举例:
▪ 春天来了当且仅当燕子飞回来了。 ▪平面上二直线平行,当且仅当这二直线不相交。 ▪2+2=4当且仅当雪是白色的。 (两者没有关系,但是确实命题)
举例: (a)P:王华的成绩很好 Q:王华的品德很好。 则PΛQ:王华的成绩很好并且品德很好。 (b P:我们去种树 Q:房间里有一台电视机 则PΛQ:我们去种树与房间里有一台电视机。 (c) P:今天下大雨 Q:3+3=6 则PΛQ:今天下大雨和3+3=6
3.析取词(或运算) (1)符号“∨” 设P、Q为二个命题,则 (P∨Q)称作P与Q的“析取”,读作: “P或Q”。
(a)P:我拿起一本书 Q:我一口气读完了这本书 P→Q:如果我拿起一本书,则我一口气读完了这本书。 (b)P:月亮出来了 Q:3×3=9 P→Q:如果月亮出来了,则 3×3=9。(善意推定)
5.双条件联结词(“等价”词、“同”联结词、 “等同”词) (1)符号“↔”设P、Q为二个命题,则P↔ Q读作:“P当且仅当Q”,“P等价 Q”,“P是Q的充分必要条件”。 (2)定义(见真值表):
(4)P,Q中,P、Q的地位是平等的,P、Q 交换位置不会改变真值表中的值。
6.命题联结词在使用中的优先级 (1)先括号内,后括号外 (2)运算时联结词的优先次序为: ¬ Λ → ↔ (由高到低) (3)联结词按从左到右的次序进行运算
∨
¬P∨(Q∨R)可省去括号,因为“V”运算是可结合的。 ( ¬P∨Q)∨R可省去括号,因为符合上述规定 而P→(Q→R)中的括号不能省去,因为“→”不满足结合律。
离散数学第四版课后答案(第4章)

第4章 习题解答4.1 A :⑤; B :③; C :①; D :⑧; E :⑩4.2 A :②; B :③; C :⑤; D :⑩; E :⑦4.3 A :②; B :⑦; C :⑤; D :⑧; E :④分析 题4.1-4.3 都涉及到关系的表示。
先根据题意将关系表示成集合表达式,然后再进行相应的计算或解答,例如,题4.1中的}2,2,1,2,2,1,1,1{},2,2,1,1{><><><><=><><=s s E I};2,2,2,1,1,1{><><><=s I而题4.2中的}.1,4,4,3,1,2,4,1,1,1{><><><><><=R为得到题4.3中的R 须求解方程123=+y x ,最终得到}.1,9,2,6,3,3{><><><=R求R R 有三种方法,即集合表达式、关系矩阵和关系图的主法。
下面由题4.2的关系分别加以说明。
1°集合表达式法将ranR ran domR domR,, 的元素列出来,如图4.3所示。
然后检查R 的每个有序对,若R y x >∈<,,则从domR 中的x 到ranR 中的y 画一个箭头。
若danR 中的x 经过2步有向路径到达ranR 中的y ,则R R y x >∈<,。
由图4.3可知}.1,3,4,2,1,2,4,4,1,44,1,1,1{><><><><>><<><=R R如果求G F ,则将对应于G 中的有序对的箭头画在左边,而将对应于F 中的有序对的箭头画在右边。
对应的三个集合分别为ranF domF ran domG ,, ,然后,同样地寻找domG 到ranF 的2步长的有向路径即可。
《离散数学》题库及标准答案

《离散数学》题库及标准答案《离散数学》题库及答案————————————————————————————————作者:————————————————————————————————日期:《离散数学》题库与答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?( )(1)?Q=>Q→P (2)?Q=>P→Q (3)P=>P→Q (4)?P∧(P∨Q)=>?P答:在第三章里面有公式(1)是附加律,(4)可以由第二章的蕴含等值式求出(注意与吸收律区别)2、下列公式中哪些是永真式?( )(1)(┐P∧Q)→(Q→?R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答:(2),(3),(4)可用蕴含等值式证明3、设有下列公式,请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ?(P→Q)=>P (6) ?P∧(P∨Q)=>?P答:(2)是第三章的化简律,(3)类似附加律,(4)是假言推理,(3),(5),(6)都可以用蕴含等值式来证明出是永真蕴含式4、公式?x((A(x)→B(y,x))∧?z C(y,z))→D(x)中,自由变元是( ),约束变元是( )。
答:x,y, x,z(考察定义在公式?x A和?x A中,称x为指导变元,A为量词的辖域。
在?x A和?x A的辖域中,x的所有出现都称为约束出现,即称x为约束变元,A中不是约束出现的其他变项则称为自由变元。
于是A(x)、B(y,x)和?z C(y,z)中y为自由变元,x和z为约束变元,在D(x)中x为自由变元)5、判断下列语句是不是命题。
若是,给出命题的真值。
( )(1)北京是中华人民共和国的首都。
(2) 陕西师大是一座工厂。
(3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。
离散数学-习题集

离散数学-习题集《离散数学》习题集第⼀部分判断题⼀、第⼀章—集合1、()已知集合A的元素个数为10,则集合A的幂集的基=102。
2、()已知两个集合A、B,若A中的元素都是B中的元素,则记为A∈B。
2、()已知集合A的元素个数为n,则集合A的幂集P(A)的元素个数为n2。
3、( ) 已知两个集合A={Ф,{Ф}},B={Ф},则A∩B={Ф}。
4、()已知两个集合A={Ф,{Ф}},B={Ф},则A∩B=Ф。
5、()已知两个集合A、B,若A中的元素都是B中的元素,则记为A∈B。
6、()已知集合A的元素个数为n,则集合A的幂集P(A)的元素个数为n2。
7、()已知集合A的元素个数为n,则A×A的幂集的元素个数为n2。
8、()已知两个集合A、B,则A-B是由属于B但不属于A的元素构成的集合。
⼆、第⼆章—⼆元关系1、()若R是A上的⼆元关系,I A是A上的恒等关系,则当且仅当I A∈R时,R是A上的⾃反关系。
2、(√)若R是集合A上的⼆元关系,且当(a,b)∈R且(a,c)∈R时,就有(b,c)∈R,则R是A 上的可传递关系。
3、()设A是集合,A1、A2、...A n都是A的⾮空⼦集,令S={A1,A2,...,A n},则如果S是集合A的⼀个划分,那么S⼀定是集合A的⼀个完全覆盖;反之亦然。
5、()R是⾮空集合A上的等价⼆元关系,则A关于R的商集A/R是集合A的⼀个划分,但不是A的⼀个完全覆盖。
6、()已知集合A有4元素,易知集合A共有24个互不相同的⼦集合,所以在集合A上⼀共可定义24个互不相同的⼆元关系。
7、()若R1和R2都是集合A上的可传递⼆元关系,则R1∪R2也是A上的传递关系。
8、()设R是有限的⾮空集合A上的偏序关系,则A必有极⼤(⼩)元和最⼤(⼩)元。
9、()若R1和R2都是集合A上的相容关系,则R1∩R2也是A上的相容关系。
10、()若R1和R2都是集合A的可传递⼆元关系,则R1∩R2也是A上的传递关系。
离散数学及其应用图论部分课后习题答案
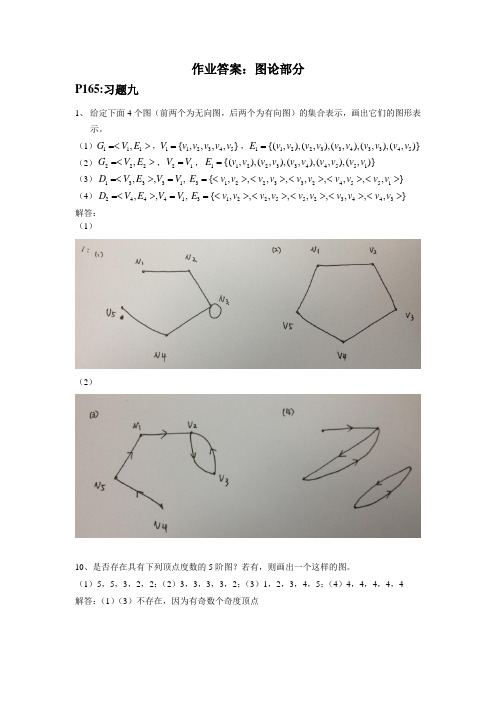
作业答案:图论部分P165:习题九1、 给定下面4个图(前两个为无向图,后两个为有向图)的集合表示,画出它们的图形表示。
(1)111,G V E =<>,112345{,,,,}V v v v v v =,11223343345{(,),(,),(,),(,),(,)}E v v v v v v v v v v = (2)222,G V E =<>,21V V =,11223344551{(,),(,),(,),(,),(,)}E v v v v v v v v v v = (3)13331,,,D V E V V =<>=31223324551{,,,,,,,,,}E v v v v v v v v v v =<><><><><> (4)24441,,,D V E V V =<>=31225523443{,,,,,,,,,}E v v v v v v v v v v =<><><><><> 解答: (1)(2)10、是否存在具有下列顶点度数的5阶图?若有,则画出一个这样的图。
(1)5,5,3,2,2;(2)3,3,3,3,2;(3)1,2,3,4,5;(4)4,4,4,4,4 解答:(1)(3)不存在,因为有奇数个奇度顶点。
14、设G 是(2)n n ≥阶无向简单图,G 是它的补图,已知12(),()G k G k δ∆==,求()G ∆,()G δ。
解答:2()1G n k ∆=--;1()1G n k δ=--。
15、图9.19中各对图是否同构?若同构,则给出它们顶点之间的双射函数。
解答:(c )不是同构,从点度既可以看出,一个点度序列为4,3,3,3,3而另外一个为4,4,3,3,1(d )同构,同构函数为12()345x a x bf x x c x d x e=⎧⎪=⎪⎪==⎨⎪=⎪=⎪⎩ 16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
离散数学习题课带答案

(P(Q∧R))∧(P(Q∧R)) (P∨(Q∧R))∧ (P∨(Q∧R)) (P∨Q)∧(P∨R))∧(P∨Q)∧(P∨R) (P∨Q∨(R∧R))∧(P∨(Q∧Q)∨R)) ∧(P∨Q∨(R∧R))∧(P∨(Q∧Q)∨R) (P∨Q∨R)∧ (P∨Q∨R))∧(P∨Q∨R) ∧ (P∨Q∨R)∧ (P∨Q∨R)∧ (P∨Q∨R)∧ (P∨Q∨R) ∧(P∨Q∨R) (P∨Q∨R)∧(P∨Q∨R))∧ (P∨Q∨R) ∧(P∨Q∨R)∧(P∨Q∨R)∧(P∨Q∨R)
(4)某些汽车比所有的火车都慢,但至少有一列火车比每辆 汽车快 C(x):x是汽车;H(x):x是火车;S(x,y): x比y慢 x(C(x)∧y(H(y)→S(x,y)))∧z(H(z)∧y(C(y) →S(y,z)))
(5)对任何整数x和y,x≤y且y≤x是x=y的充要条件 I(x):x是整数;E(x,y):x=y;G(x,y):x>y xy(I(x)∧I(y)→(G(x,y)∧G(y,x)↔ E(x,y))) (6)若m是奇数,则 2m 不是奇数 O(x):x是奇数; f(x,y)= x×y O(m) → O(f(2,m) (7)那位戴眼镜的用功的大学生在看这本大而厚的巨著 A(x):x是戴眼镜的,B(x):x是用功的,C(x):x是大学生,D(x):x是大 的,E(x):x是厚的,F(x):x是巨著, G(x,y):x在看y,a:那位,b:这本 A(a)∧B(a)∧C(a)∧D(b)∧E(b)∧F(b)∧G(a,b) (8)每个自然数都有唯一的后继数 N(x):x是自然数; L(x,y):x是y的后继数 x(N(x)→(y (N(y)∧L(y,x) ∧z (N(z)∧L(z,x)→ E(y,z)))))
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学(图论部分)1-4章习题课1. 证明:在10个人中,或有3人互相认识,或有4人互不认识。
证:设x为10人中之任意某人,则在余下9人中:(1) x至少认识其中4人,或(2) x至多认识其中3人(即至少不认识其中6人),两者必居其一。
(1) 若此x认识的4人互不相识,命题得证;否则,互相认识的2人加上x构成互相认识的3人,命题得证。
(2) 若此x不认识的6人中有3人互相认识,命题得证;否则,由Ramsey(3,3)=6知,此6人中至少有3人互不认识,此3人加上x为互不认识的4人,命题得证。
2. 设(a) V={a,b,c,d},A={<a,b>,<a,c>,<b,c>,<b,d>,<c,d>}(b) V={a,b,c,d,e},E={(a,b),(a,c),(b,c),(d,e)}画出上述图的图解。
解:略。
3. 试找出K3的全部子图,并指出哪些是生成子图。
解:K3共有17个子图。
其他略。
4. 证明:在至少有2人的团体中,总存在2个人,他们在这个团体中恰有相同数目的朋友。
解:在n个人的团体中,各人可能有的朋友数目为0, 1, 2, 3, …, n-1,共n个数,但其中0和n-1 不能共存,故n个人事实上可能的朋友数目只有n-1个。
由鸽巢原理,命题得证。
5.某次宴会上许多人互相握手。
证明:必有偶数个人握了奇数次手。
证:以人为顶点,握手关系为邻接关系构造一个无向图。
由图的性质,奇数度的顶点必为偶数个,即握了奇数次手的人数必为偶数。
6. 证明:Ramsey(3,4)=9。
(提示:题1的推广)证:在9个人中,不可能每个人都恰好认识其他的3个人(即图的9个顶点不可能每个顶点的度都为3,否则违反图的奇数度的顶点必为偶数个的性质)。
设x不会恰好认识其他的3个人(即deg(x)≠3),则在余下8人中::(1) x至少认识其中4人,或(2) x至多认识其中2人(即至少不认识其中6人),两者必居其一。
由题1的过程,命题得证。
7. 证明:图G=(V, E),n=|V|,m=|E|。
若m>12(n-1)(n-2),则G连通证:利用反证法。
设G可分解为不连通的非空的两部分G1= (V1, E1 )、G2 = (V2, E2 ),并设n1=|V1|≠0,m1=|E1|,n2=|V2|≠0,m2=|E2|则n=n1+n2,m=m1+m2若G1为完全图,则m1=12n1(n1-1),故m1≤12n1(n1-1)若G2为完全图,则m2=12n2(n2-1),故m2≤12n2(n2-1)故:m= m1+m2≤1 2n1(n1-1)+12n2(n2-1)=12(n-1)(n-2)+(n1-1)(n1-n+1) 又:1≤n1≤n-1故:(n1-1)(n1-n+1)≤0即:m≤12(n-1)(n-2) 与条件m>12(n-1)(n-2) 矛盾。
8. 证明:图G = ( V, E ),n=|V|,m=|E|。
若G连通,则m≥(n-1)证一:对n做归纳。
n=2时,m=1≥n-1成立设n=k时,命题成立。
当n=K+1时,由于G连通,任意顶点的度≥1;(1) 若任意顶点的度≥2,则2m=∑deg(vi) ≥2n,此时m≥n>n-1,命题成立。
(2) 否则,若有某顶点u的度为1,从图中去掉该顶点以及其关联边,得到的新图G1 = (V1, E1) 仍然连通,且n1=|V1|= n-1=K,m1=|E1|= m-1由归纳假设,对图G1有m1≥(n1-1)即m-1≥(n-1-1) 或m≥(n-1)由归纳原理,命题得证。
证二:由于G连通,设T= ( V, E' ) 是G的一棵生成树,则|E'|=n-1,而m≥|E'|,故。
9. 证明:n个人中,若任何2人合在一起认识其他n-2个人,则他们可以排成一排,使除首尾2人外,其余的人都和相邻的人认识。
证:以人为顶点,认识关系为邻接关系构造一个无向图,问题转化为讨论满足条件的图中Hamilton道路的存在性。
从图中任取2个顶点x和y,记deg(x,y) 为{x,y} 与其他顶点的邻接边数目。
由题意,有deg(x,y)≥n-2,这里的n-2由除了x和y外的n-2顶点中每个顶点贡献一条与x或y邻接的边得到。
(1) 若x与y认识,则deg(x)+deg(y) = deg(x,y)+2 ≥ n-2+2 = n > n-1(2) 若x与y不认识,设x认识z,z≠y,由题意x与z合在一起认识包括y的其他n-2个人,所以只能z也认识y,即在图中,顶点z与x和y同时邻接。
由之前deg(x,y) ≥ n-2的讨论可得:deg(x,y) ≥ n-2+1 = n-1,故deg(x)+deg(y) = deg(x,y) ≥ n-1综上,对任意顶点x和y,有deg(x)+deg(y) ≥n-1,由Hamilton道路存在的充分条件知图中存在一条Hamilton 道路,命题得证。
10. 用Warshall 算法求下图的道路矩阵:解:见课件的举例。
11. 若树中恰有2个顶点的度为1,则此树为一条链。
证:设 T= (V, E) 为一棵树,n=|V|,m=|E|,则 m=n -1故:deg()22(1)i i v Vv m n ∈==-∑ 且 deg (v i ) ≠0 (i =1..n)不妨设 deg (v 1)= deg (v n )=1,则 12deg()2(1)22(2)n ii v n n -==--=-∑且 deg (v i ) >1 (i =2..n -1) 所以只能 deg (v i ) =2 (i =2..n -1)即此树为从v 1到v n 的一条路。
12. 若树中有一顶点的度为k ,则树中至少有 k 个度为1的点。
证:设 T= (V, E) 为一棵树,n=|V|,m=|E|,则 m=n -1故: 1deg()22(1)n ii v m n ===-∑ 且 deg (v i) ≠0 (i =1..n) 不妨设 deg (v n ) =k ,则 11deg()2(1)n ii v n k -==--∑ 设树中有p 个度为1的顶点:deg (v n -1) = deg (v n -2)= deg (v n-p )=1则11deg()2(1)n p i i v p n k --=+=--∑ 或 11deg()2(1)n p ii v n k p --==---∑ 对余下的n -p -1个顶点,每个顶点的度至少为2,即11d e g ()2(1)n p ii v n p --=≥--∑ 所以 2(n -1)-k -p ≥ 2(n -p -1)解不等式得:p ≥ k13. 设连通图G=(V, E),T=(V, E(T))和T'=(V, E(T'))是G的两棵不同生成树且e∈E(T)-E(T'),则存在一条边e'∈E(T')-E(T),使得T-e+e' 和T'-e'+e都是G的生成树。
证:从T中去掉边e,则T被分成不连通的两部分,设其顶点集分别为V1和V2。
在T'中必存在连接V1和V2的边,记为e'∈E(T')。
∵e∈E(T)-E(T') 即e∉E(T')∴e'≠ e又:若e'∈E(T),则e不是T中割边,与T是一棵树矛盾。
∴e'∉E(T) 即e'∈E(T')-E(T)考察T+e',e和e' 在其中唯一的回路上,因此T-e+e' 构成G的一棵生成树。
同理,考察T'+e,可知T'-e'+e也构成G的一棵生成树。
14. 设图G=(V, E),定义δ(G)=min{deg(v), v∈V}为G的最小度(类似可以定义∆(G)=max{deg(v), v∈V}为G的最大度)。
若G是简单图,δ(G) ≥ k,T是一棵含k条边的树,则在G中存在与T同构的子图。
(提示:对k作归纳。
)证:对k作归纳。
易知k=1时结论成立。
设k=p时结论成立。
当k=p+1时,G是简单图,δ(G)≥p+1。
设树T含p+1条边(p+2个顶点),v0是T的一个叶子结点,u是v0的邻接点,其余顶点编号为v1~v p。
记e=(u, v0),T0=T-e,则G和T0符合归纳假设的条件,G中存在与T0同构的子图T0'。
将T0'的p+1个顶点与T0的顶点对应,编号为u', v1'~v p'。
考察顶点u',由于deg(u')≥p+1,可见u'至少与除了v1'~v p'之外的一个点邻接。
将该点编号为v0',记e'=(u', v0'),构造的T'=T0'+e'与T同V 1 V 2 V 3 V 4 V 5 构。
由归纳原理,命题得证。
15. 证明:n 阶图连通当且仅当r(B)=n -1证:必要性:课件定理[3-2-3]的证明。
充分性:设此时G 的连通分支数为k ,则经行列互换,关联矩阵B 可写成一个对角分块阵:120...00...000...k B B B B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,r(B)=r(B 1)+ r(B 2)+ … r(B k )设 第i 个连通子图的阶为n i , i=1..k 。
由必要性:r(B i )=n i -1。
故 11()(1)k k i i i i r B n n k n k ===-=-=-∑∑由条件 r(B)=n -1,故 k=1。
即图是连通的。
16. 求下图生成树的数目:解:构造关联矩阵B 划出B k ,应用Binet-Cauchy 定理得到生成树的数目|BB k T |=2417. 试画出12硬币3次求伪的判断树。
解:略。
18. 证明:对2元正则树,m=2n 0-2,其中m 为边数,n 0为树叶数。
证:树有 m=n -1二元树有 n 0 = n 2+1二元正则树有顶点数 n = n 0+n 2故: n = n 0+n 2 = n 0+(n 0-1)= 2n 0-1m=n -1=2n 0-219. 有字符串 “state seat act tea cat set a cat” ,求其最短二进制编码。
解:统计字频,建立huffman 树,构造相应的huffman 编码。
过程见课件举例。
20. 旅行商问题:用分支定界法、最近邻法、最近插入法、最远插入法求解:423352294526384930342742354131∞⎛⎫ ⎪∞ ⎪ ⎪∞ ⎪∞ ⎪ ⎪∞ ⎪ ⎪∞⎝⎭解:精确解=194最近邻法解=205最近插入法解=203最远插入法解=22921. 求下图各点到v8的最短路径(提示:利用Dijkstra 算法)解:将原图有向边反向得到新图,利用Dijkstra 算法求新图中V8到各点的最短路径。
