离散数学图论练习题
离散数学测验题--图论部分(优选.)

离散数学图论单元测验题一、单项选择题(本大题共10小题,每小题2分,共20分)1、在图G =<V ,E >中,结点总度数与边数的关系是( )(A) deg(v i )=2∣E ∣ (B) deg(v i )=∣E ∣ (C)∑∈=V v E v 2)deg( (D) ∑∈=Vv E v )deg(2、设D 是n 个结点的无向简单完全图,则图D 的边数为( )(A) n (n -1) (B) n (n +1) (C) n (n -1)/2 (D) n (n +1)/23、 设G =<V ,E >为无向简单图,∣V ∣=n ,∆(G )为G 的最大度数,则有(A) ∆(G )<n (B)∆(G )≤n (C) ∆(G )>n (D) ∆(G )≥n4、图G 与G '的结点和边分别存在一一对应关系,是G ≌G '(同构)的( )(A) 充分条件 (B) 必要条件 (C)充分必要条件 (D)既非充分也非必要条件5、设},,,{d c b a V =,则与V 能构成强连通图的边集合是( )(A) },,,,,,,,,{><><><><><=c d b c d b a b d a E(B) },,,,,,,,,{><><><><><=c d d b c b a b d a E(C) },,,,,,,,,{><><><><><=c d a d c b a b c a E6、有向图的邻接矩阵中,行元素之和是对应结点的( ),列元素之和是对应结点的() (A)度数 (B) 出度 (C)最大度数 (D) 入度7、设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100000100则G 的边数为( ).A .5B .6C .3D .48、设m E n V E V G ==>=<,,,为连通平面图且有r 个面,则r =( )(A) m -n +2 (B) n -m -2 (C) n +m -2 (D) m +n +29、在5个结点的二元完全树中,若有4条边,则有 ( )片树叶。
应用离散数学图论图的连通性题库试卷习题及答案

§5.2 图的连通性习题5.21.证明或否定:(1)简单图G 中有从点u 到点v 的两条不同的通路,则G 中有基本回路。
(2)简单图G 中有从点u 到点v 的两条不同的基本通路,则G 中有基本回路。
解:(1)简单图G 中有从点u 到点v 的两条不同的通道,则G 中有回路。
(2)简单图G 中有从点u 到点v 的两条不同的路,则G 中有回路。
解 (1)不一定:如下图,点1与点3之间有两条通道:(1、2、3)和(1、2、1、2、3),但图中没有回路。
(2)一定:设两条路分别为),,,,,(211v x x x u L m =和),,,,,(212v y y y u L n =。
若对m i ≤≤1,n j ≤≤1有j i y x ≠,则),,,,,,,,,,(12121u y y y y v x x x u n n m -是一条回路。
否则假设l k y x =且是离u 最近的一对(即对k i ≤≤1,l j ≤≤1,不存在j i y x =),则),,,,,,,,,(12121v y y y x x x u l k -是一条回路。
2.设G 是简单图,)(G δ≥2,证明G 中存在长度大于或等于1)(+G δ的基本回路。
证:以图G 中一点v 1出发,与之相邻的点设为v 2,由于)(G δ≥2,则v 2至少还有一个邻接点,设为v 3,若v 3与v 1邻接,则形成长度为1)(+G δ的基本回路,则若v 3不与v 1邻接,则至少还有一个邻接点,设为v 4,若v 4与v 1或v 2邻接,则形成长度为大于或等于1)(+G δ的基本回路,若v 4与v 1和v 2都不邻接,至少还有一个邻接点,设为v 5,…,依次类推,一定可以到达最后一个顶点v i ,由于)(G δ≥2,则除了v i -1外,一定会与前面的某个顶点邻接,就会形成长度为大于或等于1)(+G δ的基本回路。
3.证明:若连通图G 不是完全图,则G 中存在三个点w v u ,,,使E v u ∈)(,,E w v ∈)(,,E w u ∉)(,。
离散数学图论练习题(优选试题)

图论练习题一.选择题1、设G是一个哈密尔顿图,则G一定是( )。
(1) 欧拉图(2) 树(3) 平面图(4)连通图2、下面给出的集合中,哪一个是前缀码?()(1) {0,10,110,101111}(2) {01,001,000,1}(3) {b,c,aa,ab,aba}(4) {1,11,101,001,0011}3、一个图的哈密尔顿路是一条通过图中()的路。
4、设G是一棵树,则G 的生成树有( )棵。
(1) 0(2) 1(3) 2(4) 不能确定5、n阶无向完全图Kn 的边数是( ),每个结点的度数是( )。
6、一棵无向树的顶点数n与边数m关系是()。
7、一个图的欧拉回路是一条通过图中( )的回路。
8、有n个结点的树,其结点度数之和是()。
9、下面给出的集合中,哪一个不是前缀码( )。
(1) {a,ab,110,a1b11} (2) {01,001,000,1}(3) {1,2,00,01,0210} (4) {12,11,101,002,0011}10、n个结点的有向完全图边数是( ),每个结点的度数是( )。
11、一个无向图有生成树的充分必要条件是( )。
12、设G是一棵树,n,m分别表示顶点数和边数,则(1) n=m (2) m=n+1 (3) n=m+1 (4) 不能确定。
13、设T=〈V,E〉是一棵树,若|V|>1,则T中至少存在( )片树叶。
14、任何连通无向图G至少有( )棵生成树,当且仅当G 是( ),G的生成树只有一棵。
15、设G是有n个结点m条边的连通平面图,且有k个面,则k等于:(1) m-n+2 (2) n-m-2 (3) n+m-2 (4) m+n+2。
16、设T是一棵树,则T是一个连通且( )图。
17、设无向图G有16条边且每个顶点的度数都是2,则图G有( )个顶点。
(1) 10 (2) 4 (3) 8 (4) 1618、设无向图G有18条边且每个顶点的度数都是3,则图G有( )个顶点。
离散数学图论答案

离散数学图论答案【篇一:离散数学图论习题】综合练习一、单项选择题1.设l是n阶无向图g上的一条通路,则下面命题为假的是( ). (a) l可以不是简单路径,而是基本路径 (b) l可以既是简单路径,又是基本路径 (c) l可以既不是简单路径,又不是基本路径 (d) l可以是简单路径,而不是基本路径答案:a2.下列定义正确的是( ).(a) 含平行边或环的图称为多重图(b) 不含平行边或环的图称为简单图 (c) 含平行边和环的图称为多重图(d) 不含平行边和环的图称为简单图答案:d3.以下结论正确是 ( ).(a) 仅有一个孤立结点构成的图是零图 (b) 无向完全图kn每个结点的度数是n (c) 有n(n1)个孤立结点构成的图是平凡图(d) 图中的基本回路都是简单回路答案:d4.下列数组中,不能构成无向图的度数列的数组是( ). (a)(1,1,1,2,3) (b) (1,2,3,4,5) (c) (2,2,2,2,2) (d) (1,3,3,3) 答案:b5.下列数组能构成简单图的是( ). (a) (0,1,2,3)(b) (2,3,3,3)(c) (3,3,3,3)(d) (4,2,3,3) 答案:c6.无向完全图k3的不同构的生成子图的个数为(). (a) 6 (b)5(c) 4 (d) 3 答案:c7.n阶无向完全图kn中的边数为().(a)n(n?1)n(n?1)(b) (c) n (d)n(n+1) 22答案:b8.以下命题正确的是( ).(a) n(n?1)阶完全图kn都是欧拉图(b) n(n?1)阶完全图kn都是哈密顿图(c) 连通且满足m=n-1的图v,e(?v?=n,?e?=m)是树 (d) n(n?5)阶完全图kn都是平面图答案:c10.下列结论不正确是( ).(a) 无向连通图g是欧拉图的充分必要条件是g不含奇数度结点(b) 无向连通图g有欧拉路的充分必要条件是g最多有两个奇数度结点 (c) 有向连通图d是欧拉图的充分必要条件是d的每个结点的入度等于出度(d) 有向连通图d有有向欧拉路的充分必要条件是除两个结点外,每个结点的入度等1于出度答案:d11.无向完全图k4是().(a)欧拉图(b)哈密顿图(c)树答案:b12.有4个结点的非同构的无向树有 ( )个.(a) 2 (b) 3(c) 4(d) 5 答案:a13.设g是有n个结点,m条边的连通图,必须删去g的( )条边,才能确定g的一棵生成树.(a) m?n?1 (b) n?m (c) m?n?1 (d) n?m?1 答案:a14.设g是有6个结点的完全图,从g中删去( )条边,则得到树. (a) 6 (b) 9 (c) 10 (d) 15 答案:c二、填空题1.数组{1,2,3,4,4}是一个能构成无向简单图的度数序列,此命题的真值是 . 答案:02.无向完全图k3的所有非同构生成子图有个.答案:43.设图g??v,e?,其中?v??n,?e??m.则图g是树当且仅当g是连通的,且m?.答案:n-14.连通图g是欧拉图的充分必要条件是答案:图g无奇数度结点 5.连通无向图g有6个顶点9条边,从g中删去g的一棵生成树t.答案:46.无向图g为欧拉图,当且仅当g是连通的,且g中无答案:奇数度7.设图g??v,e?是简单图,若图中每对结点的度数之和,则g一定是哈密顿图.答案:?8.如图1所示带权图中最小生成树的权是.答案:12三、化简解答题1.设无向图g=v,e,v={v1,v2,v3,v4,v5,v6}, e={( v1,v2), ( v2,v2), ( v4,v5), ( v3,v4), ( v1,v3),( v3,v1), ( v2,v4)}. (1) 画出图g的图形;2图15图22(2) 写出结点v2, v4,v6的度数; (3) 判断图g是简单图还是多重图.解:(1) 图g的图形如图5所示.(2) deg(v2)?4,deg(v4)?3,deg(v6)?0.(3) 图g是多重图.作图如图2. 2.设图g=v,e,其中v={a,b,c,d,e}, e={(a,b),(b,c),(c,d), (a,e)}试作出图g的图形,并指出图g是简单图还是多重图?是连通图吗?说明理由.b e解:图g如图8所示.. 图g中既无环,也无平行边,是简单图. cd 图g是连通图.g中任意两点都连通.图3所以,图g有9个结点.作图如图3.四、计算题1.设简单连通无向图g有12条边,g中有2个1度结点,2个2度结点,3个4度结点,其余结点度数为3.求g中有多少个结点.试作一个满足该条件的简单无向图.解:设图g有x个结点,由握手定理2?1+2?2+3?4+3?(x?2?2?3)=12?23x?24?21?18?27x=9 故图g有9个结点.图4满足该条件的简单无向图如图4所示2.设图g(如图5表示)是6个结点a,b,c, d,e,f的图,试求,图g的最小生成树,并计算它的权.c 解:构造连通无圈的图,即最小生成树,用克鲁斯克尔算法:第一步:取ab=1;第二步:取af=4第三步:取fe=3;第四步:取ad=9图5 第五步:取bc=23如图6.权为1+4+3+9+23=403.一棵树t有两个2度顶点,1个3度顶点;3个4问它有几片树叶?解:设t有n顶点,则有n-1条边.t中有2个 2度顶点,1个3度顶点,3个4度顶点,其余n-2-1-3个1度顶点.五、证明题1.若无向图g中只有两个奇数度结点,则这两个结点一定是连通的.证:用反证法.设g中的两个奇数度结点分别为u和v.假若u和v不连通.即它们之间无任何通路,则g至少有两个连通分支g1,g2,且u和v分别属于g1和g2,于是g1和g2各含有一个奇数度结点.这与握手定理的推论矛盾.因而u和v一定是连通的.3【篇二:离散数学图论练习题】题1、设g是一个哈密尔顿图,则g一定是()。
离散数学图论部分经典试题及答案

离散数学图论部分经典试题及答案离散数学图论部分综合练习⼀、单项选择题1.设图G 的邻接矩阵为0101010010000011100100110则G 的边数为( ).A .6B .5C .4D .32.已知图G 的邻接矩阵为,则G 有().A .5点,8边B .6点,7边C .6点,8边D .5点,7边3.设图G =,则下列结论成⽴的是 ( ).A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v Vv 2)deg(=∑∈ D .E v Vv =∑∈)deg(4.图G 如图⼀所⽰,以下说法正确的是 ( ) . A .{(a , d )}是割边 B .{(a , d )}是边割集 C .{(d , e )}是边割集 D .{(a, d ) ,(a, c )}是边割集5.如图⼆所⽰,以下说法正确的是 ( ). A .e 是割点 B .{a, e }是点割集 C .{b , e }是点割集 D .{d }是点割集6.如图三所⽰,以下说法正确的是 ( ) .A .{(a, e )}是割边B .{(a, e )}是边割集C .{(a, e ) ,(b, c )}是边割集D .{(d , e )}是边割集οοοοοca b edο f图⼀图⼆图三7.设有向图(a )、(b )、(c )与(d )如图四所⽰,则下列结论成⽴的是 ( ).图四A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的应该填写:D8.设完全图K n 有n 个结点(n ≥2),m 条边,当()时,K n 中存在欧拉回路.A .m 为奇数B .n 为偶数C .n 为奇数D .m 为偶数 9.设G 是连通平⾯图,有v 个结点,e 条边,r 个⾯,则r = ( ).A .e -v +2B .v +e -2C .e -v -2D .e +v +2 10.⽆向图G 存在欧拉通路,当且仅当( ). A .G 中所有结点的度数全为偶数 B .G 中⾄多有两个奇数度结点C .G 连通且所有结点的度数全为偶数 D .G 连通且⾄多有两个奇数度结点11.设G 是有n 个结点,m 条边的连通图,必须删去G 的( )条边,才能确定G 的⼀棵⽣成树.A .1m n -+B .m n -C .1m n ++D .1n m -+ 12.⽆向简单图G 是棵树,当且仅当( ).A .G 连通且边数⽐结点数少1B .G 连通且结点数⽐边数少1C .G 的边数⽐结点数少1D .G 中没有回路.⼆、填空题1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是. 2.设给定图G (如图四所⽰),则图G 的点割οοοοc a b f集是.3.若图G=中具有⼀条汉密尔顿回路,则对于结点集V 的每个⾮空⼦集S ,在G 中删除S 中的所有结点得到的连通分⽀数为W ,则S 中结点数|S|与W 满⾜的关系式为.4.⽆向图G 存在欧拉回路,当且仅当G 连通且.5.设有向图D 为欧拉图,则图D 中每个结点的⼊度.应该填写:等于出度6.设完全图K n 有n 个结点(n 2),m 条边,当时,K n 中存在欧拉回路.7.设G 是连通平⾯图,v , e , r 分别表⽰G 的结点数,边数和⾯数,则v ,e 和r 满⾜的关系式.8.设连通平⾯图G 的结点数为5,边数为6,则⾯数为. 9.结点数v 与边数e 满⾜关系的⽆向连通图就是树.10.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去条边后使之变成树.11.已知⼀棵⽆向树T 中有8个结点,4度,3度,2度的分⽀点各⼀个,T 的树叶数为.12.设G =是有6个结点,8条边的连通图,则从G 中删去条边,可以确定图G 的⼀棵⽣成树.13.给定⼀个序列集合{000,001,01,10,0},若去掉其中的元素,则该序列集合构成前缀码.三、判断说明题1.如图六所⽰的图G 存在⼀条欧拉回路.2.给定两个图G 1,G 2(如图七所⽰):(1)试判断它们是否为欧拉图、汉密尔顿图?并说明理由.(2)若是欧拉图,请写出⼀条欧拉回路.v 123图六图七3.判别图G (如图⼋所⽰)是不是平⾯图,并说明理由.4.设G 是⼀个有6个结点14条边的连通图,则G 为平⾯图.四、计算题1.设图G =,其中V ={a 1, a 2, a 3, a 4, a 5},E ={,,,,}(1)试给出G 的图形表⽰;(2)求G 的邻接矩阵;(3)判断图G 是强连通图、单侧连通图还是弱连通图?2.设图G =,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1, v 2),(v 1, v 3),(v 2, v 3),(v 2, v 4),(v 3, v 4),(v 3, v 5),(v 4, v 5) },试(1)画出G 的图形表⽰;(2)写出其邻接矩阵;(2)求出每个结点的度数;(4)画出图G 的补图的图形. 3.设G =,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1,v 3),(v 2,v 3),(v 2,v 4),(v 3,v 4),(v 3,v 5),(v 4,v 5) },试(1)给出G 的图形表⽰;(2)写出其邻接矩阵;(3)求出每个结点的度数;(4)画出其补图的图形. 4.图G =,其中V ={ a , b , c , d , e },E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (c , d ), (d , e ) },对应边的权值依次为2、1、2、3、6、1、4及5,试(1)画出G 的图形;(2)写出G 的邻接矩阵;(3)求出G 权最⼩的⽣成树及其权值.5.⽤Dijkstra 算法求右图中A 点到其它各点的最短路径。
离散数学习题解答第6部分(图论)
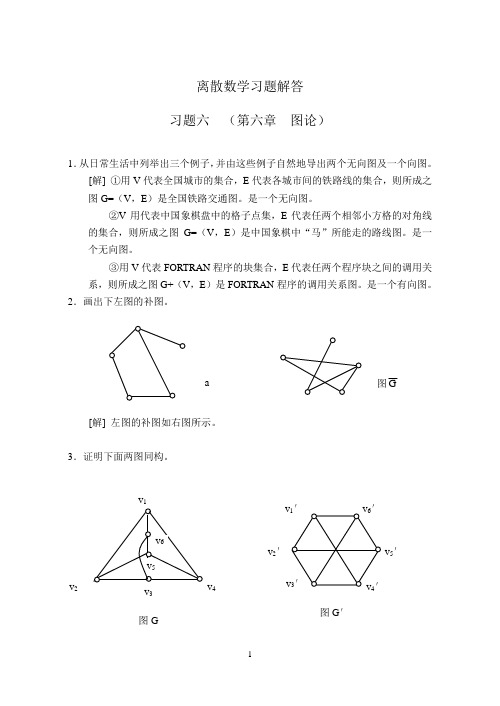
离散数学习题解答 习题六 (第六章 图论)1.从日常生活中列举出三个例子,并由这些例子自然地导出两个无向图及一个向图。
[解] ①用V 代表全国城市的集合,E 代表各城市间的铁路线的集合,则所成之图G=(V ,E )是全国铁路交通图。
是一个无向图。
②V 用代表中国象棋盘中的格子点集,E 代表任两个相邻小方格的对角线的集合,则所成之图G=(V ,E )是中国象棋中“马”所能走的路线图。
是一个无向图。
③用V 代表FORTRAN 程序的块集合,E 代表任两个程序块之间的调用关系,则所成之图G+(V ,E )是FORTRAN 程序的调用关系图。
是一个有向图。
2.画出下左图的补图。
[解] 左图的补图如右图所示。
3.证明下面两图同构。
a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1,v 2)=(v 1′,v 2′) ϕ (v 2)=v 2′ ϕ (v 2,v 3)=(v 2′,v 3′) ϕ (v 3)=v 3′ ϕ (v 3,v 4)=(v 3′,v 4′) ϕ (v 4)=v 4′ ϕ (v 4,v 5)=(v 4′,v 5) ϕ (v 5)=v 5′ ϕ (v 5,v 6)=(v 5′,v 6′) ϕ (v 6)=v 6′ϕ (v 6,v 1)=(v 6′,v 1′) ϕ (v 1,v 4)=(v 1′,v 4′) ϕ (v 2,v 5)=(v 2′,v 5′) ϕ (v 3,v 6)=(v 3′,v 6′)显然使下式成立:ψ (v i ,v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。
4.证明(a ),(b )中的两个图都是不同构的。
图G 中有一个长度为4的圈v 1v 2v 6v 5v 1,其各顶点的度均为3点,而在图G ′中却没有这样的圈,因为它中的四个度为3的顶点v 1',v 5',v 7',v 3'不成长度的4的圈。
13级离散数学(3-1图论)
【作业6】在一个部门的25个人中间,由于意见不
同,是否可能每个人恰好与其他5个人意见一致? 分析:考虑一个图,其中顶点代表人,如果两个人 意见相同,可用边连接,所以每个顶点都是5度。 解:令 25 个人分别为 v1 v2 …v25 . 则 degv1 = degv2 =…= degv25 =5 degv1 + degv2 +…+degv25 =125 是奇数 但在任何图中, 度数为奇数的结点必定是偶数, 所以是不可能的。
【作业5】求出下列各图的补图?
测试题
【测试题1】
a)画出无向完全图K4 和K6 并求出它们的边数。 b)画出完全二部图K4,2 ,和K3,3 并求出它们的边数。
【测试题2】
a)判断下列各图是否是(1)图的生成图、导出图或补图? b)画出(1)图的补图,并求出完全图K5的边数。
例:G1是无向图,deg(v1)=3,deg(v2)=1
G2是有向图,deg+(v1)=3,deg-(v1)=2,
deg(v1)=5,
v1 v2 v1
G2
v2
v3
G1
d(v1)=3(注意,环提供2
度), v2是悬挂顶点,
v4
【作业4】求下列各图顶点的度数
【注意】d-(a)=4,d+(a)=1
(环e1提供出度1,提供入度1) d(a)=4+1=5。
【说明】无向完全图:每一条边都是无向边不
含有平行边和环,每一对顶点间都有边相连。
完全图举例
K5
3阶有向完全图
4阶有向完全图
n阶无向完全图的边数为:
n(n-1)/2
【作业2】画出无向完全图K3 ,K4 和K6 并求出
它们的边数。
离散数学图论习题
第4章图论综合练习一、单项选择题1.设L是n阶无向图G上的一条通路,则下面命题为假的是( ).(A) L可以不是简单路径,而是基本路径(B) L可以既是简单路径,又是基本路径(C) L可以既不是简单路径,又不是基本路径(D) L可以是简单路径,而不是基本路径答案:A2.下列定义正确的是( ).(A) 含平行边或环的图称为多重图 (B) 不含平行边或环的图称为简单图(C) 含平行边和环的图称为多重图 (D) 不含平行边和环的图称为简单图答案:D3.以下结论正确是 ( ).(A) 仅有一个孤立结点构成的图是零图(B) 无向完全图K n每个结点的度数是n(C) 有n(n>1)个孤立结点构成的图是平凡图(D) 图中的基本回路都是简单回路答案:D4.下列数组中,不能构成无向图的度数列的数组是( ).(A) (1,1,1,2,3) (B) (1,2,3,4,5) (C) (2,2,2,2,2) (D) (1,3,3,3)答案:B5.下列数组能构成简单图的是( ).(A) (0,1,2,3) (B) (2,3,3,3) (C) (3,3,3,3) (D) (4,2,3,3)答案:C6.无向完全图K3的不同构的生成子图的个数为().(A) 6 (B) 5 (C) 4 (D) 3答案:C7.n阶无向完全图K n中的边数为().(A)2)1(+nn(B)2)1(-nn(C) n (D)n(n+1)答案:B8.以下命题正确的是( ).(A) n (n1)阶完全图K n都是欧拉图(B) n(n 1)阶完全图K n都是哈密顿图(C) 连通且满足m=n-1的图<V,E>(V=n,E=m)是树(D) n(n5)阶完全图K n都是平面图答案:C10.下列结论不正确是( ).(A) 无向连通图G是欧拉图的充分必要条件是G不含奇数度结点(B) 无向连通图G有欧拉路的充分必要条件是G最多有两个奇数度结点(C) 有向连通图D是欧拉图的充分必要条件是D的每个结点的入度等于出度(D) 有向连通图D有有向欧拉路的充分必要条件是除两个结点外,每个结点的入度等于出度 答案:D11.无向完全图K 4是( ).(A )欧拉图 (B )哈密顿图 (C )树 答案:B12.有4个结点的非同构的无向树有 ( )个. (A) 2 (B) 3 (C) 4 (D) 5 答案:A13.设G 是有n 个结点,m 条边的连通图,必须删去G 的( )条边,才能确定G 的一棵生成树.(A) 1+-n m (B) m n - (C) 1++n m (D) 1+-m n 答案:A14.设G 是有6个结点的完全图,从G 中删去( )条边,则得到树. (A) 6 (B) 9 (C) 10 (D) 15 答案:C二、 填空题1.数组{1,2,3,4,4}是一个能构成无向简单图的度数序列, 此命题的真值是 . 答案:02.无向完全图K 3的所有非同构生成子图有 个. 答案:43.设图G V ,E ,其中V n ,E m .则图G 是树当且仅当G 是连通的,且m . 答案:n -14.连通图G 是欧拉图的充分必要条件是 . 答案:图G 无奇数度结点5.连通无向图G 有6个顶点9条边,从G 中删去 条边才有可能得到G 的一棵生成树T . 答案:46.无向图G 为欧拉图,当且仅当G 是连通的,且G 中无 结点. 答案:奇数度7.设图>=<E V G ,是简单图,若图中每对结点的度数之和 ,则G 一定是哈密顿图.答案:V ≥8.如图1所示带权图中最小生成树的权是 .答案:12三、化简解答题1.设无向图G =<V ,E >,V ={v 1,v 2,v 3,v 4,v 5,v 6}, E ={( v 1,v 2), ( v 2,v 2), ( v 4,v 5), ( v 3,v 4), ( v 1,v 3),( v 3,v 1), ( v 2,v 4)}. 1 v 2 v 6 v 53 v 4图2•2 23 • 1 • 7 9 2• 8 • 6 图1(1) 画出图G 的图形;(2) 写出结点v 2, v 4,v 6的度数; (3) 判断图G 是简单图还是多重图. 解:(1) 图G 的图形如图5所示.(2) 0)deg(,3)deg(,4)deg(642===v v v .(3) 图G 是多重图.作图如图2. 2.设图G =<V ,E >,其中V ={a ,b ,c ,d ,e }, E ={(a ,b ),(b ,c ),(c ,d ), (a ,e )}试作出图G 的图形,并指出图G 是简单图还是多重图?是连通图吗?说明理由. 解:图G 如图8所示.. 图G 中既无环,也无平行边,是简单图. 图G 是连通图.G 中任意两点都连通.所以,图G 有9个结点.作图如图3.四、计算题1.设简单连通无向图G 有12条边,G 中有2个1度结点,2个2度结点,3个4度结点,其余结点度数为3.求G 中有多少个结点.试作一个满足该条件的简单无向图.解:设图G 有x 个结点,由握手定理21+22+34+3(x 223)=122 271821243=-+=x x =9 故图G 有9个结点.满足该条件的简单无向图如图4所示2.设图G (如图5表示)是6个结点a ,b ,c , d ,e ,f的图,试求,图G 的最小生成树,并计算它的权.解:构造连通无圈的图,即最小生成树,用克鲁斯克尔算法:第一步: 取ab =1;第二步: 取af =4 第三步: 取fe =3;第四步: 取ad =9 第五步: 取bc =23如图6.权为1+4+3+9+23=403.一棵树T 有两个2度顶点,1个3度顶点;3个4度顶点, 问它有几片树叶?解:设T 有n 顶点,则有n -1条边.T 中有2个 2度顶点,1个3度顶点,3个4度顶点, 其余n -2-1-3个1度顶点.由握手定理: 2·2+1·3+3·4+ (n -2-1-3)=2(n -1) 解得 n =15.于是T 有15-6=9片树叶五、证明题1.若无向图G 中只有两个奇数度结点,则这两个结点一定是连通的.证:用反证法.设G 中的两个奇数度结点分别为u 和v .假若u 和v 不连通.即它们之间无任何通路,则G 至少有两个连通分支G 1,G 2,且u 和v 分别属于G 1和G 2,于是G 1和G 2各含有一个奇数度结点.这与握手定理的推论矛盾.因而u 和v 一定是连通的.a b ec d 图3图4b • 23 1c • • a 4 • f 9 3d • •e 图6b •23 1 15 c • 25 •a 4 • f 28 9 16 3 d • 15 • e 图5。
离散数学考试题及答案
离散数学考试题及答案一、选择题1. 关于图论的基本概念,以下哪个说法是正确的?A. 无向图中的边无方向性,有向图中的边有方向性。
B. 有向图中的边无方向性,无向图中的边有方向性。
C. 无向图和有向图都是由顶点和边组成的。
D. 无向图和有向图都只由边组成。
答案:A2. “若顶点集合为V,边集合为E,那么图G可以表示为G(V, E)”是关于图的哪个基本概念的描述?A. 图的顶点B. 图的边C. 图的邻接D. 图的表示方法答案:D3. 以下哪个命题是正确的?A. 若集合A和B互相包含,则A和B相等。
B. 若集合A和B相交为空集,则A和B相等。
C. 若集合A和B相等,则A和B互相包含。
D. 若集合A和B相等,则A和B相交为空集。
答案:C二、填空题1. 有一个集合A = {1, 2, 3, 4},则集合A的幂集的元素个数为__________。
答案:162. 设A = {a, b, c},B = {c, d, e},则集合A和B的笛卡尔积为__________。
答案:{(a, c), (a, d), (a, e), (b, c), (b, d), (b, e), (c, c), (c, d), (c, e)}3. 若p为真命题,q、r为假命题,则合取范式(p ∨ q ∨ r)的值为__________。
答案:真三、计算题1. 计算集合A = {1, 2, 3, 4}和集合B = {3, 4, 5, 6}的交集、并集和差集。
答案:交集:{3, 4}并集:{1, 2, 3, 4, 5, 6}差集:{1, 2}2. 计算下列命题的真值:(~p ∨ q) ∧ (p ∨ ~q),其中p为真命题,q为假命题。
答案:真四、证明题证明:对于任意集合A和B,如果A和B互相包含,则A和B相等。
证明过程:假设A和B互相包含,即A包含于B且B包含于A。
设x为集合A中的任意元素,则x也必然存在于集合B中,即x属于B。
同理,对于集合B中的任意元素y,y也属于集合A。
(图论)离散数学习题参考答案2
解此不等式可得 n ≥ 7 , 即 G 中至少有 7 个顶点, 当为 7 个顶点时, 其度数列为 2, 2, 2, 3, 3, 4, 4 , Δ = 4, δ = 2 8. 设有 n 个顶点,由握手定理可得: ∑ d (vi ) = 2m ,即
i =1 n
1 × (3 + 5) + (n − 2) × 2 = 2 × 6
d − (v1 ) = 3, d + (v1 ) = 0; d − (v2 ) = 1, d + (v2 ) = 2; d − (v3 ) = 1, d + (v3 ) = 3; d − (v4 ) = 2, d + (v4 ) = 2
第十一次: (欧拉图与哈密顿图)P305 1.2.11.21 (无向树及其性质)P318 2.24(a), 25(b) 1. (a),(c) 是欧拉图,因为它们均连通且都无奇度顶点; (b),(d)都不是欧拉图;因为(b) 不连通,(d) 既不连通又有奇度顶点;要使(b),(d)变为欧拉图 均至少加两条边,使其连通并且无奇度顶点。如下图所示。
(1) v2 到 v5 长度为 1,2,3,4 的通路数分别为 0, 2, 0,0 条; (2) v5 到 v5 长度为 1,2,3,4 的通路数分别为 0,0,4,0 条; (3) D 中长度为 4 的通路(含回路)为 32 条; (4) D 中长度为小于或等于 4 的回路数为 12 条; (5) 因为 D 是强连通图,所以可达矩阵为 4 阶全 1 方阵,如上图所示。 46. 各点的出度和入度分别如下:
(v2,12)** (v5, 7)*
根据上表的最后一行,从 v1 到其余各点的最短路径和距离如下: v1v2, d(v1,v2)=6 v1v2v6, d(v1,v6)=12 v1v3, d(v1,v3)=3 v1v3v4v5v7, d(v1,v7)=7 v1v3v4, d(v1,v4)=5 v1v3v4v5v7v8, d(v1,v8)=10 v1v3v4v5, d(v1,v5)=6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论练习题
一.选择题
1、设G是一个哈密尔顿图,则G一定是( )。
(1) 欧拉图(2) 树(3) 平面图(4)连通图
2、下面给出的集合中,哪一个是前缀码?()
(1) {0,10,110,101111}(2) {01,001,000,1}
(3) {b,c,aa,ab,aba}(4) {1,11,101,001,0011}
3、一个图的哈密尔顿路是一条通过图中()的路。
4、设G是一棵树,则G 的生成树有( )棵。
(1) 0(2) 1(3) 2(4) 不能确定
5、n阶无向完全图Kn 的边数是( ),每个结点的度数是( )。
6、一棵无向树的顶点数n与边数m关系是()。
7、一个图的欧拉回路是一条通过图中( )的回路。
8、有n个结点的树,其结点度数之和是()。
9、下面给出的集合中,哪一个不是前缀码( )。
(1) {a,ab,110,a1b11} (2) {01,001,000,1}
(3) {1,2,00,01,0210} (4) {12,11,101,002,0011}
10、n个结点的有向完全图边数是( ),每个结点的度数是( )。
11、一个无向图有生成树的充分必要条件是( )。
12、设G是一棵树,n,m分别表示顶点数和边数,则
(1) n=m (2) m=n+1 (3) n=m+1 (4) 不能确定。
13、设T=〈V,E〉是一棵树,若|V|>1,则T中至少存在( )片树叶。
14、任何连通无向图G至少有( )棵生成树,当且仅当G 是( ),G的生成树只有一棵。
15、设G是有n个结点m条边的连通平面图,且有k个面,则k等于:
(1) m-n+2 (2) n-m-2 (3) n+m-2 (4) m+n+2。
16、设T是一棵树,则T是一个连通且( )图。
17、设无向图G有16条边且每个顶点的度数都是2,则图G有( )个顶点。
(1) 10 (2) 4 (3) 8 (4) 16
18、设无向图G有18条边且每个顶点的度数都是3,则图G有( )个顶点。
(1) 10 (2) 4 (3) 8 (4) 12
19、任一有向图中,度数为奇数的结点有( )个。
20、具有6 个顶点,12条边的连通简单平面图中,每个面都是由( )条边围成? (1) 2 (2) 4 (3) 3 (4) 5
21、在有n 个顶点的连通图中,其边数( )。
(1) 最多有n-1条 (2) 至少有n-1 条 (3) 最多有n 条 (4) 至少有n 条
22、一棵树有2个2度顶点,1 个3度顶点,3个4度顶点,则其1度顶点为( )。
(1) 5 (2) 7 (3) 8 (4) 9
23、若一棵完全二元(叉)树有2n-1个顶点,则它( )片树叶。
(1) n (2) 2n (3) n-1 (4) 2 24、下列哪一种图不一定是树( )。
(1) 无简单回路的连通图 (2) 有n 个顶点n-1条边的连通图 (3) 每对顶点间都有通路的图 (4) 连通但删去一条边便不连通的图 25、连通图G 是一棵树当且仅当G 中( )。
(1) 有些边是割边 (2) 每条边都是割边
(3) 所有边都不是割边 (4) 图中存在一条欧拉路径 26.对于无向图,下列说法中( )是正确的. A .不含平行边及环的图称为完全图
B .任何两个不同结点都有边相连且无平行边及环的图称为完全图
C .具有经过每条边一次且仅一次回路的图称为哈密尔顿图
D .具有经过每个结点一次且仅一次回路的图称为欧拉图
27.设图G 的邻接矩阵为
⎥⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100000100
则G 的边数为( ).
A .5
B .6
C .3
D .4 28.设图G =<V ,
E >,则下列结论成立的是 ( ).
A .deg(V )=2∣E ∣
B .deg(V )=∣E ∣
C .
E v V
v 2)deg(=∑∈ D .E v V
v =∑∈)deg(
29.图G 如右图所示,以下说法正确的是 ( ) .
A .{(a , d )}是割边
B .{(a , d )}是边割集
C .{(d , e )}是边割集
D .{(a, d ) ,(a, c )}是边割集
30.设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ).
A .e -v +2
B .v +e -2
C .e -v -2
D .e +v +2 31.无向图G 存在欧拉通路,当且仅当( ).
A .G 中所有结点的度数全为偶数
B .G 中至多有两个奇数度结点
C .G 连通且所有结点的度数全为偶数
D .G 连通且至多有两个奇数度结点
二、填空题
1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 .
2.设给定图G (如右图所示),则图G 的点割集是 .
3.设无向图G =<V , E >是汉密尔顿图,则V 的任意非空子集V 1,都有 ≤∣V 1∣.
4.设有向图D 为欧拉图,则图D 中每个结点的入度 .
5.设完全图K n 有n 个结点(n ≥2),m 条边,当 时,K n 中存在欧拉回路.
6.给定一个序列集合{1,01,10,11,001,000},若去掉其中的元素 ,则该序列集合构成前缀码.
ο
ο
ο ο ο
c
a
b e
d ο f
ο
ο
ο
ο ο
c
a b e d
ο f
三、计算题
1.设图G =<V ,E >,其中V ={a 1, a 2, a 3, a 4, a 5},
E ={<a 1, a 2>,<a 2, a 4>,<a 3, a 1>,<a 4, a 5>,<a 5, a 2>}
(1)试给出G 的图形表示; (2)求G 的邻接矩阵;
(3)判断图G 是强连通图、单侧连通图还是弱连通图?
2.图G =<V , E >,其中V ={a , b , c , d , e , f },E ={(a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (d , e ), (d , f ), (e , f )},对应边的权值依次为5,2,1,2,6,1,9,3及8.
(1)画出G 的图形;
(2)写出G 的邻接矩阵;
(3)求出G 权最小的生成树及其权值.
问:如果结点集是V ={a , b , c , d , e },边集E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (d , e ) },对应边的权值依次为5,2,1,2,6,1,9,那么会求吗?
3.设有一组权为2,3,5,7,11,13,17,19,23,29,31,试 (1)画出相应的最优二叉树; (2)计算它们的权值.
解:(1)最优二叉树如右图所示:
问:如果一组权为2,3,6,9,13,15,能否画出最优二叉树?
ο ο ο ο ο
c a b e
d
ο f
1
5 2 2 6
1
9
3 8
ο ο ο ο
ο
ο ο ο ο 3
2 7 1
3 5 5
11 17 34 ο ο 160 29 10 ο ο ο 23 19
42 ο ο 17 ο 24 ο 53 31
ο ο
ο 95
65。
