4整式的加减(第1课时)精品PPT课件
合集下载
整式的加减(第一课时)课件

基础练习题
总结词:巩固基础
详细描述:基础练习题主要针对整式加减法的基本规则和概念,包括同类项的合并、系数和字母的加 减等。这些题目难度较低,适合初学者熟悉基本操作。
进阶练习题
总结词:提升技能
详细描述:进阶练习题在基础练习题的基础上增加难度,涉 及更复杂的整式加减运算,如多项式的加减、去括号等。这 些题目旨在提高学生的运算能力和对整式加减法的理解。
05
06
解:$3a^2 - 2a + a^2 = (3 + 1)a^2 2a = 4a^2 - 2a$
整式的加减运算技巧
技巧一
合并同类项时,系数直接相加减 ,字母和字母的指数不变
例如
$2x + 3x = 5x$,$3a^2 2a^2 = a^2$。
技巧二
去括号时,注意符号的变化
例如
$3(x + y) = 3x + 3y$,$- (x y) = -x + y$。
整式的加减(第一课时 )ppt课件
• 整式的概念 • 整式的加减运算 • 整式的混合运算 • 整式的加减运算练习
目录
01
整式的概念
什么是整式
整式是由常数、变数、常数乘变数、常数除变数以及括号等符号组成的数学表达式 。
整式中,变数的次数可以是零次、一次或多次。
整式中,变数的指数可以是正整数、负整数或零。
步骤三:合并同类项
整式的加减运算步骤
将带有相同字母的项的系数相加或相减。 步骤四:化简
将整式化简到最简形式。
整式的加减运算实例
例1:
01
02
计算:$2x - 3x + 4x$
解:$2x - 3x + 4x = (2 - 3 + 4)x = 3x$
《整式的加减》(第1课时)课件

解:
重点、难点知识★▲
当 时,原式= 【思路点拨】先化简,再代入求值,这样更简单.
直接把
代入计算又如何?哪种方法更简便?
知识回顾 问题探究 课堂小结 随堂检测
探究三
重点、难点知识★▲
活动1
求多项式的值时, 一般先化简, 再代入指定的数值进行计算, 合并时注意系数是负数的情况,必要时要正确使用括号, 强调化简求值的格式书写.
重点、难点知识★▲
活动2 具有什么特征的几个单项式才可以合并成一个单项式? 什么叫合并同类项? 把几个同类项合并成一个单项式,叫做合并同类项.
合并同类项的依据是什么?
观察上述式子的运算,合并同类项时,几个同类项中的哪部 分在参与运算,哪部分不变? 不是同类项能不能合并?
知识回顾 问题探究 课堂小结 随堂检测
重点、难点知识★▲
活动1 回顾旧知,感受分类的作用
在一次“送温暖、献爱心”活动中,我们班同学非常积 极,其中一位同学把储钱罐捐出来,满满的一罐硬币里 有一元、五角、一角,你能以最快的方式统计一下这罐 硬币共有多少钱吗?
问题:(1)分类需要什么样的标准? (2)分类的作用又是什么?
知识回顾 问题探究 课堂小结 随堂检测
解:
(用不同的符号划出多项式中的同类项)
(加法交换律,注意交换时连同符号交换走)
(加法结合律) (乘法分配律)
(注意升降幂排列) 【思路点拨】按照同类项概念确定出多项式中同类项,再合并,注意 每一步的依据.
知识回顾 问题探究 课堂小结 随堂检测
探究三
重点、难点知识★▲
活动1
通常把一个多项式的各项按照某个字母的指数从大(小) 到小(大)的顺序排列叫做降(升)幂排列,常数项视作 字母指数为0.
重点、难点知识★▲
当 时,原式= 【思路点拨】先化简,再代入求值,这样更简单.
直接把
代入计算又如何?哪种方法更简便?
知识回顾 问题探究 课堂小结 随堂检测
探究三
重点、难点知识★▲
活动1
求多项式的值时, 一般先化简, 再代入指定的数值进行计算, 合并时注意系数是负数的情况,必要时要正确使用括号, 强调化简求值的格式书写.
重点、难点知识★▲
活动2 具有什么特征的几个单项式才可以合并成一个单项式? 什么叫合并同类项? 把几个同类项合并成一个单项式,叫做合并同类项.
合并同类项的依据是什么?
观察上述式子的运算,合并同类项时,几个同类项中的哪部 分在参与运算,哪部分不变? 不是同类项能不能合并?
知识回顾 问题探究 课堂小结 随堂检测
重点、难点知识★▲
活动1 回顾旧知,感受分类的作用
在一次“送温暖、献爱心”活动中,我们班同学非常积 极,其中一位同学把储钱罐捐出来,满满的一罐硬币里 有一元、五角、一角,你能以最快的方式统计一下这罐 硬币共有多少钱吗?
问题:(1)分类需要什么样的标准? (2)分类的作用又是什么?
知识回顾 问题探究 课堂小结 随堂检测
解:
(用不同的符号划出多项式中的同类项)
(加法交换律,注意交换时连同符号交换走)
(加法结合律) (乘法分配律)
(注意升降幂排列) 【思路点拨】按照同类项概念确定出多项式中同类项,再合并,注意 每一步的依据.
知识回顾 问题探究 课堂小结 随堂检测
探究三
重点、难点知识★▲
活动1
通常把一个多项式的各项按照某个字母的指数从大(小) 到小(大)的顺序排列叫做降(升)幂排列,常数项视作 字母指数为0.
整式的加减(公开课) ppt课件
ppt课件
6
整式的加减 去括号
ppt课件
7
知识结构:
整式的概念 整式的加减
整式的计算
单项式 多项式
系数
次数 项,项数,常数项, 最高次项 次数
同类项与合并同类项 去括号 化简求值
用字母来表示生活中的量
ppt课件
8
如何进行整式的加减呢? 八字诀
去括号、合并同类项
ppt课件
9
口诀: 去括号,看符号: 是“+”号,不变号; 是“-”号,全变号.
整式的加减整式的加减整式的整式的概念整式的整式的计算单项式单项式多项式多项式系数系数次数次数项项数常数项项项数常数项最高次项最高次项次数次数同类项与合并同类项与合并同类项去括号去括号化简求值化简求值用字母来表示生活中的量用字母来表示生活中的量10例如
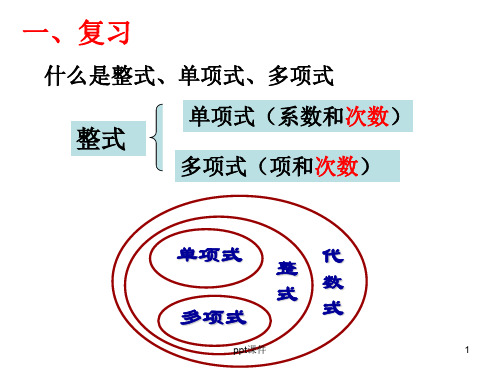
一、复习
什么是整式、单项式、多项式
整式
单项式(系数和次数) 多项式(项和次数)
合并同类项概念: _把__多__项_式__中__的__同__类_项__合__并__成__一_项_.
合并同类项法则: 1.__系_数___相加减;
2._字__母__和__字_母__的__指__数___不变。
ppt课件
5
1.下列各式中,是同类项的是:__③__⑤_⑥______
① 2x2 y3 与 x3 y2 ② x2 yz 与 x2 y
思维分析:把多项式看作一个整体,并用括号
括起来。 见多必括
解 (2x2 -3x + 1)+( -3x2 + 5x-7) = 2x2 -3x + 1 -3x2 + 5x-7
= (2x2 -3x2 )+(-3x + 5x)+(1-7)
《整式的加减》整式及其加减PPT课件下载(第1课时)

8 n+ 5 n =(8 + 5) n =13 n
-7a2b+2a2b=(-7+2)a2b=-5a2b
合并同类项的法则是: 把同类项的系数相加,字母和字母的指数不变. 讨论:-3a2b与5b2a能不能合并?
不是同类项不可以合并.
探究新知
下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)a+a=2a
(1)3a+2b-5a-b
(2)-4ab+
1 3
b2-9ab-
1 2
b2
解:(1) 3a + 2b – 5a - b
找
=(3a-5a)+(2b-b)
=(3-5)a+(2-1)b
=-2a+b
移 合并
探究新知
解:(2)-4ab+
1 3
b2-9ab-
1 2
b2
找
=(-4ab-9ab)+(
1 3
b2-12
课堂检测
拓广探索题
解:小芳说得有道理. 6x3-5x3y +2x2y +2x3+5x3y-2x2y-8x3+7
=(6+2-8)x3+(-5+5)x3y+(2-2)x2y+7
=7 即它合并同类项后的结果与x,y的取值无关, 所以题目中给出的条件x=-14,y=0.78是多余的.
课堂小结
同类项 的特点
1.都是单项式 2.所含的字母相同 3.相同字母的指数也相同
合 并 合并同类项
把同类项的系数相加,字母和字母
同
的法则
的指数不变.
类 项
1.准确地找出同类项;
-7a2b+2a2b=(-7+2)a2b=-5a2b
合并同类项的法则是: 把同类项的系数相加,字母和字母的指数不变. 讨论:-3a2b与5b2a能不能合并?
不是同类项不可以合并.
探究新知
下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)a+a=2a
(1)3a+2b-5a-b
(2)-4ab+
1 3
b2-9ab-
1 2
b2
解:(1) 3a + 2b – 5a - b
找
=(3a-5a)+(2b-b)
=(3-5)a+(2-1)b
=-2a+b
移 合并
探究新知
解:(2)-4ab+
1 3
b2-9ab-
1 2
b2
找
=(-4ab-9ab)+(
1 3
b2-12
课堂检测
拓广探索题
解:小芳说得有道理. 6x3-5x3y +2x2y +2x3+5x3y-2x2y-8x3+7
=(6+2-8)x3+(-5+5)x3y+(2-2)x2y+7
=7 即它合并同类项后的结果与x,y的取值无关, 所以题目中给出的条件x=-14,y=0.78是多余的.
课堂小结
同类项 的特点
1.都是单项式 2.所含的字母相同 3.相同字母的指数也相同
合 并 合并同类项
把同类项的系数相加,字母和字母
同
的法则
的指数不变.
类 项
1.准确地找出同类项;
人教版七年级数学上册整式的加减(第1课时)课件(共28张)

先判断每一组是否是同类项,不是的,为前者配一个.
(1)2x2y与-3x2y √
(2)2abc与2ab
3abc
(3)-3pq与3qp
x22y
(4)-4x2y与5xy
×
√
×
探究新知
归纳总结
同类项的判别方法:
(1)同类项只与字母及其指数有关,与系数无关,与
字母在单项式中的排列顺序无关;
(2)抓住“两个相同”,一是所含的字母要完全相同,
中到不同的括号内;
三并,将同一括号内的同类项相加即可.
探究新知
素养考点 2
合并同类项并且求值
例 2 ( 1 ) 求 多 项 式2
2x 5x x 4x 3x 2
2
2
的值,
其中x = .
分析:在多项式求值时,可以先将多项式中的同类项合并,
然后再代入求值,这样可以简化计算.
2
2
2
(5)3x2+2x3=5x5
√
(6)a+a-5a=-3a
注:(2)(4)(5)中的单项式不是同类项,不能合并.
(3)是同类项,但合并结果不对.
探究新知
素养考点 1 合并同类项
用不同
的标记把同
类项标出来!
例1 合并下式中的同类项.
4a 2 3b 2 2ab 3a 2 b 2 .
解: 4a 2 3b 2 2ab 3a 2 b 2
解:(1) 2 x 5 x x 4 x 3 x 2 x 2.
当x = 时,原式=− .
探究新知
(2)求多项式 3a abc 1 c 2 3a 1 c 2
(1)2x2y与-3x2y √
(2)2abc与2ab
3abc
(3)-3pq与3qp
x22y
(4)-4x2y与5xy
×
√
×
探究新知
归纳总结
同类项的判别方法:
(1)同类项只与字母及其指数有关,与系数无关,与
字母在单项式中的排列顺序无关;
(2)抓住“两个相同”,一是所含的字母要完全相同,
中到不同的括号内;
三并,将同一括号内的同类项相加即可.
探究新知
素养考点 2
合并同类项并且求值
例 2 ( 1 ) 求 多 项 式2
2x 5x x 4x 3x 2
2
2
的值,
其中x = .
分析:在多项式求值时,可以先将多项式中的同类项合并,
然后再代入求值,这样可以简化计算.
2
2
2
(5)3x2+2x3=5x5
√
(6)a+a-5a=-3a
注:(2)(4)(5)中的单项式不是同类项,不能合并.
(3)是同类项,但合并结果不对.
探究新知
素养考点 1 合并同类项
用不同
的标记把同
类项标出来!
例1 合并下式中的同类项.
4a 2 3b 2 2ab 3a 2 b 2 .
解: 4a 2 3b 2 2ab 3a 2 b 2
解:(1) 2 x 5 x x 4 x 3 x 2 x 2.
当x = 时,原式=− .
探究新知
(2)求多项式 3a abc 1 c 2 3a 1 c 2
人教版七年级数学上册《整式》整式的加减PPT课件

B.系数是1,次数是6; D.系数是-1,次数是6;
2.单项式 -4πr2 的系数及次数分别为( C )
A. -4,2
B.-4,3
C. 4π ,2
D. 4π ,3
当堂训练
3.如果 1 a2b2n1 是五次单项式,则n的值为( B )
2
A.1
B.2
C.3
D.4
课堂小结
单项式
概念:数或字母的积组成的式子 (包括单独的数或字母) 系数:单项式中的数字因数 次数:所有字母的指数的和
第四章 整式的加减
4.1 整式
第2课时 多项式和整式
学习目标
1. 掌握多项式、多项式的项、次数以及常数项 的概念. 2. 会准确迅速的确定一个多项式的项数和次数. 3. 归纳出整式的概念会区别单项式和多项式.
学习重难点
学习重点:理解多项式、多项式的项与次 数概念以及整式的概念.
学习难点:正确的找出多项式的项和次数.
单项式与多项式统称为整式。
巩固练习
用多项式填空,并指出它们的项和次数。
(1)一个长方形相邻两边长分别为a,b,则这个长方形的
周长为 2a+2b . (2)m为一个有理数,m的立方与2的差为 m3-2 .
(3)某公司向某地投放共享单车,前两年每年投放a辆,为环 保和安全起见,从第三年年初起不再投放,且每个月回b辆,第
课堂小结
巩固练习
练一练:判断下列代数式是否是单项式?
4b2
,
π,2+3m
,3xy
,
a 3
,
1 t
答:4b2
,
π,3xy
,
a 3
是单项式.
探究新知
学生活动二 【一起探究】
整式的加减ppt课件

例3
添加标题
某商店原有5袋大 米,每袋大米为x 千克.
添加标题
上午卖出3袋,下 午又购进同样包装 的大米4袋.
添加标题
进货后这个商店有 大米多少千克?
添加标题
例3(2)某商店原有5袋大米, 每袋大米为x千克.
添加标题
上午卖出3袋,下午又购进同 样包装的大米4袋.
添加标题
进货后这个商店有大米多少千 克?
这个式子的结果 是多少?
你是怎样得到的?
类比探究,学习 新知
(1)运用有理数的运算律计算.
100×2+252×2= ;
100×(-2)+252×(-2)=
.
2.类比探究, 学习新知
(1)运用有理数的运算律计算
100×2+252×2 =(100+252)×2=352×2=704; 100×(-2)+252×(-2) =(100+252)×(-2)=352×(-2)=-704.
多项式3x3-2x-5的常数项是____,一次项是 ____, 三次项的系数是_____.二次项的系数是 _____.每项的系数分别是____,每项的次 数分别是____,多项式的次数是___
用多项式__表示奇 数,三个连续奇数 可表示成____ ____
一.用单项式n表示整数,三个连续整数可表示 成________
(4)按同一个字母的降幂(或升幂排列).
例1 合并下列各式的同类项:
(1)xy 2 315.学xy 2以致用,应用新 (2) 3 x 2y 2 x 2y 3 x 知y2 2 x y2
(3)4 a 2 3 b 2 2 a b 4 a 2 4 b 2
练习1 判断下列说法是否正确,正确的
添加标题
某商店原有5袋大 米,每袋大米为x 千克.
添加标题
上午卖出3袋,下 午又购进同样包装 的大米4袋.
添加标题
进货后这个商店有 大米多少千克?
添加标题
例3(2)某商店原有5袋大米, 每袋大米为x千克.
添加标题
上午卖出3袋,下午又购进同 样包装的大米4袋.
添加标题
进货后这个商店有大米多少千 克?
这个式子的结果 是多少?
你是怎样得到的?
类比探究,学习 新知
(1)运用有理数的运算律计算.
100×2+252×2= ;
100×(-2)+252×(-2)=
.
2.类比探究, 学习新知
(1)运用有理数的运算律计算
100×2+252×2 =(100+252)×2=352×2=704; 100×(-2)+252×(-2) =(100+252)×(-2)=352×(-2)=-704.
多项式3x3-2x-5的常数项是____,一次项是 ____, 三次项的系数是_____.二次项的系数是 _____.每项的系数分别是____,每项的次 数分别是____,多项式的次数是___
用多项式__表示奇 数,三个连续奇数 可表示成____ ____
一.用单项式n表示整数,三个连续整数可表示 成________
(4)按同一个字母的降幂(或升幂排列).
例1 合并下列各式的同类项:
(1)xy 2 315.学xy 2以致用,应用新 (2) 3 x 2y 2 x 2y 3 x 知y2 2 x y2
(3)4 a 2 3 b 2 2 a b 4 a 2 4 b 2
练习1 判断下列说法是否正确,正确的
整式的加减_1PPT课件(冀教版)

2若a 1,b 1,c 3,求A B的值.
解:A B a2 b2 c2 4a2 2b2 3c2 3a2 3b2 2c2
当a 1,b 1,c 3时 A B 3 318 18
返回首页
第四章 整式的加减
4.4 整式的加减
1.填空:整式包括_单__项__式__和__多__项__式__.
2.下列各式,是同类项的一组是( A )
A.22 x2 y与 1 yx2 2
B.2m2n与2mn2
C. 1 ab与abc 2
3.去括号后合并同类项: (3a-b)+(5a+2b)-(7a+4b). =3a-b+5a+2b-7a-4b =(3+5-7)a+(-1+2-4)b =a-3b 返回首页
1.整式加减的一 般步骤并不绝对, 在具体运算中, 也可以先将同类 项合并,再去括 号(当然要按运 算顺序去做)
2.已知代数式和代数式中字 母的值,求代数式的值,一 般不直接将字母的值代入代 数式,而是先把代数式化简, 然后再代入求值.
整式的加减实质就是把合并同类项和去括号 综合起来,求两个多项式的和或差时,第一把 多项式看作一个整式,分别括在括号里;给出 整式中字母的值.求整式的值的问题,一般要先 化简,再把给定字母的值代入计算,得出整式 的值,不要把数值直接代入整式中计算.对于整 式中的应用问题,应根据题意列出算式,再进 行整式的加减运算,计算出结果.
B. x+ 3 ? 4
C.3x 1 ? 4
D.x+ 3 4
解析: 原式 x+1 2x 1 x 2x (1 1)
4
2
42
3.若m、n互为相反数,则 (3m-2n)与
(2m-3n) 的差为 0 .
解析:因为 m、n互为相反数,所以m+n=0, 所以(3m-2n)-(2m-3n) =3m-2n-2m+3n =m+n=0.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识的升华
瞧一瞧:
下列各题计算的结果对不对?如果不对, 指出错在哪里?
(1) 3a 2b 5ab ( 错 )
(2) 5 y2 2 y2 3 ( 错 )
(3) 2ab 2ba 0 ( 对 )
(4) 3x2 y 5xy2 2x2 y ( 错 )
4 xy 2 ; 5
x 2 xy 2 b 2 2ab
①找 注意符号 ②交换律 ③结合律 ④分配律
⑤合并: A.系数相加减; B.字母和字母的指数不变。
养成好习惯
求值
(1)求多项式2x2-5x+x2+4x-3x2-2的 值,其中x=2
解:2x2-5x+x2+4x-3x2-2 =(2+1-3)x2+(-5+4)x-2 =-x-2
当X=2 时,原式 =-2-2=-4
我会填:
100t+(-252)t
(1) 100t-252t= [100+(-252)] t= -152 t; (2) 3x2+2x2= 3+2 x2 = 5 x;
(3) 3ab2-4ab2= [3+(-4)] ab2 = -1 ab2 . 上述运算有什么共同特3点ab,2+你(-能4从ab中2)得出什么规律? (一) 同类项 1. 所含字母相同; 2. 相同字母的指数也分别相同; (满足这样条件)的项,叫同类项。
探究并填空:
(1)100t-252t=( 100-252 )t
(2)3 x 2 +2 =( 3+2 )
(3)3 ab2-4ab2 =( 3-4 )
上述运算有什么特点,你能从 中得出什么规律?
列式表示:
在青藏铁路线上,在格尔木到拉萨之间有一
段很长的冻土地段,根据下表提供的信息你能算 出各段的铁路及这段铁路的全长吗?
= -152t; = 5x2; = -1ab2.
2.法则要点:
含有多个不同的同
类项的多项式如何
合并呢?
①找 例:4x2 + 2x + 7 + 3x - 8x2 - 2 注意符号
②交换律 =4x2 - 8x2 + 2x + 3x + 7 - 2
③结合律 =( 4x2 - 8x2)+ (2x + 3x)+ (7 – 2)
练一练
&同类项的定义:所含___字__母__相__同_,并且__相__同__字__母_的 ___指__数也相同的项,叫做同类项。几个常数项也是 _同__类__项__。
&判断同类项:1、字母__相__同_;2、相同字母的指 数也_相__同__。与_系__数___无关,与_字__母__顺__序__无关。
几个常数项也是同类项。
1、下列各组是同类项的是( D) A 2x3与3x2 B 12ax与8bx C x4与a4 D π与-3
2、5x2y 和42ymxn是同类项,则 m=__1____, n=___2___。
随堂练习
知识的升华 1
思考: 1.判断下列各组中的两项是否是同类项: (1) -5ab3与3a3b ( )否(2)3xy与3x( ) 否 (3) -5m2n3与2n3m2是( ) (4)53与35( )是
第一课时
1.单项式,单项式的系数,次数; 2.多项式,多项式的项,多项式的次数; 3.整式的概念 。
挑战“记忆”
练习一(课前测评)
1.运用有理数的运算律计算:
100×2+252×2= (100+252)×2 =704 100×(-2)+252×(-2)= (100+252)×(-2)
=-704 有理数可以进行加减计算,那么整式能 否可以加减运算呢?怎样化简呢?
(5) x3与53 ( ) 否
&判断同类项:1、字母__相__同_;2、相同字母的指 数也_相__同__。与_系__数___无关,与_字__母__顺__序__无关。
退出 返回 上一张下一张
(二)合并同类项:
1.定义: 把多项式中的同类项 合并成一项 。
(1) 100t -252t (2) 3x2 +2x2 (3) 3ab2 -4ab2
解:(2)-3x2y+2x2y+3xy2-2xy2 =(-3+2)x2y+(3-2)xy2 =-x2y+xy2
规则:同桌之间一个直接代入求值,另一个先合并同类 项,再代入求值,看谁算得又快又对。
(1)求多项式2x 2 - 5x x 2 4x - 3x 2 - 2的值,
④分配律 =(4- 8)x2 + (2 + 3)x + (7 – 2)
在合并同类项时结果往往是一
⑤合并: = -54 x2++55 xx +-45x2 个多项式,通常把这个结果写
A.系数相加减;
成按某一个字母的升幂或降幂对不对?如果不对, 指出错在哪里?
注意:在多项式中找同类项要找齐,做 到不重,不漏(包括符号)。
提高练习:
填空: 1.如果2a2bn+1与-4amb3是同类项,则 m=___2_,n=__2__;
2.若5xy2+axy2=-2xy2,则a=_-_7_;
3.在6xy-3x2-4x2y-5yx2+x2中没有同类 的项是__6_x_y__;
× × √ x
瞧一瞧:
合并同类项法则:
合并同类项后,所得项的系数是合并前各同类项 的系数的和,且字母部分不变。
注意: 1.若两个同类项的系数互为相反数,则两项的和等于零, 如:-3ab2+3ab2=(-3+3)ab2=0×ab2=0。 2.多项式中只有同类项才能合并,不是同类项不能合并。
退出 返回 上一张下一张
冻土段
速度 (千米/时)
100
非冻土地段 120
铁路全长
时间 (小时)
t
2.1t
路程(千米)
100t
1220522t.1t
100t 252t
能化简吗?依据是什么?
单项式 + 单项式 整式 + 整式
100 t + 252 t = (100+325522) t 100× 2+252× 2 = (100+325522) ×2 100× (-2)+252× (-2) = (100+325522) ×(-2)
注:先合并同类项再求值,这样可以简化计算
例1:合并下列各式的同类项:
(1)4a2+3b2+2ab-4a2-4(2b)2-3x2y+2x2y+3xy2-2xy 解:(1)4a2+3b2+2ab-4a2-4b2
=(4a2-4a2)+(3b2-4b2)+2ab =(4-4)a2+(3-4)b2+2ab
=-b2+2ab
