卡尔曼滤波算法(含详细推导)
卡尔曼滤波五个公式推导过程

卡尔曼滤波五个公式推导过程1.系统的状态方程假设我们有一个线性动态系统,可以用如下的状态方程来描述:x(k)=Ax(k-1)+Bu(k-1)+w(k-1)其中,x(k)表示系统在时刻k的状态向量,A是系统的状态转移矩阵,B是输入变量矩阵,u(k-1)是输入变量向量,w(k-1)是过程噪声。
2.系统的测量方程假设我们的系统是通过一些传感器进行测量的,测量结果表示为:z(k)=Hx(k)+v(k)其中,z(k)是系统的测量向量,H是观测矩阵,v(k)是测量噪声。
3.状态估计的预测根据系统的状态方程,我们可以预测系统在下一个时刻的状态。
预测的结果表示为:x^(k)=Ax(k-1)+Bu(k-1)其中,x^(k)表示状态的预测向量。
4.测量更新在得到测量结果后,我们可以根据测量更新系统的状态估计。
计算出的状态估计称为卡尔曼增益。
卡尔曼增益的计算公式如下:K(k)=P^(k)H^T(HP^(k)H^T+R)^-1其中,P^(k)是状态协方差的预测值,R是测量噪声的协方差。
5.状态估计的更新通过卡尔曼增益,我们可以计算出最终的状态估计。
状态估计的更新公式如下:x(k)=x^(k)+K(k)(z(k)-Hx^(k))P(k)=(I-K(k)H)P^(k)其中,I是单位矩阵,P(k)是状态协方差的最优估计。
以上就是卡尔曼滤波的五个公式的推导过程。
通过这五个公式,我们可以根据系统的状态方程和测量方程,利用预测和更新步骤,得到最优的状态估计结果。
卡尔曼滤波在各个领域都有广泛的应用,如目标跟踪、定位导航等。
Kalman滤波原理及算法

Kalman滤波原理及算法kalman滤波器一(什么是卡尔曼滤波器卡尔曼全名Rudolf Emil Kalman,匈牙利数学家,1930年出生于匈牙利首都布达佩斯, 我们现在要学习的卡尔曼滤波器,正是源于他的博士论文和1960年发表的论文《A New Approach to Linear Filtering and Prediction Problems》(线性滤波与预测问题的新方法)。
二.卡尔曼滤波器算法的介绍以下是卡尔曼滤波器核心的5个式子。
X(k|k-1)=A X(k-1|k-1)+B U(k) (1)P(k|k-1)=A P(k-1|k-1) A’+Q (2)X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) (3)Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) (4)P(k|k)=(I-Kg(k) H)P(k|k-1) (5)下面我们详细介绍卡尔曼滤波的过程。
首先,我们要引入一个离散控制过程的系统。
该系统可用一个线性随机微分方程来描述:X(k)=A X(k-1)+B U(k)+W(k)再加上系统的测量值:Z(k)=H X(k)+V(k)上两式子中,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。
A和B是系统参数,对于多模型系统,他们为矩阵。
Z(k)是k时刻的测量值,H是测量系统的参数,对于多测量系统,H为矩阵。
W(k)和V(k)分别表示过程和测量的噪声。
他们被假设成高斯白噪声(White Gaussian Noise),他们的covariance分别是Q,R(这里我们假设他们不随系统状态变化而变化)。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。
下面我们来用他们结合他们的covariances来估算系统的最优化输出。
首先我们要利用系统的过程模型,来预测下一状态的系统。
卡尔曼滤波方程的推导

Kalman 增益推导: Kalman 滤波器是一个最小均方误差估计器,先验状态误差估计可表示为
ˆ ( k | k ),我们最小化这个矢量幅度平方的期望值 E X (k ) X ˆ (k | k ) 2 , X (k ) X
这等价于最小化后验估计协方差矩阵 P(k | k ) 的迹,通过展开合并 P(k | k ) 公式, 可得:
E[W (k )] 0或E[W (k )] W T E[W (k )W ( j )] Q(k ) kj E[V (k )] 0或E[V (k )] V T E[V (k )V ( j )] R(k ) kj
式(2)
1 (k j ) 其中 kj ,这里 Q(k ) 0 是激励噪声的一个 n n 维的协 0 ( k j )
我们通过式(11)求导的方式求得 P(k | k ) 的极值点:
tr ( P(k | k )) 2[ H (k ) P(k | k 1)]T 2 K (k ) S (k ) 0 ( K (k )) 注:这里协方差矩阵式对称矩阵 K (k ) P(k | k 1) H T (k ) S 1 (k )
1、 随机线性离散系统的状态方程和观测方程为:
X (k ) (k , k 1) X (k 1) B(k , k 1)U (k 1) (k , k 1)W (k 1) Z (k ) H (k ) X (k ) V (k )
式(1)
式中状态向量 X (k ) R n ,观测矢量 Z (k ) R m ,随机过程噪声 W (k ) R r ,随 机观测噪声 V (k ) R m ,状态转移矩阵 (k , k 1) R nn ,过程噪声输入矩阵
kalman滤波器算法原理
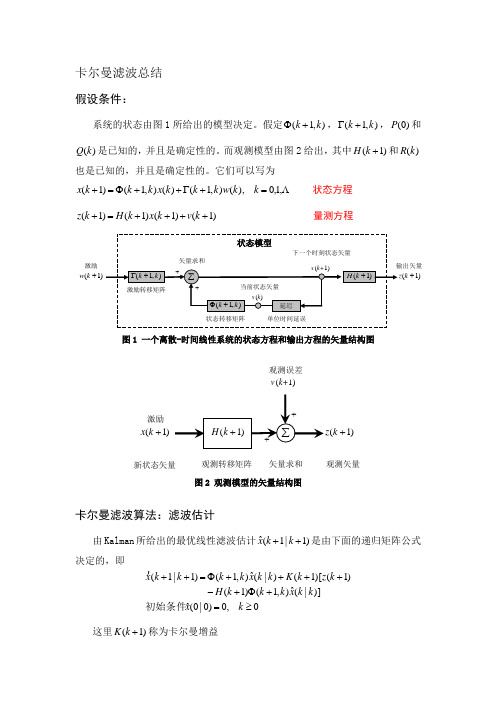
卡尔曼滤波总结假设条件:系统的状态由图1所给出的模型决定。
假定),1(k k+Φ,),1(k k+Γ,)0(P 和)(k Q 是已知的,并且是确定性的。
而观测模型由图2给出,其中)1(+kH 和)(k R 也是已知的,并且是确定性的。
它们可以写为,1,0),(),1()(),1()1(=+Γ++Φ=+k k w k k k x k k k x 状态方程)1()1()1()1(++++=+k v k x k H k z 量测方程)1(+k w激励)1(+k图1 一个离散-时间线性系统的状态方程和输出方程的矢量结构图观测转移矩阵 )1(+k xv (k+1)矢量求和激励)1(+k观测矢量 观测误差新状态矢量图2 观测模型的矢量结构图卡尔曼滤波算法:滤波估计由Kalman 所给出的最优线性滤波估计)1|1(ˆ++k k x是由下面的递归矩阵公式决定的,即,0)0|0(ˆ)]|(ˆ),1()1()1()[1()|(ˆ),1()1|1(≥=+Φ+-++++Φ=++k xk k xk k k H k z k K k k xk k k k x 初始条件这里)1(+kK 称为卡尔曼增益卡尔曼增益卡尔曼增益的表达式为,1,0,)]1()1()|1()1([)1()|1()1(1=+++++⨯++=+-k k R k H k k P k H k H k k P k K TT其中)|1(k kP +表示单步预测误差协方差矩阵。
单步预测误差协方差矩阵(单步性能)1,0)0()0|0(),1()(),1(),1()|(),1()|1(==+Γ+Γ++Φ+Φ=+k P P k k k Q k k k k k k P k k k k P TT,初始条件滤波误差的误差协方差矩阵(协方差递归形式)1,0),|1()]1()1([)1|1(=+++-=+k k k P k H k K I k k P +性能评价(系统状态的卡尔曼滤波估计的协方差矩阵)1,0],))1|1(ˆ)1(ˆ))(1|1(ˆ)1([()1|1(=++-+++-+=+k k k x k x k k xk x E k k P T+11|11|----Γ+Φ=k k k k k k kW XXkkk k V XH Z +=式中:k X —— 是一个1⨯n 维矢量,称为k t 时刻的状态矢量。
卡尔曼滤波器原理详解

卡尔曼滤波器原理详解卡尔曼滤波器是一种用于估计系统状态的滤波算法,其原理基于状态空间模型和观测模型,并结合最小均方误差准则。
它通过使用系统动态方程和观测值,对系统的状态进行估计和预测,实现对噪声和偏差的最优抑制,从而提高状态估计的精度和稳定性。
1.预测步骤:预测步骤是基于系统的动态方程,利用上一时刻的状态估计和控制输入,预测系统的状态。
预测步骤中,通过状态转移矩阵A将上一时刻的状态估计值x(k-1)预测到当前时刻的状态估计值的先验估计值x'(k):x'(k)=A*x(k-1)+B*u(k-1)其中,x(k-1)为上一时刻的状态估计值,u(k-1)为控制输入。
预测步骤还要对状态估计值的协方差矩阵P(k-1)进行更新,通过状态转移矩阵A和系统的过程噪声协方差矩阵Q的关系:P'(k)=A*P(k-1)*A'+Q2.更新步骤:更新步骤是基于观测模型,利用当前时刻的观测值和预测的状态估计值,对状态进行校正和更新。
更新步骤中,首先计算观测残差z(k):z(k)=y(k)-H*x'(k)其中,y(k)为当前时刻的观测值,H为观测模型矩阵。
然后基于观测模型矩阵H、预测的状态估计值x'(k)和状态估计值的协方差矩阵P'(k),计算卡尔曼增益K(k):K(k)=P'(k)*H'*(H*P'(k)*H'+R)^(-1)其中,R为观测噪声协方差矩阵。
最后,利用卡尔曼增益对状态估计值进行校正和更新:x(k)=x'(k)+K(k)*z(k)更新步骤还要对状态估计值的协方差矩阵P'(k)进行更新,通过卡尔曼增益K(k)和观测噪声协方差矩阵R的关系:P(k)=(I-K(k)*H)*P'(k)其中,I为单位矩阵。
卡尔曼滤波器的主要优点在于可以根据系统的动态方程和观测模型进行状态估计,对于动态系统和噪声的建模具有一定的灵活性。
卡尔曼滤波详解一维卡尔曼滤波实例解析(五个公式以及各个参数的意义)

卡尔曼滤波详解一维卡尔曼滤波实例解析(五个公式以及各个参数的意义)一、问题描述假设我们有一个一维系统,我们想要估计这个系统的状态x。
我们可以通过一维传感器获得关于这个系统的观测z,但是这个观测会存在误差。
二、基本原理三、基本公式1.状态预测:我们首先假设系统可以通过一个线性方程来描述:x(k)=Ax(k-1)+B(u(k))+w(k),其中x(k)代表系统在时刻k的真实状态,A是系统的状态转移矩阵,B是外部输入的影响矩阵,u(k)是外部输入,w(k)是系统状态预测过程中的噪声。
2.状态协方差预测:卡尔曼滤波同时也需要估计状态的不确定性,即状态协方差。
协方差可以通过以下公式进行预测:P(k)=AP(k-1)A^T+Q(k-1),其中P(k)代表状态协方差矩阵,Q(k-1)是协方差预测过程中的噪声。
3.观测预测:将状态的估计值带入观测模型中,可以预测观测值:z^(k)=Hx^(k),其中z^(k)代表预测的观测值,x^(k)代表状态的估计值,H是观测模型矩阵。
4.观测残差:观测残差即观测值与预测观测值之间的差异:y(k)=z(k)-z^(k),其中y(k)代表观测残差。
5.状态更新:基于观测残差,我们可以通过以下公式更新状态的估计值:x(k)=x^(k)+K(k)y(k),其中K(k)代表卡尔曼增益。
卡尔曼增益可以通过以下公式计算:K(k)=P(k)H^T(HP(k)H^T+R)^-1,其中R为观测噪声的方差。
四、参数含义1.状态转移矩阵A:描述系统状态k与状态k-1之间的转移关系。
2.外部输入矩阵B:外部输入对系统状态的影响矩阵。
3.外部输入u(k):外部输入,可以是控制信号或者测量噪声。
4.状态预测噪声w(k):在状态预测过程中引入的噪声。
5.状态协方差矩阵P:表示状态估计的不确定性,协方差矩阵的对角线上的元素越大,状态的不确定性越大。
6.状态协方差预测噪声Q(k):在状态协方差预测过程中引入的噪声。
卡尔曼滤波算法含详细推导.ppt

而M 1向量 v为1(过n)程噪声向量,它描述状态转移中间的
加性噪声或误差。
1、kalman滤波问题
(1)、观测方程
y(n)C (n)x(n)v2(n)....2 .)....(
式中,N 1向量y(n)表示动态系统在时间n的观测向量; N M矩阵C(n)称为观测矩阵(描述状态经过其作用,
卡尔曼滤波算法及 推导
1、kalman滤波问题
考虑一离散时间的动态系统,它由描述状态向量的过程方程 和描述观测向量的观测方程共同表示。
(1)、过程方程
x (n 1 ) F (n 1 ,n )x (n ) v 1 (n )...1 )....
式中,M 1向量x(n)表示系统在离散时间n的状态向量,它是 不可观测的;M M矩阵F(n+1,n)成为状态转移矩阵,描述
变成可预测的),要求也是已知的;v2(n)表示观测噪声向 量,其维数与观测向量的相同。过程方程也称为状态方程, 为了分析的方便,通常假定过程噪声v1(n)和观测噪声v2(n) 均为零均值的白噪声过程,它们的相关矩阵分别为:
1、kalman滤波问题
E { v 1 (n )v 1 H (k ) }Q 0 ,1 n ( n k )n , k ..3 .)...(
K (n ,n 1 ) E { e (n ,n 1 )e H (n ,n 1 )}................1 ..) ....( 7 ..
表示(一步)预测状态误差的相关矩阵
3、kalman滤波算法
由上一节的的新息过程的相关知识和信息后,即可转入 kalman滤波算法的核心问题的讨论:如何利用新息过程估计 状态向量的预测?最自然的方法是用新息过程序列a(1),…a(n) 的线性组合直接构造状态向量的一布预测:
卡尔曼滤波算法

卡尔曼滤波器不断的把covariance递归, 从而估算出最优的温度值。其运
行的很快,而且它只保留了上一时刻的covarian2c02e1/3。/28
12
三:卡尔曼滤波引例
2021/3/28
13
四:卡尔曼滤波算法数学推导
引入一个离散控制过程的系统。 该系统可用一个线性随机微分方程来描述:
X(k)=F X(k-1)+B U(k)+W(k) 加上系统的测量值:
五:卡尔曼滤波的典型应用—多传感器数据融合处理
数据融合的模型: (a)集中式融合系统;
(b)无反馈式分布融合系统;
(c)有反馈式分布融合系统; (d)有反馈的全并行系统
(c)有反馈式分布融合系统
融合中心到各传感器有反 馈通道,提高各传感器状态 估计和预测精度。
2021/3/28
27
五:卡尔曼滤波的典型应用—多传感器数据融合处理
• 卡尔曼滤波器源于他的博士论文和1960年 发表的论文《A New Approach to Linear Filtering and Prediction Problems》 (线性滤波与预测问题的新方法)。
卡尔曼将状态变量引入虑波理论,提出了递推滤波算法,建 立了后来被自动控制界称道的“卡尔曼滤波”。
25
五:卡尔曼滤波的典型应用—多传感器数据融合处理
数据融合的模型: (a)集中式融合系统;
(b)无反馈式分布融合系统;
(c)有反馈式分布融合系统; (d)有反馈的全并行系统
(b)无反馈式分布融合系统
各传感器分别滤波,将
各局部状态估计送给 融合中心进行融合,最 后给出融合结果。
2021/3/28
26
四:卡尔曼滤波算法数学推导
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、kalman滤波问题
ß 考虑一离散时间的动态系统,它由描述状态向量的过程方程 和描述观测向量的观测方程共同表示。
(1)、过程方程
x(n 1) F (n 1, n)x(n) v1(n).......(1)
式中,M 1向量x(n)表示系统在离散时间n的状态向量,它是 不可观测的;M M矩阵F(n+1,n)成为状态转移矩阵,描
述动态系统在时间n的状态到n+1的状态之间的转移,应为已
知。而M 1向量 v1(n) 为过程噪声向量,它描述状态转移中
间的加性噪声或误差。
1、kalman滤波问题
(1)、观测方程
y(n) C(n)x(n) v2(n).........(2)
式中,N 1向量y(n)表示动态系统在时间n的观测向量; N M矩阵C(n)称为观测矩阵(描述状态经过其作用,
定义滤波状态向量的误差向量,可以证明:
P(n) E{e(n)eH (n)}............................................(35)
2、新息过程
性质3 表示观测数据的随机向量序列{y(1) ,…y(n)}与表示新息
过程的随机向量序列{a(1),…a(n)} 一一对应 ,即
{y(1),...y(n)} { (1),... (n)}..........(9)
以上性质表明:n时刻的新息a(n)是一个与n上课之前的观测数 据y(1), ...,y(n-1)不相关,并具有白噪声性质的随机过程,但它却能够提
将状态方程(1)和状态向量的一步预测更新公式(25)代入式(29)中,有:
e(n 1, n) F (n 1, n)[x(n) x1(n)]
G(n)[ y(n) C(n) x1(n)] v1(n)
将观测方程(2)代入上式,并代入 e(n, n -1) x(n) x1(n) ,则有:
e(n 1, n) [F (n 1, n) G(n)C(n)]e(n, n 1)
这里使用了状态向量与观测噪声不相关的事实。进一步地,由正交原理引
理知,在最小均方误差准则下求得的一步预测估 x1(n) 与预测误差e(n,n-1)彼
此正交,即
E{x1(n)eH (N , N 1)} 0
3、kalman滤波算法
因此,由式(26)及式(27)易得:
E{x(n 1)H (n)} F(n 1,n)E{[x(n) e(n,n 1)]eH (n,n 1)}CH (n)
v1(n) G(n)v2 (n)..................(30)
3、kalman滤波算法
求式(3)所示状态向量的一步预测误差向量的相关矩阵,容易证明:
K(n 1,n) E{e(n 1,n)]eH (n 1,n)} [F(n 1,n) G(n)C(n)]K(n,n 1)[F(n 1,n) G(n)C(n)]H Q1(n) G(n)Q2(n)GH (n).............(31)
然后再用到下式得到
y 1
(n)
:
y ( n ) C ( n ) x 1 ( n )......... ..( 12 ) 1
2、新息过程
ß 将上式代入新息过程的定义式(6),可得到:
(n) y(n) C(n) x1(n)
C(n)[x(n) x1(n)] v2 (n)..........(13)
状态向量的预测?最自然的方法是用新息过程序列 a(1),…a(n)的线性组合直接构造状态向量的一布预测:
def
n
x1 (n) x (n 1 y(1),..., y(n)) W1(k) (k)
ß 式中W1(k)表示与一步预测项对应的权矩k阵1,且k为离散时间。
现在的问题是如何确定这个权矩阵?
(1)、状态向量的一布预测
式中Q2(n)是观测噪声v2(n)的相关矩阵,而
K(n,n1) E{e(n,n1)eH(n,n1)}...........................(17)
表示(一步)预测状态误差的相关矩阵
3、kalman滤波算法
ß 由上一节的的新息过程的相关知识和信息后,即可转入 kalman滤波算法的核心问题的讨论:如何利用新息过程估计
k
......(3)
E{v2 (n)v2H (k)}
Q2 (n),n 0,nk
k
......(4)
1、kalman滤波问题
ß 还假设状态的初始值x(0)与v1(n) 、 v2(n), n 0均不相关,并且噪声向量v1(n)与 v2(n)也不相关,既有:
E{v1(n)v2H (k)} 0,n, k......(5)
式中R(n)是信息过程的相关矩阵,由式(10)定义。
3、kalman滤波算法
ß (3)、Riccati方程
由式(28)表示的kalman增益与预测状态误差的相关矩阵K(n,n-1)有关,为了最后完 成kalman自适应滤波算法,还需要再推导K(n,n-1)的递推公式。
考察状态向量的预测误差:
e(n 1, n) x(n 1) x1(n 1)...........(29)
状态向量的一步预测分为非自适应(即确定)部F分(n 1, n) x(n) 和自
适应(即校正)部分G(n)a(n)。从这个意义上讲,G(n)称为kalman增益 (矩阵)是合适的。
3、kalman滤波算法
(2)、 kalman增益的计算
为了完成kalman自适应滤波算法,需要进一步推导kalman增益的实际计算
E{x(n 1) H (k)} W1(k)E{ (k) H (k)}
W1(k)R(k)
ß 由此可以求出权矩阵的表达式:
W1(k) E{x(n 1) H (k)}R1(K )............(20)
3、kalman滤波算法
ß 将式(20)代入式(18),状态向量的一步预测的最小均
方估计可表示为
变成可预测的),要求也是已知的;v2(n)表示观测噪声向 量,其维数与观测向量的相同。过程方程也称为状态方程, 为了分析的方便,通常假定过程噪声v1(n)和观测噪声v2(n) 均为零均值的白噪声过程,它们的相关矩阵分别为:
1、kalman滤波问题
E{v1(n)v1H (k)}
Q1 (n),n 0,nk
F(n 1,n)E{e(n,n 1)eH (n,n 1)}CH (n) F(n 1,n)K(n,n 1)CH (n)........(27)
将式(27)代入式(24),便得到kalman增益的计算公式如下:
G(n) F (n 1, n)K (n, n 1)C H (n)R1(n)............(28)
供有关y(n)的新息,这就上信息的内在物理含义。
2、新息过程
(2)、新息过程的计算
下面分析新息过程的相关矩阵
R(n) E{ (n) H (n)}........ .(10)
在kalman滤波中,并不直接估计观测数据向量的进一步预测
,
而是先计算状态向量的一步预测
def
x1 (n) x(n y(1),...y(n 1))........(11)
2、新息过程
ß 考虑一步预测问题,给定观测值y(1), ...,y(n-1),求观测向量y(n)的 最小二乘估计,记作
def
yˆ1(n) yˆ(n y(1),...,y(n 1))
(1)、新息过程的性质 y(n)的新息过程定义为:
(n) y(n) yˆ1(n)..........(6)
式中,N 1向量(n)表示观测数据y(n)的新的信息,简称新息。
P(n) K (n, n 1) F 1(n 1, n)G(n)C(n)K (n, n 1)........(33)
式(32)称为Riccati差分方程。
3、kalman滤波算法
若定义
x(n)
是利用已知的y(1),…,y(n)求得的状态向量的滤波估计,则
e(n) x(n) x1(n)..............................................(34)
根据正交性原理,最优预测的估计误差
e(n 1, n) x(n 1) x1(n 1)
3、kalman滤波算法
ß 应该与已知值正交,故有
E{e(n 1, n) H (k)} E{[x(n 1) x1(n 1) H (k)}
0, k 1,..., n.........(19)
ß 将式(18)代入(19),并利用新息过程的正交性,得到
2、新息过程
ß 新息 (n)具有以下性质: 性质1 n时刻的新息 (n)与所有过去的观测数据y(1), ...,
y(n-1)正交,即:
E{ (n) yH (k)} 0,1 k n 1.......(7)
性质2 新息过程由彼此正交的随机向量序列{ (n)} 组成,即
E{有 (n) H (k)} 0,1 k n 1..........(8)
n
x 1 (n 1) E{x(n 1) H (k)}R1(k) (k)
k 1
n1
E{x(n 1) H (k)}R1(k) (k)
k 1
E{x(n 1) H (n)}R1(n) (n)..............(21)
ß 注易意知到下E式{对v1(kn=)0,(k1),}… ,0, nk成立0,:1,..., n, 并利用状态方程(1),
ß 若定义
def
G(n) E{x(n 1) H (k)}R1(k)
并将式(23)和式(24)代入式(21),则得到状态向量一步预测的
更新公式:
x(n 1) F (n 1, n) x(n) G(n) (n)..............(25)
式(25)在kalman滤波算法中起着关键的作用,因为它表明,n+1时刻的
