苏教版小学数学六年级上册思考题
苏教版数学小学六年上册第一单元《长方体和正方体》试题共10套
苏教版小学数学六年级上册单元测试题姓名--------班级---------分数---------一、填空1、有一个长方体长、宽、高分别是7厘米、5厘米、3厘米，它的棱长之和是( )2、做一个长方体框架，长8厘米，宽5厘米，高4厘米，要用( )厘米的铁丝，这是求长方体的( )；如果在框架表面上贴上塑料板，要用( )平方厘米的塑料板，这是求长方体的( )，这个长方体占空间( )立方厘米，这是求长方体的( )。
3、0.7立方米=( )立方米( )立方分米4、一个长方体的体积是96立方分米，底面积是16立方分米，它的高是( )分米。
5、有一长方体木料长3厘米，宽3厘米，高2厘米。
把他切成1立方厘米的小方块可以切成( )块。
6、用一根12分米长的铁丝围成一个最大的正方体形状的框架，这个正方体得体积是( )立方分米。
7、一个正方体的棱长总和是108分米，这个正方体的表面积是( )平方分米，体积是( )立方分米。
8、一个正方体的表面积是72平方分米，占地面积是( )平方分米。
9、有一个正方体，棱长3厘米。
若将每条棱长扩大2倍，这个正方体的体积应是( )，表面积应是( )。
10、用3个棱长4分米的正方体粘合成一个长方体，长方体的表面积比3个正方体的表面积少( )平方分米。
二、判断题。
1、只有6个面都是长方体的物体才叫长方体。
2、长方体中的三条棱长分别叫做长、宽、高。
3、求一个容器的容积，就是求这个容器的体积。
4、一个正方体的棱长之和是12厘米，体积是1立方厘米。
5、一个正方体的棱长是a，所以这个正方体的体积是3a.6、长方体的体积都比正方体的体积大。
7、把2块棱长都为2厘米的正方体拼成一个长方体，表面积增加了8平方厘米。
8、因为用2个同样大小的正方体拼成的长方体的体积扩大2倍，所以表面积也扩大到原来的2倍。
9、如果两个长方体的体积相等，它们的长、宽和高的长度必须相等。
10、在不改变体积大小的前提下，地面积扩大2倍，高反而缩小2倍。
苏教版六年级数学上册 第三单元 分数除法(重点题型+单元测试+答案)
第三单元 分数除法知识点1：除法计算1. 分数除以整数（0）除外，等于分数乘这个整数的倒数。
2. 分数除以分数，可以用被除数乘除数的倒数来计算。
3. 甲数除以乙数（0）除外，等于甲数乘乙数的倒数。
例1(易错题)：声音在空气中23秒约能传播227米，一秒约能传播多少米？例2(易错题)：电影画面是有许多连续拍摄的照片，以每张124秒的速度播放形成的，照这样的速度，半秒可以播放多少张照片？一分钟呢？例3(易错题)：一种柴油45升重1625千克。
（1）1升这种柴油重多少千克？ （2）1千克这种柴油有多少升？例4(思考题)：如果x 是一个不等于零的自然数，那么1x除以三和13除以x ，这两个算式的结果相等吗？例5(拓展题)：2009÷200920092010【练习题】1. 两个真分数相除，商一定大于被除数（ ）。
2. 两个因数的积71010，其中一个因数是14，求另一个因数是多少？3. 一个正方形的周长是811米，它的边长是多少米？4. 用58吨玉米可以制成淀粉720吨，照这样计算，一吨玉米可以制成淀粉多少吨？5. 小雪把一道除法算式中的被除数扩大到原来的四倍后，再除以六，结果是118，这道除法算式中的被除数原来是多少？6. 饲养场养白兔51只，是兔子总数的35，兔子一共有（ ）只。
7. 小华看一本故事书，已经看了全书的34，正好是69页。
这本书一共有（ ）页。
8. 一条牛仔裤128元，它的价钱是一件茄克衫的45。
一件茄克衫（ ）元。
9. 一袋糖果，吃了34，正好是24颗。
这袋糖果有（ ）颗。
10. 解方程。
32x=5349x=518x ÷116=32234÷x=910知识点2：简单的分数除法实际问题1. 单位一已知，用乘法；单位一未知，用除法。
2. 已知一个数的几分之几是多少，求这个数是把这个数看作单位一，单位一的量是未知的，可以设单位一的量为x ，根据乘法意义来列方程解答。
苏教版小学数学六年级上册思考题解
二、长方体和正方体1.填空：(1)一个正方体棱长之和为36厘米，它的体积是( 27 )立方厘米，表面积是( 54 )平方厘米。
(2)一个长方体的棱长之和为36厘米，已知它的长为4 厘米，宽为3厘米，高为( 2 )厘米。
(3)一个长方体的表面积是148平方厘米，已知这个长方体底面长6 厘米，宽5 厘米，这个长方体的高是( 4 ) 厘米。
(4)一个长方体的表面积是320平方厘米，上、下两个面是周长32厘米的正方形，长方体的体积是(384 )立方厘米。
提示：底面正方形的边长是32÷4＝8(厘米)，面积是8×8＝64(平分厘米) 侧面积是 320－64×2＝192(平方厘米)长方体的高是 192÷32＝6(厘米)长方体体积是 64×6＝384(平分厘米)(5)一个长方体的侧面积为72平方分米，高是4分米，底面长是宽的2倍。
这个长方体的体积是( 72 )立方分米。
提示：底面周长是 72÷4＝18(分米)底面的宽是 18÷2÷(2＋1)＝3(分米)， 长是 3×2＝6(分米)(6)一段方钢长2米，横截面是周长为12 厘米的正方形，这块方钢的体积是 ( 1800 )立方厘米。
(7)一只木箱高5分米，底面周长3 米，下底面积是54平方分米，它的表面积是( 258 )平方分米。
(8)一个正方体的棱长缩小2倍，体积缩小到原来的21，体积缩小到原来的( 81 )，表面积缩小到原来的( 41 )。
(9)两个长方体的高相等，且甲长方体的体积是乙长方体体积的4倍，如果两个长方体的底面都是正方形，那么，当甲长方体底面边长是4厘米时，乙长方体底面边长是( 2 )厘米。
(10)一张边长 20 厘米的正方形商标纸，正好贴满底面为正方形的食品盒的侧面，这个食品盒的容积是( 500 )毫升。
提示：底面正方形边长是 20÷4＝5(厘米)(11)棱长为a的正方体，表面积是( 6a2 )，把它切成两个长方体后，表面积的和是( 8a2 )。
苏教版六年级数学上册《列方程解决实际问题》教学反思
苏教版六年级数学上册《列方程解决实际问题》教学反思第一篇：苏教版六年级数学上册《列方程解决实际问题》教学反思区教学大比武活动已经过去一周多了，但对于自己执教的《列方程解决实际问题（1）》感触仍然很多。
这节课是在五年级学生刚刚经历了等式的性质的学习和解简单的方程的基础上进行的，本节的重点是：如何分析实际问题中的数量关系和综合运用方程知识解决实际问题。
难点是：找到题目中未知量与已知量之间的数量关系、等量关系，掌握形如ax+b=c,ax-b=c的方程的解法。
人民小学的五年级学生基础知识非常扎实，不仅能熟练地解决已学的一步计算的简单方程，而且，根据课堂上练习时的观察，一半的学生在新授之前已经掌握了ax+b=c,ax-b=c的解法。
从课堂发言看，这些学生并不是运用等式的性质来解方程，有的班级学生学会了移项的方法解题，有的是根据等式中各个量间的关系来解方程，比如2x-22=64，部分学生把2x看作被减数，运用被减数=减数+差的关系式得出2x=64+22后，轻松解答方程。
可见不少班级老师已经在教学时拓展了更复杂的方程的解法。
再经过共同学习后学生已经熟练地掌握形如ax+b=c,ax-b=c的方程的解法。
但找到题目中未知量与已知量之间的数量关系、等量关系仍然是学生学习的难点，许多学生能顺利列出方程但是对等量关系式却表达不清，这种现象在历年的教学中均有体现。
用方程解决生活中的问题，关键在于让学生能正确寻找问题中的数量关系式。
掌握了数量关系式，问题便可迎刃而解。
学生在以前的学习中缺乏这样的训练，对如何分析数量关系没有一定的基础和经验。
在例1教学时，学生找等量关系的时候还是比较困难，究其原因，大多是直接把大雁塔和小雁塔的高度比较，而没有和小雁塔高度的2倍去比较。
等量关系犹如解题的拐杖，一定要让学生认真审题，仔细分析。
这就需要教师恰当地引导。
我认为教学中要做到：一、抓住关键句提高学生的分析能力。
解决实际问题首先要引导学生分析题目的条件和问题，找出题目中的关键句，根据关键句找出题目中的直接的相等关系，这样可以便于学生列出方程，解答问题。
苏教版六年级上册数学教材课后答案
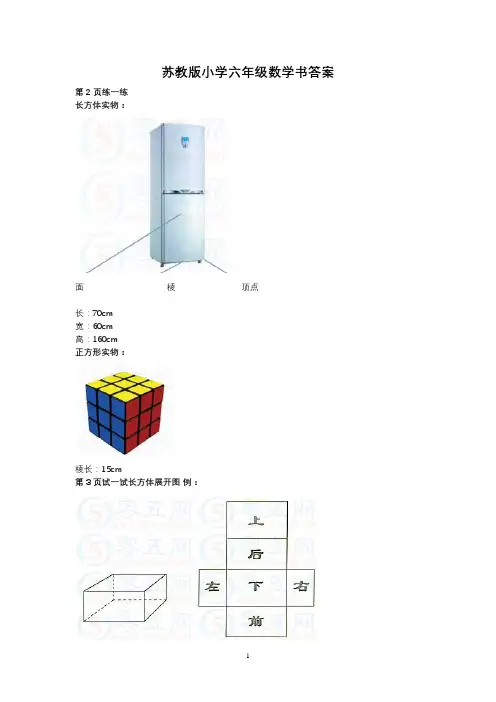
苏教版小学六年级数学书答案第2页练一练长方体实物：面棱顶点长：70cm宽：60cm高：160cm正方形实物：棱长：15cm第3页试一试长方体展开图例：练一练1.2.第1、3个第4页练习一1.（1）长是7cm；宽是4cm；高是3cm（2）长是6dm；宽是4dm；高是5dm （3）长是20dm；宽是8dm；高是8dm5. 第5页8.（1）4×10=40（平方厘米）（2）3×7=21（平方毫米）（3）4×4=16（平方厘米）9.（1）a+b+c4(a+b+c) （2）12a72动手做长方体：选择长10cm，宽8cm；长10cm，宽5cm；长8cm，宽5cm的纸片各2张。
正方体：选择边长是8厘米或10厘米的纸片6张。
第6页试一试第7页练一练第8页练习二1.（1）4，3，12（2）4，2，8（3）3，2，6（4）522.（1）5×5+5×3.5+5×3.5=60（平方分米）（2）60×2=120（平方分米）3.（25×20+25×15+20×15）×2=2350（平方厘米）4.20×20×6=2400（平方厘米）5.第9页7.解：27×31×2+27×2.5×2+31×2.5=1886.5（平方厘米）答：至少需要1886.5平方厘米。
8.10.解：长：8cm宽：5cm高：1.5cm8×5×2+8×1.5×2+5×1.5=111.5（平方厘米）8×5+8×1.5×2+5×1.5×2=79（平方厘米）答：内盒79平方厘米，外盒111.5平方厘米。
第11页试一试方法：例：将其中一个杯子倒满水，再将其倒入另一个杯中，若溢出，则此杯容积更大，反之亦然。
2022年小学数学六年级上册1.6长方体和正方体的体积(含答案)苏教版
一、预习与质疑〔课前学习区〕〔一〕预习内容：第16、17页〔二〕预习时间：10分钟〔三〕预习目标：探索并掌握长方体和正方体的体积公式，能应用公式正确计算长方体和正方体的体积，并能解决相应的简单实际问题。
〔四〕学习建议：1．自学课本第16、17页，用红笔勾画出疑惑点；独立思考完成复习和自主学习局部。
2．针对自主学习中找出的疑惑点，课上小组讨论交流，答疑解惑。
3、你能棱长为1厘米的小正方体摆成什么形状的长方体，试着摆一摆，能说出它的体积吗？想一想长方体的体积与什么有关？正方体呢？〔五〕预习检测：活动一：出示体积相近的一块橡皮和一个火柴盒，你们有什么方法比出它们的体积大小吗？用切的方法求橡皮的体积。
能用切的方法求这个火柴盒的体积吗？看来，还需要找到更简单的方法。
猜一猜，长方体的体积可能与哪些数量有关呢？怎么求长方体的体积呢？（六）生成问题：通过预习和做检测题你还有哪些疑惑请写在下面。
二、落实与整合〔课中学习区〕活动二：拼长方体，发现体积计算规律1. 明确要求，有序操作。
〔1〕提出操作要求：用假设干个1立方厘米的正方体摆成一个长方体，要求四人小组内每人摆出的长方体各不相同。
然后将摆出的长方体放在桌子上，并编号。
〔2〕学生操作。
2. 观察物体，记录数据。
〔1〕出例如9前半局部表格，并提问: 你能看出这些长方体的长、宽、高各是多少吗？〔2〕提问：怎样才能知道这些由1立方厘米的正方体摆成的长方体的体积？〔数每个长方体中包含了多少个1立方厘米的正方体的个数〕依次出示后半局部表格：〔3〕先在小组内互相说说，然后将这些数据依次记录在表格中。
〔4〕填完表格，你如果能通过观察表格，发现点什么就更好了。
3．观察数据，沟通联系。
你们是怎么看出这些长方体的长、宽、高的？你们又是怎样数出每个长方体里包含的正方体的个数的？小正方体的个数可以怎样求？正方体的个数可以这样求:活动三：探究例10（1）屏幕出例如10三个长方体，用1立方厘米的小正方体摆出下面的长方体，各需要多少个？先想一想，再摆一摆。
苏教版小学数学六年级上册思考题
二、长方体和正方体1.填空：(1)正方体棱长之和为36 厘米，它的体积是( )立方厘米，表面积是( )平方厘米。
(2)一个长方体的棱长之和为36 厘米，已知它的长为4 厘米，宽为3 厘米，高为 ( ) 厘米。
(3)一个长方体的表面积是148平方厘米，已知这个长方体底面长6 厘米，宽5 厘米，这个长方体的高是( ) 厘米。
(4)一个长方体的表面积是320平方厘米，上、下两个面是周长32厘米的正方形，长方体的体积是( )立方厘米。
(5)一个长方体的侧面积为72平方分米，高是4分米，底面长是宽的2倍。
这个长方体的体积是( )立方分米。
(6)一段方钢长 2 米， 横截面是周长为 12 厘米的正方形，这块方钢的体积是( )立方厘米。
(7)一只木箱高5 分米，底面周长3 米，下底面积是54 平方分米，它的表面积是 ( )平方分米。
(8)一个正方体的棱长缩小到原来的21，体积缩小到原来的( )，表面积缩小到原来的( )。
(9)两个长方体的高相等，且甲长方体的体积是乙长方体体积的4倍，如果两个长方体的底面都是正方形，那么，当甲长方体底面边长是4厘米时， 乙长方体底面边长是( ) 厘米。
(10)一张边长20厘米的正方形商标纸正好贴满底面为正方形的食品盒的侧面，这个食品盒的容积是( )毫升。
(11)棱长为a 的正方体，表面积是( )，把它切成两个长方体后，表面积的和是( )。
(12) 3个棱长为a 的正方体拼成一个长方体，这个长方体的表面积是( )。
(13) 有两个相同的正方体拼成一个长方体，这个长方体棱长的总和是48厘米，这个长方体的体积是( )立方厘米。
(14) 把一个正方体分成相等的64个小正方体，表面积增加了( )倍。
(15) 要拼成棱长8 厘米的正方体，需要( )个棱长2 厘米的正方体。
(16) 一个正方体的表面积是54平方分米，如果棱长增加2 分米，体积增加( )立方分米，表面积增加( )平方分米。
(17) 一个长方体，如果高增加2厘米，就变成了一个正方体。
六年级数学上册第8讲三个和尚没水喝思维突破苏教版
课堂笔记第8讲三个和尚没水喝例题练习例1 一个水池有若干相同的进水管和若干相同的排水管．如果单独打开一个进水管,那么24小时可以将空水池灌满；如果单独打开一个排水管,那么36小时可以将满池的水排光．请根据题意,回答下列问题：（1）同时打开2个进水管,多少小时可以将空水池灌满？（2）同时打开3个进水管和1个排水管,多长时间可以将空水池灌满？（3）同时打开1个进水管和2个排水管,多长时间可以将满池的水排光？练 1 一个水池有若干相同的进水管和若干相同的排水管,如果单独打开一个进水管,那么12小时可以将空水池灌满；如果单独打开一个排水管,那么18个小时可以将满池的水排光．那么,同时打开2个进水管和2个排水管,多长时间可以将空水池灌满？如果打开2个进水管和3个排水管呢？例2 一水池装有两个相同的进水管和一个排水管．如果开1个进水管,6小时可将空池灌满；如果开1个进水管和1个排水管,12小时可将空池灌满．现在将2个进水管和1个排水管同时打开,请问多少时间能灌满整个池子的二分之一？练2 一水池装有两个相同的进水管和一个排水管．如果只开1个排水管,6小时可将一池子水排空；如果开1个进水管和1个排水管,3小时可以将空池灌满．现在将2个进水管和1个排水管同时打开,请问：多少时间能将空池灌满？例3 蓄水池有甲、乙两个进水管和一个排水管．单开甲管需10小时灌满水池,单开乙管需课堂笔记12小时灌满水池,单开排水管需20小时排空水池．上午8点三个管同时打开,中间排水管因故关闭,结果到下午2点水池被灌满．问：排水管在何时被关闭？练3 蓄水池有一根进水管和一根排水管．如果想灌满整池水,单开进水管需10小时,如果想排空整池水,单开排水管需15小时．上午6点将两个管同时打开,中间排水管因故关闭,结果到下午6点水池被灌满．问：排水管在何时被关闭？例4 一个蓄水池,水从一根进水管以一定的速度流入．如果打开5个水龙头,6小时可以把满池水排空,如果打开8个水龙头,3小时可以把满池水排空．现在打开11个水龙头,问要多少时间才能把水排空？练4 一艘船破了个洞,水以一定的速度涌入．如果有3个船员排水,10分钟可以排干积水；如果有5个船员排水,5分钟可以排干积水．如果有6个船员排水,多少分钟可以排干积水？选做题1 某水库建有10个泄洪闸,现有水库的水位已经超过安全线,上游河水还在按不变的速度流入．为了防洪,需调节泄洪速度．假设每个闸门泄洪的速度相同,经测算,若打开1个泄洪闸,30小时水位降至安全线；若打开2个泄洪闸,10小时水位降至安全线．现在抗洪指挥部队要求在2.5小时使水位降至安全线以下,至少要同时打开几个闸门？课堂笔记自我巩固1．一个水池有2根排水管和1根进水管．单开一个排水管30分钟可放完全池水；单开一根进水管,20分钟注满空池．如三管齐开,_______分钟可以将满池水排空．2．蓄水池有一根进水管和一根排水管．单开进水管需4小时注满整个蓄水池,单开排水管需8小时排空整池水．开始时蓄水池没有水,小高将两个管同时打开,中间进水管因故堵住了不再进水,结果到3个小时他过来发现蓄水池恰好没水．那么进水管堵住了________小时．3．一水池装有两根出水管和一根进水管．单开一个出水管40分钟可放完全池水；单开一根进水管,30分钟注满空池．如三管齐开,________分钟可以将满池水排空．4．一水池装有两根进水管和一根出水管．单开一个进水管15分钟可注满空水池；单开一根放水管,30分钟放空这池水．如三管齐开,________分钟可以将空池注满．5．一个水池有许多相同的进水管和排水管．如果打开一个进水管,那么12小时能将空池灌满；如果打开一个排水管,那么20小时能将满池的水排光．那么,同时打开2个进水管和2个排水管,________小时能将空池灌满．6．一个水池有许多相同的进水管和排水管．如果打开一个进水管,那么10小时能将空池灌满；如果打开一个排水管,那么12小时能将满池的水排光．那么,同时打开2个进水管和3个排水管,________小时能将满池水排空．7．书店出售一批书,有一个售货员和一个进货员．售货员20天可以卖完这批书,而1个进货课堂笔记：员需要30天才能进到等量的这批书．现在书店中有只剩下了这批书的四分之一,售货员每天都卖出相同的商品,有1个进货员不断的给书店进货,________天之后可以卖完书店的这批书．8．一批货物在商店里销售,有一个售货员和一些进货员．售货员30天可以将摆满商品的商店里的全部商品卖出,而1个进货员需要90天才能将空商店摆满商品．现在商店中有一半的商品,售货员每天都卖出相同的商品,有2个进货员不断的给商店进货,________天之后可以卖完商店的商品．9．一水池装有一个进水管和一个排水管．如果单开进水管,4小时可将空池灌满；如果单开排水管,6小时可将整池水排完．现在先打开进水管,1小时后打开排水管．那么在打开进水管3小时后水池中的水占水池容积的_______．10．蓄水池有一根进水管和一根排水管．如果想灌满整池水,单开进水管需6小时；如果想排空整池水,单开排水管需8小时．上午10点将两个管同时打开,中间排水管因故关闭,结果到下午7点水池被灌满．那么排水管共打开了________小时．课堂落实1．一水池装有甲乙两根进水管．单开甲进水管30分钟可注满空池；单开乙进水管,20分钟注满空池．现在按单开甲进水管1分钟、单开乙进水管1分钟、单开甲进水管1分钟、单开乙进水管1分钟的顺序重复下去．那么灌满这个水池需要________分钟．2．一水池装有两根排水管和一根进水管．单开一个排水管20分钟可放完全池水；单开一根进水管,15分钟注满空池．如果三管齐开,________分钟可以将满池水排空．3．一个水池有许多相同的进水管和排水管．如果打开一个进水管,那么10小时能将空池灌满；如果打开一个排水管,那么15小时能将满池的水排光．那么同时打开2个进水管和2个排水管,________小时能将空池灌满．4．书店里有一个售货员和一个进货员．售货员10天可以卖完这批书,而进货员需要15天才能进到等量的这批书．现在书店中只剩下了这批书的31,售货员每天都卖出相同的商品,而进货员不断的给书店进货,那么________天之后可以卖完书店的这批书．5．一个水池,底部安有一个常开的排水管,上部安有若干个同样粗细的进水管．当打开6个进水管时,需要6小时才能注满水池；当打开5个进水管时,需要12小时才能注满水池．如果打开8个进水管,注满水池需要________小时． 作业笔记 课堂笔记第8讲三个和尚没水喝例题练习例1 一个水池有若干相同的进水管和若干相同的排水管．如果单独打开一个进水管,那么24小时可以将空水池灌满；如果单独打开一个排水管,那么36小时可以将满池的水排光．请根据题意,回答下列问题：（1）同时打开2个进水管,多少小时可以将空水池灌满？【答案】12小时【解析】一个进水管的效率是124,一个排水管的效率是136．1÷（124×2）=12小时．（2）同时打开3个进水管和1个排水管,多长时间可以将空水池灌满？【答案】1027小时【解析】1÷（124×3−136）=1027小时．（3）同时打开1个进水管和2个排水管,多长时间可以将满池的水排光？【答案】72小时【解析】1÷（136×2−124）=72小时．练1 一个水池有若干相同的进水管和若干相同的排水管,如果单独打开一个进水管,那么12小时可以将空水池灌满；如果单独打开一个排水管,那么18个小时可以将满池的水排光．那么,同时打开2个进水管和2个排水管,多长时间可以将空水池灌满？如果打开2个进水管和3个排水管呢？【答案】18小时,不能灌满【解析】进水管和排水管的效率分别是112和118．如果开2个进水管和2个排水管,进水的效率是2×112−2×118=118,需要18小时灌满．如果开2个进水管和3个排水管,进水的效率是2×112−3×118=0,永远不能灌满．例2 一水池装有两个相同的进水管和一个排水管．如果开1个进水管,6小时可将空池灌满；如果开1个进水管和1个排水管,12小时可将空池灌满．现在将2个进水管和1个排水管同时打开,请问多少时间能灌满整个池子的二分之一？【答案】2小时【解析】进水管的效率为16,排水管的效率为16−112=112,将2个进水管和1个排水管同时打开,12÷（16×2−112）=2小时能灌满整个池子的一半．练2 一水池装有两个相同的进水管和一个排水管．如果只开1个排水管,6小时可将一池子水排空；如果开1个进水管和1个排水管,3小时可以将空池灌满．现在将2个进水管和1个排水管同时打开,请问：多少时间能将空池灌满？【答案】1.2小时【解析】排水管的效率是16,进水管的效率是13+16=12．如果开2个进水管1个排水管,进水的效率是2×12−16=56,需要1÷56=1.2个小时将空池灌满．例3 蓄水池有甲、乙两个进水管和一个排水管．单开甲管需10小时灌满水池,单开乙管需12小时灌满水池,单开排水管需20小时排空水池．上午8点三个管同时打开,中间排水管因故关闭,结果到下午2点水池被灌满．问：排水管在何时被关闭？【答案】上午10点【解析】从上午8点到下午2点共6个小时,进水管的工作量为（110+112）×6=1110,多出来的工作量即是排水管的工作量,排水管工作了（1110−1）÷120=2小时,因此排水管在上午10点被关闭．练3 蓄水池有一根进水管和一根排水管．如果想灌满整池水,单开进水管需10小时,如果想排空整池水,单开排水管需15小时．上午6点将两个管同时打开,中间排水管因故关闭,结果到下午6点水池被灌满．问：排水管在何时被关闭？【答案】上午9点【解析】从上午6点到下午6点,进水管一直开着,灌进的水量为110×12=65,超过15．说明排水管一共排出的水量是15．排水管开着的时间是15÷115=3小时,那么它在上午9点就关上了．例4 一个蓄水池,水从一根进水管以一定的速度流入．如果打开5个水龙头,6小时可以把满池水排空,如果打开8个水龙头,3小时可以把满池水排空．现在打开11个水龙头,问要多少时间才能把水排空？【答案】2小时【解析】将蓄水池内的水设为单位“1”,5个水龙头的排水效率与水的进水效率差为16,8个水龙头的排水效率与水的进水效率差为13,由此可知3个水龙头的排水效率为13−16=16,1个水龙头的排水效率为118,水的进水效率为118×5−16=19,11个水龙头1÷（118×11−19）=2小时能把水放空．练4 一艘船破了个洞,水以一定的速度涌入．如果有3个船员排水,10分钟可以排干积水；如果有5个船员排水,5分钟可以排干积水．如果有6个船员排水,多少分钟可以排干积水？【答案】4分钟【解析】将船内积水设为单位“1”,3个船员的排水效率与水的进水效率差为110,5个船员的排水效率与水的进水效率差为15,由此可知2个船员的排水效率为15−110=110,1个船员的排水效率为120,水的进水效率为120×3−110=120,6个船员1÷（120×6−120）=4分钟可以排干积水．【答案】7个【解析】将超过安全线的水量设为单位“1”,1个泄洪闸与河水流入的效率差为130,2个泄洪闸与河水流入的效率差为110,由此可知1个泄洪闸的排水效率为110−130=115,河水流入的效率为115−130=130．若要2.5小时使水位降至安全线以下,泄洪闸每小时需排出的水量为1÷2.5+130=1330,需要泄洪闸1330÷115=612个,即至少需要7个泄洪闸．自我巩固1．一个水池有2根排水管和1根进水管．单开一个排水管30分钟可放完全池水；单开一根进水管,20分钟注满空池．如三管齐开,_______分钟可以将满池水排空．【答案】60【解析】1÷（130×2−120）=60分钟.2．蓄水池有一根进水管和一根排水管．单开进水管需4小时注满整个蓄水池,单开排水管需8小时排空整池水．开始时蓄水池没有水,小高将两个管同时打开,中间进水管因故堵住了不再进水,结果到3个小时他过来发现蓄水池恰好没水．那么进水管堵住了________小时．A．1.5 B．2.5 C．3.5【答案】A【解析】3小时排水管排水18×3=38,说明也进水38,所以进水管堵住了3−38÷14=1.5小时.3．一水池装有两根出水管和一根进水管．单开一个出水管40分钟可放完全池水；单开一根进水管,30分钟注满空池．如三管齐开,________分钟可以将满池水排空．【答案】60【解析】1÷（140×2−130）=60分钟.4．一水池装有两根进水管和一根出水管．单开一个进水管15分钟可注满空水池；单开一根放水管,30分钟放空这池水．如三管齐开,________分钟可以将空池注满．【答案】10【解析】1÷（115×2−130）=10分钟.5．一个水池有许多相同的进水管和排水管．如果打开一个进水管,那么12小时能将空池灌满；如果打开一个排水管,那么20小时能将满池的水排光．那么,同时打开2个进水管和2个排水管,________小时能将空池灌满．【答案】15【解析】1÷（112×2−120×2）=15小时.6．一个水池有许多相同的进水管和排水管．如果打开一个进水管,那么10小时能将空池灌满；如果打开一个排水管,那么12小时能将满池的水排光．那么,同时打开2个进水管和3个排水管,________小时能将满池水排空．【答案】20【解析】1÷（112×3−110×2）=20小时.7．书店出售一批书,有一个售货员和一个进货员．售货员20天可以卖完这批书,而1个进货员需要30天才能进到等量的这批书．现在书店中有只剩下了这批书的四分之一,售货员每天都卖出相同的商品,有1个进货员不断的给书店进货,________天之后可以卖完书店的这批书．【答案】15【解析】14÷（120−130）=15天.8．一批货物在商店里销售,有一个售货员和一些进货员．售货员30天可以将摆满商品的商店里的全部商品卖出,而1个进货员需要90天才能将空商店摆满商品．现在商店中有一半的商品,售货员每天都卖出相同的商品,有2个进货员不断的给商店进货,________天之后可以卖完商店的商品．【答案】45【解析】12÷（130−190×2）=45天.9．一水池装有一个进水管和一个排水管．如果单开进水管,4小时可将空池灌满；如果单开排水管,6小时可将整池水排完．现在先打开进水管,1小时后打开排水管．那么在打开进水管3小时后水池中的水占水池容积的_______．A．13B．512C．16【答案】B【解析】设水池的容积为“1”,14×3−16×2=512.10．蓄水池有一根进水管和一根排水管．如果想灌满整池水,单开进水管需6小时；如果想排空整池水,单开排水管需8小时．上午10点将两个管同时打开,中间排水管因故关闭,结果到下午7点水池被灌满．那么排水管共打开了________小时．课堂落实1．一水池装有甲乙两根进水管．单开甲进水管30分钟可注满空池；单开乙进水管,20分钟注满空池．现在按单开甲进水管1分钟、单开乙进水管1分钟、单开甲进水管1分钟、单开乙进水管1分钟的顺序重复下去．那么灌满这个水池需要________分钟．【答案】242．一水池装有两根排水管和一根进水管．单开一个排水管20分钟可放完全池水；单开一根进水管,15分钟注满空池．如果三管齐开,________分钟可以将满池水排空．【答案】303．一个水池有许多相同的进水管和排水管．如果打开一个进水管,那么10小时能将空池灌满；如果打开一个排水管,那么15小时能将满池的水排光．那么同时打开2个进水管和2个排水管,________小时能将空池灌满．【答案】154．书店里有一个售货员和一个进货员．售货员10天可以卖完这批书,而进货员需要15天才能进到等量的这批书．现在书店中只剩下了这批书的13,售货员每天都卖出相同的商品,而进货员不断的给书店进货,那么________天之后可以卖完书店的这批书．【答案】105．一个水池,底部安有一个常开的排水管,上部安有若干个同样粗细的进水管．当打开6个进水管时,需要6小时才能注满水池；当打开5个进水管时,需要12小时才能注满水池．如果打开8个进水管,注满水池需要________小时．【答案】3。
苏教版六年级数学上册课后思考题
苏教版六年级数学上册课后思考题2012.121.甲、乙两人沿着400米的环形报道跑步，他们同时性同一地点出发，同向而行。
甲每分跑280米，乙每分跑240米。
经过多少分甲比乙多跑1圈？2.盒子里装有同样数量的红球和白球。
每次取出6个红球和4个白球，取了若干次以后，红球正好取完，白球还有10个。
一共取了几次？盒子里原来有红球多少个？3.下面五种形状的硬纸各有若干张。
选择哪几种，每种选几张，正好可以围城一个长方体或正方体？4.下图表示用棱长1厘米的正方体摆成的物体。
（1）从上面、正面和左侧面看到的分别是什么形状？试着画一画。
（2）这个物体的表面积是多少平方厘米？（3）在这个物体上添加同样大的正方体，补成一个大正方体。
这个大正方体的表面积至少是多少平方厘米？5.你能根据正方体的体积来估计右边物体的体积吗？1cm36. 一个长方体，如果高增加2厘米，就变成一个正方体。
这时表面积比原来增加56平方厘米。
原来长方体的体积是多少立方厘米？7.把一个六面都涂上颜色的正方体木块，切成64块大小相同的小正方体（如右图）。
（1）三面涂色的小正方体有多少块？（2）两面涂色的小正方体有多少块？（3）一面涂色的小正方体有多少块？8.两根同样长的钢管，第一根用去25米，第二根用去25。
哪一根用去的长一些？9.先找规律，再填数。
（1）45，25,15, ( ) ,120, ( ) , ( ) 。
（2）23, 1 ,32,94,( ) , ( ) 。
10.先计算，在观察每组算式的得数，能发现什么规律？（1）12－13＝( )( )12×13＝( )( )（2）14－15＝( )( )14×15＝( )( )你能根据发现的规律再写几组这样的算式吗？11.一辆小汽车行32千米用汽油325升。
行1千米用汽油多少升？1升汽油可行多少千米？12.两个长方形重叠部分的面积相当于小长方形面积的14，相当于大长方形面积的16。
苏教版六年级数学上册知识点及易错题解析
第一单元长方体和正方体1、两个面相交的线叫做棱，三条棱相交的点叫做顶点。
2、长方体相交于同一顶点的三条棱的长度，分别叫做它的长、宽、高。
3、长方体的特征：面——有六个面，都是长方形（特殊情况下有两个相对的面是正方形），相对的面完全相同；棱——有12条棱，相对的棱长度相等；顶点——有8个顶点。
4、正方体的特征：面——有六个面，都是正方形，所有的面完全相同；棱——有12条棱，所有的棱长度相等；顶点——有8个顶点。
5、正方体也是一种特殊的长方体。
6、把一个长方体或正方体纸盒展开，至少要剪开7条棱。
7、长方体（或正方体）的六个面的总面积，叫做它的表面积。
8、长方体的表面积=（长×宽+宽×高+高×长）×2正方体的表面积=棱长×棱长×6。
9、物体所占空间的大小叫做物体的体积。
10、容器所能容纳物体的体积，叫做这个容器的容积。
11、常用的体积单位有立方厘米、立方分米、立方米。
1立方米=1000立方分米，1立方分米=1000立方厘米。
12、计量液体的体积，常用升和毫升作单位。
1立方分米=1升，1立方厘米=1毫升，1升=1000毫升。
13、长方体的体积=长×宽×高V =abh14、正方体的体积=棱长×棱长×棱长V =a×a×a15、长方体（或正方体）的体积=底面积×高=横截面×长V=Sh17、每相邻两个长度单位（除千米外）的进率都是10，每相邻两个面积单位之间的进率都是100，每相邻两个体积单位之间的进率都是1000。
18、正方体的棱长扩大n倍，表面积会扩大n 的平方倍，体积会扩大n 的立方倍。
第二单元分数乘法1、分数乘整数的意义与整数乘法的意义相同，是求几个相同加数的和的简便运算。
2、一个数乘分数表示求这个数的几分之几是多少，求一个数的几分之几是多少用乘法计算。
3、分数和分数相乘，用分子相乘的积作分子，分母相乘的积作分母。
2023【苏教版】小学六年级数学上册-【练习四】
苏教版六年级上册
1.计算下面长方体和正方体的体积。【选自教材P20 练习四 第1题】 9×6×5=270(cm3) 0.5×2.5×0.8=1(m3) 63=216(dm3)
2.一种冷藏车的车厢是长方体教材P20 练习四 第2题】
2×0.2×0.13=0.052(立方米)
答：长方体木料的体积是0.052立方米。
15.【选自教材P21 练习四 第15题】
376cm2 130dm2 0.62m2 96dm2
480cm3 100dm3 0.03m3 64dm3
16.一种长方体的煤气灶包装箱，长8分米，宽4分米，高1.5 分米。【选自教材P21 练习四 第16题】 （1）做这个包装箱至少要用多少平方分米硬纸板？是多少 平方米？
3.6 dm=（ 36 ）cm 3.6 dm2=（ 360 ）cm2 3.6 dm3=（ 3600）cm3
30 cm=（ 3 ）dm 600 cm2=（ 6 ）dm2 420 cm3=（ 0.42 ）dm3
11.【选自教材P21 练习四 第11题】 0.5 dm3=（ 500 ）cm3 8500 dm3=（ 8.5 ）m3 2.03 m3=（ 2030 ）dm3 6780 cm3=（ 6.78 ）dm3
18.一个花坛（如右图），高0.9米，底面是边长1.2米的正方 形，四周用木条围成。【选自教材P22 练习四 第18题】 （2）用泥土填满这个花坛，大约需要泥 土多少立方米？（木条的厚度忽略不计）
1.44×0.9=1.296(立方米)
答：大约需要泥土1.296立方米。
18.一个花坛（如右图），高0.9米，底面是边长1.2米的正方 形，四周用木条围成。【选自教材P22 练习四 第18题】 （3）做这样一个花坛，四周大约需要木 条多少平方米？
六年级上册数学月考试题-综合考练(2)-15-16江苏省苏教版
江苏省宿迁市沭阳县银河学校小学部六年级（上）月考数学试卷一、认真思考、对号入座（每题1分，共20分）1．一个正方体棱长5厘米，它的棱长总和是，表面积是，体积是．2．一根5米长的绳子对折、对折再对折，每一段是绳长的，每段长米．3．在下面的横线里填上适当的单位名称．一块橡皮的体积约是8；汽车的油箱大约能盛汽油50．4．5.04立方分米=立方厘米4.5升=立方厘米45平方米=平方分米800毫升=升．5．一个正方体的棱长总和是48厘米，它的表面积是平方厘米，体积是立方厘米．6．一个长方体方钢，横截面积是12平方厘米，长2分米，体积是立方厘米．7．一个长方体水箱，从里面量，底面积是25平方米，水深1.6米，这个水箱能装水升．8．把1.2米的长方体材料（如图），平均锯成3段，表面积比原来增加2.4平方分米，原来这根木料的体积是立方分米．9．把3个棱长是4厘米的正方体木块粘合成一个长方体，这个长方体的体积是立方厘米，表面积比原来的3个小正方体表面积的和减少平方厘米．10．一块长方体木材，长80厘米、宽20厘米、厚5厘米，若锯成最大的正方体木块（要求不能割补，不能浪费），可以锯成块，每块体积应是立方厘米．二、评判．（每题1分，共5分）11．正方体是由6个完全相同的正方形组成的图形．（判断对错）12．棱长是6厘米的正方体的表面积和体积相等．．（判断对错）13．一个长方体（不含正方体），最多有两个面面积相等．（判断对错）14．体积相等的两个正方体，它们的表面积相等．．（判断对错）15．加工一个油箱要用多少铁皮，是求这个油箱的体积．（判断对错）三、精挑细选．（每题1分，共5分）16．下面的图形中，折叠后能围成正方体的是（）A． B． C．D．17．一个正方体的棱长扩大3倍，体积扩大（）倍．A．3 B．9 C．2718．将若干个相同的小正方体拼成一个大正方体，至少需要（）个这样的小正方体．A．4 B．9 C．819．一个长方体水池，长20米，宽10米，深30分米，这个水池占地（）平方米．A．200 B．6000 C．580 D．60020．3个棱长是1厘米的正方体小方块排成一行后，它的表面积是（）A．18平方厘米B．14立方厘米C．14平方厘米D．16平方厘米四、计算．（第题8分、第二题18分、第三题8分，共34分）21．直接写出得数10﹣0.1= += 36×= 14﹣﹣=×20= ﹣= 3×= （+）×72=22．脱式计算，能简便的要简便计算27×﹣11 ﹣+﹣﹣++×16 +++×4+×4．23．计算下面长方体、正方体的表面积和体积．六、解决生活中的数学问题．（1～5题每题5分；第6题每题9分；）24．一个长方体铁块，长11分米，宽6分米，高5分米，每立方分米铁块重7.8千克，这个铁块重多少千克？25．一根铁丝，可以做成长8厘米，宽6厘米，高4厘米的长方体框架，如果用它来做一个正方体框架，做成的正方体框架棱长是多少厘米？26．一个无盖的长方体金鱼缸，长8分米，宽6分米，高7分米．制作这个鱼缸共需玻璃多少平方分米？这个鱼缸能装水多少升？（玻璃厚度忽略不计）27．有一个长20厘米、宽15厘米、高10厘米的长方体，里面盛有5厘米深的水．现在把一块石头浸没到水里，水面上升2厘米．这块石头的体积是多少立方厘米？28．有一个完全封闭的容器，里面的长是20厘米，宽是16厘米，高是10厘米，平放时里面装了7厘米深的水．如果把这个容器竖起来放，水的高度是多少？29．沭阳实验中学建一个长方体游泳池，长70米，宽30米，深2米．请你算一算．（1）游泳池的占地面积是多少平方米？（2）沿游泳池的内壁1.5米高处用白漆画一条水位线，水位线长多少米？（3）将这个游泳池注满水，大约能注水多少立方米？江苏省宿迁市沭阳县银河学校小学部六年级（上）月考数学试卷参考答案与试题解析一、认真思考、对号入座（每题1分，共20分）1．一个正方体棱长5厘米，它的棱长总和是60厘米，表面积是150平方厘米，体积是125立方厘米．【考点】长方体和正方体的表面积；长方体和正方体的体积．【分析】根据正方体的特征，12条棱的长度都相等，6个面的面积都相等，根据正方体的棱长总和=棱长×12，正方体的表面积公式：s=6a2，体积公式：v=a3，把数据代入公式解答即可．【解答】解：5×12=60（厘米）；5×5×6=150（平方厘米）；5×5×5=125（立方厘米）；答：它的棱长总和是60厘米，表面积是150平方厘米，体积是125立方厘米．故答案为：60厘米，150平方厘米，125立方厘米．2．一根5米长的绳子对折、对折再对折，每一段是绳长的，每段长米．【考点】简单图形的折叠问题；分数的意义、读写及分类．【分析】把一根绳子对折三次后，全长被平均分成了8份，根据分数的意义即可作答．【解答】解：把一根绳子对折三次后，全长被平均分成了8份，这时每段绳子是全长的；每段绳子长：5×=（米）．答：每段长米．故答案为：．3．在下面的横线里填上适当的单位名称．一块橡皮的体积约是8立方厘米；汽车的油箱大约能盛汽油50升．【考点】根据情景选择合适的计量单位．【分析】根据生活经验、对体积、容积单位和数据大小的认识，可知计量一块橡皮的体积约是8用立方厘米做单位；汽车的油箱大约能盛汽油50用升做单位；据此得解．【解答】解：一块橡皮的体积约是8 立方厘米；汽车的油箱大约能盛汽油50 升；故答案为：立方厘米，升．4．5.04立方分米=5040立方厘米4.5升=4500立方厘米45平方米=45000平方分米800毫升=0.8升．【考点】体积、容积进率及单位换算；面积单位间的进率及单位换算．【分析】把立方分米换算成立方厘米，乘以进率1000即可；高级单位升化低级单位立方厘米乘进率1000；把平方米换算成平方分米，乘以进率1000即可；把毫升换算成升，除以进率1000即可．【解答】解：5.04立方分米=5040立方厘米4.5升=4500立方厘米45平方米=45000平方分米800毫升=0.8升．故答案为：5040；4500；45000；0.8．5．一个正方体的棱长总和是48厘米，它的表面积是96平方厘米，体积是64立方厘米．【考点】长方体和正方体的表面积；长方体和正方体的体积．【分析】由正方体的特征可知：正方体有12 条棱长，且每条棱长都相等，于是可以求出正方体的棱长的长度，进而可以求出这个正方体的表面积和体积．【解答】解：48÷12=4厘米4×4×6=96平方厘米4×4×4=64立方厘米答：它的表面积是96平方厘米，体积是64立方厘米．故答案为：96；64．6．一个长方体方钢，横截面积是12平方厘米，长2分米，体积是240立方厘米．【考点】长方体和正方体的体积．【分析】根据长方体的体积公式：v=sh，把数据代入公式进行解答．【解答】解：2分米=20厘米，12×20=240（立方厘米），答：这个长方体的体积是240立方厘米．故答案为：240．7．一个长方体水箱，从里面量，底面积是25平方米，水深1.6米，这个水箱能装水40000升．【考点】长方体和正方体的体积．【分析】首先根据长方体的容积公式：v=sh，求出水箱的容积是多少立方米，再根据1立方米=1000升，换算成用升作单位即可．【解答】解：25×1.6=40（立方米），40立方米=40000升．答：这个水箱能装水40000升．8．把1.2米的长方体材料（如图），平均锯成3段，表面积比原来增加2.4平方分米，原来这根木料的体积是7.2立方分米．【考点】长方体和正方体的体积．【分析】把这个长方体平均锯成3段，需要锯2次，每锯一次就会多出2个长方体的横截面，由此可得锯成3段后表面积是增加了4个横截面的面积，由此可以求出横截面的面积是2.4÷4=0.6平方分米，再利用长方体的体积公式即可解答．【解答】解：1.2米=12分米，2.4÷4×12，=0.6×12，=7.2（立方分米），答：原来这根木料的体积是7.2立方分米．故答案为：7.2．9．把3个棱长是4厘米的正方体木块粘合成一个长方体，这个长方体的体积是192立方厘米，表面积比原来的3个小正方体表面积的和减少64平方厘米．【考点】长方体、正方体表面积与体积计算的应用．【分析】合成后长方体的体积应是原来小正方体体积的3倍，表面在粘合处少了4个，减少的面积就是这四个面．【解答】解：体积：4×4×4×3，=64×3，=192（立方厘米）；减少的表面积：4×4×4=64（平方厘米）故答案为：192，64．10．一块长方体木材，长80厘米、宽20厘米、厚5厘米，若锯成最大的正方体木块（要求不能割补，不能浪费），可以锯成64块，每块体积应是125立方厘米．【考点】简单的立方体切拼问题；长方体和正方体的体积．【分析】根据长方体切割正方体的方法可知：要使木块的体积最大，木料又不能有剩余，那么正方体木块的棱长应该是80、20和5的最大公因数，求出它们的最大公约数是5，然后根据锯出的总块数等于长宽高上锯成的块数的连乘积．由此即可解答．【解答】解：因为80、20和5的最大公约数是5，要使木块的体积最大，木料又不能有剩余，所以正方体木块的棱长应该是5厘米，（80÷5）×（20÷5）×（5÷5），=16×4×1，=64（块）；每一块的体积是：5×5×5=125（立方厘米），答：可以锯成64块，每一块的体积是125立方厘米．故答案为：64；125．二、评判．（每题1分，共5分）11．正方体是由6个完全相同的正方形组成的图形．×（判断对错）【考点】正方体的特征．【分析】根据正方体的特征可知：正方体是由6个完全相同的正方形围成的立体图形；据此判断．【解答】解：正方体是由6个完全相同的正方形围成的立体图形，而不是组成的立体图形；故答案为：×．12．棱长是6厘米的正方体的表面积和体积相等．×．（判断对错）【考点】长方体和正方体的体积；长方体和正方体的表面积．【分析】正方体的表面积和体积单位不相同，没法比较它们的大小，由此就解决即可．【解答】解：因为正方体的表面积和体积单位不相同，没法比较它们的大小，所以原题说法是错误的．故答案为：×．13．一个长方体（不含正方体），最多有两个面面积相等．×（判断对错）【考点】长方体的特征．【分析】长方体有6个面．有三组相对的面完全相同．一般情况下六个面都是长方形，特殊情况时有两个面是正方形，其他四个面都是长方形，并且这四个面完全相同，据此解答．【解答】解：由分析可知：长方体（不含正方体）最多有2个面是正方形，最多有4个面的面积相等；所以“一个长方体（不含正方体），最多有两个面面积相等”的说法是错误的．故答案为：×．14．体积相等的两个正方体，它们的表面积相等．√．（判断对错）【考点】长方体和正方体的体积；长方体和正方体的表面积．【分析】正方体的体积=棱长×棱长×棱长；正方体的表面积=棱长×棱长×6；根据正方体的体积公式可知，体积相等的两个正方体棱长一定相等，所以它们的表面积也相等，由此解决问题．【解答】解：根据正方体的体积公式可知，体积相等的两个正方体棱长一定相等，所以它们的表面积也相等．故答案为：√．15．加工一个油箱要用多少铁皮，是求这个油箱的体积．×（判断对错）【考点】长方体、正方体表面积与体积计算的应用．【分析】根据油箱的特点，加工一个长方体油箱要用多少铁皮，是求这个长方体的表面积，由此判断．【解答】解：加工一个油箱要用多少铁皮，是求这个油箱的表面积，而不是体积；原题说法错误．故答案为：×．三、精挑细选．（每题1分，共5分）16．下面的图形中，折叠后能围成正方体的是（）A． B． C．D．【考点】正方体的展开图．【分析】由平面图形的折叠及正方体的展开图解题．注意只要有“田”字格的展开图都不是正方体的表面展开图．【解答】解：A可以折叠成一个正方体，符合题意，B只要有“田”字格的展开图都不是正方体的表面展开图所以它折叠不成正方体，不符合题意，C围成几何体时，多了一个底面，少了一个侧面，所以不能围成正方体，不符合题意，D围成几何体时，有两个面重合，故不能围成正方体，不符合题意．故选：A．17．一个正方体的棱长扩大3倍，体积扩大（）倍．A．3 B．9 C．27【考点】长方体和正方体的体积．【分析】正方体的体积等于棱长的立方，它的棱长扩大几倍，则它的体积扩大棱长扩大倍数的立方倍，据此规律可得．【解答】解：正方体的棱长扩大3倍，它的体积则扩大33=27倍．故选：C．18．将若干个相同的小正方体拼成一个大正方体，至少需要（）个这样的小正方体．A．4 B．9 C．8【考点】简单的立方体切拼问题．【分析】要使所用的小正方体最少，那么大正方体的棱长最少可以由2个小正方体的棱长组成，由此即可求得小正方体的个数．【解答】解：要使所用的小正方体最少，那么大正方体的棱长最少可以由2个小正方体的棱长组成，所以使用的小正方体个数最少是：2×2×2=8（个）；故选：C．19．一个长方体水池，长20米，宽10米，深30分米，这个水池占地（）平方米．A．200 B．6000 C．580 D．600【考点】长方体、正方体表面积与体积计算的应用．【分析】水池的占地面积，就是这个长方体的底面积，根据长方体的底面积=长×宽代入数据求解．【解答】解：20×10=200（平方米）答：这个水池占地200平方米．故选：A．20．3个棱长是1厘米的正方体小方块排成一行后，它的表面积是（）A．18平方厘米B．14立方厘米C．14平方厘米D．16平方厘米【考点】长方体和正方体的表面积．【分析】3个棱长是1厘米的正方体小方块排成一行后，它的表面积减少了4个面积为1平方厘米的面，计算出原总面积减去即可．【解答】解：1×1×6×3﹣1×1×4，=18﹣4，=14（平方厘米）．故选：C．四、计算．（第题8分、第二题18分、第三题8分，共34分）21．直接写出得数10﹣0.1= += 36×= 14﹣﹣=×20= ﹣= 3×= （+）×72=【考点】小数的加法和减法；运算定律与简便运算；分数的加法和减法；分数乘法；分数除法．【分析】根据小数加减法和分数加减乘除法的计算方法解答，14﹣﹣根据减法性质进行简算，（ +）×72根据乘法分配律进行简算．【解答】解：10﹣0.1=9.9 +=36×=16 14﹣﹣=13×20=18 ﹣=3×=（+）×72=4122．脱式计算，能简便的要简便计算27×﹣11 ﹣+﹣﹣++×16 +++×4+×4．【考点】分数的四则混合运算；分数的简便计算．【分析】（1）先算乘法，再算减法；（2）根据加法交换律和结合律以及减法的性质进行简算；（3）按照从左向右的顺序进行计算；（4）先算乘法，再算加法；（5）根据加法交换律和结合律进行简算；（6）根据乘法分配律进行简算．【解答】解：（1）27×﹣11=15﹣11=4；（2）﹣+﹣/Ri466E4=（+）﹣（+）=1﹣1=0；（3）﹣+=+=；（4）+×16=+12=12；（5）+++=（+）+（+）=1+=1；（6）×4+×4=（+）×4=×4=．23．计算下面长方体、正方体的表面积和体积．【考点】长方体和正方体的体积；长方体和正方体的表面积．【分析】（1）根据正方体的表面积公式：s=6a2，体积公式：v=a3，把数据代入公式解答即可；（2）根据长方体的表面积公式：s=（ab+ah+bh）×2，体积公式：v=abh，把数据代入公式解答【解答】解：（1）8×8×6=64×6=384（平方厘米），8×8×8=64×8=512（立方厘米），答：这个正方体的表面积是384平方厘米，体积是512立方厘米．（2）12×4×4+4×4×2=48×4+16×2=192+32=224（平方分米），12×4×4=48×4=192（立方分米），答：这个长方体的表面积是224平方分米，体积是192立方分米．六、解决生活中的数学问题．（1～5题每题5分；第6题每题9分；）24．一个长方体铁块，长11分米，宽6分米，高5分米，每立方分米铁块重7.8千克，这个铁块重多少千克？【考点】长方体、正方体表面积与体积计算的应用．【分析】首先根据长方体的体积公式：v=abh，把数据代入公式求出铁块的体积，然后用铁块的体积乘每立方分米铁的质量即可．【解答】解：11×6×5×7.8=330×7.8=2574（千克），答：这个铁块重2574千克．25．一根铁丝，可以做成长8厘米，宽6厘米，高4厘米的长方体框架，如果用它来做一个正方体框架，做成的正方体框架棱长是多少厘米？【考点】长方体的特征；正方体的特征．【分析】首先根据长方体的棱长总和=（长+宽+高）×4，求出这个长方体的棱长总和，再根据正方体的棱长总和=棱长×12，用棱长总和除以12即可求出正方体的棱长．【解答】解：（8+6+4）×4÷12，=18×4÷12，=6（厘米），答：做成的正方体框架棱长是6厘米．26．一个无盖的长方体金鱼缸，长8分米，宽6分米，高7分米．制作这个鱼缸共需玻璃多少平方分米？这个鱼缸能装水多少升？（玻璃厚度忽略不计）【考点】长方体、正方体表面积与体积计算的应用．【分析】求需要的玻璃的面积，实际上是求长方体的表面积减去上盖的面积，长方体的长、宽、高已知，代入即可求解；再利用长方体的体积公式即可求出鱼缸的容积．【解答】解：（1）8×6+（8×7+6×7）×2，=48+（56+42）×2，=48+98×2，=48+196，=244（平方分米）；（2）8×6×7=336（立方分米）=336升；答：制作这个鱼缸共需玻璃244平方分米，这个鱼缸能装水336 升．27．有一个长20厘米、宽15厘米、高10厘米的长方体，里面盛有5厘米深的水．现在把一块石头浸没到水里，水面上升2厘米．这块石头的体积是多少立方厘米？【考点】长方体、正方体表面积与体积计算的应用．【分析】根据题意可知：长方体容器中上升部分水的体积等于这个石块的体积，根据长方体的体积是：v=abh，把数据代入公式解答即可．【解答】解：20×15×2=300×2=600（立方厘米），答：这块石头的体积是600立方厘米．28．有一个完全封闭的容器，里面的长是20厘米，宽是16厘米，高是10厘米，平放时里面装了7厘米深的水．如果把这个容器竖起来放，水的高度是多少？【考点】长方体和正方体的体积．【分析】平放和竖放容器内的水的体积没变，只是水在容器内体积的形状改变了；先求容器内水的体积，然后用体积除以竖放时容器的底面积，问题即可解决．【解答】解：20×16×7÷（16×10）=2240÷160，=14（厘米）；答：水的高度是14厘米．29．沭阳实验中学建一个长方体游泳池，长70米，宽30米，深2米．请你算一算．（1）游泳池的占地面积是多少平方米？（2）沿游泳池的内壁1.5米高处用白漆画一条水位线，水位线长多少米？（3）将这个游泳池注满水，大约能注水多少立方米？【考点】长方体、正方体表面积与体积计算的应用．【分析】（1）游泳池的占地面积就是这个长方体的底面积，用长乘上宽即可；（2）水位线的全长是这个泳池四壁这四个长方形长的和，也就相当于底面的周长，由此求解；（3）注满水时水的体积，也就是这个长方体的容积，根据长方体的容积（体积）的计算公式V=abh求解．【解答】解：（1）70×30=2100（平方米）答：游泳池的占地面积是2100平方米．（2）70×2+30×2=140+60=200（米）答：水位线全长200米．（3）70×30×2=4200（立方米）；答：大约能注水4200立方米．2016年8月24日。
苏教版小学数学六年级上册课后思考题
一个长方体，如果高增加2厘米，就变成一个正方体。
这时表面积比原来增加56平方厘米。
原来长方体的体积是多少立方厘米?考点：长方体和正方体的体积分析：由题意可知：高增加2厘米，就变成一个正方体．说明长方体的底面是正方形且高比底面边长少2厘米，这时表面积比原来增加56平方厘米．表面积增加的部分是高为2厘米的4个侧面的面积，由此可以求出一个侧面的面积，进而求出原来长方体的底面边长，再根据长方体的体积公式：V=abh，把数据代入公式解答．解答：底面边长：56÷4÷2=7(厘米)高：7−2=5(厘米)7×7×5=245(立方厘米)答：原来长方体的体积是245立方厘米。
分析：要使每条线上3个数的乘积都是1，即每三个分数的分子分母都能约分，观察这7个分数，分子有3个5，而分母只有15含有因数5，所以1615只能填在中间的○里，其它三个分子为5的分数，分在三条线上，然后再确定第三要填的数.解答：根据分析填图如下：分析：设小红原来有金鱼x 条，由“小明原来的金鱼比小红多8条”可知小明原来有（x+8）条，再由“小明把自己金鱼条数的1 5送给小红后，两人的金鱼条数同样多”列方程解答． 解答：设小红原来有金鱼x 条,则小明原来有(x +8)条(x +8)×(1−15)=x +(x +8)×1545x +325=x +15x +8525x =245x =12 x +8=12+8=20答：小红原来有12条，小明原来有20条。
分析：由于三角形的中线分对边的两部分相等，根据等底等高面积相等即可确定能把三角形的面积分成两个相等部分的三角形的线段是中线；要使两部分的面积是1：2，则连接三角形的一个顶点与对边的一个三等分点即可．解答：根据题干分析可得：(12-8) ÷2=2(千克)16÷2=8（元/千克）答：苹果的单价是8元/千克。
分析：根据“喜欢唱歌的有48×23=32（人），喜欢跳舞的有48×34=36（人）”可知：（32+36=68）人包括三部分，只喜欢唱歌的人数、只喜欢跳舞的人数、两种都喜欢的，所以既喜欢唱歌又喜欢跳舞的人数是：32+36-48=20（人），据此解答．解答： 48×23=32(人)48×34=36(人)32+36−48=68−48=20(人)答：既喜欢跳舞又喜欢唱歌的有20人。
苏教版-数学六年级上册-每日一题-思考题-doc
2021/3/11
21
9月26日思考题：买10个排球和4个篮球 共付510元，每个篮球比每个排球贵5元， 两种球的单价各是多少元？
2021/3/11
22
9月27日思考题：用大小相等的两个正方体拼成 一个长方体，这个长方体的棱长总和是80厘米， 每个正方体的体积是多少？
2021/3/11
23
9月28日思考题：把一根长40厘米的长方体木料 锯成3段，表面积比原来增加了24平方厘米，这 根木料原来的体积是多少？
2021/3/11
54
11月7日思考题：修一段公路，已修的长度是未修的 3/7，已修的长度比未修的少800米，这段公路全长多 少米？ （提示：根据已修的长度是未修的3/7，那么已 修的长度和未修的长度各有几份？已修的长度比未修 的长度少几份？）
2021/3/11
55
11月8日思考题：用一块30厘米的长方形铁皮，在它 的四个角各剪去一个边长3厘米的正方形，然后做成 一个容积是1008毫升的无盖长方体铁盒，原来铁皮的 宽是多少厘米？（请借助画图帮助理解题意）
2021/3/11
17
9月22日思考题：将一个长方体截下一个体积 800立方厘米的长方体后，剩下的正好是一个棱 长10厘米的正方体，原长方体的表面积是多少 平方厘米？
2021/3/11
18
9月23日思考题：一种液体饮料采用长方体塑封 纸盒密封包装，从外面量盒子长6厘米、宽4厘米、 10厘米，盒子上注明“净含量：240毫升”。你 觉得这个数据真实吗？请通过计算说明。
9月5日的思考题：甲、乙两车同时从A、B 两地相对而行，甲车每小时行80千米，乙 车每小时行100千米，两车在距中点60千米 处相遇。A、B两地相距多少千米？（可以 结合画线段图进行思考，必须先搞清楚快 车到底比慢车多行了多少千米呢？）
苏教版教材六年级数学上册思考题解析
苏教版六年级数学上册教材思考题解析1.（教材第9页）下图表示用棱长1厘米的正方体摆成的物体。
（1）从前面、上面和右面看到的分别是什么形状？试着画一画。
（2）这个物体的表面积是多少平方厘米？（3）如果添加同样的正方体，把这个物体补成一个大正方体，表面积至少是多少平方厘米？解析：（1）第（1）题从前面、上面和右面看到的图形如下所示。
（2）第（2）题这个物体的表面积就是从它的表面能数出的1平方厘米的小正方形的个数，而它表面含有的小正方形的个数正好等于从前面、上面和右面看到的图形中含有的正方形个数的和的2倍。
（7+7+6）×2=40（平方厘米）答：这个物体的表面积是40平方厘米。
（3）按要求补成的最小正方体的棱长是3厘米，所以表面积是：32×6=54（平方厘米）答：把这个物体补成一个大正方体，表面积至少是54平方厘米。
2.（教材第15页）你能根据正方体的体积来估计右边物体的体积吗？解析：要想知道右边的物体的体积，就要估一估右边的物体里面含有几个体积是1立方厘米的正方体。
上图右边的物体是一个不规则图形，我们可以根据上图左边的正方体的大小把右边的物体进行分割。
（如右图），从中可以看出题中的物体从上往下可以看作3层，每层有5个1立方厘米的正方体，体积大约是15立方厘米。
3.（教材第22页）一个长方体，如果高增加2厘米，就变成一个正方体。
这时表面积比原来增加56平方厘米。
原来长方体的体积是多少立方厘米？解析：如图，长方体的高增加2厘米，就变成了一个正方体，说明原来长方体的底面是正方形，即长方体的长和宽相等且等于现在正方体的棱长，原来长方体的高比宽均少2厘米。
表面积增加56平方厘米，其实增加的是上面高2厘米的那个小长方体的四个侧面的面积，而这四个侧面的面积完全相同。
56÷4=14（平方厘米），求出一个侧面积，再除以高2厘米，求出长为7厘米，原来长方体的宽为7厘米，高为7-2=5（厘米）。
最新版苏教版小学数学六年级上册总复习附答案解析
2022年12月11日小学数学作业学校:___________姓名：___________班级：___________考号：___________一、选择题1．下面（）图形沿虚线折叠后能围成正方体。
A．B．C．2．从A城到B城，甲车需要10小时，乙车需要8小时，乙车速度比甲车速度（）。
A．慢25%B．快25%C．慢20%3．一个三角形的三个内角的度数比是4∶5∶6，这个三角形是（）三角形。
A．锐角B．直角C．钝角4．算式2×3×4×（111234++）的正确结果是（）。
A．3B．24C．9D．265．某校六年一班有学生48人，这个班男、女生人数的比可能是（）。
A．5∶2B．7∶8C．6∶11D．9∶7二、填空题6．36千克的49是（），112米是（）米的2525升是34升的()()5 6米的()()是13米32千克比（）千克少15千克。
7．长方形菜地长与宽的比为3∶2，让菜地的长靠墙，这样围上篱笆需要140米，那么长方形菜地的长是________米，长方形菜地的面积是________平方米。
8．把一根长32米的铁丝平均截成5段，每段的长度是( )米，每段占这根铁丝的( )。
9．比16千克多14千克的是( )千克；16比( )的35少8。
10．把0.23∶4.6化成最简整数比是( )。
三、判断题11．因为231132⨯⨯=，所以1、23和32互为倒数。
( )12．足球降价10%和打九折出售，价格是一样的。
( )13．10千克减少110后，又增加110，这时是910千克。
( )14．3米的14与3个14米表示的长度相等，都是34米。
( )15．79的倒数比1小。
( )四、解答题16．比一比，再解答。
∶一件上衣，原价200元，现价160元。
现价比原价便宜了百分之几？∶一件上衣，现价160元，比原价降低了40元。
现价比原价便宜了百分之几？∶一件上衣，原价200元，现价比原价便宜了40元。
苏教版小学数学六年级上册课后思考题
一个长方体，如果高增加2厘米，就变成一个正方体。
这时表面积比原来增加56平方厘米。
原来长方体的体积是多少立方厘米?考点：长方体和正方体的体积分析：由题意可知：高增加2厘米，就变成一个正方体．说明长方体的底面是正方形且高比底面边长少2厘米，这时表面积比原来增加56平方厘米．表面积增加的部分是高为2厘米的4个侧面的面积，由此可以求出一个侧面的面积，进而求出原来长方体的底面边长，再根据长方体的体积公式：V=abh，把数据代入公式解答．解答：底面边长：56÷4÷2=7(厘米)高：7−2=5(厘米)7×7×5=245(立方厘米)答：原来长方体的体积是245立方厘米。
把34、56、57、54、98、1615、2116这七个数填入右边的◯里，使每条线上3个数的乘积都是1.考点：幻方分析：要使每条线上3个数的乘积都是1，即每三个分数的分子分母都能约分，观察这7个分数，分子有3个5，而分母只有15含有因数5，所以1615只能填在中间的○里，其它三个分子为5的分数，分在三条线上，然后再确定第三要填的数.解答：根据分析填图如下：小明和小红都养了一些金鱼,小明把自己金鱼条数的15送给小红后，两人的金鱼条数同样多。
已知小明原来的金鱼比小红多8条，小红和小明原来各有金鱼多少条?考点：[分数四则复合应用题]分析：设小红原来有金鱼x 条，由“小明原来的金鱼比小红多8条”可知小明原来有（x+8）条，再由“小明把自己金鱼条数的1 5送给小红后，两人的金鱼条数同样多”列方程解答． 解答：设小红原来有金鱼x 条,则小明原来有(x +8)条 (x +8)×(1−15)=x +(x +8)×15 45x +325=x +15x +85 25x =245x =12 x +8=12+8=20答：小红原来有12条，小明原来有20条。
把图中的三角形分成两部分，使它们的面积的比是1:1，你能分一分吗?如果要使两部分面积的比是1:2，那该怎样分呢?考点：图形的拆拼（切拼）分析：由于三角形的中线分对边的两部分相等，根据等底等高面积相等即可确定能把三角形的面积分成两个相等部分的三角形的线段是中线；要使两部分的面积是1：2，则连接三角形的一个顶点与对边的一个三等分点即可．解答：根据题干分析可得：(12-8) ÷2=2(千克)16÷2=8（元/千克）答：苹果的单价是8元/千克。
(精品试卷)新版苏教版小学数学(六年级上册)教案
第一单元长方体和正方体中预习一、教学目标：1、使学生通过观察、操作等活动认识长方体、正方体及其展开图，知道长方体和正方体的面、棱、顶点以及长、宽、高（棱长）的含义，掌握长方体和正方体的基本特征。
2、使学生通过动手实验和对具体实例的观察，了解体积（容积）的意义及其常用的计量单位，初步具有1立方米、1立方分米、1立方厘米实际大小的观念，会进行相邻体积单位的换算。
3、使学生在具体情境中，经历操作、猜想、验证、讨论、归纳等数学活动过程，探索并掌握长方体和正方体的表面积以及体积的计算方法，能解决与表面积和体积计算相关的一些简单实际问题。
4、使学生在活动中进一步积累空间与图形的学习经验，增强空间观念，发展数学思考。
5、使学生进一步体会图形学习与实际生活的联系，感受图形学习的价值，提高数学学习的兴趣和学好数学的自信心。
二、教学重点：通过观察、操作等活动认识长方体、正方体的面、棱、顶点以及长、宽、高（棱长）的含义，掌握长方体和正方体的基本特征以及表面积、体积的计算方法，能解决与表面积和体积计算相关的一些简单实际问题。
三、教学难点：在活动中进一步积累空间与图形的学习经验，增强空间观念，发展数学思考。
初步具有1立方米、1立方分米、1立方厘米实际大小的观念，探索并掌握长方体和正方体的表面积以及体积的计算方法。
四、课时安排：14课时第二单元分数乘法中预习一、教学目标：1、使学生理解分数乘法表示的意义,理解和掌握分数乘法的计算法则,并能比较熟练地计算分数乘法。
2、使学生理解求一个数的几分之几是多少的应用题的数量关系和解题思路,掌握解题方法。
3、使学生掌握分数乘法和加、减法的混合运算,理解整数乘法运算定律对于分数乘法同样适用,并能运用这些定律进行一些简便的运算，进一步提高计算能力。
4、使学生理解倒数的意义,掌握求倒数的方法,能熟练地求一个数的倒数。
二、教学重点：理解和掌握分数乘法的计算法则,并能比较熟练地计算分数乘法。
三、教学难点：运用这些定律进行一些简便的运算，进一步提高计算能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(9)两个长方体的高相等，且甲长方体的体积是乙长方体体积的4倍，如果两个长方体的底面都是正方形，那么，当甲长方体底面边长是4厘米时，乙长方体底面边长是( )厘米。
(10)一张边长20厘米的正方形商标纸正好贴满底面为正方形的食品盒的侧面，这个食品盒的容积是( )毫升。
(11)棱长为a的正方体，表面积是( )，把它切成两个长方体后，
表面积的和是( )。
(12)3个棱长为a的正方体拼成一个长方体，这个长方体的表面积是( )。
(13)有两个相同的正方体拼成一个长方体，这个长方体棱长的总和是48厘米，这个长方体的体积是( )立方厘米。
(14)把一个正方体分成相等的64个小正方体，表面积增加了( )倍。
(4)一个长方体的表面积是320平方厘米，上、下两个面是周长32厘米的正方形，长方体的体积是( )立方厘米。
(5)一个长方体的侧面积为72平方分米，高是4分米，底面长是宽的2倍。这个长方体的体积是( )立方分米。
(6)一段方钢长2米，横截面是周长为12厘米的正方形，这块方钢的体积是( )立方厘米。
(7)一只木箱高5分米，底面周长3米，下底面积是54平方分米，它的表面积是( )平方分米。
2.判断:
（）(1) a ＞a（）(2)长方体相邻两个面如果是正方形，这个长方体就成了正方体。（）(3)把棱长是a的正方体切成两个大小不等的长方体，它的表面积的
和是8a 。
（）(4)正方体的棱长扩大5倍，体积扩大15倍。（）(5)长方体的长、宽、高分别都缩小到原来的 ，表面积缩小到原来
的 。
（）(6)如果两个长方体的表面积相等，则它们的体积也相等。（）(7)一个长方体，底面周长是25厘米，高是5厘米，它的体积是125平
A. 2 B. 4 C. 8 D. 12
4.一个长方体的铁食品盒，如果围着它贴一圈商标纸(上下面不贴)，至少需要288平方厘米的长方形商标纸。已知食品盒的高是12厘米，底面为正方形，那么，做这个食品盒至少需要多少铁皮？它的容积是多少？
5.一个长方体水箱，底面为正方形，它的侧面展开是一个边长12分米的正方形，这个水箱最多能容水多少升？
(15)要拼成棱长8厘米的正方体，需要( )个棱长2厘米的正方体。
(16)一个正方体的表面积是54平方分米，如果棱长增加2分米，体积增加( )立方分米，表面积增加( )平方分米。
(17)一个长方体，如果高增加2厘米，就变成了一个正方体。表面积就增加48平方厘米，原长方体的表面积是( )平方厘米。
(18)一根长2.5米的长方体木料，把它锯成2段，表面积增加1.26平方分米，这根木料的体积是( )立方分米。
6.如图所示，一个长方体的底面是边长7厘米的正方形，
它的侧面积是500平方厘米，它的体积是多少立方厘米？
7.一个密封的长方体玻璃容器，里面装着水。从里面量，长20厘米，宽15厘
米,高10厘米，水深6厘米。如果把长方体的长20厘米，高10厘米的后侧
面作为底面放在桌子上，那么水深是多少厘米？
8.一个长方体，如果长减少2厘米，宽、高不变，它的体积减少48立方厘米；
A 40 B 50 C 80 D 400
②一个长方体木块，底面是边长1厘米的正方形，高7厘米，把它截成1立方厘米的小正方体，这7个小正方体的表面积之和比原来的长方体增加了( )平方厘米。A 49 B 42 C 12 D 7
③一个底面为正方形的长方体，如果切下一个正方体就剩下一个高4厘米的
长方体，表面积减少了36平方厘米。原长方体的表面积是( )平方厘米。A 40 B 102 C 66 D 96
④一个长方体的长、宽、高分别是a米、b米、h米，如果高增加3米后，新的长方体体积比原来增加( )立方米。
A. 3abh B. ab(h＋3) C. abh＋3 D. 3ab
又新的长方体的表面积比原来增加( )平方米。
A. 3ab B. 3(a＋b) C. 6ab D. 6(a＋b)
⑤长方体(不含正方体)最多有( )条棱长度相等，最少有( )条棱长度相等。
二、长方体和正方体
1.填空：
(1)正方体棱长之和为36厘米，它的体积是()立方厘米，表面积是( )平方厘米。
(2)一个长方体的棱长之和为36厘体的表面积是148平方厘米，已知这个长方体底面长6厘米，宽5厘米，这个长方体的高是( )厘米。
方厘米。
（）(8) 0.3 ＝0.27（）(9)正方体的体积是125立方厘米，它的棱长是5厘米。（）(10)用4个同样的正方体拼成一个大长方体，大长方体的表面积是
原来一个小正方体表面积的3倍。（）(11)如果长方体的表面积缩小到原来的 ，它的体积就缩小到原来
的 。
（）(12)把体积1立方分米的木块放在桌子上，木块占桌面的面积是1平
(22)用3个长4厘米，宽3厘米，高2厘米的同样的长方体，拼成一个表面积最大的长方体，这个大长方体的表面积是( )平方厘米。
(23)有36块棱长都为1厘米的正方体，当放成长( )厘米，宽a(24)把6个棱长2厘米的正方体拼成一个长方体，它的表面积最大是( )平方厘米。
(25)把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体，截成两个长方体，使这两个长方体的表面积之和最大，这时表面积之和是( )平方厘米。
(19)把一个长方体的小木块截成两段后，就变成两个完全相等的正方体，于是这两个正方体的棱长之和比原来长方体的棱长之和增加40厘米，原来长方体的长是( )厘米。
(20) b 是b的( )倍。b 是b的( )倍。
(21)用3个长3厘米，宽2厘米，高1厘米的同样的长方体，拼成一个表面积最小的长方体，这个长方体的表面积是( )平方厘米。
方分米。
（）(13)把体积8立方分米的正方体木块放在桌子上，木块占桌面的面积是4平方分米。
（）(14)棱长之和相等的两个长方体,它们的体积一定相等。
（）(15)正方体的棱长增加3倍，表面积就增加9倍。
3.选择：
①把一块长10厘米，宽8厘米，高5厘米的长方体木块，分割成棱长1厘米的小正方体木块，排成一排，这个长方体的长是( )厘米。