《高考风向标》2012年高考数学一轮复习 第九章 第5讲 数列的通项公式精品课件 理
【高考风向标】高考数学一轮复习 第九章 第1讲 数列的基本概念课件 文

解析:(1)该数列第 1,2,3,4 项的分母分别为 2,3,4,5,恰比项数 多 1.分子中的 22,32,42,52,恰是分母的平方,-1 不变,故它的一个 通项公式为 an=n+n+121-1.
(2)该数列各项符号是正负交替变化的,需设计一个符合因子 (-1)n,分子均为 1 不变,分母 2,6,12,20 可分解为 1×2, 2×3, 3×4, 4×5,则它的一个通项公式为 an=(-1)nnn1+1.
(3)∵0.9=1-0.1,0.99=1-0.01,0.999=1-0.001,0.999 9=
1-0.000 1,
又∵0.1=10-1,0.01=10-2,0.001=10-3,0.0001=10-4, ∴它的一个通项公式为 an=1-10-n. (4)∵这个数列前 4 项构成一个摆动数列,奇数项是 5,偶数
解析:∵a1-2=-1∉ N*,∴a2=3a1=3.∵a2-2=1=a1,
∴a3=3a2=9.∵a3-2=7,∴a4=7.∵a4-2=5,∴a5=5.∵a5-2 =3=a2,∴a6=3a5=15.
考点3 利用an 与Sn 的关系式求通项公式 例3:已知数列{an}的前 n 项和为 Sn.按照下列条件求数列的 通项公式.
已知数列的前几项求通项公式,主要从以下几个方面来考虑: ①负号用(-1)n与(-1)n+1(或(-1)n-1)来调节,这是因为n与 n+1奇偶交错;
②分数形式的数列,分子找通项,分母找通项,要充分借助 分子、分母的关系;
③对于比较复杂的通项公式,要借助于等差数列,等比数列(后 面专门学习)和其他方法解决;
函数的单调性与数列的单调性既有联系又有区别, 即数列所对应的函数单调,则数列一定单调,反之,若数列单调, 其所对应的函数不一定单调,关键是数列是定义域为正整数集的 特殊函数.所以,数列的单调性一般要通过比较an+1与an的大小 来判断,若an+1>an,则数列为递增数列,若an+1<an,则数列为递 减数列.解本题易出现的错误是由an是关于n的二次函数, 其定义域为正整数集,若数列{an}递增,则必有— k2 ≤1,故k≤2.
数列的通项公式课件高三数学一轮复习

−
= − ,
= − + =1,
所以 an=n.又 a1=1,满足通项公式,所以 an=n.
故答案为:n.
例7.已知数列{an}的前n项和为Sn.若a1=1,2Sn=an+1+1,
1 n-1
则Sn=___________.
2 (3 +1)
解析:∵a1=1,∴S1=a1=1,∵2Sn=an+1+1=Sn+1-Sn+1,
1
1
3
∴Sn+1=3Sn-1,即 Sn+1-2 =3Sn-2 =3Sn-2 ,
1
1
1
1
又 S1-2 =2 ,∴数列Sn-2 是首项为2 ,公比为 3 的等比数列,
1
1 n-1
1 n-1 1
1 n-1
∴Sn-2 =2 ·3 ,∴Sn=2 ·3 +2 =2 (3 +1).
=
=
C 1
A an
+
C 1
A an
B
A
+
B
A
六:形如a n +1 =
Aa n
Ba n + C
( A, B, C为常数) 的递推式
2
2an
n+1
例 若数列{an}满足 a1=1,an+1=
,则 an=________.
an+2
解析:因为 an+1=
所以
1
an+1
2an
,a1=1,所以 an≠0,
an+2
, =
− , ≥
方法规律总结
由 s n 求 a n 的步骤
第一步 令 n=1 得 a1
第二步 令 n 2 得 a n
高考风向标文科数一轮复习同步:第9章 第5讲 利用几类经典的递推关系式求通项公式

基础知识反馈卡·9.5时间:20分钟 分数:60分一、选择题(每小题5分,共25分)1.如图J9-5-1是关于星星的图案构成一个数列,该数列的一个通项公式是( )图J9-5-1A .a n =n 2-n +1B .a n =n (n -1)2C .a n =n (n +1)2D .a n =n (n +2)22.等差数列{a n }的公差d <0,且a 2·a 4=12,a 2+a 4=8,则数列{a n }的通项公式为( )A .a n =2n -2(n ∈N *)B .a n =2n +4(n ∈N *)C .a n =-2n +12(n ∈N *)D .a n =-2n +10(n ∈N *)3.设等比数列{a n }的公比q =2,前n 项和为S n ,则S 4a 3=( ) A .2 B .4 C.154 D.1744.已知各项均为正数的等比数列{a n },a 1a 2a 3=5,a 7a 8a 9=10,则a 4a 5a 6=( )A .5 2B .7C .6D .4 25.已知等差数列{a n }的公差为-2,且a 1+a 4+a 7+…+a 97=50,则a 3+a 6+a 9+…+a 99的值为( )A .-82B .82C .-132D .132二、填空题(每小题5分,共20分) 6.已知数列的通项a n =⎩⎨⎧3n +1 (n 为奇数),2n -2 (n 为偶数),则a 2·a 3=____. 7.等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若S n T n =3n +12n ,则a 11b 11等于________. 8.已知数列{a n }中,a 1=1,1a n +1=1a n+13,则a 10=________. 9.已知等差数列{a m }中,a m ≠0,若m >1且a m -1+a m +1-a 2m =0,S 2m -1=38,则m 等于________.6.__________ 三、解答题(共15分)10.设{a n}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110且a1,a2,a4成等比数列.(1)证明a1=d;(2)求公差d的值和数列{a n}的通项公式.基础知识反馈卡·9.51.C 2.D 3.C 4.A 5.A6.20 7.3221 8.14 9.1010.(1)证明:因a 1,a 2,a 4成等比数列,故a 22=a 1a 4.而{a n }是等差数列,有a 2=a 1+d ,a 4=a 1+3d .于是(a 1+d )2=a 1(a 1+3d ),即a 21+2a 1d +d 2=a 21+3a 1d .化简得a 1=d .(2)解:由条件S 10=110和S 10=10a 1+10×92d ,得到10a 1+45d =110.由(1)可知,a 1=d ,代入上式得55d =110,故d =2.a n =a 1+(n -1)d =2n .因此,数列{a n }的通项公式a n =2n ,(n ∈N *).。
高三一轮复习“求数列的通项公式”专题讲座

高三一轮复习“求数列的通项公式”专题讲座班级 姓名数列是高考中的重点内容之一,每年的高考题都会考察到,小题一般较易,大题一般较难。
而作为给出数列的一种形式 通项公式,在求数列问题中尤其重要。
数列通项公式直接表述了数列的本质,是给出数列的一种重要方法。
数列通项公式具备两大功能,第一,可以通过数列通项公式求出数列中任意一项;第二,可以通过数列通项公式判断一个数是否为数列的项以及是第几项等问题;因此,求数列通项公式是高中数学中最为常见的题型之一,它既考察等价转换与化归的数学思想,又能反映学生对数列的理解深度,具有一定的技巧性,是衡量考生数学素质的要素之一,求数列的通项公式是最近几年高考的热点内容之一,因而经常渗透在高考和数学竞赛中。
以下是归纳总结出的九种求解数列通项公式的方法,希望能对同学们的高三数列复习有所帮助。
一.不完全归纳法例1:求下列数列的通项公式(1)22—12 ,32—13 ,42—14 ,52—15,… (2)-11×2 ,12×3 ,-13×4 ,14×5,… (3)23 ,1,107 ,179 ,2611,… 解:(1)21)11n n a n +-=+( (2)a n = (-1)n n (n+1) (3) a n =n 2+12n +1 例2:根据数列的前4项,写出它的一个通项公式:(1)9,99,999,9999,…(2) ,17164,1093,542,211 (3) ,52,21,32,1 (4) ,54,43,32,21-- 解:(1)变形为:101-1,102―1,103―1,104―1,……∴通项公式为:110-=n n a (2);122++=n n n a n (3);12+=n a n (4)1)1(1+⋅-=+n n a n n . 评注:认真观察所给数据的结构特征,找出a n 与n 的对应关系,正确写出对应的表达式。
观察各项的特点,关键是找出各项与项数n 的关系。
《高考风向标》2012年高考数学一轮复习 第五章 第5讲 不等式的应用精品课件 理
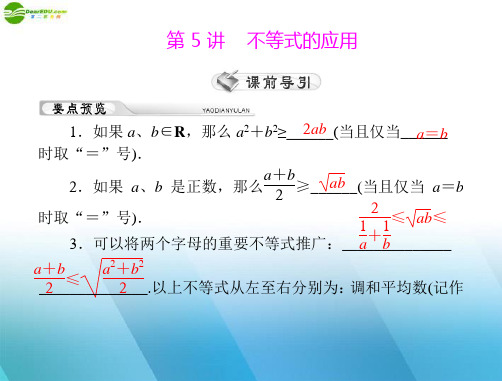
全程运输成本为 y=(a+bv2)vs=sbv+bav,v∈(0,c].
(2)依题意,有 s、b、a、v 都是正数. 因此 y=sbv+bav≥2s ab;
①若 值.
ab≤c,则当且仅当 v=bav⇒v=
的经营中,市场调研表明,该商店在经销这一产品期间第 n 天
1 的利润 an=215n
1≤n≤25 26≤n≤60
(单位:万元,n∈N*),记第 n
天的利润率 bn=前n天第投n入天的的资利金润总和,例如 b3=38+aa31+a2.
(1)求 b1、b2 的值; (2)求第 n 天的利润率 bn; (3)该商店在经销此纪品期间,哪一天的利润率最大?并
(2)方案①:年平均盈利为yx=-n-4n9+20
≤-2 n·4n9+20=6(万元). 当 n=7 时,年平均盈利最大, 若此时卖出,共获利 6×7+18=60(万元). 方案②:y=-n2+20n-49=―(n―10)2+51. 当且仅当 n=10 时,即该生产线投产后第 10 年盈利总额最 大,若此时卖出,共获利 51+9=60(万元). ∵两种方案获利相等,但方案②所需的时间长, ∴方案①较合算.
y=a4x+(14-x)·a2+2x+2×x126-14·a
=a74x+25x2-7=7a14x+3x6-1(0<x<14),
∵14x+3x6≥2 4x·3x6=6,当且仅当14x=3x6, 即 x=12 时取等号,此时 y≥35a, 即若 0<x<14,当 x=12 时总费用最少为 35a. (2)若 x≥14 时,则修旧墙的费用为 14·a4=72a 元, 建新墙费用为2x+2×x126-14·a, 故总费用为:y=72a+2x+2×x126-14·a =a2x+12x6-221(x≥14),
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【互动探究】 4.已知由正数组成的两个数列{an},{bn},如果an、an+1 是关于x的方程x2-2b2x+anbnbn+1=0的两根. n (1)求证:{bn}为等差数列; (2)已知a1=2,a2=6,分别求数列{an},{bn}的通项公 式.
解:(1)由an、an+1是关于x的方程x2-2b
2an 3.数列{an}中,a1=1,an+1= (n∈N*),则{an}的通 2+an 2 an = 项an=________. n+1
4.已知Sn是数列{an}的前n项和,log2(Sn+1)=n+1,则an
3 (n 1) n =_________. 2 (n 2)
5.已知数列{an}满足a1+3a2+3 a3+„+3 1 * an=3n(n∈N*) N ),则an的通项公式为____________.
Sn ∴数列 是以首- - (2)由(1)的结论可得 n =2n 1,∴Sn=n·n 1, 2 当n≥2时, an=Sn-Sn-1=n·n 1-(n-1)·n 2=2n 2(n+1). 2 2 由已知,a1=1,又当n=1时,2n 2(n+1)=1, ∴an=(n+1)2n 2(n∈N*). bn+1 bn+Sn bn+1 bn - * (3)由 = n (n∈N ),得 = n +2n 1, n+1 n+1 bn bn-1 - 由此式可得 n = +2n 2, n-1 bn-1 bn-2 - = +2n 3, n-1 n-2
(2)因为an=log2bn,∴3n+2=log2bn⇒bn=23n 2. bn+1 23n 5 ∴ b = 3n+2 =8,b1=32,所以{bn}是等比数列,首项为 2 n 321-8n 32 n 32,公比为8,故Tn= = 7 (8 -1). 1-8
+ +
【互动探究】
1.已知{an}是等比数列,对∀n∈N*,an>0恒成立,且 a1a3+2a2a5+a4a6=36,则a2+a5等于( D ) A.36 B.± 6 C.-6 D.6
S (1)求证:数列 n 为等比数列; n
(2)求数列{an}的通项公式及前n项和Sn; 1 bn+1 bn+Sn (3)若数列{bn}满足:b1=2, = n (n∈N*),求数列 n+1 {bn}的通项公式.
解析:(1)将an+1=Sn+1-Sn代入已知nan+1=(n+2)Sn, Sn+1 Sn 整理得 =2× n (n∈N*). n+1 S1 又由已知 1 =1,
2 两根得an+an+1=2bn,anan+1=anbnbn+1, 2 ∴2bn=bn-1bn+bnbn+1. 2 n
x+anbnbn+1=0的
∵bn>0,∴2bn=bn-1+bn+1(n>1),∴{bn}是等差数列.
2 (2)由(1)知2b1=a1+a2=8,∴b1=2,
∵a2=b1b2,∴b2=3,∴bn=n+1,∴bn-1=n, an=bn-1bn=n(n+1)(n>1). 又a1=2符合上式,∴an=n(n+1).
解析:∀n∈N*,an>0,a1a3+2a2a5+a4a6=(a2+a5)2= 36,∴a2+a5=6,故选D.
考点 2
应用迭加(迭乘、迭代)法求通项
例2:(1)已知数列{an}中,a1=2,an=an-1+2n- 1(n≥2),求数列{an}的通项公式; (2)已知Sn为数列{an}的前n项和,a1=1,Sn=n2·n,求数 a 列{an}的通项公式.
【互动探究】 2.已知数列{an}中,a1=2,(n+2)an+1-(n+1)an=0(n∈ N*),求数列{an}的通项公式.
an+1 n+1 解:由(n+2)an+1-(n+1)an=0得, a = . n+2 n an an-1 an-2 a3 a2 ∴an= · · · a · ·1 „· a a an-1 an-2 an-3 2 1 32 4 n n-1 n-2 = · · · 4·· „· 3 2= . n+1 n n-1 n+1
2
n-1
n an= 3 (n∈
考点 1 利用基本公式求数列的通项公式 例1:已知{an}是等差数列,其前n项和为Sn,已知a3=
11,S9=153. (1)求数列{an}的通项公式; (2)设an=log2bn,证明{bn}是等比数列,并求其前n项和Tn. a3=a1+2d=11 a1=5 解析:(1)由 ⇒ ⇒an=3n+2. S9=9a1+4d=153 d=3
n 2
(n≥2),
(n 1 )
.
(n 2 )
纠错反思: (1)求数列的通项公式要特别注意数列的首项,分清是第几项. (2)得到的结论Sn1 2an 1 只有在n≥2的条件下才能成立.
an1 3 a (3)当n≥2时, 成立,数列 n 不一定是等比数列. an 2
(4)正确利用数列的概念及公式解题. 【互动探究】 3.若数列{an}中,an=2n+3n,且数列 an 1-pan 为等比数
求数列通项常用数学思想有: (1)转化与化归思想;(2)整体(换元)思想;(3)方程思想.
- - - - -
„„ b3 b2 - = 2 +23 2, 3 b2 - =b1+22 2. 2 把以上各等式相加得, bn - - - - =2n 2+2n 3+„+23 2+22 2+b1. n 1 1 bn 1-2 ∵b1=2,∴ n = +2, 1-2 n n ∴bn=2(2 -1)(n∈N*).
第5讲
数列的通项公式
数列通项的常用方法 (1)利用观察法求数列的通项.
(n 1) S1 (2)利用公式法求数列的通项:①an= ; S n S n1 (n 2)
②等差数列{an}公式、等比数列{an}公式.
(3)应用迭加(迭乘、迭代)法求数列的通项: ①an+1=an+f(n);②an+1=anf(n). (4)构造等差、等比数列求通项: ①an+1=pan+q; ③an+1=pan+f(n); ②an+1=pan+qn; ④an+2=p·n+1+q·n. a a
解析:(1)方法一:(迭加法) ∵a1=2,an=an-1+2n-1(n≥2),∴an-an-1=2n-1. ∴an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+„+(a2-a1) n2n-1+1 +a1=(2n-1)+(2n-3)+(2n-5)+„+5+3+1= 2 =n2. 方法二:(迭代法) ∵a1=2,an=an-1+2n-1(n≥2), ∴an=an-1+2n-1=an-2+2(n-1)+2n-1 =an-3+2(n-2)+2(n-1)+2n-1 „
1.数列{an}的通项公式an=2n+5,则此数列是( A ) A.公差为2的等差数列 C.首项为2的等差数列 B.公差为5的等差数列 D.公差为n的等差数列
2.在数列{an}中,a1=2,a17=66,通项公式是项数 n 的一 次函数.则数列{an}的通项公式为____________. an=4n-2
+
列,求 p 的值.
解:∵数列{an+1-pan}为等比数列, ∴(an+1-pan)2=(an-pan-1)(an+2-pan+1), 将an=2n+3n代入上式并整理, 得(2-p)(3-p)×2n×3n=0, ∴p=2或p=3.
例4:已知数列{an}的前n项和为Sn,且a1=1, nan+1=(n+2)Sn (n∈N*).
(1)迭加法适用于求递推关系形如“an + 1 =an + f(n)”,迭乘法适用于求递推关系形如“an+1=an· f(n)”. (2)迭加法、迭乘法公式:①an=(an-an-1)+(an-1-an-2)+ (an-2-an-3)+„+(a2-a1)+a 1;②an= an an-1 an-2 a3 a2 · · · „· · ·1. a an-1 an-2 an-3 a2 a1
错源:使用公式an=Sn-Sn-1时未注意n≥2的条件 例3:已知Sn是数列{an}的前n项和,a1=1,Sn=2an+1-1. 求数列{an}的通项公式.
误解分析:解本题易出现的错误:(1)使用公式an=Sn-Sn-
1时未注意n≥2的条件;(2)对等比数列概念认识不够,只要式
an+1 子 a =q成立,就认为是等比数列;(3)数列{an}的首项为a2 n 时,仍然认为an是第n项.
=1+3+5+„+2(n-2)+2(n-1)+2n-1=n2, ∴an=n2. (2)∵a1=1,Sn=n2·n, a ∴当n≥2时,Sn-1=(n-1)2an-1, an n-1 ∴an=Sn-Sn-1=n an-(n-1) an-1⇒ = . an-1 n+1
2 2
a3 a 2 an an-1 an-2 ∴an= · · · a · ·1 „· a a an-1 an-2 an-3 2 1 n-1 n-2 n-3 21 = · · · 4·· „· 3 1 n+1 n n-1 2 = . nn+1
正解:由Sn=2an+1-1,得Sn-1=2an-1, an+1 3 则an=2an+1-2an,∴ a =2(n≥2). n a2 3 而a1=1,Sn=2an+1-1,得a2=1,a =1≠2,
1
∴数列{an}从第二项起是等比数列,
3 故有an=1× 2
1 ∴an= 3 n 2 2
