信号与系统4-1
信号与系统实验报告(一) 大二下

电气学科大类级《信号与控制综合实验》课程实验报告(基本实验一:信号与系统基本实验)姓名学号专业班号同组者1 学号专业班号同组者2 学号专业班号指导教师日期实验成绩评阅人综合实验和实验报告要求信号与控制综合实验,是集多门技术基础课程以及其它延伸课程理论于一体的综合性实验课程,需要综合多门学科理论知识和实验方法来体现,因此,实验目的不是简单的课程理论验证和练习,而是综合应用、研究开发、设计创新。
应采用尽可能好的设计,使所设计的电路和系统达到要实现的功能,步骤和方案自行拟定,实现对设计思路的实验验证。
完成多个实验项目的,应将实验内容整理综合后写成一份总报告,以利于锻炼整理归纳和总结能力,在总报告中以第二级标题形式依次写下所完成的实验项目、内容及实验设计过程。
实验报告按“题目、目录、正文(分所完成的各实验项目)、结论、心得与自我评价、参考文献”6个部分撰写;正文主要包括以下几个内容:任务和目标、总体方案设计(原理分析与方案设计特点,选择依据和确定)、方案实现和具体设计(过程)、实验设计与实验结果、结果分析与讨论。
(格式方面请注意:每个图应该有图号和图名,位于图的下方,同一图号的分图应在同一页,不要跨页;每个表应该有表号和表名,位于表的上方,表号表名与表(数据)也应在同一页,不要跨页;建议各部分题目采用四号黑体、设计报告内容文字采用小四号宋体)注:报告中涉及实验指导书或教材内容,只需注明引用位置,不必在报告中再加以阐述。
不得不加引用标记地抄袭任何资料。
每一基本实验部分按计划学时100分成绩计算(100%),需要完成60分的实验项目;实验报告、设计部分和创新研究内容另外计分(分别为10%、20%和10%)。
再按照学时比例与本课程其它部分实验综合成为总实验成绩。
每一部分实验均为:基本实验:0~60分,考核基本理论的掌握和基本操作技能、实验室道德规范;实验报告:0~10分,考核思考和总结表述能力;完成设计性实验:0~20分,评价设计能力;完成创新性实验:0~10分,鼓励创新。
南邮信号与系统B习题答案04

(3)
解:
s
s
2
a
2 2
a shatu (t ) 2 2 s a
由频域微分性:
d a 2as 2 tshatu(t ) 2 2 2 2 ds s a (s a )
s t shatu(t ) 由线性: 2 2 2 (s a ) 2a
4-7 用部分分式展开法求下 列函数的拉氏反变换。
1 2 3 原式 e t 2e 2t 3e 3t u t s 1 s 2 s 3
2s 4 (4) s s2 4
A Bs C 解:原式是真分式,可表示 为:原式 2 s s 4 2s 4 用遮挡法得: A 2 1 s 4 s 0
s 2 8s 10 (1) 2 s 5s 4
解:原式不是真分式,用长 除法将其分解为:
3s 6 原式 1 2 s 5s 4 3s 6 则f 0 lim s 2 3 t s 5s 4
平面,故f 存在:
由于原式的极点为 1、 4,均位于s平面的左半
s 1 1 2s 1 4 2 2s 5 Y s 2 2 s 4s 4 s 1 s 4s 4 s 22
设Y s
s 2
2
2s 5
2
s 22
A
B s 2
用遮挡法求系数 A: A s 2 Y s s 2 2s 5 s 2 6
4-3 已知f t F s ,求下列信号的拉氏变 换。
(2) e
解:
at
t f a
t f aF as a
精品文档-信号与系统分析(徐亚宁)-第4章

F2= s/(s^2+w0^2)
第4章 连续时间信号与系统的复频域分析
【例4-10】用MATLAB求解【例4-3】, 设τ=1 解 求解的代码如下: %program ch4-10 R=0.02; t=-2:R:2; f=stepfun(t, 0)-stepfun(t, 1); S1=2*pi*5; N=500; k=0:N; S=k*S1/N; L=f*exp(t′*s)*R; L=real(L);
本例中
和
的ROC均为
Re[s]>0,
极点均在s=0处。但
有一个s=0的零点,
抵消了该处的极点,相应地ROC扩大为整个s平面。
第4章 连续时间信号与系统的复频域分析 4.2.3 复频移(s域平移)特性
【例4-4】
, s0为任意常数 (4-12)
求e-atcosω0tU(t)及e-atsinω0tU(t)的象函数。
第4章 连续时间信号与系统的复频域分析
1. s 借助复平面(又称为s平面)可以方便地从图形上表示 复频率s。如图4-1所示,水平轴代表s Re[s]或σ, 垂直轴代表s的虚部,记为Im[s]或jω, 水平 轴与垂直轴通常分别称为σ轴与jω轴。如果信号f(t)绝 对可积,则可从拉氏变换中得到傅里叶变换:
f= exp(-t)+2*t*exp(-2*t)-exp(-2*t)
第4章 连续时间信号与系统的复频域分析
【例4-9】 用MATLAB求解【例4-2】 解 求解的代码如下:
%program ch4-9 syms w0t; F1=laplace(sin(w0*t)) F2=laplace(cos(w0*t))
(4-2)
山大信号与系统答案

第一章习题新闻来源:山东大学信息学院点击数:707 更新时间:2009-4-5 0:13 1—1 画出下列各函数的波形图。
(1)(2)(3)(4)1—2 写出图1各波形的数学表达式图1(1) (2)(3) 全波余弦整流(4) 函数1—3 求下列函数的值。
(1)(2)(3)(4)(5)1—4 已知,求,。
1—5 设,分别是连续信号的偶分量和奇分量,试证明1—6 若记,分别是因果信号的奇分量和偶分量,试证明,1—7 已知信号的波形如图2所示,试画出下列函数的波形。
(1)(2)图 21—8 以知的波形如图3所示,试画出的波形.图31—9 求下列各函数式的卷积积分。
(1),(2),1—10 已知试画出的波形并求。
1—11 给定某线性非时变连续系统,有非零初始状态。
已知当激励为时,系统的响应为时,系统的响应则为。
试求当初始状态保持不变,而激励为时的系统响1—12 设和分别为各系统的激励和响应,试根据下列的输入—输出关系,确定下列各⑴⑵(3)(4)第一章习题答案新闻来源:山东大学信息学院点击数:623 更新时间:2009-4-5 23:181-1 (1)(2)(3)(4)1-2(1)、(2)、或或(3)(4) =1-3(1)(2)(3)(4)(5)01-4 ,1-7 (1)(2)1-81-9(1)(2)1-101-111-12 (1)非线性、时不变系统。
(2)线性、时变系统。
(3)线性、时不变系统。
(4)线性、时变系统。
上一篇:没有上一篇资讯了下一篇:没有下一篇资讯了第二章习题新闻来源:山东大学信息学院点击数:412 更新时间:2009-4-9 22—1 已知给定系统的齐次方程是,分别对以下几种初始状态求解系1),2),3),2—2 已知系统的微分方程是当激励信号时,系统的全响应是,试确定系统的零输入2—3 已知系统的微分方程是该系统的初始状态为零。
1)若激励,求响应。
2)若在时再加入激励信号,使得时,,求系数。
(仅供参考)信号与系统第四章习题答案

e −sT
=
−sT
2 − 4e 2
+ 2e −sT
Ts 2
(f) x(t) = sin πt[ε (t)− ε (t − π )]
sin π tε (t ) ↔
π s2 + π 2
L[sin
πtε (t
−π
)]
=
L e jπt
− 2
e− jπt j
ε (t
−π
)
∫ ∫ =
1 2j
∞ π
e
jπt e−st dt
4.3 图 4.2 所示的每一个零极点图,确定满足下述情况的收敛域。
(1) f (t) 的傅里叶变换存在
(2) f (t )e 2t 的傅里叶变换存在
(3) f (t) = 0, t > 0
(4) f (t) = 0, t < 5
【知识点窍】主要考察拉普拉斯变换的零极点分布特性。 【逻辑推理】首先由零极点写出拉普拉斯变换式,再利用反变换求取其原信号,即可求取其收
= cosϕ eω0tj + e−ω0tj − sin ϕ eω0tj − e−ω0tj
2
2j
=
cos 2
ϕ
−
sin 2
ϕ j
e
ω0 t j
+
cosϕ 2
+
sin ϕ 2j
e −ω 0tj
F(s) =
L
cosϕ 2
−
sin ϕ 2j
eω0tj
+
cos 2
ϕ
+
sin ϕ 2j
e
−ω0
t
j
ε
(t
)
∫ ∫ =
信号与系统第四章习题参考答案13

《信号与系统》第四章习题参考答案4-1 解 (1)111()ataL es s a s s a -⎡⎤-=-=⎣⎦++ (2)[]2221221sin 2cos 111s s L t t s s s ++=+++++ (3)()2212tL te s -⎡⎤=⎣⎦+(4)[]21sin(2)4L t s =+,由S 域平移性质,得 ()21s i n (2)14tL e t s -⎡⎤=⎣⎦++ (5)因为1!nn n L t s +⎡⎤=⎣⎦,所以 []2211212s L t s s s++=+= 由S 域平移性质,得 ()()23121ts L t e s -+⎡⎤+=⎣⎦+(6)()2211cos sL at s s a -=-⎡⎤⎣⎦+,由S 域平移性质,得 (){}()2211cos ts L at e s s aβββ-⎡⎤-=-⎣⎦+++ (7)232222L t t s s ⎡⎤+=+⎣⎦ (8)732()327tL t es δ-⎡⎤-=-⎣⎦+ (9)[]22sinh()L t s βββ=-,由S 域平移性质,得()22sinh()atL e t s a βββ-⎡⎤=⎣⎦+-(10)由于()211cos ()cos 222t t Ω=+Ω 所以 222221111c o s ()22424ss L t s s s s ⎛⎫⎡⎤Ω=+∙=+ ⎪⎣⎦+Ω+Ω⎝⎭(11)()()()11111at t L e e a a s a s s a s βββββ--⎡⎤⎛⎫-=-= ⎪⎢⎥--++++⎣⎦⎝⎭ (12)由于()221cos()1ts L e t s ωω-+⎡⎤=⎣⎦++所以 ()()()221cos()1a t a s e L et s ωω--++⎡⎤=⎣⎦++(13)因为(2)(1)(1)(1)(1)(1)t t t te u t e t e e u t ------⎡⎤-=-+-⎣⎦且()(1)(1)2(1)(1)(1)11sst t e e L t eu t L eu t s s ------⎡⎤⎡⎤--=-=⎣⎦⎣⎦++所以 ()(1)(2)2211(2)(1)(1)11s t s s e L teu t e e s s s -----⎡⎤+⎡⎤-=+=⎢⎥⎣⎦+++⎣⎦(14)()(1)tL e f t F s -⎡⎤=+⎣⎦,由尺度变换性质,得(1)ta t L e f aF as a -⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦(15)()t L f aF as a ⎡⎤⎛⎫=⎪⎢⎥⎝⎭⎣⎦,再由s 域平移性质,得 []2()()at t L e f aF a s a aF as a a -⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦(16)31cos(6)cos (3)cos(3)2t t t -=∙13cos(9)cos(3)44t t =+32213cos (3)48149s s L t s s ⎡⎤=+⎣⎦++由s 域微分性质,得()()22322222213181327cos (3)481494819d s s s s L t t ds s s s s ⎡⎤--⎛⎫⎢⎥⎡⎤=-+=+ ⎪⎣⎦⎢⎥++⎝⎭++⎣⎦(17)[]2cos(2)4sL t s =+,连续两次应用s 域微分性质,有 []()2224cos(2)4s L t t s-=+,()3232224cos(2)4s sL t t s-⎡⎤=⎣⎦+(18)111atL es s a -⎡⎤-=-⎣⎦+,由s 域积分性质,得111111(1)at sL e ds t s s a ∞-⎛⎫⎡⎤-=- ⎪⎢⎥+⎣⎦⎝⎭⎰ln()ln ln s s a s s a ⎛⎫=+-=- ⎪+⎝⎭ (19)351135tt L ee s s --⎡⎤-=-⎣⎦++,由s 域积分性质,得 33111115ln 353t t s e e s L ds t s s s --∞⎛⎫⎡⎤-+⎛⎫=-= ⎪ ⎪⎢⎥+++⎝⎭⎣⎦⎝⎭⎰(20)()22sin aL at s a =⎡⎤⎣⎦+,由s 域积分性质,得()1122211sin 1arctan 21s s at s a s L ds d t s a a a s a π∞∞⎡⎤⎛⎫⎛⎫===-⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎛⎫⎣⎦+ ⎪⎝⎭⎰⎰ 4-2 解(1)因为()()sin ()2T f t t u t u t ω⎡⎤⎛⎫=--⎪⎢⎥⎝⎭⎣⎦()sin ()sin 22T T t u t t u t ωω⎡⎤⎛⎫⎛⎫=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以可借助延时定理,得()()sin ()sin 22T T L f t L t u t L t u t ωω⎧⎫⎡⎤⎛⎫⎛⎫=+--⎡⎤⎡⎤⎨⎬ ⎪ ⎪⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭⎣⎦⎩⎭222222221sT T s ee S S S ωωωωωω--⎛⎫=+=+ ⎪+++⎝⎭(2)因为()()()sin sin cos cos sin t t t ωϕωϕωϕ+=+ 所以()222222cos sin cos sin sin s s L t s s s ωϕϕωϕϕωϕωωω++=+=⎡⎤⎣⎦+++ 4-3 解此题可巧妙运用延时性质。
信号与系统--完整版答案--纠错修改后版本
1)
3)
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)5)
3.9、求图所示各系统的单位序列响应。
(a)
(c)
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)
4.34 某LTI系统的频率响应,若系统输入,求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入,求该系统的输出。
4.39 如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?
(1)如,求的频谱函数(或画出频谱图)。
(2)如,求的频谱函数(或画出频谱图)。
(1) (2) (3) (4) (5)
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知,试求下列函数的频谱:
(1)(3) (5)
(8)(9)
4下列方式求图4-25示信号的频谱函数 (1)利用xx和线性性质(门函数的频谱可利用已知结果)。
(1)
5-18 已知系统函数和初始状态如下,求系统的零输入响应。
(1),
(3),
5-22 如图5-5所示的复合系统,由4个子系统连接组成,若各子系统的系统函数或冲激响应分别为,,,,求复合系统的冲激响应。
5-26 如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。
5-28 某LTI系统,在以下各种情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。
(7)(8)
1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
信号与系统课后习题与解答第三章
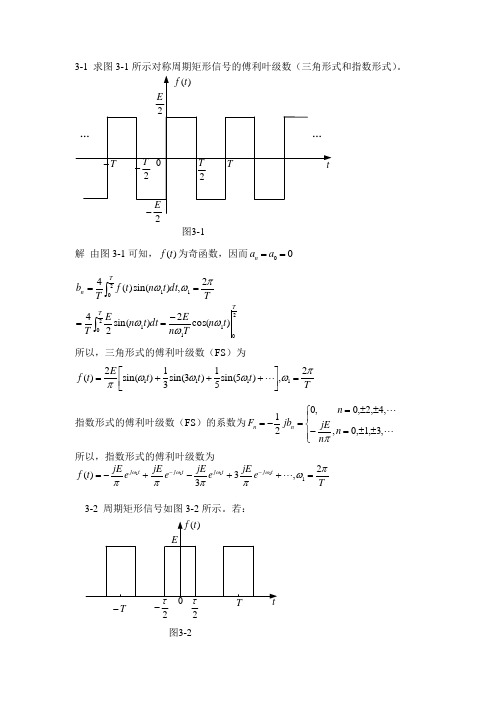
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∞ 1 ∞ & jnΩt A0 ∞ jnΩt & ∴ f (t) = ∑Ane = ∑Fne = + ∑An cos(nΩt −ϕn ) 2 n=−∞ 2 n=1 n=−∞ ∞ a0 ∞ = + ∑an cos nΩt + ∑bn sin nΩt 2 n=1 n=1
-2
y(t) =1 5 + 0.193sin( π t − 72.34°) + 0.022sin( 3π t −83.94°)) 0. R =1Ω x(t) y(t + 0.008sin( 5π t −86.36°) − −
-1
0
1
2
3
t
解:方法一:x(t)的傅里叶系数为(周期T=2, 基频ω1=2π/T=π)
第四章第1讲
12
例 3
解:
某线性非时变系统的幅频响应| (jω)|和相频响 某线性非时变系统的幅频响应|H(jω)|和相频响 应ϕ(ω)如图所示。若激励 f (t) =1+ ∑1 cosn t ,
n=1 ∞
n
求该系统的响应y(t)。 1 cos n t f (t) =1+ n=1 n |H(jω)| 1 2 =1+ cost + cos 2t +L 2 F( jω) = 2πδ(ω) +π[δ (ω +1) + δ (ω −1)] ω 2 -2 0 1 + π[δ (ω + 2) +δ (ω − 2)] +L 2
第四章第1讲 3
求解方法二
按电路分析中的方法:应用叠加定理 按电路分析中的方法: 将激励信号按傅里叶级数展开, 将激励信号按傅里叶级数展开, ∞ A f (t) = 0 + ∑An cos(nΩt −ϕn ) 2 n=1 令激励的各次谐波信号单独作用: 令激励的各次谐波信号单独作用: 直流分量激励 ⇒ 响应 r (t) 一次谐波分量激励 ⇒ 响应 r (t) 二次谐波分量激励 ⇒ 响应 r (t) 等 响应为: (t)=r (t)+… 响应为:r(t)=r0(t)+ r1(t)+ r2(t)+…
2 π 3π 5π
(计算过程见学习 1 2 2 2 指导书35面) x(t) = + sin π t + sin 3π t + sin 5π t +L
直流分量激励: y0 (t) = 0.5
R 1 2 & X1 = ⋅ = 0.193∠− 72.34° R + jωL 1+ jπ π π & & & 三次谐波分量激励:X1 = 2 ∠0° Y3 = R X3 = 1 ⋅ 2 = 0.022∠−83.94° R + j3ωL 1+ j3π 3π 3π & & 一次谐波分量激励: X1 = 2 ∠0° Y1 =
n n
写出响应y(t)的指数形式或三角函数形式的傅里叶级数, 即
∴ y(t) =
n=−∞
& ∑Y e
n
∞
jnΩt
= Y0 + 2∑Yn cos(nΩt −有效值:I = I0 + I12 + I2 +L ,或 U = U0 +U12 +U2 +L L L
总功率: P = P + P + P +L L 0 1 2 其中:P = U0I0 为直流分量的功率; 0 P =U1I1 cosϕ1 为一次谐波的功率;等。 1
第四章第1讲 8
+∞
频域系统函数
求法: 求法: 从系统的传输算子H 从系统的传输算子H(p)求,即H(jω)=H(p) | p=jω; (jω p=jω 从系统的单位冲激响应h 从系统的单位冲激响应h(t)求,即H(jω)=F [h(t)] ; (jω 根据正弦稳态分析方法从频域电路模型按H(jω 根据正弦稳态分析方法从频域电路模型按H(jω)的定 义式求。 义式求。 用实验方法求。 用实验方法求。 H(jω)可实现的条件: (jω 可实现的条件: 在时域中必须满足当t<0 在时域中必须满足当t<0时,h(t)=0,即系统必须是 因果系统。 因果系统。 在频域中,其必要条件是| (jω)|≠0 在频域中,其必要条件是| H(jω)|≠0,即必须满足佩 利-维纳准则。 利-维纳准则。
奇 n2 n为 数 a0 =1, an = 0, bn = π (计算过程见学习指导书35面) 偶 0 n为 数
系统传输函数 H( jω) =
1 1 1 H = ∠− arctg(nπ ) 即: ( jnω1) = 2 1+ jnω 1+ jω 1+ (nπ ) 1 1 1+ (nπ )
2
3 1 −2 t −t 所以: rzs1(t) = ( − 2e + e )ε (t) 2 2 3 1 −2 t −t 零状态响应为: rzs (t) = rzs1(t) − rzs1(t −1) = ( − 2e + e )ε (t) 2 2 3 1 −2 (t −1) −(t −1) − ( − 2e + e )ε (t −1) 2 2
第四章第1讲 11
例
2
s +3 (令s=jω),激励 2 s + 3s + 2
设系统的系统函数为 H(s) =
e(t)=ε(t)-ε(t-1) ,求零状态响应。
1 解: e1(t) = ε (t) ⇔ E1( jω) = πδ(ω) + jω
jω + 3 1 RZS1( jω) = H( jω)E1( jω) = π (ω) + δ jω ( jω +1)( jω + 2) 3 1 3 −2 2 δ = π (ω) + + + 2 2 jω jω +1 jω + 2
2 2 Q sgn t ⇔ , 根据对称性: ⇔ 2π sgn( −ω) = −2π sgn(ω) jω jt 1 ∴ ⇔ − jπ sgn(ω) 即有:H(jω)=F [h(t)]=-jsgn(ω) t 故得:R(jω)=H(jω) H(jω)E(jω)= [-jsgn(ω)][-jsgn(ω)]E(jω) =-sgn(ω)sgn(ω)E(jω)=-E(jω)
第四章第1讲 6
§2 非周期信号激励下的零状态响应
基本思想 全响应=零输入响应+零状态响应
n
时域分析: r(t) = ∑Cje
j =1 n
j =1
λj t
+ h(t) ∗e(t)
频域分析:rzi (t) = ∑Cje 零状态响应的求法如下:
e(t)
λj t
零输入响应的求法与时域一样。
rzs (t) = h(t) ∗e(t)
用正弦稳态分析的方法求正弦稳态传输函数H(jnΩ)。
& Yn & H 其定义为: ( jnΩ) = & 式中, Yn为响应y(t)中第n次谐波 Fn
(ω=nΩ) 的复数振幅(即相量)。
第四章第1讲 2
求解方法一
& 求响应y(t)中第 n 次谐波(ω=nΩ) 的复数振幅(即相量) Yn , & & 即 Y = H( jnΩ)F
∑
∞
ϕ(ω) π -2 0 -π 2 ω
该信号通过系统后,其响应的频谱为:
Y( jω) = H( jω)F( jω) =| H( jω) | F( jω) e jϕ(ω) ={4πδ(ω) +π[δ (ω +1) + δ (ω = 4πδ(ω) +π[δ (ω +1) + δ (ω
−j ω −1)]e 2
1 jω + 3 RZS ( jω) = H( jω)E( jω) = 1+ ( jω +1)( jω + 2) jω + 3 1 1 1 = + − jω + 3 jω +1 jω + 2
零状态响应为: rzs (t) = (e−3 t + e−t − e−2 t )ε (t)
h(t)
傅里叶变换
E( jω) H( jω)
傅里叶反变换
Rzs ( jω) = H( jω)E( jω)
其中:H(jω)=F[h(t)] 称频域系统函数。则h(t)=F -1[H(jω)]
第四章第1讲 7
频域系统函数
定义 设系统激励e(t)的傅里叶变换为E(jω),系统零状态 响应rzs(t) 的傅里叶变换为Rzs(jω), 则定义频域系统函数为: H( jω) = Rzs ( jω)
−j ω −1)]}e 2
π
π
傅里叶反变换即可得: y(t) = 2 + cos(t − ) = 2 + sin t 2
第四章第1讲 13
π
例
4
在如图所示系统中,e(t)为已知激励 , (t) = 1 。求零状态响 h πt 应 r(t)。 e(t) r(t) h(t) h(t) 解:设 e(t)⇔E(jω)
所以:r(t)= -e(t) 可见此系统为一反相器。
第四章第1讲 14
例
5
如图所示系统,已知f (t)的傅里叶变换F(jω 如图所示, 如图所示系统,已知f (t)的傅里叶变换F(jω)如图所示, 子系统的H(jω)=jsgn(ω 子系统的H(jω)=jsgn(ω)。求零状态响应 y(t)。 y(t)。 cos4t
