《非线性系统分析与控制》资料教材
合集下载
第七章 非线性控制系统分析
x0>1 x0<1
x(t)
1
x0et x0 x0et
不稳定的平衡状态
小范围稳定的平衡状态 t
起始偏离小——系统可能稳定 起始偏离大——系统可能不稳定
2. 自激振荡 在没有外界周期变化信号的作用下，系统
内产非生线的性具二有阶固系定统振: 幅x和2频(1 率的x2)稳x 定x周0期运(动，0)
返
回
3. 频率响应
在正弦信号的作用下，输出常常有倍频 和分频等谐波分量。
7.1.3 非线性系统的分析与设计方法
1. 相平面法
相平面法是基于时域的一种图解分析方法
2. 描述函数法
本
节 返
描述函数法是基于频域的等效线性化的图
回
本 解分析方法，是线性理论中频率法的一种推广。
章
返
回
7.4 描述函数法
常用的分析非线性系统的谐方波法线有性两化 种： 描述非函线数性法特性的描述函数 相典平型面非法线性特性的描述函数
改变线性部分的参数 或对线性部分进行校正
改变非线性特性 非线性特性的应用
本 章 返 回
■ 改变线性部分的参数或对线性部分进行校正
本 节 返
W (s)s[s(T m s K 1 m )( T K s1 m )(T s1 )]
回
本 章 返 回
■ 改变非线性特性
本 节 返 回 本 章 返 回
N0(X)——基准描述函数 K0——非线性特性尺度函数
本 节 返 回
K 0W (j )N 0(X ) 1 K0W(j)N01(X)
本 章
1 ——基准负倒描述函数
返 回
N 0(X)
非线性系统稳定条件： -1/N 0(X)曲线不被K 0W(j)曲线包围。
非线性控制系统分析课件
特点
非线性系统的行为复杂，难以用线性 系统的理论和方法进行分析和设计。
分类与比较
分类
根据非线性的性质，非线性控制系统可以分为连续时间非线性控制系统和离散时间非线性控制系统。
比较
连续时间非线性控制系统和离散时间非线性控制系统在分析和设计上有较大的差异。
常见非线性控制系统示例
描述：以下是一些常见的非线性控制系 统示例，包括电气系统、机械系统、化 工系统等。
非线性控制系统设
04
计
控制器设计
线性化设计方法
将非线性系统在平衡点附近线性 化，然后利用线性系统的设计方 法进行控制器设计。
反馈线性化设计方
法
通过引入适当的非线性反馈，将 非线性系统转化为线性系统，然 后进行控制器设计。
滑模控制设计方法
利用滑模面的设计，使得系统状 态在滑模面上滑动，并利用滑模 面的性质进行控制器设计。
相平面法
总结词
一种通过绘制相平面图来分析非线性系统动态特性的方法。
详细描述
相平面法通过将系统的状态变量绘制在二维平面上，直观地展示系统的动态行为，如极限环、分岔等。这种方法 适用于具有两个状态变量的系统。
平均法
总结词
一种通过将非线性系统的动态特性平均 化来简化分析的方法。
VS
详细描述
平均法通过在一定时间范围内对非线性系 统的动态特性进行平均，将非线性系统简 化为一个平均化的线性系统。这种方法适 用于具有周期性激励的非线性系统。
线性系统稳定性分析方法
通过求解特征方程或使用劳斯-赫尔维茨判 据等方法，可以判定线性系统的稳定性。
非线性系统稳定性分析
要点一
非线性系统的特性
非线性系统不具有叠加性和时不变性，其响应会受到初始 状态和输入信号的影响。
非线性系统的行为复杂，难以用线性 系统的理论和方法进行分析和设计。
分类与比较
分类
根据非线性的性质，非线性控制系统可以分为连续时间非线性控制系统和离散时间非线性控制系统。
比较
连续时间非线性控制系统和离散时间非线性控制系统在分析和设计上有较大的差异。
常见非线性控制系统示例
描述：以下是一些常见的非线性控制系 统示例，包括电气系统、机械系统、化 工系统等。
非线性控制系统设
04
计
控制器设计
线性化设计方法
将非线性系统在平衡点附近线性 化，然后利用线性系统的设计方 法进行控制器设计。
反馈线性化设计方
法
通过引入适当的非线性反馈，将 非线性系统转化为线性系统，然 后进行控制器设计。
滑模控制设计方法
利用滑模面的设计，使得系统状 态在滑模面上滑动，并利用滑模 面的性质进行控制器设计。
相平面法
总结词
一种通过绘制相平面图来分析非线性系统动态特性的方法。
详细描述
相平面法通过将系统的状态变量绘制在二维平面上，直观地展示系统的动态行为，如极限环、分岔等。这种方法 适用于具有两个状态变量的系统。
平均法
总结词
一种通过将非线性系统的动态特性平均 化来简化分析的方法。
VS
详细描述
平均法通过在一定时间范围内对非线性系 统的动态特性进行平均，将非线性系统简 化为一个平均化的线性系统。这种方法适 用于具有周期性激励的非线性系统。
线性系统稳定性分析方法
通过求解特征方程或使用劳斯-赫尔维茨判 据等方法，可以判定线性系统的稳定性。
非线性系统稳定性分析
要点一
非线性系统的特性
非线性系统不具有叠加性和时不变性，其响应会受到初始 状态和输入信号的影响。
自动控制原理第八章非线性控制系统分析
第八章非线性控制系统分析l、基本内容和要求（l）非线性系统的基本概念非线性系统的定义。
本质非线性和非本质非线性。
典型非线性特性。
非线性系统的特点。
两种分析非线性系统的方法——描述函数法和相平面法。
（2）谐波线性化与描述函数描述函数法是在一定条件下用频率特性分析非线性系统的一种近似方法。
谐波线性化的概念。
描述函数定义和求取方法。
描述函数法的适用条件。
（3）典型非线性特性的描述函数（4）用描述函数分析非线性系统非线性系统的一般结构。
借用奈氏判据的概念建立在奈氏图上判别非线性反馈系统稳定性的方法，非线性稳定的概念，稳定判据。
（5）相平面法的基本概念非线性系统的数学模型。
相平面法的概念和内容。
相轨迹的定义。
（6）绘制相轨迹的方法解析法求取相轨迹；作图法求取相轨迹。
（7）从相轨迹求取系统暂态响应相轨迹与暂态响应的关系，相轨迹上各点相应的时间求取方法。
（8）非线性系统的相平面分析以二阶系统为例说明相轨迹与系统性能间的关系，奇点和极限环的定义，它们与系统稳定性及响应的关系。
用相平面法分析非线性系统，非线性系统相轨迹的组成。
改变非线性特性的参量及线性部分的参量对系统稳定性的影响。
2、重点（l）非线性系统的特点（2）用描述函数和相轨迹分析非线性的性能，特别注重于非线性特性或线性部分对系统性能的影响。
8-1非线性控制系统分析1研究非线性控制理论的意义实际系统都具有程度不同的非线性特性，绝大多数系统在工作点附近，小范围工作时，都能作线性化处理。
应用线性系统控制理论，能够方便地分析和设计线性控制系统。
如果工作范围较大，或在工作点处不能线性化，系统为非线性系统。
线性系统控制理论不能很好地分析非线性系统。
因非线性特性千差万别，无统一普遍使用的处理方法。
非线性元件(环节)：元件的输入输出不满足(比例+叠加)线性关系，而且在工作范围内不能作线性化处理(本质非线性)。
非线性系统：含有非线性环节的系统。
非线性系统的组成：本章讨论的非线性系统是，在控制回路中能够分为线性部分和非线性部分两部分串联的系统。
非线性控制系统PPT课件
32
1. 210时
z2 cz12 1
●当t→∞时， e1t 0,e2t 0
● e2t比 e1t较 快 趋 于 零 ， 称λ2为快特征值，λ1为慢特征值
称V2为快特征向量，V1为慢特征向量
●当z1>1时，z2变化快，曲线斜率>1，当z1<1时，z2变化慢， 曲线斜率<1.
dz2 dz1
c2 1
z1(2
第一种情况 两个特征值都为实数，1 2 0
线性坐标变换： zM1x
z1 z2
1
z1
2
z2
z1 1z1 z2 2z2
zz1 2eJrt zz1 20 0e1t
z10 e2tz20
z1 (t ) z10e1t z2 (t) z20e2t
z 2 c z 1 2 1 , c z 2 0(z 1 0 )2 1
● 以上模型有一组平衡点 ● 以上模型等式右边的函数是状态变量的不连续函数。
当x2>0时以上模型简化为线性模型：
x1 x2
x2
k m
x1
c m
x2
k g
当x2<0时以上模型简化为线性模型：
x1 x2
x2
k m
x1
c m
x2
k g
20
1.2.4 负阻振荡器
h ( ) 满足以下条件： h (0 )0 , h '(0 )0 h (v) 当 v , h (v) 当 v
无摩擦单摆系统：
x1 x2 x2 10 sin x1
所有轨线或解的曲线称为系统的相图。 30
2.1 线性系统的特性
线性系统： xAx
解：
x(t)M exp(Jrt)M 1x0
1. 210时
z2 cz12 1
●当t→∞时， e1t 0,e2t 0
● e2t比 e1t较 快 趋 于 零 ， 称λ2为快特征值，λ1为慢特征值
称V2为快特征向量，V1为慢特征向量
●当z1>1时，z2变化快，曲线斜率>1，当z1<1时，z2变化慢， 曲线斜率<1.
dz2 dz1
c2 1
z1(2
第一种情况 两个特征值都为实数，1 2 0
线性坐标变换： zM1x
z1 z2
1
z1
2
z2
z1 1z1 z2 2z2
zz1 2eJrt zz1 20 0e1t
z10 e2tz20
z1 (t ) z10e1t z2 (t) z20e2t
z 2 c z 1 2 1 , c z 2 0(z 1 0 )2 1
● 以上模型有一组平衡点 ● 以上模型等式右边的函数是状态变量的不连续函数。
当x2>0时以上模型简化为线性模型：
x1 x2
x2
k m
x1
c m
x2
k g
当x2<0时以上模型简化为线性模型：
x1 x2
x2
k m
x1
c m
x2
k g
20
1.2.4 负阻振荡器
h ( ) 满足以下条件： h (0 )0 , h '(0 )0 h (v) 当 v , h (v) 当 v
无摩擦单摆系统：
x1 x2 x2 10 sin x1
所有轨线或解的曲线称为系统的相图。 30
2.1 线性系统的特性
线性系统： xAx
解：
x(t)M exp(Jrt)M 1x0
非线性控制系统分析
第一张
上一张 下一张 最后一张
结束授课
非线性系统响应还有其他与线性 系统不同的现象,无法用线性系统的 理论来解释。在一些情况下,引入某 些非线性环节,使系统获得比线性系 统更为优异的性能。实际上大多数智 能控制都属于非线性控制范畴。
应当明确指出的是：非线性系统 分析中不能使用叠加原理,也不能使用 线性系统分析中传递函数、频率特性 数学模型。
上一张 下一张 最后一张
结束授课
三、自持振荡
线性二阶系统只在阻尼比=0时给予阶跃作用，将产生周期性响应过程, 这时系统处于临界稳定状态。
实际上,一旦该系统参数发生微小变化,该周期性状态就无法维持,要么 发散至无穷大,要么衰减至零。
而非线性系统在没有外作用时,有可能产生频率和振幅一定的稳定周期 性响应。该周期响应过程物理上可实现并可保持,通常将其称为自持振荡或 自振荡,如下图所示。
但当系统的非线性特征明显且不能进行线性化处理时，就必须采用非 线性系统理论来分析。这类非线性称为本质非线性。
第一节 非线性系统的基本概念
如果一个控制系统包含一个或一个以上具有非线性特性的元件或环节, 则此系统即为非线性系统。
如系统不能进行线性化处理，或其时域响应不能用线性微分方程（一 般只能用非线性微分方程来描述,具有非线性数学模型）来描述,则称为非 线性系统，或称为本质非线性系统。这样的系统有以下特点：
如果自振荡的幅值在允许范围内, 按照李雅普诺夫关于稳定性的定义,系 统是稳定的。
自振荡是人们特别感兴趣的一个问 题,对它的研究有很大的实际意义。在 多数情况下,正常工作时不希望有振荡 存在,必须设法消除它。但在某些情况 下,特意引入自振荡,使系统有良好的稳 态、暂态性能。
第一张
上一张 下一张 最后一张
第8章-非线性系统分析
假若平衡点在坐标原点时得：
令：
方程组可改写为
特征方程
线性化方程组
在一般情况下，线性化方程在平衡点附近的相轨迹与非线性系统在平衡点附近的相轨迹具有同样的形状特征。但是，若线性化方程求解至少有一个根为零，根据李雅普诺夫小偏差理论，不能根据一阶线性化方程确定非线性系统平衡点附近的特性，此时，平衡点附近的相轨迹要考虑高阶项。
(1) 无阻尼运动（=0） 此时系统特征根为一对共轭虚根，相轨迹方程变为
对上式分离变量并积分，得
式中，A为由初始条件决定的积分常数。
初始条件不同时,上式表示的系统相轨迹是一族同心椭圆，每一个椭圆对应一个等幅振动。在原点处有一个平衡点(奇点)，该奇点附近的相轨迹是一族封闭椭圆曲线，这类奇点称为中心点。
图8-1 无阻尼二阶线性系统的相轨迹
(2)欠阻尼运动（01） 系统特征方程的根为一对具有负实部的共轭复根,系统的零输入解为 式中,A、B、为由初始条件确定的常数。时域响应过程是衰减振荡的。
可求出系统有一个位于相平面原点的平衡点（奇点），不同初始条件出发的相轨迹呈对数螺旋线收敛于该平衡点，这样的奇点称为稳定焦点。
5．李雅普诺夫法 李雅普诺夫法是根据广义能量函数概念分析非线性系统稳定性。原则上适用所有非线性系统，但对大多数非线性系统，寻找李雅普诺夫函数相当困难，关于李雅普诺夫法在现代控制理论中作祥解。 6．计算机辅助分析 利用计算机模拟非线性系统，特别上采用MATLAB软件工具中的Simulink来模拟非线性系统方便且直观，为非线性系统的分析提供了有效工具。
例1：确定非线性系统的奇点及附近的相轨迹。
解：令
求得奇点（0，0），（-2，0）。
即
由
（1）奇点（0，0） 线性化方程为
特征根
令：
方程组可改写为
特征方程
线性化方程组
在一般情况下，线性化方程在平衡点附近的相轨迹与非线性系统在平衡点附近的相轨迹具有同样的形状特征。但是，若线性化方程求解至少有一个根为零，根据李雅普诺夫小偏差理论，不能根据一阶线性化方程确定非线性系统平衡点附近的特性，此时，平衡点附近的相轨迹要考虑高阶项。
(1) 无阻尼运动（=0） 此时系统特征根为一对共轭虚根，相轨迹方程变为
对上式分离变量并积分，得
式中，A为由初始条件决定的积分常数。
初始条件不同时,上式表示的系统相轨迹是一族同心椭圆，每一个椭圆对应一个等幅振动。在原点处有一个平衡点(奇点)，该奇点附近的相轨迹是一族封闭椭圆曲线，这类奇点称为中心点。
图8-1 无阻尼二阶线性系统的相轨迹
(2)欠阻尼运动（01） 系统特征方程的根为一对具有负实部的共轭复根,系统的零输入解为 式中,A、B、为由初始条件确定的常数。时域响应过程是衰减振荡的。
可求出系统有一个位于相平面原点的平衡点（奇点），不同初始条件出发的相轨迹呈对数螺旋线收敛于该平衡点，这样的奇点称为稳定焦点。
5．李雅普诺夫法 李雅普诺夫法是根据广义能量函数概念分析非线性系统稳定性。原则上适用所有非线性系统，但对大多数非线性系统，寻找李雅普诺夫函数相当困难，关于李雅普诺夫法在现代控制理论中作祥解。 6．计算机辅助分析 利用计算机模拟非线性系统，特别上采用MATLAB软件工具中的Simulink来模拟非线性系统方便且直观，为非线性系统的分析提供了有效工具。
例1：确定非线性系统的奇点及附近的相轨迹。
解：令
求得奇点（0，0），（-2，0）。
即
由
（1）奇点（0，0） 线性化方程为
特征根
第八章 非线性控制系统分析PPT课件
2x(t)sinntd(t)
0
直流分量 n次谐波
Xn (An2Bn2)1/2
narctan(An/Bn)
描述函数的定义
e(t)Asint
x(t)X1sin(t1)
N中(在A基正) =波弦N输分(入A量)下和e，j∠输非N(入A线) 信=性XA号环1 e的节j1复的数B稳1比态Aj输A称1出 为非线性环节的描述函数
N (A )2 M A 1 (m A )2 h1 (A h)2 j2 M A 2(m h 1 )
上节重点内容回顾
描述函数的定义
e(t)Asint
x(t)X1sin(t1)
N中(在A基正) =波弦N输分(入A量)下和e，j∠输非N(入A线) 信=性XA号环1 e的节j1复的数B稳1比态Aj输A称1出 为非线性环节的描述函数
x(t)=Asinωt
死区非线性环节的描述函数
19
典型非线性特性的描述函数
2. 饱和特性的描述函数
x(t)
x(t)
0
π
2π
Kk
a
e(t) 0 ψ
ωt
0
A e x( t )
ψ
π 2π ωt
e(t)Asint
kAsint 0t
ቤተ መጻሕፍቲ ባይዱ
x(t) ka
t,Aa,Asina
kAsint t
N(A )2 k arcsina Aa A1(a A)2 ,Aa
x(t)A 1co stB 1sint X1sin(t1)
A11X021x=(t)cAos12+tdB( 12t) B 11 a1rc0t2gABx(11t)sintd(t)
负倒 描述函数
r e N(A) x G(s)
第7章非线性控制系统分析自动控制原理课件
本章将介绍的分析非线性控制系统的相平面法和描 述函数法, 是在非线性控制系统满足一定的条件下, 将 线性控制理论的某些内容给以扩充和变通后得出的, 因 此具有一定的局限性.
7-3相平面法
1. 相平面法的基本概念
所谓相平面法, 是一种二阶微分方程的图解法. 此
法即可用于线性二阶系统, 也可用于线性部分是二阶的
率为-1的直线, 见下图. •
e
0.2 p2 0.1
0.1
0
0.2
0.8
p1
特定的相轨迹为 p1 p2
1 p0
e
0
区域 :
•
e
d
•
e/ de
•
e
•
0.8 e
0.8 /(
1)
•
相轨迹与区域 类似, 但所有相轨迹均趋向于 e 0.8
直线, 见下图.
•
e
0
p3
0.8
0.2 p2 0.1 0
•
4m0 0.8 e 0.2 or e 0,e 0.1
区域 :
•
•
•
••
e
d
e
de d
e
•
e
d
e
dt dt de de
•
•
e
d
e
•
e
0.8
de
•
•
令 d e/ de, 则 e 0.8 /( 1)等倾线为一组平
•
行于 e 轴的直线. 当 0时, e 0.8
•
相轨迹为一组平行的曲线, 所由相轨迹均趋向于e 0.8
x
x0 ,
•
x
•
x0
情况下的
•
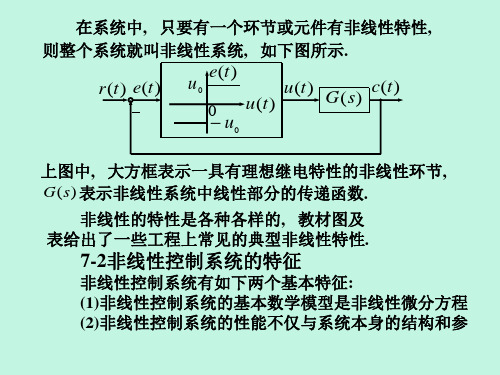
7-3相平面法
1. 相平面法的基本概念
所谓相平面法, 是一种二阶微分方程的图解法. 此
法即可用于线性二阶系统, 也可用于线性部分是二阶的
率为-1的直线, 见下图. •
e
0.2 p2 0.1
0.1
0
0.2
0.8
p1
特定的相轨迹为 p1 p2
1 p0
e
0
区域 :
•
e
d
•
e/ de
•
e
•
0.8 e
0.8 /(
1)
•
相轨迹与区域 类似, 但所有相轨迹均趋向于 e 0.8
直线, 见下图.
•
e
0
p3
0.8
0.2 p2 0.1 0
•
4m0 0.8 e 0.2 or e 0,e 0.1
区域 :
•
•
•
••
e
d
e
de d
e
•
e
d
e
dt dt de de
•
•
e
d
e
•
e
0.8
de
•
•
令 d e/ de, 则 e 0.8 /( 1)等倾线为一组平
•
行于 e 轴的直线. 当 0时, e 0.8
•
相轨迹为一组平行的曲线, 所由相轨迹均趋向于e 0.8
x
x0 ,
•
x
•
x0
情况下的
•
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
的解。因此，二次型性能指标的线性最优控制问题 称为LQR问题，即线性· 二次型· 黎卡梯问题。
非线性系统分析与控制
U
B
BU
(t ) X
A
X (t )
C
Y(t )
KX (t )
K * R 1BT P*
P*
ห้องสมุดไป่ตู้
解：PA A TP PBR 1BTP Q 0
线性二次型最优控制系统结构图
1、冯纯伯 等《非线性控制系统分析与设计》 2、曹建福 等《非线性系统理论及应用》 3、斯洛廷，李卫平译《应用非线性控制》
非线性系统分析与控制
第一章 绪论
线性系统与非线性系统的主要区别： 1.线性系统满足叠加原理，非线性系统不满足； 2.一般来说对于非线性系统不能求得完整的解，只能定 性分析； 研究非线性控制的理由： 1. 改进现有的控制系统； 2. 硬非线性特性分析； 3. 对模型不确定处理； 4. 设计简化。 §1.1 控制理论发展概述 一、古典控制理论 1.数学模型理论；2.响应分析；3.稳定性分析； 4.综合校正。
三、非线性控制理论
有一部分系统可以在基本满足工程需要的条件下 将其在某一平衡点处加以近似线性化； 也有一些系统，在分析它的大干扰稳定性与动态 品质时，就不宜把它近似地作为线性系统处理； 现代非线性科学所揭示的大量有意义的事实，例 如分叉、混沌、奇异吸引子等，均远远超过人们 熟知的非线性系统的自振现象，无法用线性系统 理论来解释。 非线性控制系统的研究几乎是与线性系统平行的， 并已经提出了许多具体方法，如相平面法、描述 函数法、绝对稳定性理论、Lyapunov稳定性理论、 输入输出稳定性理论等。
统，分析该平衡点的稳定性； 2）Lyapunov第二方法。
2.极限环
非线性系统能够在没有外激励时产生固定幅值和固定周 期的振荡，这种振荡叫极限环或自激振荡。
例 ：描述范德堡方程 的二阶微分方程（质量-弹簧-阻尼 器系统）为： 2c( x 2 1) x kx 0 m x
c 和 k 为正常数，分析该系统的特点） （ m、 • 非线性系统的极限环不同于线性系统的临界稳定或持 续振荡。 • 极限环代表了非线性系统的一种重要现象，分有害和 有益两种情况，应分别对待。
对于一个给定的线性系统，提出一个性能指标， 其一般表达式为
J (XT (t )QX(t ) UT (t ) RU(t ))dt
0
* U 问题是：要找出状态反馈规律 (X(t)) ，使得上式
给出的性能指标达到极值，这种控制称为最优 控制。 从数学上来看，就是在状态方程约束条件下求泛 函 J [X(t ), U(t )]的条件极值问题，这是一个典型的 条件变分法问题。条件变分问题中的欧拉 - 拉 格朗日（ Euler-Lagrange）方程是解决线性二 次型最优控制问题的基础。
非线性系统分析与控制
《非线性系统分析与控制》
研究生课程：32学时 授课教师：王印松
非线性系统分析与控制
主要教学内容
• • • • • 第一部分：非线性系统的主要特征； 第二部分：李雅普诺夫分析方法； 第三部分：现代稳定理论 第四部分：非线性系统的反馈线性化 第五部分：非线性系统的自适应控制 主要参考书：
d n y(t ) d n1 y(t ) h t , y(t ), y(t ), , , u (t ), t 0 n n 1 dt dt 可写成向量微分方程的形式：
(t ) f [t , x(t ), u (t )], t 0 x
上述微分方程代表最一般化的非线性控制系统的方程。如果 函数与 t 无关，则称此系统为自治的，否则称为非自治的。 在许多控制系统中输入量 u(t ) 可以从函数 f 中分列出来， 系统方程可写成以下形式： (t ) f [t , x(t )] B(t , x)u(t ), t 0 x 这类系统为仿射非线性系统。
结论分析： x0 1 系统收敛于由线性模型确定的稳定的平衡点； x0 1 系统快速地发散（有限时间逃逸问题）。
非线性系统分析与控制
100
50
0
-50
-100
-150
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
t/s
初值条件：由右到左依次为1.2,1.5,1.8,2.5
非线性系统分析与控制
例2. 线性化可以改变系统的结构，有可能变成不可控系统。
1 cos x3 x x 2 sin x3 3 x 0
0 u1 0 u2 1
某一机器人运动系统；在 x3 (t ) 0 点线性化后有：
1 1 0 x u1 x 2 0 0 u 2 x 0 1 3
特点：独特的建模方法 若有一自变量为时间
t 的函数 x(t )，使得积分
0
条件下，根据拉氏变换定义可得到
d k x (k ) st 是绝对收敛的；在初始条件为零的 e dt k dt
这样，可把由常系数线性常微分方程描述的线 性系统转换为传递函数描述。
d k x(t ) d k x(t ) st k L e dt s X ( s) dtk 0 dtk
ax x 3 0 x
当
a 由正变负时，一个平衡点分裂为三个点
（x e 0, a , a ），这表明系统的动态特性的质变，
a 0 为一临界分叉值。
4.混沌
1）混沌的解释：由确定性方程（内因）直接得到的具 有随机性的运动状态。或者说，混沌是具有随机性的非 周期性振荡。 2）混沌对初始条件非常敏感，即初始条件的微小差别 常常使轨道按指数形式分开（蝴蝶效应）。 3）混沌是一种确定性运动：无周期而有序、已发现三 条通向混沌的道路、Feigenbaum普适常数、有界性和 对初值具有很强的敏感性。 4）具有通常确定性运动所没有的统计和几何特征： 5）局部不稳定而整体稳定、无限自相似、连续功率谱、 奇怪吸引子分维数、正的Lyapunov特征指数、正测度 熵等。
* U 结论为：线性二次型最优控制规律 是状态变量
的线性函数，即
U * K * X(t )
K * 为最优增益矩阵，其表达式为
K * R 1 B T P * K *为常数矩阵；上式中 P *为黎卡梯 对线性定常系统， （Riccati）矩阵方程
AT P PA PBR1 B T P Q 0
状态空间建模理论与方法 ：将能够唯一地确定系统动力学 行为的最小的一组变量 x1 (t ), x2 (t ),, xn (t )
定义为系统的一组状态变量集合或状态向量
x(t ) x1 (t ), x2 (t ),, xn (t ) 以每一个状态变量 xi (t )为轴所形成的 n 维欧氏空间 R n 定义 为状态空间。 现代控制理论的建模方法要求用 n个一阶常微分方程所组 成的方程组去描述一个 n 阶的线性动态系统。其数学模 型的标准形式为：
特点：1、以一阶线性自变量对时间的微分方程组来对 系统进行描述的，其数学模型与分析方法是时域的； 2、所用到的数学工具主要是线性常微分方程理论与 线性代数理论； 3、它的建模理论与数学方法使得这种控制理论体系 适应于线性多输入多输出系统； 4、它建立了一整套最优控制设计原理与方法，使得 所求得的控制规律能保证系统性能指标达到极值； 5、对于参数可能在较大范围内变化的线性系统，最 优控制设计方法与线性系统参数辨识技术相结合，可 得到自适应的或称之为自动寻找最优点的控制系统。
T
(t ) AX(t ) BU(t ) X Y(t ) CX(t )
上式称为：线性动态系统的状态空间方程。
非线性系统分析与控制
• 所有线性动态系统的数学模型都可归结为上式 所示的矩阵形式的状态方程；矩阵代数（线性 代数）中的几乎所有方法都可以用来对线性动 态系统的各个问题，如可控性问题、动态品质 问题、稳定性问题、参数辨识问题以及综合校 正（即控制系统的设计问题）等问题进行分析 和研究 。 • 线性最优控制 （最有影响的分支之一）
例：分析下面非线性系统
0.1x x 5 6 sin t x (0) 4.01 (0) 4 和 x(0) 3.01, x 在初值分别为 x(0) 3, x
的特征。
4
3
2
1
0
-1
-2
-3
0
10
20
30
40
50
60
70
80
90
100
§1.4 非线性控制理论在电力系统中 的应用现状
非线性系统分析与控制
•近似线性化局限性的例题分析
例1.
(t ) x(t ) x 2 (t ) x x(0) x0
(t ) x(t ) x x(t ) x0 exp(t )
关于稳定的平衡点 x(t ) 0 ，近似线性化系统及其解可描述 为： 原系统的解：
x0 exp(t ) x(t ) 1 x0 x0 exp(t )
2、非线性系统近似线性化建模方法的局限性
近似线性化建模：在某一平衡点处加以近似线性化，从而得 到原非线性系统近似线性化的数学模型---传递函数或线性 状态方程； 要求：当非线性函数在所研究的区域内没有间断点并在所选 择的平衡点附近没有多值关系或者急剧的曲折时，允许进行 近似线性化。 实质：就是在某一选定的系统平衡点处以非线性函数的全微 分代替其增量。 工程设计中广泛采用的原因有： 1、非线性控制系统在平衡状态附近工作，近似线性化所得 到的模型可以满足需要； 2、利用线性控制理论成熟地综合校正与设计方法； 3、线性系统的反馈是状态变量或输出量的线性函数，其控 制规律易于实现。