透视式、纽曼投影式与费歇尔投影式的相互转化方法
构象间的转换
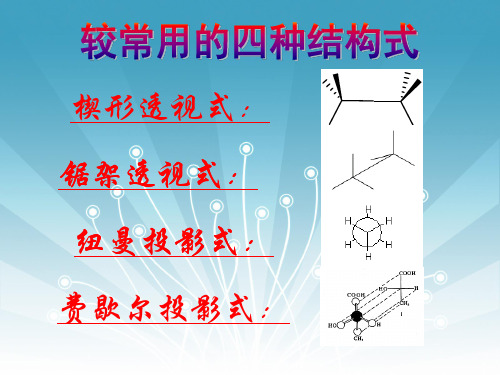
单键可以自由旋转,分子中的原子或基团 围绕单键旋转时,可以产生不同空间排布方 式,即产生不同的构象,再根据构象进行各 种结构式的转换。
H
1 CHO 2
H OH
1CHO 2
OH
H H
OH OH
3 2 4 CH2OH OHC 1
H 3
OH
=
3 H HOCH2 4 OH
4 CH2OH
眼睛由此从下向上看
由楔形式写费歇尔投影式
[1] 东北师大等五院校合编.《有机化学》(第三版) 北京:高等教育出版社,1993 [2] 邢其毅等.《基础有机化学》(第二版) 北京:高等教育出版社,1992 [3] 王积涛等.《有机化学》(第二版) 天津: 南开大学出版社,2003 [4] 邢其毅主编.《基础有机化学示范教学》 北京:北京大学出版社,1983 [5] 叶秀林.《立体化学》 北京:高等教育出版社,1982
2
OH
=
3 H OH HOCH2 4 (2)
OH CHO 1
4 CH2OH (1)
H 2
4 HOCH2 (3)
1 CHO
OH
1800 HO
2 H
3
OH
CHO 1
H
3
OH
HOCH2 4 (4) 重叠式构象
HOCH2 4 (5) 交叉式构象
1 CHO 1 CHO H HO 2 3 H 4 CH2OH 4 CH2OH (1) (2) OH H 3 HO OH 2 H
4 CH2OH ⑴
4 CH2OH ⑵
把分子立体模型放在眼前,从C-C单键的延长线上 观察,用圆心表示前面的碳原子,用圆表示后面的 0 碳原子,分别从圆心和圆上引出三条互为120 的射线 作为价键,用以连接碳原子上的三个原子或基团。
Newman投影式与Fischer投影式的转换

H O 3 H H 3 O H H 3 O H H O 3 H C 2 H 5 C 2 H 5 C 2 H 5 C 2 H 5
( 2 S , 3 S ) - 2 , 3 - 戊 二 醇 ( 2 R , 3 R ) - 2 , 3 - 戊 二 醇 ( 2 S , 3 R ) - 2 , 3 - 戊 二 醇 ( 2 R , 3 S ) - 2 , 3 - 戊 二 醇
Newman投影式与Fischer投影式的转换
根据Fischer投影式的投影规则, Fischer投影式描述的立体构 象,是Newman投影式的重叠式构象, 在 由 Newman 投 影 式 转 换 为 Fischer 投 影 式 的 过 程 中 , 当 Newman投影式为交叉式构象时,须将交叉式构象转换为重 叠式构象。
竖线基团 基团的位置关系是“横前竖后”
练习书上习题3-17
答案
①在平面内交换两个基团,变为对映体。 ②在平面上旋转90或270o,变为对映体 ③在平面内交换三个基团,构型不变。 ④在纸平面上旋转 180°,保持不变。
C H 3 C H 3 C H 3 C H 3 H 2 O H H O 2 H H 2 O H H O 2 H
构象异构体与构型异构体
• 构象异构是指在构造不变的前提下单键旋转,导致 原子或原子团的空间相对位置改变的现象。例如 交叉式和重叠式.
• 构型异构就是原子或原子团连的位置不同,不是由 单键旋转造成的。像手性分子就属于构型异构。
• 有时需要同时兼顾分子构象和构型, • 构象用Newman投影式表示, • 而涉及手性碳原子的构型则用Fischer投影式表示
构象透视式、纽曼投影式与费歇尔投影式的相互转化方法
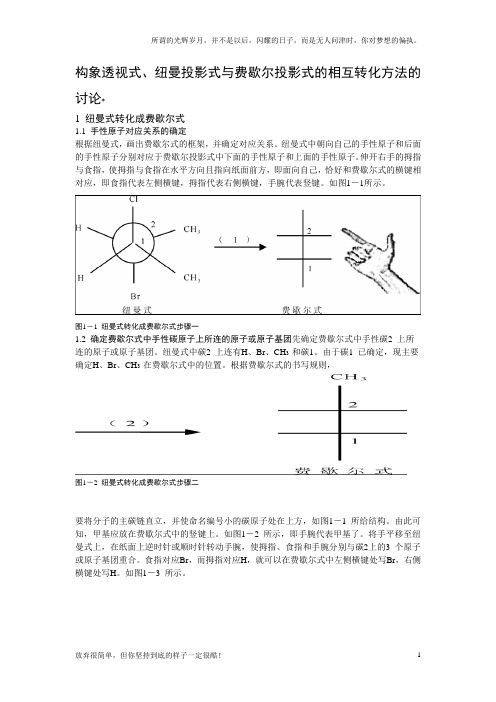
构象透视式、纽曼投影式与费歇尔投影式的相互转化方法的讨论*1 纽曼式转化成费歇尔式1.1 手性原子对应关系的确定根据纽曼式,画出费歇尔式的框架,并确定对应关系。
纽曼式中朝向自己的手性原子和后面的手性原子分别对应于费歇尔投影式中下面的手性原子和上面的手性原子。
伸开右手的拇指与食指,使拇指与食指在水平方向且指向纸面前方,即面向自己,恰好和费歇尔式的横键相对应,即食指代表左侧横键,拇指代表右侧横键,手腕代表竖键。
如图1-1所示。
图1-1 纽曼式转化成费歇尔式步骤一1.2 确定费歇尔式中手性碳原子上所连的原子或原子基团先确定费歇尔式中手性碳2 上所连的原子或原子基团。
纽曼式中碳2 上连有H、Br、CH3 和碳1。
由于碳1 已确定,现主要确定H、Br、CH3 在费歇尔式中的位置。
根据费歇尔式的书写规则,图1-2 纽曼式转化成费歇尔式步骤二要将分子的主碳链直立,并使命名编号小的碳原子处在上方,如图1-1 所给结构。
由此可知,甲基应放在费歇尔式中的竖键上。
如图1-2 所示,即手腕代表甲基了。
将手平移至纽曼式上,在纸面上逆时针或顺时针转动手腕,使拇指、食指和手腕分别与碳2上的3 个原子或原子基团重合。
食指对应Br,而拇指对应H,就可以在费歇尔式中左侧横键处写Br,右侧横键处写H。
如图1-3 所示。
图1-3 纽曼式转化成费歇尔式步骤三根据费歇尔式的书写规则可知,甲基应放在竖键上。
同理,可利用上述方法确定碳1 横键上的原子或原子基团。
所确定的费歇尔式如图1-4所示。
图1-4 纽曼式转化成费歇尔式步骤四2 透视式转化成费歇尔式2.1 手性原子对应关系的确定如图2-1 所示,透视式中朝向自己的手性原子对应于费歇尔式中下面的手性原子;透视式中后面的手性原子对应于费歇尔式中上面的手性原子。
图2-1 透视式转化成费歇尔式步骤一2.2 费歇尔式中手性碳2 上所连原子或原子基团的确定同上,根据费歇尔式的书写规则可知,甲基放在竖键上,如图2-2 所示。
费歇尔投影式转换规则

费歇尔投影式转换规则费歇尔投影式转换规则是一种用于将三维坐标系中的点转换为二维坐标系中的点的方法。
它主要用于地图制作、计算机图形学和测量学等领域中。
费歇尔投影式转换规则的原理是将三维坐标系中的点投影到一个平面上,再将该平面上的点映射到二维坐标系中。
下面将详细介绍费歇尔投影式转换规则的原理和应用。
一、费歇尔投影式转换规则的原理费歇尔投影式转换规则是一种等积映射方法,它可以将三维空间中的点投影到一个平面上,并保持点在平面上的间距和角度不变。
这种方法的原理是通过将三维坐标系中的点投影到一个平面上,再将该平面上的点映射到二维坐标系中,从而实现从三维坐标系到二维坐标系的转换。
1. 地图制作费歇尔投影式转换规则广泛应用于地图制作领域。
通过将地球表面上的经纬度坐标转换为平面坐标,可以将地球上的各种地理信息制作成平面地图。
这种转换方法能够保持地图上各点之间的相对位置和角度关系,使得地图更加准确和易于阅读。
2. 计算机图形学在计算机图形学中,费歇尔投影式转换规则常用于将三维模型投影到二维屏幕上显示。
通过将三维坐标系中的点投影到二维屏幕上,可以实现三维模型的可视化显示。
这种转换方法能够保持模型上各点之间的相对位置和角度关系,使得显示的模型更加真实和逼真。
3. 测量学在测量学中,费歇尔投影式转换规则被用于测量三维物体的形状和尺寸。
通过将三维物体投影到一个平面上,可以测量物体在平面上的长度、角度等参数,从而推断出物体的真实尺寸。
这种转换方法能够保持物体上各点之间的相对位置和角度关系,使得测量结果更加准确和可靠。
三、费歇尔投影式转换规则的优缺点费歇尔投影式转换规则具有以下优点:1. 等积映射:转换后保持点之间的相对位置和角度关系,准确性高。
2. 易于计算:转换过程简单,计算量较小。
然而,费歇尔投影式转换规则也存在一些缺点:1. 形变问题:由于将三维空间映射到二维平面上,会导致一些形变,例如面积变形、角度变形等。
2. 局限性:该规则只适用于特定的投影面,对于曲面或复杂的几何体可能不适用。
构象透视式、纽曼投影式与费歇尔投影式的相互转化方法
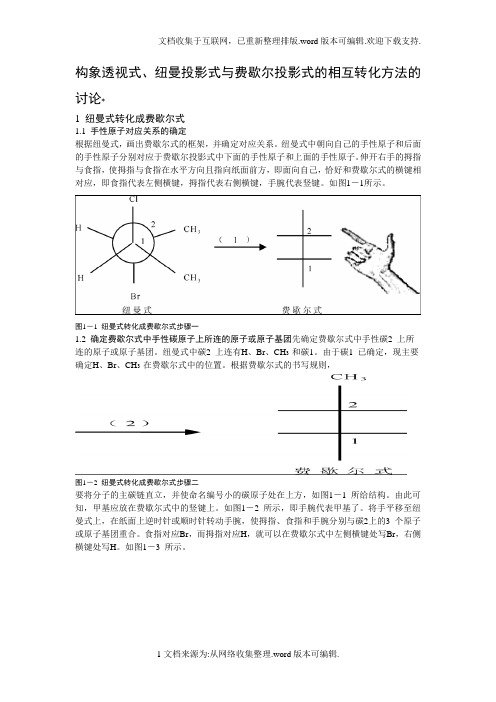
构象透视式、纽曼投影式与费歇尔投影式的相互转化方法的讨论*1 纽曼式转化成费歇尔式1.1 手性原子对应关系的确定根据纽曼式,画出费歇尔式的框架,并确定对应关系。
纽曼式中朝向自己的手性原子和后面的手性原子分别对应于费歇尔投影式中下面的手性原子和上面的手性原子。
伸开右手的拇指与食指,使拇指与食指在水平方向且指向纸面前方,即面向自己,恰好和费歇尔式的横键相对应,即食指代表左侧横键,拇指代表右侧横键,手腕代表竖键。
如图1-1所示。
图1-1 纽曼式转化成费歇尔式步骤一1.2 确定费歇尔式中手性碳原子上所连的原子或原子基团先确定费歇尔式中手性碳2 上所连的原子或原子基团。
纽曼式中碳2 上连有H、Br、CH3 和碳1。
由于碳1 已确定,现主要确定H、Br、CH3 在费歇尔式中的位置。
根据费歇尔式的书写规则,图1-2 纽曼式转化成费歇尔式步骤二要将分子的主碳链直立,并使命名编号小的碳原子处在上方,如图1-1 所给结构。
由此可知,甲基应放在费歇尔式中的竖键上。
如图1-2 所示,即手腕代表甲基了。
将手平移至纽曼式上,在纸面上逆时针或顺时针转动手腕,使拇指、食指和手腕分别与碳2上的3 个原子或原子基团重合。
食指对应Br,而拇指对应H,就可以在费歇尔式中左侧横键处写Br,右侧横键处写H。
如图1-3 所示。
图1-3 纽曼式转化成费歇尔式步骤三根据费歇尔式的书写规则可知,甲基应放在竖键上。
同理,可利用上述方法确定碳1 横键上的原子或原子基团。
所确定的费歇尔式如图1-4所示。
图1-4 纽曼式转化成费歇尔式步骤四2 透视式转化成费歇尔式2.1 手性原子对应关系的确定如图2-1 所示,透视式中朝向自己的手性原子对应于费歇尔式中下面的手性原子;透视式中后面的手性原子对应于费歇尔式中上面的手性原子。
图2-1 透视式转化成费歇尔式步骤一2.2 费歇尔式中手性碳2 上所连原子或原子基团的确定同上,根据费歇尔式的书写规则可知,甲基放在竖键上,如图2-2 所示。
透视式、纽曼投影式与费歇尔投影式的相互转化方法

透视式、纽曼投影式与费歇尔投影式的相互转化方法构象透视式、纽曼投影式与费歇尔投影式的相互转化方法的讨论*1 纽曼式转化成费歇尔式1.1 手性原子对应关系的确定根据纽曼式,画出费歇尔式的框架,并确定对应关系。
纽曼式中朝向自己的手性原子和后面的手性原子分别对应于费歇尔投影式中下面的手性原子和上面的手性原子。
伸开右手的拇指与食指,使拇指与食指在水平方向且指向纸面前方,即面向自己,恰好和费歇尔式的横键相对应,即食指代表左侧横键,拇指代表右侧横键,手腕代表竖键。
如图1,1所示。
图1,1 纽曼式转化成费歇尔式步骤一1.2 确定费歇尔式中手性碳原子上所连的原子或原子基团先确定费歇尔式中手性碳2 上所连的原子或原子基团。
纽曼式中碳2 上连有H、Br、CH3 和碳1。
由于碳1 已确定,现主要确定H、Br、CH3 在费歇尔式中的位置。
根据费歇尔式的书写规则,图1,2 纽曼式转化成费歇尔式步骤二要将分子的主碳链直立,并使命名编号小的碳原子处在上方,如图1,1 所给结构。
由此可知,甲基应放在费歇尔式中的竖键上。
如图1,2 所示,即手腕代表甲基了。
将手平移至纽曼式上,在纸面上逆时针或顺时针转动手腕,使拇指、食指和手腕分别与碳2上的3 个原子或原子基团重合。
食指对应Br,而拇指对应H,就可以在费歇尔式中左侧横键处写Br,右侧横键处写H。
如图1,3 所示。
图1,3 纽曼式转化成费歇尔式步骤三根据费歇尔式的书写规则可知,甲基应放在竖键上。
同理,可利用上述方法确定碳1 横键上的原子或原子基团。
所确定的费歇尔式如图1,4所示。
图1,4 纽曼式转化成费歇尔式步骤四2 透视式转化成费歇尔式2.1 手性原子对应关系的确定如图2,1 所示,透视式中朝向自己的手性原子对应于费歇尔式中下面的手性原子;透视式中后面的手性原子对应于费歇尔式中上面的手性原子。
图2,1 透视式转化成费歇尔式步骤一2.2 费歇尔式中手性碳2 上所连原子或原子基团的确定同上,根据费歇尔式的书写规则可知,甲基放在竖键上,如图2,2 所示。
Fischer投影式和Newman投影式的互换方法及其应用

Fischer投影式和Newman投影式的互换方法及其应用作者:黄艳仙来源:《化学教学》2009年第07期摘要:举例介绍了Fischer投影式和Newman投影式二者相互转换的简易方法及其在立体化学中判断构象间的相互关系、理解反应机理等方面的应用。
关键词:Fischer投影式;Newman投影式;转换;立体化学文章编号:1005-6629(2009)07-0072-03中图分类号:G633.479文献标识码:B立体化学是有机化学的一个重要组成部分,在基础有机化学教学中,立体化学是教学的重点和难点之一。
在讨论立体化学问题时,有时须兼及分子的构型和构象的两个方面,要求学生能熟练地相互转换Fischer投影式和Newman投影式。
构象用Newman投影式表示,而手性分子用Fischer投影式表示,两者之间该怎样互换是学生较难把握的问题[1]。
本文结合笔者的教学实践,介绍了Fischer投影式和Newman投影式二者相互转换的简易方法,并通过举例说明其在立体化学中的应用。
1 Fischer投影式和Newman投影式的相互转换方法1.1 由Newman投影式转换为Fischer投影式根据Fischer投影式的投影规则,Fischer投影式描述的立体构象都是Newman投影式的重叠式构象,所以,由Newman投影式转换为Fischer投影式时,当Newman投影式为交叉式构象时,须将交叉式构象转换为重叠式构象。
例1.将下列所示的Newman投影式转换为Fischer投影式[1]。
即当Newman投影式竖键垂直向上时,则前方向上的原子放在Fischer投影式竖线的上方;当Newman投影式竖键垂直向下时,则前方向下的原子放在Fischer投影式竖线的下方。
即:1.2 由Fischer投影式转换为Newman投影式由Fischer投影式转换为Newman投影式时,则反过来进行即可。
例2.将下列所示的 Fischer 投影式转换为Newman投影式[2]。
费歇尔投影式和纽曼式互相转化规则

费歇尔投影式和纽曼式互相转化规则1费歇尔投影式费歇尔投影式(Follmer projection),是由德国地理学家Wilhelm Follmer于1880年发明的一种地图投影法。
它既保留了地图的几何形状,又保留了地图的面积长度比例。
费歇尔投影式可以用球面投射将地球表面的图形简单化成扁平圆形,从而将三维的地球表示成二维图形,从而实现地球表面各个地方的准确位置显示。
费歇尔投影式用于航海、航空、大地测量,考虑到它的精度和准确性,也可以作为地图展示的主形式,在印刷地图上更加常用。
它主要特点是内部投影,图形简单,圆形明显,边界简单,横纵比例准确,正中心距正中心短,处处有利于准确的定点测量。
2纽曼式纽曼式(Newmann projection)是由德国空间学家吉米·纽曼(Jimmy Newman)在1874年提出的一种地图投影形式。
它是把地球以某一参照点为中心放射度量,把地球表面各个点重放到平面上实现投影的一种投影方式。
纽曼式把地球投射到一个平面上,精确却不完美,它既具有反射型投影的优势,又具有等比例投影的优势,视图角度可以随意改变,使地图看上去更加的自然。
但它的不足之处在于投射出的地形特点被放大了,偏离了实际地形,在高纬度地区会把图形拉长变形。
3互相转化规则由于费歇尔投影式和纽曼式属于投影面形式的不同,所以对于不同投影形式来说,地球表面上某个点的坐标位置是不一样的,因此在从费歇尔投影式转化为纽曼式和由纽曼式转化为费歇尔投影式时,需要一些变换方法。
具体而言,从费歇尔投影式转换为纽曼式的方法是将费歇尔投影式的横轴和纵轴进行放大,使图形延伸,最后将延伸后的图形转换为纽曼式;从纽曼式转换为费歇尔投影式则是将纽曼式的横轴和纵轴进行缩小,从而将图形内部化,然后将内部化后的图形转换为费歇尔投影式。
