matlab实验案例,节水洗衣机(优选.)
matlab实验案例节水洗衣机

1实验案例 (1)1.1案例:节水洗衣机 (1)1.1.1问题重述与分析 (2)1.1.2基本假设及说明 (2)1.1.3符号和变量说明 (2)1.1.4建模准备 (3)1.1.5模型建立 (4)1.1.6模型求解 (4)1.1.7思考题 (10)1实验案例1.1 案例:节水洗衣机问题:1996年全国赛B题节水洗衣机我国淡水资源有限,节约用水人人有责,洗衣机在家庭用水中占有相当大的份额,目前洗衣机已非常普及,节约洗衣机用水十分重要。
假设在放入衣物和洗涤剂后洗衣机的运行过程为:加水—漂洗—脱水—加水—漂洗—脱水—…—加水—漂洗—脱水(称“加水—漂洗—脱水”为运行一轮)。
请为洗衣机设计一种程序(包括运行多少轮、每轮加水量等),使得在满足一定洗涤效果的条件下,总用水量最少。
选用合理的数据进行运算,对照目前常用的洗衣机的运行情况,对你的模型和结果出评价。
洗衣机的节水优化模型摘要本文通过分析洗衣机的洗衣过程,认为是一次性溶解、多次稀释的过程。
据此建立非线性规划模型,并利用迭代公式和最优化原理,得出最少用水量的判断公式和代数解。
以海棠洗衣机为例,通过对比,利用我们的模型算出的用水量比厂家提供的数据要少,从而说明所建模型的优越性。
最后,根据模型解,给出最少用水量与脏衣服的重量的关系图,并从中得出有趣的结论,也给厂家提供一个节约用水的模型。
1.1.1问题重述与分析对洗衣机的运行进行设计,主要目的是为了节约用水量。
在满足洗涤效果的前提下使得用水量最少。
因此,这是一个典型的最优化问题,目标为洗衣总用水量最少,主要的决策为洗多少轮以及每轮加水量的问题。
而一般洗衣只是第一次加水漂洗时才放洗涤剂,而过后则是清水漂洗,通过化学原理,可以将第1轮洗涤后的各轮洗涤看成是不断的稀释过程。
为了评价洗涤效果,可用衣服上残留的污物质量与洗涤前污物质量之比作为评价指标。
在设计每轮加水量时,要考虑洗衣机本身洗衣同的最大容积,运行的最低加水量。
“节水洗衣机”问题数学建模及若干评注

“节水洗衣机”问题数学建模及若干评注随着社会的进步和科技的进步,环保意识日益增强,水资源的合理利用成为了一个重要的课题。
在平时生活中,人们对节水的需求也越来越高。
洗衣机作为家庭中常用的家电之一,其节水性能的提高对于节约水资源至关重要。
为了探究如何提高洗衣机的节水性能,我们可以运用数学建模的方法,深度分析洗衣机的工作原理和水资源利用状况,并给出相应的评注。
起首,我们需要明确洗衣机的工作原理。
一个平凡的洗衣机通常由进水管、排水管、脱水管和筒体组成。
在洗衣过程中,洗衣机需要从自来水管道中引入一定的水量,通过旋转筒体和叠加多个水平的模块化滚筒对衣物进行清洗,然后将污水排出,最后通过脱水管将衣物中的水分进行脱水处理。
基于以上的洗衣机工作原理,我们可以运用数学建模的方法来分析洗衣机的节水性能。
起首,我们可以建立一个洗衣机节水模型。
假设洗衣机每次清洗的衣物量为Q(千克),每次清洗所需的水量为W(升),那么洗衣机的节水效率(E)可以定义为:节水效率 = 1 - W / (Q * V),其中V表示洗衣机的内筒容量(升)。
通过这个模型,我们可以计算出洗衣机使用一次千克的衣物所需的平均水量。
在实际测量中,我们发现不同洗衣机型号和品牌的节水性能存在差异。
这是因为洗衣机的设计结构、清洗工艺以及水流控制等因素都会影响洗衣机的节水性能。
因此,在对洗衣机进行节水评估时,我们需要思量这些因素,并给出相应的评注。
评注可以接受数值化表达,例如可以将节水性能分为级别,给出相应的得分。
这样可以提供给消费者在采购洗衣机时进行参考,选择更加节水的型号。
除了数学建模和评注之外,我们还可以实行其他措施来提高洗衣机的节水性能。
例如,通过改进洗衣机的工艺和水流控制技术,降低每次清洗所需的水量。
此外,提高洗衣机的内筒容量,可以在一次清洗中洗更多的衣物,从而实现更高的节水效果。
另外,我们还可以通过优化洗涤剂的配方和使用方法,提高洗涤效果,缩减对屡次洗衣的需求,从而节约水资源。
智能控制实验-模糊控制

实验一 洗衣机的模糊控制仿真一、实验目的本实验要求在学生掌握模糊控制器基本工作原理和设计方法基础上,熟悉MALAB 中的模糊控制工具箱,能针对实际问题设计模糊控制器,建立模糊控制系统,训练学生综合运用计算机来解决一些实际问题的能力。
二、实验设备计算机一台、MATLAB 软件三、实验要求设计一个模糊控制器,根据衣物的泥污和油污程度,输出衣物的洗涤时间,通过改变控制参数的大小,观察模糊控制的性能。
四、实验步骤1.确定模糊控制器的结构选用两输入单输出模糊控制器,控制器的输入为衣物的泥污和油污,输出为洗涤时间。
2. 定义输入、输出模糊集 将泥污分为三个模糊集:泥污少SD 、泥污中MD 、泥污大LD ;油污分为三个模糊集:油污少SG 、油污中MG 、油污大LG ;将洗涤时间分为五个模糊集:很短VS 、短S 、中等M 、长L 、很长VL 。
3. 定义隶属度函数选用三角形隶属度函数实现泥污、油污和洗涤时间的模糊化:(50)/50050/50050(100)/505010050100(50)/50x x x x x x x x μμμμ=-⎧≤≤⎪≤≤⎧⎪==⎨⎨-<≤⎩⎪⎪<≤=-⎩SD MD 泥污LD (50)/50050/50050(100)/505010050100(50)/50x x x x x x x x μμμμ=-⎧≤≤⎪≤≤⎧⎪==⎨⎨-<≤⎩⎪⎪<≤=-⎩SG MG 油污LG(50)/50010/50010(100)/501025/501025(100)/5025402540/504060(100)/504060(50)/50x z x z x z x z x z z x z x z x μμμμμμ=-⎧≤≤⎪⎧≤≤⎪=⎨⎪-<≤⎩⎪≤≤⎧⎪==⎨⎨-<≤⎩⎪⎪≤≤⎧⎪=⎨<≤-⎪⎩⎪≤≤=-⎩SG MG MG 洗涤时间MG LG实验结果:实验分析:6.模糊推理因模糊控制规则表对称,所以上图为input1 和input2分别为50时input2和input1与洗涤时间的关系。
基于MATLAB的洗衣机模糊控制设计

基于MATLAB的洗衣机模糊控制设计MATLAB是一种功能强大的数学软件,可以用于模糊控制设计。
在本文中,我们将介绍如何使用MATLAB来设计一个基于模糊控制的洗衣机控制系统。
首先,我们需要定义洗衣机模糊控制系统的输入和输出变量。
在一个简单的洗衣机系统中,输入变量可以是衣物的脏度和水位,而输出变量可以是洗衣机的清洗时间和水温。
接下来,我们需要建立一个模糊控制器模型。
模糊控制器是一个基于模糊逻辑的控制器,能够处理模糊输入和输出变量。
在MATLAB中,我们可以使用Fuzzy Logic Toolbox来建立一个模糊控制器模型。
我们首先需要定义模糊输入变量的隶属函数。
在这个例子中,我们可以定义脏度变量的隶属函数为"低","中"和"高",水位变量的隶属函数为"低","中"和"高"。
然后,我们需要定义模糊输出变量的隶属函数。
在这个例子中,我们可以定义清洗时间变量的隶属函数为"短","适中"和"长",水温变量的隶属函数为"低","中"和"高"。
接下来,我们需要定义输入和输出变量之间的模糊规则。
在这个例子中,我们可以定义以下规则:规则1:如果脏度是低和水位是低,那么清洗时间是短和水温是低。
规则2:如果脏度是低和水位是中,那么清洗时间是适中和水温是中。
规则3:如果脏度是低和水位是高,那么清洗时间是长和水温是中。
规则4:如果脏度是中和水位是低,那么清洗时间是适中和水温是中。
规则5:如果脏度是中和水位是中,那么清洗时间是适中和水温是中。
规则6:如果脏度是中和水位是高,那么清洗时间是长和水温是高。
规则7:如果脏度是高和水位是低,那么清洗时间是长和水温是中。
规则8:如果脏度是高和水位是中,那么清洗时间是长和水温是高。
基于Matlab的洗衣机模糊控制 - 副本

基于MATLAB的洗衣机模型模糊设计控制一、问题描述随着现代社会生活节奏的不断加快和人们生活水平的不断提高,人们对各种方便、快捷的家用电器需求量越来越大,为了提高人们的生活效率,全自动洗衣机应运而生。
洗衣机的技术发展日新月异,产品类型众多,但是从总体来看,人们对洗衣机的基本要求应该是:省时、省电、省水、磨损率小、操作方便、功能完善等。
模糊控制洗衣机不仅实现了洗衣机的全面自动化,也提高了洗衣的质量,具有很强的实用性和较好的发展前景。
本设计就是围绕着智能洗衣机进行研究。
本课题的主要目的就是设计一个比较合理的洗衣机模糊控制器,这种采用模糊控制的洗衣机能够自动检测洗衣桶内水的脏污程度和污渍性质(油污或者泥污);能自动预选洗涤时间,并适时调整这些运行参数,以达到最佳的洗涤效果。
二、解决方案本课题的主要是通过模糊控制来对洗衣机进行控制,通过MATLAB对其仿真。
课题的主要目的是设计一个比较合理的洗衣机模糊控制器,这种采用模糊控制的洗衣机能够自动检测洗衣桶内水的脏污程度和污渍性质(油污或者泥污);能自动预选水位和洗涤时间,并能够进行整个洗涤过程中实施监控,并适时调整这些运行参数,以达到最佳的洗涤效果。
模糊控制器的组成框图如图1所示图1三、实现步骤本设计选用两输入单输出模糊控制器。
控制器的输入为衣物的污泥和油脂,输出为洗涤时间。
将污泥分为3个模糊集:SD(污泥少),MD (污泥中),LD (污泥多);将油脂分为3个模糊集:NG (油脂少),MG (油脂中),LG (油脂多);将输出的洗涤时间分为5个模糊集:VS (很短),S (短),M (中等),L (长),VL (很长)。
1、定义隶属函数污泥含量选用如下隶属函数:()()()()()()⎪⎪⎩⎪⎪⎨⎧-=⎩⎨⎧-=-==50/5050/10050/50/50x x x x x x x μLDMD SD μμμ污泥1005010050500500≤<≤<≤≤≤≤x x x x采用三角隶属函数可实现污泥的模糊化采用Matlab 仿真,如图2所示。
matlab-SIMULINK仿真实例
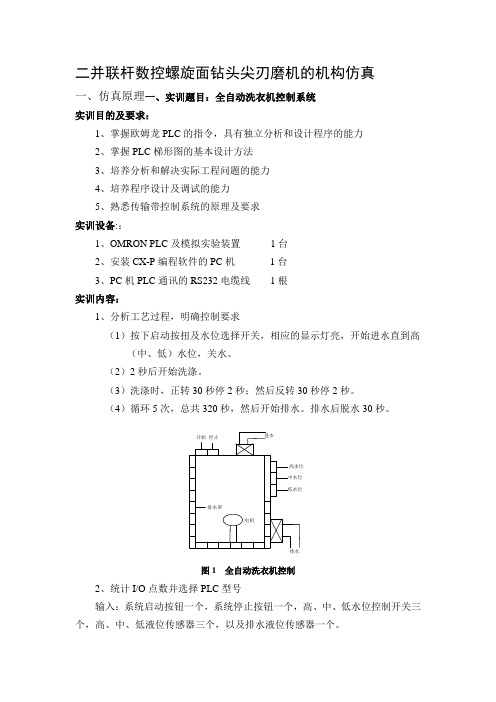
二并联杆数控螺旋面钻头尖刃磨机的机构仿真一、仿真原理一、实训题目:全自动洗衣机控制系统实训目的及要求:1、掌握欧姆龙PLC的指令,具有独立分析和设计程序的能力2、掌握PLC梯形图的基本设计方法3、培养分析和解决实际工程问题的能力4、培养程序设计及调试的能力5、熟悉传输带控制系统的原理及要求实训设备::1、OMRON PLC及模拟实验装置1台2、安装CX-P编程软件的PC机1台3、PC机PLC通讯的RS232电缆线1根实训内容:1、分析工艺过程,明确控制要求(1)按下启动按扭及水位选择开关,相应的显示灯亮,开始进水直到高(中、低)水位,关水。
(2)2秒后开始洗涤。
(3)洗涤时,正转30秒停2秒;然后反转30秒停2秒。
(4)循环5次,总共320秒,然后开始排水。
排水后脱水30秒。
图1 全自动洗衣机控制2、统计I/O点数并选择PLC型号输入:系统启动按钮一个,系统停止按钮一个,高、中、低水位控制开关三个,高、中、低液位传感器三个,以及排水液位传感器一个。
输出:进出水显示灯一盏,高、中、低水位显示灯各一盏,电机正、反转显示灯各一盏,排水、脱水显示灯灯各一盏。
PLC的型号:输入一共有9个,考虑到留有15%~20%的余量即9×(1+15%)=10.35,取整数10,所以共需10个输入点。
输出共有8个,8×(1+15%)=9.2,取整数9,所以共需9个输出点。
可以选OMRON公司的CPM1A/CPM2A 型PLC就能满足此例的要求。
3、I/O分配表1 全自动洗衣机控制I/O分配表输入输出地址名称地址名称00000 启动系统按钮01000 排水显示灯00001 高水位选择按钮01001 脱水显示灯00002 中水位选择按钮01002 进、出水显示灯00003 低水位选择按钮01003 高水位显示灯00004 排水液位传感器01004 中水位显示灯00005 停止系统按钮01005 低水位显示灯00006 高水位液位传感器01006 电机正转显示灯00007 中水位液位传感器01007 电机反转显示灯00008 低水位液位传感器4、PLC控制程序设计及分析实现功能:当按下按钮00000,中间继电器20000得电并自锁,按下停止按钮00005,中间继电器20000掉电。
节水洗衣机—数学建模
节水洗衣机—数学建模数学建模是利用数学原理建立有关普遍问题的精确模型的一种技术,可以用于研究现实问题,为决策提供重要的参考,是当前科学研究和管理决策的重要手段。
本文针对一类具有明显特点的问题——节水洗衣机,运用数学建模技术,建立分析模型,寻求有效解决方案。
节水洗衣机是基于流体动力原理技术开发的新一代洗衣机。
它利用洗涤系统的水位控制、流量控制等技术来实现多种水位的洗涤效果,避免大量水的浪费。
节水洗衣机的核心问题在于洗衣量与流体流量之间的调节,即通过控制流量如何达到最佳洗涤效果,以实现最大限度的节约用水。
本文首先根据实际情况确定模型的基本内容,完成决策变量与相关约束条件之间关系的建立。
以节水洗衣机性能指标——洗衣量为目标函数,流量为决策变量,考虑不同流量对洗衣机功耗的影响,以及不同流量处理量的变化情况,构建数学解模型,并利用数值解法求解。
将洗衣量特定函数表示如下:$Y=Y(v)=B \ln \dfrac{v}{v_0}+Kv$其中$Y$为洗涤量,$v$为流量,$v_0$为固定参数,$B$为系数,$K$为系数。
对此函数,本文采用最大化目标模型求解,即最大化洗衣量,在给定假设条件下求解流量:令求解函数$Y'=B \ln \dfrac{v}{v_0}+Kv-c=0$,解得$v=\dfrac{v_0 e^{-c/B}-Kv_0 }{K}$,将上述求解的$v$带入$Y$可得:以上所得即为节水洗衣机最优流量方案及其最优洗衣量模型,可用于实际应用。
综上所述,本文运用数学建模技术,建立分析模型,对节水洗衣机的功能进行深层次分析,寻求有效解决方案,为实际应用提供重要参考。
本文运用的数学技术也可以应用于其他类似的问题研究,可以更好的服务实际需求。
洗衣机节水设计方案 (2)
总用水量
5
1
3
20
60
2
3
21
63
3
3
26
78
4
4
20
80
5
4
21
84
显然,在其他条件确定的前提下,洗涤衣物越多则用水量越多。 根据上述讨论,建议洗衣机使用者合理安排衣物洗涤,以达到科 学用水和节约用水的目的。也建议洗衣机制造厂家适时研制能够测定 各种参数并作出合理反应的智能洗衣机,用户可以根据简明的数控面 板进行操作。 6.模型的评价 (1)模型的优点 在解决方案中利用数学模型得到最少洗涤剂剩余量,在此基础上 分析剩余洗涤剂含量与衣物重量的比值来衡量洗衣的实际效果。最终 得到比较理想的实验数据,方法简单明了。 (2)模型的缺点 在考虑到对最小用水量的影响因素中,只考虑到了衣物的重量、 洗涤剂加入量的影响,而实际洗涤过程中洗衣机的性能和洗涤剂的质 量也是相对重要的影响因素。虽然模型反映了问题的本质,但依然会
2
第一轮的注水量为。第一轮洗衣→排水之后,剩余洗涤剂为。随水排 出的洗涤剂为,可见
由此
一般地,应有
(
)
于是,第轮脱水之后衣物中剩余洗涤剂含量
我们用全部的轮洗衣完成之后衣物中剩余洗涤剂含量与衣物重量的 比值来衡量洗衣的实际效果,则比值越小,说明洗衣效果越好。可以 用限定来规定洗衣的效果要求。在特定的洗衣条件之下,应该合理确 定洗衣的轮次和每次的注水量,以便用最少的用水量达到预计的洗衣 效果。至此,问题归结为求总用水量函数的条件极值问题
摘要:本文对节水洗衣问题进行了定量分析,把洗衣效果问题简化为剩余洗涤剂剩 余含量的问题,经过多次加水洗涤过程,从而建立了节水洗衣的动态 规划模型,得到了在满足衣物洁净度要求下的最少加水总量、最佳洗 涤剂用量、最优洗涤轮次及相应的加水策略。 1.问题的重述
数学建模 节水洗衣机
数学建模节水洗衣机近年来,随着环境保护意识的提高,节水已成为一种趋势。
为此,许多研究者致力于研究如何设计一种节水洗衣机。
数学建模在研究节水洗衣机中发挥了重要作用。
本文将以数学建模的角度,介绍节水洗衣机的相关概念、原理和方法。
1. 节水洗衣机的原理节水洗衣机的原理是通过减少洗涤剂使用和优化洗涤程序来实现节水。
具体而言,它采用了以下的技术方案:(1)高效清洁技术。
通过使用高效清洁剂和配合不同风速的水流,实现高效的清洁。
(2)减少洗衣量。
减少单次洗涤量,避免浪费水资源。
(3)通过洗衣程序的调整,达到节水效果。
比如采用高速旋转,使衣物自然晾干,减少烘干次数。
2. 数学模型为了更好地实现节水,需要建立数学模型。
首先,我们需要确定优化目标,然后建立数学模型来解决问题。
(1)优化目标洗涤剂和水是实现清洁的两个重要因素,但是在实际中,它们也是造成浪费的原因之一。
因此,我们需要确定优化目标,以找到最佳的洗涤剂和水的使用方式。
在确定优化目标之后,我们可以建立数学模型。
其中,最常见的模型是线性规划模型。
通过线性规划模型,我们可以实现洗涤剂和水的最佳使用,以达到节水效果。
例如,我们可以通过线性规划模型来确定最佳的洗涤剂使用量和水的使用量,以达到清洁效果最好的同时,最大限度地减少水的使用。
3. 研究方法为了验证数学建模的有效性,我们需要采用实验方法来对其进行验证。
例如,可以通过对洗涤剂的浓度、清洁剂的种类和其他因素进行测试来获取实验数据。
然后,将这些实验数据应用于建立的数学模型中,计算最佳的洗涤剂和水的使用量,以确定节水效果。
在研究节水洗衣机的过程中,可以采用多种方法进行实验验证。
例如,可以采用洗涤机的实验样机进行实验,以明确优化目标以及验证数学模型的正确性。
4. 结论综上所述,数学建模是研究节水洗衣机的一种有效方法。
通过建立数学模型来解决清洁效果和节水效率之间的平衡关系,可以有效地为节约水资源做出贡献。
未来,我们可以进一步探讨和应用数学建模的方法来推进环保事业的发展。
matlab实验案例,节水洗衣机(优选.)
1 实验案例 (1)1.1 案例:节水洗衣机 (1)1.1.1 问题重述与分析 (2)1.1.2 基本假设及说明 (2)1.1.3 符号和变量说明 (2)1.1.4 建模准备 (3)1.1.5 模型建立 (4)1.1.6 模型求解 (4)1.1.7 思考题 (10)1实验案例1.1 案例:节水洗衣机问题:1996年全国赛B题节水洗衣机我国淡水资源有限,节约用水人人有责,洗衣机在家庭用水中占有相当大的份额,目前洗衣机已非常普及,节约洗衣机用水十分重要。
假设在放入衣物和洗涤剂后洗衣机的运行过程为:加水—漂洗—脱水—加水—漂洗—脱水—…—加水—漂洗—脱水(称“加水—漂洗—脱水”为运行一轮)。
请为洗衣机设计一种程序(包括运行多少轮、每轮加水量等),使得在满足一定洗涤效果的条件下,总用水量最少。
选用合理的数据进行运算,对照目前常用的洗衣机的运行情况,对你的模型和结果出评价。
洗衣机的节水优化模型摘要本文通过分析洗衣机的洗衣过程,认为是一次性溶解、多次稀释的过程。
据此建立非线性规划模型,并利用迭代公式和最优化原理,得出最少用水量的判断公式和代数解。
以海棠洗衣机为例,通过对比,利用我们的模型算出的用水量比厂家提供的数据要少,从而说明所建模型的优越性。
最后,根据模型解,给出最少用水量与脏衣服的重量的关系图,并从中得出有趣的结论,也给厂家提供一个节约用水的模型。
1.1.1问题重述与分析对洗衣机的运行进行设计,主要目的是为了节约用水量。
在满足洗涤效果的前提下使得用水量最少。
因此,这是一个典型的最优化问题,目标为洗衣总用水量最少,主要的决策为洗多少轮以及每轮加水量的问题。
而一般洗衣只是第一次加水漂洗时才放洗涤剂,而过后则是清水漂洗,通过化学原理,可以将第1轮洗涤后的各轮洗涤看成是不断的稀释过程。
为了评价洗涤效果,可用衣服上残留的污物质量与洗涤前污物质量之比作为评价指标。
在设计每轮加水量时,要考虑洗衣机本身洗衣同的最大容积,运行的最低加水量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 实验案例 (1)1.1 案例:节水洗衣机 (1)1.1.1 问题重述与分析 (2)1.1.2 基本假设及说明 (2)1.1.3 符号和变量说明 (2)1.1.4 建模准备 (3)1.1.5 模型建立 (4)1.1.6 模型求解 (4)1.1.7 思考题 (10)1实验案例1.1 案例:节水洗衣机问题:1996年全国赛B题节水洗衣机我国淡水资源有限,节约用水人人有责,洗衣机在家庭用水中占有相当大的份额,目前洗衣机已非常普及,节约洗衣机用水十分重要。
假设在放入衣物和洗涤剂后洗衣机的运行过程为:加水—漂洗—脱水—加水—漂洗—脱水—…—加水—漂洗—脱水(称“加水—漂洗—脱水”为运行一轮)。
请为洗衣机设计一种程序(包括运行多少轮、每轮加水量等),使得在满足一定洗涤效果的条件下,总用水量最少。
选用合理的数据进行运算,对照目前常用的洗衣机的运行情况,对你的模型和结果出评价。
洗衣机的节水优化模型摘要本文通过分析洗衣机的洗衣过程,认为是一次性溶解、多次稀释的过程。
据此建立非线性规划模型,并利用迭代公式和最优化原理,得出最少用水量的判断公式和代数解。
以海棠洗衣机为例,通过对比,利用我们的模型算出的用水量比厂家提供的数据要少,从而说明所建模型的优越性。
最后,根据模型解,给出最少用水量与脏衣服的重量的关系图,并从中得出有趣的结论,也给厂家提供一个节约用水的模型。
1.1.1问题重述与分析对洗衣机的运行进行设计,主要目的是为了节约用水量。
在满足洗涤效果的前提下使得用水量最少。
因此,这是一个典型的最优化问题,目标为洗衣总用水量最少,主要的决策为洗多少轮以及每轮加水量的问题。
而一般洗衣只是第一次加水漂洗时才放洗涤剂,而过后则是清水漂洗,通过化学原理,可以将第1轮洗涤后的各轮洗涤看成是不断的稀释过程。
为了评价洗涤效果,可用衣服上残留的污物质量与洗涤前污物质量之比作为评价指标。
在设计每轮加水量时,要考虑洗衣机本身洗衣同的最大容积,运行的最低加水量。
1.1.2基本假设及说明1.洗衣机一次用水量有最高限和最低限,能连续补充在限度内的任意水量;2.洗衣机每轮运行过程为:加水-漂洗-脱水;3.仅在第一轮运行时加上洗涤剂,在后面的运行轮中仅有稀释作用;4.洗衣时所加的洗涤剂适量,漂洗时间足够,能使污垢一次溶解,忽略不能溶解的污垢;5.脱水后的衣服质量与干衣服的重量成正比;6.每缸洗衣水只用一次;1.1.3符号和变量说明A:污物的质量(kg);i ρ:第i 轮运行时污物浓度(kg/升);n :洗衣服时洗衣机运行轮数(次); i x :第i 轮用水量(升);M :干衣服的质量(kg ); m :衣服脱水后衣服含水质量(kg );ε:衣服的清洁度(常量,洗衣的衣服上污量与0A 之比);S :洗一次衣服的总用水量(升); m ax M :洗衣机一次洗衣的最大量(kg );α:脱水后衣服含水质量与干衣服质量比(常数);显然M m α= m ax V :洗衣机一次注水最高限(升);m in V :衣服完全浸泡的状态下为洗衣机能正常运行需注入的最低水量(升);β:单位质量的衣服完全浸泡最低所需水量(常量); 1.1.4 建模准备(1) 由化学中的洗涤原理知,有助于洗涤作用的三个因素:1、 表面活性(以肥皂为代表的活性剂产生洗涤作用的各种物质之通称);2、 界面电(配入洗涤剂中的碱和磷酸盐等无机助剂的作用);3、 机械力和流水力(由于水的流动产生机械力)在洗衣过程中,一般之在第一次加入洗涤剂,在第二次及以后,不再加入洗涤剂,从而,使有助于洗涤的三个因素的前两个不存在,只剩下水的流动力的作用,洗涤作用因此很微弱。
于是假设污物的第一次被洗涤,接下来的过程只是污物的稀释过程是合理的。
(2)实际生活经验可知,在衣服完全浸泡的基础上,洗衣机还需有一定的富裕水量m in V 才能使其正常运行。
一种衣服完全浸泡所需水量是衣服质量的β倍,则质量为M 的衣服使洗衣机能洗的最少水量M V M V β+=min min )(。
脱水后剩下水量是衣服质量的α倍,M m α=。
对于普通衣服βα,可视为常数。
实验测定1kg 混合干衣服浸泡所需水量,脱水后衣服含水量与干衣服质量之比,如表1。
计算可得0.5;60.0==βα。
各次运行时,污物的浓度为:mx mmx mmx m x A n n n +=+=+==-1323212101,,,,ρρρρρρρ ,经过迭代得到)())((32110m x m x m x x m A n n n +++=- ρ 1.1.5 模型建立根据以上分析,可以建立解决洗衣机节水的非线性最优化模型。
⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤+≤≤≤≤+++==∑=.,,3,2,)()()())((..min maxmin max 1min 032101n i V m x M V V x M V A m x m x m x x m A m t s x S i n nn ni iερ(1)1.1.6 模型求解 1.1.6.1 解析求解如果(1)存在最优解**2*1,,,n x x x ,则可以证明m x m x x n +==+=**2*1 (证明从略)。
n 的取值讨论ε≤++)()(**2*1m x m x x m n n(1) 当),,3,2(,1n i m x x i =+刚好为)(min M V ,则有最多洗涤轮数。
由()ε<nnM V m )(min ,得1)(ln ln min max +⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛=M V m n ε (2) 当),,3,2(,1n i m x x i =+刚好为m ax V ,则有最少洗涤轮数。
由()ε<nnV m max ,得1ln ln max max+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛=V m n ε综上所述,n 的取值范围为max min n n n ≤≤。
1.1.6.2 其他求解方法所建立模型为非线性最优化模型,故这里采用Matlab 求解非线性规划的函数fmincon 求解。
1.1.6.3 数据初始化程序init1996b.m%1996B 洗衣机节水模型 %参数与数据初始化 %af =0.60;%脱水后衣服含水质量与干衣服质量比(常数)beta = 5.0;%单位质量的衣服完全浸泡最低所需水量(常量); Vmin = 24;%衣服完全浸泡的状态下为洗衣机能正常运行需注入的最低水量(升);ef= 0.001;%衣服的清洁度(常量,洗衣的衣服上污量与之比);M = 5;%干衣服的质量(kg);m = af*M;%衣服脱水后衣服含水质量(kg)VminM = beta*M + Vmin;Vmax = 60;%洗衣机一次注水最高限(升);1.1.6.4 模型求解程序(根据n穷举求解)程序:solv1996_1.m%initinit1996bNmin = fix( log(ef)/ log((m/Vmax)) ) + 1 Nmax = fix( log(ef)/ log(m/VminM) ) + 1opti_s = 1e6;for n= Nmin:Nmax,t1= m/(ef)^(1/n)t2= VminMonex= max(m/(ef)^(1/n),VminM);S = n*onex-(n-1)*mx=[];x(1)=onex;if n>=2,for i=2:n,x(i)=onex-m;endend%test=sum(x)-S;if S < o pti_s,opti_n = n;%洗衣轮次opti_s = S;%存储最少所需水量opti_x = x;endendopti_nopti_sopti_xm1.1.6.5 模型求解程序(直接非线性规划求解)目标函数m文件:myobj1996b.mfunction r=myobj1996b(x)%1996年B题目标函数:总需水量r= sum(x);约束条件m文件:mycon1996b.mfunction [C,Ceq]= mycon1996b(x)%1996年B题采用非线性规划求解算法求解的约束条件函数global m ef %全局变量n= length(x);%洗衣轮次tmpX = x(1);%x1if n>=2,for i=2:n,tmpX=tmpX*(x(i)+m);%x1*(x2+m)*(x3+m)*...*(xn+m) endendC=m^n -tmpX*ef ;%只有一个约束,决策变量约束用fmincon的参数lb,ub来处理%C=m^n/tmpX - ef ;%只有一个约束,决策变量约束用fmincon 的参数lb,ub来处理Ceq=[];主程序:solv1996b_2%1996B洗衣机节水模型%参数与数据初始化%initinit1996bNmin = fix( log(ef)/ log((m/Vmax)) ) + 1 Nmax = fix( log(ef)/ log(m/VminM) ) + 1opti_s = 1e6;for n=Nmin:Nmax,%穷举所有可能洗衣次数的模型lb=[];ub=[];lb(1)= VminM;ub(1)= Vmax;if n>=2,for j=2:n,lb(j) = VminM- m;ub(j) = Vmax-m;endendlbub[x,fval,exitflag]=fmincon('myobj1996b',VminM*ones (1,n),[],[],[],[],...lb,ub,'mycon1996b')if fval < opti_s,opti_n = n;opti_s = fval;opti_x = x;endendopti_nopti_sopti_xm1.1.6.6 解析法运行结果:solv1996b_1Nmin =3Nmax =3t1 =30t2 =49S =141opti_n =3opti_s =141opti_x =49 46 46m =31.1.6.7 直接非线性规划求解运行结果solv1996b_2Nmin =3Nmax =3lb =49 46 46ub =60 57 57Warning: Trust region method does not currently solve this type of problem,switching to line search.> In E:\MATLABR11\toolbox\optim\fmincon.m at line 190In F:\PROGRAM\mbookfile2002\solv1996b_2.m at line 24 Optimization terminated successfully:Search direction less than 2*options.TolX andmaximum constraint violation is less than options.TolConActive Constraints:123x =49 46 46fval =141exitflag =1opti_n =3opti_s =141opti_x =49 46 46m =3结果对比发现,两种求解方法得到的洗衣方案相同,均洗3轮,共需水141,第1,2,3轮分别加水49升,46升,46升。
