河南省长葛市第三实验高中10-11学年高一数学上学期期中考试新人教A版

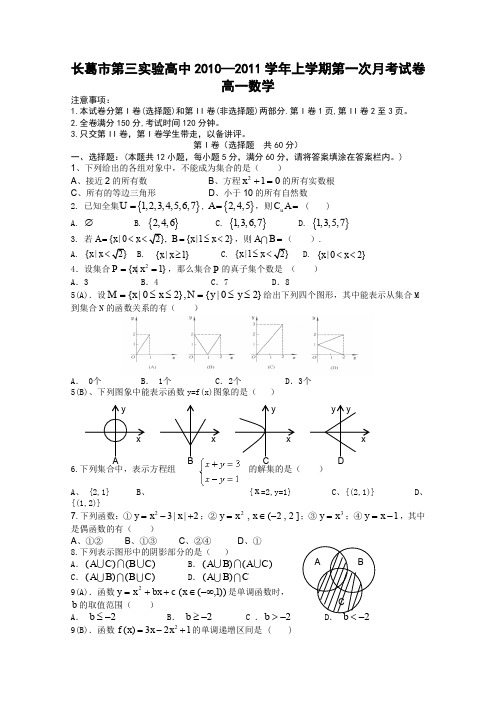
长葛市第三实验高中2010-2011学年上学期期中考试高一数学试题
注意事项：
1．本试卷分第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）和答题卷三部分。

满分150分，考试时间120分钟。

2．答卷前考生务必将自己的班级、姓名、考号和考试科目用钢笔分别填在答题卷密封线内。

3．第Ⅰ卷和第Ⅱ卷的答案务必答在答题卷中，否则不得分；答题卷用0.5毫米的黑色墨水签字笔答在上面每题对应的答题区域内，在试题卷上作答无效．．．．．．．．．。

4．考试结束后，只把答题卷交回（试题．．卷自己保留好，以．．．．．．．．备评讲．．．
）。

第I 卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只
有一项是符合题目要求的．
1. 设:||f x x →是集合A 到集合B 的映射，若{2,0,2}A =-，则A B I 等于（ ） A. {0} B. {2} C. {0,2} D. {2,0}-
2. 函数2(1)(23)y x x x =---的零点为（ ）
A. 1，2，3
B. 1，－1，3
C. 1，－1，－3
D. 无零点
3. 函数()f x =
）对称
A. x 轴
B. 原点
C. y 轴
D. 直线y x = 4. 下列不等式成立的是（ ） A.322log 2log 3log 5<< B. 322log 2log 5log 3<< C. 232log 3log 2log 5<<
D. 223log 3log 5log 2<<
5. 已知()f x 在[,]a b 是奇函数，且()f x 在[,]a b 上的最大值为m ，则函数
()()3F x f x =+在[,]a b 上的最大值与最小值之和为（ ）
A. 23m +
B. 26m +
C. 62m -
D. 6 6. 已知函数e e ()e e
x
x
x x f x ---=+，若()f a b =，则()f a -=（ ）
A.b
B.－b
C. b
1
D.－
b
1 7. 设集合U={1，2，3，4，5}，A ={1，2，3}，B ={2，5}，则U ()A C B I =（ ） A.{2}
B.{2，3}
C. {3}
D. {1，3}
8. 下列函数中，是偶函数且在区间(0,)+∞上单调递减的函数是（ ） A. ||
3x y =- B. 1
2
y x = C. 23log y x = D. 2y x x =- 2x (01)x ≤≤
9. 函数()f x = 2 (12)x << 的值域是（ ） 25x -+ (23)x ≤≤
A. R
B. [0，2]
C. [1,2)-
D. [－1， 2] 10. ()f x 是定义在R 上的奇函数，且单调递减，若(2)(4)0f a f a -+-<，则a 的取范围是（ ）
A. 1a <
B. 3a <
C. 1a >
D. 3a >
11. 若2()2f x x ax =-+与1)(+=x a
x g 在区间[1，2]上都是减函数，则a 的取值范围
是（ ）
A.)1,0()0,1(⋃-
B. ]1,0()0,1(⋃-
C.（0,1）
D. ]1,0(
12.
函数y =的定义域是（ ）
A.[1,)+∞
B. 2(,)3+∞
C. 2[,1]3
D. 2
(,1]3
第Ⅱ卷 （非选择题，共90分）
二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中的横线上。

13.
函数2
2()3()log (31)x f x x +=++的定义域是 .
14. 函数212
()log (32)f x x x =-+的单调递增区间是 .
15.设1a >，函数()log a f x x =在区间[]2a a ，上的最大值与最小值之差为
1
2
，则a =_______．
16. 已知()x x f x a a -=+ (01)a a >≠且且(1)3f =则(0)(1)(2)f f f ++＝ . 三、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及解答步
骤。

17. （本小题10分）设函数()f x 是R 上的奇函数，当0x ≥时，2()4f x x x =+． （Ⅰ）求()f x 的表达式；
（Ⅱ）证明()f x 在区间(0,)+∞上是增函数．
18. （12分）设全集2{2,3,21},{|12|,2},{7}U a a A a A =+-=-=U ð，求实数a 的值，并写出U 的所有子集.
19.（12分）若()f x 是定义在(0,)+∞上的增函数，且对一切,0x y >，满足
()()()x
f f x f y y
=-. （Ⅰ）求(1)f 的值；
（Ⅱ）若(6)1f =，解不等式1
(3)()23
f x f +-<.
20.（12分）已知偶函数()f x 在[0,)+∞上为增函数，且1
()02
f =.
求不等式(log )0a f x > (0,1)a a >≠且的解集.
21. （12分）函数2
()1ax b f x x +=
+是定义域在（－1，1）上奇函数，且12
()25
f =. （Ⅰ）确定函数()f x 的解析式；
（Ⅱ）用定义证明()f x 在（－1，1）上是增函数； （Ⅲ）解不等式(1)()0f t f t -+<.
22. （12分）某服装批发市场，销售季节性流行服装A ．当季节即将来临时，价格呈上升趋势，开始时定价为 10 元，并且每周（7 天）涨价 2 元，5 周后开始保持 20 元的平稳销售；10 周后当季节即将过去时，平均每周降价 2 元，直到 16
周末，该服装已不再销售．
（Ⅰ）试建立价格P 与周次t 之间的函数关系；
（Ⅱ）若此服装每件进价Q 与周次t 之间的关系式为21
(8)128
Q t =--+，[0,16]t ∈，
t ∈N ，问该服装第几周每件销售利润最大？
三、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及解答步
骤。

17. 解：（Ⅰ）当0x <时，0x ->，∴22()()4()4f x x x x x -=-+-=- …2分 ∵()f x 是奇函数，∴()()f x f x -=-， …………3分
∴22()()(4)4f x f x x x x x =--=--=-+， ……………4分
因此，220
4,()04,x x x f x x x x ≥⎧+=⎨<-+⎩ ． ……………5分
（Ⅱ）设120x x <<，则
2
2212211()()(4)(4)f x f x x x x x -=+-+2121()(4)x x x x =-++ …7分
∵120x x <<，∴210x x ->，2140x x ++>， ……………8分
∴21()()0f x f x ->，∴12()()f x f x <∴()f x 是(0,)+∞上的增函数， ……10分 18. 解：根据补集的概念，由{7}U A =ð知，7U ∈，且7A ∉.
∴2
217a a +-=，解得24a a ==-或
当2|12|37,3;4|12|97,9,a a U a a U a =-=≠∈=--=≠∉时，
且当时，且故的值为2. 又∵集合U 中的元素有3个，即U ＝{2，3，7}.故其所有子集的个数为328＝（个），
它们分别为：{2}{3}{7}{23}{37}{27}{237}.∅，
，，，，，，，，，，，
即：01a <<时不等的解集{|0}a x x a x a
<<>或 1a >时不等的解集{|}a x x a x ><<或0 21. 解：（Ⅰ）
2
0,10
b
=+ 1,a =
⇒ 即
22.1514
a b
+=+ 0.b = ∴2
()1x
f x x =
+. （Ⅱ）证明：任取1211x x -<<<，则2121222
1
()()11x x f x f x x x -=-++＝211222
12()(1)
(1)(1)
x x x x x x --++. ∵1211x x -<<<，∴2112120,11,10,x x x x x x ->-<<->
221210,10,x x +>+> ∴2121()()0()(),f x f x f x f x ->>即
∴()f x 在（－1，1）上是增函数.
（Ⅲ）(1)()(),f t f t f t -<-=-∵()f x 在（－1，1）上是增函数
∴111t t -<-<-<，解得1
02
t <<.。