利用matlab和数值方法实验三个案例
三个参数matlab程序,用matlab求定积分的三个实例代码
三个参数matlab程序,⽤matlab求定积分的三个实例代码⼀、符号积分符号积分由函数int来实现。
该函数的⼀般调⽤格式为：int(s)：没有指定积分变量和积分阶数时，系统按findsym函数指⽰的默认变量对被积函数或符号表达式s求不定积分；int(s,v)：以v为⾃变量，对被积函数或符号表达式s求不定积分；int(s,v,a,b)：求定积分运算。
a,b分别表⽰定积分的下限和上限。
该函数求被积函数在区间[a,b]上的定积分。
a和b可以是两个具体的数，也可以是⼀个符号表达式，还可以是⽆穷(inf)。
当函数f关于变量x在闭区间[a,b]上可积时，函数返回⼀个定积分结果。
当a,b中有⼀个是inf 时，函数返回⼀个⼴义积分。
当a,b中有⼀个符号表达式时，函数返回⼀个符号函数。
例：求函数x^2+y^2+z^2的三重积分。
内积分上下限都是函数，对z积分下限是sqrt(x*y)，积分上限是x^2*y；对y积分下限是sqrt(x)，积分上限是x^2；对x的积分下限1，上限是2，求解如下：>>syms x y z %定义符号变量>>F2=int(int(int(x^2+y^2+z^2,z,sqrt(x*y),x^2*y),y,sqrt(x),x^2),x,1,2) %注意定积分的书写格式F2 =1610027357/6563700-6072064/348075*2^(1/2)+14912/4641*2^(1/4)+64/225*2^(3/4) %给出有理数解>>VF2=vpa(F2) %给出默认精度的数值解VF2 =224.92153573331143159790710032805⼆、数值积分1.数值积分基本原理求解定积分的数值⽅法多种多样，如简单的梯形法、⾟普⽣(Simpson)法、⽜顿－柯特斯(Newton-Cotes)法等都是经常采⽤的⽅法。
它们的基本思想都是将整个积分区间[a,b]分成n个⼦区间[xi,xi+1]，i=1,2,…,n，其中x1=a，xn+1=b。
MATLAB实验报告实例
MATLAB课程设计院（系）数学与计算机学院专业信息与计算科学班级学生姓名学号指导老师赵军产提交日期实验内容： 1. Taylor逼近的直观演示用Taylor 多项式逼近y = sin x．已知正弦函数的Taylor 逼近式为∑=----=≈nkk kkxxPx1121!)12()1()(sin．实验目的：利用Taylor多项式逼近y = sin x，并用图形直观的演示。
实验结果报告（含基本步骤、主要程序清单、运行结果及异常情况记录等）：1.将k从1取到5，得到相应的P = x-1/6*x^3+1/120*x^5-1/5040*x^7+1/362880*x^9;2.用MATLAB进行Taylor逼近，取x的范围是（-3.2，3.2）；程序清单如下：syms x; y = sin(x); p = x - (x^3)/6 + (x^5)/120 - (x^7)/5040 + (x^9)/362880 x1 = -3.2:0.01:3.2;ya = sin(x1);y1 = subs(p,x,x1);plot(x1,ya,'-',x1,y1)4.程序运行正常。
思考与深入：取y = sin x 的Taylor 多项式为P 的逼近效果很良好，基本接近y = sin x 的图像，不过随着k 的取值变多，逼近的效果会越来越好。
实验内容： 2. 数据插值在(,)[8,8][8,8]x y =-⨯-区域内绘制下面曲面的图形：2222sin()x y z x y+=+并比较线性、立方及样条插值的结果。
．实验目的：学会用MATLAB对函数进行线性、立方及样条插值，并比较结果。
实验结果报告（含基本步骤、主要程序清单、运行结果及异常情况记录等）：1.用MATLAB一次进行对函数的线性、立方、及样条插值，并进行算法误差分析。
2.主要程序如下：[x,y] = meshgrid(-8:1:8,-8:1:8);z = sin((x.^2 + y.^2).^0.5)./((x.^2 + y.^2).^0.5);surf(x,y,z),axis([-8,8,-8,8,-2,3])title('z的曲面图形'); %画出z的曲面图形%选较密的插值点，用默认的线性插值算法进行插值figure;[x1,y1] = meshgrid(-8:0.4:8,-8:0.4:8);z1=interp2(x,y,z,x1,y1);surf(x1,y1,z1),axis([-8,8,-8,8,-2,3])title('线性插值');%立方和样条插值figure;z1=interp2(x,y,z,x1,y1,'cubic');z2=interp2(x,y,z,x1,y1,'spline');surf(x1,y1,z1),axis([-8,8,-8,8,-2,3])title('立方插值');figure;surf(x1,y1,z2),axis([-8,8,-8,8,-2,3])title('样条插值');%算法误差的比较z = sin((x1.^2 + y1.^2).^0.5)./((x1.^2 + y1.^2).^0.5);figure;title('误差分析1');figure;surf(x1,y1,abs(z-z2)),axis([-8,8,-8,8,0,0.025]) title('误差分析2');3.结果如下：4.程序运行正常。
数值分析matlab程序实例
1，秦九韶算法，求出P(x=3)=2+4x+5x^2+2x^3的值clear all;x=3;n=3;a(1)=2;a(2)=4;a(3)=5;a(4)=2v(1)=a(n+1);for k=2:(n+1);v(k)=x*v(k-1)+a(n-k+2);endp=v(n+1)p=,1132，一次线型插值程序：利用100.121.求115的开方。
clear all;x1=100;x2=121;y1=10;y2=11;x=115;l1=(x-x2)/(x1-x2);l2=(x-x1)/(x2-x1);p1=l1*y1+l2*y2p1=10.71433，分段插值程序，已知为S1（x)为（0，0），（1，1），（2，5）（3,8）上的分段一次插值，求S1（1.5）.clear allx=[0123];y=[0158];n=length(x);a=1.5;for i=2:nif(x(i-1)<=a<x(i));endendH1=y(i-1)+(y(i)-y(i-1))/(x(i)-x(i-1))*(a-x(i-1))H1=3.50004）曲线拟合：用一个5次多项式在区间[0，2π]内逼近函数sin(x)。
clear allX=linspace(0,2*pi,50);Y=sin(X);[P,S]=polyfit(X,Y,5)plot(X,Y,'k*',X,polyval(P,X),'k-')P=-0.00560.0874-0.39460.26850.87970.0102S=R:[6x6double]df:44normr:0.03375)求有理分式的导数clear allP=[3,5,0,-8,1,-5];Q=[10,5,0,0,6,0,0,7,-1,0,-100];[p,q]=polyder(P,Q)6）将以下数据按从小到大排序：4.3 5.7 5.2 1.89.4a=[4.35.75.21.89.4];b(1:100)=0;n=1;b(a*10)=1;for k=1:100a(n)=k/10;if b(k)>0a(n)=k/10;n=n+1;endendaa=1.8000 4.3000 5.2000 5.70009.400010.00007)用二分法求方程x 3-x-1=0在[1,2]内的近似根，要求误差不超过10-3。
Matlab技术实战案例分享
Matlab技术实战案例分享引言从Matlab在科学与工程领域的广泛应用，我们可以看出它的强大功能和实用性。
在本文中，我们将分享一些实际应用中的Matlab技术案例，通过这些案例，读者将更好地理解和掌握Matlab的实战应用技巧。
一、图像处理图像处理是Matlab应用最广泛的领域之一，它在医学影像分析、计算机视觉等方面具有广泛的应用。
通过Matlab的图像处理工具箱，我们可以轻松处理和分析各种类型的图像数据。
案例一：基于Matlab的肌肉图像分析在运动学研究中，肌肉图像分析是一个重要的课题。
我们可以通过Matlab将单帧肌肉图像进行分割，提取关键特征并进行测量分析，如肌肉纤维方向和长度等。
这为运动学研究提供了有力的工具和方法。
案例二：基于Matlab的图像增强和去噪在计算机视觉领域，图像增强和去噪是常见的图像处理任务。
我们可以通过Matlab中的图像滤波函数和增强算法，对图像进行降噪和增强处理，提高图像的质量和清晰度。
这对于图像识别、目标检测等任务具有重要意义。
二、信号处理信号处理是Matlab应用广泛的另一个领域，它在通信、音频处理等方面具有重要的应用。
通过Matlab的信号处理工具箱，我们可以进行各种类型的信号处理和分析。
案例三：基于Matlab的音频处理和音频特征提取在音频处理领域，Matlab提供了丰富的函数和算法可以用来进行音频处理和音频特征提取。
我们可以通过Matlab对音频信号进行降噪、滤波、频谱分析等处理，同时提取关键的音频特征，如音调、节奏等。
案例四：基于Matlab的时频分析时频分析是信号处理中重要的分析方法之一。
通过Matlab的时频分析工具箱，我们可以对信号的瞬时频率和幅度进行分析，了解信号在时域和频域上的特征。
这对于故障诊断、语音识别等任务具有重要意义。
三、数值计算与优化数值计算与优化是Matlab的另一个重要领域，它在工程计算、统计建模等方面具有广泛的应用。
通过Matlab的数值计算和优化工具箱，我们可以轻松进行各种复杂的数值计算和优化问题求解。
实验五 MATLAB在数值计算中的应用
实验五 MATLAB 在数值计算中的应用徐晓-应用数学10-3班-10104479实验目的在工程技术中，大量的实际问题都需要进行近似处理，从而产生不同问题的数值计算 方法。
而 MATLAB 具有强大的数值运算功能，本实验的目的是学会用 MATLAB 软件进行一些数值运算，包括代数方程求根、插值问题和曲线拟合问题等。
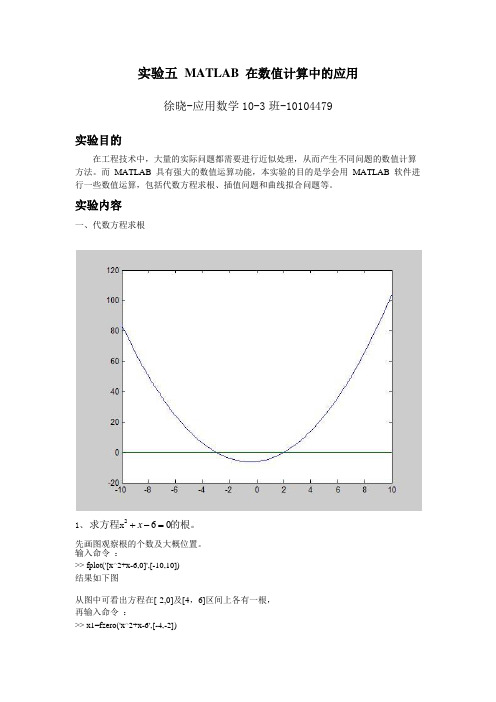
实验内容一、代数方程求根1、60x +-=2求方程x 的根。
先画图观察根的个数及大概位置。
输入命令 ：>> fplot('[x^2+x-6,0]',[-10,10])结果如下图从图中可看出方程在[-2,0]及[4，6]区间上各有一根， 再输入命令 ：>> x1=fzero('x^2+x-6',[-4,-2])x1 = -3>> x2=fzero('x^2-4*x-5',[0,4])x2 = 22、求方程3cos ln x x 的所有的根fplot('[3*cos(x)-log(x),0]',[- 50,50])%先画图，看一下确定解得大致范围 fplot('[3*cos(x)-log(x),0]',[- 30,30])%通过图形确定解得具体范围f=inline('3*cos(x)-log(x)');fsolve(f,[-19.04,-18.62,-13,-12,-7.2 ,-5.2,-1.4,1.4,5.2,7.2,12,13,18.62,19.04])%利用单个解得最近数值进行求解。
结果为：ans =Columns 1 through 4-19.7669 + 1.0760i -19.7669 + 1.0760i -13.5544 + 1.0312i -13.5544 + 1.0312iColumns 5 through 8-7.3921 + 0.9647i -7.3921 - 0.9647i -1.4453 + 0.7984i 1.4473 - 0.0000iColumns 9 through 125.3020 + 0.0000i 7.1395 + 0.0000i 11.9702 - 0.0000i 13.1064 + 0.0000iColumns 13 through 1418.6247 - 0.0000i 19.0387 + 0.0000i3、求方程的所有的根。
利用Matlab进行线性代数问题求解的方法与案例
利用Matlab进行线性代数问题求解的方法与案例引言线性代数是数学的一个重要分支，广泛应用于工程、物理、计算机科学等领域。
而Matlab作为一种功能强大的数值计算软件，提供了各种实用的工具和函数，可以方便地解决线性代数问题。
本文将介绍一些常用的线性代数问题求解方法，并通过具体的案例来展示Matlab在实际应用中的效果。
一、线性方程组的求解线性方程组是线性代数中最基础的问题之一。
Matlab提供了多种求解线性方程组的函数，如“backslash”操作符（\）和“linsolve”函数等。
下面通过一个实例来说明Matlab的线性方程组求解功能。
案例：假设有以下线性方程组需要求解：2x + 3y - 4z = 53x - 2y + z = 8x + 5y - 3z = 7在Matlab中输入以下代码：A = [2 3 -4; 3 -2 1; 1 5 -3];b = [5; 8; 7];x = A\b;通过以上代码，我们可以得到线性方程组的解x=[1; -2; 3]。
这表明在满足以上方程组的条件下，x=1，y=-2，z=3。
可以看出，Matlab在求解线性方程组时，使用简单且高效。
二、矩阵的特征值和特征向量求解矩阵的特征值和特征向量也是线性代数中的重要概念。
利用特征值和特征向量可以得到矩阵的许多性质和信息。
在Matlab中，我们可以通过“eig”函数来求解矩阵的特征值和特征向量。
案例：假设有一个2x2矩阵A，需要求解其特征值和特征向量。
在Matlab中输入以下代码：A = [2 3; 1 4];[V, D] = eig(A);通过以上代码，我们可以得到矩阵A的特征向量矩阵V和特征值矩阵D。
具体结果如下：特征向量矩阵V = [0.8507 -0.5257; 0.5257 0.8507]特征值矩阵D = [1.5858 0; 0 4.4142]由结果可知，矩阵A的特征向量矩阵V和特征值矩阵D可以提供有关该矩阵的很多信息，如相关线性变换、对称性等。
MATLAB应用实例分析例分析
MATLAB应用实例分析例分析Matlab应用例题选讲仅举一些运用MATLAB的例子，这些问题在数学建模中时常遇到，希望能帮助同学们在短时间内方便、快捷的使用MATLAB 解决数学建模中的问题，并善用这一工具。
常用控制命令:clc:%清屏; clear:%清变量; save:%保存变量; load:%导入变量一、利用公式直接进行赋值计算本金P以每年n次，每次i%的增值率(n与i的乘积为每年增值额的百分比)增加，当增加到r×P 时所花费的时间T为:(利用复利计息公式可得到下式) lnrnT() r，P,P(1，0.01i),T,r,2,i,0.5,n,12nln(1，0.01i)MATLAB 的表达形式及结果如下:>> r=2;i=0.5;n=12; %变量赋值>> T=log(r)/(n*log(1+0.01*i)) 计算结果显示为:T = 11.5813即所花费的时间为T=11.5813 年。
分析:上面的问题是一个利用公式直接进行赋值计算问题，实际中若变量在某个范围变化取很多值时，使用MATLAB，将倍感方便，轻松得到结果，其绘图功能还能将结果轻松的显示出来，变量之间的变化规律将一目了然。
若r在[1,9]变化，i在[0.5,3.5]变化;我们将MATLAB的表达式作如下改动，结果如图1。
r=1:0.5:9;i=0.5:0.5:3.5;n=12;p=1./(n*log(1+0.01*i));T=log(r')*p;plot(r,T)xlabel('r') %给x轴加标题ylabel('T') %给y轴加标题q=ones(1,length(i));text(7*q-0.2,[T(14,1:5)+0.5,T(14,6)-0.1,T(14,7)-0.9],num2str(i'))40350.5302520T 1151.510 22.55 33.50123456789r图11从图1中既可以看到T随r的变化规律，而且还能看到i的不同取值对T—r 曲线的影响(图中的六条曲线分别代表i的不同取值)。
MATLAB实验三《MATLAB在数值计算方面的应用》
《计算机仿真及应用》实验教案实验三MATLAB 在数值计算方面的应用一、实验目的1、掌握数值微积分的常用命令。
2、熟悉运用MATLAB指令进行矩阵和代数方程的求解。
3、了解 MATLAB在概率分析和统计分析方面的应用。
4、熟练掌握多项式运算和卷积运算。
5、区别符号计算和数值计算。
二、实验主要仪器与设备装配有 MA TLAB7.6软件的计算机三、预习要求做实验前必须认真复习第四章MATLAB的数值计算功能。
四、实验内容及实验步骤/ 2y(t) dt ，其中y 0.2sin t 。
试编写M脚本文件并运行之。
本例演示：trapz1、求积分s( x)用于数值积分时的的基本原理；sum 的用法及注意事项。
cleard=pi/8;%分区间的区间间隔t=0:d:pi/2;%包含 5个采样点的一维数组y=0.2+sin(t);s=sum(y);%求出的是：所有函数采样值之和s_sa=d*s;%高度为函数采样值的所有小矩形之和s_ta=d*trapz(y);disp(['sum 求得积分 ',blanks(3),'trapz 求得积分 '])disp([s_sa, s_ta])t2=[t,t(end)+d];y2=[y,nan];stairs(t2,y2,':k')hold onplot(t,y,'r','LineWidth',3)h=stem(t,y,'LineWidth',2);set(h(1),'MarkerSize',10)axis([0,pi/2+d,0,1.5])hold offshg运行结果：sum 求得积分trapz 求得积分1.5762 1.3013第1页共4页159132 6 10x 142、求方程711的解。
编写 M 脚本文件并运行之。
本例演示：如何确定解的性状315481216（唯一与否，准确与否）；如何求特解和齐次解；如何检查解的正确性。
Matlab在化工数值计算中的应用
Matlab 在化工数值计算中的应用(提纲) 基础知识Command Window 指令窗简介最简单的计算器使用方法加减乘除和幂运算符、矩阵的输入形式、常见表达式形式数值、变量和表达式数值的表示方法(十进制、科学记数)、变量命名规则(对大小写敏感，变量名的第一个字母必须为英文字母，不得含空格，但可含下划线链接符)、Matlab 默认的预定义变量(ans/inf/i 或j/pi/NaN 等)、复数和复数矩阵(把复数作为一个整体处理、real(z),imag(z),abs(z)/模,angle(z)/相角)。
例1：已知/612334,12,2i z i z i z e π=+=+=，并计算123/z z z z =计算结果的图形表示。
例2：画出衰减振荡曲线/3sin3t y e t -=及它的包络线并计算/30t y e -=。
t 的取值范围是[]04π， t=0:pi/80:4*pi; %定义自变量取值数组y0=exp(-t/3); %计算与自变量相应的y0数组y=exp(-t/3).*sin(3*t);%计算与自变量相应的y 数组plot(t,y,'-r',t,y0,':b',t,-y0,':b') %用不同颜色，不同线条绘制曲线数值计算结果的显示格式format/format short, format long, format short e, format long e, 标点符号的使用指令窗的常用控制指令clc, clear,edit, help, exit/quit, typeM 角本文件的编写与运算路径的制定帮助系统数值数组及其运算数组及其运算是Matlab 的核心内容2.1 一维数组的创建与赋值(逐个元素输入法、冒号生成法)；2.2 二维数组的创建与复制(直接输入法)2.3 执行数组运算的常用函数三角函数、反三角函数、幂指对函数、复数函数(abs,angle,conj （共厄复数）,imag,real)2.4 数组运算与矩阵运算A.’, A’,S./B,s*inv(B),A.^n,A^n,A.*B,A*B,A./B,A/B,f(A)注意运算符的小黑点。
MATLAB实验
MATLAB实验1. 引言MATLAB（Matrix Laboratory）是一种专用于数值计算和数据可视化的高级编程语言。
它在科学、工程和商业领域得到了广泛应用。
本文档将介绍一些MATLAB的基本操作和实验，帮助读者快速上手并熟悉MATLAB环境。
2. 实验一：变量和运算符2.1 变量的定义和赋值在MATLAB中，可以使用赋值运算符“=”来给变量赋值。
例如：a = 1;b = 2;2.2 运算符的使用MATLAB支持基本的数学运算符，如加法、减法、乘法、除法等。
下面是一些例子：c = a + b; % 加法d = a - b; % 减法e = a * b; % 乘法f = a / b; % 除法2.3 MATLAB函数的调用MATLAB内置了许多常用的数学函数，可以直接调用。
例如，求平方根可以使用sqrt函数：x = sqrt(a);3. 实验二：矩阵和向量操作3.1 矩阵的定义和初始化在MATLAB中，可以使用矩阵来存储和处理数据。
矩阵可以通过直接赋值来定义，也可以通过函数来初始化。
例如：A = [123; 456; 789]; % 直接定义矩阵B = zeros(3, 3); % 初始化一个3x3的全零矩阵3.2 矩阵的运算MATLAB提供了丰富的矩阵运算功能，如加法、乘法、转置等。
下面是一些例子：C = A + B; % 矩阵加法D = A * B; % 矩阵乘法E = A'; % 矩阵转置3.3 向量的操作向量是一种特殊的矩阵，只有一列或一行。
可以使用向量进行各种数学运算。
例如：v = [123]; % 定义一个行向量w = [4; 5; 6]; % 定义一个列向量dot_product = v * w; % 向量点乘cross_product = cross(v, w); % 向量叉乘4. 实验三：控制流程和函数4.1 条件语句条件语句用于根据不同的条件执行不同的操作。
MATLAB 使用if-else语句来实现条件控制。
《数学建模》实验指导4_matlab数值计算
《数学建模》实验指导4_matlab数值计算实验：matlab 数值计算实验目的：1. 掌握用matlab 进行插值、拟合、方程求解等数值计算的方法。
实验内容：1. 某气象观测站测得某日6:00-18:00之间每隔2小时的温度如下：时间 6 8 10 12 14 16 18 温度 18 20 22 25 30 28 24 试用三次样条插值求出该日6:30,8:30,10:30,12:30,14:30,16:30的温度。
2. 已知lg(x)在[1，101]区间11个整数采样点x=1:10:101的函数值lg(x)，试求lg(x)的5次拟合多项式p(x)，并分别绘制出lg(x)和p(x)在[1，101]区间的函数曲线。
提示: 对数表示: 以e 为底的是log() 以10为底的是log10() 以2为底的是log2()3. 求以下非线性方程组的解：1212122x x x x e x x e --?-=?-+=? 4. 求以下有约束最值：22min (,)120f x y x yx y x y =+?+≤?-≥?5．求0.6220.611/0.60.6y dy --?的值，画出被积函数在[-0.6,0.6]内的函数图形。
提示:绘制已经定义的函数的命令为:ezplot('fun',[a,b]).提示：● 一维插值：Y1=interp1(X,Y,X1,'method')1. 函数根据X 、Y 的值，计算函数在X1处的值。
X 、Y 是两个等长的已知向量，分别描述采样点和样本值，X1是一个向量或标量，描述欲插值的点，Y1是一个与X1等长的插值结果。
method 是插值方法，允许的取值有'linear'(线性插值)、'nearest'(最近插值)、'spline'(三次样条插值)、'cubic'（三次多项式插值），缺省值是'linear'。
实验6 Matlab数值计算实验报告
Tutorial 6 实验报告实验名称：Matlab数值计算实验目的：1、掌握数据统计与分析的方法；2、掌握数据插值和曲线拟合的方法及其应用；3、掌握多项式的常用运算。
实验内容：1.利用randn函数生成符合正态分布的10×5随机矩阵A，进行如下操作：（1）求A的最大元素和最小元素；（2）求A的每行元素的和以及全部元素的和；（3）分别对A的每列元素按升序、每行元素按降序排列。
2.用3次多项式方法插值计算1-100之间整数的平方根。
3.某气象观测站测得某日6：00-18：00之间每隔2h的室内外温度（°C）如下表所示。
使用三次样条插值分别求出该日室内外6：30-17：30之间每隔2h各点的近似温度，并绘制插值后的温度曲线。
4.已知lgx在[1,101]区间10个整数采样点的函数值如下表所示，试求lgx 的5次拟合多项式p(x)，并绘制lgx 和p(x)在[1,101]区间的函数曲线。
5. 有3个多项式(),(),()P x xx x P x x P x x x =+++=+=++4322123245223，试进行下列操作：（1） 求()()()()P x P x P x P x =+123。
（2） 求()P x 的根。
（3） 当x 取矩阵A 的每一元素时，求()P x 的值。
其中：.....A --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1121407523505256. 求函数在指定点的数值导数。
(),,f x x ==1237. 用数值方法求定积分。
（1）I π=⎰210的近似值。
（2）ln()x I dx x +=+⎰122011实验结果： 1.2.3.4.5.(1)(2)(3)6.7.(1)(2)。
数值分析matlab实验报告
数值分析matlab实验报告数值分析 Matlab 实验报告一、实验目的数值分析是研究各种数学问题数值解法的学科，Matlab 则是一款功能强大的科学计算软件。
本次实验旨在通过使用 Matlab 解决一系列数值分析问题，加深对数值分析方法的理解和应用能力，掌握数值计算中的误差分析、数值逼近、数值积分与数值微分等基本概念和方法，并培养运用计算机解决实际数学问题的能力。
二、实验内容（一）误差分析在数值计算中，误差是不可避免的。
通过对给定函数进行计算，分析截断误差和舍入误差的影响。
例如，计算函数＄f(x) ＝＼sin(x)＄在＄x ＝ 05$ 附近的值，比较不同精度下的结果差异。
（二）数值逼近1、多项式插值使用拉格朗日插值法和牛顿插值法对给定的数据点进行插值，得到拟合多项式，并分析其误差。
2、曲线拟合采用最小二乘法对给定的数据进行线性和非线性曲线拟合，如多项式曲线拟合和指数曲线拟合。
（三）数值积分1、牛顿柯特斯公式实现梯形公式、辛普森公式和柯特斯公式，计算给定函数在特定区间上的积分值，并分析误差。
2、高斯求积公式使用高斯勒让德求积公式计算积分，比较其精度与牛顿柯特斯公式的差异。
（四）数值微分利用差商公式计算函数的数值导数，分析步长对结果的影响，探讨如何选择合适的步长以提高精度。
三、实验步骤（一）误差分析1、定义函数｀compute_sin_error` 来计算不同精度下的正弦函数值和误差。
｀｀｀matlabfunction value, error ＝ compute_sin_error(x, precision)true_value ＝ sin(x)；computed_value ＝ vpa(sin(x)， precision)；error ＝ abs(true_value computed_value)；end｀｀｀2、在主程序中调用该函数，分别设置不同的精度进行计算和分析。
（二）数值逼近1、拉格朗日插值法｀｀｀matlabfunction L ＝ lagrange_interpolation(x, y, xi)n ＝ length(x)；L ＝ 0;for i ＝ 1:nli ＝ 1;for j ＝ 1:nif j ～＝ ili ＝ li （xi x(j)）／（x(i) x(j)）；endendL ＝ L ＋ y(i) li;endend｀｀｀2、牛顿插值法｀｀｀matlabfunction N ＝ newton_interpolation(x, y, xi)n ＝ length(x)；％计算差商表D ＝ zeros(n, n)；D(：， 1) ＝ y'；for j ＝ 2:nfor i ＝ j:nD(i, j) ＝（D(i, j 1) D(i 1, j 1)）／（x(i) x(i j ＋ 1)）；endend％计算插值结果N ＝ D(1, 1)；term ＝ 1;for i ＝ 2:nterm ＝ term （xi x(i 1)）；N ＝ N ＋ D(i, i) term;endend｀｀｀3、曲线拟合｀｀｀matlab％线性最小二乘拟合p ＝ polyfit(x, y, 1)；y_fit_linear ＝ polyval(p, x)；％多项式曲线拟合p ＝ polyfit(x, y, n)；％ n 为多项式的次数y_fit_poly ＝ polyval(p, x)；％指数曲线拟合p ＝ fit(x, y, ＇exp1'）；y_fit_exp ＝ p(x)；｀｀｀（三）数值积分1、梯形公式｀｀｀matlabfunction T ＝ trapezoidal_rule(f, a, b, n)h ＝（b a) ／ n;x ＝ a:h:b;y ＝ f(x)；T ＝ h （（y(1) ＋ y(end)）／ 2 ＋ sum(y(2:end 1)））；end｀｀｀2、辛普森公式｀｀｀matlabfunction S ＝ simpson_rule(f, a, b, n)if mod(n, 2) ～＝ 0error(＇n 必须为偶数'）；endh ＝（b a) ／ n;x ＝ a:h:b;y ＝ f(x)；S ＝ h ／ 3 （y(1) ＋ 4 sum(y(2:2:end 1)）＋ 2 sum(y(3:2:end 2)）＋ y(end)）；end｀｀｀3、柯特斯公式｀｀｀matlabfunction C ＝ cotes_rule(f, a, b, n)h ＝（b a) ／ n;x ＝ a:h:b;y ＝ f(x)；w ＝ 7, 32, 12, 32, 7 ／ 90;C ＝ h sum(w y)；end｀｀｀4、高斯勒让德求积公式｀｀｀matlabfunction G ＝ gauss_legendre_integration(f, a, b)x, w ＝ gauss_legendre(5)；％选择适当的节点数t ＝（b a) ／ 2 x ＋（a ＋ b) ／ 2;G ＝（b a) ／ 2 sum(w f(t)）；end｀｀｀（四）数值微分｀｀｀matlabfunction dydx ＝ numerical_derivative(f, x, h)dydx ＝（f(x ＋ h) f(x h)）／（2 h)；end｀｀｀四、实验结果与分析（一）误差分析通过不同精度的计算，发现随着精度的提高，误差逐渐减小，但计算时间也相应增加。
利用Matlab解决常见数学问题的案例分析
利用Matlab解决常见数学问题的案例分析概述：Matlab是一款流行的科学软件，广泛应用于数学建模、数据分析、图像处理等领域。
本文将通过几个实际案例，介绍如何利用Matlab解决常见的数学问题，并分析其解决方法和效果。
案例一：线性方程组的求解线性方程组是数学中常见的问题之一。
假设有如下线性方程组：3x + 2y = 14x - 3y = 5可以使用Matlab中的线性方程组求解函数`linsolve`来求解。
首先，定义系数矩阵A和常数矩阵b，并调用`linsolve`函数求解方程组：```matlabA = [3 2; 4 -3];b = [1; 5];x = linsolve(A, b);```运行上述代码后，可以得到方程组的解x为：x = 3y = -2案例二：函数曲线绘制Matlab具有强大的绘图功能，可以绘制各种函数曲线。
例如，我们可以绘制正弦函数sin(x)在区间[-2π,2π]上的曲线。
首先，定义x的取值范围，并计算对应的y 值：```matlabx = -2*pi:0.1:2*pi;y = sin(x);```接下来，使用`plot`函数将曲线绘制出来：```matlabplot(x, y);```运行代码后，可以得到正弦函数的曲线图。
案例三：最小二乘拟合最小二乘拟合是一种常见的曲线拟合方法，用于将一组数据拟合成一条曲线。
假设有一组离散的数据点，我们希望找到一个曲线来拟合这些数据。
在Matlab中，可以使用`polyfit`函数进行最小二乘拟合。
例如，假设有一组数据：x = [1 2 3 4 5];y = [0.5 2.5 2 4 3.5];可以使用`polyfit`函数进行线性拟合：```matlabp = polyfit(x, y, 1);```其中，第一个参数x是自变量的取值，第二个参数y是因变量的取值，第三个参数1表示进行一次多项式拟合。
拟合的结果保存在向量p中，p(1)为拟合曲线的斜率，p(2)为截距。
Matlab技术在物理实验设计中的应用案例分享
Matlab技术在物理实验设计中的应用案例分享1. 引言物理实验设计是物理学学科中不可或缺的一部分。
通过实验，我们可以观察和验证自然界中的物理现象，探索物理规律。
在过去的几十年中，Matlab技术逐渐在物理实验设计中得到广泛应用，它提供了强大的数值计算和数据分析工具，为实验设计和数据处理提供了更高效且准确的解决方案。
本文将分享几个物理实验中使用Matlab技术的案例，展示其在实验设计过程中的重要作用。
2. 案例一：光学实验中的传输矩阵计算在光学实验中，我们常常需要计算光线在不同光学元件中的传输矩阵，以便了解根据入射光线的参数得到出射光线的特性。
传统的计算方法需要大量的手动计算和拟合，而使用Matlab可以通过编写简洁的代码实现自动计算。
通过定义光学元件的参数和传输矩阵的运算规则，我们可以快速计算得到光线在多个元件中的传输矩阵，并进一步推导出所需的光学参数。
这种方法大大提高了实验设计的效率和精确度。
3. 案例二：力学实验中的数据拟合与分析在力学实验中，我们常常需要通过实验数据来验证力学定律和公式，并进行数据拟合和分析。
Matlab提供了丰富的数据处理和拟合函数，可以帮助我们从大量实验数据中提取所需的信息。
例如，在弹簧振动实验中，我们可以通过测量弹簧的振动周期和质量来验证胡克定律，并使用Matlab对实验数据进行最小二乘拟合，得到弹簧的劲度系数和振动频率。
这种数据处理和拟合的方法使得实验结果更加准确可靠。
4. 案例三：电路实验中的电路分析与模拟在电路实验中，我们经常需要对电路进行分析和模拟，以便了解电流、电压和功率等参数的变化规律。
Matlab提供了强大的电路分析和模拟工具，可以帮助我们建立电路模型，并通过数值计算和仿真得到电路的各种参数。
例如，在串联电路实验中，我们可以通过测量电阻和电压来验证欧姆定律，并使用Matlab进行电路模拟，得到电流和功率的变化曲线。
这种电路分析和模拟的方法大大简化了实验过程，同时提高了数据的准确性。
数值计算方法实验指导(Matlab版)
《数值计算方法》实验指导（Matlab版）学院数学与统计学学院计算方法课程组《数值计算方法》实验1报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验1 算法设计原则验证（之相近数相减、大数吃小数和简化计算步骤） 2. 实验题目(1) 取1610=z ，计算z z -+1和)1/(1z z ++，验证两个相近的数相减会造成有效数字的损失．(2) 按不同顺序求一个较大的数（123）与1000个较小的数（15310-⨯）的和，验证大数吃小数的现象．(3) 分别用直接法和九韶算法计算多项式n n n n a x a x a x a x P ++++=--1110)(在x =1.00037处的值．验证简化计算步骤能减少运算时间．对于第(3)题中的多项式P (x )，直接逐项计算需要2112)1(+=+++-+n n n 次乘法和n 次加法，使用九韶算法n n a x a x a x a x a x P ++++=-)))((()(1210则只需要n 次乘法和n 次加法． 3. 实验目的验证数值算法需遵循的若干规则． 4. 基础理论设计数值算法时，应避免两个相近的数相减、防止大数吃小数、简化计算步骤减少运算次数以减少运算时间并降低舍入误差的积累．两相近的数相减会损失有效数字的个数，用一个大数依次加小数，小数会被大数吃掉，乘法运算次数太多会增加运算时间． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab6. 实验过程(1) 直接计算并比较；(2) 法1：大数逐个加1000个小数，法2：先把1000个小数相加再与大数加； (3) 将由高次项到低次项的系数保存到数组A[n]中，其中n 为多项式次数．7. 结果与分析 (1) 计算的z z -+1= ，)1/(1z z ++．分析：(2) 123逐次加1000个6310-⨯的和是 ，先将1000个6310-⨯相加，再用这个和与123相加得．分析：(3) 计算次的多项式：直接计算的结果是，用时；用九韶算法计算的结果是，用时．分析：8. 附录：程序清单(1) 两个相近的数相减．%*************************************************************%* 程序名：ex1_1.m *%* 程序功能：验证两个相近的数相减会损失有效数字个数 *%*************************************************************z=1e16;x,y======================================================================(2) 大数吃小数%*************************************************************%* 程序名：ex1_2.m *%* 程序功能：验证大数吃小数的现象. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数z=123; % 大数t=3e-15; % 小数x=z; % 大数依次加小数% 重复1000次给x中加上ty=0; % 先累加小数% 重复1000次给y中加上ty=z + y; % 再加到大数x,y======================================================================(3) 九韶算法%*************************************************************%* 程序名：ex1_3.m *%* 程序功能：验证九韶算法可节省运行时间. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数A=[8,4,-1,-3,6,5,3,2,1,3,2,-1,4,3,1,-2,4,6,8,9,50,-80,12,35,7,-6,42,5,6,23,74,6 5,55,80,78,77,98,56];A(10001)=0; % 扩展到10001项，后面的都是分量0% A为多项式系数,从高次项到低次项x=1.00037;n=9000; % n为多项式次数% 直接计算begintime=clock; % 开始执行的时间 % 求x的i次幂% 累加多项式的i次项endtime=clock; % 完毕执行的时间time1=etime(endtime,begintime); % 运行时间disp('直接计算');disp(['p(',num2str(x),')=',num2str(p)]);disp([' 运行时间: ',num2str(time1),'秒']);% 九韶算法计算begintime=clock; % 开始执行的时间% 累加九韶算法中的一项endtime=clock; % 完毕执行的时间time2=etime(endtime,begintime); % 运行时间disp(' ');disp('九韶算法计算');disp(['p(',num2str(x),')=',num2str(p)]);disp([' 运行时间: ',num2str(time2),'秒']);《数值计算方法》实验1报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验1 算法设计原则验证（之数值稳定性） 2. 实验题目 计算定积分⎰==-1110,1,0,d n x e xI x nn ，分别用教材例1-7推导出的算法A 和B ，其中：算法A ：⎩⎨⎧≈-=-6321.0101I nI I n n 算法B ：⎪⎩⎪⎨⎧≈-=-0)1(1101I I nI n n 验证算法不稳定时误差会扩大．3. 实验目的验证数值算法需遵循的若干规则． 4. 基础理论设计数值算法时，应采用数值稳定性好的算法．数值稳定的算法，误差不会放大，甚至会缩小；而数值不稳定的算法会放大误差． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab6. 实验过程分别用数组IA[ ]和IB[ ]保存两种算法计算的结果． 7. 结果与分析 运行结果：（或拷屏）8. 附录：程序清单%*************************************************************%* 程序名：ex1_4.m *%* 程序功能：验证数值稳定性算法可控制误差. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数I=[0.856, 0.144, 0.712, 0.865, ...0.538, 0.308, 0.154, 0.938, ...0.492, 0.662, 0.843];% 保留14位小数的精确值, …是Matlab中的续行符% 算法AIA(1) = 0.6321; % Matlab下标从1开始，所以要用IA(n+1)表示原问题中的I(n）% 算法Bdisp('n 算法A 算法B 精确值');for n=1:11fprintf('%2d %14.6f %14.6f %14.6f\n',n-1,IA(n),IB(n),I(n));end% n显示为2位整数, 其它显示为14位其中小数点后显示6位的小数《数值计算方法》实验1报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验1 算法设计原则（除数绝对值不能太小） 2. 实验题目将线性方程组增广矩阵利用初等行变换可化为⎪⎪⎭⎫⎝⎛→-⎪⎪⎭⎫ ⎝⎛→-⎪⎪⎭⎫ ⎝⎛''0'0''02221112'12221121112222211121122121121b a b a r r b a b a a r r b a a b a a a a a a由此可解得'/',/'22221111a b x a b x ==．分别解增广矩阵为161011212-⎛⎫ ⎪⎝⎭和162121011-⎛⎫⎪⎝⎭的方程组，验证除数绝对值远小于被除数绝对值的除法会导致结果失真． 3. 实验目的验证数值算法需遵循的若干规则． 4. 基础理论设计数值算法时，应避免除数绝对值远小于被除数绝对值的除法，否则绝对误差会被放大，使结果失真． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab6. 实验过程用二维数组A 和B 存放方程组的增广矩阵，利用题目所给初等行变换求解方程组． 7. 结果与分析第1种顺序的方程组的解为x =，y =；第2种顺序的方程组的解为x =，y =． 分析：8. 附录：程序清单%************************************************************* %* 程 序 名：ex1_5.m * %* 程序功能：验证除数的绝对值太小可能会放大误差. * %*************************************************************clc;A=[1e-16, 1, 1; 2, 1, 2];B=[2, 1, 2; 1e-16, 1, 1]; % 增广矩阵% 方程组A% m = - a_{21}/a_{11} 是第2行加第1行的倍数% 消去a_{21}% m = - a_{12}/a_{22} 是第1行加第2行的倍数% 消去a_{12}, 系数矩阵成对角线% 未知数x1的值% 未知数x2的值disp(['方程组A的解: x1=',num2str(A(1,3)),', x2=',num2str(A(2,3))]); disp(' ');% 方程组B% m = - b_{21}/b_{11} 是第2行加第1行的倍数% 消去b_{21}% m = - b_{12}/b_{22} 是第1行加第2行的倍数% 消去b_{12}, 系数矩阵成对角线% 未知数x1的值% 未知数x2的值disp(['方程组B的解: x1=',num2str(B(1,3)),', x2=',num2str(B(2,3))]);《数值计算方法》实验2报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验2 非线性方程的迭代解法(之简单迭代法) 2. 实验题目用简单迭代法求方程010423=-+x x 在区间[1,2]的一个实根，取绝对误差限为410-．3. 实验目的掌握非线性方程的简单迭代法． 4. 基础理论简单迭代法：将方程0)(=x f 改写成等价形式)(x x ϕ=，从初值0x 开始，使用迭代公式)(1k k x x ϕ=+可以得到一个数列，若该数列收敛，则其极限即为原方程的解．取数列中适当的项可作为近似解． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程7. 结果与分析8. 附录：程序清单《数值计算方法》实验2报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验2 非线性方程的迭代解法(之Newton 迭代法) 2. 实验题目用Newton 迭代法求方程010423=-+x x 在区间[1,2]的一个实根，取绝对误差限为410-．3. 实验目的掌握求解非线性方程的Newton 迭代法． 4. 基础理论Newton 迭代法：解方程0)(=x f 的Newton 迭代公式为)(')(1k k k k x f x f x x -=+．5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程7. 结果与分析8. 附录：程序清单《数值计算方法》实验2报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验2 非线性方程的迭代解法(之对分区间法) 2. 实验题目用对分区间法求方程310x x --=在区间[1, 1.5]的一个实根，取绝对误差限为410-． 3. 实验目的掌握求解非线性方程的对分区间法． 4. 基础理论对分区间法：取[a ，b ]的中点p ，若f (p ) ≈ 0或b – a < ε，则p 为方程0)(=x f 的近似解；若f (a ) f (p ) < 0，则说明根在区间取[a ，p ]中；否则，根在区间取[p ，b ]中．将新的有根区间记为 [a 1，b 1]，对该区间不断重复上述步骤，即可得到方程的近似根． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程用宏定义函数f (x )；为了循环方便，得到的新的有根区间始终用[a ，b ]表示；由于新的有根区间可能仍以a 为左端点，这样会反复使用函数值f (a )，为减少运算次数，将这个函数值保存在一个变量fa 中；同样在判断新的有根区间时用到函数值f (p )，若新的有根区间以p 为左端点，则下一次用到的f (a )实际上就是现在的f (p )，为减少运算次数，将这个函数值保存在一个变量fp 中．算法的伪代码描述：Input ：区间端点a ，b ；精度要求（即误差限）ε；函数f （x ）；最大对分次数N Output ：近似解或失败信息7. 结果与分析8. 附录：程序清单说明: 源程序中带有数字的空行，对应着算法描述中的行号%**********************************************************%* 程序名：Bisection.m *%* 程序功能：使用二分法求解非线性方程. *%**********************************************************f=inline('x^3-x-1'); % 定义函数f(x)a=input('有根区间左端点: a=');b=input('右端点:b=');epsilon=input('误差限:epsilona=');N=input('最大对分次数: N=');1 % 对分次数计数器n置12 % 左端点的函数值给变量fafprintf('\n k p f(p) a(k) f(a(k))'); fprintf(' b(k) b-a\n');% 显示表头fprintf('%2d%36.6f%12.6f%12.6f%12.6f\n',0,a,fa,b,b-a);% 占2位其中0位小数显示步数0, 共12位其中小数6位显示各值3% while n≤ N 4 % 取区间中点p5% 求p 点函数值给变量fpfprintf('%2d%12.6f%12.6f',n,p,fp); % 输出迭代过程中的中点信息p 和f(p)6 % 如果f(p)=0或b-a 的一半小于误差限εfprintf('\n\n 近似解为:%f\n',p);% 则输出近似根p (7)return;% 并完毕程序 (7)89 % 计数器加110% 若f(a)与f(p)同号11% 则取右半区间为新的求根区间, 即a 取作p 12 % 保存新区间左端点的函数值 13% 否则14 % 左半区间为新的求根区间, 即b 取作p 15fprintf('%12.6f%12.6f%12.6f%12.6f\n',a,fa,b,b-a); %显示新区间端点与左端函数值、区间长度 16fprintf('\n\n 经过%d 次迭代后未达到精度要求.\n',N); % 输出错误信息(行17)《数值计算方法》实验2报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验2 非线性方程的迭代解法(之Aitken-Steffensen 加速法) 2. 实验题目用Aitken-Steffensen 加速法求方程010423=-+x x 在区间[1,2]的一个实根，取绝对误差限为410-．3. 实验目的熟悉求解非线性方程的Aitken-Steffensen 加速法． 4. 基础理论将方程0)(=x f 改写成等价形式)(x x ϕ=，得到从初值0x 开始的迭代公式)(1k k x x ϕ=+后，基于迭代公式)(1k k x x ϕ=+的Aitken-Steffensen 加速法是通过“迭代-再迭代-加速”完成迭代的，具体过程为kk k k k k k k k k k x y z z y x x y z x y +---===+2)(),(),(21ϕϕ． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程为了验证Aitken-Steffensen 加速法可以把一些不收敛的迭代加速成迭代收敛，我们使用将方程组变形为31021x x -=，取迭代函数31021)(x x -=ϕ，并利用宏定义出迭代函数．由于不用保存迭代过程，所以用x0表示初值同时也存放前一步迭代的值，y 和z 是迭代过程中产生的y k 和z k ，x 存放新迭代的结果．算法的伪代码描述：Input ：初值x 0；精度要求（即误差限）ε；迭代函数φ（x ）；最大迭代次数N7. 结果与分析8. 附录：程序清单%************************************************************* %* 程 序 名：Aitken_Steffensen.m * %* 程序功能：用Aitken-Steffensen 加速法求方程. * %************************************************************* clc;clear all;phi=inline('0.5 * sqrt( 10 - x^3)'); % 迭代函数x0=input('初值: x0 = ');epsilon=input('误差限: epsilon='); N=input('最大迭代次数: N=');disp(' n 迭代中间值y(n-1) 再迭代结构z(n-1) 加速后的近似值x(n)'); fprintf('%2d%54.6f\n',0,x0);% 占2位整数显示步数0, 为了对齐, 占54位小数6位显示x01 % n 是计数器2 % while n<=Ny= 3 ; % 迭代 z= 3 ; % 再迭代 x= 3 ; % 加速% x0初值与前一步的近似值, y 和z 是中间变量, x 是下一步的近似值fprintf('%2d%18.6f%18.6f%18.6f\n',n,y,z,x);%显示中间值和迭代近似值6 % 如果与上一步近似解差的绝对值不超过误差限 fprintf('\n\n 近似解 x≈x(%d)≈%f \n',n,x);% 则输出近似根 (7)， 可简略为: fprintf('\n\n 近似解 x=%f',x); return; % 并完毕程序(7) 8 % 相当于endif9 % 计数器加110 % 新近似值x 作为下一次迭代的初值 11fprintf('\n 迭代%d 次还不满足误差要求.\n\n',N); %输出错误信息(12)《数值计算方法》实验2报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验2 非线性方程的迭代解法（之Newton 下山法） 2. 实验题目用Newton 下山法求方程010423=-+x x 在区间[1,2]的一个实根，取绝对误差限为410-．3. 实验目的熟悉非线性方程的Newton 下山法． 4. 基础理论Newton 下山法：Newton 下山法公式为)(')(1k k kk k x f x f x x λ-=+，使|)(||)(|1k k x f x f <+，其中10≤<k λ．5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程定义函数f(x)和df(x)，其中df(x)是f(x)的导函数．每步迭代时先取下山因子为1，尝试迭代，判断尝试结果是否满足下山因子，若满足则作为这步的迭代结果；否则将下山因子减半，然后再尝试．为防止当前的x k 是极小值点，附近不会有满足下述条件的其它点，使尝试陷入死循环，同时计算机中能表示出的浮点数也有下界，因此我们设置了最大尝试次数．当超过最大尝试次数时，不再进行下山尝试．由于反复尝试迭代且要判断下山条件，所以f (x 0)和f ‘(x 0)会反复使用，为避免重复计算浪费运行时间，将这两个值分别保存在变量fx0和dfx0．而尝试产生的节点，判断下山条件时要用到它的函数值，若尝试成功，这个点会作为下一步的初值再使用，所以把该点的函数值也保存在变量fx 中．算法的伪代码描述：Input ：初值x 0；精度要求（即误差限）ε；函数与其导函数f （x ）和f’(x)；最大迭代次数N ；K 下山尝试最大次数Output ：近似解或失败信息7. 结果与分析8. 附录：程序清单%*************************************************************%* 程序名：NewtonDownhill.m *%* 程序功能：用Newton下山法求解非线性方程. *%*************************************************************clc;clear all;f=inline('x^3-x-1'); % 函数f(x)df=inline('3*x^2-1'); % 函数f(x)的导函数x0=input('初值: x0 = ');epsilon=input('误差限: epsilon=');N=input('最大迭代次数: N=');K=input('最大下山尝试次数: K=');1 % 迭代次数计数器2 % 存x0点函数值fprintf('\n\n n x(n) f(x(n))\n'); % 显示表头fprintf('%2d%14.6f%14.6f\n',0,x0,fx0); % 2位整数显示0, 共14位小数6位显示x0和fx03 % while n≤ Ndisp(''); % 换行显示下山尝试过程的表头disp(' 下山因子尝试x(n) 对应f(x(n)) 满足下山条件');disp('');4 % 存x0点导数值, 每次下山尝试不用重新计算ifdfx0==0 % 导数为0不能迭代disp(‘无法进行Newton迭代’);return;endlambda=1.0; % 下山因子从1开始尝试k=1; % k下山尝试次数计数器while k<=K % 下山最多尝试K次% 下山公式fx=f(x); % 函数值fprintf('%22.6f%14.6f%14.6f',lambda,x,fx); % 显示尝试结果if (abs(fx)<abs(fx0)) % 判断是否满足下山条件fprintf(' 满足\n');break; % 是, 则退出下山尝试的循环elsefprintf(' 不满足\n');endlambda=lambda/2; % 不是, 则下山因子减半k=k+1; % 计数器加1endif k>Kfprintf('\n 下山条件无法满足, 迭代失败.\n\n');return;endfprintf('%2d%14.6f%14.6f\n',n,x,fx);% 2位整数显示步数n, 共14位小数6位显示下步迭代结果22 % 达到精度要求否fprintf('\n\n 方程的近似解为: x≈%f\n\n',x); % (23)return; % 达到, 则显示结果并完毕程序(23) end % (24)% 用x0,fx0存放前一步的近似值和它的函数值, 进行循环迭代25262728fprintf('\n 迭代%d次还不满足误差要求.\n\n',N);《数值计算方法》实验2报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验2 非线性方程的迭代解法（之弦截法） 2. 实验题目用弦截法求方程010423=-+x x 在区间[1,2]的一个实根，取绝对误差限为410-． 3. 实验目的熟悉非线性方程的弦截法． 4. 基础理论将Newton 迭代法中的导数用差商代替，得到弦截法(或叫正割法)公式)()()(111k k k k k k k x f x f x f x x x x --+---=．5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程不保存迭代过程，所以始终以x 0和x 1分别存放x k -1和x k ，而x 存放新产生的迭代值x k +1，这样，下一次迭代时需要把上一步的x 1（即x k ）赋值于x 0（做新的x k -1）．这些点的函数值会重复用到，在迭代公式中也要用到，上一步的x 1作为下一步的x 0也会再一次用它的函数值，为减少重新计算该点函数值的运行时间，将x 1点的函数值保存在变量fx1中．算法的伪代码描述：Input ：初值x 0，x 1；精度要求（即误差限）ε；函数f （x ）；最大迭代次数N7. 结果与分析8. 附录：程序清单%*************************************************************%* 程序名：SecantMethod.m *%* 程序功能：用弦截法求解非线性方程. *%*************************************************************clc;clear all;f=inline('2*x^3-5*x-1'); % 函数f(x)x0=input('第一初值: x0 = ');x1=input('第二初值: x1 = ');epsilon=input('误差限: epsilon=');N=input('最大迭代次数: N=');fprintf('\n n x(n)\n'); % 显示表头fprintf('%2d%14.6f\n', 0, x0); % 占2位显示步数0, 共14位其中小数6位显示x0fprintf('%2d%14.6f\n', 1, x1); % 占2位显示步数1, 共14位其中小数6位显示x11 % 存x0点函数值2 % 存x1点函数值3 % 迭代计数器4 % while n≤ N% 弦截法公式fprintf('%2d%14.6f\n', n, x); %显示迭代过程6 % 达到精度要求否fprintf('\n\n 方程的近似解为: x≈%f\n\n', x);return; % 达到, 则显示结果并完毕程序89 % 原x1做x0为前两步的近似值10 % 现x做x1为一两步的近似值11 % x0点函数值12 % 计算x1点函数值, 为下一次循环13 % 计数器加1 14fprintf('\n 迭代%d 次还不满足误差要求.\n\n',N);《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验3 解线性方程组的直接法(之Gauss 消去法) 2. 实验题目用Gauss 消去法求解线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x ． 3. 实验目的掌握解线性方程组的Gauss 消去法． 4. 基础理论Gauss 消去法是通过对增广矩阵的初等行变换，将方程组变成上三角方程组，然后通过回代，从后到前依次求出各未知数．Gauss 消去法的第k 步(1≤k≤n -1)消元：若0≠kk a ，则依次将增广矩阵第k 行的kk ik a a /-倍加到第i 行（k+1≤i≤n），将第k 列对角线下的元素都化成0．5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程7. 结果与分析8. 附录：程序清单《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验3 解线性方程组的直接法(之Gauss 列主元消去法) 2. 实验题目用Gauss 列主元消去法求解线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x ． 3. 实验目的掌握解线性方程组的Gauss 列主元消去法． 4. 基础理论Gauss 列主元消去法也是通过对增广矩阵的初等行变换，将方程组变成上三角方程组，然后通过回代，从后到前依次求出各未知数．Gauss 列主元消去法的第k 步(1≤k≤n -1)消元：先在nk k k kk a a a ,,,,1 +中找绝对值最大的，将它所在的行与第k 行交换，然后将第k 行的kk ik a a /-倍加到第i 行（k+1≤i≤n），将第k 列对角线下的元素都化成0． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程7. 结果与分析8. 附录：程序清单《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验3 解线性方程组的直接法(之Doolittle 分解) 2. 实验题目对矩阵A 进行Doolittle 分解，其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A ．3. 实验目的掌握矩阵的Doolittle 分解． 4. 基础理论矩阵的Doolittle 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个单位下三角矩阵和一个上三角矩阵的乘积．若设⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n n n u u u u u u u u u u U l l ll l l L000000,1010010001333223221131211321323121则可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=+=-=∑∑-=-=1111,,2,1,/)(,,1,,k t kk tk it ik ik k r rj kr kj kj nk k i u u l a l nk k j u l a u其中k = 1，2，…，n ．5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程（1）按计算公式依次计算一行u 同时计算一列l ；（2）因为计算完u ij （或l ij ）后，a ij 就不再使用，为节省存储空间，将计算的u ij （和l ij ）仍存放在矩阵A 中的相应位置；（3）使用L 矩阵和U 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值．L 对角线上的元素为1，上三角部分为0，下三角部分为A 中对应的元素；U 的下三角部分为0，上三角部分为A 中对应的元素．算法的伪代码描述： Input ：阶数n ；矩阵A7. 结果与分析8. 附录：程序清单%****************************************************% 程序名: Doolittle.m *% 程序功能: 矩阵LU分解中的Doolittle分解. *%****************************************************clc;clear all;n=4; % 矩阵阶数A=[6 2 1 -1;2 4 1 0; 1 1 4 -1; -1 0 -1 3]disp('A=');disp(A);% LU分解(Doolittle分解)for k=1:n% 计算矩阵U的元素u_{kj}% (可参照下面l_{ik}的公式填写)% 计算矩阵L的元素l_{ik}% L 在A 下三角, U 在上三角(对角线为1) enddisp('分解结果：'); disp('L='); for i=1:n for j=1:nif i>j % 在下三角部分, 则取A 对于的元素显示 fprintf(' %8.4f',A(i,j));elseif i==j % 在对角线上, 则显示1 fprintf(' %8d',1);else % 在上三角部分, 则显示0 fprintf(' %8d',0); end endfprintf('\n'); % 换行 enddisp('U='); for i=1:n for j=1:nif i<=j % 在上三角部分或对角线上, 则取A 对于的元素显示 fprintf(' %8.4f',A(i,j));else % 在下三角部分, 则显示0 fprintf(' %8d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验3 解线性方程组的直接法(之LU 分解法) 2. 实验题目用LU 分解(Doolittle 分解)法求解线性方程组⎪⎩⎪⎨⎧=++=++=++104615631552162321321321x x x x x x x x x 3. 实验目的熟悉解线性方程组LU 分解法．4. 基础理论若将矩阵A 进行了Doolittle 分解，A = LU ，则解方程组b x A=可以分解求解两个三角方程组b y L=和y x U =．它们都可直接代入求解，其中b y L=的代入公式为∑-==-=11,,2,1,k j j kj k k n k y l b y而y x U=的代入公式为∑+=-=-=nk j kk j kjk k n n k u x uy x 11,,1,,/)( ．5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程（1）Doolittle 分解过程依次计算一行u 同时计算一列l 完成，并将计算的u ij （和l ij ）仍存放在矩阵A 中的相应位置；（2）求解方程组的代入公式中用到的u ij 和l ij 都直接在A 的相应位置取值即可． 算法的伪代码描述：Input ：阶数n ；矩阵A ；常数项向量b7. 结果与分析8. 附录：程序清单%**************************************************** % 程序名: LinearSystemByLU.m *% 程序功能: 利用LU分解(Doolittle分解)解方程组. *%****************************************************clc;clear all;n=3; % 矩阵阶数A=[1 2 6; 2 5 15; 6 15 46];b=[1;3;10];% LU分解(Doolittle分解)for k=1:n% 计算矩阵U的元素u_{kj}% (可参照下面l_{ik}的公式填写)% 计算矩阵L的元素l_{ik}% L在A下三角, U在上三角(对角线为1) endfor k=1:n % 用代入法求解下三角方程组Ly=by(k)=b(k);3 %∑-==-=11,,2,1,kjj kjk knkylby33enddisp('方程组Ly=b的解：y=');disp(y');for k=n:-1:1 % 回代求解上三角方程组Ux=y x(k)=y(k);6 %∑+=-=-=nkjj kjk knnkxuyx11,,1,,666 enddisp('原方程组的解：x='); disp(x');《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X成绩：1. 实验名称实验3 解线性方程组的直接法(之Cholesky 分解) 2. 实验题目对矩阵A 进行Cholesky 分解，其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A ． 3. 实验目的理解矩阵的Cholesky 分解． 4. 基础理论矩阵的Cholesky 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个下三角矩阵L 和L 转置的乘积，即A =LL T，其中L 各元素可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=-=∑∑-=-=11112,,2,1,/)(k t kktk it ik ik k r kr kk kk nk k i l l l a l l a l其中k = 1，2，…，n ．5. 实验环境操作系统：Windows xp ； 程序设计语言：VC++ 6. 实验过程（1）按计算公式依次先计算一列对角线上的元素l kk ，再计算这列其他元素l ik ，且对称位置的元素也取同一个值；（2）因为计算完l ij 后，a ij 就不再使用，为节省存储空间，将计算的l ij 仍存放在矩阵A 中的相应位置；（3）使用L 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值．L 上三角部分为0，对角线和下三角部分为A 中对应的元素．算法的伪代码描述：Input ：阶数n ；矩阵AOutput ：矩阵L (合并存储在数组A 中)行号 伪代码注释1 for k ← 1 to n2∑-=-=112k r krkk kk l a l3 for i ← k to n4 ∑-=-=11/)(k t kk tk it ik ik l l l a l计算结果存放在a ij5 endfor6 endfor7return L输出L7. 结果与分析8. 附录：程序清单%************************************************************* %* 程 序 名：Cholesky.m * %* 程序功能：对称正定矩阵的Cholesky 分解. * %*************************************************************n=4; % 矩阵阶数 A=[6,2,1,-1; 2,4,1,0; 1,1,4,-1; -1,0,-1,3];disp('A ='); for i=1:n for j=1:nfprintf('%10.4f',A(i,j)); % 共占14位endfprintf('\n');% 一行完毕换行end% Cholesky 分解 for k=1:n % 计算对角线上的l _{kk}% 计算其他的l _{ik} % 和l _{ki}end % L 在A 下三角, L^T 在上三角disp('分解结果：'); disp('L='); for i=1:n for j=1:n if i>=j % 在下三角部分或对角线上, 则取A 对于的元素显示fprintf('%10.4f',A(i,j));else % 在上三角部分, 则显示0 fprintf('%10d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X成绩：1. 实验名称实验3 解线性方程组的直接法(之改进的Cholesky 分解) 2. 实验题目对矩阵A 进行改进的Cholesky 分解，其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A ．3. 实验目的理解矩阵改进的Cholesky 分解． 4. 基础理论矩阵的改进的Cholesky 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个单位下三角矩阵L 和对角矩阵D 与L 转置的乘积，即A =LDL T，其中L 和D 各元素可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=-=∑∑-=-=11112,,2,1,/)(k t k kt it t ik ik k r kr r kk k nk k i d l l d a l l d a d其中k = 1，2，…，n ．5. 实验环境操作系统：Windows xp ； 程序设计语言：VC++ 6. 实验过程（1）按计算公式依次先计算D 的一个元素d k ，再计算L 中这列的元素l ik ，且对称位置的元素也取同一个值；（2）因为计算完d k 和l ij 后，a kk 或a ij 就不再使用，为节省存储空间，将计算的a kk 或l ij 仍存放在矩阵A 中的相应位置；（3）使用L 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值．L 对角线和上三角部分为0，下三角部分为A 中对应的元素；D 对角线为A 中对应的元素，其余都是0．算法的伪代码描述： Input ：阶数n ；矩阵AOutput ：矩阵L (合并存储在数组A 中)7. 结果与分析8. 附录：程序清单%************************************************************* %* 程 序 名：ImprovedCholesky.m * %* 程序功能：对称正定矩阵的改进的Cholesky 分解. * %*************************************************************n=4; % 矩阵阶数A=[6,2,1,-1; 2,4,1,0; 1,1,4,-1; -1,0,-1,3];disp('A =');for i=1:nfor j=1:nfprintf('%10.4f',A(i,j)); % 共占14位endfprintf('\n'); % 一行完毕换行end% Cholesky分解for k=1:n% 计算D对角线上的u_{kk}% 计算L的元素l_{ik}% 和L转置的元素l_{ki} end % L在A下三角, D在对角线disp('分解结果：');disp('L=');for i=1:nfor j=1:nif i>j % 在下三角部分, 则取A对于的元素显示fprintf('%10.4f',A(i,j));elseif i==j % 在对角线上, 则显示1fprintf('%10d',1);else % 在上三角部分, 则显示0fprintf('%10d',0);endendfprintf('\n'); % 换行enddisp('D='); for i=1:n for j=1:n if i==j % 在对角线上, 则取A 对于的元素显示fprintf('%10.4f',A(i,j));else % 其余显示0fprintf('%10d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验3 解线性方程组的直接法(之追赶法) 2. 实验题目用追赶法求解线性方程组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----101053001210023100124321x x x x 3. 实验目的熟悉解线性方程组的追赶法． 4. 基础理论对于系数矩阵为三对角矩阵的方程组，其Crout 分解可分解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=------11111211122111122211n n nn n n nn n n t t t s a s a s a s b a c b a c b a c b A这样，解方程组可以由如下2步完成：“追”：,,,3,2,/)(,,/,/,1111111111n i s y a f y t a b s s c t s f y b s i i i i i i i i i i i i =-=-====-----其中：Tn f f ),,(1 为方程组的常数项，n t 没用；“赶”：.1,,2,1,,1 --=-==+n n i x t y x y x i i i i n n5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程在“追”的过程中，向量s 和y 都有n 个元素，t 只有n -1个元素，又1s 和1y 的计算公式与其它i s 和i y 不同，所以先单独计算1s 和1y ，然后在一个n -1次循环中，求其它i s 和i y 以与i t ．由于在“追”的过程中，i b ，i c 和i f 在分别计算完对应的i s ，i t 和i y 后就不再使用，所以借用数组b ，c 和f 存储向量s ，t 和y ；同样在“赶”的过程中，i y 在计算完对应的i x 后就不再使用，所以再一次借用数组f 存储向量x ．追赶法算法的伪代码描述：Input ：阶数n ；三对角矩阵的三条对角线向量a ，b ，c ，常数项向量f Output ：方程组的解x改进的追赶法算法的伪代码描述：Input ：阶数n ；三对角矩阵的三条对角线向量a ，b ，c ，常数项向量f Output ：方程组的解x7. 结果与分析8. 附录：程序清单%*************************************************************%* 程序名：ChaseAfter.m *%* 程序功能：用追赶法求解三对角线性方程组. *%*************************************************************clc;clear all;n=4;a=[0,-1,-1,-3];b=[2, 3, 2, 5];c=[-1, -2, -1, 0];f=[0, 1, 0, 1];% "追"s(1) = b(1);y(1) = f(1); % 先单独求s_1和y_1 for k = 1 : n-1% 再求t_i(i=1,2,…,n-1)% s_i(i=2,3,…,n)% y_i(i=2,3,…,n)end% "赶"x(n) = y(n); % 先单独求x_nfor k = n-1 : -1 : 1% 再求x_i(i=n-1,n-2, (1)endx=x' % 输出解向量-------------------------------------------------------------------------------------------------------------------改进的程序:%*************************************************************%* 程序名：ChaseAfter.m *%* 程序功能：用追赶法求解三对角线性方程组. *%*************************************************************clc;clear all;n=4;a=[0,-1,-1,-3];b=[2, 3, 2, 5];c=[-1, -2, -1, 0];f=[0, 1, 0, 1];% "追"% b(1)=b(1); % s_1仍在b_1中，不用重新计算y(1)=f(1)/b(1); % 先单独y_1for k=1:n-1% 再求t_i(i=1,2,…,n-1)% s_i(i=2,3,…,n)% y_i(i=2,3,…,n)end% "赶"% f(n)=f(n); % x_n等于y_n仍在f_n中for k=n-1:-1:1% 再求x_i(i=n-1,n-2, (1)endx=f' % 输出解向量《数值计算方法》实验4报告班级：20##级####x班学号：20##2409####：##X 成绩：1. 实验名称实验4 解线性方程组的迭代法(之Jacobi迭代)2. 实验题目用Jacobi迭代法求解线性方程组1231231232251223x x x x x x x x x +-=⎧⎪++=⎪⎨++=⎪⎪⎩任取3. 实验目的掌握解线性方程组的Jacobi 迭代法． 4. 基础理论将第i （n i ≤≤1）个方程i n in i i b x a x a x a =+++ 2211移项后得到等价方程ii n in i i i i i i i i i a x a x a x a x a b x /)(11,11,11------=++--便可构造出Jacobi 迭代公式,1,0,/)()()(11,)(11,)(11)1(=------=++--+k a x a x a x a x a b x ii k n in k i i i k i i i k i i k i ． 5. 实验环境操作系统：Windows xp ； 程序设计语言：Matlab 6. 实验过程7. 结果与分析8. 附录：程序清单《数值计算方法》实验4报告班级： 20##级####x 班 学号： 20##2409#### ： ##X 成绩：1. 实验名称实验4 解线性方程组的迭代法(之Gauss-Seidel 迭代) 2. 实验题目用Gauss-Seidel 迭代法求解线性方程组。
数值方法matlab实验
数值方法matlab实验数值方法在Matlab中可以用来解决各种数学问题，包括求解方程、插值、微分、积分等。
下面是几个常见的数值方法在Matlab中的实验例子。
1. 求解方程：a. 使用二分法求解方程 f(x) = x^2 - 4 = 0。
```matlabf = @(x) x^2 - 4;[x, iter] = bisection_method(f, -5, 5, 1e-6);disp(['Root: ', num2str(x)]);disp(['Number of iterations: ', num2str(iter)]);```b. 使用牛顿法求解方程 f(x) = x^2 - 4 = 0。
```matlabf = @(x) x^2 - 4;df = @(x) 2*x;[x, iter] = newton_method(f, df, 3, 1e-6, 100);disp(['Root: ', num2str(x)]);disp(['Number of iterations: ', num2str(iter)]);```2. 插值：a. 使用拉格朗日插值多项式对给定数据点进行插值。
```matlabx = [0, 1, 2, 3];y = [1, 0, 1, 0];xx = 0:0.1:3;yy = lagrange_interpolation(x, y, xx);plot(x, y, 'o', xx, yy);```b. 使用样条插值对给定数据点进行插值。
```matlabx = [0, 1, 2, 3];y = [1, 0, 1, 0];xx = 0:0.1:3;yy = spline_interpolation(x, y, xx);plot(x, y, 'o', xx, yy);```3. 微分：a. 使用中心差分公式计算函数 f(x) = sin(x) 在某一点 x0 处的导数。
数值分析MATLAB实验报告
实验 2.1 多项式插值的震荡现象问题提出：考虑在一个固定的区间上用插值逼近一个函数。
显然Lagrange 插值中使用的节点越多，插值多项式的次数越高，我们自然关心插值多项式的次数增加时，)(x L n 是否也更加靠近被逼近的函数。
Runge 给出的一个例子是极著名并富有启发性的。
设区间[-1,1]上函数.2511)(2xx f +=实验内容：考虑空间[-1,1]的一个等距划分，分点为 nix i 21+-=， =i 0，1,2 ...,n , 则拉格朗日插值多项式为)(2511)(02x l xx L ini n ∑=+=. 其中，n i x l i ,...,2,1,0),(=是n 次Lagrange 插值基函数。
实验要求：（1）选择不断增大的分点数目,...,3,2=n 画出原函数)(x f 及插值多项式函数)(x L n 在[-1,1]上的图像，比较并分析实验结果。
（2）选择其他的函数，例如定义在区间[-5,5]上的函数 ,1)(4xxx h +=)arctan()(x x g =， 重复上述的实验看其结果如何。
首先编写拉格朗日插值函数的Matlab 实现： Matlab 程序为：function y=lagrange(x0,y0,x) %Lagrange 插值 n=length(x0); m=length(x); for i=1:m z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n if(j~=k)p=p*(z-x0(j))/(x0(k)-x0(j)); end ends=s+p*y0(k); endy(i)=s; end（1）当函数为.2511)(2xx f +=时， Matlab 程序为：x=linspace(-1,1,100); y=1./(1+25*x.^2); plot(x,y) hold on; for i=2:2:10x0=linspace(-1,1,i+1); y0=1./(1+25*x0.^2); y=laglanri(x0,y0,x); plot(x,y,'r--') hold on end运行结果：结果分析：从图上看到在区间[-1，1]的两端点附近，随着插值点数的增加，插值函数)(x L n 与)(x f 偏离的越远，而且出现了振荡现象。
数值分析在生活中应用举例及Matlab实现
一、最小二乘法,用MATLAB实现1. 数值实例下面给定地是乌鲁木齐最近1个月早晨7：00左右（新疆时间）地天气预报所得到地温度,按照数据找出任意次曲线拟合方程和它地图像.下面用MATLAB编程对上述数据进行最小二乘拟合.b5E2RGbCAP2008年10月26~11月26天数 1 2 3 4 5 6 7 8 9 10 温度9 10 11 12 13 14 13 12 11 9 天数11 12 13 14 15 16 17 18 19 20 温度10 11 12 13 14 12 11 10 9 8 天数21 22 23 24 25 26 27 28 29 30 温度7 8 9 11 9 7 6 5 3 1 下面用MATLAB编程对上述数据进行最小二乘拟合2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7,6,5,3,1];p1EanqFDPwa1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1=polyval(a1,x)b2=polyval(a2,x)b3=polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为：r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和.4、拟合曲线如下图二、线性方程组地求解（高斯-塞德尔迭代算法）1、实例：求解线性方程组（见书P233页）3612363311420238321321321xx xxx x x x x 记A x=b, 其中363320,,12361114238321bxAxx x 任取初始值Tx00,进行迭代.2、用C 语言实现,源程序如下：#include<stdio.h> #include<stdlib.h> struct Node {double value; // 矩阵非零元素值int index;// 元素地索引(序号或列标)};struct Matrix{struct Node *data; // 记录元素数据int total_elem; // 矩阵非零元素个数int total_ln; // 矩阵地总行数int total_col; // 矩阵地总列数};// 采用MSR法实现系数矩阵地存储void Create_Matrix( struct Matrix &matrix ){int index = 0, i = 0;double value = 0.0;printf( "请输入线性方程组系数矩阵地非零元素个数及总行数、总列数: " );scanf( "%d%d%d", &matrix.total_elem, &matrix.total_ln, &matrix.total_col );DXDiTa9E3dmatrix.data = (struct Node *)malloc( sizeof(struct Node)*(matrix.total_elem+1) );RTCrpUDGiTprintf( "请依次输入矩阵地主对角线元素及每行地非零非对角线元素(行优先)\n" );for( i = 0; i <= matrix.total_elem; i++ ){if( i == matrix.total_ln )value = 0;elsescanf( "%lf", &value );matrix.data[i].value = value;}printf( "\n系数矩阵地信息相关如下(Quote为添加项,表示序列号):" );printf( "\nValue:" );for( i = 0; i < matrix.total_elem + 1; i++ )printf( "%3.0lf", matrix.data[i].value );printf( "\nQuote:" );for( i = 0; i < matrix.total_elem + 1; i++ )printf( "%3d", i );printf( "\n\n" );for( i = 0; i <= matrix.total_elem; i++ ){if( i == 0 )printf( "请参照上表输入第每行第一个非零非主对角元素地序号\n " );if( i == matrix.total_ln )matrix.data[i].index = matrix.total_elem + 1;elseif( i == matrix.total_ln + 1 )printf( "请依次输入非零非对角元素地列标\n " );if( i != matrix.total_ln )scanf( "%d", &matrix.data[i].index );}}// 显示系数矩阵地相关信息void Display_Matrix( struct Matrix matrix ){int i = 0;printf( "系数矩阵采用MSR存储法地相关信息如下(Quote为添加项,表示序列号):" ); printf( "\nQuote: " );for( i = 0; i <= matrix.total_elem; i++ )printf( "%3d", i );printf( "\nvalue: " );for( i = 0; i <= matrix.total_elem; i++ )printf( "%3.0lf", matrix.data[i].value );printf( "\nIndex: " );for( i = 0; i <= matrix.total_elem; i++ )printf( "%3d", matrix.data[i].index );printf( "\n" );}// 初始化向量,使之分量全为0void Init_X( double *X, int n ){int i = 0;for( i = 0; i < n; i++ )X[i] = 0;}// 初始化右端向量void Init_b( double *b, int n ){int i = 0;Init_X( b, n );printf( "\n请输入%d个数(方程组地右端项): ", n );for( i = 0; i < n; i++ )scanf( "%lf", &b[i] );}// 初始化未知向量,得到初始值void Init_temp_X( double *temp, int n ){int i = 0;Init_X( temp, n );printf( "请输入X 向量地初始值: " );for( i = 0; i < n; i++ )scanf( "%lf", &temp[i] );}// 采用高斯-塞德尔GS迭代法求值int Calculate_X_GS( struct Matrix A, double *X, double *b )5PCzVD7HxA{int i = 0, j = 0, sum = 0;double temp = 0.0, temp_1 = 0.0, *temp_X = 0, judge = 0.0;jLBHrnAILgtemp_X = (double *)new double[A.total_ln];Init_temp_X( temp_X, A.total_ln );for( i = 0; i < A.total_ln; i++ )X[i] = temp_X[i];sum = 0;do{judge = 0.0;for( i = 0; i < A.total_ln; i++ )temp_X[i] = X[i];for( i = 0; i < A.total_ln; i++ ){temp = 0.0;temp_1 = 0.0;for( j = A.data[i].index; A.data[j].index < i && j <= A.total_elem; j++ )xHAQX74J0X temp_1 += A.data[j].value*X[A.data[j].index];for( ; j < A.data[i+1].index && j <= A.total_elem; j++ )LDAYtRyKfEtemp += A.data[j].value * temp_X[A.data[j].index];X[i] = (b[i] - temp_1- temp)/A.data[i].value;}for( i = 0; i < A.total_ln; i++ ){if( X[i]-temp_X[i] < 0 )judge = temp_X[i]-X[i]>judge ? temp_X[i]-X[i] : judge;Zzz6ZB2Ltk elsejudge = X[i]-temp_X[i]>judge ? X[i]-temp_X[i] : judge;dvzfvkwMI1 }sum++;printf( "\n\n第%d 次迭代地结果: ", sum );for( i = 0; i < A.total_ln; i++ )printf( "\nX[%d] = %g", i, X[i] );printf( "\njudge = %g", judge );}while( judge > 0.000001 );return sum;}void main( ){struct Matrix A;// 实现系数矩阵地存储及显示Create_Matrix( A );Display_Matrix( A );double *X = 0, *b = 0;X = (double *)new double[A.total_ln];b = (double *)new double[A.total_ln];Init_X( X, A.total_ln );Init_b( b, A.total_ln );int i = 0, sum = 0;sum = Calculate_X_GS( A, X, b );printf( "\n\n线性方程组地解为: " );for( i = 0; i < A.total_ln; i++ )printf( "\nX[%d] = %g", i, X[i] );printf( "\n总共迭代了%d 次\n\n", sum );}3、运行结果如下：版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some p arts, including text, pictures, and design. Copyright is personal ownership.rqyn14ZNXI 用户可将本文地内容或服务用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律地规定，不得侵犯本网站及相关权利人地合法权利.除此以外，将本文任何内容或服务用于其他用途时，须征得本人及相关权利人地书面许可，并支付报酬.EmxvxOtOcoUsers may use the contents or services of this articlefor personal study, research or appreciation, and othernon-commercial or non-profit purposes, but at the same time,they shall abide by the provisions of copyright law and otherrelevant laws, and shall not infringe upon the legitimaterights of this website and its relevant obligees. In addition, when any content or service of this article is used for otherpurposes, written permission and remuneration shall beobtained from the person concerned and the relevantobligee.SixE2yXPq5转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用，不得对本文内容原意进行曲解、修改，并自负版权等法律责任.6ewMyirQFLReproduction or quotation of the content of this articlemust be reasonable and good-faith citation for the use of news or informative public free information. It shall notmisinterpret or modify the original intention of the contentof this article, and shall bear legal liability such ascopyright.kavU42VRUs。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
产品， 而且这个投入－产出模式是稳定的；
(3) 部门 j 为生产一单位产品需要 tij 单位的产品投入其中 i n {1,2,, n}.
我们把 tij 称为投入系数，它通常被假设为不变的，用经济学的术语来说，就是投入比例是
水塔是一个高 12.2 米、直径 17.4 米的圆柱. 按照设计, 水塔水位降至约 8.2 米时, 水 泵自动启动加水; 当水位升高到约 10.8 米时, 水泵自动停止工作.
可以考虑采用用水率(单位时间的用水量)来反映用水规律, 并通过间隔一段时间测量 水塔里的水位来估算用水率.
表１给出了某个小镇某一天的真实数据, 试估计任何时刻从水塔流出的水流量, 及一 天的总用水量．
一、实验目的
三、水塔水流量的估计
了解建立数学模型的基本方法, 运用插值方法解决实际问题.
二、实验内容
美国某州的各公用水管理机构要求各社区提供各个时刻的用水率以及每天所用的总用 水量．但许多社区并没有测量流入或流出当地水塔的水量的设备，他们只能代之以每小时测 量水塔中的水位．更为重要的是，无论什么时候，只要水塔中的水位下降到某一最低水位时， 水泵就启动向水塔重新充水直到某一最高水位，但也无法得到水泵的供水量的测量数据．因 此，在水泵正在工作时，人们不容易建立水塔中水位与水泵工作时的用水量之间的关系．水 泵每天向水塔充水两次．试估计在任何时候，甚至包括水泵正在工作的时间内，水从水塔流 出的流量，并估计一天的总用水量．
d=A\ y' ;a=d(1),b=d(2)
N0=exp(a+b*t0)
x=1960:2001;yy=exp(a+b*x);
plot(x,yy,t,N,'o',2000,N0,'o')
计算结果为
a －33.0383， b 0.0186
N(2000) = 63.2336
所以取五位有效数，可得人口数据的指数拟合函数
位
上表给出了从第一次测量开始的以小时为单位的时刻，以及该时刻的高度单位为米的水塔中 水位的测量值．
三、实验原理
根据问题的要求, 关键在于确定用水率函数, 即单位时间内用水体积, 记为 f (t) . 如 果能够通过测量数据, 产生若干个时刻的用水率, 也就是 f (t) 在若干个点的函数值, 则 f (t) 的计算问题就转化为插值问题.
Байду номын сангаас
五、演示实验
根据投入产出表, 则投入系数矩阵为
0.15 0.1 0.2
T
0.3
0.05
0.3
0.2 0.3 0 .
将投入系数矩阵和对三个部门的外部需求输入 MATLAB, 程序如下: T=[0.15 0.1 0.2; 0.3 0.05 0.3; 0.2 0.3 0]; d=[50 100 100]’; A=eye(3)-T; x=A\d 得到三个部门的总产出分别为 126.7606, 204.2254, 186.6197 亿元.
由人口数据取对数（y = ln N）计算，得下表
t 1960 1961 1962 1963 1964 1965 1966 1967 1968 y 3.3918 3.4213 3.4503 3.4698 3.4763 3.4920 3.5133 3.5322 3.5505
根据表中数据及等式 a + b t k = y k ( k = 1，2，……，9)可列出关于两个未知数 a 、b 的 9 个方程的超定方程组（方程数多于未知数个数的方程组）
2
(4) 水泵第一次供水时间段为[8.97,10.95], 第二次供水时间段为[20.84, 22.96].
利用水塔截面积是常熟, 得到不同时刻水塔中水的体积如表 2.
表 2 水塔中水的体积(单位: 时刻(小时), 体积(立方米))
时 0 0.92 1.84 2.95 3.87 4.98 5.90 刻 t 体 2302 2254 2214 2171 2114 2095 2067 积 时 7.01 7.93 8.97 9.98 10.92 10.95 12.03 刻 t 水 2026 1995 1955 // // 2573 2497 位 时 12.95 13.88 14.98 15.90 16.83 17.93 19.04 刻 t 水 2428 2364 2295 2238 2183 2121 2059 位 时 19.96 20.84 22.01 22.96 23.88 24.99 25.91 刻 t 水 2005 1955 // 2573 2518 2461 2421 位
六、思考题
(1) 设有 n 个部门, 已知投入系数, 给定外部需求, 建立求解各部门总产出的模型;
(2) 设投入产出如上表所给, 如果今年对农业、工业、服务业的外部需求分别为 50, 100, 150 亿元, 问这三个部门的总产出分别为多少?
(3) 如果三个部门的外部需求分别增加 1 个单位, 它们的总产出分别增加多少个单位? (4) 可行的投入产出模型的投入系数应满足什么条件?
位
时 12.95 13.88 14.98 15.90 16.83 17.93 19.04
刻
t
水 10.21 9.94 9.65 9.41 9.18 8.92 8.66
位
时 19.96 20.84 22.01 22.96 23.88 24.99 25.91
刻
t
水 8.43 8.22 // 10.82 10.59 10.35 10.18
们可得到投入－产出平衡方程组
(I T )x d 或 Ax d ， A I T . 投入－产出分析所要解决的问题是：对已知最终需求量 d ，求出产出向量 x ， 使平衡 方程组成立. 由最终需求向量 d 于产出向量 x 的经济意义知 d 0 ， x 0 ， 因此， 一个
经济模型是可行的等价于由它确定的平衡方程组对任意的非负右端都有非负解. 以上讨论的经济模型称为 Lenontief 开模型.
在给出问题解决方法之前, 需要做下面假设.
(1) 水塔中水流量是时间的连续光滑函数, 与水泵工作无关, 流量只取决于水位表, 与水位无关;
(2) 水泵工作与否完全取决于水塔内水位的高低, 且每次加水的工作时间大约为 2 小 时;
S (17.4)2 237.8
(3) 水塔为标准圆柱体, 水塔截面积是常数
需要利用数据确定上式中系数 a，b。
四、演示实验
据统计，六十年代世界人口数据如下(单位：亿)
年 1960 1961 1962 1963 1964 1965 1966 1967 1968 人 29.72 30.61 31.51 32.13 32.34 32.85 33.56 34.20 34.83 口
单位 i 产品作为纯产出，我们称这个纯产出 di 为 i 产品的最终需求或对 i 产品的外部需求量， 而称 n 阶矩阵T (tij ) R nn 为投入矩阵. 设 x (x1, x2 ,, xn )T 和 d (d1, d2 ,, dn )T 分别表示产出向量和最终需求向量， 则我
二、实验内容
一个国家或区域的经济系统中,各部门(或企业)既有消耗又有生产,或者说既有“投 入” 又有“产出”.生产的产品供给各部门和系统外的需求,同时也消耗系统各部门所提供 的产品,消耗的目的是为了生产；生产的结果必然要创造新价值. 显然对每一部门,物资消耗 和新创造的价值等于它生产的总产值. 这就是“投入”和“产出”之间的平衡关系.
表 1 水位测量记录 (符号 // 表示水泵启动)
时
0 0.92 1.84 2.95 3.87 4.98 5.90
刻
t
水 9.68 9.48 9.31 9.13 8.98 8.81 8.69
位
时 7.01 7.93 8.97 9.98 10.92 10.95 12.03
刻
t
水 8.52 8.39 8.22 // // 10.82 10.50
利用 matlab 和数值方法实验三个案例
一、人口预测问题实验 一、实验目的
了解马尔萨斯人口模型的数学描述，熟悉数据处理的方法和技巧。
二、 实验内容
由中国人口数据资料（单位：亿）
年 1991 1992 1993 1994 1995 1996 t 数 11.58 11.72 11.85 11.98 12.11 12.24 量 N
产 农业 出
工业
服务业
最终需求 总产出
投入
农业
15
20
30
35
100
工业
30
10
45
115
200
服务业
20
60
70
150
初始投入 35
110
75
总投入
100
200
150
表中每行表示投入的分配, 每列表示投入的来源.
一般说，在对一个国家或区域的经济用投入产出法进行分析和研究时，首先根据统计数 字制定投入产出表，进而计算出有关的技术系数. 对这些系数的分析，可以了解经济系统的 结构和各部门之间的数量关系，还可通过求解方程组来获知最终需求的变动对各部门生产的 影响
三、实验原理
根据投入－产出平衡方程组
(I T )x d 或 Ax d ， A I T , 其中 x 和 d 分别表示产出向量和最终需求向量，矩阵 T 投入系数矩阵.
四、 实验任务
设整个经济由农业、工业、服务业三个部门组成, 分别生产农产品、工业品、提供服务 三种产品, 并不考虑政府干预和外来投资和输入等因素. 已知用货币计算的投入产出表如 下: (单位：亿元）
Lenontief 投入产出法讨论如下特殊的经济问题：在某种特定的经济状态中， 几个产 业部门中的每一个为了满足社会各经济部门对产品的总需求， 应具有怎样的产出水平.