_第二章连续系统的时域分析习题解答
《信号与系统》考研试题解答第二章连续系统的时域分析

X2.1 (东南大学2002年考研题)一线性时不变连续时间系统,其在某激励信号作用下的自由响应为(e-3t+e-t) (t),强迫响应为(1-e-2t) (t),则下面的说法正确的是______________(A)该系统一定是二阶系统(B)该系统一定是稳定系统(C)零输入响应中一定包含(e-3t+e-t) (t)(D )零状态响应中一定包含(1-e-2t) (t)X2.2(西安电子科技大学2005年考研题)信号f1(t)和f2(t)如图X2.2所示,f=f1(t)* f2(t),则f(-1)等于__________图X2.2X2.3 (西女电子科技大学2005年考研题)下列等式不成立的是(A) f1(t t。
)* f2(t t°) 锂) * f2(t)(B)-J—f1(t)* f2(t) dtd f1(t)dt-J* — f2(t) dt 2(C) f(t)* (t) f (t)(D) f(t)* (t) f (t)答案:X2.1[D] , X2.2[C], X2.3[B]、判断与填空题T2.1 (北京航空航天大学2001年考研题)判断下列说法是否正确,正确的打错误的打“X” 。
(1 )若y(t) f(t)*h(t),则y(2t) 2f(2t)*h(2t)。
[](2)如果x(t)和y(t)均为奇函数,贝U x(t)*y(t)为偶函数。
[](3)卷积的方法只适用于线性时不变系统的分析。
[](4 )若y(t) f(t)*h(t),则y( t) f( t)*h( t)。
[](5)两个LTI系统级联,其总的输入输出关系与它们在级联中的次序没有关系。
[]第二章、单项选择题连续系统的时域分析(C) 1.5 ( D)-0.5(A)T2.2 (华中科技大学2004年考研题)判断下列叙述或公式的正误,正确的在方括号中打“/,错误的在方括号中打“X”。
(1)线性常系数微分方程表示的系统,其输出响应是由微分方程的特解和齐次解组成,或由零输入响应和零状态响应所组成。
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第2章 连续时间系统的时域分析【圣才

Ri(t) v1(t) e(t)
Ri(t)
1 C
t
i(
)d
v1 (t )
e(t)
vo (t) v1(t)
消元可得微分方程:
6 / 59
圣才电子书
十万种考研考证电子书、题库视频学习平
1
台
C
d
dt
vo (t)
1 R
vo (t)
R
e(t)
2-2 图 2-2-2 所示为理想火箭推动器模型。火箭质量为 m1,荷载舱质量为 m2,两 者中间用刚度系数为 k 的弹簧相连接。火箭和荷载舱各自受到摩擦力的作用,摩擦系数分 别为 f1 和 f2。求火箭推进力 e(t)与荷载舱运动速度 v2(t)之间的微分方程表示。
M
di1 (t ) dt
Ri2 (t)
0
化简方程组可得微分方程:
(L2
M
2
)
d4 dt 4
vo
(t)
2RL
d3 dt 3
vo
(t)
2L C
R2
d2 dt 2
vo
(t)
2R C
d dt
vo
(t)
1 C2
vo
(t)
MR
d2 dt 2
e(t)
(3)由图 2-2-1(c)所示列写电路方程,得:
C
dv1 (t ) dt
b.自由响应由两部分组成,其中,一部分由起始状态决定,另一部分由激励信号决 定,二者都与系统的自身参数有关;当系统 0-状态为零,则零输入响应为零,但自由响应 可以不为零。
c.零输入响应在 0-时刻到 0+时刻不跳变,此时刻若发生跳变,可能为零状态响应分 量。
信号与系统王明泉版本~第二章习题解答
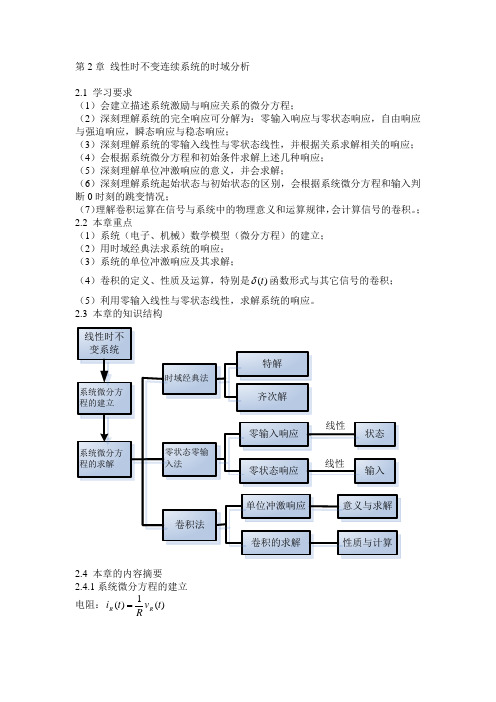
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
《信号与系统》第二章作业题答案

第二章 连续时间系统的时域分析1.与()t δ相等的表达式为:A .1()4t δ B .2(2)t δ C .(2)t δ D .1(2)2t δ解:由()t δ函数的性质1()()t t δαδα=可得,选B2.()j tet dt ωδ∞--∞'=⎰。
解:运用性质0()()()(0)t f t t dt f t f δ∞=-∞'''=-≡-⎰,得到()()j tet dt j j ωδωω∞--∞'=--=⎰。
3.两个线性时不变系统的级联,其总的输入-输出关系与它们在级联中的次序没有关系。
(正确)解:以冲击响应为例。
因为级联时,系统总的冲击响应等于各子系统冲击响应的卷积,而卷积与顺序没有关系,所以冲击响应与子系统顺序没有关系。
4.若()()()y t x t h t =*,则()()()y t x t h t -=-*-。
(错误)解:由()()()y t x h t d τττ∞-∞=-⎰,得()()()y t x h t d τττ∞-∞-=--⎰。
而()()()()()x t h t x h t d y t τττ∞-∞-*-=--+≠-⎰5.已知(21)f t -+波形如图所示,试画出()f t 的波形。
解:根据1反2展36.用图解法求图中信号的卷积()()()t f t f t f 21*=。
(03北邮A,8分)解:当10t -<时,即1t <时,由图1所示,12()()*()0f t f t f t ==图1当1020t t ->⎧⎨-<⎩时,即12t <<时,由图2所示,11201()()*()sin()[cos()1]t f t f t f t d t πττππ-===+⎰图2当1220t t -<⎧⎨->⎩时,即23t <<时,由图3所示,11222()()*()sin()cos()t t f t f t f t d t πττππ--===⎰图3当1222t t ->⎧⎨-<⎩时,即34t <<时,由图4所示,21221()()*()sin()[cos()1]t f t f t f t d t πττππ-===-⎰图4当4t >时,如图5所示,12()()*()0f t f t f t ==图57.如图所示系统由几个子系统组成,各子系统的冲激响应为)()(1t u t h =,)1()(2-=t t h δ,)()(3t t h δ-=,试求此系统的冲激响应)(t h ;若以()()t u e t e t -=作为激励信号,用时域卷积法求系统的零状态响应。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
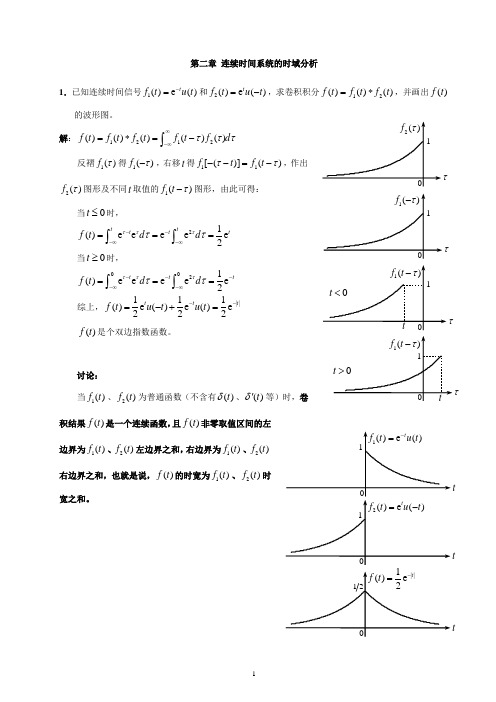
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
(NEW)吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解

目 录第1章 信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 连续系统的时域分析2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散系统的时域分析3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 傅里叶变换和系统的频域分析4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 连续系统的s域分析5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 离散系统的z域分析6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 系统函数7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 系统的状态变量分析8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第1章 信号与系统1.1 复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象,其图像为信号的波形。
根据信号的不同特性,可对信号进行不同的分类:确定信号与随机信号;周期信号与非周期信号;连续时间信号与离散时间信号;实信号与复信号;能量信号与功率信号等。
二、信号的基本运算1加法和乘法f1(t)±f2(t)或f1(t)×f2(t)两信号f1(·)和f2(·)的相加、减、乘指同一时刻两信号之值对应相加、减、乘。
2.反转和平移(1)反转f(-t)f(-t)波形为f(t)波形以t=0为轴反转。
图1-1(2)平移f(t+t0)t0>0,f(t+t0)为f(t)波形在t轴上左移t0;t0<0,f(t+t0)为f(t)波形在t轴上右移t0。
图1-2平移的应用:在雷达系统中,雷达接收到的目标回波信号比发射信号延迟了时间t0,利用该延迟时间t0可以计算出目标与雷达之间的距离。
这里雷达接收到的目标回波信号就是延时信号。
3.尺度变换f(at)若a>1,则f(at)波形为f(t)的波形在时间轴上压缩为原来的;若0<a<1,则f(at)波形为f(t)的波形在时间轴上扩展为原来的;若a<0,则f(at)波形为f(t)的波形反转并压缩或展宽至。
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
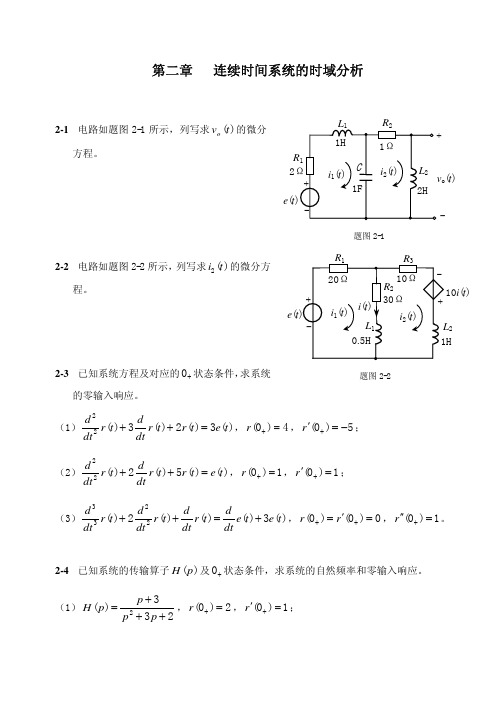
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 (1) s1 (t ) = f1 (t ) ∗ f 2 (t ) ; (2) s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ; (3) s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示,列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示, 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) , 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统,其初始状态一定,当输入 e1 (t ) = δ (t ) 时,其全响应
r1 (t ) = −3e − tU (t ) ; 当 输 入 e2 (t ) = U (t ) 时 , 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ,其中 f1 (t ) = sgn(t − 1) , f 2 (t ) = e 2-15 求下列卷积 (1) f1 (t ) = e
_第二章连续系统的时域分析习题解答

— P2-1 —第二章 连续系统的时域分析习题解答2-1 图题2-1所示各电路中,激励为f (t ),响应为i 0(t )和u 0(t )。
试列写各响应关于激励微分算子方程。
解:.1)p ( ; )1(1)p ( , 111 , 1111)( )b (;105.7)625(3 102 ;)(375)()6253(4)()()61002.041( )a (0202200204006000f i p f p u p f p p p u i f p p p ppft u pf i p pu i t f t u p t f t u p =+++=++⇒++=+=+++=++=⨯=+⇒⨯==+⇒=++-- 2-2 求图题2-1各电路中响应i 0(t )和u 0(t )对激励f (t )的传输算子H (p )。
解:.1)()()( ; 11)()()( )b (;6253105.7)()()( ; 6253375)()()( )a (220 20 40 0 +++==+++==+⨯==+==-p p p p t f t i p H p p p t f t u p H p p t f t i p H p t f t u p H f i f u f i fu2-3 给定如下传输算子H (p ),试写出它们对应的微分方程。
.)2)(1()3()( )4( ; 323)( )3(; 33)( )2( ; 3)( )1( +++=++=++=+=p p p p p H p p p H p p p H p p p H解:; 3d d 3d d )2( ; d d 3d d)1( f tf y t y t f y t y +=+=+ . d d 3d d 2d d 3d d )4( ; 3d d 3d d 2 )3( 2222t f tf y t y t y f t f y t y +=+++=+ 2-4 已知连续系统的输入输出算子方程及0– 初始条件为:.4)(0y ,0)(0y )y(0 ),()2(13)( )3(; 0)(0y ,1)(0y ,0)y(0 ),()84()12()( )2(;1)(0y ,2)y(0 ),()3)(1(42)( )1(---2---2--=''='=++==''='=+++-=='=+++=t f p p p t y t f p p p p t y t f p p p t yf (u 0(t ) (b) u 0(t ) (a)图题2-1— 2 —试求系统的零输入响应y x (t )(t /0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 连续系统的时域分析习题解答2-1 图题2-1所示各电路中,激励为f (t ),响应为i 0(t )和u 0(t )。
试列写各响解:.1)p ( ; )1(1)p ( , 111 , 1111)( )b (; 105.7)625(3 102 ;)(375)()6253(4)()()61002.041( )a (0202200204006000f i p f p u p f p p p u i f p p p ppf t u pf i p pu i t f t u p t f t u p =+++=++⇒++=+=+++=++=⨯=+⇒⨯==+⇒=++-- 2-2 求图题2-1各电路中响应i 0(t )和u 0(t )对激励f (t )的传输算子H (p )。
解:. 1)()()( ; 11)()()( )b (; 6253105.7)()()( ; 6253375)()()( )a (220 20 40 0 +++==+++==+⨯==+==-p p pp t f t i p H p p p t f t u p H p p t f t i p H p t f t u p H f i f u f i f u2-3 给定如下传输算子H (p ),试写出它们对应的微分方程。
.)2)(1()3()( )4( ; 323)( )3(; 33)( )2( ; 3)( )1( +++=++=++=+=p p p p p H p p p H p p p H p p p H解:; 3d d 3d d )2( ; d d 3d d )1( f tfy t y t f y t y +=+=+. d d 3d d 2d d 3d d )4( ; 3d d 3d d 2 )3( 2222t f tf y t y t y f t f y t y +=+++=+2-4 已知连续系统的输入输出算子方程及0– 初始条件为:. 4)(0y ,0)(0y )y(0 ),()2(13)( )3(; 0)(0y ,1)(0y ,0)y(0 ),()84()12()( )2(;1)(0y ,2)y(0 ),()3)(1(42)( )1(---2---2--=''='=++==''='=+++-=='=+++=t f p p p t y t f p p p p t y t f p p p t y 1f u 0(t )(b)1f (t )4k 6k 2Fu 0(t )(a)图题2-1试求系统的零输入响应y x (t )(t 0)。
解:,e e)( ,3 ,1 )1(32121t tA A t y p p --+=-=-=. 0 , )e 12(1)(121444200 ,)e ()( , 2 ,0 )3(. 0 , 2sin e 5.0)(905.00cos 240)sin (cos 21cos 0 ,)2cos(e )( , 2j 2 ,0 )2(;0 , e 5.1e 5.3)(5.15.3312 232132323123213 ,2123213233232132213 ,213212121 t t t y A A A A A A A A A A t A A t y p p t t t y A A A A A A A A A A A A t A A t y p p t t y A A A A A A t t t t t t ------+-=⇒⎪⎩⎪⎨⎧-=-==⇒⎪⎩⎪⎨⎧+-=-=+=++=-===⇒⎪⎩⎪⎨⎧︒-===⇒⎪⎩⎪⎨⎧=+-=+=++=±-==-=⇒⎩⎨⎧-==⇒⎩⎨⎧--=+= 2-5 已知图题2-5各电路零输入响应分别为:.0 ,V sin e6cos e2)( (b); 0 ,V e 4e 6)( )a (3343x x t t t t u t t u ttt t ----+=-=求u (0-)、i (0-)。
解:;V 246)0()0( )a (x =-==+-u u.0)66(1.0)0()0( V;202)0()0( )b (A3512)1618(61)0()0( x x x x =+-===+===++-==+-+-+-i i u u i i 2-6 图题2-6所示各电路:(a) 已知i (0-) = 0,u (0-) = 5V ,求u x (t ); (b) 已知u (0-) = 4V ,i (0-) = 0,求i x (t ); (c) 已知i (0-) = 0,u (0-) = 3V ,求u x (t ) .解:0650650)( )(2=++⇒=++⇒=p p pp p a Z61H (b) i +-图题2-511i 1H(a)16F -u+5i1H F 1 6 (a)+-(b) 1 11F1H+ u -i(c)1F+u-iH 1 41 5图题2-6.0 ,V e 10e 15)( ,10 ,1532050)0()0(' ,V 5)0(e e )(3 , 2 32212121322121---------=-==⇒⎩⎨⎧--=+=⇒===+=⇒-=-=⇒ t t u A A A A A A C i u u A A t u p p t t x x x t t x.0 ,V e e 4 ,4 ,1 ,15035)0(' ,V 3)0( ,e e ,4,1,045045: )c (. 0 ,A sin e 4)( ,2 ,4 sin cos 4cos 04401)0(' , 0)0( )cos(e )(11 , 11 022011110)( )b (4214212122121212121212-------------==-=-=+⨯-==+=-=-==++⇒=++=-==⇒⎩⎨⎧--==⇒=+⨯-==+=⇒--=+-=⇒=++⇒=+++⇒= t u A A u u A A u p p p p p p t t t i A A A A A A A A i i A t A t i j p j p p p p p p t t x x x t t x t x x x t x 同理/πY 2-7 已知三个连续系统的传输算子H (p )分别为:. )2(13 )3( ; )84()12( )2( ; )3)(1(42)1(22+++++-+++p p p p p p p p p p 试求各系统的单位冲激响应h (t )。
解:; )()e e ()(3111)( )1(3t t h p p p H t t ε--+=⇒+++=.)()e 41e 2541()(241)2(5.241)( )3(;)()2sin e 875.02cos e 8181()( 2)2(2875.0)2(8181)( 5.1,81)84(1)21()81(8481)( )2(2222222222t t t h p p p p H t t t t h p p p p H B A p p p p B p A p p B Ap p p H t t t t εε-----+=⇒+-++=-+-=⇒++⨯-++-=⇒-==⇒++--+-=++++-= 2-8 求图题2-8所示各电路中关于u (t )的冲激响应h (t 解:(a)f u pu pu u i i pui f 480422111=+⇒⎩⎨⎧=--+=- e 5.0)(125.05.0184)( 81t h p p f u p H tε-=⇒+=+==⇒24(a).V )()e 4.0e 4.2()( 64.214.0 6723115.01111311)( )c (.V )()e 2e 2()( 221223235.015.01)( )b (6222t t h p p p p p pp p p H t t h p p p p p pp p H t t t t εε-----=⇒+++-=++=+++⨯+=-=⇒+-+=++=++=2-9 求图题2-9所示各电路关于u (t )的冲激响应h (t )与阶跃响应g (t )。
解:.)(2cos 21)(0 2cos 42)(21)()( ),(2sin 42)(21)( 21)21(24121121)( )a ( t _0 222t t t tt d h t g t t t t h p p p p p pp p H εετεττεδ=⎥⎦⎤⎢⎣⎡+==-=⇒+-=+=++=-⎰),(e 41)(21)(2141211212111)( )b ( 21 t t t h p p p p p p H t εδ-+=⇒++=++=++= . )()e e ()(0]e e [)()( )e e 2()(112211122)( )c (.)()e 211()(0e 21)(21)()( 2 2_0 2 21 21 _0 t t][t t t d h t g t h p p ppp p H t t t t d h t g tt t t t εεττεεεετττττ-----------=+-==-=⇒+-+=+-+=-=-==⎰⎰2-10 如图题2-10所示系统,已知两个子系统的冲激响应分别为h 1(t )(t 1),h 2(t )(t ),试求整个系统的冲激响应h (t )。
解:求和号后的冲激响应为)1()(-+t t δδ,于是整个系统的冲激响应为:1F+-(b)+f-1 311+ u -(c) + f - F 13 图题2-8+f-1F 1F1H+ u-(a)+ f -1F 1+-(b)1+ f-1F 1H (c)12+ u -图题2-9图题2-10y (t )h 2(t ) h 1(t )f ())1()()(-+=t t t h εε2-11 各信号波形如题图2-11所示,试计算下列卷积,并画出其波形。
. )(')( )3( ; )()( )2( ; )()( )1(41 31 21t f t f t f t f t f t f ***解:.)3()3(21)1()1(23)1()1(23)3()3(21)3()3(21)1()1()1()1(21 )1()1(21)1()1()3()3(21 )1()1()(')( )3();6()6(21)5()5(21)4()4(21)3()3( )2()2(21)1()1(21)(21 )4()3()2()()( )2();4()4(21)2()2( )()2()2()4()4(21 )2()2()()( )1(2()2(21)()2()2(21)(11411113111211-----+++-++=-----+++---+++-++=--+=--+--------+------=-+---=--+---+++-++=-++=--+-++=t t t t t t t t t t t t t t t t t t t t t f t f t f t f t t t t t t t t t t t t t t t f t f t f t f t f t t t t t t t t t t t f t f t f t f t t t t t t t f εεεεεεεεεεεεεεεεεεεεεεεεε***2-12 求下列各组信号的卷积积分。
