大作业1(机电控制系统时域频域分析)
控制系统频域分析
控制系统频域分析1. 引言频域分析是控制系统理论中的重要内容之一，它可以帮助工程师们深入了解控制系统的特性和性能。
通过对系统在频域上的响应进行分析，可以得到系统的频率响应曲线和频率特性，从而更好地设计和调节控制系统。
本文将介绍控制系统频域分析的基本概念、常用方法和应用场景。
2. 控制系统频域分析的基本概念2.1 传递函数传递函数是描述系统输入与输出之间关系的数学模型。
对于线性时不变系统，其传递函数可以用拉普拉斯变换表示。
传递函数的频域特性可以通过对传递函数进行频域变换得到。
2.2 频率响应频率响应是控制系统在不同频率下的输出响应，它是描述系统在不同频率下性能的重要指标。
频率响应可以通过传递函数的频域特性来分析。
2.3 增益余弦图增益余弦图是描述控制系统增益和相位随频率变化的图形。
在增益余弦图中，横轴表示频率，纵轴表示增益和相位角。
通过分析增益余弦图，可以得到系统的幅频特性和相频特性。
3. 控制系统频域分析的常用方法3.1 简单频率响应分析简单频率响应分析是最基本也是最常用的频域分析方法之一。
它通过对系统输入信号进行正弦波信号的傅里叶变换，得到系统的频率响应曲线。
常用的频率响应曲线有幅频特性曲线和相频特性曲线。
3.2 Bode图Bode图是一种常用的频域分析方法，它将系统的增益和相位角随频率变化的情况绘制在一张图中。
通过分析Bode图，可以得到系统的幅频特性和相频特性，并进行系统的稳定性分析。
3.3 Nyquist图Nyquist图是一种用于分析系统稳定性的频域分析方法。
它将系统的传递函数关联到一个复平面上，通过对系统传递函数的频域特性进行分析，可以得到系统的稳定性信息。
Nyquist图可以帮助工程师们更好地设计和调节控制系统。
4. 控制系统频域分析的应用场景频域分析在控制系统设计和调节中有广泛的应用场景。
以下是几个常见的应用场景：4.1 控制系统稳定性分析通过对控制系统的频域特性进行分析，可以判断系统的稳定性。
自动控制 控制系统的时域和频域描述1
定义 x y u 1 0
dy du dy x2 0 1u dt dt dt dy 2 d 2u du d2y x3 2 0 2 1 2 u 2 2u dt dt dt dt
其中
0 b0 0 1 b1 a1 0 0 2 b2 a2 1 a2 0 2 3 b3 a1 2 a2 1 a3 0 7 6 2 5
第2章 控制系统的时域和频域描述
d 由y x3 x3可得到 dt d x3 a1 x3 a2 x2 a3 x1 u dt
写成矩阵形式
x1 (t ) 0 d x2 ( t ) 0 dt x3 (t ) a3 1 0 a2 0 x1 (t ) 0 1 x2 ( t ) 0 u a1 x3 (t ) 1
SISO系统的矩阵表示
其中
x1 x X 2 xn
d X (t ) AX (t ) Bu(t ) dt y (t ) C T X (t ) du(t )
1 B 2 n
C T [1 0 0] d 0 b0
间形式。
d3 d2 d d y (t ) 6 2 y (t ) 8 y (t ) 4 y (t ) 2 u(t ) 7u(t ) 3 dt dt dt dt
解：按照前面介绍的方法
d x j x j 1 j 1u dt x1 y 0u y
第2章 控制系统的时域和频域描述
解：写成标准的状态空间形式
d X (t ) AX (t ) F ( X , t ) BU (t ) dt y C T X D TU
自动控制系统的时域频域分析报告
摘要 (I)第一早绪论 (1)1.1自动控制理论发展概述 (1)1.2Matlab 简介.............................2第二早控制系统的时域分析与校正......22.1概述 (2)2.2一阶系统的时间响应及动态性能 (3)2.3二阶系统的时间响应及动态性能 (4)2.4高阶系统的阶跃响应、动态性能及近似 (11)AVV ------- *第二早控制系统的频域分析与校正 (13)3.1概述 ................................ . (13)3.2频率特性的表示方法.................. .. (14)3.3频率特性的性能指标.................. .. (15)3.4典型环节的频率特性.................. .. (17)第四章结论 (23)课程设计总结 (24)参考文献 (25)附录 (26)摘要第一章绪论1.1自动控制理论发展概述自动控制理论是在人类征服自然地生产实践活动中孕育、产生，并随着社会生产和科学技术的进步而不断发展、完善起来的。
早在古代，劳动人民就凭借生产实践中积累的丰富经验和对反馈概念的直观认识，发明了许多闪烁控制理论智慧火花的杰作。
我国北宋时代苏颂和韩公廉利用天衡装置制造的水运仪象台，就是一个按负反馈原理构成的闭环非线性自动控制理论；1681年Dennis Papin发明了用做安全调节装置的锅炉压力调节器；1765年俄国人普尔佐诺夫发明了蒸汽锅炉水位调节器。
1788年，英国人瓦特在他发明的蒸汽机上使用了离心调速器，解决了蒸汽机的速度控制问题，引起了人们对控制技术的重视。
之后，人们曾经试图改善调速器的准确性，却常常导致系统产生振荡。
1868年，英国物理学家麦克斯韦通过对调速系统线性常微分方程的建立与分析，解释了瓦特速度控制系统中出现的不稳定问题，开辟了用数学方法研究控制系统的途径。
此后，英国数学家劳斯和德国数学家古尔维茨独立的建立了直接根据代数方程的系数判别系统稳定性的准则。
控制系统频域分析
c •
K g 0 系统不稳定
在Bode图上可测取相角裕度和幅值裕度
L() dB
1
kg
20 lg h
20 lg
| Gk ( jg ) |
0dB
c
kg rad / s
20 lg | Gk ( jg ) |
F( )
00
-1800
g
rad / s
MATLAB中用来求系统幅值裕度和相位裕度的函数为 margin( )，它的调用格式有以下几种：
1
| Gk ( jg ) |
例：已知系统开环传递函数为：
Gk
s
ss
5
10.1s
1
试绘制系统Bode图并求系统相角裕量和幅值裕量。
num=[5]; den=conv (conv ([1 0],[1 1]), [0.1 1]); sys=tf (num, den); margin (sys) [Gm,Pm,Wg,Wc]=margin (sys)
系统的频域性能指标为：
Gm =2.2000；Pm =13.5709；Wg =3.1623；Wc = 2.1020
即：系统的剪切频率ωc=2.1020rad/s；相位裕度 =13.5709°，
相位穿越频率ωg=3.1623rad/s； 幅值裕量kg=20*log10(2.2)=6.8485dB。
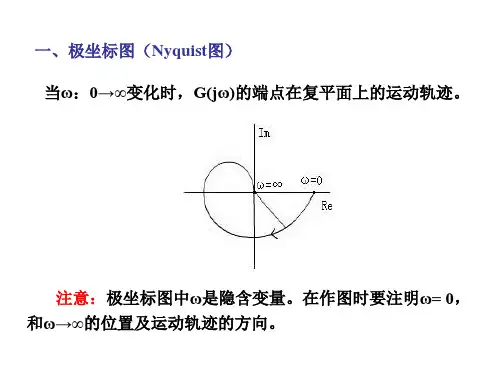
一、极坐标图（Nyquist图） 当ω：0→∞变化时，G(jω)的端点在复平面上的运动轨迹。
注意：极坐标图中ω是隐含变量。在作图时要注明ω= 0， 和ω→∞的位置及运动轨迹的方向。
MATLAB中用来绘制连续系统极坐标图的指令为 nyquist( )，其调用格式为：
nyquist (sys)——sys为由tf、zpk建立起来的控制系统数 学模型。此时绘制出来的极坐标图的默认角频率w是从 -∞~ +∞。这点与自动控制原理略有不同。
哈工大机电系统控制基础大作业Matlab时域分析
《机电系统控制基础》大作业一基于MATLAB的机电控制系统响应分析哈尔滨工业大学2013年12月12日1作业题目1. 用MATLAB 绘制系统2()25()()425C s s R s s s Φ==++的单位阶跃响应曲线、单位斜坡响应曲线。
2. 用MATLAB 求系统2()25()()425C s s R s s s Φ==++的单位阶跃响应性能指标：上升时间、峰值时间、调节时间和超调量。
3. 数控直线运动工作平台位置控制示意图如下：X i伺服电机原理图如下：LR(1)假定电动机转子轴上的转动惯量为J 1，减速器输出轴上的转动惯量为J 2，减速器减速比为i ，滚珠丝杠的螺距为P ，试计算折算到电机主轴上的总的转动惯量J ；(2)假定工作台质量m ，给定环节的传递函数为K a ，放大环节的传递函数为K b ，包括检测装置在内的反馈环节传递函数为K c ，电动机的反电势常数为K d ，电动机的电磁力矩常数为K m ，试建立该数控直线工作平台的数学模型，画出其控制系统框图；(3)忽略电感L 时，令参数K a =K c =K d =R=J=1，K m =10，P/i =4π，利用MATLAB 分析kb 的取值对于系统的性能的影响。
源代码：t=[0:0.01:5];u=t;C=[25],R=[1,4,25];G=tf(C,R);[y1,T]=step(G,t);y2=lsim(G,u,t);subplot(121),plot(T,y1);xlabel('t(sec)'),ylabel('x(t)'); grid on;subplot(122),plot(t,y2);grid on;xlabel('t(sec)'),ylabel('x(t)');仿真结果及分析：源代码：t=[0:0.001:1];yss=1;dta=0.02;C=[25],R=[1,4,25];G=tf(C,R);y=step(G,t);r=1;while y(r)<yss;r=r+1;endtr=(r-1)*0.001;[ymax,tp]=max(y);tp1=(tp-1)*0.001;mp=(ymax-yss)/yss;s=1001;while y(s)>1-dta && y(s)<1+dta;s=s-1;endts=(s-1)*0.001;[tr tp1 mp ts]仿真结果及分析：C = 25ans = 0.4330 0.6860 0.2538 1.0000由输出结果知：上升时间为0.4330秒，峰值时间为0.6860秒，最大超调量为0.2538，调整时间1.0000秒。
机电系统仿真第一次大作业试题
说 明大家所做大作业是本门课程成绩评定的依据，将来是要存档、检查的，需认真完成。
一经发现有相互抄袭现象，取消大作业成绩！一、所提交大作业要有封面，其上标注有：课程名称、第几次大作业、专业班级、姓名、学号等。
二、对问题的求解方法、过程要求有详细说明，有程序时需列出程序清单，程序求解结果。
（有问题可答疑）以下问题可设计MATLAB 程序进行求解。
题目一、电动机通过弹性轴联接惯性负载，以电动机输出力矩T m 为激励，负载转角θL 为响应。
已知235L J kg m =⋅，220m J kg m =⋅，15/k kN m rad =⋅，1.5/m c kN m s rad =⋅⋅。
对所给系统进行动力学分析（参考课件的实例分析），求解以下问题：（1）确定系统输入、输出量，选取系统状态变量，列出系统的状态空间表达式（包括状态方程和输出方程）；（2）求系统的特征值，判断系统稳定性、能控性、能观性；（3）求系统输入-输出间的传递函数；（4）求系统输入-输出间的频响函数（绘制出伯德图）；（5）求系统在单位阶跃输入时，状态变量和输出变量的时域响应（绘制出响应图线）；（6）求系统在方波信号（自行产生一方波信号数据作为输入）输入激励下的响应，绘制出状态变量和输出变量的时域响应图线。
题目二、油井钻井平台与钻孔机模型。
钻井平台向钻孔机提供驱动力矩，带动钻轴转动，钻头受被钻物体的接触力矩。
以力矩τ2为输入（驱动），以转角θ2为输出响应。
已知2130J kg m =⋅，2220J kg m =⋅，15/k kN m rad =⋅，1 1.8/c kN m s rad =⋅⋅，22/c kN m s rad =⋅⋅。
对所给系统进行动力学分析（参考课件的实例分析），求解以下问题：（1）确定系统输入、输出量，选取系统状态变量，列出系统的状态空间表达式（包括状态方程和输出方程）；（2）求系统的特征值，判断系统稳定性、能控性、能观性；（3）求系统输入-输出间的传递函数；（4）求系统输入-输出间的频响函数（绘制出伯德图）；（5）求系统在单位阶跃输入时，状态变量和输出变量的时域响应（绘制出响应图线）；（6）求系统在方波信号（自行产生一方波信号数据作为输入）输入激励下的响应，绘制出状态变量和输出变量的时域响应图线。
机电控制工程基础 第 4 章 线性系统的频域分析法
第 4 章 线性系统的频域分析法
第 4 章 线性系统的频域分析法
4. 2 频率特性的图示法
工程中常用的频率特性的图示法有以下三种。 1. 频率特性曲线 频率特性 曲 线 包 括 幅 频 特 性 曲 线 和 相 频 特 性 曲 线。幅 频 特 性 是 频 率 特 性 幅 值︱ G (j ω )︱ 随 ω 的变 化规律;相频特性描述的是频率特性相角 ∠ G ( j ω )随 ω 的 变化规律,如图 4－4 ( a )所示。
时域分析法具有直观、准确的优点,但实际系统往往都 是高阶的,求解高阶系统的微分方程以及按时域指标进行设 计并非易事。频域分析法能比较方便地由频率特性来确定系 统性能。当系统的传递函数难以确定时,可以通过实验法确 定频率特性。
第 4 章 线性系统的频域分析法
4. 1 频 率 特 性
4. 1. 1 频率特性的基本概念与定义 1. 频率特性的基本概念 首先以图 4－1 所示的 RC 滤波网络为例,建立频率特性
(3 )有关传递函数的概念和运算法则对频率特性同样适 用。
(4 )频率特性虽然是用系统稳态响应定义的,但可以用来 分析系统全过程的响应特性,这一点可以通过傅里叶变换加 以证明。
第 4 章 线性系统的频域分析法
图 4－3 频率特性、传递函数与微分方程之间的关系
第 4 章 线性系统的频域分析法
(5 )频率特性具有明显的物理意义。 传递函数表示的是系统或环节传递任意信号的性能,而 频率特性则表示系统或环节传递正弦信号的能力,并且有 3 个要素,即同频率、变幅值、相位移。因此,对于稳定的系 统,可以通过实验的方法求出其输出量的各个物理参数。即 在系统的输入端施加不同频率的正弦信号,然后测量系统的 输出稳态响应,再根据幅值比和相位差作出系统的频率特性 曲线。对于不稳定系统,输出响应稳态分量中含有由系统传 递函数的不稳定极点产生的呈发散或振荡的分量,所以不稳 定系统的频率特性不能通过实验方法确定。
机电控制工程基础课件：控制系统的时域分析
式中,(t - T )代表输出量的稳态分量 c t ( ∞ );
代表输
出量的瞬态分量,通常以 ct ( t )表示, t 趋于无穷大时,瞬态分 量趋于零。
一阶系统的单位斜坡响应曲线如图 3－4 所示。
控制系统的时域分析
图 3－4 一阶系统的单位斜坡响应曲线
控制系统的时域分析 该指数曲线的特点如下: (1 )指数曲线的初始斜率为零,因为
控制系统的时域分析
控制系统的时域分析
3. 1 典型输入信号与系统性能指标 3. 2 一阶系统的时间响应 3. 3 二阶系统的时间响应 3. 4 高阶系统的时间响应 习题
控制系统的时域分析
3. 1 典型输入信号与系统性能指标
3. 1. 1 典型输入信号 典型输入信号一般应具备两个条件:一是信号的数学表
响应曲线的初始斜率为
控制系统的时域分析
图 3－5 一阶系统的单位脉冲响应曲线
控制系统的时域分析
3. 2. 5 一阶系统的三种响应之间的关系 比较一阶系统对单位脉冲、单位阶跃和单位斜坡输入信
号的响应,可以发现这三种信号之间有以下关系:
控制系统的时域分析
即系统对输入信号导数的响应,等于系统对该输入信号 响应的导数。或者说系统对输入信号积分的响应,等于系统 对该输入信号响应的积分。这一重要特点适用于任意线性定 常系统,但不适用于线性时变系统和非线性系统。
控制系统的时域分析
图 3－1 是某二阶系统在单位阶跃函数作用下的时间响 应,即单位阶跃响应。 c (输出, r (t )表示输入。为了便于分析 和比较,假定系统在单位阶跃输入信号作用前处于静止状态, 而且输出量及各阶导数均等于零。对于大多数控制系统来说, 这种假设是符合实际情况的。描述系统性能的指标通常为:
自动控制系统的时域频域分析
目录摘要 (Ⅰ)第一章绪论 (1)1.1 自动控制理论发展概述 (1)1.2 Matlab简介 (2)第二章控制系统的时域分析与校正 (2)2.1 概述 (2)2.2 一阶系统的时间响应及动态性能 (4)2.3 二阶系统的时间响应及动态性能 (5)2.4高阶系统的阶跃响应、动态性能及近似 (9)第三章控制系统的频域分析与校正 (11)3.1 概述 (11)3.2 频率特性的表示方法 (13)3.3 频率特性的性能指标 (15)3.4 典型环节的频率特性 (16)第四章结论 (20)课程设计总结 (22)参考文献 (24)附录 (24)摘要系统利用Matlab进行控制系统时域与频域的分析与设计，对控制系统的给定数学模型，研究系统性能与系统结构、参数之间的关系。
其仿真过程是以某种算法从初态出发，逐步计算系统的响应，最后绘制出系统的响应曲线，即可分析系统的性能。
自动控制系统的计算机仿真是一门涉及到计算机技术、计算数学与控制理论、系统辨识、控制工程以及系统科学的综合性学科。
控制系统仿真就是以控制系统的模型为基础，主要用数学模型代替实际的控制系统，以计算机为工具，对控制系统进行实验和研究的一种方法。
控制系统最常用的时域分析法，就是在输入信号的作用下，求出系统的输出响应。
系统采用单位阶跃响应为输入信号，求出各典型环节（一阶、二阶及高阶）的输出响应，分析各响应在阻尼比和固有频率变化时对输出响应的影响，从而可以选择最优方案，提高系统的快速性。
而频域分析法是应用频率特性研究控制系统的一种经典方法，以此可直观的表达出系统的频率特性，其主要方法有Bode图、Nyquist曲线、Nichols图，由于编写M 文件时三种方法只需改变固定的命令，所以系统主要研究Bode图。
同样是研究响应的典型环节，及比例、微分、积分、惯性、二阶振荡与高阶环节，分析其对数幅频特性与对数相频特性。
经过对两种分析方法的对比与分析，得出了时域分析法与频域分析法的关系与区别。
hyq--机电控制系统大作业一
《机电控制系统分析与设计》课程大作业之一基于MATLAB 的直流电机 双闭环调速系统的设计与仿真1. 设置该大作业的目的在转速闭环直流调速系统中，只有电流截止负反馈环节对电枢电流加以保护，缺少对电枢电流的精确控制，也就无法充分发挥直流伺服电动机的过载能力，因而也就达不到调速系统的快速起动和制动的效果。
通过在转速闭环直流调速系统的基础上增加电流闭环，即按照快速起动和制动的要求，实现对电枢电流的精确控制，实质上是在起动或制动过程的主要阶段，实现一种以电动机最大电磁力矩输出能力进行启动或制动的过程。
此外，通过完成本大作业题目，让学生体会反馈校正方法所具有的独特优点：改造受控对象的固有特性，使其满足更高的动态品质指标。
2. 大作业具体内容设一转速、电流双闭环直流调速系统，采用双极式H 桥PWM 方式驱动，已知电动机参数为：额定功率200W ； 额定转速48V ； 额定电流4A ； 额定转速=500r/min ； 电枢回路总电阻8=R Ω； 允许电流过载倍数λ=2； 电势系数=e C 0.04Vmin/r ； 电磁时间常数=L T 0.008s ； 机电时间常数=m T 0.5；电流反馈滤波时间常数=oi T 0.2ms ； 转速反馈滤波时间常数=on T 1ms ；要求转速调节器和电流调节器的最大输入电压==**im nmU U 10V ； 两调节器的输出限幅电压为10V ；PWM 功率变换器的开关频率=f 10kHz ； 放大倍数=s K 4.8。
试对该系统进行动态参数设计，设计指标： 稳态无静差； 电流超调量≤i σ5%；空载起动到额定转速时的转速超调量σ≤ 25%； 过渡过程时间=s t 0.5 s 。
3. 设计计算1. 计算电流和转速反馈系数；根据双闭环系统静特性曲线可以看出，双闭环调速系统在稳态工作时，两个调节器都不饱和，其中各变量之间满足：*0n n U U n n αα=== *i i d dL U U I I ββ===所以可得：转速反馈系数：max 100.02(min/)500nm nm nom U U V r n n α**==== 电流反馈系数：m 101.25(/)I 24im im ax nom U U V A I βλ**====⨯ 2. 按工程设计法，详细写出电流环的动态校正过程和设计结果；电流环的结构如图1a （图148页）所示，对于反电动势E ，由于其对于电流环只是一个缓慢变化的扰动作用，所以在设计电流环时先暂时将反电动势的交叉反馈断开，不考虑其作用。
机电控制工程基础第三章时域分析法1
)
function
at2 r(t)
0
t0 t<0
r(t) at2
其拉氏变换后的像函数为：
L[r(t)]
2a s3
0
t
a=1/2时称为单位加速度函数:
L[ 1 2
t2
1(t)]ຫໍສະໝຸດ 1 s3正弦函数：x(t) aSint，式中，a 为振幅，为频率。
其拉氏变换后的像函数为：
L[a sin t]
a s2 2
100
(s)
C(s) R(s)
1
s 100 0.1
100 s 10
10 0.1s 1
s
由闭环传递函数知时间常数T=0.1秒
R(s)
-
100 s
C(s)
0.1
由公式知：ts=3T=0.3秒（D0.05）
② 可设反馈系数为k
100
1
(s)
C(s) R(s)
s 1 100 k
k 0.01 s 1
s
k
当 T 0.k01，则
分析系统特性究竟采用何种典型输入信号，取决于实际系统在 正常工作情况下最常见的工作状态。
当系统的输入具有突变性质时，可选择阶跃函数为典型输入信 号；当系统的输入是随时间增长变化时，可选择斜坡函数为典 型输入信号。若实际输入信号是脉动（冲击）式的，应该采用 脉冲函数。
讨论系统的时域性能指标时，通常选择单位阶跃信号作为典型 输入信号。
3.1.2典型输入作用 (The role of typical input )
单位脉冲函数 Unit pulse function
阶跃函数
Step function
斜坡函数（速度）函数Slope(Speed ) function
机电控制工程基础控制系统的时域分析
《机电控制工程基础控制系统的时域分析》xx年xx月xx日CATALOGUE 目录•引言•机电控制工程的基本理论•机电控制工程基础控制系统的时域分析•机电控制工程基础控制系统的稳定性分析•机电控制工程基础控制系统的性能指标与评价•机电控制工程基础控制系统设计实例01引言机电控制工程在现代化工业生产中发挥着至关重要的作用，可实现生产过程的自动化、提高生产效率和产品质量。
机电控制工程在军事、航空航天、交通运输等领域也有着广泛的应用。
机电控制工程的重要性通过研究机电控制工程基础控制系统的时域分析，旨在提高控制系统的性能和稳定性，进而提高生产工艺和设备的效率和质量。
研究机电控制工程的时域分析还可为其他相关领域的研究提供理论支撑和实践经验。
研究目的和意义研究范围本研究的重点在于研究机电控制工程基础控制系统的时域分析方法，涉及控制系统的工作原理、组成结构、性能指标等方面的研究。
研究方法本研究将采用理论分析和实验研究相结合的方法，通过建立数学模型、分析实验数据和结果，对控制系统的性能进行评估和优化。
研究范围和方法02机电控制工程的基本理论机电控制系统的基本组成接收输入信号，并按照设定的规律产生控制信号输出；控制器执行器测量元件干扰因素接收控制信号，并驱动被控对象按照设定的规律运动；检测被控对象的输出信号，反馈给控制器；影响控制效果的外部因素。
1机电控制工程的基本原理23输入信号经过控制器和执行器，不反馈被控对象的输出信号；开环控制输入信号经过控制器和执行器，反馈被控对象的输出信号，并作为下一步控制的输入信号；闭环控制比例、积分、微分控制，通过调整控制信号的幅度、相位、频率，实现高精度控制。
PID控制机电控制系统的分类被控对象和控制器之间的数学模型为线性关系；线性控制系统被控对象和控制器之间的数学模型为非线性关系；非线性控制系统被控对象需要维持在某一恒定值上；恒值控制系统被控对象跟随某一输入信号变化而变化。
随动控制系统03机电控制工程基础控制系统的时域分析描述系统在时间上的表现和行为。
控制系统的时域与频域特性分析
将时域信号转换为频域信号，通过分析频谱特性来了解信号的频率组成和变化规 律。
频域分析
通过分析系统的频率响应，了解系统在不同频率下的性能表现，有助于揭示系统 的内在特性。
控制系统设计中的时频转换
时频转换
在控制系统设计中，时频转换是一种 重要的技术手段，用于将时域特性与 频域特性相互转换，以便更好地进行 系统分析和设计。
VS
详细描述
时频联合分析结合了时域和频域分析的方 法，通过同时考虑系统的时域和频域特性 ，全面了解系统的动态特性和稳定性。例 如，对于一个控制系统，可以通过时频联 合分析计算系统的时频响应曲线，从而更 全面地评估系统的性能和稳定性。
06 结论
控制系统的时域与频域特性总结
稳定性
通过分析系统的极点和零点，可以判断系统 的稳定性。极点位于复平面的左半部分时， 系统不稳定；而零点同样影响稳定性，需要 综合考虑。
稳定性
系统在受到扰动后恢复平衡状态 的能力，分为稳定、临界稳定和 不稳定三种状态。
阶跃响应与冲激响应
阶跃响应
系统在阶跃输入信号下的动态行为， 反映系统的动态性能和调节能力。
冲激响应
系统在冲激输入信号下的动态行为， 用于评估系统的暂态性能和稳态误差 。
时域性能指标
上升时间
系统输出从稳态值的 10%上升到90%所需的
快速性
系统的快速性主要通过调节时间常数实现， 时间常数小的系统响应速度快。
控制系统的时域与频域特性总结
• 准确性：系统的准确性由最大误差决定，可通过优化系统 参数减小误差。
控制系统的时域与频域特性总结
带宽
带宽反映了系统对不同频率信号的响应能力，带 宽越大，系统对高频信号的响应越好。
机电控制系统分析与设计(大作业)答案
分析题（每小题20分，共100分）1. 简化下图所示系统的结构图，求系统的闭环传递函数。
答：2. 如下图所示，已知给定信号X（t）=1(t),试计算H（S）=1，0.1时的系统稳态误差。
答：3. 设(图题46)系统开环传递函数为G(s)，试判别闭环系统稳定与否。
（1）答：4.系统的特征方程为： ,试用劳斯判据判定系统的稳定性S5+3S4+4S3+6S2+8S+5=0答S5 1 4 8S4 3 6 0S3 2 8 0S2 -6 0S1 13.5S0 0劳斯表第一列元素有变化所以系统不稳定5.分析电容传感器的工作原理及其主要应用。
答：电容传感器的工作原理是利用力学量变化使电容器中其中的一个参数发生变化的方法来使信号变换的。
根据改变电容器的参数不同电容传感器可有3类：改变极板遮盖面积的电容传感器：改变极板遮盖面积的电容传感器：改变极板间距离的电容传感器。
在实际应用中，为了提高这类传感器灵敏度、提高测量范围和减小非线性误差，常做成差动式电容器及互感器电桥组合结构，如图3(b)所示。
两边是固定的电极板1和2，中间由弹簧片支承的活动极板3。
2个固定极板与互感器两端及交流电源U相连接，活动极板连接端子和互感器中间抽头端子为传感器的输出端，该输出端电压ΔU随着活动极板运动而变化。
若活动极板的初始位置距2个固定极板的距离均为d0，则固定极板1和活动极板3之间，固定2和活动极板3之间的初始电容相等，若令其为C0。
当活动极板3在被测物体作用下向固定极板2移动Δd时，则位于中间的活动极板到两侧的固定极板的距离分别为：由上述推导可知，活动极板和2个固定极板构成电容分别为：当他们做成差动式电容器及互感器电桥组合结构时，其等效电容为：虽然电容的变化量仍旧和位移Δd成非线性关系，但是消除了级数中的偶次项，使线性得到改善。
当时（在微小量检测中，如线膨胀测量等，一般都能满足这个条件），略去高次项，得：。
哈工大机电系统控制基础大作业一指导书
函数实现，如图 3（b）所示。
R(S)
系统1 G1(s)
+
+
系统2 G2(s)
Y(S)
T (s) Y (s) num R(s) den
（a） num1
G1(s) den1
G2 (s)
num 2 den 2
仿真时间区段 三种τ值下的
系统模型 系统响应
生成图形
图 11 MATLAB 文本
对于任意输入，例如正弦输入，应用lsim函数可以求得 =0.025时系统的时 间响应及误差曲线，如图12所示。所用MATLAB文本如图13所示。
x(t)
1 0.8 0.6 0.4 0.2
0 -0.2 -0.4 -0.6 -0.8
t=[0:0.01:0.8];
nG=[50]; tao=0;dG=[0.05 1+50*tao 50];G1=tf(nG,dG); tao=0.0125;dG=[0.05 1+50*tao 50];G2=tf(nG,dG); tao=0.025;dG=[0.05 1+50*tao 50];G3=tf(nG,dG);
y:输出响应
sys:由tf,zpk
x:状态响应
或ss建立的
（仅用于状态空间模型） 模型
u : 输入
t : 仿真时间 区段（可选）
[y, x] lsim[sys, u, t]
图 8 lsim 函数
2.4. 利用 MATLAB 绘制 Bode 图 在MATLAB中，可以用不带输出参数bode函数自动生成Bode图。而用带输
大作业1(机电控制系统时域频域分析)
《机电系统控制基础》大作业一基于MATLAB的机电控制系统响应分析哈尔滨工业大学2013年月日1作业题目1. 用MATLAB 绘制系统2()25()()425C s s R s s s Φ==++的单位阶跃响应曲线、单位斜坡响应曲线。
2. 用MATLAB 求系统2()25()()425C s s R s s s Φ==++的单位阶跃响应性能指标：上升时间、峰值时间、调节时间和超调量。
3. 数控直线运动工作平台位置控制示意图如下：X i伺服电机原理图如下：LR(1)假定电动机转子轴上的转动惯量为J 1，减速器输出轴上的转动惯量为J 2，减速器减速比为i ，滚珠丝杠的螺距为P ，试计算折算到电机主轴上的总的转动惯量J ；(2)假定工作台质量m ，给定环节的传递函数为K a ，放大环节的传递函数为K b ，包括检测装置在内的反馈环节传递函数为K c ，电动机的反电势常数为K d ，电动机的电磁力矩常数为K m ，试建立该数控直线工作平台的数学模型，画出其控制系统框图；(3)忽略电感L 时，令参数K a =K c =K d =R=J=1，K m =10，P/i =4π，利用MATLAB 分析kb 的取值对于系统的性能的影响。
2 题目11.syms sf=25/(s^2+4*s+25)*1/s;x=ilaplace(f);t=0:0.001:10;xx=subs(x);%ÔªËØÌæ»»plot(t,xx);xlabel('t') ;ylabel('x0(t)');title('µ¥Î»½×Ô¾ÏìÓ¦ÇúÏß');syms sf=25/(s^2+4*s+25)*1/s^2; x=ilaplace(f);t=0:0.001:5;xx=subs(x);%ÔªËØÌæ»»plot(t,xx);xlabel('t') ;ylabel('x0(t)');title('µ¥Î»Ð±ÆÂÏìÓ¦ÇúÏß');2．计算结果：C =1timetopeak =0.6820percentovershoot =25.3786risetime =0.4459setllingtime =1.6787源代码：num=[0,25];den=[1,4,25];G=tf(num,den);% ¼ÆËã×î´ó·åֵʱ¼äºÍËü¶ÔÓ¦µÄ³¬µ÷Á¿¡£C=dcgain(G)[y,t]=step(G);plot(t,y)grid[Y,k]=max(y);timetopeak=t(k)percentovershoot=100*(Y-C)/C% ¼ÆËãÉÏÉýʱ¼ä¡£n=1;while y(n)<Cn=n+1;endrisetime=t(n)% ¼ÆËãÎÈ̬ÏìӦʱ¼ä¡£i=length(t);while (y(i)>0.98*C)&(y(i)<1.02*C)i=i-1;endsetllingtime=t(i)3.假定工作台质量m、滚珠丝杠的转动惯量电动机、减速器、滚珠丝杠、折算到电机主轴上的总的转动惯量：(给出操作过程、仿真结果及分析、源代码) 3 题目24 题目3。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《机电系统控制基础》大作业一基于MATLAB的机电控制系统响应分析哈尔滨工业大学2013年11月4日1作业题目1. 用MATLAB 绘制系统2()25()()425C s s R s s s Φ==++的单位阶跃响应曲线、单位斜坡响应曲线。
2. 用MATLAB 求系统2()25()()425C s s R s s s Φ==++的单位阶跃响应性能指标：上升时间、峰值时间、调节时间和超调量。
3. 数控直线运动工作平台位置控制示意图如下：X i伺服电机原理图如下：LR(1)假定电动机转子轴上的转动惯量为J 1，减速器输出轴上的转动惯量为J 2，减速器减速比为i ，滚珠丝杠的螺距为P ，试计算折算到电机主轴上的总的转动惯量J ；(2)假定工作台质量m ，给定环节的传递函数为K a ，放大环节的传递函数为K b ，包括检测装置在内的反馈环节传递函数为K c ，电动机的反电势常数为K d ，电动机的电磁力矩常数为K m ，试建立该数控直线工作平台的数学模型，画出其控制系统框图；(3)忽略电感L 时，令参数K a =K c =K d =R=J=1，K m =10，P/i =4π，利用MATLAB 分析kb 的取值对于系统的性能的影响。
2 题目1单位脉冲响应曲线单位阶跃响应曲线源代码t=[0:0.01:1.6]; %仿真时间区段和输入nC=[25];dR=[1,4,25];fi=tf(nC,dR); %求系统模型[y1,T]=impulse(fi,t);[y2,T]=step(fi,t); %系统响应plot(T,y1);xlabel('t(sec)'),ylabel('x(t)'); grid on;plot(T,y2);xlabel('t(sec)'),ylabel('x(t)'); grid on; %生成图形3 题目2借助Matlab，可得：ans =0.4330 0.6860 25.3826 1.0000即源代码t=[0:0.001:1];yss=1;dta=0.02; %设定仿真时间区段和误差限nC=[25];dR=[1,4,25];fi=tf(nC,dR);y=step(fi,t); %计算系统的单位阶跃响应r=1;while y(r)<yss;r=r+1;endtr=(r-1)*0.001; %上升时间[ymax,tp]=max(y);tp=(tp-1)*0.001;%峰值时间mp=(ymax-yss)/yss*100;%最大超调量s=1001;whiley(s)>1-dta && y(s)<1+dta;s=s-1;end ts=(s-1)*0.001;%调整时间[tr,tp,mp,ts]4题目3设小齿轮所在的轴为I 轴，大齿轮所在的轴为II 轴。
1T ，2T ，3T 分别为总负载，小齿轮和大齿轮的负载，'2T 为II 轴输入转矩。
根据力平衡原理，I ，II 轴的力平衡方程分别为1112d T J T dt ω=+ ，'2223d T J T dtω=+ 1ω2ω分别为小齿轮和大齿轮的角速度.根据轴II 输入转矩2T 是由轴I 上的负载转矩获得的 ，与且它们的转速成反比，所以有：22'T iT =将工作台质量折算到I 轴。
在工作台和丝杠间，3T 驱动丝杠使工作台运动。
根据动力平衡关系，即丝杠转动一周所做的功等于工作台前进一个导程时其惯性力所做的功，有32dv T m P dt π⎛⎫= ⎪⎝⎭v 为工作台位移时的线速度，P 为导程。
又根据传动关系有： 2122P P v iωωππ== 联立以上各式有： 211111222112d d P d T J m J dt i dt i dtωωωπ⎛⎫=++ ⎪⎝⎭由于 11d T J dtω=故221222J m P J J i i π⎛⎫=++ ⎪⎝⎭（1）X i参考课本2-25得电动机至工作台的微分方程式：22(t)(t)(t)d m m d d d RJ K K K u dt dt θθ+=取拉普拉斯变换得：(s)(Ts 1)K G s =+式中m d RJ T K K =1d K K = 系统闭环传递函数11(s)(Ts 1)e a bb b KK K K K G s K K K=++式中12P K i π=（3）将已知条件带入得系统传递函数为：220(s)1020bb bK G s s K =++由二阶系统的典型传递函数222(s)(s)2o n i n n X X s ωωξω=++可知nω=ξ=K<1.25时，系统为过阻尼系统；可知：0<bK=1.25时，系统为临界阻尼系统；bK>1.25时，系统为欠阻尼系统。
b源代码syms s;t=[0:0.001:2];kb=0.1;num1=20*kb;den1=[1 10 num1];G1=tf(num1,den1);kb=1;num2=20*kb;den2=[1 10 num2];G2=tf(num2,den2);kb=10;num3=20*kb;den3=[1 10 num3];G3=tf(num3,den3);kb=100;num4=20*kb;den4=[1 10 num4];G4=tf(num4,den4); %写出Kb取不同值时的传递函数[y1,T]=impulse(G1,t);[y1a,T]=step(G1,t);[y2,T]=impulse(G2,t);[y2a,T]=step(G2,t);[y3,T]=impulse(G3,t);[y3a,T]=step(G3,t);[y4,T]=impulse(G4,t);[y4a,T]=step(G4,t); %建立相应的单位脉冲响应与阶跃响应figureplot(T,y1,'--',T,y2,'-.',T,y3,'-',T,y4,':','LineWidth',2); legend('Kb=0.1','Kb=1','Kb=10','Kb=100');title('不同Kb取值下单位脉冲响应');xlabel('t(sec)');ylabel('x(t)');grid on;figureplot(T,y1a,'--',T,y2a,'-.',T,y3a,'-',T,y4a,':','LineWidth',2); legend('Kb=0.1','Kb=1','Kb=10','Kb=100');title('不同Kb取值下单位阶跃响应');xlabel('t(sec)');ylabel('x(t)');grid on; %生成图形t=[0:0.001:5];y1=step(G1,t);y2=step(G2,t);y3=step(G3,t);y4=step(G4,t);yss=1;dta=0.02;r=1;while y1(r)<yss&r<5001;r=r+1;endtr1=(r-1)*0.001; %K b=0.1时的上升时间[ymax,tp]=max(y1);tp1=(tp-1)*0.001; %K b=0.1时的峰值时间mp1=(ymax-yss)/yss; %K b=0.1时的最大超调量s=5001;while y1(s)>1-dta&y1(s)<1+dta;s=s-1;end ts1=(s-1)*0.001; %Kb=0.1时的调整时间r=1;while y2(r)<yss&r<5001;r=r+1;endtr2=(r-1)*0.001; %Kb=1时的上升时间[ymax,tp]=max(y2);tp2=(tp-1)*0.001; %Kb=1时的峰值时间mp2=(ymax-yss)/yss; %Kb=1时的最大超调量s=5001;while y2(s)>1-dta&y2(s)<1+dta; s=s-1;end ts2=(s-1)*0.001; %Kb=1时的调整时间r=1;while y3(r)<yss;r=r+1;endtr3=(r-1)*0.001; %Kb=10时的上升时间[ymax,tp]=max(y3);tp3=(tp-1)*0.001; %Kb=10时的峰值时间mp3=(ymax-yss)/yss; %Kb=10时的最大超调量s=5001;while y3(s)>1-dta&y3(s)<1+dta;s=s-1;end ts3=(s-1)*0.001;%Kb=10时的调整时间r=1;while y4(r)<yss;r=r+1;endtr4=(r-1)*0.001;%Kb=100时的上升时间[ymax,tp]=max(y4);tp4=(tp-1)*0.001;%Kb=100时的峰值时间mp4=(ymax-yss)/yss; %Kb=100时的最大超调量s=5001;while y4(s)>1-dta&y4(s)<1+dta;s=s-1;end ts4=(s-1)*0.001;%Kb=100时的调整时间[tr1,tp1,mp1,ts1][tr2,tp2,mp2,ts2][tr3,tp3,mp3,ts3][tr4,tp4,mp4,ts4] %显示结果。