[精品]2015-2016学年浙江省杭州市下城区四季青中学七年级(上)期中数学试卷含答案
浙江省杭州市青中学七年级数学上学期期中试卷(含解析)浙教版
浙江省杭州市青中学七年级数学上学期期中试卷（含解析）浙教版一、选择题（本题有10个小题，每小题3分，共30分）1．﹣3的相反数是（）A．3 B．﹣3 C．D．﹣2．在，，π，，，中无理数的个数有（）A．1 个 B．2个C．3 个 D．4个3．稀土元素有独特的性能和广泛的应用，我国稀土资源的总储藏量约为1 050 000 000吨，是全世界稀土资源最丰富的国家．将1 050 000 000吨用科学记数法表示为（）A．1.05×1010吨B．1.05×109吨C．10.5×108吨D．0.105×1010吨4．下列四个数中，最大的一个数是（）A．2 B．C．0 D．﹣25．对于下列四个式子：①0.1；②；③；④．其中不是整式的是（）A．①B．②C．③D．④6．下列各组数中，数值相等的是（）A．32和 23B．﹣23和（﹣2）3C．﹣|23|和|﹣23| D．﹣32和（﹣3）27．已知长方形的长为（2b﹣a），宽比长少b，则这个长方形的周长是（）A．3b﹣2a B．3b+2a C．6b﹣4a D．6b+4a8．已知，则0.005403的算术平方根是（）A．0.735 B．0.0735 C．0.00735 D．0.0007359．已知m﹣n=100，x+y=﹣1，则代数式（n+x）﹣（m﹣y）的值是（）A．99 B．101 C．﹣99 D．﹣10110．己知a，b两数在数轴上对应的点如图所示，则|a|+|a﹣b|等于（）A．﹣a B．﹣b C．b﹣2a D．2a﹣b二、填空题（本题有6小题，每小题3分，共24分）11．室内温度是16℃，室外温度是﹣5℃，则室内温度比室外温度高℃．12．已知|a+2|=0，则a= ．13．﹣的立方根是，的平方根是．14．若﹣x3y a与x b y是同类项，则a+b的值为．15．已知：m与n互为相反数，c与d互为倒数，a是的整数部分，则的值是．16．任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[3]=1，现对72进行如下操作：72 []=8 []=2 []=1，这样对72只需进行3次操作后变为1，类似地：（1）对81只需进行次操作后变为1；（2）只需进行3次操作后变为1的所有正整数中，最大的是．三、简答题（本题共有7小题，共66分．）17．计算：（1）18+6+（2）（﹣24）×（﹣+）（3）6÷（﹣+﹣）（4）﹣22﹣（3﹣7）2﹣（﹣1）2009×（﹣）18．先化简再求值：（1）2（a2﹣ab）﹣3（a2﹣ab），其中a=﹣2，b=3．（2）（2x2+x）﹣[4x2﹣（3x2﹣x），其中x=﹣．19．已知|a|=4，|b|=7，且a＜b，求a﹣b的值．20．一种长方形餐桌的四周可以坐6人用餐（带阴影的小长方形表示1个人的位置）、现把n张这样的餐桌按如图方式拼接起来．（1）问四周可以坐多少人用餐？（用n的代数式表示）（2）若有28人用餐，至少需要多少张这样的餐桌？21．如图甲，把一个边长为2的大正方形分成四个同样大小的小正方形，再连接大正方形的四边中点，得到了一个新的正方形（图中阴影部分），求：（1）图甲中阴影部分的面积是多少？（2）图甲中阴影部分正方形的边长是多少？（3）如图乙，在数轴上以1个单位长度的线段为边作一个正方形，以表示数1的点为圆心，以正方形对角线长为半径画弧，交数轴负半轴于点A，求点A所表示的数是多少？22．为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：收费标准（注：水费按月份结算）每月用水量单价（元/立方米）不超出6立方米的部分 2超出6立方米不超出10立方米的部分 4超出10立方米的部分8例如：某户居民1月份用水8立方米，应收水费为2×6+4×（8﹣6）=20（元）．请根据上表的内容解答下列问题：（1）若某户居民2月份用水5立方米，则应收水费多少元？（2）若某户居民3月份交水费36元，则用水量为多少立方米？（3）若某户居民4月份用水a立方米（其中6＜a＜10），请用含a的代数式表示应收水费．（4）若某户居民5、6两个月共用水18立方米（6月份用水量超过了10立方米），设5月份用水x 立方米，请用含x的代数式表示该户居民5、6两个月共交水费多少元．23．已知b是立方根等于本身的负整数，且a、b满足（a+2b）2+|c+|=0，请回答下列问题：（1）请直接写出a、b、c的值：a= ，b= ，c=（2）a、b、c在数轴上所对应的点分别为A、B、C，点D是B、C之间的一个动点（不包括B、C两点），其对应的数为m，则化简|m+|；（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点B、点C都以每秒一个单位长度的速度向左运动，同时点A以每秒2个单位长度的速度向右运动，假设t秒钟过后，若点A与点C 之间的距离为 AC，点A与点B之间的距离为AB，请问：AB﹣AC的值是否随着t的变化而改变？若变化，请说明理由；若不变，请求出AB﹣AC的值．2016-2017学年浙江省杭州市青春中学七年级（上）期中数学试卷参考答案与试题解析一、选择题（本题有10个小题，每小题3分，共30分）1．﹣3的相反数是（）A．3 B．﹣3 C．D．﹣【考点】相反数．【专题】常规题型．【分析】根据相反数的概念解答即可．【解答】解：﹣3的相反数是3，故选：A．【点评】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣”号；一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．2．在，，π，，，中无理数的个数有（）A．1 个 B．2个C．3 个 D．4个【考点】无理数．【分析】根据无理数的三种形式，①开方开不尽的数，②无限不循环小数，③含有π的数，结合所给数据即可作出判断．【解答】解： =2，所给数据中无理数有：π，，共2个．故选B．【点评】本题考查了无理数的定义，属于基础题，解答本题的关键是熟练掌握无理数的三种形式．3．稀土元素有独特的性能和广泛的应用，我国稀土资源的总储藏量约为1 050 000 000吨，是全世界稀土资源最丰富的国家．将1 050 000 000吨用科学记数法表示为（）A．1.05×1010吨B．1.05×109吨C．10.5×108吨D．0.105×1010吨【考点】科学记数法—表示较大的数．【专题】应用题．【分析】科学记数法就是将一个数字表示成a×10的n次幂的形式，其中1≤|a|＜10，n表示整数．n 为整数位数减1，即从左边第一位开始，在首位非零的后面加上小数点，再乘以10的n次幂．【解答】解：1 050 000 000吨用科学记数法表示为1.05×109吨．故选B．【点评】用科学记数法表示一个数的方法是（1）确定a：a是只有一位整数的数；（2）确定n：当原数的绝对值≥10时，n为正整数，n等于原数的整数位数减1；当原数的绝对值＜1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．4．下列四个数中，最大的一个数是（）A．2 B．C．0 D．﹣2【考点】实数大小比较．【专题】推理填空题；实数．【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．【解答】解：根据实数比较大小的方法，可得﹣2＜0＜＜2，故四个数中，最大的一个数是2．故选：A．【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．5．对于下列四个式子：①0.1；②；③；④．其中不是整式的是（）A．①B．②C．③D．④【考点】整式．【分析】根据整式的概念对各个式子进行判断即可．【解答】解：①0.1；②；④是整式，故选C【点评】本题考查的是整式的概念，对整式概念的认识，凡分母中含有字母的代数式都不属于整式，在整式范围内用“+”或“﹣”将单项式连起来的就是多项式，不含“+”或“﹣”的整式绝对不是多项式，而单项式注重一个“积”字．6．下列各组数中，数值相等的是（）A．32和 23B．﹣23和（﹣2）3C．﹣|23|和|﹣23| D．﹣32和（﹣3）2【考点】有理数的乘方；绝对值．【分析】根据有理数的乘方及绝对值的运算将四个选项中各数计算出来，再进行比较即可得出结论．【解答】解：A、∵32=9，23=8，∴32≠23；B、∵﹣23=﹣8，（﹣2）3=﹣8，∴﹣23=（﹣2）3；C、∵﹣|23|=﹣8，|﹣23|=8，∴﹣|23|≠|﹣23|；D、∵﹣32=﹣9，（﹣3）2=9，∴﹣32≠（﹣3）2．故选B．【点评】本题考查了有理数的乘方及绝对值，熟练掌握有理数的乘方及绝对值的运算是解题的关键．7．已知长方形的长为（2b﹣a），宽比长少b，则这个长方形的周长是（）A．3b﹣2a B．3b+2a C．6b﹣4a D．6b+4a【考点】整式的加减．【分析】先求出长方形的宽，再根据长方形的周长=2×（长+宽）计算即可．【解答】解：∵长方形的长为（2b﹣a），宽比长少b，∴长方形的宽为（2b﹣a）﹣b=b﹣a，∴这个长方形的周长是：2[（2b﹣a）+（b﹣a）]=2（3b﹣2a）=6b﹣4a；故选：C．【点评】本题考查列代数式，要在给出的长的基础上把宽表示出来，进而计算出长方形周长，同时本题要注意当代数式由单位名称时要把代数式用括号括起来．8．已知，则0.005403的算术平方根是（）A．0.735 B．0.0735 C．0.00735 D．0.000735【考点】算术平方根．【专题】计算题．【分析】由于所求已知数0.005403的小数点比54.03向左移动了四位，那么则它的平方根就向左移动两位，由此即可得到结果．【解答】解：∵ =7.35∴0.005403的算术平方根是0.0735．故选B．【点评】此题主要考查了算术平方根的定义和性质，解题关键是小数点的位置，这个数的小数点向左移动了四位．则它的平方根就向左移动两位．9．已知m﹣n=100，x+y=﹣1，则代数式（n+x）﹣（m﹣y）的值是（）A．99 B．101 C．﹣99 D．﹣101【考点】整式的加减—化简求值．【专题】计算题；整式．【分析】原式去括号整理后，将已知等式代入计算即可求出值．【解答】解：∵m﹣n=100，x+y=﹣1，∴原式=n+x﹣m+y=﹣（m﹣n）+（x+y）=﹣100﹣1=﹣101．故选D．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．10．己知a，b两数在数轴上对应的点如图所示，则|a|+|a﹣b|等于（）A．﹣a B．﹣b C．b﹣2a D．2a﹣b【考点】整式的加减；数轴；绝对值．【专题】计算题．【分析】根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，去括号合并即可得到结果．【解答】解：根据题意得：b＜a＜0，∴a﹣b＞0，则原式=﹣a+a﹣b=﹣b，故选B【点评】此题考查了整式的加减，熟练掌握运算法则是解本题的关键．二、填空题（本题有6小题，每小题3分，共24分）11．室内温度是16℃，室外温度是﹣5℃，则室内温度比室外温度高21 ℃．【考点】有理数的减法．【分析】利用室内温度﹣室外温度就是室内温度比室外温度高的度数可得16﹣（﹣5），再用有理数的减法法则计算即可．【解答】解：16﹣（﹣5）=16+5=21，故答案为：21．【点评】此题主要考查了有理数的减法，关键是掌握减法法则：减去一个数，等于加上这个数的相反数．12．已知|a+2|=0，则a= ﹣2 ．【考点】绝对值．【分析】根据绝对值的意义得出a+2=0，即可得出结果．【解答】解：由绝对值的意义得：a+2=0，解得：a=﹣2；故答案为：﹣2．【点评】本题考查了绝对值的意义；熟记0的绝对值等于0是解决问题的关键．13．﹣的立方根是﹣，的平方根是±2 ．【考点】立方根；平方根．【分析】利用平方根及立方根的定义计算即可得到结果．【解答】解：﹣的立方根是﹣，的平方根是±2，故答案为﹣，±2．【点评】本题考查了立方根，平方根，以及算术平方根，熟练掌握各自的定义是解本题的关键．14．若﹣x3y a与x b y是同类项，则a+b的值为 4 ．【考点】同类项．【分析】根据同类项的概念可得方程：a=1，b=3，再代入a+b即可求解．【解答】解：∵﹣x3y a与x b y是同类项，∴a=1，b=3，∴a+b=1+3=4．故答案为：4．【点评】此题主要考查同类项的概念及性质．关键是学生对概念的记忆，属于基础题．15．已知：m与n互为相反数，c与d互为倒数，a是的整数部分，则的值是﹣1 ．【考点】实数的运算；估算无理数的大小．【分析】首先根据有理数的加法可得m+n=0，根据倒数定义可得cd=1，然后代入代数式求值即可．【解答】解：∵m与n互为相反数，∴m+n=0，∵c与d互为倒数，∴cd=1，∵a是的整数部分，∴a=2，∴=1+2×0﹣2=﹣1．故答案为：﹣1．【点评】此题主要考查了实数的运算，关键是掌握相反数和为0，倒数积为1．16．任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[3]=1，现对72进行如下操作：72 []=8 []=2 []=1，这样对72只需进行3次操作后变为1，类似地：（1）对81只需进行 3 次操作后变为1；（2）只需进行3次操作后变为1的所有正整数中，最大的是255 ．【考点】估算无理数的大小．【专题】新定义．【分析】（1）根据运算过程得出[]=9，[]=3，[]=1，即可得出答案．（2）最大的正整数是255，根据操作过程分别求出255和256进行几次操作，即可得出答案．【解答】解：（1）∵[]=9，[]=3，[]=1，∴对81只需进行3次操作后变为1，故答案为：3．（2）最大的正整数是255，理由是：∵[]=15，[]=3，[]=1，∴对255只需进行3次操作后变为1，∵[]=16，[]=4，[]=2，[]=1，∴对256只需进行4次操作后变为1，∴只需进行3次操作后变为1的所有正整数中，最大的是255，故答案为：255．【点评】本题考查了估算无理数的大小的应用，主要考查学生的理解能力和计算能力．三、简答题（本题共有7小题，共66分．）17．计算：（1）18+6+（2）（﹣24）×（﹣+）（3）6÷（﹣+﹣）（4）﹣22﹣（3﹣7）2﹣（﹣1）2009×（﹣）【考点】实数的运算．【专题】计算题；实数．【分析】（1）原式利用立方根定义计算即可得到结果；（2）原式利用乘法分配律计算即可得到结果；（3）原式先计算括号中的加减运算，再计算除法运算即可得到结果；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解：（1）原式=18+6﹣2=22；（2）原式=﹣2+20﹣9=9；（3）原式=6÷（﹣）=6÷（﹣2）=﹣3；（4）原式=﹣4﹣16﹣2=﹣22．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．18．先化简再求值：（1）2（a2﹣ab）﹣3（a2﹣ab），其中a=﹣2，b=3．（2）（2x2+x）﹣[4x2﹣（3x2﹣x），其中x=﹣．【考点】整式的加减—化简求值．【分析】根据去括号法则、合并同类项法则把原式化简，代入计算即可．【解答】解：（1）原式=2a2﹣2ab﹣2a2+3ab=ab当a=﹣2，b=3时，原式=﹣6；（2）原式=2x2+x﹣4x2+（3x2﹣x）=2x2+x﹣4x2+3x2﹣x=x2，当x=﹣时，原式=．【点评】本题考查的是整式的化简求值，掌握整式的加减混合运算法则是解题的关键．19．已知|a|=4，|b|=7，且a＜b，求a﹣b的值．【考点】有理数的减法；绝对值．【专题】常规题型．【分析】根绝绝对值的意义，a＜b确定a、b的值，再计算a﹣b．【解答】解：因为|a|=4，|b|=7，得a=±4，b=±7．由a＜b，所以a=±4，b=7当a=﹣4，b=7时，a﹣b=﹣11，当a=4，b=7时，a﹣b=﹣3．【点评】本题考查了绝对值的化简和有理数的减法．根据绝对值的意义及a＜b确定a、b的值是解决本题的关键．20．一种长方形餐桌的四周可以坐6人用餐（带阴影的小长方形表示1个人的位置）、现把n张这样的餐桌按如图方式拼接起来．（1）问四周可以坐多少人用餐？（用n的代数式表示）（2）若有28人用餐，至少需要多少张这样的餐桌？【考点】规律型：图形的变化类．【分析】（1）根据图形可知，每张桌子有4个座位，然后再加两端的各一个．于是n张桌子就有（4n+2）个座位；（2）令4n+2=28，解即可，注意要四舍五入．【解答】解：（1）（4n+2）人；（2）4n+2=28，解得n=6.5．答：至少需要7张这样的餐桌．【点评】本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．21．如图甲，把一个边长为2的大正方形分成四个同样大小的小正方形，再连接大正方形的四边中点，得到了一个新的正方形（图中阴影部分），求：（1）图甲中阴影部分的面积是多少？（2）图甲中阴影部分正方形的边长是多少？（3）如图乙，在数轴上以1个单位长度的线段为边作一个正方形，以表示数1的点为圆心，以正方形对角线长为半径画弧，交数轴负半轴于点A，求点A所表示的数是多少？【考点】正方形的性质；实数与数轴；勾股定理．【专题】计算题．【分析】（1）由大正方形分成四个同样大小的小正方形，阴影部分为大正方形的四边中点的连线形成，所以阴影部分为大正方形面积的一半，根据正方形面积公式计算即可；（2）由（1）的结论和正方形的面积公式易得到阴影部分正方形的边长；（3）先利用勾股定理得到边长为1的正方形的对角线的长度为，则OA=﹣1，而A点在原点左侧，利用数轴上数的表示方法即可得到点A表示的数．【解答】解：（1）S阴影=×22=2；（2）设图甲中阴影部分正方形的边长是a，则a2=2，∴a=，即图甲中阴影部分正方形的边长是；（3）∵以1个单位长度的线段为边作一个正方形，其对角线长为=，∴OA=﹣1，∴点A表示的数为﹣（﹣1）=1﹣．【点评】本题考查了正方形的性质：正方形的四边相等，四个角都等于90°，其面积等于边长的平分．也考查了勾股定理以及实数与数轴的关系．22．为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：收费标准（注：水费按月份结算）每月用水量单价（元/立方米）不超出6立方米的部分 2超出6立方米不超出10立方米的部分 4超出10立方米的部分8例如：某户居民1月份用水8立方米，应收水费为2×6+4×（8﹣6）=20（元）．请根据上表的内容解答下列问题：（1）若某户居民2月份用水5立方米，则应收水费多少元？（2）若某户居民3月份交水费36元，则用水量为多少立方米？（3）若某户居民4月份用水a立方米（其中6＜a＜10），请用含a的代数式表示应收水费．（4）若某户居民5、6两个月共用水18立方米（6月份用水量超过了10立方米），设5月份用水x 立方米，请用含x的代数式表示该户居民5、6两个月共交水费多少元．【考点】列代数式．【分析】（1）（2）利用用水量的范围确定单价算出结果即可；（3）36元一定用水量超出10立方米，分段计算即可；（4）分5月份不超过6m3时和5月份超过6m3时两种情况列式即可．【解答】解：（1）2×5=10元答：应收水费10元；（2）10+（36﹣2×6﹣4×4）÷8=10+1=11立方米答：用水量为11立方米；（3）（4a﹣12）元；（4）当5月份不超过6m3时，水费为（﹣6x+92）元；当5月份超过6m3时，水费为（﹣4x+80）元．【点评】此题考查列代数式，找出题目蕴含的数量关系是解决问题的关键．23．已知b是立方根等于本身的负整数，且a、b满足（a+2b）2+|c+|=0，请回答下列问题：（1）请直接写出a、b、c的值：a= 2 ，b= ﹣1 ，c= ﹣（2）a、b、c在数轴上所对应的点分别为A、B、C，点D是B、C之间的一个动点（不包括B、C两点），其对应的数为m，则化简|m+|；（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点B、点C都以每秒一个单位长度的速度向左运动，同时点A以每秒2个单位长度的速度向右运动，假设t秒钟过后，若点A与点C之间的距离为 AC，点A与点B之间的距离为AB，请问：AB﹣AC的值是否随着t的变化而改变？若变化，请说明理由；若不变，请求出AB﹣AC的值．【考点】实数与数轴；非负数的性质：绝对值；非负数的性质：偶次方；立方根；一元一次方程的应用．【分析】（1）先根据b是立方根等于本身的负整数，求出b，再根据（a+2b）2+|c+|=0，即可求出a、c；（2）先得出点A、C之间（不包括A点）的数是负数或0，得出m≤0，再化简|2m|即可；（3）先求出AB=3+3t，AC=3t+，从而得出AB﹣AC=．【解答】解：（1）∵b是立方根等于本身的负整数，∴b=﹣1．∵（a+2b）2+|c+|=0，∴a=2，c=﹣；故答案为：2，﹣1，﹣；（2）∵b=﹣1，c=﹣，a、c在数轴上所对应的点分别为A、C，∴点B、C之间（不包括A点）的数是小于的负数，∴m≤0，∴|m+|=﹣m﹣，（3）依题意得：A：2+2t，B：﹣1﹣t，C：﹣t．所以AB=3+3t，AC=3t+所以AB﹣AC=（3+3t ）﹣（3t+）=，故AB﹣AC的值不随着t的变化而改变．【点评】本题考查了数轴与绝对值，一元一次方程的应用．通过数轴把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．。
【鼓楼】15-16初一上期中数学试卷
2015-2016学年度第一学期七年级数学期中试卷一、选择题（本大题共6小题，每小题2分，共12分。
在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）1、-2的相反数是（ ）A.21B. 2C.21- D. -2 2、2008年我国的国民生产总值约为130800亿元，那么120800用科学计数法表示正确的是（ ）A. 1.308×105B. 13.08×104C. 1.308×104D. 1.308×1023、下列各组是同类项的一组是A. 5xy 与2xyzB. 2与-7C. -2x 2y 与5y 2zD.3ac 与7bc4、下列各组数中，数值相等的是A. 32和23B.-32和（-3）2C. 32）（-和32-D.)2(--和2--5、单项式222yz x -的系数和次数分别是（ ） A. -2，2 B. -2，5 C. 21-，2 D. 21-，5 6、以下各正方形的边长是无理数的是（ ）A. 面积为3的正方形B. 面积为1.44的正方形C. 面积为25的正方形D. 面积为16的正方形二、填空题（本大题共10小题，每小题2分，共20分。
不需写出解答过程，请把答案直接填写在答题卡相应位置上）7、211-的倒数是___________；2015)1(-=__________。
8、比较大小：2)43(--_______21-（填“＜”、“=”、“＞”） 9、在数轴上将点A 向右移动7个单位，再向左移动4个单位，终点恰好是原点，则点A 表示的数是_________。
10、多项式322-+-x x 的次数为_______，项数为________。
11、钢笔每支2元，铅笔每支0.5元，n 支钢笔和m 支铅笔共_____元。
12、有理数a ，b ，c 在数轴上的位置如图，化简b c b a --+的结果为________。
浙江省杭州四季青中学2015-2016学年七年级上学期期中考试科学试卷
2015学年第一学期七年级科学学科期中考试试卷试卷满分：150分考试时间：95分钟一、选择题（每小题3分，共75分，每小题只有一项最符合题意的答案，将选项序号填入答题卷）1化学实验必须规范，否则容易发生安全事故。
你认为下列实验操作正确的是（）A B C D2. 如图为2014年巴西世界杯足球赛吉祥物的动物原型——犰狳（qiúyú）。
犰狳体温恒定，妊娠期为60~120天，每胎产仔2~4只，在遇到危险时会缩成球形。
犰狳在动物分类上属于（）A．甲壳类 B．两栖类 C．爬行类 D．哺乳类3．生活处处是科学,留心观察皆学问,对需测量的科学量进行估计，是应具有的基本技能之一。
凭你的生活经验，下列估计不正确的是( )A.一个茶杯的高度大约为0.15米B.我们上课的教室内空气的体积约为35立方米C.一瓶矿泉水的体积约为600毫升D.我们的课桌高度约为750毫米4. 阿凡提的故事：一次国王故意为难阿凡提，让他在众臣面前说出眼前池塘里的水有多少桶，阿凡提略加思索后回答：若桶像池塘一样大的话，池塘里的水就只有一桶；若桶像池塘的十分之一大的话，池塘里的水就有十桶；若……这则故事说明了( )A．测量总是有误差的 B.测量前应选择合适的测量工具C. 测量的工具大小决定了物体的大小D.测量的标准不一样，结果也不一样5. 教学楼过道的消防栓箱的玻璃经常被同学不小心损坏，所以同学们下课时请不要在走廊奔跑、打闹。
那么在配破损的玻璃时，用下列哪种尺子比较好（）A．最小刻度1毫米的2米长的钢卷尺 B．最小刻度为1厘米的1.5米长的皮尺C．最小刻度1毫米的学生用三角尺 D．最小刻度为1厘米的30米长的皮尺6.骨髓移植能够治疗再生障碍性贫血，是因为健康人骨髓中的造血干细胞能不断产生新的血细胞（如图），这一过程称为细胞的（）7. 下列关于显微镜的操作，其中属于“对光”环节的是（）A B C D8.被蚊子叮咬，人会感觉到痒并用手拍打，其信息是主要依靠下图哪种细胞来传递（）9.下列岩石结构可能找到古生物化石的是（）A、玄武岩和花岗岩B、大理岩和砂岩C、石灰岩和砂岩D、砾岩和玄武岩10.地震发生时，我们可采取的应急措施有（）①保持清醒、冷静的头脑，及时将身边的书包或柔软的物品顶在头上②快速离开教室，跑到空旷地方去③迅速于高处跳楼逃生④躲到高层教学楼下面⑤来不及外逃时；双手抱头躲避在墙角或坚实的家具下，亦可转移到承重墙较多、面积较小的房间内A. ①②③B. ②③④C. ②④⑤D. ①②⑤11.若用一台显微镜观察同一标本四次，每次仅调整目镜、物镜和细准焦螺旋，结果得到下面各图。
人教版七年级上册试卷2015-2016期中测试答案.docx
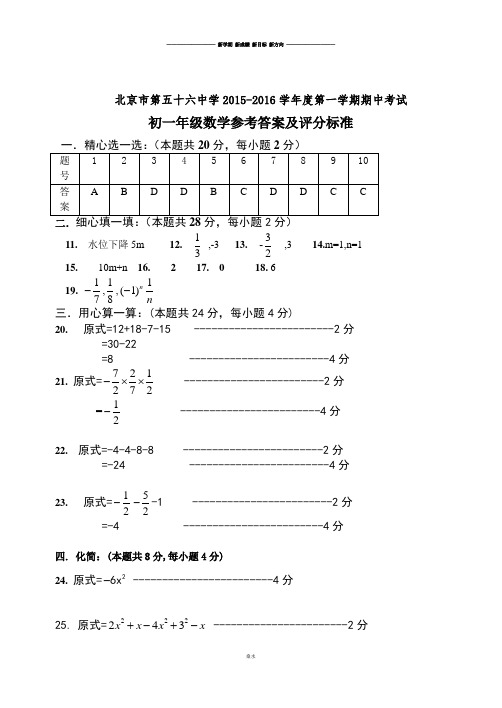
北京市第五十六中学2015-2016学年度第一学期期中考试初一年级数学参考答案及评分标准二． 11. 水位下降5m 12. 13 ,-3 13. 3-2,3 14.m=1,n=1 15. 10m+n 16. 2 17. 0 18. 619. 17-,18,1(1)-n n三．用心算一算：(本题共24分，每小题4分)20. 原式=12+18-7-15 ------------------------2分=30-22=8 ------------------------4分21. 原式=721272-⨯⨯ ------------------------2分 =12- ------------------------4分22. 原式=-4-4-8-8 ------------------------2分=-24 ------------------------4分23. 原式=12-52--1 ------------------------2分 =-4 ------------------------4分四. 化简：(本题共8分,每小题4分)24. 原式=26x - ------------------------4分25. 原式=222243+-+-x x x x -----------------------2分=229-+x ------------------------4分五．先化简，再求值：（本题共5分）26. 原式=224a 2a 64a 4a 10---++ ----------2分 = 2a+4 ----------------------------------------4分当 a=-1 时，原式= 2 ----------------------------5分六．（本题共23分）27. （1）总收入130万元,总支出35万元？-----------------2分（2）总收入+130万元,总支出-35万元 ---------------4分(3)95万元---------------5分28. 215(2) 2.50352-<--<-<<-<----------------2分 画图----------------3分29（1）剩余部分的面积24-x ab ，二次二项式，二次项系数的和是-3.----------------2分（2）22-x ab ----------------2分（3）22-x r π ----------------3分 30（1）5 ----------------2分（2）x=-1 ----------------2分（3）x=2,x=-5----------------3分初中数学试卷桑水出品。
2015-2016七年级(上)期中数学试卷
初一数学试卷一、选择题（每小题3分，共30分）1．﹣2的倒数是（）A．2 B．﹣2 C．D．﹣2．我国以2010年11月1日零时为标准计时点，进行了第六次全国人口普查，查得全国总人口约为1370000000人，请将总人口用科学记数法表示为（）×108×109 ×1010×1083．下列各组数中，互为相反数的是（）A．2和﹣2 B．﹣2和C．﹣2和D．和24．下列各数中，比﹣1小的数是（）A．0 B．1 C．﹣100 D．25．若3x n+5y与﹣x3y是同类项，则n=（）A．2 B．﹣5 C．﹣2 D．56．化简a+2b﹣b，正确的结果是（）A．a﹣b B．﹣2b C．a+b D．a+27．下列各题正确的是（）A．3x+3y=6xy B．x+x=x2C．﹣9y2+6y2=﹣3 D．9a2b﹣9a2b=08．一个多项式与x2﹣2x+1的和是3x﹣2，则这个多项式为（）A．x2﹣5x+3 B．﹣x2+x﹣1 C．﹣x2+5x﹣3 D．x2﹣5x﹣139．去括号正确的是（）A．a2﹣（a﹣b+c）=a2﹣a﹣b+c B．5+a﹣2（3a﹣5）=5+a﹣6a+10C．3a﹣（3a2﹣2a）=3a﹣a2﹣ a D．a3﹣[a2﹣（﹣b）]=a3﹣a2+b10．已知实数m、n在数轴上的对应点的位置如图所示，则下列判断正确的是（）A．m＞0 B．n＜0 C．mn＜0 D．m﹣n＞0二、填空题（每小题4分，共24分）11．计算：|﹣2|=．12．某种商品每袋4.8元，在一个月内的销售量是m袋，用式子表示在这个月内销售这种商品的收入．13．多项式2x2﹣3x+5是次项式．14．如果□×（﹣）=1，则□内应填的有理数是．15．体育委员带了500元钱去买体育用品，已知一个足球a元，一个篮球b元．则代数式500﹣3a﹣2b表示的数为．16．按下面程序计算：输入x=3，则输出的答案是．三、解答题（一）（每小题5分，共30分）17．计算：2×（﹣3）+（﹣40）÷8．（3a﹣b）﹣3（a+3b）．（﹣1）4+（﹣）÷﹣|﹣3|18．化简：（1）（2x﹣3y）+（5x+4y）（2）（8a﹣7b）﹣（4a﹣5b）．四、解答题（二）（每小题6分，共12分）19．先化简，再求值．x﹣2（x﹣y2）+（﹣x+y2），其中x=﹣2，y=．20．若A=x2﹣2x+1，B=3x﹣2，求A﹣B．五、解答题（三）（每小题8分，共24分）21．教师节当天，出租车司机小王在东西向的街道上免费接送教师，规定向东为正，向西为负，当天出租车的行程如下（单位：千米）：+5，﹣4，﹣8，+10，+3，﹣6，+7，﹣11．（1）将最后一名老师送到目的地时，小王距出发地多少千米？方位如何？（2）若汽车耗油量为0.2升/千米，则当天耗油多少升？若汽油价格为6.20元/升，则小王共花费了多少元钱？22．观察下面三行数：﹣3，9，﹣27，81，﹣243，…①0，12，﹣24，84，﹣240，…；②3，﹣9，27，﹣81，243，…．③（1）第①行数按什么规律排列？（2）第②③行数与第 ①行数分别有什么关系？（3）取每行数的第9个数，计算这三个数的和．23．小明用的练习本可以到甲、乙两家商店购买，已知两商店的标价都是每本1元，甲商店的优惠条件是购买10本以上，从第11本开始按标价的70%出售；乙商店的优惠条件是，从第一本起按标价的80%出售．（1）若小聪要购买20本练习本，则当小聪到甲商店购买时，须付款 元，当到乙商店购买时，须付款 元；（2）若设小明要购买x （x ＞10）本练习本，则当小明到甲商店购买时，须付款 元，当到乙商店购买时，须付款 元；（3）买多少本练习本时，两家商店付款相同？24. 有这样一道题，“计算)3()2()232(323323223y y x x y xy x xy y x x -+-++----的值，其中1,21-==y x ”，甲同学把“21=x 抄成了21-=x ，但计算结果是正确的，你说这是怎么回事。
【精品】[已校验]浙江省杭州市上城区英特外国语学校2015-2016学年七年级(上)期中数学试卷及答案
![【精品】[已校验]浙江省杭州市上城区英特外国语学校2015-2016学年七年级(上)期中数学试卷及答案](https://img.taocdn.com/s3/m/71ebf57e700abb68a882fb69.png)
．
16．如果 2a﹣18=0，那么 a 的算术平方根是
．
17．大于﹣ ，小于 的整数有 个．
18．已知
，则
．
19．已知﹣ 1＜x＜ 3，化简： | x+1|+
=．
20．在数轴上和有理数 a、 b、 c 对应的点的位置如图所示：
有下面四个结论：① abc＜0；②| a﹣b|+| b﹣ c| =| a﹣c| ③（a﹣ b）（b﹣c）（c﹣a）
）
A．﹣ 2005 B．
C．
D．2005
3．据《中国经济周刊》报道，上海世博会第四轮环保活动投资总金额高达
820
亿元，其中 820 亿用科学记数法表示为（
）
A．0.82×1011 B．8.2×1010 C． 8.2× 109 D． 82×108
4．计算 1﹣| ﹣2| 结果正确的是（
）
A．3 B．1 C．﹣ 1 D．﹣ 3
第 5 页（共 15 页）
故选 A．
7．在数轴上与﹣ 3 的距离等于 4 的点表示的数是（
）
A．1 B．﹣ 7 C．1 或﹣ 7 D．无数个
【考点】 数轴．
【分析】 此题注意考虑两种情况：该点在﹣ 3 的左侧，该点在﹣ 3 的右侧．
【解答】 解：根据数轴的意义可知，在数轴上与﹣ 3 的距离等于 4 的点表示的数
16．如果 2a﹣18=0，那么 a 的算术平方根是 3 ． 【考点】 算术平方根． 【分析】 先根据 2a﹣18=0 求得 a=9，再根据算术平方根的定义即可求 a 的算术 平方根． 【解答】 解：∵ 2a﹣18=0， ∴ a=9， ∴ a 的算术平方根是 3．
5．下列说法正确的是（
）
浙江省杭州市七年级(上)期中数学试卷
给出一个变换公式：
将明文转换成密文，如：4⇒
，即 R 变为 L．
11⇒
，即 A 变为 S．
将密文转换成明文，如：21⇒3×（21-17）-2=10，即 X 变为 P 13⇒3×（13-8）-1=14，即 D 变为 F． （1）按上述方法将明文 NET 译为密文； （2）若按上述方法将明文译成的密文为 DWN，请找出它的明文．
6. 若 a=77+77+77+77+77+77+77，b=78，则 a 与 b 的大小关系为（ ）
A. a＞b
B. a=b
C. a＜b
D. 无法比较
7. 有理数 a，a+2，-a-3（a＞0）的大小顺序是（ ）
A. -a-3＜a＜a+2 B. -a-3＜a+2＜a C. a＜a+2＜-a-3
D. a＜-a-3＜a+2
10. 实际测量一座山的高度时，可在若干个观测点中测量每两个相邻可视观测点的相对
高度，然后用这些相对高度计算出山的高度．下表是某次测量数据的部分记录（
用 A-C 表示观测点 A 相对观测点 C 的高度）
A-C
C-D
E-D
F-E
G-F
B-G
90 米
80 米
-60 米
50 米
-70 米
40 米
根据这次测量的数据，可得观测点 A 相对观测点 B 的高度是（ ）米．
A. 210
B. 170
C. 130
D. 50
二、填空题（本大题共 6 小题，共 24.0 分）
11. 3 是 m 的一个平方根，则 m 的另一个平方根是______，m=______．
浙江省杭州四季青中学七年级上学期期中考试数学考试卷(解析版)(初一)期中考试.doc
浙江省杭州四季青中学七年级上学期期中考试数学考试卷（解析版）（初一）期中考试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）【题文】下列各对量中，不具有相反意义的是（）A、胜3局与负4局B、收入3000元与支出2000元C、气温升高4℃与气温升高10℃D、转盘逆时针转3圈与顺时针转5圈【答案】C【解析】试题分析：解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量，一般情况下一对反义词具有相反意义．一般情况下一对反义词具有相反意义，气温升高和气温降低具有相反意义．因为气温升高和气温升高不具有相反意义，所以气温升高4℃与气温升高10℃不是一对具有相反意义的量．故选C．考点：正数和负数．【题文】下列各数：其中无理数有（）A、2个 B、3个 C、4个 D、5个【答案】C【解析】试题分析：此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0．1010010001…，等有这样规律的数．无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．由无理数的定义可知．故选C．考点：无理数．【题文】对于有理数有下列几种说法，其中正确的个数有（）①若，则与互为相反数；②若，则与异号；③若与同号，则；④若，且与同号，则．A、3个B、2个C、1个D、0个【答案】C【解析】试题分析：此题考查了有理数的混合运算，有理数的混合运算首先弄清运算顺序，其次运用各种运算法则进行运算，本题要求学生掌握判断一个命题的真假的方法，可利用举反例的方法说明一个命题为假命题，即满足题中的条件，但与结论矛盾．熟练掌握运算法则是解本题的关键．①根据相反数的意义：只有符号不同的两个数互为相反数，若a+b=0，移项可得a=-b，满足相反数的定义，故a与b互为相反数，本选项正确；②举一个反例满足a+b＜0，可以取a与b同时为负数满足条件，但a与b不异号，本选项错误；③举一个反例满足a+b＞0，可以取a与b同时为负数满足条件，但a+b＜0，本选项错误；④举一个反例，a与b两数都为负数，a的绝对值大于b的绝对值满足条件，但是a+b小于0，本选项错误．①若a+b=0，则a=-b，即a与b互为相反数，本选项正确；②若a+b＜0，若a=-1，b=-2，a+b=-3＜0，但是a与b同号，本选项错误；③若a与b同号，a+b＞0，只有同时为正，故只能a＞0，b＞0，但是a，b也可以同时去负数，本选项错误；④若|a|＞|b|，且a，b同号，例如a=-3，b=-2，满足条件，但是a+b=-5＜0，本选项错误．则正确的结论有1个．故选A．考点：1．有理数的加法；2．绝对值．【题文】若，则的大小关系是（）A、 B、 C、 D、【答案】D【解析】试题分析：本题主要考查数值的大小比较,根据指数和绝对值等的运算进行判断取值范围，然后比较大小．∵a=-2-6=-8，b=-9,c=-，∴c＞a＞b．故选：D．考点：1．有理数指数幂的化简求值；2．绝对值；3．对数值大小的比较．【题文】的平方根是（）A、-4B、4C、D、【答案】C【解析】试题分析：根据平方根的定义即可解得．∵=16，42=16，∴的平方根是，故选C．考点：平方根．【题文】下列说法正确的是（）A、是负数B、一定是非负数C、不论为什么数，D、一定是分数【答案】B【解析】试题分析：任何数的绝对值一定是非负数．注意字母可以表示任意实数．根据代数式和绝对值的定义和取值判断各项．a是0时，-a还是0，所以A错误；|a|一定是非负数，正确的是B．当a=0时，没有倒数，所以C错误；当a=0时，是0，所以D错误．故选B．考点：代数式．【题文】有下列代数式，，，，，，，其中多项式的个数为（）A、2B、3C、4D、5【答案】B试题分析：本题考查了多项式的定义，注意理解几个单项式的和叫做多项式．根据多项式的定义，进行判断即可．所给各式中多项式有：，，，共3个．故选B．考点：多项式．【题文】将整式去括号，得（）A、 B、C、 D、【答案】A【解析】试题分析：本题考查去括号的方法：去括号时，运用乘法的分配律，先把括号前的数字与括号里各项相乘，再运用括号前是”+“，去括号后，括号里的各项都不改变符号；括号前是”-“，去括号后，括号里的各项都改变符号。
浙江版七年级数学上册2015-2016学年度上期期中复习综合练习及答案
2015-2016学年第一学年初一数学期中复习综合练习一、 选择题（10⨯3=30）1．向东行驶3km ，记作+3km ，向西行驶2km 记作…………………………………………（ ）A ．+2kmB ．-2kmC ．+3kmD ．-3km2.一种面粉包装袋上的质量标识为“25±0.5kg ”，则下列四袋面粉中不合格的是……（ ）A ．24.5kgB ．25.5kgC ．24.8kgD ．26.1kg3．为促进义务教育办学条件均衡，某市投入480万元资金为部分学校添置实验仪器及音、体、美器材，480万元用科学记数法表示为………………………………………………（ ）A ．448010⨯元；B ．54810⨯元；C ．64.810⨯元；D ．70.4810⨯元；4. 若32n x y 与5m x y -是同类项，则m ，n 的值为……………………………………（ ）A.3,1m n ==-； B ．3,1m n ==；C ．3,1m n =-=-； D ．3,1m n =-=；5.下列各数：0，227，13-，0.74573，1.32，3.4545545554….其中无理数有……………（ ） A ．1个 ； B ．2个 ； C ．3个； D.4个；6.下列说法正确的是………………………………………………………………………（ ）A ．单项式2342x y 的次数是9；B ． 1a x x++不是多项式； C ．322223x x y y -+是三次三项式； D ．单项式232r π的系数是32； 7.已知x-2y=3，则代数式6-2x+4y 的值为………………………………………………（ ）A ．0B ．-1C ．-3D ．38．如果()2210a b ++-=，那么代数式()2011a b +的值是………………………………( )A ．－1B ．2011C ．－2011D ．19．一列数1a ，2a ，3a ，…，其中1a =12，n a =111n a --（n 为不小于2的整数），则100a =( ) A ．12；B ．2 ；C ．-1 ；D ．-2； 10.如图1，将一个边长为a 的正方形纸片剪去两个小矩形，得到一个“”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为…………………………（ ）A ．2a-3b ；B ．4a-8b ；C ．2a-4b ；D ．4a-10b ；二、填空题（10⨯3=30） 11. 213-的倒数是 ，相反数是 ，绝对值是 . 12.写出在122-和1之间的所有负整数： . 13.比较大小：23- 34-.（填“＞”“＜”“=”） 14.设x 表示一个两位数，如果在x 左边放一个数字8，那么得到的一个三位数是 .15.对正有理数a ，b ，定义运算★如下：a ★b ab a b=+，则3★4= ； 16.当m = 时，多项式22232x xy y mx ++-中不含2x 项.17.根据规律填上合适的数：（1）1、8、27、64、 、216；（2）2、5、10、17、 、37；18.同学们玩过算24的游戏吧!下面就来玩一下．我们约定的游戏规则是：黑色扑克牌为正数，红色扑克牌为负数，只能用加、减、乘、除四种运算，每张扑克牌只能用一次，来算24．现在有下面的4张扑克牌，请你用这四张扑克牌来算24，在横线上写出运算的过程 .19．小亮按如图所示的程序输入一个数x 等于10，最后输出的结果为_______．20. 如图所示，圆的周长为4个单位长度，在圆的4等分点处标上字母A ，B ，C ，D ，先将圆周上的字母A 对应的点与数轴的数字1所对应的点重合，若将圆沿着数轴向左滚动．那么数轴上的-2009所对应的点将与圆周上字母 所对应的点重合．二、解答题（本题满分70分）21．计算(4+5+5+5分，共19分)(1) 2111943+-+--； （2）()()35263005-⨯---÷⎡⎤⎣⎦；(3)36926521⨯⎪⎭⎫⎝⎛-- ； (4) ()285150.813-÷-⨯+-；22. （本题5分）化简求值()22222322x y xy xy x y ⎡⎤-++⎣⎦，其中12x =，2y =-．23. （本题5分）已知4a b +=，2ab =-，求代数式()()4326a b ab a b ab -----的值.24. （本题6分）某一出租车一天下午以鼓楼为出发地在东西方向营运，向东走为正，向西走为负，行车里程（单位：km ）依先后次序记录如下：+5；-6；-4.5；+7；+3.5；+6；+10；-4（1）将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼的什么方向？（2）若每千米的价格为2.4元，司机一个下午的营业额是多少？25. （本题6分）小强在计算一个整式减去-3ab+5bc-1时，因为粗心，把减去误作加上，得结果为ab-3bc+6，试问：（1）这是一个怎样的整式？（2）原题的正确结果应是多少？26. （本题8分）1张长方形桌子可坐6人，按如图方式将桌子拼在一起：①两张桌子拼在一起可坐多少人？3张桌子呢？10张桌子呢？②一家餐厅有40张这样的长方形桌子，按上图方式每5张拼成一张大桌子，则一共可坐多少人？③在（2）中若改成每8张桌子拼成一张大桌子，共可坐多少人？27. （本题6分）已知多项式238x my +-与多项式227nx y -++的差中，不含有x 、y ，求mn mn +的值．28．（本题6分）图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面-层有一个圆圈，以下各层均比上-层多一个圆圈，一共堆了n 层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=()12n n +．如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是 ；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数-23，-22，-21，…，求图4中所有圆圈中各数的绝对值之和．29. （本题9分）如图：在数轴上A 点表示数a ，B 点示数b ，C 点表示数c ，b 是最小的正整数，且a 、c 满足()2270a c ++-=.（1）a= ，b= ，c= ；（2）若将数轴折叠，使得A 点与C 点重合，则点B 与数 表示的点重合；（3）点A 、B 、C 开始在数轴上运动，若点A 以每秒1个单位长度的速度向左运动，同时，点B 和点C 分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t 秒钟过后，若点A 与点B 之间的距离表示为AB ，点A 与点C 之间的距离表示为AC ，点B 与点C 之间的距离表示为BC ．则AB= ，AC= ，BC= ．（用含t 的代数式表示）（4）请问：3BC-2AB 的值是否随着时间t 的变化而改变？若变化，请说明理由；若不变，请求其值．2015-2016学年第一学年初一数学期中复习综合练习参考答案一、选择题：1.B ；2.D ；3.C ；4.B ；5.A ；6.B ；7.A ；8.A ；9.A ；10.B ；二、填空题：11. 35- ，213 ，213 ；12.-2，-1；13.＞；14. 800x + ；15. 127；16.3；17.125，26；18. ()36104+⨯---+⎡⎤⎣⎦ ；19.256；20.C ；三、解答题：21.（1）3；（2）-1060；（3）-4；（4）215； 22. 22259x y xy --=-；23.14；24.（1）17，在鼓楼东17米；（2）46×2.4=110.4元；25. （1）487-+；ab bc-+；（2）7138ab bc26.（1）8，10，24；（2）112人；（3）100人；27. 原式=()()2n x m y++--，依题意得23215+=3；n=-；m n mnm=，328.（1）67；（2）1761；29.（1）-2，1，7；（2）4；（3）33t+；t+，59t+，26（4）12；不变。
2015-2016学年浙江省杭州市下城区启正中学七年级(上)期中数学试卷(解析版)
2015-2016学年浙江省杭州市下城区启正中学七年级（上）期中数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．（3分）实数、2、、、3.14、、、0中，无理数有（）A．2个 B．3个 C．4个 D．5个2．（3分）下列式子计算正确的是（）A．（﹣3）﹣（﹣6）=﹣9 B．﹣42=﹣16 C．=﹣2 D．=±33．（3分）三峡工程的水库的库容可达393500000000m3，用科学记数法表示，精确到十亿位为（）m3．A．3.938×1011B．3.93×1011C．3.94×1011D．0.394×10174．（3分）若a的倒数是它本身，b的平方根等于它本身，那么（a2+b）2的值是（）A．1 B．8 C．±1 D．±85．（3分）若=2，则（x+3）2的平方根是（）A．4 B．8 C．±4 D．±86．（3分）下列多项式中，各项系数的积是30的是（）A．﹣x2+5x+6 B．2x2+2x﹣5 C． D．﹣32x+y+5z7．（3分）有下列说法：①任何无理数都是无限小数；②有理数与数轴上的点一一对应；③是3的平方根；④在1和3之间的无理数有且只有，，，这4个；⑤是分数，它是有理数，⑥1+是多项式．其中正确的个数是（）A．1 B．2 C．3 D．48．（3分）已知a，b，c是有理数，且a+b+c=0，abc（乘积）是负数，则的值是（）A．3 B．﹣3 C．1 D．﹣19．（3分）如图，数轴上的A，B，C三点所表示的数是分别是a、b、c，其中AB=BC，如果|a|＞|b|＞|c|，那么该数轴的原点O的位置应该在（）A．点A的左边B．点A与点B之间C．点B与点C之间D．点B与点C之间（靠近点C）或点C的右边10．（3分）已知如图，观察数表，横排为行，竖排为列，根据前五行所表达的规律，说明这个分数位于（）A．第18行，第7列B．第17行，第7列C．第17行，第11列D．第18行，第11列二、填空题（本题有10小题共10空，每空2分，共20分）11．（2分）相反数的立方根是．12．（2分）如果m＞0，n＜0，m＜|n|，那么m、n、﹣m、﹣n的大小关系是．13．（2分）把一个长、宽、高分别为40 cm，8 cm，25 cm的长方体铁块锻造成一个立方体铁块，则立方体铁块的棱长为．14．（2分）若单项式x a﹣1y2与﹣3xy b﹣1是同类项，那么a+b的值为．15．（2分）已知（a﹣3）x3y a﹣2是关于x，y的四次单项式，求a的值．16．（2分）定义运算a⊕b=b2﹣a2+1，那么（5⊕4）⊕3=．17．（2分）若实数x，y，z满足：|x3+8|+（y﹣）2+=0，则y x+z=．18．（2分）若14x+5﹣21x2=﹣2，则6x2﹣4x+5=．19．（2分）已知关于x，y的多项式（mx2+nxy﹣3x+y﹣1）﹣（x2﹣mxy﹣3x﹣1）的值与x的取值无关，则（﹣1）100+m+n|m﹣n+（﹣n）m|的值为．20．（2分）如图，用火柴棍摆出一列正方形图案，若按这种方式摆下去，摆出第n个图案用根火柴棍（用含n的代数式表示）．三、解答题（共70分）21．（24分）计算（1）﹣4﹣（﹣3）﹣（﹣6）+（﹣2）（2）1﹣（﹣）+（﹣+）（3）已知A，B关于x的多项式，且A=x2﹣2x+1，A﹣B=2x2﹣6x+3，求A+B．（4）先化简，再求值：（﹣4x2+2x﹣8y）﹣（﹣x﹣2y），其中x=，y=2015．22．（8分）已知数轴上A、B、C三个互不重合的点，若A点对应的数为a，B 点对应的数为b，C点对应的数为c．（1）若a是最大的负整数，B点在A点的左边，且距离A点2个单位长度，把B点向右移动3+个单位长度可与C点重合，请在数轴上标出A，B，C点所对应的数．（2）在（1）的条件下，化简﹣﹣|a﹣b|+|c﹣a|．23．（8分）如图，四边形ABCD和CEFB都是正方形，且正方形ABCD的边长为a，正方形CEFG的边长为b，连接BD，BF和DF后得到三角形BDF．（1）请用含字母a和b的代数式表示三角形（阴影部分）的面积（结果要求化成最简）（2）当a=，b=时，求三角形BDF（阴影部分）的面积．24．（12分）求下列各代数式的值（1）已知|=2，求+﹣3的值．（2）实数10+的整数部分是x，小数部分是y，求x﹣y的值．（3）若a、b互为相反数，a、c互为倒数，并且m的平方等于它的本身，试求+ac的值．25．（10分）某商场购进一批西服，进价为每套250元，原定每套以290元的价格销售，这样每天可销售200套，如果每套比原销售价降低10元销售，则每天可多销售100套，该商场为了确定销售价格，作了如下测算，请你参加测算，并由此归纳得出结论．（每套西服的利润=每套西服的销售价﹣每套西服的进价）．（1）按原销售价销售，每天可获利润元；（2）若每套降低10元销售，每天可获利润元；（3）如果每套销售价降低10元，每天就多销售100套，每套销售价降低20元，每天就多销售200套，按这种方式：若每套降低10x元（0≤x≤4，x为正整数）．①则每套的销售价格为元（用代数式表示）；②则每天可销售套西服（用代数式表示）；③则每天共可以获利润元（用代数式表示）④根据以上的测算，如果你是该商场的经理，你将如何确定商场的销售方案，使每天的获利最大？26．（8分）已知x1，x2，…，x2012都是不等于0的有理数，请你探究以下问题：（1）若y1=，则y1=．（2）若y2=+，则y2=；（3）若y3=++，则y3=．（4）由以上探究可知，在y2012这些不同的值中，最大值和最小值的差等于．（5）y2012=++…+，则y2012共有个不同的值．2015-2016学年浙江省杭州市下城区启正中学七年级（上）期中数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．（3分）实数、2、、、3.14、、、0中，无理数有（）A．2个 B．3个 C．4个 D．5个【解答】解：、是无理数，故选：A．2．（3分）下列式子计算正确的是（）A．（﹣3）﹣（﹣6）=﹣9 B．﹣42=﹣16 C．=﹣2 D．=±3【解答】解：A、（﹣3）﹣（﹣6）=﹣3+6=3，所以选项A不正确；B、﹣42=﹣16，所以选项B正确；C、没有意义，选项C不正确；D、=3，选项D不正确；故选：B．3．（3分）三峡工程的水库的库容可达393500000000m3，用科学记数法表示，精确到十亿位为（）m3．A．3.938×1011B．3.93×1011C．3.94×1011D．0.394×1017【解答】解：393500000000精确到十亿位用科学记数法表示为3.94×1011，故选：C．4．（3分）若a的倒数是它本身，b的平方根等于它本身，那么（a2+b）2的值是（）A．1 B．8 C．±1 D．±8【解答】解：∵a的倒数是它本身，∴a=±1，a2=1，∵b的平方根等于它本身，∴b=0，∴（a2+b）2=（1+0）2=1．故选：A．5．（3分）若=2，则（x+3）2的平方根是（）A．4 B．8 C．±4 D．±8【解答】解：∵=2，∴x+3=4．∴（x+3）2=42=16．∵16的平方根是±4，∴（x+3）2的平方根是±4．故选：C．6．（3分）下列多项式中，各项系数的积是30的是（）A．﹣x2+5x+6 B．2x2+2x﹣5 C． D．﹣32x+y+5z 【解答】解：A、﹣1×5×6=﹣30，故选项错误；B、2×2×（﹣5）=﹣20，故选项错误；C、×（﹣）×（﹣）=30，故选项正确；D、﹣32××5=﹣30，故选项错误．故选：C．7．（3分）有下列说法：①任何无理数都是无限小数；②有理数与数轴上的点一一对应；③是3的平方根；④在1和3之间的无理数有且只有，，，这4个；⑤是分数，它是有理数，⑥1+是多项式．其中正确的个数是（）A．1 B．2 C．3 D．4【解答】解：①任何无理数都是无限小数，故①符合题意；②实数与数轴上的点一一对应，故②不符合题意；③是3的平方根，故③符合题意；④在1和3之间的无理数有无数个，故④不符合题意；⑤是无理数，故⑤不符合题意；⑥1+是无理数，故⑥不符合题意；故选：B．8．（3分）已知a，b，c是有理数，且a+b+c=0，abc（乘积）是负数，则的值是（）A．3 B．﹣3 C．1 D．﹣1【解答】解：由题意知，a，b，c中只能有一个负数，另两个为正数，不妨设a ＜0，b＞0，c＞0．由a+b+c=0得出：a+b=﹣c，b+c=﹣a，a+c=﹣b，代入代数式，原式==1﹣1﹣1=﹣1．故选：D．9．（3分）如图，数轴上的A，B，C三点所表示的数是分别是a、b、c，其中AB=BC，如果|a|＞|b|＞|c|，那么该数轴的原点O的位置应该在（）A．点A的左边B．点A与点B之间C．点B与点C之间D．点B与点C之间（靠近点C）或点C的右边【解答】解：∵|a|＞|b|＞|c|，∴点A到原点的距离最大，点B其次，点C最小，又∵AB=BC，∴在点B与点C之间，且靠近点C的地方或点C的右边，故选：D．10．（3分）已知如图，观察数表，横排为行，竖排为列，根据前五行所表达的规律，说明这个分数位于（）A．第18行，第7列B．第17行，第7列C．第17行，第11列D．第18行，第11列【解答】解：观察数表，发现：①第一行的每个数的分子、分母的和为2，第二行的每个数的分子、分母的和为3，第三行的每个数的分子、分母的和为4，…，由此可知，就是每行各数的分子、分母的和为行数加1，②每行的第一个数的分母为1，第二个数的分母为2，…，即分母是几就是第几个数；所以所在的行数为11+7﹣1=17，即第17行中，位于自左至右第7个数．故选：B．二、填空题（本题有10小题共10空，每空2分，共20分）11．（2分）相反数的立方根是﹣2．【解答】解：相反数的立方根是﹣2，故答案为：﹣2．12．（2分）如果m＞0，n＜0，m＜|n|，那么m、n、﹣m、﹣n的大小关系是﹣n＞m＞﹣m＞n．【解答】解：根据正数大于一切负数，只需分别比较m和﹣n，n和﹣m．再根据绝对值的大小，得﹣n＞m＞﹣m＞n，故答案为：﹣n＞m＞﹣m＞n．13．（2分）把一个长、宽、高分别为40 cm，8 cm，25 cm的长方体铁块锻造成一个立方体铁块，则立方体铁块的棱长为20cm．【解答】解：立方体的体积是：40×25×8=8000（cm3）则立方体的棱长是=20（cm）．立方体铁块的棱长为20cm．故答案为：20cm．14．（2分）若单项式x a﹣1y2与﹣3xy b﹣1是同类项，那么a+b的值为5．【解答】解：由题意，得a﹣1=1，b﹣1=2．解得a=2，b=3．a+b=2+3=5，故答案为：5．15．（2分）已知（a﹣3）x3y a﹣2是关于x，y的四次单项式，求a的值无解．【解答】解：依题意有3+a﹣2=4且a﹣3≠0，故a无解．故答案为：无解．16．（2分）定义运算a⊕b=b2﹣a2+1，那么（5⊕4）⊕3=﹣54．【解答】解：（5⊕4）⊕3=（42﹣52+1）⊕3=（﹣8）⊕3=32﹣（﹣8）2+1=9﹣64+1=﹣54故答案为：﹣54．17．（2分）若实数x，y，z满足：|x3+8|+（y﹣）2+=0，则y x+z=3．【解答】解：由题意得，x3+8=0，y﹣=0，z﹣4=0，解得x=﹣2，y=，z=4，所以，y x+z=（）﹣2+4=3．故答案为：3．18．（2分）若14x+5﹣21x2=﹣2，则6x2﹣4x+5=7．【解答】解：∵14x+5﹣21x2=﹣2，即21x2﹣14x=7，∴3x2﹣2x=1，∴6x2﹣4x+5，=2（3x2﹣2x）+5，=7．故答案是：7．19．（2分）已知关于x，y的多项式（mx2+nxy﹣3x+y﹣1）﹣（x2﹣mxy﹣3x﹣1）的值与x的取值无关，则（﹣1）100+m+n|m﹣n+（﹣n）m|的值为3．【解答】解：（mx2+nxy﹣3x+y﹣1）﹣（x2﹣mxy﹣3x﹣1），=mx2+nxy﹣3x+y﹣1﹣x2+mxy+3x+1，=（m﹣1）x2+（ny﹣3+my+3）x+y，∵原多项式的值与x的取值无关，∴，∴，（﹣1）100+m+n|m﹣n+（﹣n）m|，=（﹣1）100×|1+1+1|，=3．20．（2分）如图，用火柴棍摆出一列正方形图案，若按这种方式摆下去，摆出第n个图案用2n（n+1）或4（1+2+3+…n）根火柴棍（用含n的代数式表示）．【解答】解：设摆出第n个图案用火柴棍为S n．①图，S1=4；②图，S2=4+3×4﹣（1+3）=4+2×4=4（1+2）；③图，S3=4（1+2）+5×4﹣（3+5）=4（1+2+3）；…；第n个图案，S n=4（1+2+3+…+n﹣1）+（2n﹣1）×4﹣（2n﹣3+2n﹣1）=4（1+2+3+…+n ﹣1）+8n﹣4﹣4n+4=4（1+2+3+…+n﹣1）+4n=4（1+2+3+…+n﹣1+n）=4×=2n（n+1）．三、解答题（共70分）21．（24分）计算（1）﹣4﹣（﹣3）﹣（﹣6）+（﹣2）（2）1﹣（﹣）+（﹣+）（3）已知A，B关于x的多项式，且A=x2﹣2x+1，A﹣B=2x2﹣6x+3，求A+B．（4）先化简，再求值：（﹣4x2+2x﹣8y）﹣（﹣x﹣2y），其中x=，y=2015．【解答】解：（1）原式=﹣4+3+6﹣2=﹣1+4=2；（2）原式=1++﹣+=1；（3）∵A=x2﹣2x+1，A﹣B=2x2﹣6x+3，∴A+B=2A﹣（A﹣B）=2（x2﹣2x+1）﹣（2x2﹣6x+3）=2x﹣1；（4）原式=﹣x2+x﹣2y+x+2y=﹣x2+x，当x=时，原式=．22．（8分）已知数轴上A、B、C三个互不重合的点，若A点对应的数为a，B 点对应的数为b，C点对应的数为c．（1）若a是最大的负整数，B点在A点的左边，且距离A点2个单位长度，把B点向右移动3+个单位长度可与C点重合，请在数轴上标出A，B，C点所对应的数．（2）在（1）的条件下，化简﹣﹣|a﹣b|+|c﹣a|．【解答】解：（1）∵a是最大的负整数，∴a=﹣1，∵B点在A点的左边，且距离A点2个单位长度，∴﹣1﹣b=2，∴b=﹣3，∵把B点向右移动3+个单位长度可与C点重合，∴c﹣（3+）=﹣3，∴c=，A，B，C点在数轴上所对应的数如图：（2）﹣﹣|a﹣b|+|c﹣a|=﹣a+（a+b）﹣（a﹣b）+（c﹣a）=﹣a+a+b﹣a+b+c﹣a=﹣2a+2b+c=﹣2×（﹣1）+2×（﹣3）+=﹣4+．23．（8分）如图，四边形ABCD和CEFB都是正方形，且正方形ABCD的边长为a，正方形CEFG的边长为b，连接BD，BF和DF后得到三角形BDF．（1）请用含字母a和b的代数式表示三角形（阴影部分）的面积（结果要求化成最简）（2）当a=，b=时，求三角形BDF（阴影部分）的面积．【解答】解：（1）解：S=S△BCD+S梯形CEFB﹣S△DEF△BFD=a2+（a+b）b﹣（a+b）b=a2（2）当a=时，由（1）可知：阴影部分面积为：24．（12分）求下列各代数式的值（1）已知|=2，求+﹣3的值．（2）实数10+的整数部分是x，小数部分是y，求x﹣y的值．（3）若a、b互为相反数，a、c互为倒数，并且m的平方等于它的本身，试求+ac的值．【解答】解：（1）∵|=2，∴=±2，当=2时，=，+﹣3=2×2+3×=5.5；当=﹣2时，=﹣，+﹣3=2×（﹣2）+3×（﹣）=﹣5.5；（2）∵2＜＜3，∴12＜10+＜13，∴x=12，y=10+﹣12=﹣2，∴x﹣y=12﹣（﹣2）=14﹣；（3）∵a、b互为相反数，a、c互为倒数，并且m的平方等于它的本身，∴a+b=0，ac=1，m=0或1，当m=0时，+ac=0+1=1；当m=1时，+ac=0+1=1；即+ac=1．25．（10分）某商场购进一批西服，进价为每套250元，原定每套以290元的价格销售，这样每天可销售200套，如果每套比原销售价降低10元销售，则每天可多销售100套，该商场为了确定销售价格，作了如下测算，请你参加测算，并由此归纳得出结论．（每套西服的利润=每套西服的销售价﹣每套西服的进价）．（1）按原销售价销售，每天可获利润8000元；（2）若每套降低10元销售，每天可获利润9000元；（3）如果每套销售价降低10元，每天就多销售100套，每套销售价降低20元，每天就多销售200套，按这种方式：若每套降低10x元（0≤x≤4，x为正整数）．①则每套的销售价格为（290﹣10x）元（用代数式表示）；②则每天可销售（200+100x）套西服（用代数式表示）；③则每天共可以获利润（40﹣10x）（200+100x）元（用代数式表示）④根据以上的测算，如果你是该商场的经理，你将如何确定商场的销售方案，使每天的获利最大？【解答】解：（1）按原销售价销售，每天可获利润为：（290﹣250）×200=8000（元），故答案为：8000；（2）若每套降低10元销售，每天可获利润为：（290﹣10﹣250）（200+100）=9000（元），故答案为：9000；（3）①由题意可得，每套的销售价格为：（290﹣10x）元，故答案为：（290﹣10x）；②每天可销售：（200+100x）套，故答案为：（200+100x）；③每天共可以获利润为：（290﹣10x﹣250）（200+100x）=（40﹣10x）（200+100x）元，故答案为：（40﹣10x）（200+100x）；④利润为W元，则W=（40﹣10x）（200+100x）=﹣1000（x﹣1）2+9000，∴当x=1时，W取得最大值，此时W=9000，即每套比原销售价降低10元销售，可使每天的获利最大．26．（8分）已知x1，x2，…，x2012都是不等于0的有理数，请你探究以下问题：（1）若y1=，则y1=±1．（2）若y2=+，则y2=±2或0；（3）若y3=++，则y3=±3，±1．（4）由以上探究可知，在y2012这些不同的值中，最大值和最小值的差等于4024．（5）y2012=++…+，则y2012共有2013个不同的值．【解答】解：（1）x1＜0时，y1==﹣1，x1＞0时，y1==﹣1，则y1=±1；（2）若x1＞0，x2＞0时，y2=+=2，x1＞0，x2＜0时，y2=+=0，x1＜0，x2＜0时，y2=+=﹣2，综上所述，y2=±2或0；（3）x1＞0，x2＞0，x3＞0，y3=++=3，x1＞0，x2＞0，x3＜0，y3=++=1x1＞0，x2＜0，x3＜0，y3=++=﹣1，x1＜0，x2＜0，x3＜0，y3=++=﹣3综上所述，y3=±1，±3；（4）由以上探究可知，在y2012这些不同的值中，最大的值和最小的值的差等于2012﹣（﹣2012）=4024；（5）由以上探究可知，y2012=++…+，则y2012共有2013个不同的值．故答案为：±1；±2或0；±3或±1，4024；2013．。
2016年浙江省杭州市下城区四季青中学七年级上学期数学期中试卷和解析答案
2015-2016学年浙江省杭州市下城区四季青中学七年级（上）期中数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）下列各对量中，不具有相反意义的是（）A．胜3局与负4局B．收入3000元与支出2000元C．气温升高4℃与气温升高10℃D．转盘逆时针转3圈与顺时针转5圈2．（3分）下列各数：，﹣π，0，，，，0.1010010001…，，1.414，0.，其中无理数有（）A．2个 B．3个 C．4个 D．5个3．（3分）对于有理数a，b有下列几种说法，其中正确的个数有（）①若a+b=0，则a与b互为相反数；②若a+b＜0，则a与b异号；③若a与b同号，则a+b＞0；④若|a|＞|b|，且a与b同号，则a+b＞0．A．3个 B．2个 C．1个 D．0个4．（3分）若a=﹣2+2•（﹣3），b=﹣32，c=﹣|﹣|，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b5．（3分）（﹣4）2的平方根是（）A．﹣4 B．4 C．±4 D．±26．（3分）下列说法正确的是（）A．﹣a是负数B．|a|一定是非负数C．不论a为什么数，D．一定是分数7．（3分）有下列代数式4，，，x2﹣2xy+y2，，5m，﹣3xy+1，其中多项式的个数为（）A．2 B．3 C．4 D．58．（3分）将整式﹣[a﹣（b+c）]去括号，得（）A．﹣a+b+c B．﹣a+b﹣c C．﹣a﹣b+c D．﹣a﹣b﹣c9．（3分）已知a是两位数，b是一位数，把b接写在a的后面，就成为一个三位数．这个三位数可表示成（）A．10a+b B．ab C．100a+b D．a+10b10．（3分）等边△ABC在数轴上的位置如图所示，点A，C对应的数分别为0和﹣1，若△ABC绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1；则翻转2006次后，点B所对应的数是（）A．2005 B．2006 C．2007 D．2008二、专心填一填（6小题，每小题4分，共24分）11．（4分）单项式πr2的系数是；当r=3时，这个代数式的值是（结果保留到0.01）12．（4分）我们要深入领会胡锦涛总书记关于社会主义荣辱观的重要论述，树立起节约光荣、浪费可耻的观念．如果每人每天浪费水0.32升，那么100万人每天浪费的水，可用科学记数法表示为升，数量是多么惊人啊！13．（4分）当x=，y=时，+=0．14．（4分）写出两个无理数，使它们的和为有理数，；写出两个无理数，使它们的积为有理数，．15．（4分）已知|a|＞|b|，且a＜0，b＞0，试利用数轴比较a，b，﹣a，﹣b 的大小：（用“＜”连接），本题用到的数学思想是．16．（4分）已知n是自然数，多项式x n+3x3﹣2x+4x2是三次三项式，那么n可以取的数是．三、认真解一解（7小题共66分）17．（6分）观察下列等式：回答问题：①=1+﹣=1②=1+﹣=1③=1+﹣=1，…（1）根据上面三个等式的信息，猜想=；（2）请按照上式反应的规律，试写出用n表示的等式；（3）验证你的结果．18．（10分）计算：①2.75﹣[（﹣5）﹣（﹣0.5）+（﹣3）]；②（﹣）×（﹣）÷（﹣）；③﹣7×（﹣）+26×（﹣）﹣2×；④﹣12﹣÷（﹣）+5×（﹣2）2．19．（8分）化简：（1）2（2x﹣3y）﹣（3x+2y+1）（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]．20．（8分）（1）已知mn﹣n=15，m﹣mn=6，求：代数式m﹣n的值；（2）已知x2+2x﹣5=3，求：代数式2x2+4x+8的值；（3）已知x2﹣x﹣1=0，求：代数式﹣x3+2x2+2015的值．21．（10分）（1）利用如图4×4方格，作出面积为8平方单位的正方形．（2）已知3m﹣4与7﹣4m是N的平方根，求﹣2﹣N的立方根．22．（12分）如图是某住宅的平面结构示意图，图中标注了有关尺寸（墙体厚度勿略不计，单位：m）．（1）该住宅的面积是多少？（2）该房的主人计划把卧室以外的地面都铺上地砖，若他所选的地砖的价格是60元/m2，他买地砖至少需要多少元？23．（12分）这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行．”国王以为要不了多少粮食，就随口答应了，结果国王输了．（1）我们知道，国际象棋共有64个格子，则在第64格中应放多少米？（用幂表示）（2）请探究第（1）中的数的末位数字是多少？（简要写出探究过程．）（3）你知道国王输给了阿基米德多少粒米吗？为解决这个问题，我们先来看下面的解题过程：用分数表示无限循环小数：．解：设①．等式两边同时乘以10，得10x=②．将②﹣①得：9x=2，则．∴请参照以上解法求出国王输给阿基米德的米粒数（用幂的形式表示）2015-2016学年浙江省杭州市下城区四季青中学七年级（上）期中数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）下列各对量中，不具有相反意义的是（）A．胜3局与负4局B．收入3000元与支出2000元C．气温升高4℃与气温升高10℃D．转盘逆时针转3圈与顺时针转5圈【解答】解：A、胜3局与负4局，是相反意义的量；B、收入3000元与支出2000元，是相反意义的量；C、气温升高4℃与气温升高10℃，不是相反意义的量；D、转盘逆时针转3圈与顺时针转5圈，是相反意义的量，故选：C．2．（3分）下列各数：，﹣π，0，，，，0.1010010001…，，1.414，0.，其中无理数有（）A．2个 B．3个 C．4个 D．5个【解答】解：，﹣π，，0.1010010001…，是无理数，故选：CD．3．（3分）对于有理数a，b有下列几种说法，其中正确的个数有（）①若a+b=0，则a与b互为相反数；②若a+b＜0，则a与b异号；③若a与b同号，则a+b＞0；④若|a|＞|b|，且a与b同号，则a+b＞0．A．3个 B．2个 C．1个 D．0个【解答】解：∵互为相反数的两个数的和是0，∴若a+b=0，则a与b互为相反数，∴①正确；∵若a+b＜0，则a、b有可能都是负数，∴a与b不一定异号，∴②不正确；∵若a与b同号，则a、b有可能都是负数，∴此时a+b＜0，∴③不正确；∵若|a|＞|b|，且a与b同号，则a、b有可能都是负数，∴此时a+b＜0，a+b＞0不一定成立，∴④不正确．综上，可得对于有理数a，b有下列几种说法，其中正确的个数有1个：①．故选：C．4．（3分）若a=﹣2+2•（﹣3），b=﹣32，c=﹣|﹣|，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b【解答】解：∵a=﹣2+2•（﹣3）=﹣8，b=﹣32=﹣9，c=﹣|﹣|=﹣，∴c＞a＞b，故选：D．5．（3分）（﹣4）2的平方根是（）A．﹣4 B．4 C．±4 D．±2【解答】解：∵（﹣4）2=16，∴16的平方根是±4．故选：C．6．（3分）下列说法正确的是（）A．﹣a是负数B．|a|一定是非负数C．不论a为什么数，D．一定是分数【解答】解：a是0时，﹣a还是0，所以A错误；|a|一定是非负数，正确的是B．当a=0时，没有倒数，所以C错误；当a=0时，是0，所以D错误．故选：B．7．（3分）有下列代数式4，，，x2﹣2xy+y2，，5m，﹣3xy+1，其中多项式的个数为（）A．2 B．3 C．4 D．5【解答】解：多项式有，x2﹣2xy+y2，﹣3xy+1，故选：B．8．（3分）将整式﹣[a﹣（b+c）]去括号，得（）A．﹣a+b+c B．﹣a+b﹣c C．﹣a﹣b+c D．﹣a﹣b﹣c【解答】解：根据去括号法则：﹣[a﹣（b+c）]=﹣（a﹣b﹣c）=﹣a+b+c．故选：A．9．（3分）已知a是两位数，b是一位数，把b接写在a的后面，就成为一个三位数．这个三位数可表示成（）A．10a+b B．ab C．100a+b D．a+10b【解答】解：根据题意可得这个三位数可表示成10a+b，故选：A．10．（3分）等边△ABC在数轴上的位置如图所示，点A，C对应的数分别为0和﹣1，若△ABC绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1；则翻转2006次后，点B所对应的数是（）A．2005 B．2006 C．2007 D．2008【解答】解：因为2006=668×3+2=2004+2，所以2006次翻折对应的数字和2005对应的数字相同是2005．故选：A．二、专心填一填（6小题，每小题4分，共24分）11．（4分）单项式πr2的系数是π；当r=3时，这个代数式的值是18.85（结果保留到0.01）【解答】解：∵π是数字不是字母，∴单项式πr2的系数是π．代数式的值=×32=6π≈18.85．故答案为：π；18.85．12．（4分）我们要深入领会胡锦涛总书记关于社会主义荣辱观的重要论述，树立起节约光荣、浪费可耻的观念．如果每人每天浪费水0.32升，那么100万人每天浪费的水，可用科学记数法表示为 3.2×105升，数量是多么惊人啊！【解答】解：0.32×100×104=3.2×105升．13．（4分）当x=3，y=5时，+=0．【解答】解：由题意得，3﹣x=0，y﹣5=0，解得x=3，y=5．故答案为：3；5．14．（4分）写出两个无理数，使它们的和为有理数2﹣，3+；写出两个无理数，使它们的积为有理数3，2．【解答】解：（1）可以先写出任意一个无理数如2﹣，若两个无理数的和是4，则另一个无理数是：4﹣（2﹣）=2+；（2）可以先写出任意一个无理数如3，若两个无理数的积是12，则另一个无理数是：12÷3．故答案为：2﹣，2+；3，．15．（4分）已知|a|＞|b|，且a＜0，b＞0，试利用数轴比较a，b，﹣a，﹣b 的大小：a＜﹣b＜b＜﹣a（用“＜”连接），本题用到的数学思想是数形结合．【解答】解：已知|a|＞|b|，且a＜0，b＞0，如图所示：则a＜﹣b＜b＜﹣a，本题用到的数学思想是数形结合．16．（4分）已知n是自然数，多项式x n+3x3﹣2x+4x2是三次三项式，那么n可以取的数是1，2，3．【解答】解：由于该多项式已经有一、二和三次项，因此xn可以是一次项或者二次项或者三次项，所以n=1，2，3；三、认真解一解（7小题共66分）17．（6分）观察下列等式：回答问题：①=1+﹣=1②=1+﹣=1③=1+﹣=1，…（1）根据上面三个等式的信息，猜想=1；（2）请按照上式反应的规律，试写出用n表示的等式；（3）验证你的结果．【解答】解：（1）根据上面三个等式的信息，猜想=1，故答案为：1；（2）=1+﹣．（3）=====1+﹣．18．（10分）计算：①2.75﹣[（﹣5）﹣（﹣0.5）+（﹣3）]；②（﹣）×（﹣）÷（﹣）；③﹣7×（﹣）+26×（﹣）﹣2×；④﹣12﹣÷（﹣）+5×（﹣2）2．【解答】解：①原式=2.75+5.5﹣0.5+3.25=6+5=11；②原式=﹣××=﹣；③原式=﹣×（﹣7+26+2）=﹣×21=﹣66；④原式=﹣1+4+20=23．19．（8分）化简：（1）2（2x﹣3y）﹣（3x+2y+1）（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]．【解答】解：（1）原式=4x﹣6y﹣3x﹣2y﹣1=（4﹣3）x﹣（6+2）y=x﹣8y﹣1；（2）原式=﹣（3a2﹣4ab）+[a2﹣4a﹣4ab]=﹣3a2+4ab+a2﹣4a﹣4ab=﹣2a2﹣4a．20．（8分）（1）已知mn﹣n=15，m﹣mn=6，求：代数式m﹣n的值；（2）已知x2+2x﹣5=3，求：代数式2x2+4x+8的值；（3）已知x2﹣x﹣1=0，求：代数式﹣x3+2x2+2015的值．【解答】解：（1）∵mn﹣n=15，m﹣mn=6，∴两式相加得到：m﹣n=21；（2）∵x2+2x﹣5=3，∴x2+2x=8，∴2x2+4x+8=2（x2+2x）+8=24；（3）∵x2﹣x﹣1=0，∴x2=x+1，﹣x2+x=﹣1，∴﹣x3+2x+2015=﹣x（x+1）+2x+2015=﹣x2﹣x+2x+2015=﹣x2+x+2015=2014．21．（10分）（1）利用如图4×4方格，作出面积为8平方单位的正方形．（2）已知3m﹣4与7﹣4m是N的平方根，求﹣2﹣N的立方根．【解答】解：（1）如图所示：（2）由题意得：3m﹣4+7﹣4m=0，解得：m=3．则N=（3×3﹣4）2=25，﹣2﹣N=﹣2﹣15=﹣27，﹣27的立方根是﹣3．22．（12分）如图是某住宅的平面结构示意图，图中标注了有关尺寸（墙体厚度勿略不计，单位：m）．（1）该住宅的面积是多少？（2）该房的主人计划把卧室以外的地面都铺上地砖，若他所选的地砖的价格是60元/m2，他买地砖至少需要多少元？【解答】解：（1）该住宅的面积是2x•4y+x•2y+x•y+2x•2y=15xy；（2）他买地砖需要60×（2x•4y+x•2y+•x•y）=660xy元．23．（12分）这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行．”国王以为要不了多少粮食，就随口答应了，结果国王输了．（1）我们知道，国际象棋共有64个格子，则在第64格中应放多少米？（用幂表示）（2）请探究第（1）中的数的末位数字是多少？（简要写出探究过程．）（3）你知道国王输给了阿基米德多少粒米吗？为解决这个问题，我们先来看下面的解题过程：用分数表示无限循环小数：．解：设①．等式两边同时乘以10，得10x=②．将②﹣①得：9x=2，则．∴请参照以上解法求出国王输给阿基米德的米粒数（用幂的形式表示）【解答】解：（1）第64个格子，应该底数是2，指数63，所以为263；（2）∵21=2，22=4，23=8，24=16，25=32…∵63÷4=15…3，∴263的末位数字与23的末位数字相同，是8；（3）设x=1+2+22+…+263①．等式两边同时乘以2，得2x=2+22+23+ (264)②﹣①，得x=264﹣1．答：国王输给阿基米德的米粒数为264﹣1．赠送初中数学几何模型【模型一】“一线三等角”模型： 图形特征：运用举例：1.如图，若点B在x轴正半轴上，点A(4，4)、C(1，－1)，且AB＝BC，AB⊥BC，求点B的坐标；xyBCAO2.如图，在直线l上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S、2S、3S、4S，则14S S+=．ls4s3s2s13213. 如图，Rt△ABC中，∠BAC=90°，AB=AC=2，点D在BC上运动（不与点B，C重合），过D作∠ADE=45°，DE交AC于E．（1）求证：△ABD∽△DCE；（2）设BD=x，AE=y，求y关于x的函数关系式，并写出自变量x的取值范围；（3）当△ADE是等腰三角形时，求AE的长．B4.如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。
浙江省杭州市上城区四校2015-2016学年七年级上学期期中联考数学试题解析(解析版)
考生须知：1． 试卷满分为120试时间为100分钟.2． 本卷答案必须做在答题卷相应的位置上，做在试卷上无效. 3． 请用2B 铅笔.钢笔或圆珠笔将相关内容填涂在答题卷的相应位置上.一. 选择题：（每小题3分，共30分）1.比－4小2的数是（ ）A ．－2 B.－1 C.－6 D.0 【答案】C.考点：有理数的减法.2.下列各式中正确的是（ ）A.33-=-B.)1(1--=-C.12-<-D.22-+=+-【答案】B. 【解析】试题分析：选项A,333-≠=-,选项A 错误；选项B,)1(11--==-,选项B 正确；选项C ，12-- ，选项C 错误；选项D ，222-+≠-=+-，选项D 错误，故答案选B.考点：绝对值的计算.3.用代数式表示：“x 的5倍与y 的和的一半”可以表示为（ ） A.152x y +B.1(5)2x y +C.1(5)2x y + D.5x y + 【答案】B. 【解析】试题分析:根据题意可得“x 的5倍与y 的和的一半”可以表示为1(5)2x y +，故答案选B.考点：列代数式.4．用科学记数法表示数2350为（ ）A. 2.350×103B. 0.2350×104C. 0.2350×103D. 2.350×104【答案】A. 【解析】试题分析：科学记数法的表示形式为a ×10n的形式，其中1≤|a|＜10，n 为整数．确定n 的值时为这个数的整数位数减1，这里a=2.35，n=3，所以2350=2.35×103．故答案选A.考点：科学计数法.5．亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会，并在会上投票选出2022年第19届亚运会举办城市为杭州.5个城市的国际标准时间（单位：时）在数轴上表示如图所示，那么北京时间2015年9月16日20时应是（ ）智利 伦敦 巴黎 曼谷 杭州A.伦敦时间2015年9月16日11时B.巴黎时间2015年9月16日13时C.智利时间2015年9月16日5时D.曼谷时间2015年9月16日18时 【答案】B.考点：数轴.6．在4-，3.14 ，π ，10，∙∙15.1 ，722中无理数的个数是（ ） （A ） 5个 （B ） 4个 （C ） 3个 （D ） 2个 【答案】D. 【解析】试题分析：无理数是无限不循环小数，根据无理数的定义可得在4-，3.14 ，π ，10，∙∙15.1 ，722中无理数有π，10，共2个，故答案选D. 考点：无理数.7．设a 是最小的自然数，b 是最大的负整数，c 是绝对值最小的有理数，则c b a +-=（ ） A.1 B.2 C.0 D.以上都不对 【答案】A. 【解析】试题分析：由a 是最小的自然数，b 是最大的负整数，c 是绝对值最小的有理数，可得a=0,b=-1,c=0,所以c b a +-=0-（-1）+0=1.故答案选A.考点：有理数.8．已知a =12.3是由四舍五入得到的近似数，则a 的取值范围是（ ） A.12.25≤a ≤12.35 B.12.25≤a ﹤12.35 C.12.25﹤a ≤12.35 D.12.25﹤a ﹤12.35 【答案】B.考点：近似数.9．下列说法中，正确的．．．是（ ） ①3243-〉- ②a 一定是正数 ③无理数一定是无限小数 ④ 16.8万精确到十分位 ⑤2)8(-的算术平方根是 8 A.①②③ B.④⑤ C.②④ D.③⑤ 【答案】D. 【解析】试题分析：根据两个负数，绝对值大的反而小可得3243--，①错误；a 是正数或0，②错误；无理数一定是无限小数，③正确；16.8万精确到千位，④错误；2)8(-的算术平方根是8，⑤正确.所以正确的有③⑤两个，故答案选D.考点：有理数.10．有理数a ，b 在数轴上对应的位置如图所示，那么代数式-+-的值是( )A.-1B.0C.1D.2【答案】D. 【解析】试题分析：由图可以看出，-1＜a ＜0，∴a+1＞0，|a+1|=a+1,同理，|a|=-a ，|a-b|=-（a-b ）=b-a ，|b-1|=-（b-1）=1-b,所以原式=211111111=-++=-----+--++bba b a b a a a a ，故答案选D. 考点：数轴；绝对值.二. 填空题：（每空2分，共30分）11．如果水位升高3m 时水位变化记作+3米，则水位下降5米时水位变化记作：________米. 【答案】-5. 【解析】试题分析：因为"正"和"负"相对，所以水位升高3米时水位变化记作+3米，水位下降5米时水位变化记作-5米.考点：正负数的意义.12．81-的相反数是________，绝对值是2的数是________，-412的倒数是________. 【答案】81，±2，94-.考点：相反数；倒数；绝对值.13．计算：⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛-3132=________ , 364=____________，2)4(4-+=__________. 【答案】-1,4,8. 【解析】试题分析：131323132-=--=⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛-, 4643=，844)4(42=+=-+. 考点：有理数的减法；立方根；平方根.14．在数轴上与表示-1的点的距离为3个单位长度的点所表示的数是______________. 【答案】-4或2. 【解析】试题分析：当点在-1的左侧时，在数轴上与表示-1的点的距离为3个单位长度的点所表示的数是-4；当点在-1的右侧时，在数轴上与表示-1的点的距离为3个单位长度的点所表示的数是2.考点：数轴.15．单项式853ab -的系数是________,次数是________，多项式5732--x x 的次数是________.【答案】85-,4，2.考点：单项式；多项式.16．已知实数,x y 满足0114=++-y x ，则代数式x y -=_____________.【答案】15. 【解析】试题分析：已知0114=++-y x ，可得x=4，y=-11，所以x-y=4+11=15.考点：a a 和的非负性. 17．若92=x ,则x=________，,92=x则x=________.【答案】±3，±9. 【解析】试题分析：由92=x 可得3±=x ，由92=x可得x=±9.考点：平方根；二次根式a2的化简.18．假设一家旅馆一共有30个房间，分别编以1-30号三十个号码，现在要在每个房间的钥匙上刻上数字，要求所刻数字必须使服务员很容易辨认是哪一个房间的钥匙，而使外人不容易猜到，现在有一种编码方法是：在每把钥匙上刻上两个数字，左边的一个数字是这把钥匙原来的房间号除以5所得的余数，而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数，那么刻的数是36的钥匙所对应的原来房间应该是___________号.【答案】13.【解析】试题分析：一共有30个房间，分别编以1～30三十个号码，左边的一个数字是这把钥匙原来的房间号码除以5所得的余数，由于1-30中，除以5余3的数有8，13，18，23，28．右边的一个数字是这把钥匙原来的房间号码除以7所得的余数，其中除以7余6的数只有13．所以这个刻的数是36的钥匙所对应的原来房间应该是13．考点：有理数的除法.三.解答题：（共60分）19．（8分）在数轴上表示下列各数以及它们的相反数，并把这些数和它的相反数按从小到大的顺序用“＜”号连接.0， -2， 2.5，【答案】详见解析.考点：相反数；数轴；有理数的大小比较.20．（12分）计算.（1）－9＋6÷（－2）（2）49 3510⎛⎫⨯-÷⎪⎝⎭（3）22350(5)1--÷-- （4）用简便方法计算：1799918⨯【答案】(1)-12;(2)38-；(3)-12;(4)899.5. 【解析】试题分析：(1)(2)(3)题，根据有理数的运算顺序依次计算即可；（4）把181799化为100-181，再根据乘法分配律计算即可.试题解析：解：（1）原式=-9+（-3）=-12； （2）原式= 910)54(3⨯-⨯=38-； （3）原式=-9-2-1=-12； （4）原式=（100-181）×9=900-21=899.5. 考点：有理数的混合运算.21．（8分）一座圆形花坛的半径为r ，中间喷水池是面积为4的正方形.（1）用关于r 的代数式写出该花坛的实际种花面积，并求出当r=2时花坛的实际种花面积（π取3.14，结果精确到0.1）.（2）现需要将喷水池缩小为面积为2的正方形，请在图中画出缩小后的正方形，使它的顶点在网格的格点上.【答案】(1)4π-4；（2）详见解析. 【解析】试题分析：(1)用花坛的面积减去正方形的面积即可；（2）再图中画出一个边长为2的正方形即可. 试题解析：（1）实际种花面积为：π42-r ,当2=r 时，原式=4π-4；（2）如图，考点：列代数式.22.（10分） 2015年9月30日杭州西湖景区某公园人流量为7万，每张门票80元，“十一黄金周”景区迎来了旅游高峰期，游客从各个省市来到杭州，该公园统计：十一黄金周期间，游客人数与前一天相比，增加和减少的情况如下表：（记增加为正）.（1）10月2号该公园的人流量是多少万人？（2）“十一黄金周”期间，人流量最多和最少分别出现在哪一天？（3）该公园的所有门票收入均要缴纳百分之五的税，求“十一黄金周”期间，该公园的实际收入.【答案】(1)10.8万人；（2）最多5号:17.7万人;最少2号:10.8万人；（3）7600万元.考点：正负数的意义；有理数的运算.23．（10分）24点游戏是一种使用扑克牌来进行的益智类游戏，游戏内容是：从一副扑克牌中抽去大小王剩下52张，任意抽取4张牌，把牌面上的数运用你所学过的运算得出24.每张牌都必须使用一次，但不能重复使用.（1）在玩“24点”游戏时，小明抽到以下4张牌：请你帮他写出运算结果为24的算式：(写出2个)_______________________； _______________________；（2）如果.表示正，.表示负，请你用（1）中的4张牌表示的数写出运算结果为24的算式(写出2个)：__________________________； __________________________；（3）如果小明抽到以下4张牌：请你用这4张牌表示的数写出运算结果为24的一个算式：__________________________.【答案】（1）2×4×（6-3）；3×4+6×2；（2）2×（-4）×[3+(-6）]；（-4）×（-6）×（3-2）；（3）(3÷7+3)×7.【解析】试题分析：根据有理数的运算顺序依次写出即可.试题解析：（1）2×4×（6-3）；3×4+6×2；（2）2×（-4）×[3+(-6）]；（-4）×（-6）×（3-2）；（3）(3÷7+3)×7.(答案不唯一)考点：有理数的运算.24.（12分）（1）在数1.2.3.4.5.6.7.8前添加“+”，“-”并依次运算，所得结果可能的最小非负数是多少？（列式计算，列出一个算式即可）（2）在数1.2.3……2015前添加“+”，“-”并依次运算，所得结果可能的最小非负数是多少？（列式计算，列出一个算式即可）（3）在数1.2.3……n前添加“+”，“-”并依次运算，所得结果可能的最小非负数是多少？（只写出答案即可）【答案】(1)(1-2-3+4)+(5-6-7+8)=0 ；(2)(1+2-3)+(4-5-6+7)+……+（2012-2013-2014+2015）=0；（3）当n是4的倍数时，结果可能的最小非负数为0；当n除以4余1时，结果可能的最小非负数为1；当n除以4余2时，结果可能的最小非负数为1；当n除以4余3时，结果可能的最小非负数为0.试题解析：解：(1)(1-2-3+4)+(5-6-7+8)=0 ；(2)(1+2-3)+(4-5-6+7)+……+（2012-2013-2014+2015）=0；（3）当n是4的倍数时，结果可能的最小非负数为0；当n除以4余1时，结果可能的最小非负数为1；当n除以4余2时，结果可能的最小非负数为1；当n除以4余3时，结果可能的最小非负数为0.考点：有理数的运算.高考一轮复习：。
2016学年浙江省杭州市下城区安吉路实验学校七年级(上)数学期中试卷带参考答案
2015-2016学年浙江省杭州市下城区安吉路实验学校七年级（上）期中数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）小马虎在下列计算中，只做对了一道题，他做对的题目是（）A．﹣（a﹣6）=﹣a﹣6 B．a3+a2=a5C．a3+a3=2a3D．x2y+xy2=2x3y32．（3分）一个点从数轴上的原点开始，先向右移动3个单位，再向左移动7个单位长度，这时点所对应的数是（）A．3 B．1 C．﹣2 D．﹣43．（3分）x=2是方程ax﹣6=0的解，则a的取值是（）A．2 B．3 C．4 D．54．（3分）下列各组数中，互为相反数的一组是（）A．﹣2与﹣B．﹣2与C．﹣2与D．|﹣2|与5．（3分）若|x+2|+，则xy的值为（）A．﹣8 B．﹣6 C．5 D．66．（3分）有理数a等于它的倒数，有理数b等于它的相反数，则a2009+b2009等于（）A．1 B．﹣1 C．±1 D．27．（3分）以下各数中是无理数的个数是（）A．2 B．3 C．4 D．58．（3分）有一批画册，若3人合看一本，则多余2本；若2人合看一本，就有9人没有，设人数为x，则列出的方程是（）A．3x+2=2x﹣9 B．﹣2=C．+2=D．+2=﹣99．（3分）有下列说法：①任何无理数都是无限小数；②有理数与数轴上的点一一对应；④是分数，它是有理数．⑤近似数7.30所表示的准确数a的范围是：7.295≤a＜7.305．其中正确的个数是（）A．1 B．2 C．3 D．410．（3分）如图，某人沿着边长为90米的正方形，按A→C→D→B→A…方向运动，甲从A以64米/分的速度，乙从C以90米/分的速度行走，当乙第一次追上甲时在正方形的（）A．AB边上 B．CA边上 C．DC边上 D．BD边上二、认真填一填（本题有6个小题，每小题4分，共24分）11．（4分）单项式﹣的系数是，多项式是次二项式．12．（4分）用代数式表示a除以b加1为．13．（4分）（1）3.256精确到十分位为，（2）用科学记数法表示372000为．14．（4分）的算术平方根是．一个正方形的面积是13，估计它的边长大小接近于整数．15．（4分）已知|x﹣y|=y﹣x，|x|=3，y=2，则（x+y）3=．16．（4分）如图是一个数值转换机的示意图，若输出的数y=5，则输入的数x=．三、全面答一答（本题有7个小题，共66分）解答应按要求写出必要的解答步17．（12分）计算下列各式①﹣﹣+2﹣+②﹣+33③﹣14﹣（1﹣0.5）××[2﹣（﹣3）2]④4﹣（﹣36）×（+﹣）18．（12分）解下列方程：①2（2x﹣1）=1﹣（3﹣x）②﹣1=③﹣=﹣1.6④4x﹣3+6（3﹣4x）=7（4x﹣3）19．（7分）（1）先化简再求值：x2﹣（x2+2xy﹣y2）+5（y2﹣3xy），其中x=，y=．（2）已知m﹣n=6，求﹣4（m﹣n）+3m﹣3n+8的值．20．（7分）已知单项式2x3y m﹣1与x m﹣2n y4是同类项，求代数式：（m﹣2n）﹣2（2n﹣m）+m﹣5的值．21．（7分）已知下面两个方程3（x+2）=5x，①4x﹣3（a﹣x）=6x﹣7（a﹣x）②有相同的解，试求a的值．22．（7分）1千瓦时电（即通常所说的1度电）可供一盏40瓦的电灯点亮25小时．（1）1千瓦时的电量可供n瓦的电灯点亮多少时间？（2）若每度电的电费为a元，一个100瓦的电灯使用12时的电费是几元？23．（7分）一个工厂接受﹣项任务，需要在12天内完成，如果由第一车间独做，正好按期完成；如果由第二车间单独完成，就要超过规定日期3天，如果由两个车间合作几天后，剩下的任务由第二车间单独去做，正好在规定日期完成，问两个车间共合作了几天？（前段工作量+后段工作量=总工作量）24．（7分）从2012年7月1日起浙江执行新版居民阶梯电价，小坤同学家收到电费支出与新政前相比是多了还是少了？”于是，小坤同学上网了解了有关电费的收费情况，得到如下两表：2004年1月至2012年6月执行的收费标准：2012年7月起执行的收费标准：（1）若小坤家2012年7月份的用电量为200度，则小坤家7月份的电费支出是多少元？比新政前少了多少元？（2）若小坤家2012年8月份的用电量为480度，则电费支出与新政前相比有什么变化？请计算说明．（3）若新政后小坤家的月用电量为a度，请你用含a的代数式表示当月的电费支出．2015-2016学年浙江省杭州市下城区安吉路实验学校七年级（上）期中数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）小马虎在下列计算中，只做对了一道题，他做对的题目是（）A．﹣（a﹣6）=﹣a﹣6 B．a3+a2=a5C．a3+a3=2a3D．x2y+xy2=2x3y3【解答】解：A、﹣（a﹣6）=﹣a+6，错误；B、字母的指数不同，不是同类项，不能合并，错误；C、正确；D、字母的指数不同，不是同类项，不能合并，错误．故选：C．2．（3分）一个点从数轴上的原点开始，先向右移动3个单位，再向左移动7个单位长度，这时点所对应的数是（）A．3 B．1 C．﹣2 D．﹣4【解答】解：根据题意，得0+3﹣7=﹣4．故选：D．3．（3分）x=2是方程ax﹣6=0的解，则a的取值是（）A．2 B．3 C．4 D．5【解答】解：把x=2代入方程得：2a﹣6=0，解得：a=3，故选：B．4．（3分）下列各组数中，互为相反数的一组是（）A．﹣2与﹣B．﹣2与C．﹣2与D．|﹣2|与【解答】解：A、绝对值不同不是相反数，故A错误；C、只有符号不同的两个数互为相反数，故C正确；D、都是2，故D错误；故选：C．5．（3分）若|x+2|+，则xy的值为（）A．﹣8 B．﹣6 C．5 D．6【解答】解：∵|x+2|≥0，≥0，而|x+2|+=0，∴x+2=0且y﹣3=0，∴x=﹣2，y=3，∴xy=（﹣2）×3=﹣6．故选：B．6．（3分）有理数a等于它的倒数，有理数b等于它的相反数，则a2009+b2009等于（）A．1 B．﹣1 C．±1 D．2【解答】解：∵有理数a等于它的倒数，∴a=±1，∵有理数b等于它的相反数，∴b=0，当a=1、b=0时，a2009+b2009=12009+02009=1，当a=﹣1、b=0时，a2009+b2009=（﹣1）2009+02009=﹣1，综上所述，a2009+b2009等于±1．故选：C．7．（3分）以下各数中是无理数的个数是（）A．2 B．3 C．4 D．5【解答】解：无理数有：，﹣共有2个．故选：A．8．（3分）有一批画册，若3人合看一本，则多余2本；若2人合看一本，就有9人没有，设人数为x，则列出的方程是（）A．3x+2=2x﹣9 B．﹣2=C．+2=D．+2=﹣9【解答】解：设人数为x，可列方程为：+2=．故选：C．9．（3分）有下列说法：①任何无理数都是无限小数；②有理数与数轴上的点一一对应；③在1和3之间的无理数有且只有这4个；④是分数，它是有理数．⑤近似数7.30所表示的准确数a的范围是：7.295≤a＜7.305．其中正确的个数是（）A．1 B．2 C．3 D．4【解答】解：①任何无理数都是无限小数，故说法正确；②实数与数轴上的点一一对应，故说法错误；③在1和3之间的无理数有无数个，故说法错误；④不是分数，它不是有理数，故说法错误．⑤近似数7.30所表示的准确数a的范围是：7.295≤a＜7.305，故说法正确．故选：B．10．（3分）如图，某人沿着边长为90米的正方形，按A→C→D→B→A…方向运动，甲从A以64米/分的速度，乙从C以90米/分的速度行走，当乙第一次追上甲时在正方形的（）A．AB边上 B．CA边上 C．DC边上 D．BD边上根据题意得：（90﹣64）x=90+90+90，解得：x=，∴64x=64×≈756.33．∵90+90+90+90+90+90≈651.78＜756.33＜779.04≈90+90+90+90+90+90+90，∴当乙第一次追上甲时在正方形的BD边上．故选：D．二、认真填一填（本题有6个小题，每小题4分，共24分）11．（4分）单项式﹣的系数是﹣，多项式是2次二项式．【解答】解：单项式﹣的系数是﹣，多项式的次数为2，故答案为：﹣；212．（4分）用代数式表示a除以b加1为．【解答】解：数a除以b为，加1为：．13．（4分）（1）3.256精确到十分位为 3.3，（2）用科学记数法表示372000为 3.72×105．【解答】解：（1）3.256精确到十分位为3.3；（2）372000用科学记数法表示为3.72×105，故答案为3.3，3.72×105．14．（4分）的算术平方根是2．一个正方形的面积是13，估计它的边长大小接近于整数4．【解答】解：∵=4，∴的算术平方根是2，∵正方形的面积是13，∵＜＜，∴3＜＜4，∴与最接近的整数是4，故答案为：2，4．15．（4分）已知|x﹣y|=y﹣x，|x|=3，y=2，则（x+y）3=﹣125．【解答】解：∵|x﹣y|=y﹣x，∴x﹣y＜0，即x＜y．∵|x|=3，y=2，∴x=±3．∵x＜y，∴x=﹣3，y=2，∴（x+y）3=（﹣3﹣2）3=﹣125．故答案为：﹣125．16．（4分）如图是一个数值转换机的示意图，若输出的数y=5，则输入的数x= 9或10．【解答】解：若x是奇数，则（x+1）÷2=5，解得x=9，若x是偶数，则x÷2=5，解得x=10，所以，输入的数x=9或10．故答案为：9或10．三、全面答一答（本题有7个小题，共66分）解答应按要求写出必要的解答步骤17．（12分）计算下列各式②﹣+33③﹣14﹣（1﹣0.5）××[2﹣（﹣3）2]④4﹣（﹣36）×（+﹣）【解答】解：①原式=﹣1+2=1；②原式=4﹣5+27=26；③原式=﹣1﹣××（﹣7）=﹣1+=；④原式=4+6+20﹣21=9．18．（12分）解下列方程：①2（2x﹣1）=1﹣（3﹣x）②﹣1=③﹣=﹣1.6④4x﹣3+6（3﹣4x）=7（4x﹣3）【解答】解：①去括号得：4x﹣2=1﹣3+x，移项，合并同类项得：3x=0；解得：x=0．②去分母得：3（3x﹣1）﹣12=2（5x﹣7），去括号得：9x﹣3﹣12=10x﹣14，移项得：9x﹣10x=﹣14+3+12，合并同类项得：﹣x=1，系数化为1得：x=﹣1．③原方程化为：5x+2﹣（2x﹣6）=﹣1.6，去括号得：5x+2﹣2x+6=﹣1.6，移项得：5x﹣2x=﹣1.6﹣2﹣6，合并同类项得：3x=﹣9.6，系数化为1得：x=﹣3.2．④去括号得：4x﹣3+18﹣24x=28x﹣21，移项得：4x﹣24x﹣28x=﹣21+3﹣18，合并同类项得：﹣48x=﹣36，19．（7分）（1）先化简再求值：x2﹣（x2+2xy﹣y2）+5（y2﹣3xy），其中x=，y=．（2）已知m﹣n=6，求﹣4（m﹣n）+3m﹣3n+8的值．【解答】解：（1）原式=x2﹣x2﹣2xy+y2+y2﹣15xy=6y2﹣15xy，当x=，y=时，原式=6×﹣15××=；（2）原式=﹣4（m﹣n）+3m﹣3n+8=﹣4（m﹣n）+3（m﹣n）+8，=﹣（m﹣n）+8当m﹣n=6时，原式=﹣6+8=2．20．（7分）已知单项式2x3y m﹣1与x m﹣2n y4是同类项，求代数式：（m﹣2n）﹣2（2n﹣m）+m﹣5的值．【解答】解：∵单项式2x3y m﹣1与x m﹣2n y4是同类项，∴，解得，∴（m﹣2n）﹣2（2n﹣m）+m﹣5=m﹣n﹣4n+2m+m﹣5=m﹣n﹣5=×5﹣﹣5=8．21．（7分）已知下面两个方程3（x+2）=5x，①4x﹣3（a﹣x）=6x﹣7（a﹣x）②有相同的解，试求a的值．【解答】解：由方程①可求得3x﹣5x=﹣6，所以x=3．由已知，x=3也是方程②的解，根据方程解的定义，把x=3代入方程②时，应有：4×3﹣3（a﹣3）=6×3﹣7（a﹣3），解得：a=4．22．（7分）1千瓦时电（即通常所说的1度电）可供一盏40瓦的电灯点亮25小时．（1）1千瓦时的电量可供n瓦的电灯点亮多少时间？（2）若每度电的电费为a元，一个100瓦的电灯使用12时的电费是几元？【解答】解：（1）1千瓦时=40瓦×25小时．所以1千瓦时的电量可供n瓦的电灯点亮时；（2）一个100瓦的电灯使用12时的所耗费的电量为100瓦×12小时=1.2千瓦时，所以电费为1.2a元．23．（7分）一个工厂接受﹣项任务，需要在12天内完成，如果由第一车间独做，正好按期完成；如果由第二车间单独完成，就要超过规定日期3天，如果由两个车间合作几天后，剩下的任务由第二车间单独去做，正好在规定日期完成，问两个车间共合作了几天？（前段工作量+后段工作量=总工作量）【解答】解：设两个车间共合作了x天．则++×（12﹣x）=1，解得x=．答：两个车间共合作了天．24．（7分）从2012年7月1日起浙江执行新版居民阶梯电价，小坤同学家收到了新政后的第一张电费单，小坤爸爸说：“小坤，请你计算一下，我家这个月的电费支出与新政前相比是多了还是少了？”于是，小坤同学上网了解了有关电费的收费情况，得到如下两表：2004年1月至2012年6月执行的收费标准：2012年7月起执行的收费标准：多少元？比新政前少了多少元？（2）若小坤家2012年8月份的用电量为480度，则电费支出与新政前相比有什么变化？请计算说明．（3）若新政后小坤家的月用电量为a度，请你用含a的代数式表示当月的电费支出．【解答】解：（1）新政前：0.538×50+0.568×150=112.1（元），新政后：0.538×200=107.6（元），107.6﹣112.1=﹣4.5（元），答：小坤家7月份的电费支出是107.6元，比新政前少4.5元．（2）新政前：0.538×50+0.568×150+0.638×280=290.74元，新政后：0.538×230+0.588×170+0.838×80=290.74元，答：小坤家2012年8月份的用电量为480度时，则电费支出与新政前相比没有变化．（3）当0＜a≤230时，当月的电费支出为0.538a元，当230＜a≤400时，当月的电费支出为0.538×230+0.588（a﹣230）=（0.588a﹣11.5）元，当a＞400时，当月的电费支出为0.538×230+0.588×170+0.838（a﹣400）=0.838a﹣111.5（元）．赠送初中数学几何模型【模型五】垂直弦模型：图形特征：运用举例：1.已知A、B、C、D是⊙O上的四个点.(1)如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证AC⊥BD；(2)如图2，若AC⊥BD，垂足为E，AB＝2，DC＝4，求⊙O的半径.O DAB CEAOD CB2.如图，已知四边形ABCD内接于⊙O，对角线AC⊥BD于P，设⊙O的半径是2。
2014-2015学年浙江省杭州市下城区春蕾中学七年级(上)期中数学试卷
第1页（共16页）2014-2015学年浙江省杭州市下城区春蕾中学七年级（上）期中数学试卷、选择题（3分）下列各对数中互为相反数的是（A . 32 与-23(-3 2)2 与 23 (-3)法表示为（ ）的个数有（ ）（3分）欢欢发烧了，妈妈带她去看医生，结果测量出体温是 39.2 C ，用了退-23与(-2)32 2C . -3 与(-3)2. （3分）备受关注的象山港跨海大桥总投资约 77亿元, 77亿元用科学记数3.9 ―.A . 7.7 10 兀B .（3分）-.16的平方根与 14.（ 3分）在 ，7.7 1010元C . 0.77 1010元11 ―..0.77 10 兀-3 -8的算术平方根的和是（ 一0， 3.14， - 2，3二，76.0123456（数部分由连续的正整数组成）中，无理数（3分）用四舍五入法按要求对 504920.96 分别取近似值,其中错误的是（A . 504900 （精确到百位）505000 （精确到千位） C . 504921 (精 确到个位)504921.9 (精确到 0.1)(3 分)若 a =-(-2)2，b =—(-3)3， c = -(-4)2，则 -[a-(b-c)]的值为()A . -39C . 15D . 47烧药后，以每15分钟下降0.2 C的速度退烧，则两小时后，欢欢的体温是（第3页（共16页）)C -A . 38.2B . 37.2C . 38.6D . 37.68. （3分）数n 的平方根是x ，则 n 1的平方根是（）2A . x 1B . 、x 2 1C. x 1D . x 2 19. （3分）随着通讯市场竞争的日益激烈，某通讯公司的手机市话收费按原标准 每分钟降低了 m 元后，再次下调了 25%，现在的收费标准是每分钟n 元，则 原收费标准每分钟为多少元（）4 3C. （ n m ）D . （一 n m ）34第一个图中有3根火柴棒和1个三145 根、100 个二、填空题要注意认真看清题目的条件和要填写的内容， 尽量完整地填写答案. 111. （3分）--的倒数是313. （3分）实验员把1个细菌放在盛有营养液的器皿中，经过24小时，这个细菌分裂成两个， 并且每经过24小时，1个细菌都分裂成两个， 如果第33天细菌刚好充满整个器皿， 问细菌刚好达到器皿容积一半时是第天.14. （3分）若A 与B 都是三次多项式，贝U 关于A 与B 的差，有下列说法：① 一定是三次式；②可能是六次式；③可能是一次式；④可能是非零常数；其第2页（共16页）A . (5n —m)元 410. (3分)5 B . （一 n m ） 4 如图是用火柴棒摆出的图形,角形,第二个图中有9根火柴棒和 4个三角形， 第三个图中有18根火柴棒和 9个三角形…， 则第10个图形中，火柴棒根数及三角形个数分别165 根、100 个B . 165 根、55 个C .135根、8512. （3分）—航2肯&是3项式，最高次项的系数为中不正确的是 _______ .15. （3分）如图， 一个饮料瓶的容积为800mL （1升二1000mL ），小明把这一满 瓶饮料喝掉一部分后，将饮料瓶正放时瓶内饮料的高度是14cm ，倒放时空余 部分的高度为6cm （如图所示）.现将剩余的饮料倒入另一个长方体饮料 盒中时，盒子内的饮料高度为10cm ，则小明喝掉了 __________________ ml 的饮料，长方体饮料盒的底面积是 ____ cm 2 .16. （ 3分）如图所示，数轴上点C 表示的数是1 ,点F 表示的数是-2 ,CD=1, 以CD ，CF 为边作长方形CDEF ，以C 为圆心、CE 的长为半径画弧交数轴 于A 、B 两点，则点A 表示的数是 ________________ ，点B 表示的数是 _______ .三、全面答一答解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以. 17. 计算:1 1 5(—66)( )2 3 115 [、、3-2 ( .5-2)](精 确到 0.1 ， ■. 3 1.732，5 ： 2.236)A Y三三(1)(5) (2) (3)(4)+ 2 V 2 + 8 - V918. 把下列代数式的序号填入相应的横线上:第5页（共16页）。
浙江省杭州市下城区七年级数学上学期期中试题-人教版初中七年级全册数学试题
下城区2016学年第一学期七年级数学期中测试卷考生须知：1．本试卷分试题卷和答题卷两部分。
满分120分，考试时间100分钟。
2．必须在答题纸的对应答题位置上答题。
3．不允许使用计算器进行计算，凡题目中没有要求取精确值的，结果中应保留根号或π． 一．仔细选一选（本题有10小题，每小题3分，共30分．下面每小题给出的四个选项中，只有一个是正确的， 注意可以用多种不同的方法来选取正确答案．） 1． 自然数3的相反数是（ ▲） A ．﹣3 B ．3C ．D ．2．用代数式表示：“x 的5倍与y 的和的一半”可以表示为(▲ ) A ．B ．C ．D ．5x+y3．在实数：4-，1415926.3，π，10，.5.1.3，722，38中， 无理数的个数为（ ▲）A ．2个B ．3个C ．4个D. 5个4．中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为（ ） A ．44×108B ．4.4×109C ．4.4×108D ．4.4×10105．下列各对数中，数值相等的数是（ ▲ ）A ．32-与32-B ．2233--与（）C ．33(32)32⨯⨯与D ．332(2)--与6．下列运算正确的是 （ ▲ ） A ．525±= B.525-=- C.55=-- D.2552=-7.若有理数m 在数轴上对应的点为M ，且满足1m m <<-，则下列数轴表示正确的是（）（第10题）8．有长为l 的篱笆，利用他和房屋的一面墙围成如图形状的长方形园子，园子的宽为t ，则所围成的园子面积为（ ）A ．（l ﹣）tB ．（l ﹣t ）tC ．（﹣t ）tD ．（l ﹣2t ）t9．有下列说法：①任何无理数都是无限小数； ②有理数与数轴上的点一一对应；③在数轴上，原点两旁的两个点所表示的数都是互为相反数； ④3π是分数，它是有理数． ⑤81的算术平方根是9. 其中正确的个数是（ ） A ．1B ．2C ．3D ．410．在两个形状、大小完全相同的大长方形内，分别互不重叠地放入四个如图③的小长方形后得图①，图②，已知大长方形的长为a ，两个大长方形未被覆盖部分分别用阴影表示，则图①阴影部分周长与图②阴影部分周长的差是（ ）（用a 的代数式表示）A ．a -B ．aC ．a 21-D ．a 21二．认真填一填（本题有6个小题，每小题4分，共24分．注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．） 11. ﹣的倒数是▲．12．计算：（1）=364▲（2）=-+2)4(4▲．mB10MxD C AM 10mx10M xm 10Mxm13．（1）请你写出一个同时符合下列条件的代数式，①同时含有字母,a b ；②是一个4次单项式；③它的系数是一个负无理数， 你写出的一个代数式是▲ .（2）多项式32322-+-ab b a 是▲次多项式，最高项的系数是▲。
浙江省杭州四季青中学2015-2016学年七年级上学期期中考试语文试卷
2015学年第一学期七年级语文学科期中考试卷（问卷）时间：１２０分钟满分：1２0分一、语言积累与运用（27分）1.书写：认真书写下面的文字，力求工整漂亮。
（3分）生活有多广阔，语文就有多广阔。
在生活中学习语文，在语文中品味生活。
2.下列加点字中注音正确的一项是（）（3分）A．憔．悴jiāo 瘫．痪tān 匿．笑nì B.菡．萏hàn 感慨．gài 尴尬．gàC．须臾．yú愠．怒ǎo 逾．越yú D.笃．信dǔ股肱．gōng 喜好．hào3．下列词语中有错别字的一项是（）（3分）A．荫蔽覆盖心绪自作主张 B. 阴影分歧取决截然不同C．时晨纠纷狡猾恍然大悟 D. 冷漠威慑开拓整装待发4．下列各句中所运用的修辞手法不同于其他三句的一项是（）（3分）A．但花朵从来都稀落，东一穗西一串伶仃地挂在树梢，好像在试探什么。
B．每一朵盛开的花就像是一个小小的张满了的帆，帆下带着尖底的舱。
C．花朵儿一串挨着一串，一朵接着一朵，彼此推着挤着，好不活泼热闹。
D．仔细看时，才知道那是每一朵花中的最浅淡的部分，在和阳光互相挑逗。
5．依次填入下面一段文字横线处的词语，最恰当的一项是（）（3分）文学如泉，越品越见；文学如茶，越品越知；文学如酒，越品越感。
在文学的陶冶下，你会发现自己少了一份浮躁，多了一份宁静；少了一份庸俗，多了一份雅致；少了一份世故，多了一份纯真。
A.醇厚幽远清冽B.清冽醇厚幽远C.醇厚清冽幽远D.清冽幽远醇厚6．下列语序排列正确的一项是（）（3分）①另外，树木年轮里，还储存着当地的气候、火山爆发和水灾旱灾等丰富的自然信息。
②人们所熟知的年轮，是树木的年龄。
③因此，科学家十分重视从树木的年轮里获取蕴藏着的科学信息资料。
④一棵树被锯倒了，数一数树墩上有多少圈条纹，人们就知道这棵树有多大年龄了。
A．②④①③ B．④②①③ C．②①④③ D．③②④①7 .下列与作家、作品及其相关内容衔接正确的一项是（）(3分)A.《秋天的怀念》——怀念母亲——史铁生B.《金色花》——英国——泰戈尔C.《世说新语》——宋朝——刘义庆D. 《论语》——道家经典——孔子8．古诗文默写。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2015-2016学年浙江省杭州市下城区四季青中学七年级（上）期中数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）下列各对量中，不具有相反意义的是（）A．胜3局与负4局B．收入3000元与支出2000元C．气温升高4℃与气温升高10℃D．转盘逆时针转3圈与顺时针转5圈2．（3分）下列各数：，﹣π，0，，，，0.1010010001…，，1.414，0.，其中无理数有（）A．2个 B．3个 C．4个 D．5个3．（3分）对于有理数a，b有下列几种说法，其中正确的个数有（）①若a+b=0，则a与b互为相反数；②若a+b＜0，则a与b异号；③若a与b同号，则a+b＞0；④若|a|＞|b|，且a与b同号，则a+b＞0．A．3个 B．2个 C．1个 D．0个4．（3分）若a=﹣2+2•（﹣3），b=﹣32，c=﹣|﹣|，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b5．（3分）（﹣4）2的平方根是（）A．﹣4 B．4 C．±4 D．±26．（3分）下列说法正确的是（）A．﹣a是负数B．|a|一定是非负数C．不论a为什么数，D．一定是分数7．（3分）有下列代数式4，，，x2﹣2xy+y2，，5m，﹣3xy+1，其中多项式的个数为（）A．2 B．3 C．4 D．58．（3分）将整式﹣[a﹣（b+c）]去括号，得（）A．﹣a+b+c B．﹣a+b﹣c C．﹣a﹣b+c D．﹣a﹣b﹣c9．（3分）已知a是两位数，b是一位数，把b接写在a的后面，就成为一个三位数．这个三位数可表示成（）A．10a+b B．ab C．100a+b D．a+10b10．（3分）等边△ABC在数轴上的位置如图所示，点A，C对应的数分别为0和﹣1，若△ABC绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1；则翻转2006次后，点B所对应的数是（）A．2005 B．2006 C．2007 D．2008二、专心填一填（6小题，每小题4分，共24分）11．（4分）单项式πr2的系数是；当r=3时，这个代数式的值是（结果保留到0.01）12．（4分）我们要深入领会胡锦涛总书记关于社会主义荣辱观的重要论述，树立起节约光荣、浪费可耻的观念．如果每人每天浪费水0.32升，那么100万人每天浪费的水，可用科学记数法表示为升，数量是多么惊人啊！13．（4分）当x=，y=时，+=0．14．（4分）写出两个无理数，使它们的和为有理数，；写出两个无理数，使它们的积为有理数，．15．（4分）已知|a|＞|b|，且a＜0，b＞0，试利用数轴比较a，b，﹣a，﹣b 的大小：（用“＜”连接），本题用到的数学思想是．16．（4分）已知n是自然数，多项式x n+3x3﹣2x+4x2是三次三项式，那么n可以取的数是．三、认真解一解（7小题共66分）17．（6分）观察下列等式：回答问题：①=1+﹣=1②=1+﹣=1③=1+﹣=1，…（1）根据上面三个等式的信息，猜想=；（2）请按照上式反应的规律，试写出用n表示的等式；（3）验证你的结果．18．（10分）计算：①2.75﹣[（﹣5）﹣（﹣0.5）+（﹣3）]；②（﹣）×（﹣）÷（﹣）；③﹣7×（﹣）+26×（﹣）﹣2×；④﹣12﹣÷（﹣）+5×（﹣2）2．19．（8分）化简：（1）2（2x﹣3y）﹣（3x+2y+1）（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]．20．（8分）（1）已知mn﹣n=15，m﹣mn=6，求：代数式m﹣n的值；（2）已知x2+2x﹣5=3，求：代数式2x2+4x+8的值；（3）已知x2﹣x﹣1=0，求：代数式﹣x3+2x2+2015的值．21．（10分）（1）利用如图4×4方格，作出面积为8平方单位的正方形．（2）已知3m﹣4与7﹣4m是N的平方根，求﹣2﹣N的立方根．22．（12分）如图是某住宅的平面结构示意图，图中标注了有关尺寸（墙体厚度勿略不计，单位：m）．（1）该住宅的面积是多少？（2）该房的主人计划把卧室以外的地面都铺上地砖，若他所选的地砖的价格是60元/m2，他买地砖至少需要多少元？23．（12分）这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行．”国王以为要不了多少粮食，就随口答应了，结果国王输了．（1）我们知道，国际象棋共有64个格子，则在第64格中应放多少米？（用幂表示）（2）请探究第（1）中的数的末位数字是多少？（简要写出探究过程．）（3）你知道国王输给了阿基米德多少粒米吗？为解决这个问题，我们先来看下面的解题过程：用分数表示无限循环小数：．解：设①．等式两边同时乘以10，得10x=②．将②﹣①得：9x=2，则．∴请参照以上解法求出国王输给阿基米德的米粒数（用幂的形式表示）2015-2016学年浙江省杭州市下城区四季青中学七年级（上）期中数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）下列各对量中，不具有相反意义的是（）A．胜3局与负4局B．收入3000元与支出2000元C．气温升高4℃与气温升高10℃D．转盘逆时针转3圈与顺时针转5圈【解答】解：A、胜3局与负4局，是相反意义的量；B、收入3000元与支出2000元，是相反意义的量；C、气温升高4℃与气温升高10℃，不是相反意义的量；D、转盘逆时针转3圈与顺时针转5圈，是相反意义的量，故选：C．2．（3分）下列各数：，﹣π，0，，，，0.1010010001…，，1.414，0.，其中无理数有（）A．2个 B．3个 C．4个 D．5个【解答】解：，﹣π，，0.1010010001…，是无理数，故选：CD．3．（3分）对于有理数a，b有下列几种说法，其中正确的个数有（）①若a+b=0，则a与b互为相反数；②若a+b＜0，则a与b异号；③若a与b同号，则a+b＞0；④若|a|＞|b|，且a与b同号，则a+b＞0．A．3个 B．2个 C．1个 D．0个【解答】解：∵互为相反数的两个数的和是0，∴若a+b=0，则a与b互为相反数，∴①正确；∵若a+b＜0，则a、b有可能都是负数，∴a与b不一定异号，∴②不正确；∵若a与b同号，则a、b有可能都是负数，∴此时a+b＜0，∴③不正确；∵若|a|＞|b|，且a与b同号，则a、b有可能都是负数，∴此时a+b＜0，a+b＞0不一定成立，∴④不正确．综上，可得对于有理数a，b有下列几种说法，其中正确的个数有1个：①．故选：C．4．（3分）若a=﹣2+2•（﹣3），b=﹣32，c=﹣|﹣|，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b【解答】解：∵a=﹣2+2•（﹣3）=﹣8，b=﹣32=﹣9，c=﹣|﹣|=﹣，∴c＞a＞b，故选：D．5．（3分）（﹣4）2的平方根是（）A．﹣4 B．4 C．±4 D．±2【解答】解：∵（﹣4）2=16，∴16的平方根是±4．故选：C．6．（3分）下列说法正确的是（）A．﹣a是负数B．|a|一定是非负数C．不论a为什么数，D．一定是分数【解答】解：a是0时，﹣a还是0，所以A错误；|a|一定是非负数，正确的是B．当a=0时，没有倒数，所以C错误；当a=0时，是0，所以D错误．故选：B．7．（3分）有下列代数式4，，，x2﹣2xy+y2，，5m，﹣3xy+1，其中多项式的个数为（）A．2 B．3 C．4 D．5【解答】解：多项式有，x2﹣2xy+y2，﹣3xy+1，故选：B．8．（3分）将整式﹣[a﹣（b+c）]去括号，得（）A．﹣a+b+c B．﹣a+b﹣c C．﹣a﹣b+c D．﹣a﹣b﹣c【解答】解：根据去括号法则：﹣[a﹣（b+c）]=﹣（a﹣b﹣c）=﹣a+b+c．故选：A．9．（3分）已知a是两位数，b是一位数，把b接写在a的后面，就成为一个三位数．这个三位数可表示成（）A．10a+b B．ab C．100a+b D．a+10b【解答】解：根据题意可得这个三位数可表示成10a+b，故选：A．10．（3分）等边△ABC在数轴上的位置如图所示，点A，C对应的数分别为0和﹣1，若△ABC绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1；则翻转2006次后，点B所对应的数是（）A．2005 B．2006 C．2007 D．2008【解答】解：因为2006=668×3+2=2004+2，所以2006次翻折对应的数字和2005对应的数字相同是2005．故选：A．二、专心填一填（6小题，每小题4分，共24分）11．（4分）单项式πr2的系数是π；当r=3时，这个代数式的值是18.85（结果保留到0.01）【解答】解：∵π是数字不是字母，∴单项式πr2的系数是π．代数式的值=×32=6π≈18.85．故答案为：π；18.85．12．（4分）我们要深入领会胡锦涛总书记关于社会主义荣辱观的重要论述，树立起节约光荣、浪费可耻的观念．如果每人每天浪费水0.32升，那么100万人每天浪费的水，可用科学记数法表示为 3.2×105升，数量是多么惊人啊！【解答】解：0.32×100×104=3.2×105升．13．（4分）当x=3，y=5时，+=0．【解答】解：由题意得，3﹣x=0，y﹣5=0，解得x=3，y=5．故答案为：3；5．14．（4分）写出两个无理数，使它们的和为有理数2﹣，3+；写出两个无理数，使它们的积为有理数3，2．【解答】解：（1）可以先写出任意一个无理数如2﹣，若两个无理数的和是4，则另一个无理数是：4﹣（2﹣）=2+；（2）可以先写出任意一个无理数如3，若两个无理数的积是12，则另一个无理数是：12÷3．故答案为：2﹣，2+；3，．15．（4分）已知|a|＞|b|，且a＜0，b＞0，试利用数轴比较a，b，﹣a，﹣b 的大小：a＜﹣b＜b＜﹣a（用“＜”连接），本题用到的数学思想是数形结合．【解答】解：已知|a|＞|b|，且a＜0，b＞0，如图所示：则a＜﹣b＜b＜﹣a，本题用到的数学思想是数形结合．16．（4分）已知n是自然数，多项式x n+3x3﹣2x+4x2是三次三项式，那么n可以取的数是1，2，3．【解答】解：由于该多项式已经有一、二和三次项，因此xn可以是一次项或者二次项或者三次项，所以n=1，2，3；三、认真解一解（7小题共66分）17．（6分）观察下列等式：回答问题：①=1+﹣=1②=1+﹣=1③=1+﹣=1，…（1）根据上面三个等式的信息，猜想=1；（2）请按照上式反应的规律，试写出用n表示的等式；（3）验证你的结果．【解答】解：（1）根据上面三个等式的信息，猜想=1，故答案为：1；（2）=1+﹣．（3）=====1+﹣．18．（10分）计算：①2.75﹣[（﹣5）﹣（﹣0.5）+（﹣3）]；②（﹣）×（﹣）÷（﹣）；③﹣7×（﹣）+26×（﹣）﹣2×；④﹣12﹣÷（﹣）+5×（﹣2）2．【解答】解：①原式=2.75+5.5﹣0.5+3.25=6+5=11；②原式=﹣××=﹣；③原式=﹣×（﹣7+26+2）=﹣×21=﹣66；④原式=﹣1+4+20=23．19．（8分）化简：（1）2（2x﹣3y）﹣（3x+2y+1）（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]．【解答】解：（1）原式=4x﹣6y﹣3x﹣2y﹣1=（4﹣3）x﹣（6+2）y=x﹣8y﹣1；（2）原式=﹣（3a2﹣4ab）+[a2﹣4a﹣4ab]=﹣3a2+4ab+a2﹣4a﹣4ab=﹣2a2﹣4a．20．（8分）（1）已知mn﹣n=15，m﹣mn=6，求：代数式m﹣n的值；（2）已知x2+2x﹣5=3，求：代数式2x2+4x+8的值；（3）已知x2﹣x﹣1=0，求：代数式﹣x3+2x2+2015的值．【解答】解：（1）∵mn﹣n=15，m﹣mn=6，∴两式相加得到：m﹣n=21；（2）∵x2+2x﹣5=3，∴x2+2x=8，∴2x2+4x+8=2（x2+2x）+8=24；（3）∵x2﹣x﹣1=0，∴x2=x+1，﹣x2+x=﹣1，∴﹣x3+2x+2015=﹣x（x+1）+2x+2015=﹣x2﹣x+2x+2015=﹣x2+x+2015=2014．21．（10分）（1）利用如图4×4方格，作出面积为8平方单位的正方形．（2）已知3m﹣4与7﹣4m是N的平方根，求﹣2﹣N的立方根．【解答】解：（1）如图所示：（2）由题意得：3m﹣4+7﹣4m=0，解得：m=3．则N=（3×3﹣4）2=25，﹣2﹣N=﹣2﹣15=﹣27，﹣27的立方根是﹣3．22．（12分）如图是某住宅的平面结构示意图，图中标注了有关尺寸（墙体厚度勿略不计，单位：m）．（1）该住宅的面积是多少？（2）该房的主人计划把卧室以外的地面都铺上地砖，若他所选的地砖的价格是60元/m2，他买地砖至少需要多少元？【解答】解：（1）该住宅的面积是2x•4y+x•2y+x•y+2x•2y=15xy；（2）他买地砖需要60×（2x•4y+x•2y+•x•y）=660xy元．23．（12分）这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行．”国王以为要不了多少粮食，就随口答应了，结果国王输了．（1）我们知道，国际象棋共有64个格子，则在第64格中应放多少米？（用幂表示）（2）请探究第（1）中的数的末位数字是多少？（简要写出探究过程．）（3）你知道国王输给了阿基米德多少粒米吗？为解决这个问题，我们先来看下面的解题过程：用分数表示无限循环小数：．解：设①．等式两边同时乘以10，得10x=②．将②﹣①得：9x=2，则．∴请参照以上解法求出国王输给阿基米德的米粒数（用幂的形式表示）【解答】解：（1）第64个格子，应该底数是2，指数63，所以为263；（2）∵21=2，22=4，23=8，24=16，25=32…∵63÷4=15…3，∴263的末位数字与23的末位数字相同，是8；（3）设x=1+2+22+…+263①．等式两边同时乘以2，得2x=2+22+23+ (264)②﹣①，得x=264﹣1．答：国王输给阿基米德的米粒数为264﹣1．。