(青岛版五年制)二年级上册数学计算能力测试题
二年级上册数学单元测试-3.角的初步认识 青岛版(含答案)

二年级上册数学单元测试-3.角的初步认识一、单选题1.下面四句话中,错误的一句是()A. 0既不是正数也不是负数B. 1既不是素数也不是合数C. 假分数的倒数不一定是真分数D. 角的两边越长,角就越大2.一个三角形只能有( )直角跟2个锐角A. 2B. 1C. 53.左图中有()个角。
A. 8B. 7C. 64.用一副三角板不能拼出()。
A. 75B. 20C. 135D. 1505.图中直角的个数为()个。
A. 4B. 8C. 10D.12二、判断题6.量角器上的两个相邻刻度间所对的角是1°.7.小于90度的角叫锐角.8.角的两边越长,角就越大.9.角的两条边越长,角越大.三、填空题10.下面的图形中共有________个直角。
11.________是锐角.________是钝角.46°180°360°100°12.下面图中直角、锐角、钝角各有多少个?直角有________个锐角有________个钝角有________个13.图∠1=120°,∠2=________14.如图,在直角三角形中,∠1=________,∠2=________.四、解答题15.已知∠1=35°,∠1+∠2=180°,∠2是多少度?16.描出所有的平行四边形五、应用题17.填上角的各部分名称参考答案一、单选题1.【答案】D【解析】【解答】解:角的大小与角叉开的角度有关,与角两边的长短无关.故选D.【分析】A、B、C都对;D、角的大小与角的两边的长短无关,与角叉开的角度有关,因此错了.2.【答案】B【解析】【解答】一个三角形只能有一个直角或者钝角,2个锐角。
【分析】角的认识能力考查。
3.【答案】A【解析】4.【答案】B【解析】【解答】解:A、把45°和30°的角拼在一起组成75°的角;B、不能拼出20°的角;C、把90°和45°的角拼在一起组成135°的角;D、把90°和60°的角拼在一起组成150°的角.故答案为:B【分析】一副三角板中角的度数有:90°、60°、30°、45°,把这些角组合后就能拼出一定度数的角.5.【答案】C【解析】【解答】解:两个直角边的交叉点处公有8个直角,再加上2个,共10个直角.故答案为:C【分析】直角是90°的角,除了标出的两个直角外,两条直角边相交成的4个角也是直角.二、判断题6.【答案】正确【解析】【解答】解:根据量角器的知识可知,量角器上的两个相邻刻度间所对的角是1°,原题说法正确. 故答案为:正确【分析】量角器上有180个刻度,共能测量180°的角,相邻的两个刻度间所对的角是1°.7.【答案】正确【解析】【解答】小于90度的角角锐角,所以原题说法正确.故答案为:正确.【分析】根据锐角的定义进行判断即可.8.【答案】错误【解析】【解答】解:角的大小与边的长短无关.所以一个角的两边越长,这个角就越大.故是错误的.故答案为:错误.【分析】角的大小与边的长短无关.所以一个角的两边越长,这个角就越大.是错误的.本题考查角的定义.由两条具有公共端点的射线组成的图形叫做角.角的大小与边的长短无关.9.【答案】错误【解析】【解答】解:角的大小和边长无关.故答案为:错误.【分析】依据角的定义就可填出正确答案.三、填空题10.【答案】2【解析】11.【答案】46°;100°【解析】【解答】解:根据角的分类知识可知,46°是锐角,100°是钝角.故答案为:46°;100°【分析】直角是90°的角,平角是180°的角,周角是360°的角,小于90°的角是锐角,大于90°小于180°的角是钝角.由此给角分类即可.12.【答案】2;2;1【解析】13.【答案】60【解析】【解答】解:∠2=180°-120°=60°故答案为:60【分析】∠1和∠2组成平角,平角是180°的角,,因此用180°减去∠1的度数即可求出∠2的度数. 14.【答案】60°;30°【解析】【解答】∠1=180120=60∠2=90∠1=9060=30故答案为:60,30【分析】因为∠1和120的角合起来是平角,所以∠1=180120=60,因为在直角三角形中两个锐角的和是90,也就是所以∠1和∠2的和是90,所以∠2=90∠1=9060=30。
二年级上册数学试题-第五单元美丽的校园——认识方向青岛版(五年制)_含答案

第五单元美丽的校园——认识方向【例1】早晨,面对太阳升起的方向,你的前面是()方,你的后面是()方,左面是()方,右面是()方。
晚上,面向北极星的方向,你的后面是()方,左面是()方,右面是()方。
思路分析:本题考查的知识点是根据已知条件用相对的方法确定方向,解答时抓住给出的可以判断已知方向的条件找到标准方向是解答此类问题的关键。
早晨,面对太阳升起的方向,前面应是东方,和东相对的是西,所以后面是西;这时左面应是北,右面是南。
晚上,面向北极星的方向应是北方,这时后面应是和北相对的方向南方,左面应是西方,右面是东方。
解答:东西北南南西东【例2】小强、小军、小林和小乐去森林公园玩。
回家时,小强向西走,小军向北走,小林和小乐一起向南走,他俩分开后,小林向西走,小乐向东走。
请你根据他们回家的路线,在图中标出他们各自的家。
思路分析:这道题直接用方向板为工具来判断方向,根据上北下南左西右东,小强回家时向西走,就是向左走,然后向上(北)走,所以红色的房子是小强的家;小军回家时向北走,就是向上走,然后向右(东)走,所以蓝色的房子是小军的家;小林和小乐回家时一起向南走,就是向下走,他俩分开后,小林向西走,就是向左走,所以绿色的房子是小林的家;小乐向东走,就是向右走,所以紫色的房子是小乐的家。
解答:【例3】(1)邮局在公园的( )面,学校在公园的( )面。
(2)小娟家在学校的( )面,小娟家在小峰家的( )面。
(3)体育场在博物馆的( )面,体育场在学校的( )面。
思路分析:(1)根据箭头提示,明确平面图的绘制方向(上北下南、 左西右东),然后确定不同的观测点。
(2)邮局在公园的右面,即东面;学校在公园的上面,即北面;小娟家在学校的下面,即南面;小娟家在小峰家右面,即东面;体育场在博物馆的上面,即北面;体育场在学校的左面,即西面。
解答:(1)东 北 (2)南 东 (3)北 西【例4】壮壮从家出发先向( )走到图书馆,再向( )走到体育馆,然后和强强一起往( )走到文化馆,最后往( )走到展览馆。
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)

每个笼子里有几只蝴蝶?
15÷3=5(只)
答:每个笼子里有5只蝴蝶。
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
课堂练习
1.计算。
4
28 8 0
5
5 25 25 0
3
4 12 12 0
4
4 16 16 0
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
课堂练习
1.计算。
3
39 9 0
2
24 4 0
5
3 15 15 0
4
5 20 20 0
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
2.数住旅馆。
如果都住3人间,男生需要几个房间?女生呢?还可以怎样 安排?
青岛版(五年制) 数学 二年级 上册
6 制作标本——表内除法
除法竖式计算
情境导入
探究新知
课堂练习
课堂小结
课后作业
情境导入
算一算。
15÷5= 3 20÷4= 5 9÷3= 3
4÷2= 2 12÷3= 4 16÷4= 4
1÷1= 1 14÷2= 7 6÷3= 2
探究新知
例 每个笼子里有几只蝴蝶?
求每个笼子里有几只蝴蝶, 就是把15平均分成3份,求 每份是多少,用除法计算。
二年级上册数学- 除法竖式计算 青岛版(五年制)(16张)
课堂小结
这节课你们都学会了哪些知识?
用竖式求商的方法:
5 ……商 除数…… 3 1 5 ……被除数
二年级上册数学单元测试-4.除法的初步认识 青岛版(五年制)(含答案)

二年级上册数学单元测试-4.除法的初步认识一、判断题1.判断对错.某个数除以1,仍得某个数.2.把18分成2份,每份是93.三位数除以两位数,被除数末尾有0,商的末尾也一定有0.()4.被除数的中间有0,商的中间就有0。
(判断对错)二、填空题5.36是2的________倍6.根据题意,先解答,再写出数量关系青山水泥厂生产水泥960吨.如果用一条运64吨的船来运,几次可以运完?算式:________÷________=________(次)数量关系:________÷工效=次数7.一根钢管长3米,重4千克.(用分数表示。
填写分数时,先写分子,后写分母)(1)这样的钢管每米重________千克;(2)1千克这样的钢管长________米。
8.□60÷48,要使商是两位数,□里最小填________.9.________是冠军?三、单选题10.连一连.(1)96÷24()A. 96B. 24C. 4 (2)24×4()A. 96B. 24C. 4 (3)96÷4()A. 96B. 24C. 411.商中间有0,且没有余数,可以填()A. 7B. 8C. 912.老师有62支钢笔奖励给2个同学,平均每个同学奖励()支。
A. 32B. 31C. 3013.王娟买了一本科幻小说,共374页,如果每天看8页,()天能看完.A. 46B. 47C. 4814.先把估商写在上面的括号里,再算出准确的商. ()A. 700B. 782C. 728D. 87 2四、解答题15.在□里填数字.(自上而下,自左向右填)五、综合题16.批发玩具。
(1)张叔叔带着720元钱去批发小飞机,可以批到多少架(2)赵阿姨有455元,最多能批到多少辆小汽车?还剩多少元?六、应用题17.母鸡有384只,公鸡有6只,母鸡的只数是公鸡的几倍?18.一台笔记本的价格是3535元,是一台打印机的7倍,打印机又是小音响的5倍,那么小音响的价格是多少元?参考答案一、判断题1.【答案】正确【解析】【解答】任何数除以1,还得原数,原题说法正确.故答案为:正确.【分析】一个数除以1,结果还是原数,据此判断.2.【答案】错误【解析】【解答】只有平均分才能用除法求解,题目中没有说是平均分成2份。
2022-2023学年山东省青岛市西海岸新区高二年级上册学期期中学业水平检测数学试题【含答案】

2022-2023学年山东省青岛市西海岸新区高二上学期期中学业水平检测数学试题一、单选题1.某校把纸笔测试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例记入学期总评成绩,90分以上为优秀,甲、乙、丙三人的各项成绩如下表(单位:分):纸笔测试实践能力成长记录甲908395乙889095丙908890则学期总评优秀的是( )A .甲B .乙、丙C .甲、乙D .甲、丙C【分析】根据比例关系直接计算每个学的成绩,对比得到答案.【详解】甲的;9050%8320%9530%90.1⨯+⨯+⨯=乙的;、8850%9020%9530%90.5⨯+⨯+⨯=丙的成绩.9050%8820%9030%89.6⨯+⨯+⨯=故选:C2.数列的一个通项公式是( )234513579,,,,A .B .21n na n =+21n n a n =-C .D .23n n a n =-23n n a n =+B【分析】根据数列分子分母的规律求得通项公式.【详解】由于数列的分母是奇数列,分子是自然数列,故通项公式为.21n n a n =-故选:B3.某社会调查机构就某地居民的月收入情况调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出200人作进一步调查,则在(元)月收入段应抽出人数是[)2500,3000( )A .100B .50C .40D .25B【分析】直接根据分层抽样的比例关系计算得到答案.【详解】区间[2500,3000)的频率为,抽取人数为.0.00055000.25p =⨯=2000.2550⨯=故选:B4.已知一组数据:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,6,6,则其第70百分位数为( )A .3B .4C .5D .6C【分析】按百分位数的计算过程计算.第1步,按从小到大排列原始数据.第2步,计算 .%i n p =⨯第3步,若i 不是整数,而大于i 的比邻整数为j ,则第p 百分位数为第j 项数据;若i 是整数,则第p 百分位数为第i 项与第(i +1)项数据的平均数.【详解】第1步,按从小到大排列原始数据.第2步,计算 .2170%14.7i ⨯==第3步,因i 不是整数,故取大于14.7的比邻整数为15,则第70百分位数为第15项数据5;故选:C5.从一批产品(其中正品、次品都多于两件)中任取两件,观察正品件数和次品件数,下列事件是互斥事件的是①恰有一件次品和恰有两件次品;②至少有一件次品和全是次品;③至少有一件正品和至少有一件次品;④至少有一件次品和全是正品.A .①②B .①④C .③④D .①③B【详解】试题分析:∵从一批产品中任取2件,观察正品件数和次品件数,其中正品、次品都多于2件,∴恰有一件次品和恰有两件次品是互斥的,至少有一件次品和全是正品是互斥的,∴①④是互斥事件.互斥事件和对立事件.6.若数列,,,,是等比数列,则的值是( )9-m x n 16-x A .12B .C .D .12±12-12.5-C【分析】根据等比数列得到,结合得到答案.()2916x =-⨯-290x q =-⨯<【详解】数列,,,,是等比数列,则,故,9-m x n 16-()2916x =-⨯-12x =±,故.290x q =-⨯<12x =-故选:C7.集合论是德国数学家康托尔于十九世纪末创立的,希尔伯特赞誉其为“数学思想的惊人产物,在纯粹理性范畴中人类活动的最美表现之一”.取一条长度为1的线段,将它三等分,去掉中间一段,留下的两段分割三等分,各去掉中间一段,留下更短的四段,……,将这样操作一直继续下去,直至无穷.由于在不断分割舍弃过程中,所形成的线段的数目越来越多,长度越来越小,在极限情况下,得到一个离散的点集,称为康托尔三分集.若在前次操作中共去掉的线段长度之和不小于,n 2930则的最小值为( )n (参考数据:,)lg 20.3010=lg 30.4771=A .9B .8C .7D .6A【分析】通过归纳法归纳出每次舍弃的线段的长度,然后由等比数列的前项和公式求得前次舍n n 弃的线段的和,然后列不等式求解.【详解】第一次操作去掉的线段长度为,第二次操作去掉的线段长度和为,第三次操作去132133⨯掉的线段长度和为,…,第操作去掉的线段长度和为,221333⨯⨯n 121(33n -⋅由此得,121()12121123()1(2333333313nn n --+⨯++⨯=⨯=-- 所以,,2291()330n -≥21(330n ≤,,2lg lg 303n ≤-lg 301lg 310.47718.4lg 3lg 2lg 3lg 20.47710.3010n ++≥==≈---所以的最小值是9.n 故选:A .二、多选题8.对划艇运动员甲、乙二人在相同的条件下进行了6次测试,测得他们最大速度的数据如下,甲:27,38,30,37,35,31;乙:33,29,38,34,28,36.根据以上数据,下列说法正确的是( )A .他们最大速度的平均值相等B .他们最大速度的中位数相等C .同样情况下,甲运动员的发挥比乙更稳定D .同样情况下,乙运动员的发挥比甲更稳定AD【分析】直根据题意,分别计算甲乙两个人的平均数,中位数,方差,可得甲的方差大于乙的方差;结合方差的意义,判断即可.【详解】解:甲的平均数,(273830373531)633=+++++÷=乙的平均数,(332938342836)633=+++++÷=甲的中位数为:,乙的中位数为:,则他们最大速度的中位数不相等,3135332+=333433.52+=,(22222221[(2733)(3833)(3033)(3733)(3533)3133)15.76S ⎤=-+-+-+-+-+-=⎦甲,(22222221[(3333)(2933)(3833)(3433)(2833)3633)12.76S ⎤=-+-+-+-+-+-=⎦乙22S S > 甲乙乙比甲稳定.∴故选:AD.9.已知数列是公比的正项等比数列,是与的等比中项,是与等差中项,{}n a 1q ≠M 3a 11a N 5a 9a 则下列说法正确的是( )A .B .72a N =227a M =C .D .M N <M N>BC【分析】首先利用等差,等比中项的定义,判断AB ;再利用基本不等式判断CD.【详解】由等比中项的定义可知,,223117M a a a =⋅=等差中项的定义可知,, 故A 错误,B 正确;592N a a =+592a a N +=若是负数,则,若是正数,则,因为数列是公M M N <M M ==592a a N +={}n a 比的正项等比数列,所以,根据基本不等式可知,故C 正确;D 错误.1q ≠59a a ≠M N <故选:BC10.如图,由到的电路中有4个元件,分别标为元件1,元件2,元件3,元件4,电流能通M N 过元件1,元件2的概率都是,电流能通过元件3,元件4的概率都是0.9,电流能否通过各元件p 相互独立.已知元件1,元件2中至少有一个能通过电流的概率为0.96,则( )A .B .元件1和元件2恰有一个能通的概率为45p =425C .元件3和元件4都通的概率是0.81D .电流能在与之间通过的概率为0.9504M N ACD【分析】根据独立事件的概率乘法公式以及互斥事件的概率的加法公式,可得答案.【详解】对于A ,由题意,可得,整理可得,则()122C 10.96p p p -+=220.960p p -+=,则,故A 正确;()()1.20.80p p --=40.85p ==对于B ,,故B 错误;()()11228C 1C 0.810.80.3225p p -=⨯⨯-==对于C ,,故C 正确;0.90.90.81⨯=对于D ,元件3,元件4中至少有一个能通过电流的概率为,()12222C 0.910.9C 0.90.99⨯⨯-+⨯=则电流能在与之间通过的概率为,故D 正确.M N 0.960.990.9504⨯=故选:ACD.11.已知数列满足:,,,3,4,…,则下列说法正确的是( ){}n a 12a =112n n a a -=-2n =A .565a =B .对任意,恒成立*n ∈N 1n n a a +<C .不存在正整数,,使,,成等差数列p qr pa r a q a D .数列为等差数列11n a ⎧⎫⎨⎬-⎩⎭ABD【分析】首先判断D ,根据数列的递推关系,通过D 构造等差数列的定义,即可判断;根据等差数列的通项公式,得到数列的通项公式,再通过代入的方法,判断ABC.{}n a 【详解】因为,(),所以,(),112n n a a -=-*2,N n n ≥∈112n n a a +=-*N n ∈即,因为,1111n n a a +-=-1110a -=≠所以,1111111111n n n n na a a a a +===+----得,,111111+-=--n n a a 1111a =-所以数列是首项为1,公差为1的等差数列,即,11n a ⎧⎫⎨⎬-⎩⎭11=-n n a 得,故D 正确;11n a n =+A.,故A 正确;516155a =+=B.,所以,故B 正确;()111111011n n a a n n n n +⎛⎫⎛⎫-=+-+=-< ⎪ ⎪++⎝⎭⎝⎭1n n a a +<C. 若存在正整数,,使,,成等差数列,则,p qr pa r a q a 2r p q a a a =+即,得,令,满足等式,所以C 错误;21122r p q +=++211r p q =+3,4,6p r q ===故选:ABD三、填空题12.对某种新品电子元件进行寿命终极度实验,统计情况如下:寿命(h )100-200200-300300-400400-500500-600个数2030804030估计优质品(寿命300h 以上者)的概率为______.##0.7534【分析】直接计算频率得到答案.【详解】.804030150320308040302004p ++===++++故答案为.3413.已知从某班学生中任选两人参加农场劳动,选中两人都是男生的概率是,选中两人都是女生14的概率是,则选中两人中恰有一人是女生的概率为______.25##7200.35【分析】根据对立事件概率的求法,可得答案.【详解】由题意,选出的两个人只有两男、两女、一男一女三种情况,则选中两人中恰有一人是女生的概率为.12714520--=故答案为.72014.已知等差数列的公差为2,且,,是等比数列的前三项,则数列的前{}n a 1a 2a 5a {}n b {}n n a b 项和______.n n S =1(1)3nn +-⋅【分析】根据等比数列的性质求得得通项公式,从而可求得,然后由错位相减法求和.1a n a n b 【详解】等差数列的公差为2,且,,是等比数列的前三项,{}n a 1a 2a 5a {}n b 所以,,,2215a a a =2111(2)(8)a a a +=+11a =所以,,,即,,,21n a n =-23a =59a =11b =23b =213b q b ==所以,13n n b -=,1(21)3n n n a b n -=-⋅,21113353(21)3n n S n -=⨯+⨯+⨯++-⋅ ,2131333(23)3(21)3n n n S n n -=⨯+⨯++-⋅+-⋅ 相减得,1213(13)21232323(21)312(21)313n n nnn S n n ----=+⨯+⨯++⨯--⋅=+⨯--⋅- 2(22)3n n =---⋅所以.1(1)3nn S n =+-⋅故.1(1)3nn +-⋅四、双空题15.已知某区甲、乙、丙三所学科基地学校的数学强基小组人数分别为24,8,16人,在一次统一中,该区三所学校强基学生的平均分分别为118,120,114,方差分别为15,12,21,则该区所有数学强基学生成绩的平均数______,方差______.x ==2S 117 21.5【分析】根据总体均值与总体方差的计算公式求解即可.【详解】解:甲、乙、丙三所学科基地学校的数学强基小组人数分别为24,8,16人,则甲、乙、丙三所学科基地学校的人数占比分别为:,,241248162=++81248166=++161248163=++所以,111118120114117263x =⨯+⨯+⨯=方差的公式为,所以()2211n i i S x xn ==-∑()2222211112n n i i i i i S x x x x x x n n ===-+=-∑∑所以,()1112222222242424111511811815242424i i i i i i s x x x x ====∑-⇒=∑-⇒∑=+⨯甲甲,()1112222222888111212012012888i i i i i i s x x x x ====∑-⇒=∑-⇒∑=+⨯乙乙()111222222161616112111411421161616i i i i i i s x x x x ====∑-⇒=∑-⇒∑=+⨯丙丙则.()()()2222211181524120128114211611721.548S ⎡⎤=+⨯++⨯++⨯-=⎣⎦故117;21.5.五、解答题16.有6个相同的小球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字为2”,乙表示事件“第二次取出的球的数字为3”,丙表示事件“两次取出的球的数字之和为8”,丁表示事件“两次取出的球的数字之和为7”,则( )A .丙与丁相互独立B .甲与丙相互独立C .乙与丙相互独立D .乙与丁相互独立D【分析】计算各事件概率,再根据独立事件概率的关系依次判断每个选项得到答案.【详解】两次取出的球的数字之和为8,有5种情况,()()()()()2,6,3,5,4,4,5,3,6,2;()556636P ==⨯丙两次取出的球的数字之和为7,有6种情况,()()()()()()1,6,2,5,3,4,4,3,5,2,6,1;()61666P ==⨯丁;()()1=6P P =甲乙,A 错误;,B 错误;()()()0P P P =≠⋅丙丁丙丁()()()136P P P =≠⋅甲丙甲丙,C 错误;,D 正确.()()()136P P P =≠⋅乙丙乙丙()()()1=36P P P =⋅乙丁乙丁故选:D.17.袋子中放有大小和形状相同的小球若干个,其中红色小球1个,黄色小球1个,蓝色小球个,n 从袋子中随机抽取1个小球,设取到蓝色小球为事件,且事件发生的概率是.M M 12(1)求的值;n (2)从袋子中不放回地随机抽取2个小球,若每次取到红色小球得0分,取到黄色小球得1分,取到蓝色小球得2分,设第一次取出小球后得分为,第二次取出小球后得分为,记事件为“a b N ”,求事件发生的概率.2a b +=N (1)2n =(2)13【分析】(1)袋子中随机抽取1个小球,共有个结果,得到,解得答案.2n +()122n P M n ==+(2)红色小球记为,黄色的小球记为,蓝色小球记为,,列举出所有情况共12种,满A B 1C 2C足条件共有4种,得到概率.【详解】(1)由题意,从袋子中随机抽取1个小球,共有个结果,每个结果可能性相同,2n +其中事件发生有种结果,所以,解得.M n ()122n P M n ==+2n =(2)把红色小球记为;黄色的小球记为;蓝色小球记为,;A B 1C 2C 则两次不放回地取出小球的组合情况可用表格表示为AB1C 2C A×(),A B ()1,A C ()2,A C B(),B A ×()1,B C ()2,B C 1C ()1,C A ()1,C B ×()12,C C 2C ()2,C A ()2,C B ()21,C C ×共12个样本点,其中事件包含的样本点有,,,,共4个,N ()1,A C ()2,A C ()1,C A ()2,C A 所以.()41123P N ==18.某学校高一级部根据同年龄段女生的身高数据绘制了频率分布直方图,其中身高的变化范围是(单位:厘米),样本数据分组为,,,,[)150,180[)150,155[)155160,[)160165,[)165170,,.[)170175,[)175,180(1)求值;x (2)已知样本中身高大于175厘米的人数是36,求出样本总量的数值和身高超过170厘米的人数N;n (3)求样本中位数的值.0x (1)0.03x =(2)1200;216(3)0164x =【分析】(1)直接根据频率和为1计算得到答案.(2)计算身高大于厘米的样本的频率是,再计算样本总量,身高超过170厘米的1750.031200N =频率为,得到答案.0.18(3)判断身高位于的频率为,身高位于的频率为,再根据[)150,1600.220.5<[)150,1650.570.5>中位数公式计算得到答案.【详解】(1)由频率分布直方图的性质,解得()0.0040.040.070.050.00651x +++++⨯=0.03x =(2)身高大于厘米的样本的频率是,所以样本总量,1750.00650.03p =⨯=3612000.03N ==身高超过170厘米的频率为,()0.0060.0350.18p =+⨯=所以身高超过170厘米的人数.0.181200216n =⨯=(3)因为身高位于的频率为[)150,160()0.040.00450.220.5+⨯=<身高位于的频率为[)150,165()0.0040.040.0750.570.5++⨯=>所以中位数应该,由,[)0160,165x ∈()()00.040.00451600.070.5x +⨯+-⨯=分解得.0164x =19.已知是数列的前项和,且.n S {}n a n 214n S n n =-(1)求的通项公式;{}n a (2)若,求.123n nT a a a a =++++ n T (1)152n a n=-(2)2214,171498,7n n n n T n n n ⎧-≤≤=⎨-+>⎩【分析】(1)由与的关系求解;n a n S (2)分段讨论后由等差数列的前项和公式求解.n 【详解】(1)()214N *n S n n n =-∈当时,,1n =211141113a S ==⨯-=当时,,2n ≥()()221141411152n n n a S S n n n n n-⎡⎤=-=-----=-⎣⎦也符合上式,所以,1a 152n a n =-(2)因为,所以时,;时,,152n a n =-17n ≤≤0n a >7n >0n a <当时,,17n ≤≤()212312313152142n n n n n n T a a a a a a a a S n n +-=++++=++++===- 当时,7n >()123123789n n n T a a a a a a a a a a a =++++=++++-+++ .()()212371237897221498n n a a a a a a a a a a a S S n n =++++-++++++++=-=-+ 综上:2214,171498,7n n n n T n n n ⎧-≤≤=⎨-+>⎩20.某区,,三所学校有意愿报考名校自招的人数分别为24,8,16人,受疫情因素影响,A B C 该区用分层随机抽样的方法从三所学校中抽取了6名学生,参加了该区统一举办的现场小范围自招推介说明会.(1)从这6名中随机抽取2名学生进行座谈和学情调查,求这2名学生来自不同学校的概率;(2)若考生小张根据自身实际,报考了甲乙两所名校的自招,设通过甲校自招资格审核的概率为,23通过乙校自招资格审核的概率为,已知通过两所学校自招资格审核与否是相互独立的,求小张至45少能通过一所学校自招资格审核的概率.(1)1115(2)1415【分析】(1)首先确定三所学校被抽到的人数,再利用编号,列举的方法,即可所求概率;(2)首先求两所学校都没有通过的概率,再利用对立事件概率公式,即可求解.【详解】(1)用分层随机抽样的方法从三个学校中一共抽取了6名选手参加全市集训,现三所学校应该抽取的人数分别为3,1,2设来自学校的三名学生分别为,,;来自学校的学生为;来自学校的两名学生分A 1A 2A 3AB BC 别为,1C 2C 从这6名中随机抽取2名学生进行座谈和学情调查,样本空间()()()()(){()()()()1213111122322122,,,,,,,,,;,,,,,,,;Q A A A A A B A C A C A A A B A C A C =()()()()()()}331321212,,,,,;,,,,,A B A C A C B C B C C C 共包含15个样本点Ω记这2名学生来自不同学校为事件,D 事件含,,;,,;,,,D ()1,A B ()11,A C ()12,A C ()2,A B ()21,A C ()22,A C ()3,A B ()31,A C ()32,A C ,共11个样本点,()1,B C ()2,B C 所以()()()1115n D P D n ==Ω(2)记小张至少能通过一所学校自招资格审核为事件,通过甲学校自招资格审核为事件,通E M 过乙学校自招资格审核为事件,则事件“至少通过一所学校自招资格审核”的对立事件是“两所N E 学校都通不过”,因为与相互独立,所以与相互独立M N M N 所以()()()()2414111113515P E P M N P M P N ⎛⎫⎛⎫=-=-=---=⎪⎪⎝⎭⎝⎭答:小张至少能通过一所学校自招资格审核的概率为141521.已知为数列的前项和,,为数列的前项和,.n S {}n a n 12n n S a +=n T {}n b n 12nn n n b S S +=(1)求数列的通项公式;{}n a (2)若对任意恒成立,求正实数的取值范围.220232024n T λλ-≥*N n ∈λ(1)12n n a -=(2)2024λ≥【分析】(1)根据与的关系求解数列的通项公式即可;n a n S {}n a (2)由得,按照列项求和法,再根据含参不等式求解正实数的取值范围即可.n S n b n T λ【详解】(1)解:由题意,对任意,有①*N n ∈12n n S a +=当时,,可得,,所以1n =11S a =1112a a +=11a =当时,②2n ≥1112n n S a --+=①-②得:122n n n a a a -=-所以,即12nn a a -=12nn a a -=所以,对任意,数列是以1为首项,以2为公比的等比数列*n ∈N {}n a 所以11122n n n a --=⨯=(2)解:因为2121nn n S a =-=-所以()()111221121212121n n n n n n n n n b S S +++===-----所以1231111111111337212121n n n n n T b b b b ++=++++=-+-++-=---- 可以看出,随着的增大而增大,所以,且对任意,n T n 1n T →*n ∈N 1n T <所以恒成立,有,220232024n T λλ-≥220232024λλ-≥所以,所以()()202410λλ-+≥2024λ≥22.已知数列满足:,,.{}n a 11a =22a=2132n n n a a a ++=-(1)证明:数列为等比数列,并求数列的通项公式;{}1n n aa +-{}n a (2)证明:;222222334411111123n n a a a a a a a a ++++++<---- (3)若正整数,,记.1122k k x b a b a b a =⋅+⋅++⋅ {}0,1k b ∈()12k W x b b b =+++ (ⅰ)求;()21n W -(ⅱ)证明.()()432W n W n +=+(1)证明见解析,12n n a -=(2)证明见解析(3)(ⅰ);(ⅱ)证明见解析()21n W n-=【分析】(1)根据递推关系式结合等比数列的定义证明数列为等比数列,再按照迭代法即{}1n n aa +-可求解数列的通项公式;{}n a (2)将通项放大成等比求和的式子,按照等比数列的和求解证明即可;(3)根据结合等比运算即可求和证明.()12kW x b b b =+++ ()21n W -()()432W n W n +=+【详解】(1)解:因为,所以213n n n a a a ++=-()2112n n n n a a a a +++-=-又因为所以是以1为首项,2为公比的等比数列2110a a -=≠{}1n n a a +-所以所以112n n n a a -+-=()()21121111222n n n n n a a a a a a ---=+-++-=++++= (2)解:因为()2121111111142222221n n n n n n n n n a a --++==≤=--⋅-所以2222211223344111111111124122314nnk k n n a a a a a a a a -=++⎛⎫-⎪++++≤=⨯<⎪---- ⎪-⎝⎭∑ (3)解:(ⅰ)由题知:112221n n -+++=- 又因为01121121212n n --=⋅+⋅++⋅ 所以()21111n W n-=+++= (ⅱ)因为()12kW n b b b =+++ 又因为()01101231121243422231212222k k k k n b b b b b b -++=⋅+⋅++⋅+=⋅+⋅+⋅+⋅++⋅ 所以()()()1243112k W n b b b W n +=+++++=+。
小学数学二年级上册计算题综合训练卷(二年级)同步测试.doc
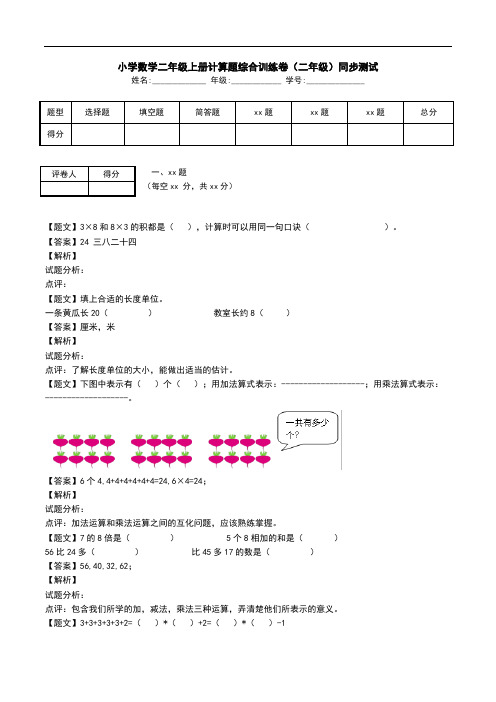
小学数学二年级上册计算题综合训练卷(二年级)同步测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】3×8和8×3的积都是(),计算时可以用同一句口诀()。
【答案】24 三八二十四【解析】试题分析:点评:【题文】填上合适的长度单位。
一条黄瓜长20()教室长约8()【答案】厘米,米【解析】试题分析:点评:了解长度单位的大小,能做出适当的估计。
【题文】下图中表示有()个();用加法算式表示:-------------------;用乘法算式表示:-------------------。
【答案】6个4,4+4+4+4+4+4=24,6×4=24;【解析】试题分析:点评:加法运算和乘法运算之间的互化问题,应该熟练掌握。
【题文】7的8倍是() 5个8相加的和是()56比24多()比45多17的数是()【答案】56,40,32,62;【解析】试题分析:点评:包含我们所学的加,减法,乘法三种运算,弄清楚他们所表示的意义。
【题文】3+3+3+3+3+2=()*()+2=()*()-1评卷人得分【答案】5、3、6、3【解析】试题分析:点评:这道题是用了两种不同的方法计算的,哪种方法都该熟悉并掌握【题文】看镜子写数【答案】634【解析】试题分析:点评:这类题目把试卷翻过来看到数字就是镜子外的数字了【题文】在○里填上“>”、“<”或“=”。
1米○100厘米 2米30厘米○3米59 - 8○50 36 + 7○43【答案】= 〈〉=【解析】试题分析:注意不同单位之间比较的时候要进行单位的换算哟!点评:【题文】4只有()条腿,4只鸡共有()只脚。
【答案】【解析】试题分析:6 8;点评:【题文】下图中共有()条线段;共有()个角,其中有()个是直角;这个图形()(填:是或不是)对称图形。
二年级数学青岛版期末试卷【含答案】

二年级数学青岛版期末试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 1千米等于多少米?A. 100B. 1000C. 10,000D. 1,000,0003. 下列哪个图形是四边形?A. 三角形B. 正方形C. 圆形D. 梯形4. 下列哪个数是质数?A. 12B. 17C. 20D. 215. 下列哪个数是立方数?A. 8B. 12C. 16D. 18二、判断题(每题1分,共5分)1. 5 + 5 = 10 ()2. 1小时等于60分钟。
()3. 0是最小的自然数。
()4. 9是3的平方根。
()5. 圆的周长是其直径的两倍。
()三、填空题(每题1分,共5分)1. 7 + 8 = __2. 1千米等于__米。
3. 一个正方形的四边相等,且每个角都是__度。
4. 4的平方是__。
5. 圆的面积计算公式是__。
四、简答题(每题2分,共10分)1. 请简述偶数和奇数的区别。
2. 什么是质数?3. 请解释加法交换律。
4. 什么是平行四边形?5. 请解释π的值及其在圆的计算中的作用。
五、应用题(每题2分,共10分)1. 小明有5个苹果,他吃掉了2个,还剩下多少个?2. 一个长方形的长是8厘米,宽是4厘米,求其面积。
3. 一个班级有20名学生,其中有10名女生,求男生的人数。
4. 一个圆形的半径是5厘米,求其周长。
5. 一个数的平方是36,求这个数。
六、分析题(每题5分,共10分)1. 请分析以下数的因数分解:18, 24, 30。
2. 请分析如何计算一个三角形的面积,并给出一个例子。
七、实践操作题(每题5分,共10分)1. 请测量一下你的书桌长度,并计算其面积。
2. 请用硬纸板剪出一个正方形,并计算其周长和面积。
八、专业设计题(每题2分,共10分)1. 设计一个实验,验证物体在斜面上滑动的加速度与斜面角度的关系。
2. 设计一个课程计划,教授基础的概率论知识,包括随机事件、概率分布等。
小学二年级数学上册第二单元测试题

小学二年级数学上册第二单元测试题一、选择题(每题4分,共20分)1. 下列哪个数是这样的数:它比4大,比6小?A. 2B. 5C. 8D. 102. 13比10多几个数?A. 2B. 3C. 4D. 53. 7、9、11、13、15依次循环出现的是第几个数?A. 第1个数B. 第2个数C. 第3个数D. 第4个数4. 下面哪个数是偶数?A. 7B. 9C. 12D. 155. 下面哪个数是奇数?A. 16B. 17C. 20D. 22二、填空题(每题4分,共20分)1. 34比28 ________。
2. 21比14 ________。
3. 28比32 ________。
4. 36比30 ________。
5. 19比20 ________。
三、判断题(每题4分,共20分)1. 12是偶数。
( )2. 45比43小。
( )3. 25比23大。
( )4. 16比19小。
( )5. 31比30大。
( )四、计算题(每题10分,共40分)1. 23+15=______2. 42-17=______3. 16+25=______4. 47-8=______5. 29+11=______答案解析:一、选择题1. B2. D3. A4. C5. B二、填空题1. 62. 73. 84. 65. 1三、判断题1. 对2. 对3. 对4. 错5. 对四、计算题1. 382. 253. 414. 395. 40在这个小学二年级数学上册第二单元测试题中,我们练习了一些基本的数学概念和运算。
首先,我们进行了选择题,检验学生对数字大小的理解和判断能力。
选择题测试了学生对数字大于、小于的掌握以及奇偶数的判断能力。
接下来,我们进行了填空题,要求学生根据给定的两个数字,判断它们之间的大小关系。
这个练习可以帮助学生巩固数字大小的概念,并加强他们对比数字大小的能力。
然后,我们进行了一些判断题,要求学生判断给定的两个数字之间的大小关系。
