2016届浙江省杭州市萧山区高考命题比赛模拟(六)数学(文)试题
浙江省杭州市萧山区2016届高三高考命题比赛数学试卷15

2016年高考模拟试卷数学卷命题双向细目表说明:题型及考点分布按照《2016考试说明》参考样卷。
说明1、本试卷的命题方向和命题意图主要从以下几点为出发点:(1)强化主干知识,强化知识之间的交叉,渗透和综合:基础知识全面考,重点知识重点考,注意信息的重组及知识网络的交叉点。
(2)淡化特殊技巧,强调数学思想方法。
考查与数学知识联系的基本方法、解决数学问题的科学方法。
(3)深化能力立意,突出考察能力与素质,对知识的考察侧重于理解和运用。
淡化繁琐、强调能力,提倡学生用简洁方法得出结论。
(4)控制难度. “易︰中︰难=3︰5︰2” .(5)新增知识考查力度及所占分数比例可略超课时比例。
基础题象“会考”,压轴题似“竞赛”.2、试卷结构与2016年样卷保持一致(1)题型结构为, 8道选择、7道填空、5道解答的结构;(2)赋分设计为,选择每题5分、填空题单空体每题4分,多空题每题6分,解答题共74分;(3)考查的内容,注重考查高中数学的主干知识:函数,三角函数和解三角形,立体几何,解析几何,数列等。
3、立足基础,突出主干命题把重点放在高中数学课程中最基础、最核心的内容上,充分关注考生在学习数学和应用数学解决问题中必须掌握的核心观念、思想方法、基本概念和常用技能。
对基础知识的考查主要集中在小题上,具体知识点分布在集合、向量、直线与圆、数列、函数图像、函数性质、线性规划、三视图、三角函数、圆锥曲线性质、空间角等内容上,而且小题的考查直接了当,大部分是直接考查单一知识点,试卷对中学数学的核心内容和基本能力,特别是对高中数学的主干知识进行较为全面地考查。
注重了知识之间的内在联系,重点内容重点考,没有片面追求知识及基本思想、方法的覆盖面,反映了新课程的理念。
4、试题难度适中,层次分明试卷在三种题型中体现出明显的层次感,选择题、填空题、解答题,层层递进。
试卷的入口题和每种题型的入口题较好的把握了难度。
试卷对较难的解答题利用分步给分的设计方法,在化解难度的同时,又合理区分不同层次的考生。
浙江省杭州市萧山区2016届高三高考命题比赛数学试卷21

2016年高考模拟试卷数学卷(理科)本试题卷分选择题和非选择题两部分.全卷共4页,选择题部分1至2页,非选择题部分2至4页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上.参考公式:柱体的体积公式:V Sh =其中S 表示柱体的底面积,h 表示柱体的高 锥体的体积公式:13V Sh =其中S 表示锥体的底面积,h 表示锥体的高台体的体积公式:)(312211S S S S h V ++=其中S 1、S 2分别表示台体的上下底面积,h 表示台体的高球的表面积公式:24S R π=球的体积公式:334R V π= 其中R 表示球的半径选择题部分(共40分)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项符合题目要求。
1、【原创】设全集(0,1,2,3,4}U =,集合{0,2,4},{0,1,3}A B ==,则( )(A )()U A C B U =U (B ) ()U C A B =ΦI (C ) ()()U U C A C B U =I (D ) ()()U U C A C B =ΦI2、【原创】已知条件2:430p x x -+>,条件:q x a >,且p ⌝是q ⌝的充分不必要条件,则实数a 的取值范围可以是( )(A )3a ≥ (B )3a > (C )1a ≤ (D )1a < 3、【原创】已知函数()sin (0)f x x ωω=>在[,]63ππ上是单调减函数,则ω满足的条件是( )(A )(0,3] (B )9[3,]2(C )9(0,]2 (D )[3,)+∞4、【原创】若点(,)P x y 满足线性约束条件⎪⎩⎪⎨⎧≥≥+-≤-002202y y x y x ,则11y u x -=+的取值范围是( )(A )1(,]5-∞ (B )[1,)+∞ (C )1[,1]5 (D )1(,]5-∞U [1,)+∞5、【原创】如图,三棱锥P ABC -,已知⊥PA 面ABC ,BC AD ⊥于D ,1===AD CD BC ,设PD x =,θ=∠BPC ,记函数()f x =tan θ,则下列表述正确的是( )(A )()f x 是关于x 的增函数 (B )()f x 是关于x 的减函数 (C )()f x 关于x 先递增后递减 (D )()f x 关于x 先递减后递增6、【改编】已知1F 、2F 分别是双曲线1C :22221x ya b -=(0a >, 0b >)的左、右焦点,且2F 是抛物线2C :22y px =(0p >)的焦点,双曲线1C 与抛物线2C 的一个公共点是P .若线段2PF 的中垂线恰好经过焦点1F ,则双曲线1C 的离心率是( )(A )23+ (B )12+ (C )22+ (D )13+7、【改编】你拿着两个鸡蛋站在120层的大楼上。
浙江省杭州市萧山区2016届高三高考命题比赛数学试卷15
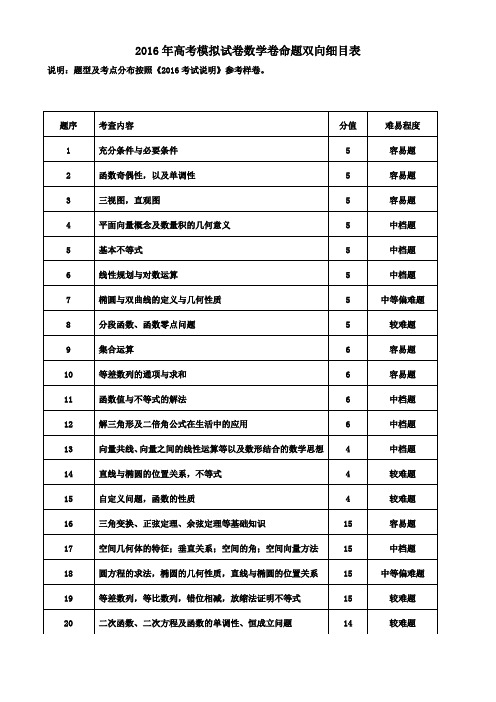
2016年高考模拟试卷数学卷命题双向细目表说明:题型及考点分布按照《2016考试说明》参考样卷。
说明1、本试卷的命题方向和命题意图主要从以下几点为出发点:(1)强化主干知识,强化知识之间的交叉,渗透和综合:基础知识全面考,重点知识重点考,注意信息的重组及知识网络的交叉点。
(2)淡化特殊技巧,强调数学思想方法。
考查与数学知识联系的基本方法、解决数学问题的科学方法。
(3)深化能力立意,突出考察能力与素质,对知识的考察侧重于理解和运用。
淡化繁琐、强调能力,提倡学生用简洁方法得出结论。
(4)控制难度. “易︰中︰难=3︰5︰2” .(5)新增知识考查力度及所占分数比例可略超课时比例。
基础题象“会考”,压轴题似“竞赛”.2、试卷结构与2016年样卷保持一致(1)题型结构为, 8道选择、7道填空、5道解答的结构;(2)赋分设计为,选择每题5分、填空题单空体每题4分,多空题每题6分,解答题共74分;(3)考查的内容,注重考查高中数学的主干知识:函数,三角函数和解三角形,立体几何,解析几何,数列等。
3、立足基础,突出主干命题把重点放在高中数学课程中最基础、最核心的内容上,充分关注考生在学习数学和应用数学解决问题中必须掌握的核心观念、思想方法、基本概念和常用技能。
对基础知识的考查主要集中在小题上,具体知识点分布在集合、向量、直线与圆、数列、函数图像、函数性质、线性规划、三视图、三角函数、圆锥曲线性质、空间角等内容上,而且小题的考查直接了当,大部分是直接考查单一知识点,试卷对中学数学的核心内容和基本能力,特别是对高中数学的主干知识进行较为全面地考查。
注重了知识之间的内在联系,重点内容重点考,没有片面追求知识及基本思想、方法的覆盖面,反映了新课程的理念。
4、试题难度适中,层次分明试卷在三种题型中体现出明显的层次感,选择题、填空题、解答题,层层递进。
试卷的入口题和每种题型的入口题较好的把握了难度。
试卷对较难的解答题利用分步给分的设计方法,在化解难度的同时,又合理区分不同层次的考生。
浙江省杭州市萧山区2016届高三高考命题比赛数学试卷6

2016年浙江省普通高中高考模拟试卷数 学 (文科)本试卷分选择题和非选择题两部分。
考试时间120分钟。
参考公式:球的表面积公式 柱体的体积公式24R S π= V Sh =球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高334R V π=球台体的体积公式 其中R 表示球的半径121()3V Sh S S =椎体的体积公式 其中12,S S 分别表示台体的上、下底面积13V Sh = h 表示台体的高其中S 表示椎体的底面积,h 表示椎体的高选择题部分一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. [原创]已知ln x π=,1log ey π=,12z e-=,则( )A .x y z <<B .z x y <<C .z y x <<D .y z x <<2. [原创] 已知直线l 、m 与平面α、β,βα⊂⊂m l ,,则下列命题中正确的是 A .若m l //,则必有βα// B .若m l ⊥,则必有βα⊥ C .若β⊥l ,则必有βα⊥ D .若βα⊥,则必有α⊥m3. [原创]为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位4. [原创]若实数,x y 满足约束条件24122x y x y x y +≥⎧⎪-≥⎨⎪-≤⎩,目标函数z tx y =+有最大值6,则t 的值为A .3 B.-3 C .1 D .1-5.[改编] 已知等比数列}{n a 前n 项和为n S ,则下列一定成立的是A .若03>a ,则20150a <B .若04>a ,则20160a <C . 若03>a ,则20150S >D .若04>a ,则20160S > 6.[改编] 已知0,0,3x y x y <<+=-若11z x y=+则z 的最值为 ( ) A .最小值-2 B .最小值-4 C .最大值-4 D .最大值-2 7. [改编]已知函数(](]1,1()12,1,3x f x x x ⎧∈-⎪=⎨--∈⎪⎩ ,其a >0,且函数-1(2)()f x f x -=+,若函数()g x =3()f x -x 恰有5个零点,则实数a 的取值范围是(A.(3B. 8)33C. 4(3D. 48(,)338. 正方体D C B A ABCD ''''-中,M 为BC 边的中点, 点P 在底面D C B A ''''和侧面C D CD ''上运动并且使C PA C MA '∠='∠,那么点P 的轨迹是( )A.两段圆弧B.两段椭圆弧C.两段双曲线弧D.两段抛物线弧非选择题部分二、填空题(本大题7小题,多空题每题6分,单空题每题4分,共36分.)9.[原创] 若集合A= {x Z ∈∣} B=(2|2x x x ->0},则__________,A ⋂(R CB )的子集个数为________个.10. [原创]设函数()2sin(2),6f x x π=+则该函数的最小正周期为________,单调递减区间为_______________.11. [改编]已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是__________,表面积是____________.B '12. [改编]过点(2,0)A 作直线l 交圆22:9C x y +=于两点,过其中任一点P 作直线l 的垂线交圆于点Q ,当直线l 绕点A 转动时,则PQ 最长为___________,此时直线方程为_________________.13.[原创] 已知||2,||3a b ==,且它们的夹角为120°,当||()a b R λλ+∈取最小值时,λ=___________.14.[改编]已知实数,x y 满足221,x y +≤则|22||623|x y x y +-+--的最大值是_____.15.[改编]过曲线1C :()222210,0y x a b a b-=>>的下焦点1F 作曲线2C :222x y a +=的切线,设切点为P ,延长1F P 交曲线3C :22x py =于点Q ,其中曲线1C 与3C 有 一个共同的焦点,若1||PF ||PQ =,则曲线1C 的离心率为___________.三、解答题(本大题共5小题,共74分。
浙江省杭州市萧山区2016年高三高考命题比赛数学试卷2

2016年高考模拟试卷数学(理)卷(时间 120 分钟 满分150 分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知正项等比数列{a n }中,若a 1a 3=2,a 2a 4=4,则a 5=( ) A .±4 B .4 C .±8 D .82.已知条件p :x ≤1,条件q :<1,则q 是¬p 成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既非充分也非必要条件3.已知,函数y=f (x+φ)的图象关于(0,0)对称,则φ的值可以是( ) A . B . C . D .4.若直线xcos θ+ysin θ﹣1=0与圆(x ﹣cos θ)2+(y ﹣1)2=相切,且θ为锐角,则这条直线的斜率是( ) A .B .C .D .5.若m 、n 为两条不重合的直线,α、β为两个不重合的平面,则下列命题中的真命题个数是( ) ①若m 、n 都平行于平面α,则m 、n 一定不是相交直线; ②若m 、n 都垂直于平面α,则m 、n 一定是平行直线;③已知α、β互相垂直,m 、n 互相垂直,若m ⊥α,则n ⊥β; ④m 、n 在平面α内的射影互相垂直,则m 、n 互相垂直.A .1B .2C .3D .46.设0,0),0,(),1,(),2,1(>>-=-=-=b a b OC a OB OA ,O 为坐标原点,若A 、B 、C 三点共线,则ba21+的最小值是( ) A .2 B .4 C .6D .87.已知点P (3,3),Q (3,﹣3),O 为坐标原点,动点M (x ,y )满足,则点M 所构成的平面区域的面积是( )A .12B .16C .32D .64 8.已知F 1、F 2分别是双曲线的左右焦点,A 为双曲线的右顶点,线段AF 2的垂直平分线交双曲线与P ,且|PF 1|=3|PF 2|,则该双曲线的离心率是( ) A .B .C .D .二、填空题(本大题共7小题,9-12小题每小题6分,13-15每小题4分,共36分) 9.设全集集U=R ,集合M={x|﹣2≤x ≤2},N={x|y=},那么M ∩N= ,C U N= .10.一空间几何体的三视图如图所示,则该几何体的体积为 , 表面积为 .11.已知{a n }为等差数列,若a 1+a 5+a 9=8π,则前9项的和S 9= , cos (a 3+a 7)的值为 .12.已知函数f (x )=﹣,则f (x )的递增区间为 , 函数g (x )=f (x )﹣的零点个数为 个.13. 过抛物线22(0)x py p =>的焦点作斜率为1的直线与该抛物线交于A,B 两点,A,B 在x 轴上的正射影分别为D,C.若梯形ABCD的面积为,则p = .14. 方程x x f =)(的根称为)(x f 的不动点,若函数)2()(+=x a xx f 有唯一不动点,且10001=x ,)1(11nn x f x =+ *N n ∈,则=2016x .15.已知a <b ,二次不等式ax 2+bx+c ≥0对任意实数x 恒成立,则M=的最小值为 .三、解答题(本大题共5小题,共74分) 16.(14分) 在∆A B C 中,a b c ,,分别是∠∠∠A B C ,,的对边长,已知a b c ,,成等比数列, 且ac a c b c 22-=-,求∠A的大小及b Bcsin 的值.17.(15分)如图,已知四棱锥P-ABCD ,底面ABCD 为菱形,PA ⊥平面ABCD ,∠ABC=60°,E ,F 分别是BC ,PC 的中点。
浙江省杭州市萧山区高考模拟试卷6(数学文)

浙江省杭州市萧山区高考模拟试卷6数 学(文科)本试卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页,非选择题部分3至4页。
满分150分,考试事件120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
参考公式:球的表面积公式 棱柱的体积公式24S R π= V Sh =球的体积公式 其中S 表示棱柱的底面积,h 表示棱柱的高343V R π= 棱台的体积公式其中R 表示球的半径 11221()3V h S S S S =++棱锥的体积公式 其中12,S S 分别表示棱台的上、下底面积,13V Sh = h 表示棱台的高其中S 表示棱锥的底面积,h 表示棱锥的高 如果事件,A B 互斥,那么 ()()()P A B P A P B +=+一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. (北京文改编)设集合{}12≤=x x A ,{}0>=x x B ,则=B A ( ) A .{}10≤<x x B .{}01<≤-x x C .{}1-≥x x D .{}1≤x x 2. (浙江文改编)已知函数()11+=-x e x f ,若()2=a f ,则=a ( )A .0B .1C .2D .33. (北京理改编)在复平面内,复数i iz -=12对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限4.(浙江文改编)设βα,是两个不同的平面,l 是一条直线,则β⊥l 的一个充分条件是( )A .βαα⊥⊥,lB .βαα⊥,//lC .βαα//,⊥lD .βαα//,//l5. (江西文改编)等比数列{}n a 的首项11=a ,且2a ,15+a ,6a 成等差数列,则数列的前5项之和是( )A. 15B. 31C. 53D. 836.(浙江文改编)某程序框图如图所示,该程序运行后 输出的k 的值是( )A .4B .5C .6D .77.(全国卷Ⅱ文改编)双曲线()0,1222>=-m my x的渐近线与圆()2222=+-y x 相切,则=m ( )A .22B .2C .1D .28. (中学数学教学参考改编)已知实数y x ,满足1≤+y x ,则y x +2的最大值为( ) A .31 B .21C .1D .29. 0≠=b a ,且关于x 的函数()1213123+•++=x b a a x x f 在R 上有极值,则a 与b 的夹角范围为( ) A .⎪⎭⎫⎢⎣⎡6,0π B .⎥⎦⎤ ⎝⎛ππ,6 C .⎥⎦⎤ ⎝⎛ππ,3 D .⎥⎦⎤⎝⎛32,3ππ10.(数学学报改编)已知函数()()0,ln 22>-=a x a x x f ,令()()ax x f x g 2-=,若()x g 有两个零点,则a 的取值范围是( )A .⎪⎭⎫⎝⎛+∞,21 B .⎪⎭⎫⎝⎛1,21 C .⎪⎭⎫ ⎝⎛∞-21,D .⎥⎦⎤⎝⎛1,21 开始 k=0 S=1S<100? S=S ﹡2s k=k+1是 输出k 结束否非选择题部分(共100分)注意事项:1. 用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
浙江省杭州市萧山区2016届高三高考命题比赛语文试卷6

2016年高考模拟试卷语文卷注意事项:1.本试卷共7页,满分为150分,考试用时为150分钟。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色签字笔写在试卷及答题卡上。
3.请认真核对学校、姓名、准考证号。
4.作答非选择题,必须用0.5毫米黑色签字笔在答题纸上的指定位置作答,在其他位置作答一律无效。
一、语言文字运用(共24分,其中选择题每小题3分)1、下列词语中加点的字,注音全都正确的一项是【原创】()A.漩.(xuán)涡滂.(pāng)沱紧箍.(gū)咒叱咤.(chà)风云B.发酵.(jiào)鬈.发(quán) 涮.(shuàn)羊肉载.(zài)歌载舞C.顷.(qǐng)刻模.(mó)板露.(lòu)马脚消弭.(mǐ)灾祸D.要挟.(xié)拙.(zhuó)见一掊.(póu)土不着.(zhuó)边际2、下列各句中,没有错别字的一项是【原创】()A.辩论双方唇枪舌剑,针锋相对,相持不下,后来正方二辩出其不意地抛出三个有力论据,令反方措手不及,只好甘败下风。
B.市场经济体制遵循灵活变通的法则,一些企业如果还抱残守缺,只会“为渊驱鱼,为丛驱雀”,最终会无法在市场中生存。
C.他虽年逾古稀,但是精神矍烁,体育馆里处处是他矫健的身姿,让人由衷佩服。
D.近来在银屏上出现的明星真人秀节目有泛滥的趋势,一些卫视为了追求收视率频频复制同类型节目,导致真人秀节目粗制滥造、良莠不齐。
3、下列各句中,加点的词语运用不正确的一项是【原创】()A.她吸取了上次比赛失败的经验教训,每日刻苦训练,终于在这次网球锦标赛中跻身..女子第二名。
B 我不会操船驾舵,可是..倘使你在辽远的海滨,我也会冒着风波寻访你这颗珍宝。
C在空灵悠远的音乐声中,杨丽萍行云流水....般的孔雀舞,迎来了观众的阵阵喝彩。
D 在新媒体快速发展的今天,一些纸质媒体为了博得读者的眼球,往往编造一些耸人听闻....的消息。
浙江省杭州市萧山区2016届高三高考命题比赛数学试卷28

2016年高考模拟试卷数学卷(理)考试时间:120分钟 满分:150分选择题部分(共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R =,集合{}3|≥=x x A ,}2log {2<=x x B ,则()=B A C U I ( ) A .{}13x x << B .}3{<x xC .}43{<≤x xD .}30{<<x x (原创)2.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸, 则该几何体的体积是( )A .2B .4C .6D .123.命题“]1,2[-∈∀x ,02≤-a x 恒成立”为真命题的一个充分不必要 条件是( )A .4a ≥B .4a ≤C .5a ≥D .5a ≤ (改编)4.无穷等差数列}{n a 的前n 项和为n S ,其中*N n ∈,则下列命题不正确...的是( ) A .若0>n a ,则n S 0> B .若n S 0>,则0>n aC .若0>n a ,则}{n S 是单调递增数列D .若}{n S 是单调递增数列,则0>n a5.设函数21(),()(,,0)f x g x ax bx a b R a x==+∈≠,若()y f x =的图象与()y g x =图象有且仅有两个不同的公共点1122(,),(,)A x y B x y ,则下列判断正确的是( )A .当0a <时,12120,0x x y y +<+>B .当0a <时,12120,0x x y y +>+<C .当0a >时,12120,0x x y y +<+<D .当0a >时,12120,0x x y y +>+>6.已知1=xy ,且220<<y ,则y x y x 2422-+的最小值为( )A .4B .29C .22D .24 (改编)7.已知集合22{(,)|1}M x y x y =+≤,若实数,λμ满足:对任意的(,)x y M ∈,都有(,)x y M λμ∈,则称(,)λμ是集合M 的“和谐实数对”.则以下集合中,存在“和谐实数对”的是( ) A .}4|),{(=+μλμλB .}4|),{(22=+μλμλ 俯视图2(第4题)侧视图正视图(第2题图)8.已知1F ,2F 是双曲线C :)0,0(12222>>=-b a by a x 的左、右焦点,4||21=F F ,点A 在双曲线的右支上,线段1AF 与双曲线左支相交于点B ,AB F 2∆的内切圆与边2BF 相切于点E .若||2||12BF AF =,22||=BE ,则双曲线C 的离心率为( )A .22 B .2C .3D .2(改编)非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.已知圆04222=++-+m y x y x C :,则其圆心坐标是_________,m 的取值范围是___________.(原创) 10.已知)cos (sin 212cos ααα+=,则cos sin αα-= ,sin2α= . (根据2016届嵊州市高三上期末试卷第9题改编)11.知函数()21,0,=1,0,x x f x x x ⎧-≤⎪⎨->⎪⎩()=21x g x -,则()()2f g = ,()g f x ⎡⎤⎣⎦的值域为 .12.正项等比数列}{n a 的前n 项和为n S ,若)(412312-+++=n n a a a S Λ,且27321=a a a ,则=5a ___________.13.如图,在正方体ABCD -A 1B 1C 1D 1中,M 为BB 1的中点,则直线MC 与平面1ACD 所成角的正弦值为___________.(根据2015年浙江省数学竞赛第3题改编)14.设R m ∈,实数y x ,满足⎪⎩⎪⎨⎧≤--≥+-≥.0623,0632,y x y x m y ,若182≤+y x ,则实数m 的取值范围是___________.(根据2016届金丽衢十二校第一次联考第6题改编)15.已知向量,a b r r 的夹角为3π,6=-b a ϖϖ,向量c a -r r ,c b -r r 的夹角为23π,c a -=r r a ϖ与c ϖ的夹角为__________,a c ⋅r r的最大值为 .(根据2015年浙江省高中数学竞赛16题改编)A 1(第13题图)16.(本题满分14分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知cos (cos 3sin )cos 0C A A B +-=.(Ⅰ)求角B 的大小;(Ⅱ)若2=+c a ,求b 的取值范围.(根据慈溪中学2016届高三上期中试卷16题改编)17.(本题满分15分)如图,已知长方形ABCD 中,1,2==AD AB ,M 为DC 的中点. 将ADM ∆沿AM 折起,使得平面⊥ADM 平面ABCM . (Ⅰ)求证:BM AD ⊥;(Ⅱ)若)10(<<=λλDB DE ,当二面角D AM E --大小为3π时,求λ的值.18.(本题满分15分)已知函数c bx ax x f ++=2)(,当1≤x 时,1)(≤x f 恒成立. (Ⅰ)若1=a ,c b =,求实数b 的取值范围;(Ⅱ)若a bx cx x g +-=2)(,当1≤x 时,求)(x g 的最大值. (原创)19.(本题满分15分)设点P 是椭圆14:221=+y x C 上任意一点,过点P 作椭圆的切线,与椭圆)1(14:22222>=+t t y t x C 交于B A ,两点. (Ⅰ)求证:PB PA =;(Ⅱ)OAB ∆的面积是否为定值?若是,求出这个定值;若不是,请说明理由. (原创) A(第17题图)B AOy xP20.(本题满分15分)正项数列}{n a 满足121223+++=+n n n n a a a a ,11=a .(Ⅰ) 求2a 的值;(Ⅱ) 证明:对任意的*N n ∈,12+≤n n a a ;(Ⅲ)记数列}{n a 的前n 项和为n S ,证明:对任意的*N n ∈,32121<≤--n n S .(根据宁波效实中学2015届高考模拟测试卷20题改编)2016年高考模拟试卷数学(理)答题卷本次考试时间120分钟,满分150分,所有试题均答在答题卷上一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9、 , ; 10、 , ; 11、 , ;12、 ; 13、 ; 14、 ;15、 , .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.学校_______________班级 学号 姓名A (第17题图)2016年高考模拟试卷数学(理)参考答案和评分标准一、选择题:本题考查基本知识和基本运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双向细目表2016年高考模拟试卷 数学(文科)卷本试题卷分选择题和非选择题两部分。
考试时间120分钟,满分150分。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
参考公式: 球的表面积公式S=42R π 球的体积公式 V=334R π 其中R 表示球的半径 锥体的体积公式 V=13Sh其中S 表示锥体的底面积,h 表 示锥体的高 柱体的体积公式 V=Sh其中S 表示柱体的底面积,h 表示柱体的高台体的体积公式V=11221()3h S S S S其中12,S S 分别表示台体的上、下底面积,h 表示台体的高选择题部分一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合}02|{2>-+=x x x A ,}log |{2x y x B ==,则=⋂B A C R )( [原创](A )),2[+∞- (B )]1,0[ (C )),0(+∞ (D ))1,0(2. 已知a R ∈,则0)2)(1(>--a a 是11>a成立的 [原创] (A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 3. 已知βα,是不同的两个平面,b a ,是不同的两条直线,则下列命题中不正确...的是[原创] (A )若α⊥a b a ,//,则α⊥b (B )若βα⊥⊥a a ,,则βα// (C )若βα⊂⊥a a ,,则αβ⊥ (D )若b a =⋂βαα,//,则b a // 4. 一个几何体的三视图如右图所示,其中正视图是一个正三 角形,则这个几何体的体积是 [原创](A )3 (B )33 (C )2 (D )32 5. 函数)0,0)(2sin(πϕωϕω<<>+=x y 的最小正周期为π,且函数图像关于点)0,6(π-对称,则函数的解析式为 [原创](A ))32sin(π+=x y (B ))322sin(π+=x y(B ))34sin(π+=x y (D ))324sin(π+=x y6. 已知椭圆)0(12222>>=+b a by a x 上一点A 关于原点的对称点为B ,F 为其左焦点,AF ^BF ,设6π=∠ABF ,则该椭圆的离心率为 [原创](A )22 (B )33 (C )13- (D )231-7. 已知平面向量b a ,,其中b 为非零向量,a 为单位向量,且b 与a b -的夹角为150,则||b 的取值范围为 [原创](A ))23,0( (B )]1,0[ (C ))3,0( (D ))1,0( 8. 定义“正对数”:ln +x =⎩⎪⎨⎪⎧0,0<x <1,ln x ,x ≥1.现有四个命题:①若a >0,b >0,则ln +(a b )=b ln +a ②若a >0,b >0,则ln +(ab )=ln +a +ln +b ③若a >0,b >0,则ln +⎝⎛⎭⎫a b ≥ln +a -ln +b ④若a >0,b >0,则ln +(a +b )≤ln +a +ln +b +ln 2 其中的真命题有________。
[根据2013年山东卷第16改编](A )①④ (B )③④ (C )①③④ (D )①②④非选择题部分二、填空题:本大题共7小题,其中第9题每空2分,第10、11、12题每空3分,第13、14、15题每空A 1B 1C 1D 1ABCD E (第14题)9.已知20πα<<,31sin =α,则______cos =α;______)4sin(=+πα;______2cos =α。
[原创]10.已知n S 为等差数列{}n a 的前n 项和,若11S =,424S S =,则数列{}n a 的通项n a =_________;64S S =______。
[原创] 11.设不等式组⎪⎩⎪⎨⎧≥≤+-≤-1255334x y x y x 表示的平面区域为Ω,若点),(y x P 是该平面区域内的动点,则y x z -=的最小值是______;若直线)2(:+=x k y l 上存在区域Ω内的点,则k 的取值范围是______。
[原创]12.已知F 是双曲线17222=-y x 的左焦点,)2,1(A 是双曲线 外一点,P 是双曲线右支上的动点,则||||PA PF +的最小值为 ,此时点P 的坐标为 。
[原创]13.在平面直角坐标系下,曲线222(||||)x y x y +=+围成的图形的面积为______。
[根据必修2课本第144页B 组第3题改编] 14.长方体1111D C B A ABCD -的底面是边长为a 的正方形,若在侧 棱1AA 上至少存在一点E ,使得︒=∠901EB C ,则侧棱1AA 的长 的最小值为______。
[根据数学教学研究第8题改编]15.已知函数()()20f x ax bx c a =++>的零点为()1212,x x x x <,且()f x 的最小值[)012,y x x ∈,则函数()()y f f x =的零点个数是 。
[根据杭高2013届高考模拟测试数学(文科)试题卷第10题改编]三、解答题:本大题共5小题,共74分。
解答应写出文字说明、证明过程或演算步骤。
16.(本题14分)已知,,a b c 分别是ABC ∆的三个内角,,A B C 的对边,且满足cos sin 0b CC a c +--=。
(Ⅰ)求B ;(Ⅱ)若b =,求c a +的取值范围。
[原创]17.(本题15分)单调递增数列{}n a 的前n 项和为n S ,满足21()2n n S a n =+, (Ⅰ)求1a ,2a ,并求数列{}n a 的通项公式;(Ⅱ)设1211, 132 1 n n n an a c n -+⎧⎪-=⎨⎪⨯+⎩为奇数为偶数,求数列{}n c 的前20项和20T 。
18.(本题15分)已知正四棱锥ABCD P -中,底面是边长为2的正方形,高为2,M 为线段PC 的中点。
(Ⅰ) 求证:PA ∥平面MDB ;(Ⅱ) N 为AP 的中点,求CN 与平面MBD 所成角的正弦值。
[根据2014学年温州十校文科数学期初联考第18题改编]19.(本题15分)已知抛物线的顶点在坐标原点,焦点在y 轴上,且过点(2,1), (Ⅰ)求抛物线的标准方程及焦点坐标;(Ⅱ)与圆1)1(22=++y x 相切的直线t kx y l +=:交抛物线于不同的两点N M ,,若抛物线上一点C 满足)(ON OM OC +=λ)0(>λ,求λ的取值范围。
[根据浙江省丽水市2013届高三高考第一次模拟测试第22题改编](第19题)20.(本题15分)已知a ∈R ,函数()221f x x ax =-+.(Ⅰ)若2a ≤,求()f x 在区间[]1,2上的最小值()m a ,并求()m a 的取值范围;(Ⅱ)记()()g x f x x a =+-,若()g x 在[]12,上恰有一个零点,求a 的取值范围。
[根据嵊州市2015学年第一学期期末教学质量检测数学(文)第20题改编]A DCMPN (第18题)2016年高考模拟试卷数学(文科)卷答题卷题号一、选择题二、填空题三、解答题总分结分人16 17 18 19 20得分一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.题号 1 2 3 4 5 6 7 8答案二、填空题:本大题7小题,9-12题每题6分,13-15每题4分,共36分,把答案填在题中的横线上.9. ___________;__________ ;___________10.___________;_________ 11. __________ ;__________ 12. __________;__________13.___________14._________15. __________三、解答题:本大题共5小题,共74分.解答题应写出必要的文字说明、证明过程或演算步骤.17.解:PMND CA B(第18题) 19.解:(第19题)20.解:2016年高考模拟试卷 数学(文科)参考答案及评分标准一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只二、填空题:本大题共7小题,其中第9题每空2分,第10、11、12题每空3分,第13、 14、15题每空4分,共36分。
9.322; 624+ ;97 10.12-n ; 4911. 3 __;]1522,72[ 12.24; )57,58(13. π48+ 14.a 215. _2或3__三、解答题:本大题共5小题,共74分。
解答应写出文字说明、证明过程或演算步骤。
16.(本题14分)本题主要考查正、余弦定理及三角函数的性质等基础知识,同时考查运算求解能力。
解:(Ⅰ)由正弦定理知:sin cos sin sin sin 0B C B C A C +--= C B C B C B A sin cos cos sin )sin(sin +=+= 代入上式sin cos sin sin 0B C B C C --= ………………………………2分1π(0,)B π∈ 3B π∴=………………………………6分(Ⅱ)由正弦定理2sin sin sin ===A b C c A a ………………7分 )]3sin([sin 2)sin (sin 2π++=+=+∴A A C A c a )6sin(32)cos 23sin 23(2π+=+=A A A ………………10分 320π<<A 6566πππ<+<∴A 1)3sin(21≤+<∴πA ………………13分 所以c a +的取值范围为]32,3( ………………14分 17.(本题15分)本题主要考查等比数列的通项公式及等差、等比数列的求和公式、不等式等基础知识,同时考查运算求解能力。
解:(Ⅰ)1n =时,2111(1)2a a =+ 得11a =………………………………2分 2=n 时,)2(21222+=a s 得22=a 当2n ≥时,2111(1)2n n S a n --=+- 得2211(1)2n n n a a a -=-+ 化为221(1)0n n a a ---=11n n a a --=或11n n a a -+= (2n ≥) ……………………………4分又因为{}n a 单调递增数列,故11n n a a --=所以{}n a 是首项是1,公差为1的等差数列,n a n = …………………………7分 (Ⅱ)1211, 132 1 n n n a n a c n -+⎧⎪-=⎨⎪⨯+⎩为奇数,为偶数131********[]3(222)102141(20)1n T =++++++++---……………9分 =101112(14)3101335192114-++++⨯+⨯⨯⨯- ……………11分 =101111111()2(41)10213351921-+-+-+-+ ……………13分 =2121101782822121++=+ ……………………15分18.(本题15分)本题主要考查空间点、线、面位置关系,线面所成角等基础知识,同时考查空间想象能力和推理论证能力。
