九年级(初三)物理3.4 互易定理§3.4 互易定理例求图示电路中的电流I。
四、互易定理
四、互易定理对于线性单一激励的不含受控源的线性电阻电路(即仅有一个独立源作用的电阻电路)还有一个很重要的性质互易性,反映互易性的原理称作互易原理。
此原理有三种形式。
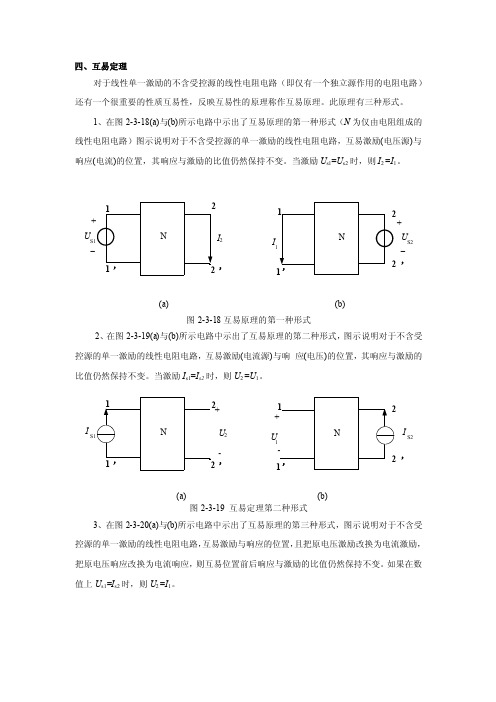
1、在图2-3-18(a)与(b)所示电路中示出了互易原理的第一种形式(N 为仅由电阻组成的线性电阻电路)图示说明对于不含受控源的单一激励的线性电阻电路,互易激励(电压源)与响应(电流)的位置,其响应与激励的比值仍然保持不变。
当激励U s1=U s2时,则I 2 =I 1。
_U ’I 2 S2 (a) (b)图2-3-18互易原理的第一种形式2、在图2-3-19(a)与(b)所示电路中示出了互易原理的第二种形式,图示说明对于不含受控源的单一激励的线性电阻电路,互易激励(电流源)与响 应(电压)的位置,其响应与激励的比值仍然保持不变。
当激励I s1=I s2时,则U 2 =U 1。
I ’U 2S2+- (a) (b)图2-3-19 互易定理第二种形式3、在图2-3-20(a)与(b)所示电路中示出了互易原理的第三种形式,图示说明对于不含受控源的单一激励的线性电阻电路,互易激励与响应的位置,且把原电压激励改换为电流激励,把原电压响应改换为电流响应,则互易位置前后响应与激励的比值仍然保持不变。
如果在数值上U s1=I s2时,则U 2 =I 1。
_U S1+ ’U 2 S2 -(a) (b)图2-3-20【例15】:电路如图2-3-21(a)所示,试求电流I 。
(a) (b)图2-3-21例15电路图【解】:原电路为一不平衡桥式电路,但为仅有一个独立源单独作用的线性电阻电路,可使用互易定理进行分析。
互易后的电路如右图所示。
此时应注意互易前后对应支路上的电压电流的参考方向必须同时关联或非关联。
在图2-3-21(b)中可以求得:A I 224241212281=+⨯++⨯+=根据分流公式:A I I 3221112=+=A II 3442413=+=由KCL 可得:A I I I 3223=-=∴原电路中所求电流AI 32=d 8V。
电路中的定理

电路中的定理下载温馨提示:该文档是小编精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!电路中的定理主要涉及对电路分析和设计的基本原理,以下是其中一些重要的定理及其简要解释:1. 欧姆定律:①定义:在同一电路中,通过某段导体的电流跟这段导体两端的电压成正比,跟这段导体的电阻成反比。
②公式:I = V / R(其中I是电流,V是电压,R是电阻)③重要性:欧姆定律揭示了电路中电流、电压和电阻之间的定量关系,是分析和计算电路问题的基本工具。
2. 叠加定理:①定义:在线性电路中,任一支路的电流或电压是电路中各个独立源分别作用时在该支路中产生的电流或电压的代数和。
②应用:通过分别考虑电路中每个独立源的作用,然后将其效果叠加,可以简化电路分析。
③注意事项:叠加定理只适用于线性电路,且不能用于计算功率。
3. 替代定理:①定义:允许在一个复杂的电路中,用一个更简单的电路或元件来替代其中的一个或多个部分,前提是替代前后的电路在外部看来具有相同的电压和电流关系。
②应用:通过替代定理,可以将复杂的电路问题简化为更简单的问题进行解决。
4. 戴维南定理(诺顿定理):①定义:戴维南定理(也称为诺顿定理)是一种将任意线性有源二端网络等效为一个电压源(或电流源)和电阻串联(或并联)的电路模型的方法。
②应用:通过戴维南定理,可以将复杂的电路简化为一个更简单的等效电路,从而便于分析和计算。
5. 最大传输定理:①定义:最大传输定理涉及到电路中的功率传输效率,即如何在源和负载之间实现最大功率传输。
②重要性:最大传输定理在电路设计、信号处理和通信系统中具有重要的应用价值。
6. 特勒根定理:①定义:特勒根定理是关于电路功率的一种定理,它表述了电路中电源和负载之间的功率平衡关系。
②应用:特勒根定理可以用于分析电路中的功率流动和能量转换。
7. 互易定理:①定义:互易定理是关于电路网络的一种性质,它表述了当网络中两个端点的角色互换时,网络的某些性质保持不变。
第四章 电路定理 互易定理

–
d
2A
(c)
a Req
b
线性 电阻 网络 NR
c
a I 5 5 + 5V – 戴维宁等 效电路
(d)
d
b
Req u1 2 10 2 5
(2) 结合a图,知c 图的等效电阻:
I 5 55 0.5A
解2
应用特勒根定理:
ˆ ˆ u1i1 u2 i2 u1 i1 u 2 i2
求(a)图电流I ,(b)图电压U。 2 4 + I 12V – (a) 1 + I 6
12V
+ 6A
U
4 2 (b)
-
-
6A 1 + 6 U –
解
I
利用互易定理
12 1 6 // 6 1 2 1.5A
U 3 2 6V
例2 解
I'
求电流I 。
利用互易定理
ˆ ˆ 10i1 5 ( 2) 5i1 ( 2) u 2 0
ˆ i1 I 0.5 A
如要电路具有互易性,则: U ab U cd
( 1) 3 ( 3 )
2
一般有受控源的电 路不具有互易性。
例3
测得a图中U1=10V,U2=5V,求b图中的电流I 。
a 2A
b 解1
+ 线性 电阻 u1 网络 –
NR
c
+ – d u2
a
5
I
(a)
b
线性 电阻 网络 NR
c + – 2A
(b)
d
a – b
(1) 利用互易定理知c 图的
互易定理

互易定理在线性无源电路中,若只有一个独立电源作用,则在一定的激励与响应的定义(电压源激励时,响应是电流;电流源激励时,响应是电压)下,二者的位置互易后,响应与激励的比值不变。
根据激励和响应是电压还是电流,互易定理有三种形式: 4.5.1 互易定理的第一种形式图4-14(a )所示电路N 在方框内部仅含线性电阻,不含任何独立电源和受控源。
接在端子11'-的支路1为电压源S u ,接在端子22'-的支路2为短路,其中的电流为2i ,它是电路中唯一的激励(即S u )产生的响应。
如果把激励和响应位置互换,如图4-14(b )中的Nˆ,此时接于22'-的支路2为电压源S u ˆ,而响应则是接于'11-支路1中的短路电流1ˆi 。
假设把图(a )和(b )中的电压源置零,则除N 和Nˆ的内部完全相同外,接于11'-和22'-的两个支路均为短路;就是说,在激励和响应互换位置的前后,如果把电压源置零,则电路保持不变。
S uS u ˆ+-(a )N (b )Nˆ 图4-14 互易定理的第一种形式对于图4-14(a )和(b )应用特勒根定理,有∑==++bk k k i u i u i u 322110ˆˆˆ∑==++bk k k i u i u i u322110ˆˆˆ 式中取和号遍及方框内所有支路,并规定所有支路中电流和电压都取关联参考方向。
由于方框内部仅为线性电阻,故k k k i R u =、k k k i R u ˆˆ=(b k 、、 3=),将它们分别代入上式后有:∑==++bk k k k i i R i u i u 322110ˆˆˆ∑==++bk k k k i i R i u i u322110ˆˆˆ 故有22112211ˆˆˆˆi u i u iu i u +=+ (4-12)对图4-14(a ),S u u =1,02=u ;对图(b ),0ˆ1=u,S u u ˆˆ2=,代入上式得 21ˆˆi ui u S S = 即S S ui u i ˆˆ12=如果21ˆˆi ui u S S =,则12ˆi i =。
人教版物理九年级全册《串、并联电路中电流的规律》

A.0.1A C.0.3A
B.0.2A D.0.4A
典型例题
(2019兰州市)将两只不同规格的灯泡L1、L2接在如图所示的电路中,闭合开关
S1、S2后,下列说法中正确的是( ) D
A.电流表测量干路电流
B.L1与L2的亮度一定相同 C.通过L,和L,的电流一定相等
D.只断开S2,L1发光且亮度不变
B点电流IB/A 0.32 0.38 0.42
5.得出结论:串联电路中各处电流都相等
IC=IA=IB
C点电流IC/A 0.32 0.38 0.42
理解与运用
如图所示,小阳用电流表探究串联电路中的电流关系,他分别用电流表测电路
0.2 A 中A、B、C三处的电流,得知IA=0.2 A,则IB=___0_._2__A,IC=_______。
课堂活动
3.进行测量,将测量数据记录在表格中; 实验数据
次数 1 2 3
A点电流IA/A
B点电流IB/A
C点电流IC/A
问题:实验中为什么要换用不同的灯泡,多次测量? 换用不同的灯泡,是为了避免 特殊性;而多次测量是为了避免 偶然,性结论才具有
普遍。性
课堂活动
4.分析实验数据
次数 1 2 3
A点电流IA/A 0.32 0.38 0.42
实验探究
3.进行测量,将测量数据记录在表格中 实验数据
次数 1 2 3
A点电流IA/A
B点电流IB/A
C点电流IC/A
3次测量中,可以选择1次实验用规格一样的灯泡,其余2次用规格不一样的灯泡。
实验探究
4.分析实验数据
次数 1 2 3
A点电流IA 0.2 0.28 0.4
B点电流IB 0.2 0.32 0.3
3-4 互易定理

3.4 互易定理1. 互易定理的内容互易定理:对于一个线性电阻网络而言,如果只有一个激励和一个响应,那么当激励与响应互换位置后,激励与响应的比值保持不变。
这里的激励指电压源或电流源,响应指电压或电流。
互易定理的示意图如图1所示。
u 1i 2u 2i 1212u u i i =图1 互易定理示意图根据互易定理和图1,1212(u u i i =激励)(互换位置后的激励)(响应)(互换位置后的响应) (1)由式(1)可以看出,如果激励(电压源电压)相同,则互换位置后的响应(电流)也相同。
这是互易定理的一种特殊情况。
由互易定理的内容可以看出,互易定理是很难自己想象出来的。
由于互易定理很难想象,要证明互易定理自然也是一件非常困难的事情。
不过,为了令人信服,下面我们来证明一下互易定理。
2. 互易定理的证明在证明互易定理之前,需要先证明两个定理和一个定理推论,即特勒根定理1、特勒根定理2和特勒根定理2推论。
特勒根定理1的内容是,任意一个电路,如果每一条支路的电流参考方向都是从电压参考方向的正极流入,则所有支路的电压电流乘积加起来一定等于零。
电压电流乘积就是功率,可见特勒根定理1的物理含义就是任何一个电路总的功率为零,也就是发出功率等于吸收功率,即功率守恒。
下面我们来证明特勒根定理1。
假设任意一个电路总计有b 条支路,n 个结点,第p 、q 个结点之间的电压记为pq u ,电流记为pq i ,则1111111111111()02222bn n n n n n nnk kpq pq p q pq p pq q pq k p q p q p q q p u i u i u u i u i u i ===========−=−=∑∑∑∑∑∑∑∑∑ (2)由式(2)即证明了特勒根定理1。
式(2)乍一看很难理解,下面对其中的细节进行解释。
式(2)中第一个等号是将支路电压电流乘积之和转化为结点与结点之间电压与电流乘积之和。
第9讲 特勒根定理和互易定理
电压源
开路
KCL
14
对偶电路
is2
( R1 R2 )i1 R2 i2 us1
R2i1 + ( R3 R2 )i2 us2
(G1 G2 )u1 G2u2 is1
G2u1 + (G2 G3 )u2 -i s2
比较这两组方程, 可看出, 它们的形式相同, 对应变量 为对偶元素, 所以通常把这两组方程称为对偶方程组。电路
u1i1 u2i2 u3i3 u4i4 u5i5 u6i6 u7i7 (u1 u2 u3 )i2 (u4 u5 u7 )i4 u6i6 u6 (i2 i4 i6 ) 0
+ u3 _
i2 i4 i6 0
KVL和KCL可知:
u
k 1
b
k k
i 0
u
k 1
b
k k
i 0
具有功率的量纲, 但不表示任何支路的功 率,称为拟功率。 率,称为拟功率 特勒根定理一是当特勒根定理二中电路N与
3 ^ 为同一电路的特例。 N
证明: 选节点d为参 考节点, 对 独立节点a 、b、 c列出电路的 KCL方程为
i i i 0 1 3 4
中把像这样一个电路的节点方程与另一个电路的网孔方程对
偶的两电路称为对偶电路。
15
第9讲 特勒根定理、互易定理、电路的对偶性
结
束
作业:P123 2-28、2-30 自行学习:P104~117----2.10和2.11 复习:第1 、2章
16
k 1
支路吸收的功率
特勒根定理一:
是功率守恒的具体体现
1
电路的互易定理

电路的互易定理
什幺是互易定理
在只含一个电压源(或电流源),不含受控源的线性电阻电路中,电压源(或电流源)与电流表(电压表)互换位置,电流表(电压表)读数不变。
这种性质称为互易定理。
在电磁学上,互易定理为洛仑兹互易定理(Lorentz Reciprocity Theorem),由卡森(J.R. Carson)导出而被称为卡森形式的互易定理。
互易定理即论述某些网络具有的互易性质的定理。
互易性质表现为:将网络的输入和特定输出互换位置后,输出不因这种换位而有所改变。
具有互易性质的网络称为互易网络。
互易性不仅一些电网络有,某些声学系统、力学系统等也有。
互易定理是一个较有普遍意义的定理。
互易定理的性质
从图中可以得出结论,图(a)的电压u2=R21/S与图(b)的电压
u1=R12/S相同。
也就是说,在互易网络中电流源与电压表互换位置,电压表读数不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N
uβ
iβ
uˆα
N
uˆβ
uSβ
iα
α'
β'
α'
β'
若uSβ的值 iSα的值,则uˆα的值 iβ的值
§3.4 互易定理
证明方法同定理1
α
β
α
β
iSα
uα
N
uβ
iβ
uˆα
N
uˆβ
uSβ
iα
α'
β'
α'
β'
根据特勒根定理有
uαiˆα uβiˆβ uˆαiα uˆβiβ iα iSα,uβ 0,iˆα 0,uˆβ uSβ
α'
电流源变换位置后电路结构改变(接入15的电阻),故不能直接用互易定 理。
由已知,N0的等效电阻Req=5;由互易定理,’的开路电压uOC=5V。用 戴维宁定理求得i=0.25A。
§3.4 互易定理
证明方法同定理1
α
β
α
β
iSα
uα
N
uβ
uˆα
N
uˆβ
iSβ
iα
α'
β'
α'
根据特勒根定理有
β'
iˆβ
uαiˆα uβiˆβ uˆαiα uˆβiβ iα iSα,iβ 0,iˆα 0,iˆβ iˆSβ
uβiSβ uˆαiSα
应用互易定理时,不仅有量的大小问题,而且还有方向问题。一般电源 的移动方法为:平移法和旋转法。
互易定理用于解平衡电桥电路和对称电路较方便。
互易性与无源性是互不相干的,回转器是无源器件,但不能互易。
§3.4 互易定理
例 求图示电路中的电流I。
解 所示为复杂电路,用互易定理可化简成 串并联方法求解的简单电路。
b
uˆαiα uˆβiβ uˆkik 0 k 1
由于电路N由线性非时变电阻组成,所以 uk Rkik,uˆk Rkiˆk
b
则有
uαiˆα
u1
b
uˆαiα uˆβiβ Rkiˆkik 0 k 1
α
β
uSα
uα
N
iS
R1 u1 gmu1 R u2
u2≠0
u1=0
iS R1 u1 gmu1 R
iS
u2 u2≠0 u1=0
u1
iS
§3.4 互易定理
互易定理在应用时要注意,前两种形式中,当激励是 电压,响应为电流;当激励是电流,响应就是电压; 第3 种形式,一边激励、响应都是电流,另一边激励、 响应都是电压。从总体上说,不能全是电流或全是电 压。(注意,互易定理中各次观测的响应均为零状态响 应)
从外界送入回转器的功率为
u1i1 u2i2 i2i1 i1i2 0
这说明回转器是既不发出功率,又不消耗功率的元件。所以,回转器是 无源元件。
1A
i1 i2
i1 i2
1A
u2 u2= u1= - u1
这说明,互易定理不适用回转器。所以说,互异性与无源性是没有关联关 系的,即不相干的。
互易定理2 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮’和’,若在端口’施加输入电流, 在端口’可得输出电压,如图所示。反之,对’施加 输入电压,可在’得到输出电流,如图所示。
α
β
α
β
iSα
uα
N
uβ
uˆα
N
uˆβ
iSβ
iα
a'
β'
α'
β'
iˆβ
若 iSβ iSα,则 uˆα uβ
I1=2A,I2=4/3A,I3=2/3A KCL:I=I2-I3=2/3A
此例也说明,同电位不等于无电流。
4
+ 8V
2 2
1
2 I
I2 I1
4
2
I
2
I3
1
2
8V
§3.4 互易定理
例
i1 i2
u1
u2
u1 u2
0
i1
0
i2
电路基础
第三章 电路定理
上海交通大学本科学位课程
§3.4 互易定理
互易定理1 对内部不含独立源和受控源的线性电阻电路
N,任取两对端钮’和’,如果在端口’施加输入 电压,在端口’可得到输出电流,如图所示。反之,对 ’施加输入电压,可在’得到输出电流,如图所示。
α
β
α
β
usα
uα
因此,当iSβ iSα时,uˆα uβ
§3.4 互易定理
互易定理3 对内部不含独立源和受控源的线性电阻电路N, 任取两对端钮’和’,若在端口’施加输入电流,在 端口’可得输出电流,如图所示。反之,对’施加输 入电压,可在’得到输出电压,如图所示。
α
β
α
β
iSα
uα
0 uˆαiSa uSβiβ
uˆαiSα uSβiβ
因此,当uSβ的值 iSα的值时,uˆα的值 iβ的值
§3.4 互易定理
互易定理的适用范围是比较窄的,它只适用于无源线性非时 变电路。如果电路中有独立源或受控源,非线性元件,时变 元件等,该电路就不能运用互易定理。这是因为线性非时变 电路保证了电路的电阻矩阵和电导矩阵具有对称性,才使互 易性得以成立。
uβ
iβ
uαiˆα uβiˆβ uˆαiα uˆβiβ
α'
β'
uα uSα,uβ 0,uˆα 0,uˆβ uSβ
α
β
iˆα
uˆα
N
uˆβ
uSβiβ uSαiˆα
uSβ
因此,当uSβ uSα时,iˆα iβ
α'
β'
§3.4 互易定理
N
uβ
iβ
iˆα
uˆα
N
uˆβ
usβ
α'
β'
α'
β'
若usβ usα,则iˆα iβ
§3.4 互易定理
证明:设电路中有b条支路,连接’和’的支路电压和电流分别
为
uα,iα,uβ,iβ, uˆα,iˆα, uˆβ,iˆβ
根据特勒根定理
b
uαiˆα uβiˆβ ukiˆk 0 k 1
§3.4 互易定理
例 一线性无源电阻电路N0,引出两对端钮测量。当输 入2A电流时,输入端电压为10V,输出端电压为5V; 若把电流源接在输出端,同时在输入端跨接一个15
的电阻,求流过15电阻的电流。
α
β
α
β
2A
10V N0
5V 5V N0
2A
α'
β' α'
β'
αi
5 u 5V 15
