解析几何专题一轨迹问题.
解析几何求轨迹方程

例1:设圆()11:22=+-y x C ,过原点O 作圆的任意弦,求所作弦的中点的轨迹方程.变式1:已知C B A ,,是直线l 上的三点,切6==BC AB ,圆Q 切直线l 于点A ,又过C B ,作圆Q 异于直线l 的两切线,设这两切线交于点P ,求点P 的轨迹方程.变式2:设动直线l 垂直于x 轴,且与椭圆4222=+y x 交于B A ,两点,P 是直线l 上满足1=⋅PB PA 的点,求点P 的轨迹方程.变式3:ABC ∆的顶点A 固定,点A 的对边BC 的长是a 2,边BC 上的高为b ,边BC 沿一条定直线移动,求ABC ∆外心的轨迹方程.例2:自抛物线x y 22=上任意一点P 向其准线l 引垂线,垂足为Q ,连接顶点O 与P 的直线和连接焦点F 与Q 的直线交于R 点,求R 点的轨迹方程.变式4:已知抛物线x y C 4:2=的焦点为F .(1)点P A ,满足2-=.当点A 在抛物线C 上运动时,求点P 的轨迹方程.(2)在x 轴上是否存在点Q 关于直线x y 2=的对称点在抛物线C 上?如果存在,求所有满足条件的点Q 的坐标;如果不存在,请说明理由.例3:过点()0,2-M 作直线l 交双曲线122=-y x 于B A ,两点,已知OB OA OP +=.求点P 的轨迹方程,并说明轨迹是什么曲线.变式5:设椭圆方程为1422=+y x ,过点()1,0M 的直线l 交椭圆于点B A ,,O 是坐标原点,l 上的动点P 满足()OB OA OP +=21,当l 绕点M 旋转时,求动点P 的轨迹方程.例4:已知抛物线的方程为()022>=p py x ,过点()p P ,0的直线l 与抛物线相交于B A ,两点,分别过点B A ,作抛物线的两条切线21,l l ,记21,l l 交于点M .(1)证明:直线21,l l 的斜率之积为定值;(2)求点M 的轨迹方程.变式6:已知抛物线x y C 4:2=的焦点为F ,过点()0,1-K 的直线l 与C 相交于B A ,两点,点A 关于x 轴的对称点为D .证明:点F 在直线BD 上.。
解析几何求圆的轨迹方程专题一师用

专题一求圆的轨迹方程教学目标:1、掌握直线与圆的标准方程与一般方程,能根据问题的条件选择适当的形式求圆的方程;2、掌握直线与圆的位置关系,可以应用直线与圆的位置关系求圆的方程3、理解圆的标准方程与一般方程之间的关系,会进行互化。
教学重难点:1、掌握圆的标准方程与一般方程,能根据问题的条件选择适当的形式求圆的方程;2、会求曲线的轨迹方程(圆)教学过程:第一部分知识点回顾一、圆的方程 :1 .圆的标准方程:x a? y b2 r2o2 •圆的一般方程:x2 y2 Dx Ey F 0(D2+ E2—4F 0)特别提醒:只有当D2+ E2—4F 0时,方程x2 y2 Dx Ey F 0才表示圆心为(D, E),半径为1~E2~4F的圆2 2 2思考:二元二次方程Ax2 Bxy Cy2 Dx Ey F 0表示圆的充要条件是什么?答案:(A C 0,且 B 0 且D2 E2 4AF 0 ));3 .圆的参数方程:y a r s°s(为参数),其中圆心为(a,b),半径为r 。
圆的参数方程的主要应用是三角换元:(3) 已知P( 1, -3)是圆y ;;煮(为参数,02 )上的点,则圆的普通方程为,P 点对应的 值为,过P 点的圆的切线方程是(答:x 2 y 2=4 ; — ; x ,3y 4 0);3(4) 如果直线l 将圆:x 22-240平分,且不过第四象限,那么I 的斜率 的取值范围是_(答: [0 , 2]);(5) 方程x 22- 0表示一个圆,则实数k 的取值范围为(答:k 丄); (6) 若 M {(x, y) | y 3sos (为参数,0)}, N (x, y) | y x b ,若MN ,则b 的取值范围是(答:-33& )二、点与圆的位置关系:已知点M x 0,y 0及圆C: x-a $ y b ? r 2 r 0 ,(1) 点 M 在圆 C 外 |CM | r x 0 a 2 y 。
立体几何中的轨迹问题(总结+讲义+练习)
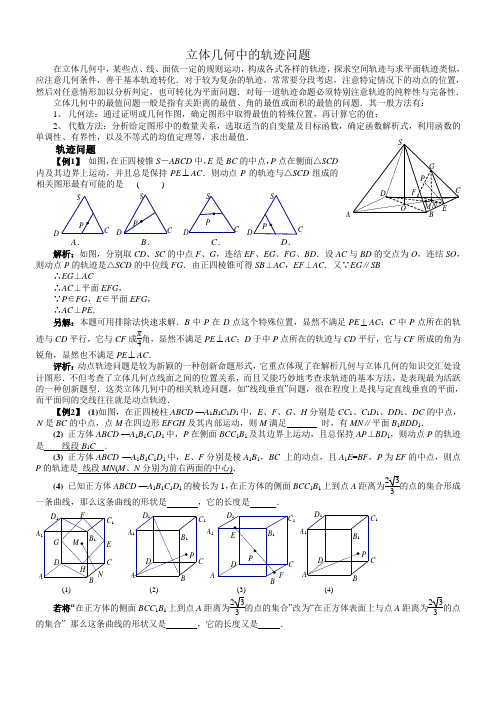
立体几何中的轨迹问题在立体几何中,某些点、线、面依一定的规则运动,构成各式各样的轨迹,探求空间轨迹与求平面轨迹类似,应注意几何条件,善于基本轨迹转化.对于较为复杂的轨迹,常常要分段考虑,注意特定情况下的动点的位置,然后对任意情形加以分析判定,也可转化为平面问题.对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性.立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题.其一般方法有: 1、 几何法:通过证明或几何作图,确定图形中取得最值的特殊位置,再计算它的值;2、 代数方法:分析给定图形中的数量关系,选取适当的自变量及目标函数,确定函数解析式,利用函数的单调性、有界性,以及不等式的均值定理等,求出最值.轨迹问题【例1】 如图,在正四棱锥S -ABCD 中,E 是BC 的中点,P 点在侧面△SCD 内及其边界上运动,并且总是保持PE ⊥AC .则动点P 的轨迹与△SCD 组成的相关图形最有可能的是 ( )解析:如图,分别取CD 、SC 的中点F 、G ,连结EF 、EG 、FG 、BD .设AC 与BD 的交点为O ,连结SO ,则动点P 的轨迹是△SCD 的中位线FG .由正四棱锥可得SB ⊥AC ,EF ⊥AC .又∵EG ∥SB∴EG ⊥AC∴AC ⊥平面EFG ,∵P ∈FG ,E ∈平面EFG , ∴AC ⊥PE .另解:本题可用排除法快速求解.B 中P 在D 点这个特殊位置,显然不满足PE ⊥AC ;C 中P 点所在的轨迹与CD 平行,它与CF 成π4角,显然不满足PE ⊥AC ;D 于中P 点所在的轨迹与CD 平行,它与CF 所成的角为锐角,显然也不满足PE ⊥AC .评析:动点轨迹问题是较为新颖的一种创新命题形式,它重点体现了在解析几何与立体几何的知识交汇处设计图形.不但考查了立体几何点线面之间的位置关系,而且又能巧妙地考查求轨迹的基本方法,是表现最为活跃的一种创新题型.这类立体几何中的相关轨迹问题,如“线线垂直”问题,很在程度上是找与定直线垂直的平面,而平面间的交线往往就是动点轨迹.【例2】 (1)如图,在正四棱柱ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 分别是CC 1、C 1D 1、DD 1、DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 满足 时,有MN ∥平面B 1BDD 1.(2) 正方体ABCD —A 1B 1C 1D 1中,P 在侧面BCC 1B 1及其边界上运动,且总保持AP ⊥BD 1,则动点P 的轨迹是 线段B 1C .(3) 正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是棱A 1B 1,BC 上的动点,且A 1E =BF ,P 为EF 的中点,则点P 的轨迹是 线段MN (M 、N 分别为前右两面的中心).(4) 已知正方体ABCD —A 1B 1C 1D 1的棱长为1,在正方体的侧面BCC 1B 1上到点A 距离为233的点的集合形成一条曲线,那么这条曲线的形状是 ,它的长度是 .若将“在正方体的侧面BCC 1B 1上到点A 距离为23 3 的点的集合”改为“在正方体表面上与点A 距离为233的点的集合” 那么这条曲线的形状又是 ,它的长度又是 .1AC C 1AEC C 1A AB1A 1(1)(2)(3)(4)DDA .B .C .D . A【例3】 (1)(04北京)在正方体ABCD -A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是 ( D )A . A 直线B .圆C .双曲线D .抛物线 变式:若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1:2(或2:1)”, 则动点P 的轨迹所在的曲线是 椭圆 (双曲线). (2)(06北京)平面α的斜线AB 交α于点B ,过定点A 的动直线l 与AB 垂直,且交α于点C ,则动点C 的轨迹是 (A )A .一条直线B .一个圆C .一个椭圆D .双曲线的一支解:设l 与l 是其中的两条任意的直线,则这两条直线确定一个平面,且斜线AB 垂直这个平面,由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内,故动点C 都在这个平面与平面α的交线上,故选A . (3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1,M 在棱AB 上,且AM =13,点P 到直线A 1D 1的距离与点P 到点M 的距离的平方差为1,则点P 的轨迹为 抛物线 .(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3,长为2的线段MN 点一个端点M 在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 π6. 【例4】 (04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与△ABC 组成图形可能是:( D )【例5】 四棱锥P -ABCD ,AD ⊥面P AB ,BC ⊥面P AB ,底面ABCD 为梯形,AD =4,BC =8,AB =6,∠APD =∠CPB ,满足上述条件的四棱锥的顶点P 的轨迹是( )A .圆B .不完整的圆C .抛物线D .抛物线的一部分 分析:∵AD ⊥面P AB ,BC ⊥平面P AB ∴AD ∥BC 且AD ⊥P A ,CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴AD P A =CB PB ∴PB =2P A在平面APB 内,以AB 的中点为原点,AB 所在直线为x 轴建立平面直角坐标系,则A (-3,0)、B (3,0),设P (x ,y )(y ≠0),则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0) ∴P 的轨迹是(B )BABCDA3P A BC D立体几何中的轨迹问题(教师版)1.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等,则动点P 所在曲线的形状为(D ).A .线段B .一段椭圆弧C .双曲线的一部分D .抛物线的一部分 简析 本题主要考查点到直线距离的概念,线面垂直及抛物线的定义.因为B 1C 1⊥面AB 1,所以PB 1就是P 到直线B 1C 1的距离,故由抛物线的定义知:动点的轨迹为抛物线的一段,从而选D .2.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2:1,则动点P 所在曲线的形状为(B ).A .线段B .一段椭圆弧C .双曲线的一部分D .抛物线的一部分3.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1:2,则动点P 所在曲线的形状为(C ).A .线段B .一段椭圆弧C .双曲线的一部分D .抛物线的一部分4.在正方体ABCD-A 1B 1C 1D 1中,E 为AA 1的中点,点P 在其对角面BB 1D 1D 内运动,若EP 总与直线AC 成等角,则点P 的轨迹有可能是(A ).A .圆或圆的一部分B .抛物线或其一部分C .双曲线或其一部分D .椭圆或其一部分 简析 由条件易知:AC 是平面BB 1D 1D 的法向量,所以EP 与直线AC 成等角,得到EP 与平面BB 1D 1D 所成的角都相等,故点P 的轨迹有可能是圆或圆的一部分.5.已知正方体ABCD A B C D -1111的棱长为a ,定点M 在棱AB 上(但不在端点A ,B 上),点P 是平面ABCD 内的动点,且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2,则点P 的轨迹所在曲线为(A ). A .抛物线B .双曲线C .直线D .圆简析在正方体ABCD A B C D -1111中,过P 作PF ⊥AD ,过F 作FE ⊥A 1D 1,垂足分别为F 、E ,连结PE .则PE 2=a 2+PF 2,又PE 2-PM 2=a 2,所以PM 2=PF 2,从而PM =PF ,故点P 到直线AD 与到点M 的距离相等,故点P 的轨迹是以M 为焦点,AD 为准线的抛物线.6.在正方体ABCD A B C D -1111中,点P 在侧面BCC 1B 1及其边界上运动,总有AP ⊥BD 1,则动点P 的轨迹为__________. 简析 在解题中,我们要找到运动变化中的不变因素,通常将动点聚焦到某一个平面.易证BD 1⊥面ACB 1,所以满足BD 1⊥AP 的所有点P 都在一个平面ACB 1上.而已知条件中的点P 是在侧面BCC 1B 1及其边界上运动,因此,符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上,故所求的轨迹为线段B 1C .本题的解题基本思路是:利用升维,化“动”为“静”,即先找出所有点的轨迹,然后缩小到符合条件的点的轨迹.7.在正四棱锥S-ABCD 中,E 是BC 的中点,点P 在侧面∆SCD 内及其边界上运动,总有PE ⊥AC ,则动点P 的轨迹为_______________.答案 线段MN (M 、N 分别为SC 、CD 的中点)8.若A 、B 为平面α的两个定点,点P 在α外,PB ⊥α,动点C (不同于A 、B )在α内,且PC ⊥AC ,则动点C 在平面内的轨迹是________.(除去两点的圆) 9.若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与∆ABC 组成的图形可能是:(D )A A AP PP PB C B C B C B C A B C D简析 动点P 在侧面ABC 内,若点P 到AB 的距离等于到棱BC 的距离,则点P 在∠ABC 的内角平分线上.现在P 到平面BCD 的距离等于到棱AB 的距离,而P 到棱BC 的距离大于P 到底面BCD 的距离,于是,P 到棱AB 的距离小于P 到棱BC 的距离,故动点P 只能在∠ABC 的内角平分线与AB 之间的区域内.只能选D . 10.已知P 是正四面体S-ABC 的面SBC 上一点,P 到面ABC 的距离与到点S 的距离相等,则动点P 的轨迹所在的曲线是(B ). A .圆 B .椭圆 C .双曲线 D .抛物线解题的要领就是化空间问题为平面问题,把一些重要元素集中在某一个平面内,利 用相关的知识去解答,象平面几何知识、解析几何知识等.11.已知正方体ABCD A B C D -1111的棱长为1,在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线,那么这条曲线的形状是_________,它的长度为__________. 简析以B 为圆心,半径为33且圆心角为π2的圆弧,长度为36π. 12.已知长方体ABCD A B C D -1111中,AB BC ==63,,在线段BD 、A C 11上各有一点P 、Q ,PQ 上有一点M ,且PM MQ =2,则M 点轨迹图形的面积是 . 提示轨迹的图形是一个平行四边形.13.已知棱长为3的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点在DD 1上运动,另一个端点N 在底面ABCD 上运动,求MN 中点P 的轨迹与正方体的面所围成的几何体的体积.简析 由于M 、N 都是运动的,所以求的轨迹必须化“动”为“静”,结合动点P 的几何性质,连结DP ,因为MN=2,所以PD=1,因此点P 的轨迹是一个以D 为球心,1为半径的球面在正方体内的部分,所以点P 的轨迹与正方体的表面所围成的几何体的体积为球的体积的18,即1843163⨯⨯=ππ. 14.已知平面//α平面β,直线l α⊂,点l P ∈,平面α、β间的距离为4,则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是( ) 简析:如图,设点P 在平面β内的射影是O ,则OP 是α、β的公垂线,OP=4.在β内到点P 的距离等于5的点到O 的距离等于3,可知所求点的轨迹是β内在以O 为圆心,3为半径的圆上.又在β内到直线l 的距离等于29的点的集合是两条平行直线m 、n ,它们到点O 的距离都等于32174)29(22<=-,所以直线m 、n 与这个圆均相交,共有四个交点.因此所求点的轨迹是四个点,故选C .16.在四棱锥ABCD P -中,⊥AD 面PAB ,⊥BC 面PAB ,底面ABCD 为梯形,AD=4,BC=8,AB=6,CPB APD ∠=∠,满足上述条件的四棱锥的顶点P 的轨迹是( )A .圆B .不完整的圆C .抛物线D .抛物线的一部分简析:因为⊥AD 面PAB ,⊥BC 面PAB ,所以AD//BC ,且︒=∠=∠90CBP DAP . 又8BC ,4AD ,CPB APD ==∠=∠,可得CPB tan PB CB PA AD APD tan ∠===∠,即得2ADCBPA PB == 在平面PAB 内,以AB 所在直线为x 轴,AB 中点O 为坐标原点,建立平面直角坐标系,则A (-3,0)、B(3,0).设点P (x ,y ),则有2y )3x (y )3x (|PA ||PB |2222=+++-=,整理得09x 10y x 22=+++由于点P 不在直线AB 上,故此轨迹为一个不完整的圆,选B .17.如图,定点A 和B 都在平面α内,定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点.且AC PC ⊥,那么动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点简析:因为PC AC ⊥,且PC 在α内的射影为BC ,所以BC AC ⊥,即︒=∠90ACB .所以点C 的轨迹是以AB 为直径的圆且去掉A 、B 两点,故选B .18.如图,在正方体1111D C B A ABCD -中,P 是侧面1BC 内一动点,若P 到直线BC 与直线11D C 的距离相等,则动点P 的轨迹所在的曲线是( )A .直线B .圆C .双曲线D .抛物线简析:因为P 到11D C 的距离即为P 到1C 的距离,所以在面1BC 内,P 到定点1C 的距离与P 到定直线BC 的距离相等.由圆锥曲线的定义知动点P 的轨迹为抛物线,故选D .19.已知正方体1111D C B A ABCD -的棱长为1,点P 是平面AC 内的动点,若点P 到直线11D A 的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是( )A .抛物线B .双曲线C .椭圆D .直线简析:如图4,以A 为原点,AB 为x 轴、AD 为y 轴,建立平面直角坐标系.设P (x ,y ),作AD PE ⊥于E 、11D A PF ⊥于F ,连结EF ,易知1x |EF ||PE ||PF |2222+=+=又作CD PN ⊥于N ,则|1y ||PN |-=.依题意|PN ||PF |=, 即|1y |1x 2-=+,化简得0y 2y x 22=+- 故动点P 的轨迹为双曲线,选B .20.如图,AB是平面a的斜线段,A为斜足,若点P在平面a内运动,使得△ABP的面积为定值,则动点P的轨迹是()(A)圆(B)椭圆(C)一条直线(D)两条平行直线分析:由于线段AB是定长线段,而△ABP的面积为定值,所以动点P到线段AB 的距离也是定值.由此可知空间点P在以AB为轴的圆柱侧面上.又P在平面内运动,所以这个问题相当于一个平面去斜切一个圆柱(AB是平面的斜线段),得到的切痕是椭圆.P的轨迹就是圆柱侧面与平面a的交线.21.如图,动点P在正方体1111ABCD A B C D-的对角线1BD上.过点P作垂直于平面11BB D D的直线,与正方体表面相交于M N,.设BP x=,MN y=,则函数()y f x=的图象大致是()分析:将线段MN投影到平面ABCD内,易得y为x一次函数.22.已知异面直线a,b成︒60角,公垂线段MN的长等于2,线段AB两个端点A、B分别在a,b上移动,且线段AB长等于4,求线段AB中点的轨迹方程.图5简析:如图5,易知线段AB的中点P在公垂线段MN的中垂面α上,直线'a、'b为平面α内过MN的中点O分别平行于a、b的直线,'a'AA⊥于'A,'b'BB⊥于'B,则P'B'AAB=⋂,且P也为'B'A的中点.由已知MN=2,AB=4,易知,2AP,1'AA==得32'B'A=.则问题转化为求长等于32的线段'B'A的两个端点'A、'B分别在'a、'b上移动时其中点P的轨迹.现以'OB'A∠的角平分线为x轴,O为原点建立如图6所示的平面直角坐标系.A BCDMNPA1 B1C1D1yxOyxOyxOyxO图6设)y ,x (P ,n |'OB |,m |'OA |==, 则)n 21,n 23('B ),m 21,m 23('A - )n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++- 消去m 、n ,得线段AB 的中点P 的轨迹为椭圆,其方程为1y 9x 22=+.点评:例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起,相互交汇和渗透,有利于培养运用多学科知识解决问题的能力.立体几何中的轨迹问题1.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分2.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2:1,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分3.在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1:2,则动点P 所在曲线的形状为 ( ) A .线段 B .一段椭圆弧 C .双曲线的一部分 D .抛物线的一部分4.在正方体ABCD-A 1B 1C 1D 1中,E 为AA 1的中点,点P 在其对角面BB 1D 1D 内运动,若EP 总与直线AC 成等角,则点P 的轨迹有可能是 ( ) A .圆或圆的一部分 B .抛物线或其一部分 C .双曲线或其一部分 D .椭圆或其一部分 5.已知正方体ABCD A B C D -1111的棱长为a ,定点M 在棱AB 上(但不在端点A ,B 上),点P 是平面ABCD 内的动点,且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2,则点P 的轨迹所在曲线为( ) A .抛物线B .双曲线C .直线D .圆6.若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与∆ABC 组成的图形可能是 ( ) A A AP PP PB C B C B C B CA B C DA B C D 7.已知P 是正四面体S-ABC 的面SBC 上一点,P 到面ABC 的距离与到点S 的距离相等,则动点P 的轨迹所在的曲线是 ( )A .圆B .椭圆C .双曲线D .抛物线8.已知平面//α平面β,直线l α⊂,点l P ∈,平面α、β间的距离为4,则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是( )A .一个圆B .两条平行直线C .四个点D .两个点9.在四棱锥ABCD P -中,⊥AD 面PAB ,⊥BC 面PAB ,底面ABCD 为梯形,AD=4,BC=8,AB=6,CPB APD ∠=∠,满足上述条件的四棱锥的顶点P 的轨迹是( ) A .圆 B .不完整的圆 C .抛物线 D .抛物线的一部分 10.如图,定点A 和B 都在平面α内,定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点.且AC PC ⊥,那么动点C 在平面α内的轨迹是( )A .一条线段,但要去掉两个点B .一个圆,但要去掉两个点C .一个椭圆,但要去掉两个点D .半圆,但要去掉两个点11.已知正方体1111D C B A ABCD -的棱长为1,点P 是平面AC 内的动点,若点P 到直线11D A 的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是( )A .抛物线B .双曲线C .椭圆D .直线12.如图,AB 是平面a 的斜线段,A 为斜足,若点P 在平面a 内运动,使得△ABP 的面积为定值,则动点P 的轨迹是( )A .圆B .椭圆C .一条直线D .两条平行直线 13.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上.过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设BP x =,MN y =,则函数()y f x =的图象大致是( )14.在正方体ABCD A B C D -1111中,点P 在侧面BCC 1B 1及其边界上运动,总有AP ⊥BD 1,则动点P 的轨迹为________.15.在正四棱锥S-ABCD 中,E 是BC 的中点,点P 在侧面∆SCD 内及其边界上运动,总有PE ⊥AC ,则动点P 的轨迹为_______________.16.若A 、B 为平面α的两个定点,点P 在α外,PB ⊥α,动点C (不同于A 、B )在α内,且PC ⊥AC ,则动点C 在平面内的轨迹是________.17.已知正方体ABCD A B C D -1111的棱长为1,在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线,那么这条曲线的形状是_________,它的长度为__________.18.已知长方体ABCD A B C D -1111中,AB BC ==63,,在线段BD 、A C 11上各有一点P 、Q ,PQ 上有一点M ,且PM MQ =2,则M 点轨迹图形的面积是 .19.已知棱长为3的正方体ABCD A B C D -1111中,长为2的线段MN 的一个端点在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是 .20.已知异面直线a ,b 成︒60角,公垂线段MN 的长等于2,线段AB 两个端点A 、B 分别在a ,b 上移动,且线段AB 长等于4,求线段AB 中点的轨迹方程.ABC D MNP A 1B 1C 1D 1 yxOyxOyxOyx O。
解析几何中的曲线的运动与轨迹

解析几何中的曲线的运动与轨迹在解析几何中,曲线的运动和轨迹是一个重要的概念。
曲线的运动指的是曲线上的点在一定的条件下随时间变化的过程,而轨迹则是曲线上所有点组成的总体路径。
本文将通过对曲线的运动和轨迹的详细解析,帮助读者更好地理解这一概念。
一、曲线的运动曲线的运动是指曲线上的点在时间变化下的位置变化。
在解析几何中,曲线的运动通常与各种参数有关。
具体而言,我们可以通过改变参数的数值,来观察曲线上的点是如何随着时间变化而发生位移的。
例如,我们考虑平面直角坐标系中的抛物线y = ax^2。
其中a是一个实数,表示抛物线的开口方向和大小。
在这个例子中,曲线的运动是由参数a决定的。
当a的取值为正时,抛物线的开口向上;当a的取值为负时,抛物线的开口向下。
此外,曲线的运动还可以通过其他参数来改变,比如平移、旋转和缩放等。
通过这些参数的调整,我们可以观察到曲线上的点如何在平面中发生位置的变化。
二、曲线的轨迹曲线的轨迹是指曲线上所有点的总体路径。
当曲线上的点随时间变化而发生位移时,它们形成的路径就是曲线的轨迹。
通过对曲线的运动进行分析,我们可以确定曲线的轨迹的一些特性。
例如,考虑直线y = kx + b,其中k和b都是实数。
当k为0时,直线变成了水平线,其轨迹是一条与x轴平行的直线。
当k为正数时,直线的斜率为正,轨迹是一条从左下方向右上方倾斜的直线。
当k为负数时,直线的斜率为负,轨迹是一条从左上方向右下方倾斜的直线。
除了直线,其他曲线的轨迹也可以通过对曲线的运动进行观察和分析来确定。
通过观察曲线上的点随时间变化而发生的位移,我们可以得到曲线的轨迹的一些性质,比如形状、方向和大小等。
三、实例分析为了更好地理解曲线的运动和轨迹,我们来看一个具体的例子:圆的运动与轨迹。
考虑平面直角坐标系中的一个单位圆x^2 + y^2 = 1。
我们可以通过改变圆心的坐标来观察圆的运动和轨迹。
当圆心的坐标为(0,0)时,圆的轨迹是一个以原点为中心的单位圆。
解析几何中的轨迹问题

解析几何中的轨迹问题求轨迹方程的一般方法:1、待定系数法(定义法):如果动点P 的运动规律合乎我们已知的某种曲线(如圆、椭圆、双曲线、抛物线、圆、直线)的定义,则可先设出轨迹方程,再根据已知条件,待定方程中的常数,即可得到轨迹方程,也有人将此方法称为定义法。
2、直译法:如果动点P 的运动规律是否合乎我们熟知的某些曲线的定义难以判断,但点P 满足的等量关系易于建立,则可以先表示出点P 所满足的几何上的等量关系,再用点P 的坐标(x ,y )表示该等量关系式,即可得到轨迹方程。
3、代入法(相关点轨迹法):如果动点(,)P x y 的运动是由另外某一点'00(,)P x y 的运动引发的,而点'00(,)P x y 的运动规律已知,(该点坐标满足某已知曲线方程),则用动点(,)P x y 表示出相关点'00(,)P x y 的坐标,然后把'00(,)P x y 的坐标代入已知曲线方程,即可得到动点P 的轨迹方程。
4、几何法:若所求的轨迹满足某些几何性质(如线段的垂直平分线,角平分线的性质等),可以用几何法,列出几何式,再代入点的坐标较简单。
5、参数法:如果采用直译法求轨迹方程难以奏效,则可寻求引发动点P 运动的某个几何量t ,以此量作为参变数,分别建立P 点坐标x ,y 与该参数t 的函数关系x =f (t ),y =g (t ),进而通过消参化为轨迹的普通方程F (x ,y )=0。
6、交轨法(两条动曲线交点的轨迹):在求动点轨迹时,有时会出现要求两动曲线交点的轨迹问题,这类问题通常通过解方程组得出交点(含参数)的坐标,再消去参数求得所求的轨迹方程(若能直接消去两方程的参数,也可直接消去参数得到轨迹方程),该法经常与参数法并用。
课前练习:1、已知两点M (-2,0)、N (2,0),点P 坐标平面内的动点,满足0MN MP MN MP ⋅+⋅=uuu r uuu r uuu r uuu r,则动点P的轨迹方程为( )A 、28y x = B 、28y x =- C 、24y x = D 、24y x =-2、 P 是椭圆5922y x +=1上的动点,过P 作椭圆长轴的垂线,垂足为M ,则PM 中点的轨迹中点的轨迹方程为:( )A 、159422=+y xB 、154922=+y xC 、120922=+y x D 、53622y x +3、圆心在抛物线)0(22>=y x y 上,且与抛物线的准线及x 轴都相切的圆的方程是( )A 、041222=---+y x y xB 、01222=+-++y x y xC 、01222=+--+y x y xD 、041222=+--+y x y x 4、一动圆M 与圆O :122=+y x 外切,而与圆C :08622=+-+x y x 内切,那么动圆的圆心M 的轨迹是:( )A 、抛物线B 、圆C 、椭圆D 、双曲线一支5、在平面直角坐标系中,A (3,1)、B (-1,3),若点C 满足12OC OA OB λλ=+uuu r uu r uu u r ,其中1λ、2λ是实数,且1λ+21λ=,则点C 的轨迹方程是典型例题:例1、(1)已知ABC ∆的顶点A 、B 的坐标分别为(-4,0),(4,0),C 为动点,且满足,sin 45sin sin C A B =+则点C 的轨迹方程(2)△ABC 的顶点为A(5-,0)、B(5,0),△ABC 的内切圆圆心在直线3=x 上, 则顶点C 的轨迹方程是( )A 、116922=-y x B 、191622=-y x C 、116922=-y x )3(>x D 、191622=-y x )4(>x 例2、过点P (2,4)作两条互相垂直的直线l 1、l 2,若l 1交x 轴于A 点,l 2交y 轴于B 点,求线段AB 的中点M 的轨迹方程。
解析几何轨迹与方程

?? x ? R ?cos? ? ? sin ? ?
? ?
y
?
R?sin ?
?
?
cos ?
?
(4)椭圆的参数方程
设椭圆的方程为 x2 ? y2 ? 1
a 2 b2
第一种参数方程以角度 ?
为参数:?? ?
x y
? ?
a cos? bsin ?
, ???
?
?
?
?
?
?
? ? a b 2 ? a 2 t 2
ห้องสมุดไป่ตู้
其参数方程为 ? x ? 2Rcos? (1? cos? )
? ?
y
?
2Rsin ?
(1?
cos?
)
(3)把线绕在一个固定的圆周上,将线头拉紧后向反方向旋转,以把线从 圆周上解放出来,使放出来的部分成为圆的切线,则线头的轨迹所形成 的曲线叫做圆的渐伸线或切展线(involute)
其坐标式参数方程为
一、曲面的方程
定义 2.2.1 如果一个方程 F ?x, y, z?? 0 或 z ? f ?x, y?与一个曲面
? 有着关系:
①满足方程 ? F ?x, y, z?? 0 或 z ? f ?x, y?的 ?x, y, z?是曲面 ?
上的点的坐标;
②曲面 ? 上的任何一点的坐标 ?x, y, z?满足方程 F ?x, y, z?? 0 或 z ? f ?x, y?, 那么方程 F ?x, y, z?? 0 或 z ? f ?x, y?就叫做曲面 ? 的方程,而曲 面 ? 叫做方程 F ?x, y, z?? 0 或 z ? f ?x, y?的图形.
一一对应的关系叫做 柱坐标系,或称空间半极坐标系 ,并把有序
平面解析几何中的轨迹方程求解练习题

平面解析几何中的轨迹方程求解练习题1. 直线的轨迹方程求解1.1 已知两点P1(x1, y1)和P2(x2, y2),求过这两点的直线的轨迹方程设直线的斜率为k,根据直线的斜截式方程可得: y - y1 = k(x - x1) (1)将点P2(x2, y2)代入方程(1),得:y2 - y1 = k(x2 - x1) (2)整理方程(2)可得:y = kx - kx1 + y1 (3)所以轨迹方程为y = kx - kx1 + y11.2 已知直线方程Ax + By + C = 0,求直线的轨迹方程将直线方程改写为斜截式方程可得:y = -A/B * x - C/B (4)所以轨迹方程为y = -A/B * x - C/B2. 圆的轨迹方程求解2.1 已知圆的圆心坐标为O(a, b),半径为r,求圆的轨迹方程设圆上任意一点P(x, y),根据点到圆心的距离公式可得:OP² = (x - a)² + (y - b)² (5)OP² = r² (6)将方程(6)代入方程(5)可得:(x - a)² + (y - b)² = r² (7)所以轨迹方程为(x - a)² + (y - b)² = r²2.2 已知圆的直径的两个端点分别为P1(x1, y1)和P2(x2, y2),求圆的轨迹方程设圆的圆心为O(x, y),半径为r,根据圆心到直径的中点的距离等于半径可得:((x + x1)/2 - x)² + ((y + y1)/2 - y)² = r² (8)((x + x2)/2 - x)² + ((y + y2)/2 - y)² = r² (9)将方程(8)和方程(9)进行化简,可得:(x - (x1 + x2)/2)² + (y - (y1 + y2)/2)² = ((x2 - x1)² + (y2 - y1)²)/4 (10)所以轨迹方程为(x - (x1 + x2)/2)² + (y - (y1 + y2)/2)² = ((x2 - x1)² + (y2 - y1)²)/43. 抛物线的轨迹方程求解3.1 已知抛物线的焦点为F(p, q),准线为直线y = -p,且焦距为4a,求抛物线的轨迹方程设抛物线上任意一点P(x, y),根据焦点到准线的距离等于焦距可得:PF² = (x - p)² + (y - q)² (11)y + p = 2a (12)PF = 4a (13)将方程(12)代入方程(11)和方程(13),可得:(x - p)² + (y - q)² = (y + p - 2a)² (14)所以轨迹方程为(x - p)² + (y - q)² = (y + p - 2a)²3.2 已知抛物线的顶点为V(h, k),对称轴为直线x = h,求抛物线的轨迹方程设抛物线上任意一点P(x, y),根据顶点到抛物线上任意一点的距离公式可得:PV² = (x - h)² + (y - k)² (15)PX = PH (16)将方程(16)代入方程(15),可得:(x - h)² + (y - k)² = (x - h) (17)所以轨迹方程为(x - h)² + (y - k)² = x - h综上所述,平面解析几何中直线、圆和抛物线的轨迹方程求解方法分别为以上所示。
专题:解析几何中的动点轨迹问题

专题:解析几何中的动点轨迹问题学大苏分教研中心 周坤轨迹方程的探求是解析几何中的基本问题之一,也是近几年各省高考中的常见题型之一。
解答这类问题,需要善于揭示问题的内部规律及知识之间的相互联系。
本专题分成四个部分,首先从题目类型出发,总结常见的几类动点轨迹问题,并给出典型例题;其次从方法入手,总结若干技法(包含高考和竞赛要求,够你用的了...);然后,精选若干练习题,并给出详细解析与答案,务必完全弄懂;最后,回顾高考,列出近几年高考中的动点轨迹原题。
OK ,不废话了,开始进入正题吧...Part 1 几类动点轨迹问题一、动线段定比分点的轨迹例1 已知线段AB 的长为5,并且它的两个端点A 、B 分别在x 轴和y 轴上滑动,点P 在段AB 上,(0)AP PB λλ=>,求点P 的轨迹。
()()()00P x y A a B b 解:设,,,,,,()()011101a a xx y b b y λλλλλλλ+⋅⎧⎧=+=⎪⎪⎪+⎨⎨++⋅=⎪⎪=⎩⎪+⎩, 2225a b +=代入()()222221125y x λλλ+++=()()222221252511x y λλλ+=++222514P x y λ=+=当时,点的轨迹是圆;① 1P y λ>当时,点的轨迹是焦点在轴上的椭圆;②01P x λ<<当时,点的轨迹是焦点在轴上的椭圆③;例2 已知定点A(3,1),动点B 在圆O 224x y +=上,点P 在线段AB 上,且BP:PA=1:2,求点P 的轨迹的方程.()()113P x y B x y AB BP =-解:设,,,,有()()()()1133131313x x y y ⎧+-=⎪+-⎪⎨+-⎪=⎪+-⎩11332312x x y y -⎧=⎪⎪⎨-⎪=⎪⎩化简即:22114x y +=代入223331422x y --⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭得 所以点P 的轨迹为()22116139x y ⎛⎫-+-= ⎪⎝⎭二、两条动直线的交点问题例3 已知两点P (-1,3),Q (1,3)以及一条直线:l y x =,设长为2的线段AB 在l 上移动(点A 在B 的左下方),求直线PA 、QB 交点M 的轨迹的方程 ()()()11M x y A t t B t t ++解:设,,,,,, ()()1313PM x y PA t t =+-=+-,,,, ()()131113QM x y QB t t =--=+-+-,,,, ////PM PAQM QB ∴,,()()()()()()()1313123x t t y x t t y ⎧+-=+-⎪∴⎨--=-⎪⎩34222x y t x y x t x y +⎧=⎪-+⎪⎨-⎪=⎪-+⎩32242x y x x y x y +-=-+-+()()()()32422x y x y x y x +-+=-+-228y x -=例4 已知12A A 、是双曲线22221(0,0)x y a b a b-=>>的两个顶点,线段MN 为垂直于实轴的弦,求直线1MA 与2NA 的交点P 的轨迹()()()()()11111200P x y M x y N x y A a A a --解:设,,,,,,,,,,1122A P A MA P A N k k k k =⎧⎪⎨=⎪⎩ 1111y yx a x ay y x a x a⎧=⎪++⎪⎨-⎪=⎪-+⎩ 1111y y y yx a x a x a x a-⋅=⋅+-+- 22122221y y x a x a =--- 2211221x y a b -= 22221112221y x x a b a a-∴=-= 2212221y b x a a=- 22222y b x a a ∴=-- 222222a y b x a b =-+()2222010x y a b x x a b >>+=≠当时,是焦点在轴上的椭圆,;2220a b x y a =>+=当时,是圆;()2222010x y b a y x a b>>+=≠当时,是焦点在轴上的椭圆,;三、动圆圆心轨迹问题例5 已知动圆M 与定圆2216x y +=相切,并且与x 轴也相切,求动圆圆心M 的轨迹()()0M x y y ≠解:设,,224M x y y +=-当圆与定圆内切时,,224M x y y +=+当圆与定圆内切时, 224x y y ∴+=±222168x y y y +=±+2816y x ±=-M 的轨迹是两条抛物线(挖去它们的交点) ()()2211202088y x y y x y =-≠=-+≠或例6 已知圆221:(3)4C x y ++=,222:(3)100C x y -+=,圆M 与圆1C 和圆2C 都相切,求动圆圆心M 的轨迹()()11113,0,3,0,6,C C C C -=解:,M r 设动圆的半径为12(1),,M C C 若圆与外切与内切则122,10MC r MC r ⎧=+⎪⎨=-⎪⎩121112,MC MC C C +=>12M C C 的轨迹是以、为焦点的椭圆,2126263a a c c ====,,,,22227b a c =-=,2213627x y +=椭圆的方程为12,M C C (2)若圆与、都内切则12210MC r MC r⎧=-⎪⎨=-⎪⎩ 12118MC MC C C +=>12M C C 的轨迹是以、为焦点的椭圆2222842637a a c c b a c =====-=,,,,, 221167x y +=椭圆的方程为四、动圆锥曲线中相关点的轨迹例7 已知双曲线过(3,0)A -和(3,0)B ,它的一个焦点是1(0,4)F -,求它的另一个焦点2F 的轨迹()2F x y 解:设,,2121AF AF BF BF -=-由双曲线定义, ()()()()2222113004530045AF BF =--+-==-+-=,,2255AF BF -=-若,222255AF BF AF BF ∴-=-=,,204F x y =≠±的轨迹是直线()2255AF BF -=-+若,22106AF BF AB +=>=,2F A B 的轨迹是以、为焦点的椭圆,210,5,26,3,4,a a c c b ===== 22142516x y y +=≠±椭圆方程为()22204142516x y F x y y =≠±+=≠±的轨迹是直线()或椭圆()例8 已知圆的方程为224x y +=,动抛物线过点(1,0)A -和(1,0)B ,且以圆的切线为准线,求抛物线的焦点F 的轨迹方程()F x y l M 解:设焦点,,准线与圆相切于,1111AA l A BB l B ⊥⊥作于,于,1124AF BF AA BB OM +=+==,F A B 的轨迹是以、为焦点的椭圆,2422213a c AB a c b ======,,,,,()221043x y F y +=≠轨迹的方程是Part 2 求动点轨迹的十类方法一、直接法根据已知条件及一些基本公式如两点间距离公式、点到直线的距离公式、直线的斜率公式、切线长公式等,直接列出动点满足的等量关系式,从而求得轨迹方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、直接法
解析几何专题一
轨迹问题
建系一一设点一一列式一一代换一一化简一一检验 例1长为2a 的线段AB 的两个端点分别在x 轴、 列式 y 轴上移动,求AB 中点P 的轨迹方程。
例2已知两个定点 A(-1,0)、B(2,0),求使 MBA 2 MAB 的点的轨迹方程。
例3 一动圆被直线x+2y=0和x-2y=0截得的弦长分别为8和4,求动圆圆心的轨迹方程。
二、定义法 例4动点P 到直线x+4=0的距离减去它到点M(2,0)的距离之差等于2,则P 的轨迹是() (A)直线 (B)椭圆(C)双曲线(
D)抛物线 例5求经过原点,并以F(2,0)为它的一个焦点,长轴长为6的椭圆中心的轨迹方程。
例6已知两个圆O i 和02,它们的半径分别是1和2,且|OQ 2 | 4,动圆M 与圆O i 内切,又与圆 02外切,建立适当的坐标系,求动圆圆心 M 的轨迹方程,并说明轨迹是什么曲线。
、代入法
2 2
例7 P 在以F 1、F 2的双曲线—L 1上运动,则叶汗2P 的重心G 的轨迹方程为
16 9 U
y 2 36内一点,A 、B 是圆上两个动点且满足 APB 90,求矩形APBQ
2
仝1,过点M (0,1)的直线l 交椭圆于A 、B 两点,O 是坐标原点,点P
4 满足oP i (oA OB ),点N 的坐标为(1,1),当I 绕点M 旋转时,求: (1)动点P 的轨迹方程;(2)
|NP 丨的最值。
例8已知P (4,0)是圆X 2
的顶点Q 的轨迹方程。
四、参数法
例9已知点M 在圆13x 2 13y 2 15x 36y 0上,点N 在射线OM 上,且满足| OM | |ON | 12 ,
求动点N 的轨迹方程。
例10设椭圆方程为X 2
2. ABC 中,A 为动点,B 、C 为定点,B( a ,0),C(a ,0)且满足条件
2 2
轨迹方程是
16x 2 16y 2
16y 2
16x 2
A. 2
c 2
1(y 0)
B.」 c 2
1(x 0)
a 3a
a 3a
C 16x 2 C. a 2
16y 2
3a 2
1的左支(y 0)
D 16
y 2
a 2
16y 2 3a 2
1的右支(y 0)
3.设圆(x
1)2
y 2
25的圆心为C,A(1,0)是圆内 定点, Q 为圆周上一动点,线段 AQ 的垂直平分线 与CQ 交于M ,则M 的轨迹方程为
A.4x 2
4y
2
1 B.4X 2
4y 2
1 4x 2
C.4x
4y 2
1 D.4x 2
4y 2
1 21 25 21 25 25 21 25 21 4. F 1> F 2是椭圆的两个焦点,M 是椭圆上任一点, 从任一焦点向 F 1MF 2顶点M 的外角平分线引垂线,
作业:
一、选择题
1.已知两点A 迹方程为
A.(x 2)2
C.(x 2)2
(2,0), B (1,0),动点P 不在x 轴上,且
y
2
4(y 0)
y 2
4(y 0)
B.(x D.(x APO
1)2 1)2
2
y
2
y
BPO ,其中0为原点,则点P 的轨 1( y 0) i(y 0) sinC si nB
1
-si nA,贝U 动点A
的
垂足为P ,则P 点的轨迹为
A 圆
B.椭圆
C 双曲线 D.抛物线
5.设动点P 是抛物线y
是
2x 2
1上任意一点,定点A(0,1),点M 分PA 所成的比为2,则点M 的轨迹方程
A.y 6x
2
6.已知圆x
2
迹方程是
1 3
2
y
A.x 2
y 2
1 3
ABC 内接与圆,且 B.y 3x
2
1 点 A(1,0), C.y
3x 2
D.y 6x 2
BAC 60 , 当BC 在圆上运动时, 3
BC 中点的轨 2
1 y 4
4x 的顶点O 作两条互相垂直的直线
B.X 2
C.x 2
7. 过抛物线y 2
轨迹方程是
A.y 2
2x
8. 设动点P 在直线x 动点Q 的
轨迹是
A 圆 B.两条直线
1/ 1、 —(X -) 4 4
分别交抛物与A 、B 两点,则线段AB 的中点P 的
y 2
2(x 1)
D.x 2
y 2
8 B.y 2 2x 8
C.y 2 2x 8
D.y 2
2 8
1上, O 为坐标原点,以OP 为直角边、点O 为直角顶点作等腰直角 OPQ ,则
C.抛物线 D 双曲线
9.已知动点P(x, y)满足5j (x A.两条相交直线 10若ac 1,则抛物线y A.y 0( x 0)
二、填空题
11 .两条直线ax
2 2
1) (y 2) B.抛物线 2
ax
B.x 0(y
2x c 的焦点
0) 12点P 在以F i 、 y 1
0 和 x ay 1
2
F 2为焦点的双曲线
x
16
0(a
2
y
9
|3x 4y 12 |,则P 点的轨迹是
D.椭圆
c 双曲线
F 的轨迹方程
C.x 4y 0( x 0) 1)的交点的轨迹方程是
D.4x y 0(x
0)
1上运动,则 F 1F 2P 的重心G 的轨迹方程是 13 .过抛物线y 2
程是
4x 的顶点O 作相互垂直的弦
OA 、OB ,则抛物线顶点 0在AB 上的射影M 的轨迹方
为圆心的圆与椭圆 x 2 2y 2
14. 设以 P (2,2) 三、解答题
15. 设 2 m 0,在直角坐标系中,通过点
佼于A 、B 两点,贝y AB 的中点M 的轨迹方程是
M ( m,0)的直线I 与双曲线x 2 y 2 4有唯一的交点P ,
(1)设X 为点P 的横坐标,证明|F1 P| a - x
a
(2)求点T 的轨迹方程
10:两条直线则抛物线1 y0和ax<2 ayx 1C 的焦点 F1的轨迹方勺轨迹方程是
A.y 0( x 0)
二、•点填在以F 1、
B.x 0©2 0) 2 F 2为焦点的双曲线 x y
16 9
4x 的顶点和O 作相互垂直的弦 2 y 2 C.x 4y 0( x 0) D.4x y 0(x 0) 1上运动,则 F 1F 2P 的重心G 的轨迹方程是 0A 的交点的轨迹方程顶点 0在AB 上的射影M 的轨迹方
2 F 2为焦点的双曲线 — 为圆心的圆与椭圆 16 2勺 4x 的顶点0作相互垂直的弦 12 •程是在以F 1、
14. 设以 P (2,2) 三.过抛物线y 程是
15设 2一 系中,通
14
.而与双(线的渐近线交勺圆与椭圆B 两点
三、解求直线I 的方程
15. 设2 m 0,在直角坐标系中,通 而与双曲线
的渐近线交 于A 、B 两点 (1)
求直线I 的方程
当m 变化时,求
当m 变化时,求
X 2
16 •已知-V a
过点 2y 2 过点 1上运动,则 F I F 2P 的重心G 的轨迹方程是
1交于A 、B 两点,贝y AB 的中点M 的轨迹方程 OA 、OB ,则抛物线顶点 0在AB 上的射影M 的轨迹方 M ( m,0)的直线I 与双曲线x 2 y 2
4有唯一的交点P , 佼于A 、B
两点,贝y AB 的中点M 的轨迹方程是
M ( m,0)的直线I 与双曲线x 2 y 2 4有唯一的交点P ,
ABC 的重心的轨迹方程
ABC 的重心的轨迹方程
2
詩1(a b IF 1QI 2a ,点P 是线段F 1Q 与该椭圆的交点,点
0)的左、右焦点分别是 b 0)的左、右焦点分别是
Fi( c,0)、F 2(C ,0).Q 是椭圆外的动点,满足 T 在线段F 2Q 上,并且满足 PT TF 2 0, ITF 2I 0 F i( c,0)、F2(C ,0).Q 是椭圆外的动点,满足 T 在线段F 2Q 上,并且满足 PT TF 2
0, ITF 2I 0
2
2
F I Q 与该椭圆的交点,点
(3)试问:在点T的轨迹C上,是否存在点M,使F1MF2的面积S b2,若存在,求F1MF2的正切值;若不存在,请说明理由。
